The use of data-derived label hierarchies in multi-label classification

Abstract

Instead of traditional (multi-class) learning approaches that assume label independency, multi-label learning approaches must deal with the existing label dependencies and relations. Many approaches try to model these dependencies in the process of learning and integrate them in the final predictive model, without making a clear difference between the learning process and the process of modeling the label dependencies. Also, the label relations incorporated in the learned model are not directly visible and can not be (re)used in conjunction with other learning approaches. In this paper, we investigate the use of label hierarchies in multi-label classification, constructed in a data-driven manner. We first consider flat label sets and construct label hierarchies from the label sets that appear in the annotations of the training data by using a hierarchical clustering approach. The obtained hierarchies are then used in conjunction with hierarchical multi-label classification (HMC) approaches (two local model approaches for HMC, based on SVMs and PCTs, and two global model approaches, based on PCTs for HMC and ensembles thereof). The experimental results reveal that the use of the data-derived label hierarchy can significantly improve the performance of single predictive models in multi-label classification as compared to the use of a flat label set, while this is not preserved for the ensemble models.

1 Introduction

Multi-label learning is concerned with learning from examples, where each example is associated with multiple labels. For instance, a document can belong to multiple categories in text categorization, a gene may be associated with multiple functions in bioinformatics, an image may belong to multiple semantic categories in image classification etc. Instead of traditional learning approaches that assume label independency and learn independent mapping functions between the input space and the corresponding labels from the output space, multi-label learning approaches should deal with the existing label dependencies and relations.

In recent years, many different approaches have been developed for solving multi-label problems (Zhang and Zhou 2014; Gibaja and Ventura 2015). Tsoumakas and Katakis (2007) summarize them into two main categories: a) algorithm adaptation methods, and b) problem transformation methods. Algorithm adaptation methods extend specific learning algorithms to handle multi-label data directly. Problem transformation methods, on the other hand, transform the multi-label classification problem into one or more single-label classification problems (where each example is associated with a single label). Madjarov et al. (2012) extend the categorization of multi-label methods with a third group of methods, namely, ensemble methods. This group of methods consists of methods that use ensembles to make multi-label predictions and their base classifiers belong to either problem transformation or algorithm adaptation methods. Methods that belong to this group are RAkEL (Tsoumakas and Vlahavas 2007), ensembles of classifier chains (ECC) (Read et al. 2009), ensembles of Predictive Clustering Trees (Kocev et al. 2007; Kocev 2011), ensembles of multi-label C4.5 trees (Clare and King 2001), Variable Pairwise Constraint projection for Multi-label ensembles (Li et al. 2013), ensembles of Fading Random Trees (Kong and Yu 2011), etc.

In addition, Madjarov et al. (2012) presented an extensive experimental evaluation of the most popular methods for multi-label learning using a wide range of evaluation measures on a variety of datasets. The results reveal that the best performing methods over all evaluation measures are the ensemble method Random Forests of Predictive Clustering Trees for Multi-target Classification (RF-PCTs for MTC) (Kocev 2011) and the single predictive model Hierarchy Of Multi-label classifiERs (HOMER) (Tsoumakas et al. 2008), followed by Binary Relevance (BR) (Tsoumakas and Katakis 2007), also a single predictive model.

BR decomposes the flat multi-label output space into n single-label output spaces (where n is the total number of labels in the original multi-label learning problem). It builds one classifier for each transformed output space, using all the examples labeled with the label from that space as positive examples and all remaining examples as negative examples. On the other hand, HOMER structures the flat multi-label output space into a tree-shaped hierarchy first, and after that utilizes BR approach for solving the classification problems defined in each node of the hierarchy. We believe that the better predictive performance of HOMER as compared to BR comes as a result of the transformed output space that HOMER is using while learning and during prediction.

As a consequence of this believe, Madjarov et al. (2015) investigated and evaluated the utility of four different data-derived label hierarchies in the context of predictive clustering trees for HMC in a global setting (Silla Carlos and Freitas 2011). The experimental results show that the use of data-derived hierarchies results in improved predictive performance and that more balanced hierarchies offer better representation of the label relationships. Multi-branch hierarchy (defined by balanced k-means clustering) outperforms binary hierarchies (defined by agglomerative clustering with single and complete linkage and PCTs) on datasets with higher number of labels used in the experiments.

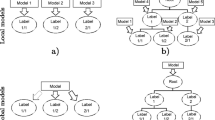
This paper extends the aforementioned study on evaluation of different data-derived label hierarchies in multi-label classification (Madjarov et al. 2015). We explore the use of data-derived label hierarchies, constructed by using clustering approaches from the label sets that appear in the annotations of the training examples. Firstly, we investigate the utility of the data-derived hierarchies in the context of single predictive models. Four different types of single predictive models (Fig. 1) were constructed that correspond to: binary classification, hierarchical single-label classification, multi-label classification and hierarchical multi-label classification. The first two approaches construct (an architecture of) local predictive models, while the last two approaches construct global models. Secondly, we evaluate and analyze the influence that the use of data-derived label hierarchies has on ensemble approaches for HMC (in particular Random Forest ensemble method for MLC and HMC in a local and a global setting). Finally, we investigate whether the conclusions from the investigation on single models carry over to the ensemble models and whether it is more beneficial to extract and use data-derived label hierarchies or just use the original, flat organization of the labels in multi-label classification problems.

Fig. 1

Schematic representation of the four different modeling tasks we consider to investigate how exploitation of label hierarchy affects the performance. Single label classification a, builds a separate model for each label, while hierarchical single label classification b, builds a separate model for each edge of the artificially generated label hierarchy (each model is trained by using only data that is relevant to that edge). Both models build local classifier. Multi-label classification c and hierarchical multi-label classification d build one global model which considers all the classes at once: the former approach (c) directly solves the flat multi-label classification task, while the latter approach (d) exploits information about the artificially generated label hierarchy

In order to answer to all of these questions we have compared:

• 1. The best performing problem transformation methods for MLC: the BR method (Tsoumakas and Katakis 2007) and the HOMER method (Tsoumakas et al. 2008) utilizing SVMs as a base classifiers,

• 2. Three different approaches based on PCTs (Blockeel et al. 1998), one for solving classical MLC problems (Kocev 2011) and two for solving HMC problems by using a local and a global setting (Vens et al. 2008)), and

• 3. Ensembles of PCTs (Kocev 2011) for MLC (one of the best performing methods for MLC (Madjarov et al. 2012)) and ensembles of PCTs for HMC (in a local and a global setting).

The experimental evaluation is made on 11 benchmark multi-label datasets using 16 evaluation measures. The datasets come from five application domains: two from image classification, one from gene function prediction, six from text classification, one from music classification and one from video classification. The predictive performance of the methods is assessed using six example-based measures, six label-based measures and four ranking-based measures.

The remainder of this paper is organized as follows. Section 2 defines the tasks of multi-label classification, multi-label ranking and hierarchical multi-label classification. An overview of the base level algorithms for MLC and the approaches for HMC that are experimentally compared in this work are given in Section 3 and Section 4. The general use of data derived label hierarchies in multi-label classification is proposed in Section 5. Section 6 describes the multi-label datasets, the evaluation measures and the experimental setup, while Section 7 presents and discusses the experimental results. Finally, the conclusions and directions for further work are presented in Section 8.

2 The tasks of multi-label and hierarchical multi-label classification

In this section, we first define the task of multi-label learning and then the task of hierarchical multi-label learning.

2.1 The task of multi-label classification (MLC)

Multi-label learning is concerned with learning from examples, where each example is associated with multiple labels. These multiple labels belong to a predefined set of labels. We can distinguish two types of tasks: multi-label classification and multi-label ranking.

In the case of multi-label classification, the goal is to construct a predictive model that will provide a list of relevant labels for a given, previously unseen example. On the other hand, the task of multi-label ranking is understood as learning a model that associates with a query example both a ranking of the complete label set and a bipartite partition of this set into relevant and irrelevant labels (Brinker et al. 2006).

The task of multi-label learning is defined as follows (Kocev et al. 2013):

Given::

• An input space $\mathcal {X}$ that consists of vectors of values of primitive data types (nominal or numeric), i.e., $\forall \mathbf {x_{i}} \in \mathcal {X}, \mathbf {x_{i}} = (\mathbf {x}_{\mathbf {i}_{1}},\mathbf {x}_{\mathbf {i}_{2}}, ...,\mathbf {x}_{\mathbf {i}_{D}}), 1 \leq \mathbf {i} \leq N$, where N is the number of vectors in the input space and D is the size of the vector (or number of descriptive attributes),

• an output space $\mathcal {Y}$ that is defined as $\mathcal {Y} = 2^{\mathcal {L}}$, i.e. the set of subsets of finite set of different labels $\mathcal {L} = \{\lambda _{1},\lambda _{2},. . .,\lambda _{Q}\}$ (Q>1 and $\mathcal {Y}_{\mathbf {i}} \subseteq \mathcal {L}$)

• a set of examples E, where each example is a pair of a vector and a label set from the input and output space respectively, i.e., $E = \{(\mathbf {x_{i}}, \mathcal {Y}_{\mathbf {i}}) | \mathbf {x_{i}} \in \mathcal {X}, \mathcal {Y}_{\mathbf {i}} \subseteq \mathcal {L}, 1 \leq \mathbf {i} \leq N \}$ where N is the number of examples of E ($N = |E| = |\mathcal {X}|$), and

• a quality criterion q, which rewards models with high predictive performance and low computational complexity.

If the task at hand is multi-label classification, then the goal is to

Find: :

a function h: $\mathcal {X} \rightarrow 2^{\mathcal {L}}$ from the input space to the label power-set (which assigns a set of labels to each example) such that h maximizes q.

On the other hand, if the task is multi-label ranking, then the goal is to

Find: :

a function f: $\mathcal {X} \times \mathcal {L} \rightarrow \mathcal {R}$, such that f maximizes q, where $\mathcal {R}$ gives the ranking for a given label and for a given example. $\mathcal {R}$ is a set of values on which a total strict order exists, typically a set of real non-negative values which can be totally ordered.

An extensive bibliography of learning methods for solving multi-label learning problems can be found in Madjarov et al. (2012), Zhang and Zhou (2014), and Gibaja and Ventura (2015).

2.2 The task of hierarchical multi-label classification (HMC)

Hierarchical classification differs from the multi-label classification in the following: the labels are organized in a hierarchy. An example that is labeled with a given label is automatically labeled with all its ancestor-labels (this is known as the hierarchy constraint (Vens et al. 2008)). Furthermore, an example can be labeled simultaneously with multiple labels that can follow multiple paths from the root label. This task is called hierarchical multi-label classification (HMC).

Here, the output space $\mathcal {Y}$ is defined with a label hierarchy $(\mathcal {L}, \leq _{h})$, where $\mathcal {L}$ is a set of labels and ≤ _h is a partial order representing the ancestor-descendant relationship ($\forall \ \lambda _{1}, \lambda _{2} \in \mathcal {L}: \lambda _{1} \leq _{h} \lambda _{2}$ if and only if λ ₁ is an ancestor of λ ₂) structured as a tree (Kocev et al. 2013). Each example from the set of examples E is a pair of a vector and a set from the input and output space respectively, where the set satisfies the hierarchy constraint, i.e., $E = \{(\mathbf {x_{i}}, \mathcal {Y}_{i})| \mathbf {x_{i}} \in \mathcal {X}, \mathcal {Y}_{i} \subseteq \mathcal {L}, \lambda \in \mathcal {Y}_{i} \Rightarrow \forall \lambda ^{\prime } \leq _{h} \lambda :\lambda ^{\prime } \in \mathcal {Y}_{i}, 1 \leq i \leq N \}$ where N is the number of examples of E (N=|E|). The quality criterion q, rewards models with high predictive performance and low complexity as in the task of multi-label classification.

An extensive bibliography of learning methods for hierarchical classification scattered across different application domains is given by Silla Carlos and Freitas (2011).

3 Algorithms for multi-label classification

In this section we give a detailed description of the algorithms for MLC that are used in the experimental comparison in this work.

3.1 Binary relevance

The simplest strategy in the multi-label setting is the one-against-all strategy, also referred to as the Binary Relevance (BR) method (Tsoumakas and Katakis 2007). It addresses the multi-label learning problem by learning one classifier for each label, using all the examples labelled with that label as positive examples and all remaining examples as negative. When making a prediction, each binary classifier predicts whether its label is relevant for the given example or not, resulting in a set of relevant labels. In the ranking scenario, the labels are ordered according to the probability associated to each label by the respective binary classifier.

The most important and widely relevant advantage of BR is its low computational complexity relative to other methods. It is theoretically simple and intuitive. Its assumption of label independence makes it suited to contexts where new examples may not necessarily be relevant to any known labels or where label relationships may change over the test data. Given a constant number of examples, BR scales linearly with the size of the known label set.

3.2 Predictive clustering trees

Predictive Clustering Trees (PCTs) (Blockeel et al. 1998)¹ are a generalization of the decision tree approach (Breiman et al. 1984). They can be used for a variety of learning tasks including different types of prediction and clustering. This includes both multi-target/multi-label classification and hierarchical multi-label classification.

The PCT framework views a decision tree as a hierarchy of clusters. The top-node of a PCT corresponds to one cluster containing all data, which is recursively partitioned into smaller clusters while moving down the tree. The leaves represent the clusters at the lowest level of the hierarchy and each leaf is labeled with its cluster’s prototype (prediction).

PCTs are built using greedy recursive top-down induction (TDI) algorithm, similar to that of C4.5 (Quinlan 1993) or CART (Breiman et al. 1984). The learning algorithm starts by selecting an attribute (feature) test for the root node. Based on this test, the training set is partitioned into subsets according to the test outcome. This is recursively repeated to construct the subtrees. The partitioning process stops when a stopping criterion is satisfied (e.g., the number of instances in the induced subsets is smaller than some predefined value; the length of the path from the root to the current subset exceeds some predefined value, etc.). In that case, the prediction is calculated and stored in a leaf.

One of the most important steps in the TDI algorithm is the test selection procedure. For each node, an attribute (test) is selected from the input space by using a heuristic function computed on the training examples. The goal of the heuristic is to guide the algorithm towards small trees with good predictive performance. The heuristic used in this algorithm for selecting the attribute tests in the internal nodes is the reduction in variance caused by partitioning the instances, where the variance V a r(E) is defined by (1) for multi-target classification and (3) for hierarchical multi-label classification. Maximizing the variance reduction maximizes cluster homogeneity and improves predictive performance.

3.2.1 PCTs for multi-target classification

Multi-target prediction (Kocev 2011) is concerned with learning from examples, where each example is associated with multiple targets. If the targets are continuous variables then the task is referred to as multi-target regression. If the targets are discrete variables, then we have a task of multi-target classification. In the multi-label scenario, each discrete target variable is a binary variable (it holds 1 if the corresponding label is relevant to the instance and 0 otherwise).

For the task of predicting of discrete targets, the variance function V a r(E) is computed as the sum of the Gini indices (Breiman et al. 1984) of the variables from the target vector, i.e.,

$$ Var(E)=\sum\limits_{i=1}^{T} \mathit{Gini(E,{\Lambda}_{i})} $$

(1)

where T is the number of target attributes and Λ _i is the i-th target attribute. $\mathit {Gini(E,{\Lambda }_{i})}= 1 - {\sum }_{j=1}^{M} {p_{j}^{2}}$ where p _j is the fraction of records in E of the j-th class in the Λ _i target attribute and M is the number of classes in the same target attribute. The prototype function returns a vector of probability distributions over the values for each discrete target. In the case of multi-label learning, it returns a vector of probabilities that an example is labeled with each of the labels from the original label set $\mathcal {L}$. An example arriving in the leaf is labeled with label λ _i if its corresponding probability from the vector of probabilities is above some threshold τ (e.g. chosen by a domain expert).

3.2.2 Random forests of PCTs for MTC

In this subsection, we explain how PCTs for MTC are used in the context of an ensemble classifier. An ensemble is a set of (base) classifiers. A new example is classified by the ensemble by combining the predictions of the member classifiers. The predictions can be combined by taking the average (for regression tasks), the majority vote (for classification tasks) (Breiman 2001), or more complex combinations.

Averaging is applied to combine the predictions of the different trees. The leaf’s prototype is the proportion of examples of different classes that belong to it. As for the single PCT, a threshold should be specified to make a prediction.

We consider the random forest ensemble learning technique that constructs different classifiers by making different bootstrap samples (Breiman 1996) of the training set on one hand, and by randomly changing the feature set during learning on the other hand. More precisely, at each node in the decision tree, a random subset of the input attributes is taken, and the best feature is selected from this subset (instead of the set of all attributes). The number of attributes that are retained is given by a function f of the total number of input attributes x (e.g., $f(x)=x, f(x)=\sqrt {x}, f(x)=\left \lfloor \log _{2}x \right \rfloor +1$, ...).

4 The use of hierarchies in hierarchical multi-label classification

An extensive bibliography of learning methods for hierarchical classification scattered across different application domains is given by Silla Carlos and Freitas (2011). Based on the existing literature, they propose a unifying framework for hierarchical classification, including a taxonomy of hierarchical classification problems and methods, and clarify the similarities and differences between a number of types of problems and methods. They also present a conceptual comparison of these types of problems and methods at a high level of abstraction, discussing their advantages and disadvantages.

One of the dimensions along which the hierarchical classification methods differ is the way of using (exploring) the hierarchical label structure in the learning and prediction phases. Silla Carlos and Freitas (2011) reviewed three different approaches: the top-down (or local) approach that uses local information to create a set of local classifiers; the global (or big-bang) approach, where a single classifier coping with the entire class hierarchy is learned; or the flat approach, that ignores the class relationships, typically building models that predict only the leaf nodes.

4.1 Local approaches for solving HMC problems

In the task of hierarchical multi-label classification, there are three different types of local approaches that can be used (Silla Carlos and Freitas 2011): Local classifiers per level, local classifiers per node, and local classifiers per parent node. The local classifiers per level approach constructs one classifier for each level of the hierarchy. The local classifiers per node approach constructs a classifier for each node from the hierarchy, except the root. There are several policies for selecting the positive and negative examples that can be used to train the local classifiers. The local classifiers per parent node approach constructs a classifier for each non-leaf node from the hierarchy. A multi-label classifier for each parent node is learned, e.g. by transforming the MLC problem by using the binary relevance scheme and learning binary classifiers for each child node in the hierarchy.

4.1.1 Architectures of PCTs and random forests of PCTs for hierarchical classification

Vens et al. (2008) investigated the performance of the local classifiers per node and per parent node approaches over a large collection of (native) hierarchical multi-label datasets from functional genomics. The conclusion of the study was that the last approach (called hierarchical single-label classification - HSC) performs better in terms of predictive performance, smaller total model size and faster induction times.

We will keep the notation HSC here, but would like to emphasize that this approach performs hierarchical multi-label classification and not hierarchical single-label classification as the term suggests.

The approach of Predictive Clustering Trees for Hierarchical Single-label Classification (PCTs for HSC) by Vens et al. (2008), constructs a decision tree classifier for each edge (connecting a label λ with its direct parent label parent(λ))² in the hierarchy, thus creating an architecture of classifiers. The corresponding tree predicts membership to label λ, using the instances that belong to parent(λ). The construction of this type of tree uses few instances: only instances labeled with parent(λ) are used for training. The instances labeled with label λ are positive instances, while the ones that are labeled with parent(λ), but not with λ are negative. The resulting tree predicts the conditional probability P(λ|parent(λ)), where for the top-level labels, all training examples are used.

To make predictions for a new instance, PCTs for HSC use the product rule P(λ) = P(λ|parent(λ))⋅P(parent(λ)) (for non top-level labels). This rule applies the trees recursively for each node (label) of the hierarchy, starting from the tree for a top-level label.

Kocev (2011) extends the approach of Vens et al. (2008) of using PCTs for HSC by applying ensembles as local classifiers at each branch, instead of single decision trees (PCTs). The method of Random Forests of PCTs for HSC (RF-PCTs for HSC) constructs a random forest ensembles of PCTs for each edge (connecting a label λ with its direct parent label parent(λ)) in the hierarchy, thus creating an architecture of ensembles. All other settings for this method are the same as for the PCTs for HSC. We will refer to the two approaches as HSC architectures of PCTs and ensembles of PCTs.

4.1.2 The hierarchy architecture of SVM classifiers in HOMER

The approach taken by HOMER is to use local classifiers for solving HMC tasks. After learning a hierarchy on the flat label space by applying an unsupervised (clustering) approach to the label part of the data, HOMER constructs a hierarchical architecture of SVM classifiers that follows the hierarchy on the label space. In each internal node of the hierarchy, a BR architecture of binary SVMs is created. Since the BR architecture contains one SVM for each descendant label of the internal node, this architecture is the same as the HSC architecture, the only difference being that PCTs for binary classification are used in PCTS for HSC and SVMs for binary classification are used in HOMER.

In the hierarchy (tree) on the label space used by HOMER, the leaves represent the labels of the original MLC problem, while each internal node m contains the union of the label sets of its children (i.e., the meta-label μ _m ). In the learning phase, a training example is considered annotated with a meta-label μ _m , if it is annotated with at least one of the (original) labels from μ _m . An example hierarchy of labels and classifiers produced by HOMER for a multi-label classification task with 8 labels is given in Fig. 2.

Fig. 2

An example of label hierarchy defined over the flat label space of the emotions dataset by using balanced k-means clustering method where k is set to 2 (λ _i - original label, μ _i - artificially defined meta-label)

In the prediction phase, HOMER starts from the root and follows a recursive process forwarding the test instance x to the child node m only if μ _m is among the predictions of the multi-label classifier. The union of the predicted labels in the leaves of the tree are the relevant labels for an instance x. For example, let’s say that according to the predictions obtained by the multi-label classifiers in the nodes of the tree from Fig. 2 the labels μ ₁, μ ₂, λ ₃, μ ₅ and λ ₅ were assigned to an example x. Only the leaf labels λ ₃ and λ ₅ are declared as relevant labels for that example x.

While the prediction phase of HOMER is similar to that of PCTs for HSC, there is an important difference. HOMER only forwards a testing instance to the child nodes that correspond to the meta-labels predicted to be relevant for the instance. As a consequence, no probability (and ranking) is produced for the original labels that belong to meta-labels predicted to be irrelevant.

4.2 Global approaches for solving HMC problems

Although the problem of hierarchical multi-label classification can be tackled by the local approaches, learning a single global model for all labels (in the hierarchy) can have some advantages (Kocev 2011). The total size of the global classification model is typically smaller as compared to the total size of all the local models learned by any of the local classifier approaches. Also, in the global classifier approach, a single classification model is built from the training set, taking into account the label hierarchy and relationships. During the test phase, each test example is classified using the induced model, in a process that can assign labels to a test example at potentially every level of the hierarchy.

4.2.1 PCTs and random forests of PCTs for hierarchical multi-label classification

To apply PCTs to the task of HMC, the example labels are represented as vectors with Boolean components. The components in the vector correspond to the labels in the hierarchy traversed in a depth-first manner. The k-th component of the vector is 1 (v _k =1) if the example is labeled with label λ _k and 0 otherwise. If v _k =1, then v _j =1 for all v _j ’s on the path from the root to v _k .

The variance of a set of examples E is defined as the average squared distance between each example’s label vector v _i and the mean label vector $\bar {\mathbf {v}}$ of the set, i.e.,

$$ \bar{\mathbf{v}}=\frac{1}{|E|}\sum\limits_{\mathbf{i} = 1}^{|E|}{\mathbf{v_{i}}} $$

(2)

$$ Var(E)=\frac{1}{|E|}\underset{\mathbf{e_{i}} \in E}{\sum}{d(\mathbf{v_{i}}, \bar{\mathbf{v}})}^{2} $$

(3)

where each component of $\bar {\mathbf {v}}$ is the proportion of examples $\bar {v_{k}}$ in the leaf that are labeled with label λ _k .

The higher levels of the hierarchy are more important: an error at the upper levels costs more than an error at the lower levels. Considering this, a weighted Euclidean distance is used (4):

$$ d(\mathbf{v_{1}},\mathbf{v_{2}})=\sqrt{\sum\limits_{k}^{|\mathbf{v}|}{w(\lambda_{k})(\mathbf{v}_{\mathbf{1}_{k}}-\mathbf{v}_{\mathbf{2}_{k}})^{2}}} $$

(4)

where $\mathbf {v}_{\mathbf {i}_{k}}$ is the k’th component of the class vector v _i of the instance e _i , and w(λ _k ) are the class weights. The class weights decrease with the depth of the class in the hierarchy, w(λ _k ) = w ₀⋅w(λ _j ), where λ _j is the parent of λ _k .

Each leaf in the tree stores the mean $\bar {\mathbf {v}}$ of the vectors of the examples that are sorted into that leaf. An example arriving in the leaf can be labeled with label λ _k if $\bar {v_{k}}$ is above some threshold t _k (that can be chosen by a domain expert).

Random forests of PCTs for HMC are considered in the same manner as the random forest of PCTs for MTC. In the case of HMC the ensemble is a set of PCTs for HMC. A new example is classified by the ensemble by combining the predictions of the member classifiers by taking the majority vote (Breiman 2001). Like in PCTs for HMC, the predictions of the random forest ensemble of PCTs for HMC satisfy the hierarchy constraint (an example that is labeled with a given label is automatically labeled with all its ancestor-labels).

5 The use of data derived label hierarchies in multi-label classification

In this study we investigate the use of label hierarchies, constructed in a data-driven manner in conjunction with HMC approaches (local and global) (Silla Carlos and Freitas 2011) and ensemble methods capable for solving HMC classification problems.

In particular, we derive label hierarchies considering the label sets that appear in the annotations of the training examples from the original (flat) classification problem. In this way, we first structure the label co-occurrence relationships that exist hidden in the output space of the multi-label classification problems in a hierarchy and after that, use that (data-derived) hierarchy to map the original classification problem into a hierarchical multi-label one. This artificially generated hierarchical multi-label classification problem could be considered as a separate (newly defined) hierarchical multi-label classification task and it could be tackled by global (big-bang) (Madjarov et al. 2015) or local approaches (Silla Carlos and Freitas 2011) for HMC.

An example hierarchy of labels generated by using the balanced k-means clustering method from the emotions multi-label classification task (used in the experimental evaluation) is given in Fig. 2. The original label space of the emotions dataset has six labels {λ ₁,λ ₂,…,λ ₆} and each example from the dataset originally is labeled with one or more labels. Table 1 shows five examples from the emotions dataset with their original labels (third column - original labels) and the corresponding hierarchical labels (fourth column - hierarchical labels) obtained by using the label hierarchy from Fig. 2 ($\mathcal {HL} = \{\mu _{1}, \mu _{2}, \mu _{3}, \mu _{4}, \mu _{5}, \lambda _{1}, \lambda _{2}, \lambda _{3}, \lambda _{4}, \lambda _{5}, \lambda _{6}\}$). Each example in the transformed, HMC dataset is actually labeled with multiple paths of the hierarchy, defined from the root to the leaves (represented by the relevant labels for the corresponding example in the original MLC dataset).

Table 1 Five examples from the emotions dataset with their original labels and the corresponding hierarchical labels obtained by using the label hierarchy from Fig. 2

5.1 Generating a label hierarchy on a multi-label output space

There exist many possible ways to structure the output space of a flat MLC problem. This process is critical for the good performance of the HMC methods on the transformed problems. One can use classical hierarchical clustering algorithms, such as hierarchical agglomerative and divisive clustering, some partitioning algorithms employed at each node of the hierarchy, or graph-based clustering approaches (Madjarov et al. 2015).

When we build the hierarchy over the label space, there is only one constraint that we should take care of: the original MLC task should be defined by the leaves of the label hierarchy. In particular, the labels from the original MLC problem represent the leaves of the tree hierarchy (Fig. 2), while the labels that represent the internal nodes of the tree hierarchy are so-called meta-labels (that model the correlation among the original labels).

In this work, we employ the approach of balanced k-means proposed by Tsoumakas et al. (2008) for deriving the hierarchy on the output space of the (original) MLC problem. It showed best performance in comparison between four different approaches that was recently made by Madjarov et al. (2015). In that comparison, only global approaches for HMC were considered.

The balanced k-means clustering approach extends the well-known k-means algorithm with an explicit constraint on the size of each cluster. The algorithm consider only the label data W _n of the examples at the current node n of the hierarchy. $\mathbf {W}_{n} = [w_{{i}_{j}}]$, where the value of $w_{{i}_{j}}$ (i=1...|E _n | and $j=1 ... |\mathcal {L}_{n}|$) is 1 if the i-th example of E _n is labeled with the label $\lambda _{j} \in \mathcal {L}_{n}$ and 0 otherwise. E _n is the set of examples that belong to the node n and $\mathcal {L}_{n} \subseteq \mathcal {L}$ is the set of labels considered in the node n (for the top level node - root node $\mathcal {L}_{n} = \mathcal {L}$). For example, for the node of the hierarchy on Fig. 2, corresponding to the meta-label μ ₃ only the label data from λ ₄,λ ₅ and λ ₆ is considered.

For the node n, the algorithm accepts as input the set of labels $\mathcal {L}_{n}$, the label data W _n of the examples that belong to that node, the number of partitions (clusters) k and the number of iterations it. It outputs k disjoint subsets of $\mathcal {L}_{n}$ with approximately equal sizes. Figure 3 shows the balanced k-means algorithm in pseudo-code.

Fig. 3

Balanced k-Means

The distance between the label λ _j ($\lambda _{j} \in \mathcal {L}_{n}$, $j=1 ... |\mathcal {L}_{n}|$) and the r-th cluster center c _r (out of k) within the labels data W _n in the n-th node is calculated by (5).

$$ distance(\lambda_{j}, c_{r}, \mathbf{W}_{n}) = \sqrt{\sum\limits_{i=1}^{|E_{n}|}{(c_{{r}_{i}} - w_{{i}_{j}})}^{2}} $$

(5)

5.2 Solving MLC problems by using global approaches for HMC

Figure 4 gives the pseudo-code of the general scenario for solving a MLC problem by using data-derived label hierarchies and global approaches for HMC. The scenario first defines the hierarchy, then solves the HMC problem by using a global approach for HMC. It finally transforms the HMC predictions P _H of the global model into a flat MLC representation.

Fig. 4

The general scenario for solving flat MLC problems by using local/global approaches for HMC: Line 10 is used for the local approaches, and line 11 for the global ones

E ^train and E ^test are the training and testing examples, while W ^train is only the label part (label data) of the training set. Using the label hierarchy derived from the label data, W ^train is transformed into new hierarchically organized label data $\mathbf {W}^{train}_{H}$. ${E}^{train}_{H}$ and $E^{test}_{H}$ are the corresponding hierarchical multi-label datasets obtained by transforming the original (flat) multi-label datasets (E ^train and E ^test) into hierarchical form.

P _H are the predictions for the examples of the hierarchical multi-label dataset $E^{test}_{H}$, while P are the predictions for the original labels. P _H are represented as vectors of probabilities (one vector for one example), where each probability is associated to only one label from the hierarchy (meta-label representing an internal node or original label representing a leaf). In the context of global approaches for HMC, predictions P in the original multi-label scenario can be obtained by using different approaches for transforming the hierarchical multi-label predictions P _H . In this work, we propose the simplest approach: only the probabilities for the leaves from the hierarchical predictions P _H are evaluated, while the other probabilities (for the meta-labels) are simply ignored.

5.3 Solving MLC problems by using local approaches for HMC

After the transformation of the original MLC problem into a HMC one, the new HMC problem can be also solved by a hierarchical multi-label local learning approach. There are different ways of using local information to create local classifiers, and although most of them are referred to as top-down in the literature, they are very different during the training phase and slightly different in the test phase.

Only line 10 of the pseudo-code in Table 4 needs to be changed (with line 11) to obtain an algorithm for solving MLC problems by using data-derived label hierarchies with local approaches for HMC. The algorithm still defines the label hierarchy first and then solves the HMC problem by using a local approach for HMC. It also extracts the predictions for the leaves of the hierarchy (that are actually the predictions for the original labels) and evaluates the performance (instead of the global one).

6 Experimental design

In this section, we present the experimental design used to compare the methods for flat MLC and for MLC via HMC. In particular, we compare:

• The BR method and the HOMER method (BR as a flat MLC approach and HOMER as MLC via local HMC approach, both of them using SVM architectures as base classifiers);

• PCTs for multi-target classification (as flat MLC approach), HSC architectures of PCTs for binary classification (as a MLC via local HMC approach) and PCTs for HMC (as a MLC via global HSC approach).

We also compare ensembles of PCTs in the same settings as the single trees:

• ensembles of PCTs for multi-target classification with HSC architectures of ensembles of PCTs for binary classification and

• ensembles of PCTs for HMC (the latter two based on the artificially defined label hierarchy).

We first briefly describe the benchmark multi-label datasets. We then give a short overview of the evaluation measures typically applied to asses the predictive performance of methods for multi-label learning. Next, we present the specific setup and the instantiation of the parameters for the compared multi-label learning methods. Finally, we present the procedure for statistical evaluation of the experimental results.

6.1 Datasets

We use eleven multi-label classification benchmark problems used in previous studies and evaluations of methods for multi-label learning. We include benchmark datasets of different size and from different application domains. Table 2 presents the basic statistics of the datasets. We can note that the datasets vary in size from 391 to 60000 training examples, from 202 to 27856 testing examples, from 72 to 2150 features, from 6 to 983 labels, and from 1.07 to 19.02 labels per example on average (i.e., label cardinality (Tsoumakas and Katakis 2007)). The datasets come pre-divided into training and testing parts as used by other researchers. In our experiments, we use these partitions in their original format. The training part usually comprises around 2/3 of the complete dataset, while the testing part consists of the remaining 1/3 of the dataset.

Table 2 Description of the benchmark problems in terms of application domain (domain), number of training (# t r.e.) and test (# t.e.) examples, number of features (D), total number of labels (Q) and label cardinality (l _c )

The datasets come from three domains: biology, multimedia and text categorization. From the biological domain, we have the yeast dataset (Elisseeff and Weston 2005). It is a widely used dataset, where genes are instances in the dataset and each gene can be associated with 14 biological functions (labels).

The datasets that belong to the multimedia domain are: emotions (Trohidis et al. 2008), scene (Boutell et al. 2004), corel5k (Duygulu et al. 2002) and mediamill (Snoek et al. 2006). The domain of text categorization is represented with 6 datasets: medical (Read et al. 2009), enron (Klimt and Yang 2004), tmc2007 (Srivastava and Zane-Ulman 2005), bibtex (Katakis et al. 2008), delicious (Tsoumakas et al. 2008) and bookmarks (Katakis et al. 2008).

6.2 Evaluation measures

Performance evaluation for multi-label learning systems differs from that of classical single-label learning systems. In any multi-label experiment, it is essential to include multiple and contrasting measures because of the additional degrees of freedom that the multi-label setting introduces. In our experiments, we used various evaluation measures that have been suggested by Tsoumakas and Katakis (2007).

In particular, we used six example-based evaluation measures (Hamming loss, accuracy, precision, recall, F ₁ score and subset accuracy) and six label-based evaluation measures (micro precision, micro recall, micro F ₁, macro precision, macro recall and macro F ₁). Note that these evaluation measures require predictions stating that a given label is present or not (binary 1/0 predictions). However, most predictive models predict a numerical value for each label and the label is predicted as present if that numerical value exceeds some pre-defined threshold τ. The performance of the predictive model thus directly depends on the selection of an appropriate value of τ. To this end, we applied a threshold calibration method by choosing the threshold (6) that minimizes the difference in label cardinality between the training data and the predictions for the test data (Read et al. 2009).

$$ \tau= \underset{\tau \in 0.00, 0.05, ..., 1.00}{argmin}{|LabelCard(E^{train})-LabelCard(H_{\tau}(E^{test}))|} $$

(6)

where E ^train is the training set and a classifier H _τ has made predictions for test set E ^test under threshold τ. We do not use the output space of the test set while calculating the threshold.

Also, we used four ranking-based evaluation measures (one-error, coverage, ranking loss and average precision) that compare the predicted ranking of the labels with the ground truth ranking. A detailed description of the evaluation measures is given in the Appendix A.

6.3 Experimental setup

The comparison of the multi-label learning methods was performed using the MULAN ³ library for the machine learning framework WEKA (Hall et al. 2009) and CLUS⁴ system for predictive clustering. The MULAN library was used for BR and HOMER, and the CLUS system for the PCTs based methods. All experiments were performed on a server with an Intel Xeon processor at 2.50GHz and 64GB of RAM with the Fedora 14 operating system. In the remainder of this section, we first state the base classifiers that were used for the HOMER and the BR methods and then the parameter instantiations of all methods.

HOMER uses Support Vector Machines (SVM) as base classifiers for solving the partial binary classification problems. Binary Relevance classifier is used as a multi-label classifier in the internal nodes of the HOMER. For training the SVMs, we used the implementation from the LIBSVM library (Chang and Lin 2001). In particular, we used SVMs with a radial basis kernel.

The kernel parameter gamma and the penalty C were determined for each dataset by 10-fold cross validation using only the training sets. The values 2⁻¹⁵,2⁻¹³,...,2¹,2³ were considered for gamma and 2⁻⁵,2⁻³,...,2¹³,2¹⁵ for the penalty C. For tuning the parameters we have used the Hamming loss evaluation measure. After determining the best parameters values on each dataset, the classifiers were trained using all available training examples and were evaluated by recognizing all test examples from the corresponding dataset.

The same settings (experimental design and setup) were used for the global BR approach. For the single PCT approaches (PCTs for multi-target classification - MTC, HSC architecture of binary classifiers and PCTs for HMC) we used the default settings of CLUS. The ensemble methods PCTs for multi-target classification, PCTs for hierarchical single-label learning and PCTs for hierarchical multi-label learning learn 100 models as suggested by Bauer and Kohavi (1999). For the size of the feature subsets needed for construction of the base classifiers for the ensembles we selected f(x)=⌊0.1⋅|x|+1⌋ as recommended by Kocev (2011). The weight parameter w ₀ for all PCTs based approaches for solving HMC problems is set to 0.75.

HOMER, HSC and the HMC methods require one additional parameter to be configured: the number of clusters k for the balanced k-means clustering algorithm. For this parameter, five different values (2–6) were considered for HOMER in the cross-validation (Tsoumakas et al. 2008). After determining the best value of k on every dataset (via cross-validation on the training dataset), HOMER was trained using all available training examples and was evaluated by recognizing all test examples from the corresponding dataset. The same hierarchies (the same values for k obtained for HOMER) were used for the HSC and HMC methods. The values of the parameter k are 3 for most of the datasets, 2 for the emotions dataset, 5 for the yeast dataset, and 4 for the enron and delicious datasets.

To investigate the utility of the data-derived hierarchy we perform pairwise comparison between the methods that use the hierarchy and their counterparts that do not use the hierarchy. In each of the comparisons the performance is compared in terms of the 16 different performance measures. To assess whether the difference in performance are statistically significant, we have employed the non-parametric Wilcoxon test for statistical significance (Demšar 2006).

7 Results and discussion

In this section, we present the results from the experimental evaluation. Table 3 shows the values for the statistical significance level (p) of the difference (as measured by the non-parametric Wilcoxon test for statistical significance) between the methods that use the data-defined label hierarchy and the methods that don’t. In particular, the following pairs of methods are compared:

• BR and HOMER

• PCTs for multi-target classification (labeled as MTC) and hierarchical architecture of binary PCTs (labeled as HSC)

• PCTs for multi-target classification (labeled as MTC) and PCTs for hierarchical multi-label classification (labeled as HMC)

• Random forests of PCTs for multi-target classification (labeled as RFMTC) and HSC architectures of random forests of PCTs for hierarchical classification (labeled as RFHSC)

• Random forests of PCTs for multi-target classification (labeled as RFMTC) and random forests of PCTs for hierarchical multi-label classification (labeled as RFHMC)

Table 3 The values of the significance level p from the non-parametric Wilcoxon test of statistical significance for the difference in performance along 16 performance evaluation measures

In this experimental evaluation, we did not include the BR approach that use single PCTs and ensembles of PTCs (in particular, Random Forest of PCTs) as base classifiers. This decision was made as a result of a recent experimental evaluation (Levatić et al. 2014) in which the authors show that the predictive performance of this combination (denoted as single-label classification) is clearly the worst for single predictive models, and only comparable to the other methods for ensembles.

The first column of the table lists the evaluation measures, while the other two columns show the values of the significance level p. The sign ‘ >’ in the 3rd, 6th, 9th, 12th and 15th columns indicates that the first method (out of the two compared methods in the corresponding pairwise comparison) is better than the second method, while the sign ‘ <’ indicates that the second method is better than the first method. The difference between the methods’ performance is statistically significant if the value of the significance level (p) is lower than 0.05. These values are shown in boldface.

The results clearly show that the methods that use the data-derived hierarchies outperform the methods that do not use those hierarchies. The methods that use the data-derived hierarchies have 31 significant wins against only 3 significant wins of the methods that do not use the hierarchies. Both, local and global approaches show similar improvements which are more pronounced on single models than ensembles.

Inspecting Table 3 (BR vs HOMER), we note that HOMER performs better than BR on example-based and label-based measures overall (8 wins vs 4 losses, 5 significant wins vs. 1 significant loss). It performs better on all recall-based measures, F ₁-based measures, accuracy and subset accuracy and worse on Hamming loss and precision-based measures. HOMER is significantly better on recall, micro recall, F ₁ score, micro F ₁ and accuracy, and worse on macro precision.

Moving on to the results for comparing single PCTs that use and don’t use the data-derived hierarchies (MTC vs HSC and MTC vs HMC), we can immediately see that both (local and global) single PCTs models that use the hierarchies perform consistently better than single PCTs for MTC (that don’t use the hierarchies). The HSC architectures perform better on 14 evaluation measures (significantly on 10) and worse (but not significantly) on 2. PCTs for HMC beat PCTs for MTC even more convincingly, performing better on all but one evaluation measure: In terms of significant wins, the score is 13:0.

Finally, the comparisons RFMTC vs RFHSC and RFMTC vs RFHMC concern the use of the label hierarchy in the context of learning PCT ensembles (Random Forest of PCTs), both HSC architectures of binary PCT ensembles and ensembles of PCTs for HMC. As a baseline, we use ensembles (RFs) of PCTs for MTC. The HSC architecture actually performs slightly worse than RFs of PCTs for MTC (the significant wins score is 0:2). RFs of PCTs for HMC, however, perform better than RFs of PCTs for MTC (better on 12 and worse on 4 evaluation measures, significant wins score 3:0). It is obvious that the difference in the predictive performance is not emphasized as for the single models. Much larger improvements of performance are hard to achieve, given that RFs of PCTs for MTC were the best performing approach from a recent comparative study (Madjarov et al. 2012) (that did not use a label hierarchy).

The results in our research reveal that, if we have a very strong classifier and it can exploit in deep the label relationships, it will always produce good predictive performance. But, by using the label relationships (in particular, represented by data-derived hierarchies) as an additional input to the classifiers, we can improve (and not decrease) the predictive performance. In our work, this is emphasized especially for the single decision trees (which are not powerful classifiers, but very important because of their knowledge extraction and representation capabilities) and less emphasized for the ensembles and SVM-based methods.

In the Appendix A, we have also shown the average ranking diagrams depicting the relative performance of the 8 methods considered in the experiments: BR, HOMER, PCTs for MTC, HSC of PCTs, PCTs for HMC, RFs of PCTs for MTC, HSC of RFs of PCTs, RFs of PCTs for HMC. These indicate that HOMER performs best on recall-related measures (incl. recall, micro recall and macro recall), micro F ₁, macro F ₁, and accuracy. RFs for HMC, on the other hand, perform best on precision and ranking-related measures (incl. micro precision and macro precision, Hamming loss, subset accuracy, ranking loss, one-error, coverage and average precision).

A more detailed analysis of the results, looking at the performance figures of each methods for individual datasets (given in Appendix B) provides additional insight. The methods that use the data-derived hierarchy (both local and global approaches for HMC), generally show better performance on datasets with a large number of labels. Also, the analysis show that for the datasets with a large number of labels, many labels have only few examples (the labels space is sparse) and the data-derived hierarchy reduces the sparsity of the label space. We believe that this is the main reason that the balanced k-means approach works better than the hierarchical agglomerative clustering methods (work presented by Madjarov et al. 2015). In particular, balanced k-means tries to create more balanced clusters in terms of the number of labels and their co-occurrence in the partial classification problems defined in each node of the tree. That means that the number of examples in a particular node among the different labels is similar and the new (hierarchical) classification problem is more balanced in comparison to the classification problem defined by the original (flat) organization of the labels. Figures 5a, b visualize the hierarchies of the tmc2007 and enron datasets and the number of examples in each node of the hierarchy. The size of the circles corresponds to the number of the examples in the training set labeled with a particular label. Circles of the original labels are annotated, while the circles that represent the meta-labels are not annotated.

Fig. 5

Visualization of the hierarchies of the tmc2007 and enron datasets and the number of examples in the nodes of the hierarchies represented by the size of the circles. Circles of the original labels are annotated, while the circles that represent the meta-labels are not annotated

8 Conclusions and further work

In this paper, we have investigated the use of label hierarchies, constructed in a data-driven manner, in multi-label classification. We consider flat label-sets and construct label hierarchies from the label sets that appear in the annotations of the training data by using a hierarchical clustering approaches based on balanced k-means clustering. The hierarchies are then used in conjunction with hierarchical multi-label classification approaches (in a global and a local setting) in the hope of achieving better multi-label classification.

While the use of hierarchies constructed in this manner has been proposed a few years ago, it has only been considered in conjunction with a local model approach to HMC (Tsoumakas et al. 2008). In particular, a binary relevance hierarchical MLC architecture based on SVMs has been considered and evaluated on two datasets in the light of a few performance measures. We conduct a much more thorough study, investigating the utility of the hierarchy in the context of two local and two global model approaches to HMC, on a large collection of datasets, through the prism of a large number of performance measures.

In particular, we investigate the utility of the hierarchy in the context of two hierarchical architectures that use binary relevance classifier based on SVMs and decision trees (predictive clustering trees for binary classification), and the global model approaches of PCTs for HMC and ensembles thereof. The experimental results clearly show that the use of the hierarchy results in improved performance.

The performance is improved both in the context of local approaches and the context of global approaches for HMC. For the local approaches, the performance is improved when using a binary relevance architecture with SVMs (significantly better performance along 5 measures). It results in even more obvious improvements for a binary relevance architecture with decision trees (PCTs, significantly better performance along 10 measures).

In the context of global approaches, the label hierarchy used in PCTs for HMC greatly improves the performance of PCTs for multi-target classification (as used for MLC): The results show improvement in performance on 15 of the 16 measures considered, significantly for 13 measures (and insignificantly worse on one measure). For ensembles (RFs) of PCTs, the use of the hierarchy improves performance along 12 of the 16 measures, but the difference is significant for only 3 measures. However, note that RFs of PCTs perform very well already even without the hierarchy, being the best performing method among many MLC methods considered in a recent extensive experimental comparison.

We also believe that the use of the label hierarchies can lead to better understanding of the learned predictive models, but we have to investigate this in our further work. Additionally, we plan to extend this study by comparison of hierarchies constructed by humans and hierarchies generated in a data-driven fashion. For HMC problems, we can consider the MLC task defined by the leaves of the provided label hierarchy. We can then construct label hierarchies automatically, as described above, and compare these hierarchies (and their utility) to the originally provided label hierarchy. Also, some other types of structures (such as DAG, DMOZ hierarchy and etc.) could be considered for capturing the dependencies and relations between the labels of the original multi-label classification problems.

Appendices

Appendix A: Evaluation measures

In this section, we present the measures that are used to evaluate the predictive performance of the compared methods in our experiments. In the definitions below, $\mathcal {Y}_{i}$ denotes the set of true labels of example x _i and h(x _i ) denotes the set of predicted labels for the same examples. All definitions refer to the multi-label setting.

1.1 A.1 Example based measures

Hamming loss evaluates how many times an example-label pair is misclassified, i.e., label not belonging to the example is predicted or a label belonging to the example is not predicted. The smaller the value of h a m m i n g_l o s s(h), the better the performance. The performance is perfect when h a m m i n g_l o s s(h)=0. This metric is defined as:

$$ hamming\_loss(h)=\frac{1}{N}\sum\limits^{N}_{i=1}\frac{1}{Q}\left|h(\mathbf{x_{i}}){\Delta} \mathcal{Y}_{i}\right| $$

(7)

where Δ stands for the symmetric difference between two sets, N is the number of examples and Q is the total number of possible class labels.

Accuracy for a single example x _i is defined by the Jaccard similarity coefficients between the label sets h(x _i ) and $\mathcal {Y}_{i}$. Accuracy is micro-averaged across all examples.

$$ accuracy(h)=\frac{1}{N}\sum\limits^{N}_{i=1}\frac{\left|h(\mathbf{x_{i}})\bigcap \mathcal{Y}_{i}\right|}{\left|h(\mathbf{x_{i}})\bigcup \mathcal{Y}_{i}\right|} $$

(8)

Precision is defined as:

$$ precision(h)=\frac{1}{N}\sum\limits^{N}_{i=1}\frac{\left|h(\mathbf{x_{i}})\bigcap \mathcal{Y}_{i}\right|}{\left|h(\mathbf{x_{i}})\right|} $$

(9)

Recall is defined as:

$$ recall(h)=\frac{1}{N}\sum\limits^{N}_{i=1}\frac{\left|h(\mathbf{x_{i}})\bigcap \mathcal{Y}_{i}\right|}{\left|\mathcal{Y}_{i}\right|} $$

(10)

F ₁ score is the harmonic mean between precision and recall and is defined as:

$$ F_{1}=\frac{1}{N}\sum\limits^{N}_{i=1}\frac{2 \times \left|h(\mathbf{x_{i}}) \cap \mathcal{Y}_{i}\right|}{\left|h(\mathbf{x_{i}})\right| + \left|\mathcal{Y}_{i}\right|} $$

(11)

F ₁ is an example based metric and its value is an average over all examples in the dataset. F ₁ reaches its best value at 1 and worst score at 0.

Subset accuracy or classification accuracy is defined as follows:

$$ subset\_accuracy(h)=\frac{1}{N}\sum\limits^{N}_{i=1}I(h(\mathbf{x_{i}})=\mathcal{Y}_{i}) $$

(12)

where I(t r u e) = 1 and I(f a l s e) = 0. This is a very strict evaluation measure as it requires the predicted set of labels to be an exact match of the true set of labels.

1.2 A.2 Label based measures

Macro precision (precision averaged across all labels) is defined as:

$$ macro\_precision=\frac{1}{Q}\sum\limits^{Q}_{j=1}\frac{tp_{j}}{tp_{j} + fp_{j}} $$

(13)

where t p _j , f p _j are the number of true positives and false positives for the label λ _j considered as a binary class.

Macro recall (recall averaged across all labels) is defined as:

$$ macro\_recall=\frac{1}{Q}\sum\limits^{Q}_{j=1}\frac{tp_{j}}{tp_{j} + fn_{j}} $$

(14)

where t p _j , f p _j are defined as for the macro precision and f n _j is the number of false negatives for the label λ _j considered as a binary class.

Macro F ₁ is the harmonic mean between precision and recall, where the average is calculated per label and then averaged across all labels. If p _j and r _j are the precision and recall for all λ _j ∈h(x _i ) from $\lambda _{j} \in \mathcal {Y}_{i}$, the macro F ₁ is

$$ macro\_F_{1}=\frac{1}{Q}\sum\limits^{Q}_{j=1}\frac{2\times p_{j} \times r_{j}}{p_{j} + r_{j}} $$

(15)

Micro precision (precision averaged over all the example/label pairs) is defined as:

$$ micro\_precision=\frac{{\sum}^{Q}_{j=1}{tp_{j}}}{{\sum}^{Q}_{j=1}{tp_{j}} + {\sum}^{Q}_{j=1}{fp_{j}}} $$

(16)

where t p _j , f p _j are defined as for macro precision.

Micro recall (recall averaged over all the example/label pairs) is defined as:

$$ micro\_recall=\frac{{\sum}^{Q}_{j=1}{tp_{j}}}{{\sum}^{Q}_{j=1}{tp_{j}} + {\sum}^{Q}_{j=1}{fn_{j}}} $$

(17)

where t p _j and f n _j are defined as for macro recall.

Micro F ₁ is the harmonic mean between micro precision and micro recall. Micro F ₁ is defined as:

$$ micro\_F_{1}=\frac{2 \times micro\_precision \times micro\_recall}{micro\_precision + micro\_recall} $$

(18)

1.3 A.3 Ranking based measures

One error evaluates how many times the top-ranked label is not in the set of relevant labels of the example. The metric o n e_e r r o r(f) takes values between 0 and 1. The smaller the value of o n e_e r r o r(f), the better the performance. This evaluation metric is defined as:

$$ one\_error(f)=\frac{1}{N}\sum\limits^{N}_{i=1}\left[\!\!\!\left[\hspace{1 mm}\left[\arg\max_{\lambda \in \mathcal{Y}} f(\mathbf{x_{i}}, \lambda)\right] \notin \mathcal{Y}_{i} \hspace{1 mm}\right]\!\!\!\right] $$

(19)

where $\lambda \in \mathcal {L} = \left \{\lambda _{1}, \lambda _{2}, ..., \lambda _{Q}\right \}$ and [ [π] ] equals 1 if π holds and 0 otherwise for any predicate π. Note that, for single-label classification problems, the One Error is identical to ordinary classification error.

Coverage evaluates how far, on average, we need to go down the list of ranked labels in order to cover all the relevant labels of the example. The smaller the value of c o v e r a g e(f), the better the performance.

$$ coverage(f)=\frac{1}{N}\sum\limits^{N}_{i=1}\max_{\lambda \in \mathcal{Y}_{i}} rank_{f}(\mathbf{x_{i}}, \lambda) - 1 $$

(20)

where r a n k _f (x _i ,λ) denotes the position of the label λ in the ranking. It maps the outputs of f(x _i ,λ) for any $\lambda \in \mathcal {L}$ to {λ ₁,λ ₂,...,λ _Q } so that f(x _i ,λ _m )>f(x _i ,λ _n ) implies r a n k _f (x _i ,λ _m )<r a n k _f (x _i ,λ _n ). The smallest possible value for c o v e r a g e(f) is l _c , i.e., the label cardinality of the given dataset.

Ranking loss evaluates the average fraction of label pairs that are reversely ordered for the particular example given by:

$$ ranking\ loss(f)=\frac{1}{N}\sum\limits^{N}_{i=1}\frac{\left| D_{i}\right|}{\left| \mathcal{Y}_{i}\right|\left|\bar{\mathcal{Y}_{i}}\right|} $$

(21)

where $D_{i} = \{(\lambda _{m}, \lambda _{n}) | f(\mathbf {x_{i}}, \lambda _{m}) \leq f(\mathbf {x_{i}}, \lambda _{n}), (\lambda _{m}, \lambda _{n}) \in \mathcal {Y}_{i} \times \bar {\mathcal {Y}_{i}}\}$, while $\bar {\mathcal {Y}}$ denotes the complementary set of $\mathcal {Y}$ in $\mathcal {L}$. The smaller the value of r a n k i n g_l o s s(f), the better the performance, so the performance is perfect when r a n k i n g_l o s s(f)=0.

Average Precision is the average fraction of labels ranked above an actual label $\lambda \in \mathcal {Y}_{i}$ that actually are in $\mathcal {Y}_{i}$. The performance is perfect when a v g_p r e c i s i o n(f)=1; the larger the value of a v g_p r e c i s i o n(f), the better the performance. This metric is defined as:

$$ avg\_precision(f)=\frac{1}{N}\sum\limits^{N}_{i=1}\frac{1}{\left| \mathcal{Y}_{i}\right|}\sum\limits_{\lambda \in \mathcal{Y}_{i}}\frac{\left| \mathcal{L}_{i}\right|}{rank_{f}(\mathbf{x_{i}}, \lambda)} $$

(22)

where $\mathcal {L}_{i}=\{\lambda ^{\prime }| rank_{f}(\mathbf {x_{i}}, \lambda ^{\prime }) \leq rank_{f}(\mathbf {x_{i}}, \lambda ), \lambda ^{\prime } \in \mathcal {Y}_{i}\}$ and r a n k _f (x _i ,λ) is defined as in coverage above.

1.4 B.1 Results on the example-based evaluation measures

Table 4 The performance of the multi-label classification approaches in terms of the examples-based evaluation measures

Table 5 The performance of the multi-label classification approaches in terms of the examples-based evaluation measures

Fig. 6

The critical diagrams for the example-based evaluation measures: The results from the Nemenyi post-hoc test at 0.05 significance level on all the datasets

1.5 B.2 Results on the label-based evaluation measures

The big difference between the micro-based and macro-based evaluation measures appears due to the averaging strategy of the obtained predictions. It is more emphasized on the large datasets that have highly unbalanced number of examples per label. Namely, the averaging in the micro-based measures is made across the predictions per example for all labels, while the averaging in the macro-based measures is made across the predictions per label for all examples, which means that for macro-based measures the labels with small number of examples are equally important as the labels with large number of examples.

Table 6 The performance of the multi-label classification approaches in terms of the label-based evaluation measures

Table 7 The performance of the multi-label classification approaches in terms of the label-based evaluation measures

Fig. 7

The critical diagrams for the label-based evaluation measures: The results from the Nemenyi post-hoc test at 0.05 significance level on all the datasets

1.6 B.3 Results on the ranking-based evaluation measures

Fig. 8

The critical diagrams for the ranking-based evaluation measures: The results from the Nemenyi post-hoc test at 0.05 significance level on all the datasets

Table 8 The performance of the multi-label classification approaches in terms of the ranking-based evaluation measures

Appendix B: Complete results from the experimental evaluation

In this section, we present the complete results from the experimental evaluation. We present the results based on the evaluation measures. Tables 4, 5, 6, 7 and 8 give the performance of the compared methods on each of the datasets measured in terms of the example based, label based and ranking based evaluation measures. The first column of the tables lists the dataset, while the remaining columns show the performance of each method for every dataset. The best results per dataset are shown in boldface. For the bookmarks dataset, HOMER did not manage to construct a predictive model within one week under the available resources. The corresponding entries in the tables with the results are marked with DNF (Did Not Finish).

To assess whether the overall differences in performance across the different approaches are statistically significant, we also employed the corrected Friedman test (Friedman 1940) and the post-hoc Nemenyi test (Nemenyi 1963) as recommended by Demšar (2006). We present the results from the Nemenyi post-hoc test with average rank diagrams (Demšar 2006). These are given in Figs. 6, 7 and 8. A critical diagram contains an enumerated axis on which the average ranks of the algorithms are drawn. The algorithms are depicted along the axis in such a manner that the best ranking ones are at the right-most side of the diagram. The lines for the average ranks of the algorithms that do not differ significantly (at the significance level of p=0.05) are connected with a line. For the bookmarks dataset, we penalize HOMER that does not finish by assigning it the lowest value (i.e., the lowest rank value) for each evaluation measure.