1 Introduction

The spatial competition model, originally established by Hotelling (1929), is widely used in business analysis. Among the applications, a particular feature of the benchmark Hotelling model is that each consumer is assumed to buy one unit from one seller exclusively. As a result, the model implies that either an increase of the level of product differentiation or brand-loyalty brings about market power. The unit-demand restriction is relaxed by recent studies such as Kim and Serfes (2006) and Jeitschko et al. (2017) and Anderson et al. (2017), where consumers are allowed to buy from both sellers (multi-brand purchase). They show that the governing force on pricing is the degree of multi-brand complementarity relative to product differentiation—a new equilibrium emerges when the incremental value for product diversity exceeds a threshold, where duopolists offer lower prices in exchange for quantities, and profits are decreasing in consumer heterogeneities.

In their pioneer works, each consumer is allowed to buy at most one unit from each seller—this might be perfectly applicable to the examples such as newspapers, iPad versus Kindle or software—but in some other markets, buying multiple units from the same seller is also pervasive (within-brand multi-purchase), e.g., food, credit cards, furniture, and services. Some customers may buy from both brands for enjoying the variety of brand-specific services (functionalities, styles, tastes), and meanwhile, some customers—e.g., loyal individuals or corporate clients—may buy multiple units of the same product for extra needs (e.g., additional capacities). Among the competing platforms, both multi-homing and repeated purchases are prevalent.

In addition to multi-brand purchase, will the previous results still hold (or under what circumstances) when within-brand multi-unit purchase is taken into account? And how should sellers respond to a change of the relative demand for the two types of multi-purchase? Combining the above studies that focus on inter-brand multi-purchase only, and the fact that some consumers may also buy multiple units from each brand, we study the pricing and location strategies by considering the within-brand multi-purchase in addition to multi-brand purchase, to extend the applicability of the Hotelling model that can be adapted to analyze different demand patterns in different markets. Neglecting the coexistence of within-brand and inter-brand multi-purchase is not innocuous, because the intensity of competition varies contingent upon the relative forces between the two types of multi-purchase.

In the textbook Hotelling model where each consumer is “restricted” to have unit-demand, it is implicitly assumed that the “marginal” or incremental utility of consuming the second unit is sufficiently small. That is, buying two units is not worthwhile because twice the price will be paid without bringing additional surplus. In Section 2, we allow consumers’ incremental utilities of consuming the same product for a second time to be heterogeneous such that some consumers are willing to purchase from the same seller twice. If owning more units of the same product does not affect the preference for diversity, and when the demand for within-brand multi-purchase is below a threshold, an increase of within-brand multi-purchase intensifies competition, resulting in a lower price and profit of the rival firm. As the quantity purchased from the same seller further increases above the threshold, duopolists find it more profitable to switch from offering higher prices as strategic complements to charging lower prices independently, in order to extract the willingness to pay from those who potentially buy from both sellers. Besides, a greater level of product differentiation weakens the effects of both types of multi-purchase.

Ostensibly, introducing within-brand multi-purchase does not significantly alters the direction for price-switch proposed by the previous studies, i.e., when the demand for brand-diversity exceeds a threshold, lower prices are offered. However, in Section 3, we show that such one-dimensional cutoff condition is incomplete and might even be misleading in inferring equilibrium patterns. In particular, when consumers have limited demand for total quantities purchased, owning more units of the same product reduces the desirability for diversity. Therefore, buying the same product again makes it less necessary to buy from the rival, and an increase of within-brand multi-purchase directly crowds out the demand for multi-brand purchase. As a result, an increase of within-brand multi-purchase induces the incentives to eliminate multi-brand equilibrium evaluated above a threshold, where prices are jumped upward. Therefore, without considering within-brand multi-purchase may not provide an accurate prediction of the market outcome when the demand structure varies.

Our approach can be applied to incorporate product selection and quadratic disutility for product differentiation. In Section 4, we consider a two-stage-game where sellers choose locations in the first stage and then offer prices simultaneously in the second stage. When the two types of multi-purchase are independent, the subgame perfect equilibria exhibit similar properties compared with d’Aspremont et al. (1979) and Kim and Serfes (2006), i.e., fixing the demand for multi-brand, a lower degree of within-brand multi-purchase leads to maximum differentiation whereby a greater level of within-brand multi-purchase yields minimum differentiation.

2 Model

A unit mass of consumers are uniformly distributed over x ∈ [0,1]. Firm A supplying brand A locates at 0 and firm B supplying brand B locates at 1. Firms are engaged into a Bertrand game and the per-unit price, pA and pB are announced simultaneously.Footnote 1

A consumer’s preference over brands is represented on the x-axis: each consumer incurs a disutility from not being able to purchase one’s ideal product, and such disutility is tx (resp., t(1 − x)) if brand A (resp., B) is chosen. Therefore, owning both brands incurs tx + t(1 − x) = t. The quadratic form of disutility from differentiation, studied in Section 4, adds technical complexities without providing new insights when location choices are not considered in the current section.

Let v ≫ 0 be the reservation value of making arbitrary purchases, such that each consumer must buy at least one unit (stay in the market). Upon owning brand i already, additional purchases made from brand − i give β, i.e., the incremental value for brand-variety, in addition to the disutility incurred from consuming the non-ideal products designed by − i.

For those who own one unit of brand i already, there will be many causes leading some buyers to prefer to buy a second i rather than buy one unit of i only, and the ensemble of such additional benefits perceived by a consumer who consumes a second i is here symbolized by μi. In previous studies, the preference for diversity (i.e., here we use β) and the preference for brands (i.e., location) are assumed to be independent—similarly, we also let μi and x be independent, in order to stress the unique role played by each of the driving forces (β, μi and t). For example, the distuility is already incurred during the choices for differentiated brands, whereby what we focus here is the within-brand quantity-difference that is exclusively captured by μi.

The choice of whether buying one unit or two units of i could be heterogeneous among different consumers; hence, μi is assumed to be ranged from [0,μ]. In the following, in order to characterize the properties of the equilibrium evaluated at explicit solutions, assume that μA and μB are independently distributed according to Bernoulli distribution: for the \( r_{i}:=\Pr \left (\mu _{i}=\mu \right ) \) fraction of those who buy brand i, their incremental valuation on the second unit of i is μ > pi and therefore each of them buy two units of i; for the remaining \( 1-r_{i} =\Pr \left (\mu _{i}=0\right ) \) fraction, 0 < pi hence each of them buys one unit of i only.Footnote 2

For the purpose of stressing the question of our interest, buying at most two units from one seller is sufficient to show the effects of a variation of within-brand quantities, and therefore we normalize the incremental value of purchasing more than two units from one seller to be zero. Before Section 3, we assume that buying a second unit of the same product does not affect the benefits from holding two different brands. Therefore, given a particular β, a consumer with valuations {μA,μB} chooses one of the purchase options: {A}, {B}, {AA}, {BB}, {AB}, {AAB}, {ABB}, and {AABB}, based on his/her brand-preference (x) and prices. The resulting utilities are summarized in Table 1.

Table 1 Utility function
Full size table

Remarks: (i) instead of being interpreted as the per-unit value, v should be the value of buying (regardless of brand(s) and quantity) in this market; (ii) a higher β indicates a greater level of the inter-brand complementarity; (iii) within brand i, the incremental value delivered by consuming an additional unit of the same product is perceived to be μi for a particular consumer. For instance: (1) buying the first A (AA battery) incurs − tx (for a particular device), but for a consumer who needs two pieces of AA batteries, buying a second A gives μA (additional power) instead of costing an additional tx because the first and the second A only differ in quantities but do not differ in brand-specific functionalities; (2) brand A differs from brand B (button cells filled in a watch); hence, choosing both brands incurs − tx − t(1 − x) + β (owning batteries for both devices), irrespective of the quantities purchased from each brand—an extra μi can be obtained only by the second unit bought within brand i.

The textbook Hotelling model where the driving force is t (i.e., product differentiation) is a special case when β and μi are absent; without considering within-brand multi-purchase, the “marginal” (incremental) utility of buying an additional unit of the same product, μi, can be regarded as sufficiently small—the consequences of relaxing this assumption is of our primary interest.

2.1 Analysis

The decision margins can be found by comparing each pair among the choice set listed in Table 1. Notice that since μi is orthogonal to x, hence upon buying a unit from i already, whether a consumer chooses to buy a second i is conditional on \( \mu _{i}-p_{i} \gtrless 0 \). Clearly, firm B will not receive any payments from consumers who never buy brand B. Therefore, from the view of firm B, the expected utility of those who may choose either {A} or {AA} is

$$ \begin{array}{@{}rcl@{}} &&(1-r_{A})\underbrace{\left( v-tx-p_{A}\right)}_{\text{buy $ \{A\} $}}+r_{A}\underbrace{\left( v+\mu-tx-2p_{A}\right)}_{\text{buy $ \{AA\} $}}\\ &&=v-tx +\underbrace{r_{A}\mu}_{\text{expected value of the second $ A $}}-\underbrace{(1+r_{A})p_{A}}_{\text{total expected payments for brand $ A $}}. \end{array} $$

Similarly, from the view of firm A, the expected utility of those who never buy A is v − t(1 − x) + rBμ − (1 + rB)pB.

Buying from both brands is less attractive if the per-unit price is relatively high compared with β. Conditional on a zero demand for multi-brand, a potential “brand-switching” consumer who is indifferent between choosing brand A and B is expected to be located at

$$ \hat{x}^{S}(\mu,p_{A},p_{B}):=\frac{1}{2}+\frac{p_{B}-p_{A}}{2t}+\frac{r_{A}}{2t}\left( \mu-p_{A}\right)-\frac{r_{B}}{2t}\left( \mu-p_{B}\right), $$
(1)

where the last two terms are absent without within-brand multi-purchase. The market share for firm A (resp., B), i.e., the left (resp., right) side of \( \hat {x}^{S} \), is a function of μ and prices of both firms.

When products are relatively cheaper compared with β, some consumers will buy both brands. Among those who buy both brands, (1 − rA)(1 − rB) of them buy {AB}; rA(1 − rB) fraction of them buy {AAB}; (1 − rA)rB fraction buy {ABB} and rArB fraction buy {AABB}. The expected utility of those who buy both brands is

$$ v+\underbrace{\beta -t}_{\text{brand-variety}} +\underbrace{\left( r_{A}+r_{B}\right)\mu}_{\text{expected value of the second $ i $}} -\underbrace{ \left( 1+r_{A}\right)p_{A} - \left( 1+r_{B}\right)p_{B} }_{\text{expected payments}}. $$

Combining those who buy brand A only, firm A sells 1 + rA units to those who locate on the left side of the margin where a consumer is indifferent between buying brand B only and buying both brands, i.e.,

$$ \hat{x}_{A}(\beta,\mu,p_{A}):=\frac{\beta-p_{A}}{t}+\frac{r_{A}}{t}\left( \mu-p_{A}\right), $$
(2)

conditional on a positive demand for multi-brand purchase. Analogously, ruling out those who buy brand A only and never buy B’s products, firm B sells 1 + rB units to those who locate on the right side of

$$ \hat{x}_{B}(\beta,\mu,p_{B}):=1-\frac{\beta-p_{B}}{t}-\frac{r_{B}}{t}\left( \mu-p_{B}\right). $$
(3)

Comparing (2) and (3), if \( \hat {x}_{B} < \hat {x}_{A} \Leftrightarrow (1+r_{A})p_{A} + (1+r_{B})p_{B} < 2\beta + (r_{A}+r_{B})\mu -t \), i.e., the demand for multi-brand purchase emerges with relatively lower prices, then firm A’s (resp., B’s) demand is \( \left (1+r_{A}\right )\hat {x}_{A} \) (resp., \( \left (1+r_{B}\right ) (1-\hat {x}_{B}) \)), which is independent of the rival’s price (sharing the customers located between \( \hat {x}_{B} \) and \( \hat {x}_{A} \)). If the degree of inter-brand complementarity is relatively lower (\( \hat {x}_{B} \geq \hat {x}_{A} \)), nobody purchases both brands and A’s (resp., B’s) demand becomes \( \left (1+r_{A}\right )\hat {x}^{S} \) (resp., \( \left (1+r_{B}\right )\left (1-\hat {x}^{S}\right ) \)), which is determined by the prices of both firms.

Firm i solves

$$ \max_{p_{i}}(1+r_{i})p_{i} \left( \frac{1}{2}+\frac{p_{-i}-p_{i}}{2t}+\frac{r_{i}}{2t}(\mu-p_{i})-\frac{r_{-i}}{2t}(\mu-p_{-i})\right), $$
(4)

if the rival offers p−i such that \( \hat {x}_{B} > \hat {x}_{A}\Leftrightarrow (1+r_{i})p_{i}+(1+r_{-i})p_{-i} > 2\beta +(r_{i}+r_{-i})\mu -t \), i.e., the Bertrand firms compete in prices. The best response derived from Eq. 4 is \( {p_{i}^{S}}(p_{-i}):=\frac {(1+r_{-i})p_{-i}+(r_{i}-r_{-i})\mu +t}{2(1+r_{i})} \), where the superscript S is short for “strategic complements” or “single-brand” purchase. Evaluated at \( \hat {x}_{B}<\hat {x}_{A}\Leftrightarrow (1+r_{i})p_{i}+(1+r_{-i})p_{-i} < 2\beta +(r_{i}+r_{-i})\mu -t\), firm i solves

$$ \max_{p_{i}}(1+r_{i})p_{i} \left( \frac{\beta-p_{i}}{t}+\frac{r_{i}}{t}\left( \mu-p_{i}\right) \right). $$
(5)

The optimization problem for each firm as shown in Eq. 5 is independent of the rival’s, and the first-order condition gives \( {p_{i}^{M}}:=\frac {\beta +r_{i}\mu }{2(1+r_{i})} \), where the superscript M is short for “local monopoly” or “multi-brand” purchase.

That is, given the rival’s price p−i, firm i has two options: charging \( {p_{i}^{S}} \) according to Eq. 4 gives profit \( {\pi _{i}^{S}}(p_{-i})= \frac {\left [(1+r_{-i})p_{-i}+(r_{i}-r_{-i})\mu +t \right ]^{2}}{8t} \) provided that \( \hat {x}_{B} > \hat {x}_{A} \); or charging \( {p_{i}^{M}} \) according to Eq. 5 gives profit \( {\pi _{i}^{M}}= \frac {(\beta +r_{i}\mu )^{2}}{4t} \) provided that \(\hat {x}_{B}<\hat {x}_{A}\). Evaluated exactly at \( p_{-i}=\hat {p}_{-i}:= \frac {\sqrt {2}(\beta +r_{i}\mu )-(r_{i}-r_{-i})\mu -t}{1+r_{-i}} \), the two options are equally profitable, i.e., \( {\pi _{i}^{S}}(\hat {p}_{-i})={\pi _{i}^{M}} \). Therefore, the best reply correspondence of firm i is a step function contingent upon a threshold of the rival’s price, \( \hat {p}_{-i} \):

$$ {p}_{i}^{BR}=\left\{\begin{array}{ll} {{p}_{i}^{S}}(p_{-i})& p_{-i} >\hat{p}_{-i}\\ {{p}_{i}^{M}}&p_{-i} <\hat{p}_{-i} \end{array}\right.. $$
(6)

When \( p_{-i}>\hat {p}_{-i} \), \( {{p}_{A}^{S}} \) and \( {{p}_{B}^{S}} \) are offered as strategic complements \(\left (\frac {d{p_{i}^{S}}}{dp_{-i}}>0 \right )\); when \( p_{-i}<\hat {p}_{-i} \), each firm offers \( {p_{i}^{M}} \) independently \(\left (\frac {d{p_{i}^{M}}}{dp_{-i}}=0 \right )\). When \( {p}_{A}^{BR} \) and \( {p}_{B}^{BR} \) hold simultaneously, the equilibrium strategies are denoted by \( \left ({{{p}_{A}^{M}}}^{*},{{{p}_{B}^{M}}}^{*}\right ) \) or \( \left ({{{p}_{A}^{S}}}^{*},{{{p}_{B}^{S}}}^{*}\right ) \).

2.2 Equilibrium

The equilibrium can be found by checking the intersections of \( {p}_{A}^{BR} \) and \( {p}_{B}^{BR} \) expressed in Eq. 6, and eliminate the profit-dominated options when multiple-Nash-equilibria arise. To make it technically rigorous, we derive the equilibrium by assuming rA ≥ rB. The symmetric equilibrium (see Corollary 1 for rA = rB) is a special case which is less informative about the relative advantages brought by within-brand multi-purchase.

Proposition 1 (Asymmetry)

For the utility class shown in Table 1, the equilibrium prices and profits are

$$ \left\{\begin{array}{l} {{p_{i}^{S}}}^{*}=\frac{3t+(r_{i}-r_{-i})\mu}{3(1+r_{i})},~{\pi_{i}^{S}}=\frac{\left[3t+(r_{i}-r_{-i})\mu\right]^{2}}{18t},~~~~\beta+\left( 1-\frac{\sqrt{2}}{3}\right)\max\{r_{i},r_{-i}\}\mu+\frac{\sqrt{2}}{3}\min\{r_{i},r_{-i}\}\mu <\sqrt{2}t\\ {{p_{i}^{M}}}^{*}=\frac{\beta+r_{i}\mu}{2(1+r_{i})},~{\pi_{i}^{M}}=\frac{(\beta+r_{i}\mu)^{2}}{4t},~~~~\beta+\left( 1-\frac{\sqrt{2}}{3}\right)\max\{r_{i},r_{-i}\}\mu+\frac{\sqrt{2}}{3}\min\{r_{i},r_{-i}\}\mu >\sqrt{2}t\\ {{p_{i}^{M}}}^{*}=\frac{\beta+r_{i}\mu-t}{1+r_{i}},~ {\pi_{i}^{M}}=\beta+r_{i}\mu-t~~~~\beta+r_{i}\mu\geq 2t \end{array}\right.. $$
(7)

Proof

First notice that the intersection of \( {{p}_{B}^{S}}\left ({{p}_{A}^{M}}\right ) < \hat {p}_{B} \) and \( {{p}_{A}^{M}} > \hat {p}_{A} \) is an empty set; hence, \( \left ({{p}_{A}^{M}},{{p}_{B}^{S}}\right ) \) cannot be an equilibrium; Similarly, \( \left ({{p}_{A}^{S}},{{p}_{B}^{M}}\right ) \) cannot be an equilibrium because \( {{p}_{B}^{M}} >\hat {p}_{B} \) and \( {{p}_{A}^{S}}\left ({{p}_{B}^{M}}\right ) < \hat {p}_{A} \) cannot hold simultaneously. That is, it is impossible that at equilibrium, one firm prices according to \( \hat {x}_{B}<\hat {x}_{A} \) whereas the other prices according to \( \hat {x}^{S} \).

For firm A, offering \( {{p}_{A}^{S}} \) evaluated at \( \hat {p}_{B} \) implies \( {{p}_{A}^{S}}\left (\hat {p}_{B}\right ) = \frac {\sqrt {2}(\beta +r_{A}\mu )}{2(1+r_{A})} =\sqrt {2}{{p}_{A}^{M}} >{{p}_{A}^{M}} \); For firm B, offering \( {{p}_{B}^{S}} \) evaluated at \( \hat {p}_{A} \) implies \( {{p}_{B}^{S}}\left (\hat {p}_{A}\right ) = \frac {\sqrt {2}(\beta +r_{B}\mu )}{2(1+r_{B})} =\sqrt {2}{{p}_{B}^{M}}> {{p}_{B}^{M}} \), i.e., price jumps at the kink between monopoly and strategic pricing. Hence, the relative positions of \( {{p}_{B}^{M}} \), \( \sqrt {2}{{p}_{B}^{M}} \), and \( \hat {p}_{B}\) are critical for firm A’s response; and firm A knows that firm B’s response will be contingent upon the relative positions of \( {{p}_{A}^{M}} \), \( \sqrt {2}{{p}_{A}^{M}} \), and \( \hat {p}_{A} \). Thanks to \( \sqrt {2} > 1 \), there are 9 possible combinations left to be checked, as shown in Fig. 1.Footnote 3

  1. (a)

    When \( \hat {p}_{A} <{{p}_{A}^{M}}<\sqrt {2}{{p}_{A}^{M}} \):

    1. (1)

      if \( \hat {p}_{B} < {{p}_{B}^{M}}<\sqrt {2}{{p}_{B}^{M}} \), the unique intersection point is \( \left ({{{p}_{A}^{S}}}^{*},{{{p}_{B}^{S}}}^{*}\right ) \).

    2. (2)

      \( {{p}_{B}^{M}}<\hat {p}_{B}<\sqrt {2}{{p}_{B}^{M}} \) and \( \hat {p}_{A} <{{p}_{A}^{M}}<\sqrt {2}{{p}_{A}^{M}} \) cannot hold simultaneously.

    3. (3)

      \( {{p}_{B}^{M}}<\sqrt {2}{{p}_{B}^{M}} <\hat {p}_{B} \) and \( \hat {p}_{A} <{{p}_{A}^{M}}<\sqrt {2}{{p}_{A}^{M}} \) cannot hold simultaneously.

  2. (b)

    When \({{p}_{A}^{M}}< \hat {p}_{A} < \sqrt {2}{{p}_{A}^{M}} \):

    1. (1)

      if \( \hat {p}_{B} <{{p}_{B}^{M}}<\sqrt {2}{{p}_{B}^{M}} \), the unique equilibrium is \( \left ({{{p}_{A}^{S}}}^{*},{{{p}_{B}^{S}}}^{*}\right ) \).

    2. (2)

      if \( {{p}_{B}^{M}} < \hat {p}_{B}< \sqrt {2}{{p}_{B}^{M}} \), \( {{p}_{A}^{M}} \) and \( {{p}_{B}^{M}} \) intersect at \( \left ({{p}_{A}^{M}},{{p}_{B}^{M}}\right ) \) whereas \( {{p}_{A}^{S}} \) and \( {{p}_{B}^{S}} \) intersect at \( \left ({{{p}_{A}^{S}}}^{*},{{{p}_{B}^{S}}}^{*}\right ) \). Compared with \( \left ({{p}_{A}^{M}},{{p}_{B}^{M}}\right ) \), deviating to \( \left ({{{p}_{A}^{S}}}^{*},{{{p}_{B}^{S}}}^{*}\right ) \) give both firms higher profits, which survives to be an equilibrium.

    3. (3)

      the subcase where \( {{p}_{B}^{M}}<\sqrt {2}{{p}_{B}^{M}} < \hat {p}_{B} \) is critical, because at least \( \left ({{{p}_{A}^{M}}},{{{p}_{B}^{M}}}\right ) \) is a candidate equilibrium. Moreover, a potential intersection of \( {p}_{A}^{BR} \) and \( {p}_{B}^{BR} \) may exist at somewhere along \( {{p}_{A}^{S}} \) and \( {{p}_{B}^{S}} \), because from A’s view, the slope of \( d{p}_{A}^{BR}/dp_{B}=\frac {1}{2}\frac {1+r_{B}}{1+r_{A}} \) is flatter than the slope of \( dp_{A}/d{p}_{B}^{BR} = 2\frac {1+r_{B}}{1+r_{A}} \) from B’s view. That is, an intersection point of \( {{p}_{A}^{S}} \) and \( {{p}_{B}^{S}} \) exists if \({{{p}_{B}^{S}}}|_{\sqrt {2}{{p}_{A}^{M}}} =\frac {\sqrt {2}(\beta +r_{A}\mu )-2(r_{A}-r_{B})\mu +2t}{4(1+r_{B})} > \hat {p}_{B}=\frac {\sqrt {2}(\beta +r_{A}\mu )-(r_{A}-r_{B})\mu -t}{1+r_{B}}\Leftrightarrow \beta +r_{A}\mu - \frac {\sqrt {2}}{3}(r_{A}-r_{B})\mu < \sqrt {2}t \).

      1. (i)

        when \( {{p}_{B}^{S}}|_{\sqrt {2}{{p}_{A}^{M}}}>\hat {p}_{B} \), the intersection point of \( {{p}_{A}^{S}} \) and \( {{p}_{B}^{S}} \) is \( \left ({{{p}_{A}^{S}}}^{*},{{{p}_{B}^{S}}}^{*}\right )>\left (\sqrt {2}{{p}_{A}^{M}},\hat {p}_{B}\right ) \), and charging \( {{p_{i}^{S}}}^{*} \) is more profitable than charging \( {{p_{i}^{M}}} \) for each firm.

      2. (ii)

        when \( {{p}_{B}^{S}}|_{\sqrt {2}{{p}_{A}^{M}}}<\hat {p}_{B} \), the unique equilibrium is \( \left ({{{p}_{A}^{M}}}^{*},{{{p}_{B}^{M}}}^{*}\right ) \).

  3. (c)

    When \( {{p}_{A}^{M}}<\sqrt {2}{{p}_{A}^{M}} < \hat {p}_{A} \):

    1. (1)

      \( \hat {p}_{B}<{{p}_{B}^{M}}<\sqrt {2}{{p}_{B}^{M}} \) and \( {{p}_{A}^{M}}<\sqrt {2}{{p}_{A}^{M}} <\hat {p}_{A} \) cannot hold simultaneously.

    2. (2)

      \( {{p}_{B}^{M}}<\hat {p}_{B}<\sqrt {2}{{p}_{B}^{M}} \) and \( {{p}_{A}^{M}}<\sqrt {2}{{p}_{A}^{M}} <\hat {p}_{A} \) cannot hold simultaneously;

    3. (3)

      if \( {{p}_{B}^{M}}<\sqrt {2}{{p}_{B}^{M}}<\hat {p}_{B} \), the unique intersection point is \( \left ({{{p}_{A}^{M}}}^{*},{{{p}_{B}^{M}}}^{*}\right ) \).

Fig. 1
figure 1

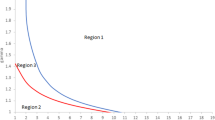
Asymmetrically Conditional Reactions. The changes of the relative positions of the determinant variables in conditional reactions, from case (a-1) to case (c-3), correspond to an increase of rA from 0 to 1, whereby the normalizations are made for the purpose of visualization: rB = 0, \( \beta < \sqrt {2}t \) and μ = 3t

Full size image

Finally, we check the boundary conditions of parameters to make the above arguments valid, given 1 ≥ rA ≥ rB ≥ 0: (i) firm B’s profit is non-negative provided that \( 0<\hat {x}^{S}\leq 1\Leftrightarrow 0 < (r_{A}-r_{B})\mu \leq 3t \). The incremental surplus from buying the same product for a second time is non-negative provided that \( {{p}_{A}^{S}} < \mu \Leftrightarrow \mu >\frac {3t}{2r_{A}+r_{B}+3} \), i.e., we restrict μ ∈ [t,3t] such that \( {{p}_{B}^{S}}\geq 0 \) and \( {{p}_{A}^{S}}\leq \mu \) hold. Evaluated at \( \beta +r_{A}\mu <\frac {\sqrt {2}}{3}(r_{A}-r_{B})\mu +\sqrt {2}t \Rightarrow \beta +r\mu _{A} < \frac {1}{2}(r_{A}-r_{B})\mu +\frac {3}{2}t \), the condition for \( \hat {x}_{B}({{p}_{B}^{S}})>\hat {x}_{A}({{p}_{A}^{S}}) \) holds; (ii) evaluated at \( \beta +r_{A}\mu >\frac {\sqrt {2}}{3}(r_{A}-r_{B})\mu +\sqrt {2}t \Rightarrow \beta +r\mu _{A} > \frac {1}{2}(r_{A}-r_{B})\mu +t \), the condition for \( \hat {x}_{B}({{p}_{B}^{M}})<\hat {x}_{A}({{p}_{A}^{M}}) \) holds; (iii) the corner solution is obtained from \( \hat {x}_{A}(p_{A}) = 1 \); hence, the interior solutions exist provided that \( \hat {x}_{A}({{p}_{A}^{M}}) < 1\Leftrightarrow \beta +r_{A}\mu <2t \), evaluated at which, the condition β + rAμ < (2 + rA + rB)μ < 2(1 + rA)μ holds such that \( {p_{i}^{M}}<\mu \). □

Corollary 1 (Symmetry)

When rA = rB = r, the symmetric equilibrium (and interior) is

$$ \left\{\begin{array}{l} {{p_{i}^{S}}}^{*}=\frac{t}{1+r},~{\pi_{i}^{S}}=\frac{t}{2},~~~~\beta+r\mu<\sqrt{2}t\\ {{p_{i}^{M}}}^{*}=\frac{\beta+r\mu}{2(1+r)},~{\pi_{i}^{M}}=\frac{(\beta+r\mu)^{2}}{4t},~~~~\beta+r\mu>\sqrt{2}t \end{array}\right.. $$
(8)

2.3 Comparative Statics

The relative values of r (within-brand multi-purchase), β (multi-brand purchase), and t (product differentiation) are essential to determine the equilibrium patterns. Fixing β and t, consider how firms would respond when some consumers choose to purchase more units from the same seller.

Single-Brand Equilibrium

When the demand for multi-purchase is low relative to product differentiation such that \(\beta +r\mu <\sqrt {2}t\), duopolistic products are substitutes—firms compete head on for consumers. An increase of r pushes prices downward \(\left (\frac {\partial {{p_{i}^{S}}}^{*}}{\partial r} < 0 \right )\). When nobody buys from both sellers and if price is not offered to be sufficiently attractive, a firm will lose a marginal consumer who switches to buy twice from the rival firm, resulting in an intensified competition. In particular, fixing ri, an increase of r−i steals firm i’s market share (\( \frac {\partial {{p_{i}^{S}}}^{*}}{\partial r_{-i}} < 0 \)), and such price dispersion is amplified by a higher μ: for ri < r−i, \( \frac {\partial {{p_{i}^{S}}}^{*}}{\partial \mu } < 0 \) and \( \frac {\partial {p_{-i}^{S}}^{*}}{\partial \mu } > 0 \). Moreover, prices are supermodular in ri and r−i, i.e., \( \frac {\partial ^{2} {{p_{i}^{S}}}^{*}}{\partial r_{i} \partial r_{-i}} > 0 \) due to strategic complements.

Regime Switch

A further increase of within-brand multi-purchase leads to two effects: First, fixing β, when r exceeds a threshold such that \( \beta +r\mu >\sqrt {2}t \), duopolistic prices switch from single-brand equilibrium to multi-brand equilibrium (extensive margin), and lower prices \( \left ({{{p}_{A}^{M}}}^{*},{{{p}_{B}^{M}}}^{*}\right )<\left ({{{p}_{A}^{S}}}^{*},{{{p}_{B}^{S}}}^{*}\right ) \) are offered non-cooperatively. In the previous studies of multi-brand purchase without within-brand multi-purchase, firms charge higher (resp., lower) prices when β is below (resp., exceeds) \( \sqrt {2}t \). When some consumers buy more units from one seller, a lower price is offered, which in turn, makes it also cheaper for buying from both sellers—when someone begins to buy both, prices are no longer strategic complements. Therefore, a lower β is needed to trigger market sharing—this can be visualized in Fig. 2, where the threshold (rA as a function of β) is negatively sloped.

Fig. 2
figure 2

Equilibria: Independence. When \( \beta > \sqrt {2}t \), only multi-brand equilibrium exists. When \(\beta < \sqrt {2}t\), both multi-brand and single-brand equilibrium may arise: fixing β and r−i, as ri increases, the equilibrium changes from high-price single-brand to low-price multi-brand

Full size image

Multi-brand Equilibrium

Second, within the intensive margin of multi-brand equilibrium, a higher ri increases the size of market sharing: \( \frac {\partial \left (\hat {x}_{A}-\hat {x}_{B}\right )}{\partial r_{i}} > 0 \), benefiting firm i unambiguously without affecting the rival \(\left (\frac {\partial {\pi _{i}^{M}}}{\partial r_{i}} > 0= \frac {\partial \pi _{-i}^{M}}{\partial r_{i}} \right )\). Clearly, a higher degree of inter-brand complementarity, β, benefits both firms but for the same magnitude of an increase of β, the firm with a relatively higher ri has a weaker incentive to increase price because, in addition to β, within-brand multi-purchase becomes an alternative canal to extract consumer surplus. That is, price is submodular in both types of multi-purchase \(\left (\frac {\partial ^{2} {{p_{i}^{M}}}^{*}}{\partial r_{i} \partial \beta } < 0 \right )\) and profit is supermodular \(\left (\frac {\partial ^{2} {\pi _{i}^{M}}}{\partial r_{i}\partial \beta } > 0 \right )\). The within-brand multi-purchase from the rival is irrelevant.Footnote 4

Product Differentiation

In addition, product differentiation counteracts both types of multi-purchase. When products are substitutes and nobody buys both brands, an increase of t makes consumers less likely to switch between brands, adjusting prices for within-brand multi-purchase is less urgent. That is, price is submodular in ri and t: \( \frac {\partial ^{2} {{p_{i}^{S}}}^{*}}{\partial r_{i} \partial t} < 0 \). When products are complements and some consumers buy from both brands, profit is submodular in ri and t because given prices, a higher degree of differentiation reduces the incentives of holding different products: \( \frac {\partial ^{2} {\pi _{i}^{M}}}{\partial r_{i} \partial t} < 0 \).

The comparative statics described above, i.e., the effects of within-brand multi-purchase on equilibrium outcome, can be briefly summarized in the following proposition:

Proposition 2

As the demand for within-brand multi-purchase (specified as ri in Bernoulli distribution) increases:

  1. (i)

    When ri is relatively low resulting in single-brand equilibrium, a marginal increase of ri intensifies competition, i.e., \( \frac {\partial ^{2} {{p_{i}^{S}}}^{*}}{\partial r_{i} \partial r_{-i}}>0 \). In particular, at symmetric equilibrium, \( \frac {\partial {{p_{i}^{S}}}^{*}}{\partial r} < 0 \);

  2. (ii)

    When ri exceeds a threshold, pricing strategies are switched from single-brand to multi-brand, and lower prices \( {{p_{i}^{M}}}^{*}<{{p_{i}^{S}}}^{*} \) are offered;

  3. (iii)

    Evaluated at multi-brand equilibrium, a marginal increase of ri leads to a higher (resp., lower) price of firm i if μ is greater (resp., less) than β, i.e., \( \text {sign}\left (\frac {\partial {{p_{i}^{M}}}^{*}}{\partial r_{i}}\right )= \text {sign}\left (\mu -\beta \right ) \); and such price adjustment is orthogonal to the rival’s choice, i.e., \( \frac {\partial ^{2} {{p_{i}^{M}}}^{*}}{\partial r_{i} \partial r_{-i}} = 0 \).

Moreover, product differentiation counteracts within-brand multi-purchase, i.e., \( \frac {\partial ^{2} p_{i}^{*}}{\partial r_{i}\partial t}\leq 0 \) and \( \frac {\partial ^{2} \pi _{i}^{*}}{\partial r_{i}\partial t}\leq 0 \).

3 Quantity Restriction

In Section 2, from the consumer side, the incremental value of buying the same product for a second time is assumed to be independent of buying a different product—evaluated at prices that offered to be relatively low, some consumers will buy three or four units. Consider an alternative demand pattern where each consumer needs at most two units. That is, the incremental consumption value brought by the third unit is zero—upon owning one unit already, for one who is going to buy a second unit, “buying the same product again” and “buying (a) different product(s)” are mutually exclusive.

Formally, in such a case, it is equivalent to say that each consumer cannot obtain β and μi simultaneously, whereby the utilities derived from choosing {A}, {B}, {AA}, {BB}, and {AB} are identical to those in Table 1. For example, upon owning {AA} already, buying a unit of B gives − t(1 − x) − pB < 0; upon owning {AB} already, buying an additional unit of A gives − pA < 0. Therefore, the option {AAB} will never be chosen (and neither {ABB} nor {AABB} will be chosen). We normalize rA = rB = r to characterize a symmetric equilibrium.

When μ is large relative to β, nobody buys both brands. A marginal brand-switching consumer locates at \( \hat {x}^{S} \). When β is large relative to μ, some consumers buy both brands, i.e., choosing {AB}. A marginal consumer who is indifferent between choosing brand A only and {AB}, and one who is indifferent between choosing {AB} and brand B only, locate at

$$ \tilde{x}_{B}:=1-\frac{\beta-p_{B}}{t}+\frac{r(\mu-p_{A})}{t},~\tilde{x}_{A}:=\frac{\beta-p_{A}}{t}-\frac{r(\mu-p_{B})}{t}, $$

respectively. Because products become substitutes for the second unit, \( \tilde {x}_{B} \) and \( \tilde {x}_{A} \) are functions of both prices. The mass of multi-brand demand, \( \tilde {x}_{A}-\tilde {x}_{B} \), is decreasing in prices and increasing in β − rμ, which is a crucial value that measures the substitutability between the two types of multi-purchase.

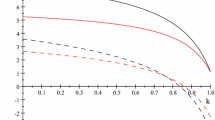
When \(\tilde {x}_{B} > \tilde {x}_{A} \Leftrightarrow \beta -r\mu < \frac {1}{2}(1-r)(p_{A}+p_{B})+\frac {t}{2} \), firms solve Eq. 4 simultaneously, i.e., single-brand pricing (regime S). Alternatively, when \( \beta -r\mu > \frac {1}{2}(1-r)(p_{A}+p_{B})+\frac {t}{2} \), firm A solves \( \max_{p_{A}}p_{A}\left ((1+r)\tilde {x}_{B}+(\hat {x}_{A}-\tilde {x}_{B})\right ) \), and firm B solves \( \max_{p_{B}}p_{B}\left ((1+r)(1-\tilde {x}_{A})+(\tilde {x}_{A}-\tilde {x}_{B})\right ) \), i.e., multi-brand pricing (regime M). Notice that firms are not independent in both regimes—the best responses are given by (Fig. 3)

$$ p_{i}^{BR}=\left\{\begin{array}{l} {p_{i}^{S}}(p_{-i})=\frac{(1+r)p_{-i}+t}{2(1+r)},~~~~\hfill p_{-i}>\tilde{p}_{-i}\\ {p_{i}^{M}}(p_{-i})=\frac{2rp_{-i}+rt-(1-r)(\beta-r\mu)}{2(1+r^{2})},~~~~\hfill p_{-i} < \tilde{p}_{-i} \end{array}\right., $$
(9)

where \( \tilde {p}_{-i}:=\frac {4r+(1+r)\sqrt {2(1+r^{2})}}{(1-r)(1+4r+r^{2})}(\beta -r\mu )-\frac {(1+2r)+r(\sqrt {2(1+r^{2})}-r)}{(1-r)(1+4r+r^{2})} \) is the cutoff of the rival’s price that makes single-brand pricing and multi-brand pricing equally profitable. In both regimes, the reaction curve is upward sloping and \( p_{i}^{BR} \) jumps upward from \( p_{-i}<\tilde {p}_{-i} \) to \( p_{-i}>\tilde {p}_{-i} \). The process for deriving the following symmetric equilibrium is provided in the Appendix.

Fig. 3
figure 3

Best Reply Correspondence with Quantity Restriction. Fixing β, as r increases, the equilibrium changes from case (ii), to (iii) then to (i), gradually crowding out multi-brand purchases

Full size image

Proposition 3

When each consumer is restricted to buy at most two units, the symmetric equilibrium is

$$ \left\{\begin{array}{l} {{p_{i}^{S}}}^{*} = \frac{t}{1+r},~{\pi_{i}^{S}}=\frac{t}{2},~~~~\hfill \beta-r\mu < \frac{(1+r)\sqrt{2(1+r^{2})}-3r-r^{2}}{(1-r)(1+r)}t \\ {{p_{i}^{M}}}^{*}=\frac{1}{2}\frac{(1-r)(\beta-r\mu)+rt}{1-r(1-r)},~{\pi_{i}^{M}}=\frac{(1+r^{2})\left( (1-r)(\beta-r\mu)+rt\right)}{4t(1-r+r^{2})^{2}},~~~~\hfill \beta-r\mu > \frac{(1+r)\sqrt{2(1+r^{2})}-3r-r^{2}}{(1-r)(1+r)}t \end{array}\right.. $$
(10)

Regime Switch: a Comparison

When consumers are allowed to buy more than two units (i.e., {AAB}, {ABB}, and {AABB} are available), as shown in Corollary 1, an increase of r will not directly crowd out the demand for multi-brand purchase—other things equal, a higher r is simply a symptom that implies a higher demand for more quantities, which also enhances market sharing that neutralizes competition (Fig. 2). In particular, the expected quantity that is sold by each seller to those who buy both brands is \( 1\cdot \left [(1-r)^{2}+(1-r)r\right ]+2\cdot \left [r(1-r)+r^{2}\right ]=1+r \), which is no less than 1 when each consumer has to choose one brand for the second and the last unit to be purchased.

In contrast, when consumers are restricted to buy two units, firm A’s products and firm B’s products become close substitutes during the second purchase (Fig. 4). Fixing β, an increase of r directly reduces the relative attractiveness of holding two different units, pushing multi-brand equilibrium to single-brand equilibrium. Nevertheless, whenever the preferences for within-brand and inter-brand multi-purchase are substitutes or independent, both types of multi-purchase counteract product differentiation, i.e., \( \frac {\partial ^{2} p_{i}^{*}}{\partial r \partial t} < 0 \) and \( \frac {\partial ^{2} p_{i}^{*}}{\partial \beta \partial t} < 0 \).

Fig. 4
figure 4

Equilibria: Substitutes. When \( \beta < \sqrt {2}t \), only single-brand equilibrium exists. When \(\beta > \sqrt {2}t\), both single-brand and multi-brand equilibrium may arise. Fixing β, as r increases, the equilibrium changes from low-price multi-brand to high-price single-brand

Full size image

The difference between Section 2 and 3 highlights the additional dimension that determines the cutoff condition for the switch of equilibria, which is previously neglected by considering multi-brand purchase only. By setting ri = 0, the condition for single-brand equilibrium is \( \beta < \sqrt {2}t \); and multi-brand equilibrium arises when \( \beta > \sqrt {2}t \), i.e., the cutoff condition of the rival’s pricing decisions can be inferred simply along the β-dimension. However, such condition is misleading when ri > 0. When within-brand multi-purchase and multi-brand purchase are independent (Fig. 2), both multi-brand and single-brand equilibrium exist when \( \beta < \sqrt {2}t \), and only multi-brand equilibrium exists when \( \beta > \sqrt {2}t \). In contrast, when the two types of multi-purchase are substitutes (Fig. 4), multi-brand equilibrium does not exist when \( \beta < \sqrt {2}t \) and both multi-brand and single-brand equilibrium may arise when \( \beta > \sqrt {2}t \).

4 The Choice of Differentiation

Our analysis is robust with location choices and quadratic disutility. Consider a two-stage game. In stage 1, firm A and B choose locations, denoted by a ∈ [0,1] and b ∈ [0,1], respectively. In stage 2, prices are announced simultaneously. According to d’Aspremont et al. (1979), the disutility from consuming the non-ideal brands, which is previously assumed to be linear in distance, is now replaced by the quadratic form to avoid the instability in stage 1, i.e., t(y − x)2 is incurred from choosing a brand located at y. In addition, μA and μB are assumed to be identically distributed following the Bernoulli distribution, i.e., rA = rB = r for simplicity.

Following the similar manner as shown by Proposition 1, when locations are fixed, the equilibrium prices with quadratic costs are provided in the Appendix. In the following, we derive the subgame perfect equilibria when firms choose locations strategically before setting prices. The results in this section can be regarded as an extended version of Kim and Serfes (2006).

First, consider the pricing strategies in stage 2, given location a ≤ b. When the demand for multi-brand purchases is zero, the expected demand margin is

$$ \hat{x}^{s}:=\frac{a+b}{2}+\frac{p_{B}-p_{A}}{2t(b-a)}+\frac{r(p_{B}-p_{A})}{2t(b-a)}. $$

Duopolists maximize profits by choosing prices, i.e., when \( {{p}_{A}^{S}}=\arg \max_{p_{A}}(1+r)p_{A}\hat {x}^{s} \) and \( {{p}_{B}^{S}}=\arg \max_{p_{B}}(1+r)p_{B}(1-\hat {x}^{s}) \) hold simultaneously, it gives

$$ \left\{\begin{array}{l} {{p}_{A}^{S}}(a,b)=\frac{(b-a)(2+a+b)t}{1+r},~{\pi_{A}^{S}}(a,b)=\frac{(b-a)(2+a+b)^{2}t}{18}\\ {{p}_{B}^{S}}(a,b)=\frac{(b-a)(4-a-b)t}{1+r},~{\pi_{B}^{S}}(a,b)=\frac{(b-a)(4-a-b)^{2}t}{18} \end{array}\right., $$
(11)

where \( \frac {\partial {\pi _{A}^{S}}}{\partial a} < 0 \) and \( \frac {\partial {\pi _{B}^{S}}}{\partial b} > 0 \), i.e., maximum differentiation. By replacing a = 0 and b = 1 into Eq. 11, it gives \( {{p_{i}^{S}}}^{*}|_{a=0,b=1}=\frac {t}{1+r} \) and \( {\pi _{i}^{S}}|_{a=0,b=1}=\frac {t}{2} \).

When the demand for multi-brand purchase is positive, the demand margins are given by

$$ \begin{array}{@{}rcl@{}} &\hat{x}_{b}:=b-\frac{\sqrt{t\left[\beta-p_{B}+r(\mu-p_{B})\right]}}{t}<b\\ &\hat{x}_{a}:=a+\frac{\sqrt{t\left[\beta-p_{A}+r(\mu-p_{A})\right]}}{t} > a. \end{array} $$

Firm A solves \( \max_{p_{A}}(1+r)p_{A}\hat {x}_{a} \) and firm B solves \( \max_{p_{B}} (1+r)p_{B}(1-\hat {x}_{b}) \), which gives

$$ \begin{array}{@{}rcl@{}} &&\left\{\begin{array}{l} {{p}_{A}^{M}}(a,b)=\frac{2}{9}\frac{3(\beta+r\mu)-a^{2}t +\sqrt{(a^{2}t)^{2}+3a^{2}(\beta+r\mu)t} }{1+r}\\ {{p}_{B}^{M}}(a,b)=\frac{2}{9}\frac{3(\beta+r\mu) -(1-b)^{2}t +\sqrt{((1-b)^{2}t)^{2} + 3(1-b)^{2}(\beta+r\mu)t } }{1+r} \end{array}\right.\\ {\pi_{A}^{M}}(a,b)&=&\frac{2t}{27}\left( 3(\beta + r\mu) - a^{2}t+a\sqrt{a^{2}t^{2} + 3(\beta + r\mu)t} \right)\left( 2at + \sqrt{a^{2}t^{2}+3(\beta+r\mu)t} \right)\\ {\pi_{B}^{M}}(a,b)&=&\frac{2t}{27}\left( 3(\beta+r\mu)-(1-b)^{2} t +\sqrt{((1-b)^{2}t)^{2} + 3(1-b)^{2}(\beta+r\mu)t } \right)\\ &&\left( 2(1-b)t + \sqrt{(1-b)^{2}t^{2} + 3 (\beta+r\mu) t} \right) \end{array} $$
(12)

It can be verified that \( \frac {\partial {\pi _{A}^{M}}}{\partial a} > 0 \) and \( \frac {\partial {\pi _{B}^{M}}}{\partial b} < 0 \), i.e., minimum differentiation. By replacing \( a=b=\frac {1}{2} \) into Eq. 12, it gives \( {{p_{i}^{M}}}^{*}|_{a=b=\frac {1}{2}} = \frac {12 (\beta +r\mu ) +\sqrt {\left [12(\beta +r\mu )+t \right ] t} -t}{18(1+r)} \) and

$$ {\pi_{i}^{M}}|_{a=b=\frac{1}{2}} = \frac{1}{108t}\left( 12(\beta+r\mu) - t +\sqrt{\left[12(\beta+r\mu) + t\right]t} \right)\left( 2t+ \sqrt{t^{2}+12 (\beta+r\mu) t} \right). $$

Proposition 4

The subgame perfect equilibria is

$$ \left\{\!\!\begin{array}{l} {{p_{i}^{S}}}^{*} = \frac{t}{1+r},~a=0,~b=1,~~~~\hfill \beta+r\mu \!<\! -\frac{t}{12} + \frac{t}{12}\left[(28+3\sqrt{87})^{\frac{1}{3}} + \frac{1}{(28+3\sqrt{87})^{\frac{1}{3}}}-1\right]^{2}\\ {p_{i}^{M}}^{*} = \frac{12 (\beta+r\mu) +\sqrt{\left[12(\beta+r\mu)+t \right] t}-t }{18(1+r)},~a = b = \frac{1}{2},~\beta+r\mu \!>\! -\frac{t}{12} + \frac{t}{12}\left[(28+3\sqrt{87})^{\frac{1}{3}} + \frac{1}{(28+3\sqrt{87})^{\frac{1}{3}}} - 1\!\right]^{2} \end{array}\right.\!\!. $$
(13)

5 Conclusion

We enrich the studies on multi-purchase behavior in a horizontally differentiated duopoly, where the equilibrium patterns are characterized by comparing the demand for multi-brand purchase and within-brand multi-unit purchase. If the utility derived from buying multiple units from the same seller is independent of the preference for product variety, an increase of the demand for within-brand multi-purchase first intensifies competition and then triggers multi-brand equilibrium that neutralizes competition evaluated above a threshold. However, if the demand for qualities is restricted, an increase of the within-brand multi-purchase might eliminate multi-brand equilibrium.

The comparison between multi-brand equilibrium and single-brand equilibrium might sound similar to the previous studies that focus on multi-brand purchase only, but we show that a variation of quantities brings about not only a quantitatively asymmetric result, but more importantly, it is critical for firms to clarify that whether a higher demand for quantities will crowd out the demand of the rival’s products or it is a symptom that indicates a higher demand for both. For example, without considering within-brand multi-purchase, the multi-brand equilibrium calls for lower prices whereby single-brand equilibrium corresponds to higher prices. However, the reverse is true when the two types of multi-purchase are substitutes.

Such extension provides insights into other marketing strategies particularly in the Internet era, where both multi-homing among competing platforms and price discrimination on repeated purchases based on big data are pervasive. In the future, the interaction between the two types of multi-purchase can be incorporated with dynamic settings, where price discrimination could be an effective way to capture loyal customers who would like to make repeated purchases (Conitzer et al. 2012).