License and Entry Strategies for an Outside Innovator Under Duopoly with Combination of Royalty and Fixed Fee

Abstract

We consider a choice of options for an innovating firm to enter the market with or without licensing its new cost-reducing technology to an incumbent firm using a combination of royalty and fixed license fee, or to license its technology without entry. When the innovating firm licenses its technology to the incumbent firm without entry, the optimal royalty rate for the innovating firm is zero. When the innovating firm enters the market with a license, its optimal royalty rate is positive. In that case if cost functions are concave, the optimal royalty rate is one such that the incumbent firm drops out of the market with negative fixed fee, and license without entry strategy and entry with license strategy are optimal; if cost functions are strictly convex, there is an internal solution of positive optimal royalty rate with positive or negative fixed fee and entry with license strategy is optimal.

1 Introduction

We consider a choice of options for an innovating firm to enter the market with or without licensing its new cost-reducing technology to the incumbent firm using a combination of a royalty per output and a fixed license fee, or to license its technology without entry also using a combination of a royalty per output and a fixed license fee.

In Proposition 4 of Kamien and Tauman (1986), assuming linear demand and cost functions and fixed license fee, it was argued that in an oligopoly when the number of firms is small (or large), entry with license strategy by the innovating firm, which is a strategy to enter the market and at the same time license its cost-reducing technology to an incumbent firm, is more profitable than license without entry strategy, which is a strategy to license its technology to an incumbent firm without entering the market. We think that their definition of license fee in the case where the innovating firm licenses its technology to an incumbent firm and does not enter the market is not appropriate. Interpreting their analysis in a duopoly model, they defined the license fee by the difference between the profit of an incumbent firm in that case and its monopoly profit before entry and license by the innovating firm. However, we can think that if the negotiation between the innovating firm and an incumbent firm about the license fee breaks down, the innovating firm can enter the market without license to an incumbent firm. If the innovating firm does not enter the market nor license, its profit is zero. But, if it enters the market, its profit is positive. Therefore, such a threat is credible, and hence an incumbent firm must pay the difference between its profit in the license without entry case and its profit in the entry without license case as a license fee.

In Hattori and Tanaka (2018), using an alternative definition of a license fee taking the above point into account, the following results about duopoly with a linear demand function and only a fixed license fee have been shown.

• 1. Linear cost functions (constant marginal costs):

  If the incumbent firm does not drop out when the innovating firm enters the market without license, license without entry strategy is optimal for the innovating firm. This result is converse to that in Kamien and Tauman (1986). If the incumbent firm drops out when the innovating firm enters the market without license, both license without entry strategy and entry without license strategy are optimal.¹

• 2. Quadratic cost functions:

  If the magnitude of the innovation is large (cost of the new technology is sufficiently low), license without entry strategy is optimal for the innovating firm, and if the magnitude of the innovation is small, entry with license strategy is optimal.

In this paper we consider a more general situation of duopoly with an innovating firm and an incumbent firm, in which the innovating firm imposes a combination of a royalty per output and a fixed license fee to the incumbent firm. We analyse a case of general demand and cost functions as well as a case of general demand and concave cost functions and a case of general demand and strictly convex cost functions. We will show the following results.

1.1 General Demand and Cost Functions Case

• 1. When the innovating firm licenses its technology to the incumbent firm without entry, the optimal royalty rate per output for the innovating firm is zero.

• 2. When the innovating firm enters the market and at the same time licenses its technology to the incumbent firm, there exists a positive optimal royalty rate per output.

• 3. Entry without license strategy is not optimal for the innovator. (Lemma 3)

1.2 General Demand and Concave Cost Functions Case

• 1. If the innovating firm enters the market and at the same time licenses its technology to the incumbent firm, and the cost functions of the firms are concave, the optimal royalty rate per output for the innovating firm is one such that the output of the incumbent firm is zero.

• 2. The fixed license fee is negative.

• 3. Boh license without entry strategy and entry with license strategy are optimal for the innovator. However, if the license fee is determined according to the rule in Kamien and Tauman (1986), only the entry with license strategy is optimal because the license fee when the innovator licenses its technology to the incumbent firm and does not enter the market according to their definition is smaller than that according to our definition.

1.3 General Demand and Strictly Convex Cost Functions Case

• 1. If the innovating firm enters the market and at the same time licenses its technology to the incumbent firm, and the cost functions of the firms are strictly convex, the optimal royalty rate per output for the innovating firm is positive but smaller than one such that the output of the incumbent firm is zero.

• 2. The equilibrium output of the innovating firm is larger than that of the incumbent firm.

• 3. Entry with license strategy is optimal for the innovator.

In this case the fixed license fee may be positive or negative. Please see an example in Section 5.

In the next section we review some related studies. In Section 3 we describe the model of this paper. In Section 4 we present the main results, and in Section 5 we study a case of linear demand and quadratic cost functions as an example of the strictly convex function case.

2 Literature Review

Various studies focus on technology adoption or R&D investment in duopoly or oligopoly. Most of them analyze the relation between the technology licensor and licensee. The difference of means of contracts, which comprise royalties, upfront fixed fees, combinations of these two, and auctions, are well discussed (Katz and Shapiro 1985). Kamien and Tauman (2002) showed that outside innovators prefer auctions, but industry incumbents prefer royalty. This topic is discussed by Kabiraj (2004) under the Stackelberg oligopoly in which the licensor does not have production capacity. Wang and Yang (2004) considered the case when the licensor has production capacity under the Stackelberg duopoly. Sen and Tauman (2007) compared the license system in detail, namely, when the licensor is an outsider and when it is an incumbent firm, using the combination of royalties and fixed fees. However, the existence of production capacity was externally given, and they did not analyze the choice of entry. Therefore, the optimal strategies of outside innovators, who can use the entry as a threat, require more discussion. Regarding the strategies of new entrants to the market, Duchene et al. (2015) focused on future entrants with old technology, and argued that a low license fee can be used to deter the entry of potential entrants. However, the firm with new technology is incumbent, and its choice of entry is not analyzed. Also, Chen (2016) analyzed the model of the endogenous market structure determined by the potential entrant with old technology and showed that the licensor uses the fixed fee and zero royalty in both the incumbent and the outside innovator cases, which are exogenously given. Creane et al. (2013) examined a firm that can license its production technology to a rival when firms are heterogeneous in production costs, and showed that a complete technology transfer from one firm to another always increases joint profit under weakly concave demand when at least three firms remain in the industry.

A Cournot oligopoly with fixed fee under cost asymmetry was analyzed by La Manna (1993). He showed that if technologies can be replicated perfectly, a lower cost firm always has an incentive to transfer its technology, and while a Cournot-Nash equilibrium cannot be fully asymmetric, there exists no non-cooperative Nash equilibrium in pure strategies. On the other hand, using cooperative game theory, Watanabe and Muto (2008) analyzed bargaining between a licensor with no production capacity and oligopolistic firms. Recent research focuses on market structure and technology improvement. Boone (2001) and Matsumura et al. (2013) found a non-monotonic relation between intensity of competition and innovation. Also, Pal (2010) showed that technology adoption may change the market outcome. The social welfare is larger in Bertrand competition than in Cournot competition. However, if we consider technology adoption, Cournot competition may result in higher social welfare than Bertrand competition under a differentiated goods market. Hattori and Tanaka (2015, 2016a) studied adoption of new technology in Cournot duopoly and Stackelberg duopoly. Rebolledo and Sandonís (2012) presented an analysis of the effectiveness of research and development (R&D) subsidies in an oligopolistic model in the cases of international competition and cooperation in R&D. Hattori and Tanaka (2016b) analyzed problems about product innovation, that is, introduction of higher quality good in a duopoly with vertical product differentiation. Recently, Sen and Stamatopoulos (2016) presented an analysis of royalty and fixed fee under duopoly with general demand and cost functions. They did not considered an option of the innovator whether it enter the market or not.

In this paper we will show that a combination of non-negative royalty and negative or positive fixed fee is optimal for the innovator under duopoly with options for the innovator to enter or not to enter the market with or without license. On the other hand, Liao and Sen (2005) showed that negative royalty can be optimal under oligopoly with one innovator and two incumbent firms. When the innovator is holding relatively insignificant new technology, licensing it to only one firm with negative royalty is optimal. This strategy leads licensee more aggressive and getting more profit which is paid to licensor as a fixed license fee. This negative royalty may result in more social welfare than that where negative royalty is prohibited.²

3 The Model

There are two firms Firms A and B. Firm A is an innovating firm and Firm B is an incumbent firm. Although at present only Firm B produces a good and Firm A is an outside innovator, after entering the market Firm A also produces the same good. It has a superior new technology and can produce the good at lower cost than Firm B.

Firm A have three options. The first option is to enter the market without license to Firm B, the second option is to license its superior technology to Firm B using a combination of a royalty per output and a fixed license fee, and the third option is to enter the market with license to Firm B also using a combination of a royalty per output and a fixed license fee. If Firm A enters, the market becomes a duopoly.

Let p be the price, x_A and x_B be the outputs of Firms A and B. The inverse demand function of the good is written as

$$p(x_{A}+x_{B}). $$

We assume Cournot type behavior of the firms. The cost function of Firm B before adoption of the new technology is c_B(x_B), and its cost function after adoption of the new technology is c_A(x_B). The cost function of Firm A is c_A(x_A). c_A(x_A) < c_B(x_B) and $c_{A}^{\prime }(x_{A})<c_{B}^{\prime }(x_{B})$ for x_A = x_B. We assume c_B(0) = 0 when Firm B drops out of the market. We analyze a case of general demand and cost functions, and also a case of general demand and concave cost functions and a case of general demand and strictly convex cost functions. Furthermore, as an example, we will consider a case of linear demand and quadratic cost functions.

The structure of the game is as follows.

• 1. In the first stage Firm A determines whether it enters the market or not, whether it sells a license to Firm B or not, (if it sells) the royalty rate and the fixed fee which can be accepted by Firm B.

• 2. In the second stage. Firm B determines whether it accepts the offer of the license or not.

• 3. In the third stage. Firms A and B determine their outputs, or, if Firm A does not enter the market, only Firm B determines its output.

We consider the sub-game perfect equilibrium of the game.

4 The Main Results

4.1 Entry Without License

Suppose that Firm A enters the market without license to Firm B. The inverse demand function in this case is written as p(x_A + x_B). The profits of Firms A and B are

$$\pi_{A}=p(x_{A}+x_{B})x_{A}-c_{A}(x_{A}), $$

and

$$\pi_{B}=p(x_{A}+x_{B})x_{B}-c_{B}(x_{B}). $$

The first order conditions for profit maximization of Firms A and B are

$$p+p^{\prime}x_{A}-c_{A}^{\prime}(x_{A})= 0, $$

and

$$p+p^{\prime}x_{B}-c_{B}^{\prime}(x_{B})= 0. $$

The second order conditions are

$$2p^{\prime}+p^{\prime\prime}x_{A}-c_{A}^{\prime\prime}(x_{A})<0, $$

and

$$2p^{\prime}+p^{\prime\prime}x_{B}-c_{B}^{\prime\prime}(x_{B})<0. $$

We assume that the second order conditions are satisfied in each case. Denote the equilibrium profit of Firm B in this case by ${\pi _{B}^{e}}$.

4.2 License Without Entry

Next suppose that Firm A licenses its technology to Firm B using a combination of a royalty per output and a fixed license fee, and does not enter the market. Denote the fixed license fee by L and the royalty rate per output by r. The inverse demand function is p(x_B). The profit of Firm B is

$$\pi_{B}=px_{B}-c_{A}(x_{B})-rx_{B}-L. $$

The first order condition for profit maximization of Firm B is

$$p+p^{\prime}x_{B}-c_{A}^{\prime}(x_{B})-r = 0. $$

The second order condition is

$$2p^{\prime}+p^{\prime\prime}x_{B}-c_{A}^{\prime\prime}(x_{B})<0. $$

From these conditions we obtain

$$\frac{dx_{B}}{dr}=\frac{1}{2p^{\prime}x_{B}+p^{\prime\prime}x_{B}-c_{A}^{\prime\prime}(x_{B})}<0. $$

If the negotiation between Firm A and Firm B about the license fee breaks down, Firm A can enter the market without license. When Firm A does not enter nor sell a license, its profit is zero; however, when it enters the market without license, its profit is positive. Therefore, such a threat is credible, and Firm B must pay the difference between its profit net of the royalty and its profit in the previous entry without license case as a fixed license fee. The total license fee is the sum of the royalty and the fixed license fee. L is determined so that $\pi _{B}={\pi _{B}^{e}}$ is satisfied. Thus, it is written as

$$L=px_{B}-c_{A}(x_{B})-rx_{B}-{\pi_{B}^{e}}. $$

Note that ${\pi _{B}^{e}}$ is a constant number. Denote the total license fee, which is L + rx_B, by TL. Then,

$$TL=px_{B}-c_{A}(x_{B})-{\pi_{B}^{e}}. $$

Firm A chooses r so as to maximize TL. The condition for maximization of TL with respect to r is

$$\frac{dTL}{dr}=(p+p^{\prime}x_{B}-c_{A}^{\prime}(x_{B}))\frac{dx_{B}}{dr}=r\frac{dx_{B}}{dr}= 0. $$

Since $\frac {dx_{B}}{dr}<0$, we get the optimal royalty rate per output, $\tilde {r}^{l}$, for the innovating firm as follows.

$$\tilde{r}^{l}= 0. $$

We have shown the following result.

Lemma 1

When the innovating firm licenses its technology to the incumbent firm without entry, the optimal royalty rate per output for the innovating firm is zero.

4.3 Entry with License

Suppose that Firm A enters the market and at the same time licenses its technology to Firm B using a combination of a royalty per output and a fixed license fee. The cost function of Firm B is c_A(⋅) in this case. Similarly to the previous case, we denote the fixed license fee by L and the royalty rate per output by r. The inverse demand function is p(x_A + x_B). The profits of Firms A and B are

$$\pi_{A}=px_{A}-c_{A}(x_{A}), $$

and

$$\pi_{B}=px_{B}-c_{A}(x_{B})-rx_{B}-L. $$

The first order conditions for profit maximization of Firms A and B are

$$ p+p^{\prime}x_{A}-c_{A}^{\prime}(x_{A})= 0, $$

(1)

and

$$ p+p^{\prime}x_{B}-c_{A}^{\prime}(x_{B})-r = 0. $$

(2)

The second order conditions are

$$2p^{\prime}+p^{\prime\prime}x_{A}-c_{A}^{\prime\prime}(x_{A})<0, $$

and

$$2p^{\prime}+p^{\prime\prime}x_{B}-c_{A}^{\prime\prime}(x_{B})<0. $$

Differentiating (1) and (2) with respect to r yields

$$(2p^{\prime}+p^{\prime\prime}x_{A}-c_{A}^{\prime\prime}(x_{A}))\frac{dx_{A}}{dr}+(p^{\prime}+p^{\prime\prime}x_{A})\frac{dx_{B}}{dr}= 0, $$

and

$$(p^{\prime}+p^{\prime\prime}x_{B})\frac{dx_{A}}{dr}+(2p^{\prime}+p^{\prime\prime}x_{B}-c_{B}^{\prime\prime}(x_{B}))\frac{dx_{B}}{dr}-1 = 0. $$

Solving them, we obtain

$$\frac{dx_{A}}{dr}=-\frac{1}{{\Delta}}(p^{\prime}+p^{\prime\prime}x_{A}), $$

and

$$\frac{dx_{B}}{dr}=\frac{1}{{\Delta}}(2p^{\prime}+p^{\prime\prime}x_{A}-c_{A}^{\prime\prime}(x_{A}))<0, $$

where

$${\Delta}=(2p^{\prime}+p^{\prime\prime}x_{A}-c_{A}^{\prime\prime}(x_{A}))(2p^{\prime}+p^{\prime\prime}x_{B}-c_{A}^{\prime\prime}(x_{B}))-(p^{\prime}+p^{\prime\prime}x_{A})(p^{\prime}+p^{\prime\prime}x_{B}). $$

We assume

$$ |2p^{\prime}+p^{\prime\prime}x_{A}-c_{A}^{\prime\prime}(x_{A})|>|p^{\prime}+p^{\prime\prime}x_{A}|, $$

(3)

and

$$ |2p^{\prime}+p^{\prime\prime}x_{B}-c_{A}^{\prime\prime}(x_{B})|>|p^{\prime}+p^{\prime\prime}x_{B}|. $$

(4)

They imply

$${\Delta}>0. $$

These assumptions are obtained from the stability conditions for the equilibrium of duopoly.³ Equations (3) and (4) mean that the slopes of the reaction curves of the firms are smaller than one. Then,

$$p^{\prime}-c_{A}^{\prime\prime}(x_{A})<0,\ p^{\prime}-c_{A}^{\prime\prime}(x_{B})<0. $$

Hence,

$$\frac{dx_{A}}{dr}+\frac{dx_{B}}{dr}=\frac{1}{{\Delta}}(p^{\prime}-c_{A}^{\prime\prime}(x_{A}))<0, $$

and

$$ \left|\frac{dx_{B}}{dr}\right|>\left|\frac{dx_{A}}{dr}\right|. $$

(5)

We have $\frac {dx_{A}}{dr}>0$ when p^′ + p^″x_A < 0 and $\frac {dx_{A}}{dr}<0$ when p^′ + p^″x_A > 0. In the former case the goods of the firms are strategic substitutes, and in the latter case they are strategic complements.

Similarly to the previous case, Firm B must pay the difference between its profit net of the royalty and its profit in the entry without license case as a fixed license fee. The fixed license fee should be equal to

$$L=px_{B}-c_{A}(x_{B})-rx_{B}-{\pi_{B}^{e}}. $$

The total license fee is

$$TL=px_{B}-c_{A}(x_{B})-{\pi_{B}^{e}}. $$

The total profit of Firm A is the sum of the total license fee and its profit as a firm in the duopoly. It is equal to

$$\pi_{A}+TL=px_{A}-c_{A}(x_{A})+px_{B}-c_{A}(x_{B})-{\pi_{B}^{e}}. $$

${\pi _{B}^{e}}$ is constant. Firm A chooses r so as to maximize π_A + TL. Differentiating π_A + TL with respect to r, using (1) and (2), yields

$$\begin{array}{@{}rcl@{}} \frac{d}{dr}(\pi_{A}+TL)&=&(p+p^{\prime}x_{A}-c_{A}^{\prime}(x_{A})+p^{\prime}x_{B})\frac{dx_{A}}{dr}\\ &&+(p+p^{\prime}x_{B}-c_{A}^{\prime}(x_{B})+p^{\prime}x_{A})\frac{dx_{B}}{dr}=p^{\prime}x_{B}\frac{dx_{A}}{dr}+(r+p^{\prime}x_{A})\frac{dx_{B}}{dr}.\\ \end{array} $$

(6)

If there is an internal solution of r which satisfies (6) = 0, it is

$$\tilde{r}^{el}=-\frac{p^{\prime}}{\frac{dx_{B}}{dr}}\left( x_{A}\frac{dx_{B}}{dr}+x_{B}\frac{dx_{A}}{dr}\right). $$

We show that there exists a positive optimal royalty rate.

Lemma 2

When the innovating firm enters the market and at the same time licenses its technology to the incumbent firm, there exists a positive optimal royalty rate so long as the output of Firm B is positive.

Proof

Suppose r = 0. Then, (1) and (2) mean x_A = x_B. Even when r < 0, |x_B − x_A| is small so long as |r| is small. Then, from (5)

$$x_{A}\frac{dx_{B}}{dr}+x_{B}\frac{dx_{A}}{dr}<0. $$

Thus,

$$\frac{d}{dr}(\pi_{A}+TL)=p^{\prime}\left( x_{B}\frac{dx_{A}}{dr}+x_{A}\frac{dx_{B}}{dr}\right)>0. $$

Therefore, there exists a positive optimal royalty rate. □

Next we show the following result.

Lemma 3

Entry with license strategy is more preferable than entry without license strategy for Firm A.

Proof

Denote the outputs of Firms A and B and the profit of Firm A in the entry without license case by ${x_{A}^{e}}$, ${x_{B}^{e}}$ and ${\pi _{A}^{e}}$. Let r be the royalty per output in the entry with license case. If we determine the value of r so that $r=c_{B}^{\prime }({x_{B}^{e}})-c_{A}^{\prime }({x_{B}^{e}})$ holds, then the first order conditions for Firms A and B in the entry with license case are as follows.

$$p+p^{\prime}x_{A}-c_{A}^{\prime}(x_{A})= 0, $$

and

$$p+p^{\prime}x_{B}-c_{A}^{\prime}(x_{B})-r=p+p^{\prime}x_{B}-c_{B}^{\prime}({x_{B}^{e}})= 0. $$

They are the same as the first order conditions in the entry without license case. Thus, the outputs of both firms in the entry with license case are equal to those in the entry without license case, that is, $x_{A}={x_{A}^{e}}$ and $x_{B}={x_{B}^{e}}$. Also the profit of Firm A in the entry with license case is equal to that in the entry without license case. The fixed license fee is

$$L=p{x_{B}^{e}}-c_{A}({x_{B}^{e}})-r{x_{B}^{e}}-{\pi_{B}^{e}}=c_{B}({x_{B}^{e}})-c_{A}({x_{B}^{e}})-r{x_{B}^{e}}. $$

Then, the total payoff of Firm A in the entry with license case is

$${\pi_{A}^{e}}+r{x_{B}^{e}}+c_{B}({x_{B}^{e}})-c_{A}({x_{B}^{e}})-r{x_{B}^{e}}={\pi_{A}^{e}}+c_{B}({x_{B}^{e}})-c_{A}({x_{B}^{e}}). $$

Since $c_{B}({x_{B}^{e}})>c_{A}({x_{B}^{e}})$, this is larger than ${\pi _{A}^{e}}$, and entry with license strategy is more preferable than entry without license strategy for Firm A. □

Now we consider two specific cases.

4.4 Concave Cost Functions Case

Assume that the cost functions of Firms A and B before adoption of the new technology are c_A(x_A) and c_B(x_B) such that c_A(x_A) < c_B(x_B) for x_A = x_B, $c^{\prime \prime }_{A}(\cdot )\leq 0$ and $c^{\prime \prime }_{B}(\cdot )\leq 0$, or $c^{\prime }_{A}(x)\leq c^{\prime }_{A}(y)$ and $c^{\prime }_{B}(x)\leq c^{\prime }_{B}(y)$ for x > y. The cost function of Firm B after adoption of the new technology is c_A(x_B). From (1) and (2)

$$p+p^{\prime}x_{A}-c^{\prime}_{A}(x_{A})= 0,\ p+p^{\prime}x_{B}-c^{\prime}_{A}(x_{B})-r = 0. $$

Suppose x_B = 0. Then,

$$r=p-c^{\prime}_{A}(0). $$

Denote this value of r by $\bar {\bar {r}}$. It is a value of the royalty rate such that the output of Firm B is just zero, that is, it drops out of the market. We call such a royalty rate per output prohibitive. Also, by (1), we have

$$\bar{\bar{r}}+p^{\prime}x_{A}=c_{A}^{\prime}(x_{A})-c^{\prime}_{A}(0)\leq 0. $$

Substituting this and x_B = 0 into (6) yields

$$\frac{d}{dr}(\pi_{A}+TL)=(c_{A}^{\prime}(x_{A})-c^{\prime}_{A}(0))\frac{dx_{B}}{dr}\geq 0. $$

However, it is nonsense to impose a royalty larger than $\bar {\bar {r}}$ because x_B = 0 and $\frac {dx_{B}}{dr}<0$. Therefore, the optimal royalty rate per output is $\bar {\bar {r}}$. In this case $\tilde {r}^{el}=-p^{\prime }x_{A}$. Comparing $\bar {\bar {r}}$ and $\tilde {r}^{el}$,

$$\bar{\bar{r}}-\tilde{r}^{el}=c_{A}^{\prime}(x_{A})-c^{\prime}_{A}(0)\leq 0. $$

However, $\tilde {r}^{el}$ is optimal only when x_B > 0.⁴

The fixed license fee in this case is negative as the following inequality shows

$$L=px_{B}-c_{A}(x_{B})-rx_{B}-{\pi_{B}^{e}}=-c_{A}(0)-{\pi_{B}^{e}}<0. $$

It compensates the profit of Firm B in the case of entry without license.

With Lemma 2 we have shown the following result.

Theorem 1

• 1. If the innovating firm enters the market and at the same time licenses its technology to the incumbent firm, and the cost functions of the firms are concave, the optimal royalty rate per output for the innovating firm is one such that the output of the incumbent firm is zero, that is, the royalty rate per output is prohibitive.

• 2. The fixed license fee in this case is negative.

4.5 Strictly Convex Cost Functions Case

Assume that the cost functions of Firms A and B before adoption of the new technology are c_A(x_A) and c_B(x_B) such that c_A(x_A) < c_B(x_B) for x_A = x_B, $c^{\prime \prime }_{A}(\cdot )>0$ and $c^{\prime \prime }_{B}(\cdot )>0$, or $c^{\prime }_{A}(x)>c^{\prime }_{A}(y)$ and $c^{\prime }_{B}(x)>c^{\prime }_{B}(y)$ for x > y. The cost function of Firm B after adoption of the new technology is c_A(x_B). Remind the first order conditions for the firms.

$$ p+p^{\prime}x_{A}-c_{A}^{\prime}(x_{A})= 0, $$

(7)

and

$$ p+p^{\prime}x_{B}-c_{A}^{\prime}(x_{B})-r = 0. $$

(8)

Suppose x_B = 0. Then,

$$r=p-c^{\prime}_{A}(0)=\bar{\bar{r}}, $$

and

$$\bar{\bar{r}}+p^{\prime}x_{A}=c_{A}^{\prime}(x_{A})-c^{\prime}_{A}(0)>0. $$

Substituting this and x_B = 0 into (6) yields

$$\frac{d}{dr}(\pi_{A}+TL)=(c_{A}^{\prime}(x_{A})-c^{\prime}_{A}(0))\frac{dx_{B}}{dr}<0. $$

Therefore, there is an internal solution of the optimal royalty rate, $\tilde {r}^{el}$, and it is smaller than $\bar {\bar {r}}$. From (1) and (2), x_A is larger than x_B.

With Lemma 2 we have shown the following result.

Theorem 2

• 1. If the innovating firm enters the market and at the same time licenses its technology to the incumbent firm, and the cost functions of the firms are strictly convex, the optimal royalty rate per output for the innovating firm is positive and smaller than one such that the output of the incumbent firm is zero.

• 2. The equilibrium output of Firm A is larger than that of Firm B.

The fixed license fee in this case may be positive or negative. Please see an example in the next section.

4.6 The Optimal Strategy for the Innovator

In this subsection we consider the optimal strategy for the innovating firm. The results depend on the form of cost functions.

4.7 Concave Cost Functions Case

When the cost functions of the firms are concave, entry with license strategy and license without entry strategy are equivalent. In both cases the monopolistic situation is realized. In the license without entry case the monopolist is Firm B, and in the case of entry with license it is Firm A. From Lemma 3 license without entry strategy and entry with license strategy are optimal.

The monopoly profit including royalty revenue is maximized at zero royalty rate. Thus, the optimal royalty rate in the case of license without entry is zero. On the other hand, in the case of entry with license the market is duopolistic with positive royalty rate. When the cost functions are concave, the monopolistic situation is optimal for the innovating firm. Therefore, the innovating firm gets larger profit by driving out the incumbent firm from the market with prohibitive royalty rate. Then, we need negative fixed fee to compensate the profit of the incumbent firm that it can get in the case of entry without license.

4.8 Strictly Convex Cost Functions Case

In the case where Firm A enters the market with license, setting the value of r as one such that the output of Firm B is zero, the monopolistic situation which is the same as that in the case of license without entry can be realized. On the other hand, the optimal royalty rate per output is different from such a value. Therefore, entry with license strategy is optimal.

Summarizing the results in the following theorem;

Theorem 3

• 1. When the cost functions of the firms are concave, license without entry strategy and entry with license strategy are optimal for the innovating firm.

• 2. When the cost functions of the firms are strictly convex, entry with license strategy is optimal for the innovating firm.

In the case of entry with license the market is duopolistic, and when the cost functions of the firms are strictly convex, the payoff of the innovating firm in duopolistic situation is larger than that in monopolistic situation because partition of production between two firms is more efficient than concentration of production to one firm under strictly convex cost functions. There is a positive internal solution of the optimal royalty rate which is not prohibitive.

5 An Example of Linear Demand and Quadratic Cost Functions Case

The cost functions of Firms A and B before adoption of the new technology are $c_{A}{x_{A}^{2}}$ and $c_{B}{x_{B}^{2}}$ with 0 < c_A < c_B. The cost function of Firm B after adoption of the new technology is $c_{A}{x_{B}^{2}}$.

5.1 Entry Without License

Suppose that Firm A enters the market without license to Firm B. The inverse demand function is assumed to be

$$p=a-x_{A}-x_{B}. $$

The profits of Firms A and B are

$$\pi_{A}=(a-x_{A}-x_{B})x_{A}-c_{A}{x_{A}^{2}},\ \pi_{B}=(a-x_{A}-x_{B})x_{B}-c_{B}{x_{B}^{2}}. $$

The conditions for profit maximization of Firms A and B are

$$a-2x_{A}-x_{B}-2c_{A}x_{A}= 0,\ a-x_{A}-2x_{B}-2c_{B}x_{B}= 0. $$

The equilibrium outputs, price and profits are

$$x_{A}=\frac{a(2c_{B}+ 1)}{4c_{A}c_{B}+ 4c_{B}+ 4c_{A}+ 3},\ x_{B}=\frac{a(2c_{A}+ 1)}{4c_{A}c_{B}+ 4c_{B}+ 4c_{A}+ 3}, $$

$$p=\frac{a(2c_{A}+ 1)(2c_{B}+ 1)}{4c_{A}c_{B}+ 4c_{B}+ 4c_{A}+ 3}, $$

$$\pi_{A}=\frac{a^{2}(c_{A}+ 1)(2c_{B}+ 1)^{2}}{(4c_{A}c_{B}+ 4c_{B}+ 4c_{A}+ 3)^{2}},\ \pi_{B}=\frac{a^{2}(2c_{A}+ 1)^{2}(c_{B}+ 1)}{(4c_{A}c_{B}+ 4c_{B}+ 4c_{A}+ 3)^{2}}. $$

Denote π_A and π_B in this case by ${\pi _{A}^{e}}$ and ${\pi _{B}^{e}}$.

5.2 License Without Entry

Next suppose that Firm A licenses its technology to Firm B using a combination of a royalty per output and a fixed license fee, and does not enter the market. The inverse demand function is

$$p=a-x_{B}. $$

The profit of Firm B is

$$\pi_{B}=(a-x_{B})x_{B}-c_{A}{x_{B}^{2}}-rx_{B}-L. $$

The equilibrium output, price and profit are

$$x_{B}=\frac{a-r}{2(c_{A}+ 1)},\ p=\frac{a+r + 2ac_{A}}{2(c_{A}+ 1)},\ \pi_{B}=\frac{(a-r)^{2}}{4(c_{A}+ 1)}-L. $$

Firm B must pay the difference between its profit net of the royalty and its profit in the previous entry without license case as a fixed license fee. The fixed license fee, L, is determined so that $\pi _{B}={\pi _{B}^{e}}$ is satisfied. Thus,

$$L=\frac{(a-r)^{2}}{4(c_{A}+ 1)}-\frac{a^{2}(2c_{A}+ 1)^{2}(c_{B}+ 1)}{(4c_{A}c_{B}+ 4c_{B}+ 4c_{A}+ 3)^{2}}=\frac{A}{4(c_{A}+ 1)(4c_{A}c_{B}+ 4c_{B}+ 4c_{A}+ 3)^{2}}, $$

where

$$\begin{array}{@{}rcl@{}} A&=&16{c_{A}^{2}}{c_{B}^{2}}r^{2}+ 32c_{A}{c_{B}^{2}}r^{2}+ 16{c_{B}^{2}}r^{2}+ 32{c_{A}^{2}}c_{B}r^{2}+ 56c_{A}c_{B}r^{2}\,+\,24c_{B}r^{2}\,+\,16{c_{A}^{2}}r^{2}+ 24c_{A}r^{2}\\ &&+\,9r^{2}-32a{c_{A}^{2}}{c_{B}^{2}}r-64ac_{A}{c_{B}^{2}}r-32a{c_{B}^{2}}r\,-\,64a{c_{A}^{2}}c_{B}r\,-\,112ac_{A}c_{B}r\,-\,48ac_{B}r\,-\,32a{c_{A}^{2}}r\\ &&-\,48ac_{A}r\,-\,18ar+ 16a^{2}{c_{A}^{2}}{c_{B}^{2}}\,+\,32a^{2}c_{A}{c_{B}^{2}}+ 16a^{2}{c_{B}^{2}}\,-\,16a^{2}{c_{A}^{3}}c_{B}+ 36a^{2}c_{A}c_{B}\,+\,20a^{2}c_{B}\\ &&-\,16a^{2}{c_{A}^{3}}-16a^{2}{c_{A}^{2}}+ 4a^{2}c_{A}+ 5a^{2}. \end{array} $$

Denote the total license fee by TL^l. Then,

$$TL^{l}=L+rx_{B}=\frac{B}{4(c_{A}+ 1)(4c_{A}c_{B}+ 4c_{B}+ 4c_{A}+ 3)^{2})}, $$

where

$$\begin{array}{@{}rcl@{}} B&=&16a^{2}{c_{A}^{2}}{c_{B}^{2}}+ 32a^{2}c_{A}{c_{B}^{2}}+ 16a^{2}{c_{B}^{2}}-16a^{2}{c_{A}^{3}}c_{B}+ 36a^{2}c_{A}c_{B}+ 20a^{2}c_{B}-16a^{2}{c_{A}^{3}}\\ &&-\,16a^{2}{c_{A}^{2}}+ 4a^{2}c_{A}+ 5a^{2}\,-\,16{c_{A}^{2}}{c_{B}^{2}}r^{2}\,-\,32c_{A}{c_{B}^{2}}r^{2}\,-\,16{c_{B}^{2}}r^{2}\,-\,32{c_{A}^{2}}c_{B}r^{2}\,-\,56c_{A}c_{B}r^{2}\\ &&-\,24c_{B}r^{2}-16{c_{A}^{2}}r^{2}-24c_{A}r^{2}-9r^{2}, \end{array} $$

Maximizing TL^l with respect to r, the optimal royalty rate is obtained as follows.

$$\tilde{r}^{l}= 0. $$

The fixed fee and the total license fee are equal to

$$L=\!TL^{l}=\frac{a^{2}(16{c_{A}^{2}}{c_{B}^{2}}\,+\,32c_{A}{c_{B}^{2}}\,+\,16{c_{B}^{2}}\,-\,16{c_{A}^{3}}c_{B}\,+\,36c_{A}c_{B}\,+\,20c_{B}\,-\,16{c_{A}^{3}}\,-\,16{c_{A}^{2}}\,+\,4c_{A}\,+\,5)}{4(c_{A}+ 1)(4c_{A}c_{B}+ 4c_{B}+ 4c_{A}+ 3)^{2}}. $$

5.3 Entry with License

Suppose that Firm A enters the market and at the same time licenses its technology to Firm B using a combination of a royalty per output and a fixed license fee. The inverse demand function is

$$p=a-x_{A}-x_{B}. $$

The profits of Firms A and B are

$$\pi_{A}=(a-x_{A}-x_{B})x_{A}-c_{A}{x_{A}^{2}},\ \pi_{B}=(a-x_{A}-x_{B})x_{B}-c_{A}{x_{B}^{2}}-rx_{B}-L. $$

The conditions for profit maximization of Firms A and B are

$$a-2x_{A}-x_{B}-2c_{A}x_{A}= 0,\ a-x_{A}-2x_{B}-2c_{A}x_{B}-r = 0. $$

The equilibrium outputs, price and profits are

$$x_{A}=\frac{a+r + 2ac_{A}}{(2c_{A}+ 1)(2c_{A}+ 3)},\ x_{B}=\frac{a-2c_{A}r-2r + 2ac_{A}}{(2c_{A}+ 1)(2c_{A}+ 3)},\ p=\frac{a+r + 2ac_{A}}{2c_{A}+ 3}, $$

$$\pi_{A}=\frac{(c_{A}+ 1)(r + 2ac_{A}+a)^{2}}{(2c_{A}+ 1)^{2}(2c_{A}+ 3)^{2}},\ \pi_{B}=\frac{(c_{A}+ 1)(2c_{A}r + 2r-2ac_{A}-a)^{2}}{(2c_{A}+ 1)^{2}(2c_{A}+ 3)^{2}}-L. $$

Also in this case Firm B must pay the difference between its profit net of the royalty and its profit in the entry without license case as a fixed license fee. The fixed license fee should be equal to

$$\begin{array}{@{}rcl@{}} L&=&\frac{(c_{A}+ 1)(2c_{A}r + 2r-2ac_{A}-a)^{2}}{(2c_{A}+ 1)^{2}(2c_{A}+ 3)^{2}}-\frac{a^{2}(2c_{A}+ 1)^{2}(c_{B}+ 1)}{(4c_{A}c_{B}+ 4c_{B}+ 4c_{A}+ 3)^{2}}\\ &=&\frac{C}{(2c_{A}+ 1)^{2}(2c_{A}+ 3)^{2}(4c_{A}c_{B}+ 4c_{B}+ 4c_{A}+ 3)^{2}}. \end{array} $$

The total license fee is

$$TL=L+rx_{B}=\frac{D}{(2c_{A}+ 1)^{2}(2c_{A}+ 3)^{2}(4c_{A}c_{B}+ 4c_{B}+ 4c_{A}+ 3)^{2}}. $$

The total profit of Firm A is equal to

$$\pi_{A}+TL=\frac{E}{(2c_{A}+ 1)^{2}(2c_{A}+ 3)^{2}(4c_{A}c_{B}+ 4c_{B}+ 4c_{A}+ 3)^{2}}. $$

About details of C, D and E please see Appendix. Firm A chooses r so as to maximize π_A + TL. We get the optimal royalty rate as follows.

$$\tilde{r}^{el}=\frac{4a{c_{A}^{2}}+ 4ac_{A}+a}{8{c_{A}^{3}}+ 24{c_{A}^{2}}+ 18c_{A}+ 2}>0. $$

With this royalty rate the outputs of Firms A and B are

$$x_{A}=\frac{a\left( 4{c_{A}^{2}}+ 6c_{A}+ 1\right)}{2(c_{A}+ 1)\left( 4{c_{A}^{2}}+ 8c_{A}+ 1\right)}>0, $$

$$x_{B}=\frac{2ac_{A}}{4{c_{A}^{2}}+ 8c_{A}+ 1}>0. $$

x_B is positive and smaller than x_A because

$$x_{A}-x_{B}=\frac{a(2c_{A}+ 1)}{2(c_{A}+ 1)\left( 4{c_{A}^{2}}+ 8c_{A}+ 1\right)}>0. $$

The price of the good is

$$p=\frac{a(2c_{A}+ 1)\left( 4{c_{A}^{2}}+ 6c_{A}+ 1\right)}{2(c_{A}+ 1)\left( 4{c_{A}^{2}}+ 8c_{A}+ 1\right)}. $$

Comparing p with $\tilde {r}^{el}$ yields

$$p-\tilde{r}^{el}=\frac{2ac_{A}(2c_{A}+ 1)}{4{c_{A}^{2}}+ 8c_{A}+ 1}>0. $$

Thus, $0<\tilde {r}^{el}<p$.

The fixed license fee and the total profit of Firm A are

$$L=\frac{a^{2}F}{\left( 4{c_{A}^{2}}+ 8c_{A}+ 1\right)^{2}(4c_{A}c_{B}+ 4c_{B}+ 4c_{A}+ 3)^{2}}, $$

and

$$\pi_{A}+TL=\frac{a^{2}G}{4(c_{A}+ 1)(4{c_{A}^{2}}+ 8c_{A}+ 1)(4c_{A}c_{B}+ 4c_{B}+ 4c_{A}+ 3)^{2}}, $$

where

$$\begin{array}{@{}rcl@{}} F&=&64{c_{A}^{5}}{c_{B}^{2}}+ 192{c_{A}^{4}}{c_{B}^{2}}+ 192{c_{A}^{3}}{c_{B}^{2}}+ 64{c_{A}^{2}}{c_{B}^{2}}-64{c_{A}^{6}}c_{B}-192{c_{A}^{5}}c_{B}-208{c_{A}^{4}}c_{B}\\ &&-\,96{c_{A}^{3}}c_{B}\,-\,44{c_{A}^{2}}c_{B}\,-\,20c_{A}c_{B}\,-\,c_{B}\,-\,64{c_{A}^{6}}\,-\,256{c_{A}^{5}}\,-\,400{c_{A}^{4}}\,-\,284{c_{A}^{3}}\,-\,104{c_{A}^{2}}\,-\,20c_{A}\!-1, \end{array} $$

and

$$\begin{array}{@{}rcl@{}} G&=&128{c_{A}^{4}}{c_{B}^{2}}+ 384{c_{A}^{3}}{c_{B}^{2}}+ 400{c_{A}^{2}}{c_{B}^{2}}+ 160c_{A}{c_{B}^{2}}+ 16{c_{B}^{2}}-64{c_{A}^{5}}c_{B}+ 352{c_{A}^{3}}c_{B}\\ &&+\,464{c_{A}^{2}}c_{B}+ 196c_{A}c_{B}+ 20c_{B}-64{c_{A}^{5}}-128{c_{A}^{4}}-32{c_{A}^{3}}+ 72{c_{A}^{2}}+ 44c_{A}+ 5. \end{array} $$

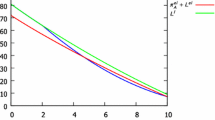
The fixed license fee, L, in this case may be negative. Assume c_B = 10, and denote c_A = tc_B, 0 < t < 1. Then, we obtain the relation between t and L as depicted in Fig. 1.

Fig. 1

Relation between t and L

L is negative when $0<t<\frac {96475}{33554432}\approx 0.00586$ or $1>t>\frac {30113483}{33554432}\approx 0.89745$. Thus, when the magnitude of the innovation is small or is very large, the fixed license fee is negative.

Denote the profit of Firm A in the market and the total license fee in this case by $\pi _{A}^{el}$ and TL^el.

5.4 The Optimal Strategy for the Innovator

Let us compare $\pi _{A}^{el}+TL^{el}$ and TL^l;

$$\left( \pi_{A}^{el}+TL^{el}\right)-TL^{l}=\frac{a^{2}{c_{A}^{2}}}{(c_{A}+ 1)\left( 4{c_{A}^{2}}+ 8c_{A}+ 1\right)}>0. $$

Compare TL^l and ${\pi _{A}^{e}}$;

$$TL^{l}-{\pi_{A}^{e}}=\frac{a^{2}H}{4(c_{A}+ 1)\left( 4{c_{A}^{2}}+ 8c_{A}+ 1\right)(4c_{A}c_{B}+ 4c_{B}+ 4c_{A}+ 3)^{2}}>0, $$

where

$$\begin{array}{@{}rcl@{}} H&=&64{c_{A}^{4}}{c_{B}^{2}}+ 128{c_{A}^{3}}{c_{B}^{2}}+ 64{c_{A}^{2}}{c_{B}^{2}}-64{c_{A}^{5}}c_{B}-64{c_{A}^{4}}c_{B}+ 96{c_{A}^{3}}c_{B}+ 128{c_{A}^{2}}c_{B}\\ &&+\,36c_{A}c_{B}+ 4c_{B}-64{c_{A}^{5}}-144{c_{A}^{4}}-96{c_{A}^{3}}-12{c_{A}^{2}}+ 4c_{A}+ 1\\ &=&64{c_{A}^{4}}c_{B}(c_{B}-c_{A})+ 64{c_{A}^{3}}\left( 2{c_{B}^{2}}-c_{A}c_{B}-{c_{A}^{2}}\right)+ 16{c_{A}^{2}}\left( 4{c_{B}^{2}}+ 6c_{A}c_{B}-9{c_{A}^{2}}\right)\\ &&+\,32{c_{A}^{2}}(4c_{B}-3c_{A})+ 12c_{A}(3c_{B}-c_{A})+ 4(c_{B}+c_{A})+ 1>0. \end{array} $$

Therefore, entry with license strategy is the optimal strategy for the innovating firm.

6 Conclusion

We summarize the results of this paper as follows.

6.1 Concave (Including Linear) Cost Function Case

In the license without entry case the optimal royalty rate is zero because in this case the incumbent firm is the monopolist. The fixed license fee is positive, and the net profit of the incumbent firm is equal to its profit when the innovator enters the market without license.

In the entry with license case the optimal royalty rate is positive, and it is one such that the output of the incumbent firm is zero. The fixed license fee should be negative to compensate the profit of the incumbent firm when the innovator enters the market without license. The net profit of the innovator in this case is equal to the fixed license fee in the license without entry case. Thus, both the entry with license strategy and the license without entry strategy are optimal for the innovator, and the market structure in this case is also monopoly. The negative fixed fee may seem to be unrealistic. Liao and Sen (2005) showed the possibility of negative royalty as the optimal strategy of the innovator which also seems to be unrealistic. We think negative fixed fee is also worth to be considered.

If the license fee is determined according to the rule in Kamien and Tauman (1986), only the entry with license strategy is optimal because the license fee when the innovator licenses its technology to the incumbent firm and does not enter the market according to their definition is smaller than that according to our definition.

In this case we need not consider an example.

6.2 Strictly Convex Cost Function Case

The license without entry case is the same as above.

In the entry with license case we can determine the royalty rate such that the output of the incumbent firm is zero, and then the net profit of the innovator is equal to the fixed license fee in the license without entry case. However, if the cost function is strictly convex, the optimal royalty rate is positive but smaller than the prohibitive level at which the output of the incumbent firm is zero. Therefore, only the entry with license strategy is the optimal strategy for the innovator, and the market structure in this case is duopoly.

The fixed licensee fee in this case may be positive or negative depending on the difference between the cost of the innovator and the cost of the incumbent firm. We consider an example in order to show this result. Therefore, the cost function in the example must be strictly convex, and then the optimal strategy is entry with license.

We obtain different conclusions in the concave cost function case and the strictly convex cost function case. It is the main contribution of this paper. These results are stated in Theorem 1, 2, 3. Thus, we must consider general nonlinear cost functions.

Appendix: Details of Calculation

$$\begin{array}{@{}rcl@{}} C&=&64{c_{A}^{5}}{c_{B}^{2}}r^{2}+ 320{c_{A}^{4}}{c_{B}^{2}}r^{2}+ 640{c_{A}^{3}}{c_{B}^{2}}r^{2}+ 640{c_{A}^{2}}{c_{B}^{2}}r^{2}+ 320c_{A}{c_{B}^{2}}r^{2}+ 64{c_{B}^{2}}r^{2}\\ &&+\,128{c_{A}^{5}}c_{B}r^{2}\,+\,608{c_{A}^{4}}c_{B}r^{2}\,+\,1152{c_{A}^{3}}c_{B}r^{2}\,+\,1088{c_{A}^{2}}c_{B}r^{2}\,+\,512c_{A}c_{B}r^{2}\,+\,96c_{B}r^{2}\,+\,64{c_{A}^{5}}r^{2}\\ &&+\,288{c_{A}^{4}}r^{2}+ 516{c_{A}^{3}}r^{2}+ 460{c_{A}^{2}}r^{2}+ 204c_{A}r^{2}+ 36r^{2}-128a{c_{A}^{5}}{c_{B}^{2}}r-576a{c_{A}^{4}}{c_{B}^{2}}r\\ &&-\,1024a{c_{A}^{3}}{c_{B}^{2}}r-896a{c_{A}^{2}}{c_{B}^{2}}r-384ac_{A}{c_{B}^{2}}r-64a{c_{B}^{2}}r-256a{c_{A}^{5}}c_{B}r-1088a{c_{A}^{4}}c_{B}r\\ &&-\,1824a{c_{A}^{3}}c_{B}r\!-1504a{c_{A}^{2}}c_{B}r\,-\,608ac_{A}c_{B}r-96ac_{B}r\,-\,128a{c_{A}^{5}}r-512a{c_{A}^{4}}r\,-\,808a{c_{A}^{3}}r\\ &&-\,628a{c_{A}^{2}}r-240ac_{A}r-36ar+ 64a^{2}{c_{A}^{5}}{c_{B}^{2}}+ 256a^{2}{c_{A}^{4}}{c_{B}^{2}}+ 400a^{2}{c_{A}^{3}}{c_{B}^{2}}+ 304a^{2}{c_{A}^{2}}{c_{B}^{2}}\\ &&+\,112a^{2}c_{A}{c_{B}^{2}}\,+\,16a^{2}{c_{B}^{2}}\,-\,64a^{2}{c_{A}^{6}}c_{B}\,-\,192a^{2}{c_{A}^{5}}c_{B}\,-\,144a^{2}{c_{A}^{4}}c_{B}\,+\,96a^{2}{c_{A}^{3}}c_{B}\,+\,188a^{2}{c_{A}^{2}}c_{B}\\ &&+\,92a^{2}c_{A}c_{B}\,+\,15a^{2}c_{B}-64a^{2}{c_{A}^{6}}\,-\,256a^{2}{c_{A}^{5}}-400a^{2}{c_{A}^{4}}\,-\,300a^{2}{c_{A}^{3}}-108a^{2}{c_{A}^{2}}\,-\,15a^{2}c_{A}, \end{array} $$

$$\begin{array}{@{}rcl@{}} D\!&=&96a^{2}{c_{A}^{3}}c_{B}+ 188a^{2}{c_{A}^{2}}c_{B}+ 92a^{2}c_{A}c_{B}+ 15a^{2}c_{B}-64a^{2}{c_{A}^{6}}-256a^{2}{c_{A}^{5}}-400a^{2}{c_{A}^{4}}\\ &&-\,300a^{2}{c_{A}^{3}}-108a^{2}{c_{A}^{2}}-15a^{2}c_{A}-64{c_{A}^{5}}{c_{B}^{2}}r^{2}-320{c_{A}^{4}}{c_{B}^{2}}r^{2}-608{c_{A}^{3}}{c_{B}^{2}}r^{2}\\ &&-\,544{c_{A}^{2}}{c_{B}^{2}}r^{2}-224c_{A}{c_{B}^{2}}r^{2}-32{c_{B}^{2}}r^{2}-128{c_{A}^{5}}c_{B}r^{2}-608{c_{A}^{4}}c_{B}r^{2}-1088{c_{A}^{3}}c_{B}r^{2}\\ &&-\,912{c_{A}^{2}}c_{B}r^{2}\,-\,352c_{A}c_{B}r^{2}\,-\,48c_{B}r^{2}\,-\,64{c_{A}^{5}}r^{2}\,-\,288{c_{A}^{4}}r^{2}\,-\,484{c_{A}^{3}}r^{2}\,-\,380{c_{A}^{2}}r^{2}\,-\,138c_{A}r^{2}\\ &&-\,18r^{2}-32a{c_{A}^{3}}{c_{B}^{2}}r-80a{c_{A}^{2}}{c_{B}^{2}}r-64ac_{A}{c_{B}^{2}}r-16a{c_{B}^{2}}r-64a{c_{A}^{3}}c_{B}r-144a{c_{A}^{2}}c_{B}r\\ &&-\,104ac_{A}c_{B}r-24ac_{B}r-32a{c_{A}^{3}}r\!-64a{c_{A}^{2}}r-42ac_{A}r\,-\,9ar+ 64a^{2}{c_{A}^{5}}{c_{B}^{2}}\,+\,256a^{2}{c_{A}^{4}}{c_{B}^{2}}\\ &&+\,400a^{2}{c_{A}^{3}}{c_{B}^{2}}+ 304a^{2}{c_{A}^{2}}{c_{B}^{2}}+ 112a^{2}c_{A}{c_{B}^{2}}+ 16a^{2}{c_{B}^{2}}-64a^{2}{c_{A}^{6}}c_{B}-192a^{2}{c_{A}^{5}}c_{B}\\ &&-\,144a^{2}{c_{A}^{4}}c_{B}, \end{array} $$

$$\begin{array}{@{}rcl@{}} E&\!=&336a^{2}{c_{A}^{4}}c_{B}+ 800a^{2}{c_{A}^{3}}c_{B}+ 692a^{2}{c_{A}^{2}}c_{B}+ 268a^{2}c_{A}c_{B}+ 39a^{2}c_{B}-64a^{2}{c_{A}^{6}}\\ &&-\,192a^{2}{c_{A}^{5}}\,-\,176a^{2}{c_{A}^{4}}\,+\,8a^{2}{c_{A}^{3}}\,+\,100a^{2}{c_{A}^{2}}\,+\,54a^{2}c_{A}\,+\,9a^{2}\!-64{c_{A}^{5}}{c_{B}^{2}}r^{2}-320{c_{A}^{4}}{c_{B}^{2}}r^{2}\\ &&-\,592{c_{A}^{3}}{c_{B}^{2}}r^{2}-496{c_{A}^{2}}{c_{B}^{2}}r^{2}-176c_{A}{c_{B}^{2}}r^{2}-16{c_{B}^{2}}r^{2}-128{c_{A}^{5}}c_{B}r^{2}-608{c_{A}^{4}}c_{B}r^{2}\\ &&-\,1056{c_{A}^{3}}c_{B}r^{2}\!-824{c_{A}^{2}}c_{B}r^{2}\,-\,272c_{A}c_{B}r^{2}-24c_{B}r^{2}\,-\,64{c_{A}^{5}}r^{2}\,-\,288{c_{A}^{4}}r^{2}\!-468{c_{A}^{3}}r^{2}\\ &&-\,340{c_{A}^{2}}r^{2}-105c_{A}r^{2}-9r^{2}+ 64a{c_{A}^{4}}{c_{B}^{2}}r + 192a{c_{A}^{3}}{c_{B}^{2}}r + 208a{c_{A}^{2}}{c_{B}^{2}}r\!+ 96ac_{A}{c_{B}^{2}}r\\ &&+\!\,16a{c_{B}^{2}}r\,+\,128a{c_{A}^{4}}c_{B}r\,+\,352a{c_{A}^{3}}c_{B}r\,+\,352a{c_{A}^{2}}c_{B}r\,+\,152ac_{A}c_{B}r+\!24ac_{B}r\,+\,64a{c_{A}^{4}}r\\ &&+\,160a{c_{A}^{3}}r + 148a{c_{A}^{2}}r + 60ac_{A}r + 9ar+ 128a^{2}{c_{A}^{5}}{c_{B}^{2}}+ 512a^{2}{c_{A}^{4}}{c_{B}^{2}}+ 800a^{2}{c_{A}^{3}}{c_{B}^{2}}\\ &&+\,608a^{2}{c_{A}^{2}}{c_{B}^{2}}+ 224a^{2}c_{A}{c_{B}^{2}}+ 32a^{2}{c_{B}^{2}}-64a^{2}{c_{A}^{6}}c_{B}-64a^{2}{c_{A}^{5}}c_{B}, \end{array} $$