Modeling resistive switching materials and devices across scales

Abstract

Resistance switching devices based on electrochemical processes have attractive significant attention in the field of nanoelectronics due to the possibility of switching in nanosecond timescales, miniaturization to tens of nanometer and multi-bit storage. Their deceptively simple structures (metal-insulator-metal stack) hide a set of complex, coupled, processes that govern their operation, from electrochemical reactions at interfaces, diffusion and aggregation of ionic species, to electron and hole trapping and Joule heating. A combination of experiments and modeling efforts are contributing to a fundamental understanding of these devices, and progress towards a predictive understanding of their operation is opening the possibility for the rational optimization. In this paper we review recent progress in modeling resistive switching devices at multiple scales; we briefly describe simulation tools appropriate at each scale and the key insight that has been derived from them. Starting with ab initio electronic structure simulations that provide an understanding of the mechanisms of operation of valence change devices pointing to the importance of the aggregation of oxygen vacancies in resistance switching and how dopants affect performance. At slightly larger scales we describe reactive molecular dynamics simulations of the operation of electrochemical metallization cells. Here the dynamical simulations provide an atomic picture of the mechanisms behind the electrochemical formation and stabilization of conductive metallic filaments that provide a low-resistance path for electronic conduction. Kinetic Monte Carlo simulations are one step higher in the multiscale ladder and enable larger scale simulations and longer times, enabling, for example, the study of variability in switching speed and resistance. Finally, we discuss physics-based simulations that accurately capture subtleties of device behavior and that can be incorporated in circuit simulations.

1 Introduction

Nanoscale devices that can undergo reversible resistance switching driven by electrochemical processes hold great promise as memory and logic elements in future nanoelectronics devices. They have the potential to contribute to the extension of Moore’s law beyond the rapidly approaching if not ongoing end of scaling and even enable neuromorphic computing [1,2,3]. Resistance- and threshold-switching cells are fascinating devices that can reversibly switch between low-resistance state (LRS) and a high-resistance state (HRS) via the application of an external electrochemical potential. Their simple structure, consisting of two metallic electrodes separated by a solid dielectric or electrolyte, seems at odds with the wide range of I-V characteristics that can be achieved by the appropriate choice of materials [4]: from linear to non-linear bipolar and nonpolar resistance switching to threshold switching [5] (an abrupt but reversible change in resistance), see Fig. 1. These devices can exhibit switching in nanosecond timescales [6] and scaling to approximately ten nanometers [7], where the distinction between material and device becomes meaningless. Ultra-fast switching, scalability to the few nanometer regime and compatibility with CMOS processing make resistance switching materials especially attractive for memory applications. These resistive random access memories (RRAM) store information using electrical resistance as the state variable as opposed to the charge stored in a capacitor currently used in SRAM, DRAM and Flash [8].

Fig. 1

Atomistic structure of pristine ECM (top left) and one in the low-resistance with a conductive filament. Bottom panels: various possible I-V characteristics of electrochemical cells

Excellent review papers and perspectives on the electrical characteristics, physics, chemistry and application of these devices have been published in recent years, see for example Refs. [8, 9]; this paper presents a review the state of the art in predictive modeling of electrochemical RRAM devices across scales. We cover recent progress in theoretical and simulation work, from electronic structure calculations that revealed the role of point defects in resistance switching in oxides, and reactive molecular dynamics capable of describing electrochemical reactions with atomistic resolution, to continuum modeling of the electronic characteristics of the entire devices. A brief description of the physics and operation of these devices is provided for completeness.

Resistive switching devices

The wide range of characteristics exhibited by this class of devices is an example of emergent phenomena originating from a set of underlying materials processes: electrochemical reactions at electrolyte/cathode and electrolyte/anode interfaces, electrochemical dissolution and deposition of metallic ions, transport and aggregation of ions and defects, injection, trapping and migration of electrons and holes, changes in composition, phase and valence change in the electrolytes, Joule heating and electromigration. How these underlying processes conspire to result in the rich set of behaviors observed remains not fully understood [9]. Due to the variety of dominant mechanisms these devices are loosely classified into electrochemical metallization cells [10] (ECM), valence change memory [11] (VCM), atomic switches and threshold switching materials [4].

VCM cells involve oxides such as HfO _x , TiO _x , TaO _x [12,13,14] separating electro-inactive metallic electrodes, their simplicity and materials widely used in the semiconductor industry make them particularly attractive. A pristine device is initially FORMED via the application of a voltage larger than the operating voltage to induce a soft breakdown of the oxide and a transition to the LRS, is called the forming step and is done normally at a voltage V _{F O R M} significantly higher than the device normal operating voltages. Once a device has been formed, it can be reversibly switched between the LRS state (ON) via the so-called SET process and switched back to the HRS (OFF) by a RESET process [13, 15,16,17]. The low resistance state has been associated with the formation of a conductive filament of oxygen vacancies that forms and dissolves driven by the injection and trapping of electrons from the electrodes [12].

ECM cells operate in a similar fashion, but involve a metallic filament. These devices consist of an electro-active electrode (typically Cu or Ag) separated by an electro-inactive one (often W, Pt or Au) by an oxide (SiO₂ or Al₂ O ₃) or electrolyte (chalcogenides GeS/GeSe or Ag₂S) [10]. The application of an external voltage of appropriate polarity results in the dissolution of the electro-active metal into the dielectric, the transport of ions towards the inactive electrode and their aggregation. This process eventually results in the formation of a conductive metallic filament that short-circuits the electrodes leading to a significant reduction in resistance. A compliance current limits the current in the ON state and its value governs the resistance of the ON state. Increasing compliance current leads to lower resistance (attributed to the formation of thicker filaments), enabling multilevel bit storage and neuromorphic computing.

While in some cases debate persists about the switching mechanisms, interfacial reactions, and the nature of the conducting paths, recent experiments and theoretical work are helping build a quantitative picture of the operating processes. Electrochemical tests like cyclic voltammetry have provided information about the redox reactions as well as the mobility and charge state of the ions [18, 19]. The mechanisms associated with filament growth have also been investigated intensively. Electrical measurements show that the resistance of the ON state is independent of device cross-sectional area, which is interpreted as indicating that a single filament dominates transport but the decrease in resistance with increasing compliance current could indicate multiple filaments under certain conditions [6]. Given the complexity of the processes involved in filament formation, imaging has played an important role and high-resolution transmission electron microscopy imaging and scanning tunneling microscopy have provided key insight into the formation of conductive filaments. [14, 20,21,22] Filaments at various stages of formation have been imaged, including under in situ conditions [23] providing important insight into the formation of the conductive filaments. Despite such progress, these experimental techniques are not without limitations and the interpretation of the results often require complex models; these limitations are particularly challenging when dealing with devices at their miniaturization limit (few nanometers) and operating at ultra-fast speeds (nanoseconds). Thus, physics based models at electronic, atomic and device scales are a key complement to experiments and are contributing to a complete understanding of these fascinating devices.

Predictive, multiscale modeling of materials

The descrip- tion of materials from first principles without empirical parameters became possible with the development of quantum mechanics in the first decades of the 1900s. Paul Dirac famously (and perhaps optimistically) stated in paper published in 1929: “The fundamental laws necessary for the mathematical treatment of a large part of physics and the whole of chemistry are thus completely known, and the difficulty lies only in the fact that application of these laws leads to equations that are too complex to be solved” [24]. Connecting the fundamental physics that describe the interactions between electrons and ions to materials properties and device characteristics has proved to be a gargantuan endeavor and required significant developments in theory and computation, from the development of efficient electronic structure methods, and potentials and algorithms for large-scale molecular dynamics (MD) simulations to finite elements. Bridging results across scales via multiscale modeling is the avenue of choice today to realize Dirac’s vision, see, for example. de Pablo and Curtin [25]. The field has attracted significant attention in the last few decades as compute power and advances in methods enabled quantitative predictions for realistic materials. Multiscale modeling often starts with a quantum mechanical description of electronic structure of the material of interest; methods like density functional theory (DFT) are generally applicable to any material of interest and provides results with the accuracy required for many (but not all) applications [26]. Unfortunately, the computational intensity of these methods preclude the simulation of large systems and long timescales and a hierarchy of methods are often used to connect ab initio predictions with materials and device performance. The first step in this multiscale ladder is often MD simulations with interatomic potentials developed from electronic structure calculations; here electrons are averaged out and the time evolution of the atoms in the material are solved using classical equations of motion. Multi-million atom MD simulations are common today and billion-simulations are possible [27]. However, even using the largest supercomputers MD is unable to achieve the length scales and, more often, the timescales required to describe many materials and device processes. Thus, information from ab initio and MD simulations are often passed to continuum models capable of connecting fundamental processes to the device world. Multiscale models have been developed to describe, among other processes, mechanical [28,29,30,31], electronic [32, 33], chemical [34] properties of materials. In this review paper we cover recent progress on modeling resistive switching materials at the various scales mentioned above and describe the insight, power and limitations of each approach. Our aim is not to provide a comprehensive review of all work in the field but to provide a perspective of the current state of the art and challenges.

Manuscript organization

We begin the paper with recent advances in DFT studies of VCM, Section 2. These calculations have provided key insight into the nature, formation and dissolution of the conductive filament and Section 3 discusses how doping can be used to engineer the response of these devices. Recent advances in reactive MD simulations enable the simulation of electrochemical processes with time and spatial scales that match those of RRAM devices at their scaling limit and operating at nanosecond timescales. Section 4 describes reactive MD simulations and Section 5 their application to ECM cells. Kinetic Monte Carlo simulations enable achieving length and timescales beyond those of MD while maintaining some description of atomic processes and their variability, these methods are discussed in Section 6. Since the early works, many models have been developed to explain the resistive switching properties and the dependence from operational parameters such as the external applied voltage or the maximum allowed current in the device, also called as compliance current, or I _C . Section 7 reviews a selection of the many physical models of resistive switching, including both analytical and numerical models and the observation of random telegraph noise in Section 8.

2 Density functional theory: methods

An important class of RRAM devices, valence change devices based on transition metal-oxide resistance-change random access memory, and hafnium oxide (HfO₂) in particular, have shown great potential for applications in next generation of nonvolatile memory and neuromorphic computing [35,36,37,38,39,40]. Along rapid developments on the experimental side, quantum mechanical based simulations [13, 15, 16, 41,42,43,44,45,46,47,48,49,50,51] have provided insight regarding the nature of the conductive channel, the formation energy of intrinsic defects and impurity ions, the drift and diffusion mobilities of ions in a defective matrix, the charge trapping effects near impurities and defects, and the electronic structure of doped oxides.

In this section we briefly introduce density functional theory, the theory underlying the calculation of electronic structure of these materials, and how it is applied to characterize the defects involved in VCM resistance switching. Section 3 then describes the application of the technique to understand the effect of doping on resistance switching.

2.1 Density functional theory: first principles simulations of valence change memory devices

In density functional theory [52], the electronic structure is often obtained by solving the Kohn-Sham equations [53]. They replace the full many body electron system with one of particles that interact with each other via a mean field approximation, and are subjected to an effective external potential; this mapping is, in principle, exact for the ground state density and energy. The Kohn-Sham equations are expressed as:

$$ \left( - \frac{\hbar^{2}}{2m_{e}}\nabla^{2} + V_{eff}(r)\right) {\Psi}_{i}(r) = \epsilon_{i} {\Psi}_{i}(r), \quad n(r) = \sum\limits_{i} |{\Psi}_{i}(r)|^{2}, $$

(1)

where V _{e f f} (r) is the effective potential that includes contributions from the external potential due to the nuclei, the electron-electron Coulomb potential and the exchange-correlation potential, Ψ _i is the wavefunction of electron i and 𝜖 _i is the energy of electron i.

The total energy of a system E[n] is expressed as a functional of the charge density n(r)

$$ E[n] = T_{s}[n] + \int dr V_{ext}(r)n(r)+E_{Hartree}[n]+E_{II}+E_{XC}[n], $$

(2)

where T _s is the Kohn-Sham kinetic energy of a system with density n(r) assuming there are no electron-electron interactions, V _{e x t} (r) is the external potential due to the nuclei and any other external fields, E _{H a r t r e e} is the Coulomb interaction energy of the interacting electron density n(r) known as the Hartree energy, E _{I I} is the interaction energy between nuclei, and E _{X C} is the exchange-correlation energy.

With this formalism, the ground state energy of a system E[n] and its corresponding electron density n(r) can be calculated if suitable approximations for the exchange-correlation energy E _{X C} [n] and the external potential V _{e x t} (r) can be found. Two early approximations for the exchange-correlation energy E _{X C} [n] were the local density approximation (LDA) and the generalized gradient approximation (GGA). Developed later, the L D A + U approach is based on LDA, but incorporates empirical on-site Coulomb corrections. The simplified, rotationally invariant equation for the L D A + U total energy is given by [54]:

$$\begin{array}{@{}rcl@{}} E_{LDA+U}&=&E_{LDA}+ \frac{U-J}{2}\sum\limits_{\sigma}\left( \sum\limits_{m_{1}} n^{\sigma}_{m_{1},m_{1}}\right.\\ && -\left.\sum\limits_{m_{1},m_{2}}{ \widehat{n}}^{\sigma}_{m_{1},m_{2}} \widehat{n}^{\sigma}_{m_{2},m_{1}}\right) \end{array} $$

(3)

Where E _{L D A} and E _{L D A + U} are the total energies calculated using LDA and L D A + U, U and J are the correction factors, m and σ are the magnetic and spin quantum numbers, and n is the on-site occupancy matrix. Using an optimal combination of orbital-specific correction factors U and J, it is possible to perform calculations with a computational demand typical for LDA or GGA, but reaching desired accuracies on predicting band gaps and electronic structures [43] comparable to hybrid functionals [55,56,57,58], which include exact exchange.

2.2 Relative formation energy function for dopant energetics in HfO₂

The defect types analyzed in this study are oxygen vacancies (V_O), cation substitutional dopants (D_Hf), and interstitial dopants (D_I). The formation reaction in Kröger-Vink notation for a neutral cation substitutional dopant D on the Hf site can be written as:

$$ n\text{Hf}_{Hf}^{x} + \mathrm{D}_{bulk}^{x} \Leftrightarrow (n-1)\text{Hf}_{Hf}^{x} + \mathrm{D}_{Hf}^{x}+ \text{Hf}_{bulk}^{x} $$

(4)

In order to facilitate comparison between different defect sites, in the following the equations are rewritten in terms of the chemical potential of oxygen, $\mu _{O}=\frac {1}{2}O_{2}(g)$:

For oxygen vacancy:

$$ \mathrm{V_{O}}: \, \mathrm{O}_{O}^{x} \Leftrightarrow \mathrm{V}_{O}^{x}+ \frac{1}{2}O_{2}(g) $$

(5)

For substitutional dopant D on the Hf site:

$$\begin{array}{@{}rcl@{}} \mathrm{D_{Hf}}: \, (n-1)\text{Hf}_{Hf}^{x} + 2(n - 1)\mathrm{O}_{O}^{x}+\mathrm{D}_{bulk}^{x}\\ + O_{2}(g) \Leftrightarrow (n-1)\text{Hf}_{Hf}^{x} + 2n\mathrm{O}_{O}^{x} +\mathrm{D}_{Hf}^{x} \end{array} $$

(6)

For interstitial dopant D:

$$ \mathrm{D_{I}}: \ \text{Hf}_{Hf}^{x} +2\mathrm{O}_{O}^{x}+ \mathrm{D}_{bulk}^{x} \Leftrightarrow \text{Hf}_{Hf}^{x}+2\mathrm{O}_{O}^{x} + \mathrm{D}_{i}^{x} $$

(7)

where n is the number of formula units in the supercell (e.g. one unit cell of m-HfO₂ contains four formula units). Thus, the corresponding defect formation energy equations are:

$$\begin{array}{@{}rcl@{}} &\mathrm{V_{O}}: \, \, E_{Form}(\mathrm{V_{O}}) = E(\mathrm{V_{O}}) - \left( E_{0} - \frac{1}{2}E(\mathrm{O}_{2})\right) \end{array} $$

(8)

$$\begin{array}{@{}rcl@{}} &\mathrm{D_{Hf}}: \, \, E_{Form}(\mathrm{D_{Hf}}) = E(\mathrm{D_{Hf}}) - \left( \left( \frac{n-1}{n}\right)E_{0} + E(\mathrm{D}) + E(\mathrm{O}_{2}) \right) \end{array} $$

(9)

$$\begin{array}{@{}rcl@{}} &\mathrm{D_{I}}: \, \, E_{Form}(\mathrm{D_{I}}) = E(\mathrm{D_{I}}) - \left( E_{0} +E(\mathrm{D})\right) \end{array} $$

(10)

Where E _{F o r m} (x) is the formation energy of defect x,E(V_O) and E(D_x) are the total energies of the defective HfO₂ supercells containing defects V_O and D_x, E ₀ is the total energy of the pristine supercell, and E(O₂) and E(D) are the chemical potentials of O₂ and defect D. For the chemical potential of O₂ we used half of the binding energy of an O₂ molecule −5.375 eV. The advantage of using the equations above for the E _{F o r m} is that the relative formation energy of a dopant at interstitial versus substitutional sites, E _r , is obtained effectively and the dopant chemical potential dependence is eliminated.

$$\begin{array}{@{}rcl@{}} E_{r}(\mathrm{D_{I},D_{Hf}}) &=& E_{Form}(\mathrm{D_{I}}) - E_{Form}(\mathrm{D_{Hf}})\\ &=& E(\mathrm{D_{I}}) - E(\mathrm{D_{Hf}}) + E(\mathrm{O_{2}}) - \frac{1}{n}E_{0} \end{array} $$

(11)

E _r (D_I,D_x) > 0 eV indicates dopant D favors the interstitial site I over the substitutional site x, and E _r (D_I,D_x) > 0 eV indicates the substitutional site is favored.

2.3 Computational setup

Spin-polarized density functional theory calculations using the Vienna ab initio Simulation Package (VASP) were carried out on monoclinic HfO₂ (m-HfO₂, space group P21/c) [59]. Projector augmented-wave pseudopotentials [60], periodic boundary conditions, and an energy cutoff of 367.38 eV were employed. K-point integration used 2x2x2 gamma-centered Monkhorst-Pack grids, and all ions were relaxed to an energy convergence of 10⁻³ eV/atom and forces less than 0.01 eV/ Å per ion. A unit cell of m-HfO₂ contains 12 atoms: 4 sevenfold-coordinated Hf, 4 threefold-coordinated (3C) O, and 4 fourfold-coordinated (4C) O atoms. We used up to 3x3x3 supercells containing 324 atoms in our calculations. The optimum combination of U parameters for monoclinic HfO₂ was found to be U d = 6.6 eV and U p = 9.5 eV [48, 49].

3 Role of doping on VCM switching

3.1 Conductive filaments and CVM general characteristics

RRAM devices exhibit nonvolatile resistive switching under an applied bias, they can reversibly switch between a high-resistance state (HRS) and a low-resistance state (LRS), representing the OFF and ON states. Switching in VCM devices is hypothesized to be due to the formation and rupture of a conductive filament through the oxide as depicted in Fig. 2. An RRAM device that has never been resistively switched is referred to as being in the pristine state. The first switching step, which induces a soft breakdown of the oxide and a transition to the LRS, is called the forming step and is done normally at a voltage V _{F O R M} significantly higher than the device normal operating voltages. Once a device has been formed, it can now be reversibly switched between the ON and OFF states through the act of switching from the HRS to the LRS referred to as the SET process, and switched back from LRS to HRS by a RESET process [13, 15,16,17].

Fig. 2

Schematics of VCM RRAM operation

According to the prevailing theory of VCM operation shown in Fig. 2, the soft breakdown of the oxide is due to the formation of a conductive filament of oxygen vacancies through the oxide. The formation of the conductive filament thus corresponds to a local reduction of the oxide (SET), while the rupture of the filament corresponds to reoxidation of the filamentary region (RESET) [13, 41]. The ratio between the resistance in the HRS and that in the LRS is referred to as the ON/OFF ratio, or alternatively as the switching window. Generally, it is advantageous for a device to have as large a switching window as possible. In contrast, ECM devices operate via the formation and dissolution of metallic filaments and ab initio simulations have been used to address some of the of its characteristics features [61].

Our discussion here is focused on the bulk properties altered by the dopants, for a complete picture interface effects should also be taken into account as recently depicted by O’Hara [62] for Hf/HfO₂ oxygen interface diffusion. Moreover, the equilibrium charge state of the dopants and vacancies will also affect the relative stability as has been shown that oxygen vacancy charge states dramatically alter during the SET and RESET operation [16, 46, 50, 51].

3.2 Substitutional vs interstitial stability of dopants in monoclinic HfO₂

For tuning device characteristics one possible option is to introduce preferable dopants either during deposition or by implantation. Doped RRAM devices have been shown to induce changes to the forming voltage, SET voltage, power dissipation, ON/OFF ratio, variability, retention, and endurance [44, 63,64,65,66,67,68,69,70,71,72,73]. Moreover, dopants reducing the oxygen vacancy (V_O) formation energy in their immediate vicinity were linked to a strong impact on device behavior [44, 64, 67, 73]. The preferred lattice site of dopant ions will be investigated in detail to shed light on the implications as substitutional dopants can contribute to V_O filament formation and enhance VCM-type switching, while interstitial dopants may form competing dopant conductive filaments, which are not useful for VCM but are useful for ECM cells (also called conductive bridge random access memory, CBRAM) [74,75,76]. The relative energy of dopants in substitional and interstitial (E r) based on Eq. 11 shows a strong dependence on the dopant ion and valence. The more isovalent a dopant ion is with the species it is replacing, the more stable the dopant will be on the substitutional site. And conversely, the more heterovalent ions tend to be more stable on interstitial defect sites. From Fig. 3, we observe a clear periodicity in the relative formation energy of cation dopants, pointing to isovalency with Hf as being a critical factor in their relative stabilities. These calculations agree with existing experimental and other theoretical evidence [65, 67, 69, 70]: Al, Si, and Zr were reported to favor cation substitutional sites in HfO₂, while interstitial sites are favored by Ag, B, Cu, and Ni. On the other hand H, F, and N are all known to favor anion substitutional sites.

Fig. 3

Relative energy for substitutional and interstitial site preference of dopants in monoclinic HfO₂

3.2.1 Vacancy formation energy in monoclinic HfO₂ with cation dopants

Oxygen vacancies in HfO₂ can be either in the 3C or 4C coordinated configuration, with the 3C coordination being slightly more energetically favorable. Figure 4 shows the supercell of HfO₂ containing a single oxygen vacancy in the 3C configuration. Next, to simulate the formation of filaments in VCM devices a column of oxygen vacancies was removed in a supercell HfO₂. In Fig. 5 we show how this filament structure is modified with the introduction of increasing concentration of titanium ions. To assess the electronic charge transfer effects with the introduction of dopants near the filament, the partial charge distribution of the electronic states associated with the filament and dopants are plotted in Fig. 6. This quantity is obtained by calculating the spatial distribution of electronic states with energies between the valence and conduction bands of m-HfO₂, i.e. through defect states induced in the band gap. The filament formation is clearly visible as a conductive channel formed by delocalized electrons from the metal ions in the neighborhood of interacting oxygen vacancies. With the introduction of Ti dopants a partial electronic localization is observed in the immediate vicinity of Ti.

Fig. 4

Supercell structure of monoclinic HfO₂ with one oxygen vacancy in the 3C position

Fig. 5

Oxygen vacancy filament in monoclinic HfO₂ with one and two dopants

Fig. 6

Partial charge density of gap states for a monoclinic HfO₂ with an oxygen vacancy filament and two Ti dopant ions

The ultimate goal of VCM doping is to tune the energetics of oxygen vacancy formation within the device. In this section, the dopant effect on V _O formation energy was calculated for both 3C and 4C oxygen vacancies in HfO₂ according to Eq. 8. As seen in Fig. 7, the presence of dopants generally reduce the formation energy of nearby V _O , however the magnitude of the change strongly depends upon the dopant species. It was found that the effect of cation dopants on V _O formation energy depended heavily upon their valence relative to Hf, with strongly n-type or p-type dopants causing the greatest reductions in V _O formation energy. On the opposite, the effect of anions on V _O formation is generally weaker and is less affected by the particular dopant species.

Fig. 7

Formation energy of single oxygen vacancies near dopants and clustered oxygen vacancies with one and two dopants in monoclinic HfO₂

Relative to their localized single vacancy effects, the energetics and charge stability of oxygen vacancies when they form extended defects like clusters or filaments, can be significantly altered. This has been shown to take place due to a number of factors including the Coulomb repulsion between the vacancies, constraints on lattice relaxation, and delocalization of unpaired Hf 5d electrons across neighboring Hf ions. Therefore, it is informative to inspect the impact of dopants on the filament energetics. From Fig. 7 a similar trend in the oxygen vacancy formation energy dependence on dopants species is noted relative to their effect on single vacancies. The overall effect is slightly weaker though, because the formation energy is being spatially averaged over the length of the entire filament, whereas the dopant induces a strong local effect.

Based on this data, implications on device performances can be derived, which suggest that dopants presence in a VCM switching oxide may induce preferential sites for the formation of conductive filaments and therefore could be beneficial to improve on the uniformity of devices. During the forming step, the conductive channel nucleation can now happen around dopants, since the formation energy of oxygen vacancies near dopants is reduced compared to Hf-sites. Moreover, if the same current compliance is used for un-doped and doped devices then a more robust filament can be achieved with dopants, which ultimately may improve on the variability, retention and endurance characteristics of VCM devices.

4 Reactive molecular dynamics simulations of electrochemistry

MD simulations with reactive interatomic potentials enable multi-million atoms simulations and the description of complex chemistry, including combustion, decomposition of explosives [77, 78], growth of carbon nanotubes [79], among others [80]. The ability of reactive force fields like REBO [81], COMB [82] and ReaxFF [83] to describe the dissociation and formation of bonds lies in two key concepts: i) the use of partial bond orders [84, 85] to describe covalent interactions, and ii) environment dependent partial atomic charges that are computed based on the atomic positions at each step of the simulation [86, 87]. This section introduces the electrochemical dynamics with implicit degrees of freedom (EChemDID) method; an extension of reactive MD simulations to describe electrochemical reactions driven by the application of an external voltage between electrodes and, the generalization of the reactive force field ReaxFF to describe discreet electron processes. Section 5 describes the application of EChemDID to simulate the dynamics of resistance switching in ECM cells.

4.1 Reactive MD simulations of electrochemistry: EChemDID

The discussion of EChemDID here is based on the ReaxFF force field, but the method is applicable to any reactive potential (for example, a similar extension to COMB is described in Ref. [88]). ReaxFF was chosen since it has been successfully applied to model a wide range of materials [80] including metals [89], semiconductors [90], organic molecules [91] and interfaces [92].

Interatomic potentials describe the total energy of the system as a function of atomic positions from which, atomic forces are obtained to solve Newton’s equations of motion in MD simulations. In ReaxFF, the total energy is decomposed as the sum of many-body covalent interactions (including bond stretch, bond angles, torsions) and pairwise non-bonded interactions including van der Waals and electrostatics based on environment-dependent partial atomic charges. In the charge equilibration formalism (QEq) [86, 87], the total electrostatic energy is written as:

$$ E\left( \{R_{i}\},\{q_{i}\}\right) = \sum\limits_{i}\left( {\chi_{i}^{0}}q_{i}+\frac{1}{2}H_{i}{q_{i}^{2}}\right)+\sum\limits_{i<j}q_{i}q_{j}J(R_{ij}) $$

(12)

where ${\chi _{i}^{0}}$ and H _i represent the electronegativity and hardness of each atoms, respectively and J(R _{i j} ) is the shielded (to avoid close range over-contributions) Coulomb function. Interatomic charges {q _i } are calculated self-consistently, at every step of the simulation, by equating the electronic chemical potential {∂ E/∂ q _i } on each atom, assuming charge neutrality.

The effect of an electrochemical potential difference Φ₀ applied between two electrodes can be modelled by changing the electronegativity of the atoms on one electrode to ${\chi _{i}^{0}}{\rightarrow \chi _{i}^{0}}+{\Phi }_{0}/2$ and to ${\chi _{i}^{0}}{\rightarrow \chi _{i}^{0}}-{\Phi }_{0}/2$ on the other. As can be seen from Eq. 12, the external potential imposes an energy difference of Φ₀e between electrons in either electrode. The challenge in describing electrochemical reactions lies in the dynamical evolution of the electrodes due to dissolution and deposition of atoms, consequence of Redox reactions. Thus, the composition of each electrode evolves in time; an atom in the electro-positive electrode of an ECM cell may dissolve into the dielectric, migrate and merge to the inactive electrode. In the original description [93], a distance-based cluster analysis was performed to identify the atoms belonging to each electrode and the electronegativities were adjusted accordingly. This approach was later generalized [94] by considering the local electrochemical potential on atom i, Φ _i (t) as a dynamical variable whose time evolution depends on the electrochemical potential of nearby atoms. As a consequence, the atomic electronegativities used for charge equilibration also become time dependent quantities $\chi _{i}(t){\rightarrow \chi _{i}^{0}}+{\Phi }_{i}(t)$. Onofrio et al. proposed a diffusive equation to describe the equilibration of electrochemical potential within connected metallic regions:

$$ \dot{\Phi}_{i}(t) = k\nabla^{2}{\Phi}_{i}(t) $$

(13)

where k is an effective diffusivity for the electrochemical potential and ∇² is the Laplacian operator. In this approach, the ultrafast equilibration of voltage, described rigorously by Maxwell’s equations, is described via fictitious, but computationally convenient, diffusion equation. The key to the EChemDID approach is that the electrochemical potential equilibration remains faster than the atomic processes. An important by-product of using a diffusive equation is the possibility to estimate electrical currents when a potential difference is applied across a metallic system and one can choose the effective diffusivity k to match the resistivity of the electrode’s materials. A complete description of EChemDID is presented in Ref. [94] including a series of validation tests and applications.

Practically, Eq. 13 is solved numerically at each step of the simulation and the updated atomic electronegativity χ _i (t) is used to perform the charge equilibration Eq. 12. EChemDID is implemented as a LAMMPS user package which can be downloaded from the authors’ webpage [95].

4.2 Explicit electrons in reactive MD simulations: eReaxFF

The charge equilibration method discussed above describes electron transfer between atoms, but is incapable of describing discreet electron processes like the trapping of an electron or a hole by a defect. As discussed above, these processes are believed to critical in the operation of VCM and in ECM cells where a dissolved Cu atom can be in the 1 + or 2 + states. An atomistic modeling for a proper theoretical description of physical systems that involve explicit electron is also critical in rechargeable battery interfaces and ferro-/piezoelectric materials. Ab initio electronic structure methods are well established to provide the most accurate description of such systems and processes. However, the physical length and timescale required to model electron flow driven processes are often prohibitive. The classical reactive force field, such as ReaxFF, treatment of charge transfer is inadequate to describe discreete electron transfer associated reactive events [80, 96]. Recently, FF methods that include aspects of explicit valence electrons have been developed, such as the electron force field (eFF) [97] and the LEWIS [98] force-field. But, their capability to describe complex reactions or materials have not been demonstrated yet. The split-charge equilibration (SQE) has also been extended to describe integer charge transfer in reactive dynamics [99,100,101], but not applied to complex chemical reactions yet. Islam et al. [102] recently extended the ReaxFF method to incorporate an explicit electronic DOF. In the eReaxFF development, basic framework and functional forms of the ReaxFF were retained to ensure transferability of the existing ReaxFF parameters to the eReaxFF [102].

Theory

A limited pseudoclassical electron/hole DOF has been introduced in the eReaxFF method as a complement to the implicit treatment of electrons in the ReaxFF method. New energy functionals were designed to compute the electrostatic interactions for explicit electrons and core charges. The explicit electron- and hole- like particles carry negative (−e) and positive (+ e) charges, respectively. The pairwise electrostatic interaction between the electron and core-charge was described as [103]

$$ E_{nucl(i)-elec(j)}=-\frac{1}{4\pi\varepsilon_{o}}\beta\sum\limits_{i,j}^{}\frac{Z_{i}}{R_{ij}}erf(\sqrt{2\alpha }R_{ij}) $$

(14)

where Z _i is the nuclear charge, R _{i j} is the distance between the electron and nucleus, α (Gaussian exponent), and β are constants that depends on the atom type. The core-charge is the charge corresponding to the atomic number of an atom. In addition to the electron-electron interactions as Coulomb point charges, short-range Gaussian repulsion functions were also employed. In contrast to the ReaxFF method, the explicit electron/hole results in variable valencies and number of lone electron pairs of host atoms. The variable atom valency was determined using an electron-nuclear distance-dependent function; that also allows an electron to virtually split itself among its neighboring atoms as such resembles a partial delocalization. To accommodate the electron-induced variable atom valency on the bonded interactions, modified over/undercoordination energy functional were used. The implementation of the charge-valency coupling enabled eReaxFF method to describe chemical bonding involving charged species more accurately via the appropriate change in valence when calculating the degree of over or under coordination of the host atoms. The ACKS2 charge calculation scheme [104] was implemented to circumvent unrealistic long range charge transfer issues of the Electronegativity Equalization Method (EEM) [86].

The capability of the eReaxFF method has been demonstrated through capturing electron affinities (EAs) of a wide range of chemical species [102]. Figure 8 shows that eReaxFF method qualitatively reproduces experimental [105, 106] and ab initio values of EAs of all the saturated, unsaturated, and radical species considered in the study, which is a notable improvement in contrast to the corresponding ReaxFF predictions. The authors employed the developed force field to study electron transfer dynamics in model hydrocarbon radicals, and good agreement with the Ehrenfest dynamics simulations was established.

Fig. 8

Electron affinities of various species as calculated using the eReaxFF method and comparison with the experimental [105, 106] and ab initio data. Adapted from [102]

In Li-ion batteries (LIBs), during the first charge cycle, reductive decomposition of the electrolyte molecules generates a thin passivation layer, which is known as solid electrolyte interphase (SEI). Atomistic modeling of such reduction reactions requires treatment of explicit electrons. The eReaxFF method enabled investigation of the SEI formation mechanisms via its explicit electronic DOF. In a recent study, Islam et al. [107] applied the eReaxFF to describe all the major reduction reaction pathways of SEI formation with ethylene carbonate (EC) molecule. The EC/Li chemistry initiates through oxidation of lithium followed by the reduction of EC. The EC⁻/Li⁺ complex undergoes EC ring opening reactions and produces o-EC⁻/Li⁺ radical. The eReaxFF predicted energetics of the radical formation and termination reactions were in good agreement with literature data. In dynamic simulations of EC/Li systems, di-lithium butyl dicarbonate (Li₂BDC), and di-lithium ethyl dicarbonate (Li₂EDC) formation were observed, which are considered as dominant components of anode-side SEI. Figure 9 represents simulation snapshots of initial, generated o-EC⁻/Li⁺ radicals, and Li₂BDC, Li₂EDC formation as observed during 600K NVT MD simulations. Overall, the eReaxFF predicted EC/Li chemistries were in better agreement with literature data compared to other ReaxFF studies on LIBs electrolytes [96, 108]. The eReaxFF method with its ability to adequately describe redox reaction is predicted to be a powerful method for understanding the dynamics of explicit electrons in physical and chemical systems.

Fig. 9

Snapshot of the simulation cell at (a) t = 0 ps, (b) the generated o-EC⁻/Li⁺ radicals are highlighted, t = 25 ps. EC and Li which are not participated in the electron transfer event are displayed as line, (c) The formation of Li2BDC, Li2EDC and C2H4 gas as observed in the MD simulations. Color scheme: cyan: carbon, white: hydrogen, red: oxygen, purple: Li + , large blue sphere: electron. Adapted from [107]

5 Atomistic modeling of resistance switching in ECM cells

Since ECM cells have been demonstrated to operate at ultrafast (nanosecond) timescale [6] and can be scaled down to the nanoscale [7], EChemDID provides the unique tool to study resistive switching with unprecedented spatial and temporal resolutions. EChemDID was used to study Cu/a-SiO₂ ECM cells; a common materials combination that has received particular attention in the field because of its compatibility with CMOS fabrication [109]. Details on the atomistic models and annealing procedure are described in Refs. [93, 110]. Here we describe the key atomistic steps identified for stable resistance switching, discuss the kinetics and stability of the nanoscale filament and show how EChemDID can be extended and applied across the scales of atomistic simulations.

Figure 10 shows snapshots of the atomic structure of an ECM cell operation corresponding to forming, reset and set sequences. The switching mechanism can be summarized as follow. When a voltage of the appropriate polarity is applied between metallic electrodes, Cu atoms dissolve inside the solid electrolyte, often aggregate into small clusters and are electric-field driven toward the inactive electrode, where they undergo successive reduction reactions. This process leads to a nanoscale filament growing from the inactive electrode toward the active one until a stable metallic bridge is formed. When the voltage is reversed, the filament breaks at the inactive electrode leaving a partial filament connected to the active electrode. During a subsequent set voltage, the partial filament at the active electrode rapidly dissolves and another metallic bridge is established within shorter timescale than that of the forming sequence. Details on the mechanism are discussed in Ref. [93].

Fig. 10

Snapshots of the atomic structure during forming, reset and set phases of a Cu/SiO₂ ECM cell. The top scale represents the switching state of the cell as a function of the simulation time ranging from high resistivity (HR) to low resistivity (LR). The colors represent atomic charges ranging from −0.3e (red) to + 0.3e (blue). The solid electrolyte has been hidden for clarity. Adapted from Ref. [93]

While EChemDID simulations, at sub-10 nm and ultrafast scales, indicate the formation of small Cu clusters and their stabilization by reduction to be the rate-limiting step, depending on materials and conditions, experimental studies show the existence of a critical nucleus size (ranging from few to tens of atoms) corresponding to a nucleation and growth process [22, 111, 112]. DFT calculations show that aggregation of Cu atoms into clusters to be energetically favorable in silica for all sizes without a critical nucleus size. Thus, given the relatively low activation energy for diffusion, clusterization is the rate limiting in such nanoscale device [113]. We note that these DFT simulations consider only neutral states under no bias and it is often observed that nucleation is mainly rate limiting at low applied voltages (up to 0.5 V) [18, 111, 112] and the voltage window depends on the materials and operating conditions.

Simulations over an ensemble of statistically independent ECM cells show that approximately 50% of the devices can be formed in less than 5 ns under 8 V and that the discrepancy in switching times is directly due to the atomic variability of the amorphous structure of the electrolyte. Interestingly, the dissolution and aggregation of Cu ions inside silica does not generate point defects, ruling out the formation of permanent nanoscale voids and channels during the forming phase. The comparison of switching timescales between different electrode geometries suggest that nanoscale roughness leads to larger dissolution rate and therefore shorter switching times [93, 110]. Finally, various shapes of the nanoscale filament have been observed and many simulations suggest that single atom chain bridges are metastables at room temperature.

Although EChemDID does not describe electrons explicitly, it is possible to extend its application across the scales by coupling the formalism with first principles and semi-empirical methods. The evolution of the electronic density of states (DoS), calculated from DFT, at various timestep during switching of a small ECM cell with EChemDID shows an increase of the number of Cu states at the Fermi energy. The change in the electronic structure of the electrolyte is directly responsible for transport in the device [110, 114]. However, the high computational cost of DFT restricts this approach to small ECM cells composed of few hundreds of atoms. In another approach [115], the (QEq) charges generated during an EChemDID simulation were used to calculate the electrostatic potential described by the Poisson equation and, an empirical tight-binding (TB) Hamiltonian was reconstructed. Following this procedure, the electronic structure of large ECM cells has been resolved and accurate electronic currents have been computed from the transmission spectrum. The TB study of Cu/a-SiO₂ ECM cells shows a dramatic increase of the transmission at the Fermi energy as soon as Cu atoms start to dissolve and clusterize inside the electrolyte. A current ratio of approximately 200 was calculated between pristine and formed cells.

To conclude, EChemDID has enabled the first atomistic simulations of ECM cell operation and, the analysis of switching in Cu/a-SiO₂ cells has provided a clear picture of the corresponding atomic mechanism. EChemDID is not without limitation and, the description of atomistic electrochemistry from a classical theory involves obviously some approximations. An improved version of the reactive force field including integer charge transfer and the explicit treatment of electron which has been discussed in the previous section appears as one of the most appealing route to improve EChemDID.

6 Kinetic Monte Carlo models

Timescales beyond tens of nanoseconds are beyond the reach of MD simulations and exploring such regimes (for example multiple switching events or slower switching) requires coarser-grained approaches. One such method is kinetic Monte Carlo (KMC) that describes the stochastic evolution of a system given possible reactions and the associated transition rates, which can be computed from ab initio simulations. KMC has been applied to VCM cells and describe the resistance switching through a random network of resistances [116] or traps [117,118,119], each contributing to conduction by trap-assisted tunneling. Also ECM systems have been studied through KMC simulations [120,121,122,123]. Guan et al. [118] proposed a model to describe switching dynamics and variability. In this model, the oxide layer between the electrodes is considered as oxygen-vacancy (V _O ) rich. V _O behave as traps which assist electronic conduction through trap-assisted-tunneling, or TAT. Depending on the concentration and distribution of V _O , different configurations are obtained, which lead to different high- and low-resistance states, therefore giving an interpretation of RRAM variability of the resistive states.

In this framework, the application of a voltage causes the migration of oxygen ions, leading to generation and recombination of V _O and thus causing current and resistance variability. The study is performed on a 2D geometry, as shown in Fig. 11. Recently, 3D KMC models have also been proposed [124, 125]. Figure 11(a) shows the area between the biased electrode, on the right, and the grounded electrode, on the left. The random points between them represent the initial V _O before forming. Figure 11(b) shows the calculated forming current, while Fig. 11(c) shows the new V _O generated by local fields, which arise when biasing the device. The V _O generated create conductive filaments and percolation paths where electronic conduction is favored. The model is also capable of explaining the increasing resistance states obtained by applying decreasing negative stop voltages, namely, the maximum negative voltage applied to the device. Figure 11(d) shows the calculated reset I-V curves, which display a gradual reset, and corresponding increasing high-resistance states for decreasing stop voltage from −2.5 V to −3 V. This dependence is interpreted by the formation of a gap with a negligible concentration of V _O due to the V _O -oxygen recombination, since negative oxygen ions are rejected by the negative electrode on the right. The formed gap obstacles electrons motion, since there are no traps aiding electron transport, thus rising the device resistance.

Fig. 11

RRAM switching model presented by Guan et al. [118]. (a) shows a 2D plane with the pre-forming oxide, with few V _O . The forming I-V curve (b) leads to the creation of percolation paths formed by V _O (c). Decreasing the stop voltage leads to increasing high resistance levels (d) due to the increased tunneling gap. The tunnel length increases for decreasing stop voltage (e–f), reducing the probability of electron transport through the gap. The model also accounts for set transition (g). Higher I _C leads to the creation of more percolation paths (h–i). Adapted from [118]

Current fluctuations during reset transition are also explained by the model: in the gap, the electric field is high, hence sometimes there is some V _O generation which allows electrons to reach the left electrode, increasing the current. However, since the recombination probability is high because the oxygen concentration is elevated at the left electrode, the generated V _O will rapidly recombine. In addition, the model can also account for set transition: Fig. 11(g) shows two set I-V curves for different compliance currents I _C . Higher I _C leads to the creation of more percolation paths, as shown in Fig. 11(h,i), thus lowering the device resistance.

7 Continuum models of filamentary resistance switching

7.1 Analytical models

Analytical models have a particular appeal due to the ability to describe complex physical processes with just a few equations which can be easily solved. The main idea is to describe only the relevant dependence of resistive switching from the evolution of few parameters, such as CF diameter [126,127,128], CF oxide gap [128,129,130,131,132,133,134] or CF top and bottom reservoir [135]. Note that the three are geometrical parameters, which allow for an immediate translation in electrical resistance. The fast evaluation of resistance and current dependence on voltage allows to implement such models in circuit simulators, e.g., SPICE, thus enabling the study of Monte-Carlo variability issues [136,137,138], memory [1, 139, 140] logic [9] and novel neuromorphic networks [141,142,143] with a high degree of accuracy, at a manageable computational load.

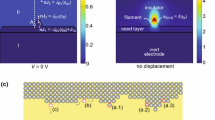
In the work by Ambrogio et al. [129], resistive switching is geometrically described as the growth of a CF with an increasing diameter ϕ during set transition, namely the switching from the high- to the low-resistance state. In the same model, reset transition, namely the reverse switching from low- to high-resistance state, is instead obtained by means of an oxide gap growth of length Δ inside the CF, which causes the rupture of the conductive path, leading to an increased resistance. A schematical representation of the reset transition is shown in Fig. 12. Figure 12(a) shows a full set state, represented by a cylinder, which also corresponds to the initial condition. The CF is composed by defects, for example oxygen vacancies V _O , metal ions (Hf in HfO _x RRAM) or other impurities. The top and bottom electrodes are fabricated in TiN, and the top electrode shows a Ti layer, also called vacancy-rich layer, or, equivalently, oxygen depletion layer, which acts as a defects reservoir. The application of a negative voltage −V _A at the top electrode leads to a migration of defects driven by the applied electric field and accelerated by temperature. The migration starts from the CF point at highest temperature, which corresponds to the center of the CF, Fig. 12(b), since top and bottom electrodes act as heat sinks. This leads to a subsequent opening of an oxide gap of length Δ, Fig. 12(c), which increases the CF resistance. The growth rate of the gap can be modeled by an Arrhenius process:

$$ \frac{d{\Delta}}{dt} = Ae^{-\frac{E_{A}}{kT_{z1}}}, $$

(15)

Fig. 12

Geometrical representation of the reset transition (a-b-c) which is caused by the gradual opening of an oxide gap, and of the set transition (d-e-f), characterized by the growth of a sub-CF inside the gap region. Adapted from [129]

where A represents a pre-exponential factor and k is the Boltzmann constant. The energy barrier E _A , which defects need to overcome to migrate, is lowered by the applied electric field:

$$ E_{A} = E_{A0}-\alpha qV, $$

(16)

and E _A 0 is the zero-field barrier, showing values around 1 eV [144]. α is the barrier lowering factor, q is the electron charge and V is the applied voltage on the gap region, which drives the migration. Temperature T in Eq. 15 is calculated by solving the steady-state Fourier equation:

$$ k_{th}{d^{2} T \over dz^{2}} + J^{2}\rho = 0, $$

(17)

which is consistently calculated in the three domains (top CF stub, gap, bottom CF stub) by using the corresponding CF and gap thermal conductivities k _{t h} [145] and resistivities ρ. J is the current density flowing into the CF region. In Eq. 15, temperature is calculated at the bottom CF stub, z₁, since migration of defects starts here, hence z₁ represents the defect injection point. The final reset state shown in Fig. 12(c) also acts as the initial state for the set transition, Fig. 12(d). During set transition, a sub-CF of diameter ϕ nucleates and grows inside the gap region, Fig. 12(e), eventually leading to a complete set state, Fig. 12(f). Since defects are still field driven and temperature activated, the corresponding ϕ growth rate can be still modeled as an Arrhenius process:

$$ \frac{d\phi}{dt} = Ae^{-\frac{E_{A}}{kT_{z2}}}. $$

(18)

Parameters are identical to the reset transition, but temperature is now calculated at the z₂ edge, since now defects are injected from the top CF stub towards the bottom electrode. The model I-V curve result is shown in Fig. 13, obtaining good quantitative results, particularly regarding switching voltages V _{s e t} and V _{r e s e t} , corner voltage V _C and reset current I _{r e s e t} . Abrupt set transition is explained through a positive thermal feedback: as the sub-CF grows, the current flowing increases, leading to a temperature increase which accelerates defects migration and the consequent CF growth, thus leading to more current. Also gradual reset is well captured. It is instead modeled through a negative thermal feedback: the growth of an oxide barrier increases the resistivity and cools the CF. Therefore, to activate a further defect migration and continue the reset transition, voltage must be increased to increase T again.

Fig. 13

Experimental and calculated with the analytical model in [129] I-V curves. The model can capture the abrupt set transition and the gradual reset transition. Adapted from [129]

Another example of analytical model is the dynamic ‘hour glass’ model for resistive switching proposed by Degraeve et al. [135]. In this model, set and reset switching kinetics are caused by the migration of oxygen vacancies V _O . The model schematizes the CF geometry as a V _O top reservoir (TR), a bottom reservoir (BR) and a thin bottleneck called constriction where conduction happens through a quantum point contact, as shown in Fig. 14.

Fig. 14

Initial device structure (a), after forming (b) and schematized geometry adopted in the “hour glass”i model (c). Adapted from [135]

7.2 Numerical models

Numerical models represent an extension of the one-dimensional analytical models previously shown, since they solve a set of equations on a 2D or 3D domain [146,147,148]. From one side, the computational load increases due to a more complex geometry and a denser space mesh, which poses limitations in the use of numerical models for Monte Carlo approaches, e.g., for variability and statistics. From the other side, however, numerical models allow for a much deeper understanding and description of the physical process. The partial differential equations describing the system physics, e.g., charge and defect transfer and heat transfer, are consistently solved through a finite element method in a 2D or 3D geometry. Many numerical models have been proposed, which include boundary effects, such as the impact of electrodes [149] or space charges [150]. An example of numerical model is the one which has been proposed by Larentis et al. [146]. The switching mechanism is explained as the motion of ionized defects, following drift-diffusion equations. In this model, the electrostatic field is calculated by solving the Poisson equation:

$$ \nabla\sigma\nabla{\Psi} = 0, $$

(19)

where σ = 1/ ρ is the electrical conductivity and Ψ is the local electrostatic potential. Note that no free space charge has been considered, therefore the second term is zero. Ψ is linked to the electric field F through:

$$ -\nabla{\Psi} = F. $$

(20)

Heat transfer is taken into account by solving the steady-state Fourier equation:

$$ -\nabla k_{th}\nabla T = |\sigma \nabla{\Psi}|^{2}. $$

(21)

The right-hand side of Eq. 21 represents the local dissipated power density, which is compared to the space variation of the heat-flow caused by thermal conduction in the left-hand side of Eq. 21. No thermal transient effects have been considered since, for the CF region, the thermal constant is much faster than any resistance switching effect [126]. The calculated temperature allows to obtain both diffusivity D and mobility μ of defects, which are related through the Einstein relation and are thermally activated. All these parameters are linked in the drift-diffusion equation which describes the motion of defects during resistive switching:

$$ \frac{\partial n_{D}}{\partial t} = \nabla(D\nabla n_{D}-\mu Fn_{D}), $$

(22)

where n _D represents the concentration of defects. Finally both local k _{t h} and σ depend on n _D . Since n _D defects behave like a dopant in an oxide layer, a high concentration of n _D , as in the CF, leads to high values of k _{t h} and σ. Instead, depleted regions with a low n _D concentration behave like an oxide layer, with low k _{t h} and σ.

Figure 15 plots both experimental and calculated reset I-V curves, showing a good agreement. Note that reset transition is shown for positive voltages, however this is due to a different voltage sign convention, no physical changes arise with respect to Fig. 13. The two experimental I-V curves were obtained for different I _C , causing two initial low resistance states of 0.4 and 1 k Ω. Increasing the voltage from 0 up to 0.4 V leads in a linear behavior since the cell shows no migration of defects. At V = V _{r e s e t} = 0.4 V, resistance starts to increase due to the onset of migration activated by temperature and field driven. Then, for increasing voltage, resistance gradually increases up to a saturation of the resistance at around 1 V. The model can closely capture these dynamics also for different initial resistance states. Four different points are highlighted in the I-V curve of Fig. 15 corresponding to an initial resistance of 0.4 k Ω, namely points A, B, C and D along the calculated curve. These points are selected to study the evolution of reset transition. Figure 16 shows the corresponding 2D maps calculated with the numerical model related to the four points for (a) defect concentration n _D in the CF region, (b) temperature T and (c) potential Ψ profile. At point A, the applied voltage is slightly below reset voltage, therefore immediately before the reset onset. The CF n _D concentration is almost continuous and the temperature profile shows a parabolic shape with a temperature maximum at the centre of the CF. The corresponding potential Ψ map reveals a uniform voltage drop on the CF region. Immediately after reset, which is represented by point B, the CF is broken and a gap appears in the n _D map, with a migration of defects from top to bottom, as shown by the blue gap and red high density spot. Note that the defect migration is opposite to Fig. 12 since the geometry is rotated. The temperature shows an increase in correspondence of the gap region, causing a thermal activation of migration. Also the potential starts to be localized on the same region, which is consistent with a field-driven defect migration. This localization is more pronounced for higher voltages, which can be evidenced by maps at points C and D.

Fig. 15

Measured and calculated reset I-V curves for different I _C . Figure 16 refers to points A, B, C and D. Adapted from [146]

Fig. 16

Calculated 2D maps of defect concentration n _D (a), temperature T (b) and potential Ψ (c) for increasing reset states A, B, C and D in Fig. 15. Adapted from [146]

8 Random telegraph noise

One of the major concerns regarding RRAM reliability is the ability to properly work at low current, e.g below 10 μ A. In this regime, variability in switching time and resistance increase [136] resulting in Random Telegraph Noise (RTN) and complicating the read operation. As an example, Fig. 17(a) shows three different read resistances for different compliance currents I _C of 45 μ A, 12 μ A and 4 μ A. As discussed above, decreasing I _C results in an increase in overall resistance but also in ΔR the difference between high R _{o f f} and low R _{o n} resistance levels. Figure 17(b) shows the corresponding normalized ΔR as a function of the mean R of the device. Data from different materials, HfO₂, NiO, and Cu-based CBRAM, show a linear increase for low resistance, followed by a saturation at high resistance, above 100 k Ω. To tackle this dependence, several models have been proposed [151,152,153,154,155]. The numerical model proposed by Ambrogio et al. [151], considers the CF as a semiconductor-like material. Through a 3D numerical simulator, electron transport equations are consistently solved to obtain the flowing current. In this model, the presence of a bistable trap near or inside the CF modifies the device potential profile. In particular, the trap, which can be a point defect, a dangling bond, or some impurity, can fluctuate between a neutral and a negatively charged state. In its neutral state, the defect does not affect electronic conduction; however, when it is negatively charge a section of the CF is depleted, reducing the effective CF diameter available for conduction and rising the device resistance. The calculated electron density n _D concentration maps are shown in Fig. 18 for two different CF sizes, hence corresponding to different I _C . Figure 18(a) represents a relatively high I _C : the depleted region, represented in blue, partially depletes the CF cross-section, giving rise to the linear slope in the calculated results in Fig. 17(b). Figure 18(b) shows instead a low-I _C CF. In this latter case, the CF cross-section is completely depleted, hence the difference between R _{o n} and R _{o f f} is high, giving a saturated regime for high resistance in Fig. 17(b). In addition, Fig. 17(b) reports different calculated results for variable CF doping density N _D , from 10¹⁸ to 10²¹ cm⁻³. Negligible differences arise, meaning that the size-dependence of RTN is mainly a geometrical effect.

Fig. 17

Experimental measurement of RTN for different I _C , (a). When I _C decreases, the relative amplitude of resistance fluctuation ΔR = R _{o f f} -R _{o n} increases. The measured and calculated relative ratio ΔR/R as a function of R is shown in (b) for different materials, revealing an initial slope for low resistance, followed by a saturation at R > 100 k Ω. The inset shows a schematic representation of the CF with a depleted region caused by the bistable defect. Adapted from [151]

Fig. 18

Calculated electron density n _D maps inside the CF region, for low- (a) and high- (b) resistance states. Adapted from [151]

9 Conclusions and outlook

Modeling and simulations at scales ranging from electrons to those of the device have contributed significantly to our understanding of the operation of resistance switching devices. From the characterization of the electronic and atomic unit processes that result in resistance switching to the interplay between heat generation and dissipation and the growth and dissolution of a conductive filament at the device level, ab initio simulations, molecular dynamics and continuum modeling are today an indispensable partner to experiments. Both simulations and experimental techniques have limitations, involve approximations and assumptions, and only their synergistic combination will result in a complete understand of these devices and enable their rational optimization.

Ab initio simulations, such as those described in Sections 2 and 3 provide the most fundamental and broadly applicable description of RRAM. Their explicit description of electronic degrees of freedom enabled, for example, the description of how charge trapping results in the formation of conductive filaments in VCM. In addition, being applicable to a wide range of materials ab initio methods have been used to explore how doping affects the performance of these devices. While very accurate, ab initio simulations cannot capture the spatial and temporal scales involved in the switching of realistic devices. Fortunately, MD simulations with reactive interatomic potentials provide a less computational intense alternative and dynamical switching with spatial and temporal scales matching those of devices at the limit of scalability were recently demonstrated in ECM cells, Section 5. These simulations simplify the description of electronic degrees of freedom and often neglect discreet electron events however, recent developments (Section 4) show promise in the ability to capture such processes. One step higher in the multiscale hierarchy, kinetic Monte Carlo models, Section 6, have been developed to describe the migration and aggregation of charge species. These models can be parameterized from ab initio and MD simulations and enable studying multiple switching and characterize the intrinsic variability in the devices. Finally, numerical and analytical continuum models, Section 7 follow the evolution of the conductive filament and temperature fields in the device and can be used within circuit simulations in design experiments.

We are unaware of the systematic integration of the various models and data across scales within a predictive modeling framework for the prediction, design and optimization of RRAM. We believe that the individual models are mature enough for this integration and that such a modeling framework together with appropriate experimental fabrication and characterization can accelerate the development of RRAM devices with improved properties.