Electrodiffusion models of synaptic potentials in dendritic spines

Abstract

The biophysical properties of dendritic spines play a critical role in neuronal integration but are still poorly understood, due to experimental difficulties in accessing them. Spine biophysics has been traditionally explored using theoretical models based on cable theory. However, cable theory generally assumes that concentration changes associated with ionic currents are negligible and, therefore, ignores electrodiffusion, i.e. the interaction between electric fields and ionic diffusion. This assumption, while true for large neuronal compartments, could be incorrect when applied to femto-liter size structures such as dendritic spines. To extend cable theory and explore electrodiffusion effects, we use here the Poisson (P) and Nernst-Planck (NP) equations, which relate electric field to charge and Fick’s law of diffusion, to model ion concentration dynamics in spines receiving excitatory synaptic potentials (EPSPs). We use experimentally measured voltage transients from spines with nanoelectrodes to explore these dynamics with realistic parameters. We find that (i) passive diffusion and electrodiffusion jointly affect the dynamics of spine EPSPs; (ii) spine geometry plays a key role in shaping EPSPs; and, (iii) the spine-neck resistance dynamically decreases during EPSPs, leading to short-term synaptic facilitation. Our formulation, which complements and extends cable theory, can be easily adapted to model ionic biophysics in other nanoscale bio-compartments.

1 Introduction

Dendritic spines, nanoscale protrusions located along dendrites of principal neurons, form the primary site of excitatory synaptic input in the mammalian brain (Harris and Kater 1994; Yuste 2011; Yuste 2010). Their function and plasticity are likely essential for neuronal function, memory formation and brain development (Yuste and Majewska 2001; Yang et al. 2009). Excitatory neurotransmitters released during synaptic transmission activate receptors on the spine head, which causes ion channels to open and current to flow into the spine. This current charges the spine causing an excitatory post-synaptic potential (EPSP), which subsequently integrates in the dendrite and summates with other excitatory or inhibitory synaptic potentials on its way to the soma and axon initial segment (Stuart and Spruston 2015). When this summation crosses a threshold, the neuron fires an action potential (AP). Spines thus present the first node in the path of neuronal integration, and voltage dynamics (i.e. rise time, fall time and amplitude) within a spine during synaptic input determine the characteristics of the downstream signal. Voltage recordings from this nanoscale neuronal subdomain have been challenging, and measurements have often been at odds with each other, specifically with regard to the spine head EPSP magnitude (Popovic et al. 2015; Jayant et al. 2017; Grunditz et al. 2008; Acker et al. 2016; Harnett et al. 2012; Cartailler et al. 2017a) and neck resistance values (Popovic et al. 2015; Jayant et al. 2017; Cartailler et al. 2017a; Svoboda et al. 1996; Tønnesen et al. 2014; Beaulieu-Laroche and Harnett 2017; Araya et al. 2006). Recently however, optical and electrical recordings have reported fast and large EPSP values in the spine (Jayant et al. 2017; Acker et al. 2016; Beaulieu-Laroche and Harnett 2017; Kwon et al. 2017). But, given that spines exhibit a stereotypical, but highly variable geometry (Arellano et al. 2007) comprising a bulbous head (volume ranges ~ 0.01–0.3 μm³) connected to the parent dendrite across a narrow neck (length ranges ~ 0.1–5 μm; diameter ranges ~ 5–200 nm), there is a need for models to explore the relationship between geometry and voltage dynamics during synaptic inputs. Such models may help reconcile the different values that have been experimentally procured and possibly help develop an intuition on particular functions carried out by different types of spines.

Traditionally, spine biophysics and the EPSP integration in a neuron are modeled using cable theory (Segev and Rall 1998; Koch 1984; Koch and Poggio 1983; Koch and Segev 1998; Jack et al. 1975), where neuronal compartments, such as dendritic spines and dendrites, are regarded as being passive electrical cables. Cable equations treat the membrane as an RC circuit and compute the time evolution of the signal in the form of partial differential equations. Traditionally, cable theory neglects the effect of concentration gradients, which is a reasonable assumption for large neuronal compartments (such as the original squid giant axon) but may fail to accurately describe electrostatics in nanoscale structures such as dendritic spines. In addition, the spine neck resistance has been indirectly estimated with fluorescence recovery after photo-bleaching (FRAP) (Svoboda et al. 1996; Tønnesen et al. 2014; Bloodgood and Sabatini 2005; Miyazaki and Ross 2017) (i.e. charged or uncharged dye molecules diffusing back into the spine head upon a spine head photo-bleaching). Here, the mean escape time τe of a single diffusive molecule (with diffusion coefficient D) from the spine head into the dendrite can be described by the relation (Schuss et al. 2007) ${\tau}_e={D}^{-1}\left(\frac{V}{4r}+\frac{L^2}{2}+\frac{VL}{\pi {r}^2}\right)+O\left({V}^{\frac{2}{3}}{D}^{-1}\right)$, where V is the volume of the spine head, r the radius of the cylindrical neck and L its length. For a typical spine with head volume V = 0.1 μm³, neck length L = 1 μm, neck radius r = 50 nm and a diffusion constant D = 0.5 × 10³ μm² s⁻¹ (corresponding to the measured coefficient of sodium ions in cytoplasm) (Kushmerick and Podolsky 1969), we obtain that $\frac{V}{4 Dr}\approx \frac{L^2}{2D}=1\ ms$ and $\frac{VL}{D\pi {r}^2}=25\ ms$. Thus, in most spine geometries we can approximate ${\tau}_e\approx \frac{VL}{D\pi {r}^2}$, which is then used to fit the exponential decay rate of the FRAP transient. Neck resistance is finally estimated with ${R}_{neck}={R}_{cyt}\frac{L}{\pi {r}^2}={R}_{cyt}\frac{D{\tau}_e}{V}$, where R_cyt, the longitudinal cytoplasmic resistivity, is assumed to be constant ≈1 − 1.5 Ω. m (Harnett et al. 2012; Koch and Segev 1998)

While both cable theory and FRAP measurements are elegant formulations to model and extract spine biophysical parameters (Popovic et al. 2015; Tønnesen et al. 2014; Koch and Poggio 1983; Miyazaki and Ross 2017), they do have limitations and, indeed, many of the estimated values are at odds with many experiments (Grunditz et al. 2008; Harnett et al. 2012; Bloodgood and Sabatini 2005). One critical aspect that is ignored in both approaches is electrodiffusion (Qian and Sejnowski 1989; Savtchenko et al. 2017; Sylantyev et al. 2013; Sylantyev et al. 2008), i.e. the effect of the electric field on the concentration gradient, which is important when large longitudinal voltage gradients and concentration changes occur. This aspect becomes more critical in the small dendritic spines where sizeable voltage swings, large concentration changes on the order of ~mM, and appreciable electric field gradients across a nanoscale neck can occur within a few milliseconds. Such effects could modulate both voltage and current transmission at a fundamental level and need to be better understood.

To extend cable theory and accurately describe electrolyte dynamics in biological micro-domains, we use the Poisson-Nernst-Planck (PNP) formalism (Savtchenko et al. 2017; Schuss et al. 2001; Holcman and Yuste 2015) and explicitly account for the effect of geometry and electrodiffusion. PNP equations have been extensively used to model thin ion channels (Chen et al. 1997), and, in addition, their steady-state analysis led to the well-known Goldman-Hodgkin-Katz formula and the definition of the reversal potential. However, the PNP equations cannot be analytically solved in complex three-dimensional structures, such as dendritic spines or extracellular space (Halnes et al. 2016; Pods et al. 2013). Previous work modelling electrodiffusion effect in spines (Qian and Sejnowski 1989; Holcman and Yuste 2015) have either captured the effects of the PNP purely through numerical simulations (Cartailler et al. 2017a), examined dynamics under non-electroneutral conditions [12], or solved PNP equations only in cylindrical geometries (Qian and Sejnowski 1989). Here, we use singular perturbation theory and derive coarse-grained PNP equations to describe voltage and ion concentration dynamics in the spine head during synaptic input, explicitly accounting for the effect of geometry and electrodiffusion. We use recently published measurements of spontaneous EPSP transients from spines to highlight these effects under different geometries. We find that electrodiffusion can indeed play a significant role in determining the overall EPSP magnitude and time scales. In addition, changes in ion concentration on a millisecond time scale can modulate current across the neck, which suggests that the neck resistance can dynamically vary as a function of synaptic current. We also find that the spine geometry affects its voltage dynamics and that trains of EPSPs could increase voltage responses.

2 Methods

2.1 PNP formalism

We used singular perturbation theory and analyzed the dynamics of both positive and negative ionic charges inside the spine head and neck (Fig. 1a), and derived a novel coarse-grained system of equations that fully captures the coupled dynamics of ions and voltage with the PNP formalism. It uses a coupled system of two differential equations to describe the interacting ion and electrical potential dynamics: (1) the Poisson (P) equation (Eq. (1)) that computes the electrical potential rising from the local differences between the concentrations of negative c⁻(x, t) and positive c⁺(x; t) charges,

$$ {\varDelta}_x\varPhi \left(x,t\right)=\frac{e}{\epsilon_0{\epsilon}_c}\left({c}^{-}\left(x,t\right)-{c}^{+}\left(x,t\right)\right) $$

(1)

Fig. 1

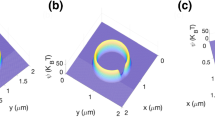
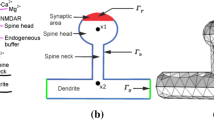
Modeling the dendritic spine geometry and its electro-diffusional properties a) Spine head contains ion channels. It is connected to the parent dendrite with a thin cylindrical neck. Membrane is modeled as an impermeable dielectric with small electrical permittivity compared to cytoplasm (ϵ_m ≪ ϵ_c). At resting state, the spine head is polarized with negative electrical potential Φ₀ ≈  − 60 mV compared to external potential Φ_ext ≈ 0 mV. Ion concentration c_head(t) also varies compared to bulk concentration c₀. Bulk is electroneutral except for a thin boundary layer near the membrane- i.e. the Debye layer (inset), where positive (red line) and negative (blue line) ion concentrations differ due to local variation of the electrical potential (black line). Most of the electrical potential drops through the poorly conducting cell membrane. Equivalent circuit describing the dendritic spine electrostatics is represented: C_m denotes the capacitance of the head membrane, C_neck and R_neck denote the membrane capacitance and the longitudinal cytoplasmic resistance of the spine neck. C_dend and R_dend denote the membrane and resistance of the dendrite. An additional membrane resistance R_leak models the ion leaks through the dendrite membrane. All of which combine to determine the voltage dynamics inside the spine head. b) Geometrical determinants of passive spine neck resistance (ion diffusion coefficient and concentration are respectively fixed to $D=\frac{1}{4}{D}_0=0.5\ {10}^{-9}{m}^2{s}^{-1}$and c₀ = 150 mM). c) Physiological determinants of spine neck resistance (neck length and radius are respectively fixed to L = 1 μm and r₀ = 50 nm)

Where, ${\varDelta}_x={\nabla}_x^2$is the Laplacian operator, e the elementary electrical charge, ε₀ the vacuum permittivity and ε_c the relative permittivity of the cytoplasm, and (2), the Nernst-Planck (NP) equation (Eq. (2)) which captures the contribution of the electrical field on the concentration gradient;

$$ \frac{\partial c}{\partial t}\left(x,t\right)=D\nabla .\left[\nabla c+ v\gamma c\nabla \varPhi \right]\left(x,t\right) $$

(2)

Where, D is the diffusion constant (that we assumed to be the same for both positive and negative charges), $\gamma =\frac{e}{kT}$, and v =  ± 1, is the ionic valence. An analytical solution to the full system of PNP equations is not possible and hence must be either numerically computed or asymptotically estimated.

2.2 Modeling electrostatics in the spine head and neck

We approximated the geometry of the dendritic spine with a ball (spine head, radius R) connected to the parent dendrite across a cylindrical thin neck (length L, cross-section S = πa², with a, the neck radius, that we assumed to be constant (Fig. 1a). We also assumed that the neck radius is smaller than the head radius a < R, as corroborated by ultra-structural reconstructions (Arellano et al. 2007) and super-resolution microscopy of living spines (Tønnesen et al. 2014). We modeled the spine head membrane as an impermeable membrane (no ion leak), with thickness d and small electrical permittivity ϵ_m ≪ ϵ_c (Fig. 1a, inset) (Table 1). We also assumed the continuity of the electrical field (derivative of the electrical potential) at the membrane boundary, a boundary layer condition employed to solve electrostatic equations across dielectric layers (Jayant et al. 2013; Jayant et al. 2014). Finally, boundary conditions for the potential and ion concentrations at the neck entrance were matched to physiological solutions inside the spine neck.

Table 1 Parameters of electrodiffusion model

Using asymptotic analysis of the Poisson equation, we first show that, apart from the thin boundary layer near the membrane, the spine head is electro-neutral with constant concentration c⁺(r, t) ≈ c⁻(r, t) ≈ c_head(t), and iso-potential Φ(r, t) ≈ Φ_head(t) (Fig. 1a) (see SI-II-A for details). This constant potential approximation in the bulk was also confirmed in recent numerical simulations using finite element, steady-state simulations (Cartailler et al. 2017a), and is true for the entire spine microdomain, except for a thin boundary layer near the membrane- i.e. the Debye layer (Fig. 1a, inset). Thus, as traditionally represented in electrical circuit analogy, the spine head behaves like a small capacitor connected to the parent dendrite through a resistive neck (Tsay and Yuste 2004). To obtain the full solution for the potential and the ion concentrations inside the entire spine head domain (i.e. bulk and boundary layer), we compute the inner solutions near the membrane that both match the boundary conditions and the asymptotic solutions in the bulk. Due to the small electrical permittivity of the membrane, the maximal potential drop occurs across the membrane bilayer, and bulk potential is given by the capacitor formula

$$ {\varPhi}_{head}(t)=\frac{\left({n}^{+}(t)-{n}^{-}(t)\right)e}{4\pi {c}_m{R}^2} $$

(3)

Here n⁺(t) and n⁻(t) are the total number of positive and negative ions inside the spine head at time t, and c_m is the membrane capacitance per unit of surface. Typically, c_m ≈ 0.01 Fm⁻² (Table 1), and therefore small differences between the total number of positive and negative charges inside the head lead to significant changes of the spine head potential. For example, inside a spherical spine head with radius R = 500 nm, the resting potential Φ₀ ≈  − 60 mV corresponds to a net excess of ≈12,000 negative charges, while the total number of ions is equal to $\frac{4}{3}\pi {R}^3{c}_0\approx 50x{10}^6$ ions. To put this in context, a typical single ion channel can flux several thousand ions per millisecond (Tovar and Westbrook 2012). Thus, due to the small capacitance of the spine head, the entry of relatively few positive charges during synaptic input, even due to a single channel opening, will result in a rapid depolarization.

The dynamics of ion concentration and potential inside the spine head critically depends on the ionic fluxes with the parent dendrite across the neck. To analyze these fluxes, we followed the methodology developed for modeling ion channels (Chen et al. 1997; Kosińska et al. 2008) and reduced PNP equations to one-dimensional equations along the neck’s principal axis from the spine head to the dendritic shaft (Fig. 1a, see SI-II-B-1 for details). The total flux J⁺(t) of positive and J⁻(t) of negative ions are the solution of the transport Nernst-Planck equation and thus comprise of a diffusion term J_neck(t), which describes the flux due to concentration gradient, and a current term I_neck(t), which describes the flux of ions driven by the electric field:

$$ {J}^{+}(t)=\frac{1}{2}\left({J}_{neck}(t)+{I}_{neck}(t)\right)\kern0.5em \mathrm{and}\ {J}^{-}(t)=\frac{1}{2}\left({J}_{neck}(t)-{I}_{neck}(t)\right) $$

(4)

We highlight that, under electro-neutral conditions, the diffusion flux J_neck(t) = J⁺(t) + J⁻(t) drives an equal amount of positive and negative charges in the same direction, and thus results in no net electrical current. On the other hand, the electrical current results from positive and negative ions that move in opposite directions I_neck(t) = J⁺(t) − J⁻(t). Mathematical analysis of PNP equations inside the neck leads to (see SI-II-B-2 for details)

$$ {J}_{neck}(t)=\frac{2 DSe}{L}\left({c}_{head}(t)-{c}_0\right) $$

(5)

and,

$$ {I}_{n\mathrm{e} ck}(t)={R}_{neck}^{-1}\left({c}_{head}(t)\right)\left({\varPhi}_{head}(t)-{\varPhi}_0\right) $$

(6)

with neck resistance

$$ {R}_{neck}\left({c}_{head}(t)\right)=\frac{L}{2\gamma DSe\left({c}_{head}(t)-{c}_0\right)}\ln \left(\frac{c_{head}(t)}{c_0}\right) $$

(7)

Previous expressions for the diffusion flux and the current inside the neck were obtained after the 1D reduction of PNP equations and their asymptotic approximation. These mathematical techniques are similar to those used for modeling ion channels (Chen et al. 1997; Kosińska et al. 2008; Goldman 1943) and remain accurate as long as the Debye length λ_D (see Table 1) is small compared to the dimensions (length and diameter) of the neck. Otherwise, full 3D numerical simulations are required or, if the Debye length is actually large compared to neck diameter, other type of asymptotic analysis can be applied (Singer and Norbury 2009). Based on previous expressions, we highlight the following findings: First, the asymptotic diffusion flux (Eq. (5)) is the expression normally used to interpret FRAP experiments. This formulation captures only diffusion and neglects the contribution of the electric field on ion dynamics. Second, electrodiffusion predicts that changes in ion concentration modulate the neck resistance which is not solely dependent on geometry as usually assumed in cable theory (Fig. 1b) but also critically depends on the ion concentration inside the spine head (Fig. 1c and Eq. (7)). For constant ion concentration, neck resistance reduces to

$$ {R}_{neck}\left({c}_0\right)=\frac{L}{2\gamma D{Sc}_0e}. $$

(8)

3 Results

3.1 Fast electrical and slow diffusional dynamics inside the dendritic spine

During synaptic input, both AMPA and NMDA receptors are activated. For the sake of computational simplicity, we chose to neglect NMDA receptors given that AMPA receptors are assumed to be the major source of Na⁺ current. Moreover, by considering the relative permeability of AMPA receptors to main ions and Goldman-Hodgkin-Katz equation, we computed that the reversal potential of AMPA receptors is ${\varPhi}_{reversal}(t)\approx {\gamma}^{-1}\ln \left(\frac{c_0}{c_{head}(t)}\right)$ (see SI-II-C-1 for details), and that the synaptic current is governed by the Nernst –Planck equation of transport:

$$ {I}_{synaptic}(t)=-{g}^{+}(t)\left({\varPhi}_{head}(t)-{\gamma}^{-1}\ln \left(\frac{c_0}{c_{head}(t)}\right)\right). $$

(9)

Here g⁺(t) is the time-dependent conductance of AMPA receptors. The ionic influx is thus maximum at resting potential Φ₀ ≈  − 60 mV and concentration c₀ and collapses when the spine head potential and concentration increase.

Using charge conservation principles for both positive and negative charges inside the spine head (see SI-II-C-1 for details), together with the capacitance relation (4), we obtained the coarse-grained system of differential equations

$$ e{v}_{h\mathrm{e} ad}\frac{d\ {c}_{head}(t)}{dt}=\frac{1}{2}\left(\ {I}_{synaptic}(t)-{J}_{neck}(t)\right) $$

(10)

and

$$ {c}_m{s}_{head}\frac{d{\varPhi}_{head}(t)}{dt}={I}_{synaptic}(t)-{I}_{neck}(t) $$

(11)

where diffusive gradient J_neck(t) and neck current I_neck(t) are respectively given by Eq. (5) and (6), and synaptic current I_synaptic(t) is given by Eq. (9). Here ${v}_{head}=\frac{4}{3}\pi {R}^3$and s_head = 4πR² are the volume and the surface area of the spine head respectively. Equation (10) describes the gradual increase of ion concentration inside the spine head during channel opening, while eq. (11) captures the potential dynamics. Equations (10) and (11) are non-trivially coupled because synaptic and neck current depend on spine head potential and concentration.

The coarse-grained system of eqs. (10–11) is a slow-fast dynamical system. The time constant of concentration changes ${\tau}_c=\frac{v_{head}L}{SD}\approx 10-100\ \mathrm{ms}$ is much longer than the time scale of voltage transients, which is due to the charging/discharging of the spine head (capacitor) through the neck resistance (time constant ${\tau}_{\varPhi }={c}_m{s}_{head}\left({R}_{neck}+\frac{1}{g^{+}(t)}\right)\approx 10-100\ \upmu \mathrm{s}$) (Supplementary Fig. 1). Thus, for a Heaviside step function input (constant channel conductance, g⁺(t) = g⁺), voltage increase is rapid at the onset of ion-channel opening, with significant depolarization values and reaches a plateau given by ${\varPhi}_{head}=\frac{\varPhi_0}{1+{g}^{+}{R}_{neck}\left({c}_0\right)}$in less than 100 μs (Fig. 2a). We termed the first few hundred microseconds of the transient as the electrostatic phase, which is accurately described by cable theory. The rapid voltage depolarization during the electrostatic phase causes a decrease in synaptic current (Eq. (9) and Fig. 2e), mirrored by an increase in neck current (Fig. 2f) which plateaus as voltage reaches a steady state. Synaptic and neck currents are then equal. Yet, while the synaptic current only involves an influx of positive ions, the neck current is composed of positive and negative ions moving in opposite directions (positive ions are pushed out the spine head and negative ions are pushed in). If we assume that positive and negative ions have the same diffusivity, only half of the entering positive ions are actually pushed out the spine, while the other half stays inside the spine head and is counter-balanced by incoming negative ions. Thus, due to current conservation, there are twice more positive ions that enter the spine than ions that are pushed out, and positive ions that stay inside the spine head are counter-balanced by incoming negative ions (so electro-neutrality is preserved). After few milliseconds, the concomitant accumulation of positive and negative ions inside the spine head leads to a significant increase of ion concentration, corresponding to the electrodiffusion phase (Fig. 2b). Thus, concentration changes during the electrostatic phase are negligible and voltage dynamics can be described accurately by cable theory, but become significant during the electrodiffusion phase. Increased ion concentration has two main effects: the decrease of effective neck resistance (Eq. (7) and Fig. 2c) and of reversal potential (Fig. 2d). Synaptic (and neck) current subsequently decreases with concentration, as reversal potential decreases and reduces the synaptic electromotive force.

Fig. 2

Slow-fast dynamics of ion concentration and electrical potential within the spine head during a step entry of positive ions (constant synaptic conductance g⁺(t) = 3 nS). a) Log plot of the voltage dynamics within different spine geometries, with large (R = 600 nm, dashed line) and small (R = 300 nm, solid lines) head, and different neck diameters (140 nm (red, R_neck(c₀) = 368 MΩ) and 80 nm (grey, R_neck(c₀) = 120 MΩ)). The electrostatics forces dominate at small time scales (<100 μs) and diffusion at larger time scales (> 1 ms). Note the deflection of the electrical potential due to concentration changes and diffusion. b) Log plot of the concentration dynamics. c) Log plot of the neck resistance dynamics. d) Log plot of the synaptic reversal potential dynamics. e) Log plot of the synaptic current dynamics. f) Log plot of the neck current dynamics. g) Dynamical model of synaptic and neck currents. h) I-V curve of dendritic spine for two different neck diameter (140 nm (grey, R_neck(c₀) = 368 MΩ) and 80 nm (black, R_neck(c₀) = 120 MΩ)). The discrepancy between the spine I-V curve (dashed line, (Δc > 0) when ion concentration change and Ohm’s law with constant resistance (solid line, Δc = 0) is highlighted. For thin and highly resistive neck, the spine behaves like a diode (inset scheme)

At steady-state, the amplitude of current through the neck I_neck(∞) is equal to the amplitude of the synaptic current I_synaptic(∞) and also to twice the diffusive outflux J_neck(∞), where ∞ denotes the steady state value for t ≫ τ_c. These relations lead to an implicit equation for the steady state current that is solved numerically (see SI-II-C-2 for details), and I-V relationship across the spine neck (Fig. 2h and Supplementary Fig. 2)

$$ {\varPhi}_{head}\left(\infty \right)={\varPhi}_0+{R}_{neck}\left(\infty \right)I\left(\infty \right)={\varPhi}_0+{\gamma}^{-1}\log \left(1+\frac{LI\left(\infty \right)}{2 DS{c}_0e}\right) $$

(12)

We stress that steady state voltage and net ion concentration depend solely on spine neck geometry (Eq. 70–72 in supplementary material and Fig. 2 a-b), whereas their dynamics is controlled by the size of the spine head, through its volume and membrane capacitance (time constants on the left hand side of the dynamical system (11–12) and transition phases in Fig. 2).

Equation (12) shows an highly non-linear relation, similar to current rectification observed in nanofluidic diodes (Schoch et al. 2008) (Fig. 2h, inset). Such a non-linear relationship - a consequence of the PNP, was also observed with finite element simulations (Cartailler et al. 2017a) of spine neck electrostatics, albeit with the assumption that only positive ions contribute to the overall current. This is an important electrodiffusion effect that arises as ion concentration changes.

Finally, the long and sustained synaptic input (Heaviside function) that leads to significant, long-term changes in spine head concentration and neck resistance is a condition that we used only to illustrate the slow-fast dynamics of the coarse-grained system of eqs. (10–11). Indeed, the kinetics of opening and closure of AMPA channels is rather of the order of few milliseconds (Koch and Segev 1998). To explore whether changes in concentration and neck resistance are already significant at this time scale during spontaneous synaptic activity, in the following section, we used recent electrical recordings of voltage transients in spine heads and estimated the corresponding currents and changes in ion concentration for different putative spine geometries.

3.2 Exploring the role of electrodiffusion with electrical recording data

Recently, we demonstrated the first direct measurements of spontaneous EPSP from spines using nanopipettes (Jayant et al. 2017). These recordings revealed voltage changes on a millisecond time scale with a fast rising phase (≈1 ms), followed by a slower decay phase (≈10 ms). A recent study measuring synaptic input currents revealed a similar time scale (Beaulieu-Laroche and Harnett 2017), providing further evidence that spine electrical transients can be large and fast. These time-scales are much slower than the estimated charging and discharging time constants of the spine head capacitor (tens of micro-seconds). Thus, the rising and decay phases likely correspond to the opening and closing kinetics of ion channels. We used the time course of this published data, along with models of the rising and decay phase of ion channels (Koch and Segev 1998), to explore the effect of electrodiffusion under different spine geometries. Although these recordings were made on spines with relatively long (>1 μm) necks, the large, fast, and spontaneous millisecond apart EPSPs could be used as a test input to explore the role of electrodiffusion on different spines geometries. We modeled the rising phase of synaptic conductance g⁺(t) with a sigmoidal function followed by a mono-exponential decay phase: ${g}^{+}(t)=\frac{g_0\exp \left(-\frac{t}{\tau_2}\right)}{1+\exp \left(-\frac{t-\mu }{\tau_1}\right)}$ (Fig. 3a-1). To determine the conductance parameters for each EPSP, we used the following grid-search fitting procedure: First, we considered four different putative spine geometries with either a large (600 nm) or small (300 nm) head diameter, and either a large (70 nm) or thin (40 nm) neck radius (neck length is fixed to L = 1 μm). Then, for each individual EPSP and each spine geometry, we determined manually the initial time t_i of rising phase and corresponding resting potential Φ₀(t_i) that slightly varies around −58 mV for each EPSP. We then computed synaptic conductance ${g}_{\left[{g}_0,\mu, {\tau}_1,{\tau}_2\right]}^{+}(t)$ for a large range of conductance parameters [g₀, μ, τ₁, τ₂] (grid search), and solved the dynamical system of equations (10–11) with a finite-elements scheme (time step 0.1 μs), over time intervals [t_i; t_i + 10 ms]. We then compared the computed head voltage Φ_head(t) for each set [g₀, μ, τ₁, τ₂] of conductance parameters with the measured voltage. Finally, the optimal set of parameters for each EPSP was then determined by minimizing the least-square distance between computed and measured voltage over each time interval [t_i; t_i + 10 ms] (Fig. 3a-2). We found similar kinetics parameters for the different spine geometries and EPSPs, with a rapid opening kinetics (median of the 4 EPSPs: μ = 0.52 ms and τ₁ = 0.11 ms) followed by a slower decay (median τ₂ = 3.95 ms) (Fig. 3a-3 and Table 1). On the other hand, we found that the conductance amplitude increased with the EPSP amplitude, and was also modulated by the spine geometry: first, synaptic conductance decreased in spines with high neck resistance (small diameter), as a lower current is needed for the head voltage to reach measured value. Moreover, for dendritic spines with smaller head volume, we found that, due to increased head concentration during EPSPs (Fig. 3b), the estimated synaptic conductance was significantly higher (up to +30% for small neck diameter (high resistance/low current) and + 200% for larger necks). Because the measured head voltage is equal to the product of the current and the neck resistance, the increased synaptic conductance actually compensated the lower reversal potential and neck resistance due to higher ion concentration (Fig. 3b). Finally, we compared the electrodiffusion response of the different spine geometries for a single EPSP with median kinetics parameters (μ = 0.52 ms, τ₁ = 0.11 ms and τ₂ = 3.95 ms) and increasing conductance g₀ = 2 → 9 nS (Fig. 4).

Fig. 3

Estimation of synaptic conductance and changes in ionic concentration during experimentally measured EPSPs a) Estimating the synaptic conductance during spontaneous activity. 1- Conductance of AMPA receptors is modeled with sigmoidal opening (parameters μ and τ₁) and single-exponential closure (parameter τ₂). 2- Optimal conductance parameters [g₀, μ, τ₁, τ₂] for each EPSP are estimated with a multi-dimensional grid-search algorithm where the conductance g⁺(t), the synaptic current (Eq. 9) and the voltage (Eq. 11) are computed for a large range of parameters. Best conductance parameters are those minimizing the distance between the computed and measured EPSPs (Jayant et al. 2017). 3- Boxplots show fitted parameters for the 4 EPSPs recorded experimentally, and optimal conductance is plotted for the different spine geometries (large (diameter = 140 nm, R_neck(c₀) = 120 MΩ, red) and thin (diameter = 80 nm, R_neck(c₀) = 368 MΩ, grey) spine neck, and large (diameter = 600 nm, dashed line) and small (diameter = 300 nm, solid line) spine head). b) Dynamics of synaptic current, head concentration, neck resistance and reversal potential as reflected by coarse-grained electro-diffusion model during spontaneous spine activity in the different spine geometries (large (diameter = 140 nm, red) and thin (diameter = 80 nm, grey) spine neck, and large (diameter = 600 nm, dashed line) and small (diameter = 300 nm, solid line) spine head)

Fig. 4

Electrodiffusion simulation of a single EPSP with increased synaptic conductances. Simulations of single EPSPs (conductance ${\mathrm{g}}^{+}\left(\mathrm{t}\right)=\frac{{\mathrm{g}}_0\exp \left(-\frac{\mathrm{t}}{\uptau_2}\right)}{1+\exp \left(-\frac{\mathrm{t}-\upmu}{\uptau_1}\right)}$, with increasing conductance (from g₀ = 2 nS to g₀ = 9 nS) and dynamical parameters μ = 0.52 ms, τ₁ = 0.11 and τ₂ = 3.95 ms) in 4 different spine geometries

Variations of ion concentration were particularly significant within spines with small head (reduced volume) and large necks (high current), leading to important modulation of synaptic current. The dynamics of concentration variations was much slower than the EPSP time course, and, for large EPSPs, we observed that the head concentration did not necessarily return to its resting state c₀ before the arrival of a second EPSP. We thus predict that the concentration increase (i.e. resistance decrease) could result in a significant reduction in neck resistance during repeated synaptic stimulations at high-frequency (≥50 Hz) (Fig. 5). This finding has one important implication, i.e., that the effective electrical resistance of the spine neck is fundamentally dynamic as it may vary with synaptic activity and associated changes in concentration. Lacking other compensatory or homeostatic mechanisms, the reduction in neck resistance during a train of EPSPs will effectively reduce the filtering effect of the neck resistance, leading to synaptic facilitation.

Fig. 5

Incremental increase of ionic concentration and associated neck resistance decrease during high-frequency synaptic stimulation. a) Relative variations of ion concentration in the spine head (R = 300 nm) and associated neck resistance for a 20 Hz synaptic stimulation (geometrical neck resistances (i.e. at concentration c₀): 500 MΩ (blue) and 100 MΩ (red)). The kinetics of the synaptic conductance is ${\mathrm{g}}^{+}\left(\mathrm{t}\right)={\mathrm{g}}^{+}\frac{\exp \left(-\frac{\mathrm{t}}{\uptau_2}\right)}{1+\exp \left(-\frac{\mathrm{t}-\upmu}{\uptau_1}\right)}$ with g⁺ = 2 nS, μ = 0.55 ms, τ₁ = 0.12 ms and τ₂ = 4 ms. b) Relative variations for 50 Hz synaptic stimulation

4 Discussion

The spine neck appears to be an important diffusional barrier, but its role in electrically shaping EPSPs has remained controversial due to the lack and difficulty in performing precise experimental measurements from dendritic spines. This has led to an incomplete and often contradictory understanding of spine electrical properties (Popovic et al. 2015; Jayant et al. 2017; Acker et al. 2016; Harnett et al. 2012; Tønnesen et al. 2014; Kwon et al. 2017; Tsay and Yuste 2004; Yuste 2013). One way to overcome this problem is with accurate biophysical models. This has been traditionally attempted with cable theory modeling, which is widely used in simulations of neuronal biophysics. However, cable equations traditionally neglect local changes in ionic concentration and the role of electrodiffusion (i.e. electric field effect on ionic gradients), which can become appreciable in small neuronal compartments such as spines (Holcman and Yuste 2015). To explore this, we use an electrodiffusion framework and fully model the electrostatics inside the spine during synaptic stimulation. We emphasize that our model does not discard cable theory but actually extends it by considering possible changes in ion concentration at millisecond time-scale in femto-liter compartments such as dendritic spines. Following previous efforts using non electroneutral conditions (Holcman and Yuste 2015) or numerical simulations (Cartailler et al. 2017a), here, using singular perturbation theory of the PNP equations to model dynamics, we derive a coarse-grained model that fully captures the coupled dynamics of ion concentration and potential inside the spine head. Specifically, we find that (i) diffusion and electrodiffusion jointly govern the dynamics of spine excitatory post-synaptic potentials (EPSPs); (ii) the spine geometry (both head and neck) plays a key role in shaping the EPSP time course; and, (iii) that the current-voltage relationship across the spine-neck is non-linear, which results in the neck resistance varying as a function of ion concentration and can lead to synaptic facilitation for high frequency EPSPs. We briefly discuss the functional implications of the above findings.

4.1 Effect of electrodiffusion on synaptic potentials in dendritic spines

Using a coupled slow-fast dynamical system analysis with a Heaviside step input waveform, we find that the EPSP voltage transient at a spine head can be divided into an electrostatic phase - lasting a few hundred microseconds; and a electrodiffusional phase - lasting several milliseconds. Our results show that, during an EPSP, the electrical voltage first rises very fast due to fast charging of the spine head (due to a low membrane capacitance), with a steady-state value determined by I_syn × R_neck, while the diffusion of ions begins to occur only a few milliseconds later. If the EPSP is sufficiently large, it adds a significant electromotive force on the ions, driving them out of the spine head through the neck, contributing to a fast and large synaptic current. After few microseconds (Fig. 2g), the spine head capacitor is charged and the neck current equilibrates with synaptic current. The amplitude of the synaptic current is proportional to the receptors’ conductance but also to the difference between head potential and reversal potential, a difference which decreases as ion concentration builds-up in the spine head (Eq. (9)). Because of this, the synaptic current also depends on spine geometry and neck resistance. Moreover, increased ion concentration inside the dendritic spine raises the electrical conductivity of the spine neck, i.e. lowers its electrical resistance. Together, decreases of synaptic current and neck resistance as ion concentration builds-up inside the spine head synergistically lower the head potential over millisecond time-scales (Fig. 2a). This down-regulation might have important downstream effects by regulating ion flux of voltage dependent receptors. In particular, we hypothesize that concentration builds-up and voltage decrease might down-regulate the influx of calcium ions through NMDAs receptors and its associated synaptic plasticity. Finally, as neck resistance is inversely proportional to the apparent neck cross-section (Eq. 52 in SI), the local membrane curvature and constriction of the neck, or the reduction of the apparent cross-section due to crowding with organelles such as spine apparatus (Bourne and Harris 2008), can further increase the neck resistance and the increase voltage gradients across the spine neck.

4.2 Regulation of spine neck resistance by ionic concentration

As expected, we find that the rapid voltage increase during the opening of AMPA receptors drives electrical currents through the spine neck. The neck current here corresponds to an exchange between positive ions flowing from the spine head to the dendrite with negative ions flowing from the dendrite to the spine head. After few microseconds, when the head capacitor is charged, synaptic and neck currents equalize. But, as synaptic current only involves positive ions, whereas neck current results from an exchange between positive and negative ions, a fraction of entering sodium ions remains inside the spine, and their relatively slow diffusion through the neck enables a gradual sodium accumulation inside the head during receptors opening. At the same time, an inward neck current of negative ions maintains the overall electro-neutrality.

Our model predicts that the currents associated with recorded EPSPs increases ion concentration inside the spine by up to 90%. This agrees with recent experiments using fluorescent sodium indicators that reported a up to 5 mM concentration increase leading to a ~ 9 mM maximal concentration following the AMPA receptors opening during EPSPs (Miyazaki and Ross 2017) and large synaptic conductance’s ranging between 2 and 8 nS measured from spines (Beaulieu-Laroche and Harnett 2017). It is important to point out that we made two major assumptions when modeling ion dynamics: First, we neglected the specific dynamics of the different ionic species such as protons, or potassium and calcium ions, which could further change the electrostatic landscape and signaling. For example, potassium ions could enter the spine neck from the dendrite via SK channel dependent shunting (Ngo-Anh et al. 2005). This current could counter the decrease in spine neck resistance due to the increased sodium concentration and thus tune the net synaptic current. The second important assumption of our model is that negative charges were only accounted for by chloride ions, while it is known that negative charges are also partly accounted for by less mobile proteins (Delpire and Staley 2014). An important effect of lower negative charges’ motility and inward negative current would be to down-regulate changes in ion concentration and electrodiffusion effects (i.e. lowering neck resistance and reversal potential) (Fig. 6). Moreover, decreased motility of negative ions would reduce the neck current (see SI-II-B-3 for details). However, as the neck resistance would be increased and electrodiffusion effect decreased, the voltage in the spine head during the EPSP would, overall, reach higher values (Fig. 6). We highlight that we did not consider the extreme scenario where the negative charges would be completely immobile (diffusion coefficient D⁻ = 0). Indeed, in that case, positive charges might not be well-mixed in the bulk and shall accumulate near immobile negative charges, and our mathematical analysis would not be valid anymore as it relies on the bulk electro-neutrality and the accumulation of excess charges within a small Debye layer. This extreme scenario has been discussed in (Holcman and Yuste 2015) and treated mathematically in (Cartailler et al. 2017b; Cartailler et al. 2017c). Finally, as diffusive extrusion of accumulated ions from the spine head is relatively slow (ten’s to hundreds of milliseconds), we predict that high-frequency synaptic inputs will lead to a significant decrease in neck resistance, as the rate of ion concentration buildup in the spine nanodomain will exceed the rate of diffusion through the neck, leading to increase in the effect of the synaptic potentials on the dendrite. Our analysis thus reveals that electrodiffusion could be a novel physiological mechanism of post-synaptic facilitation on a millisecond time scale.

Fig. 6

Electrodiffusion simulation of a single EPSP for decreased diffusivity of negative ions. Simulations of single EPSPs (conductance ${\mathrm{g}}^{+}\left(\mathrm{t}\right)=\frac{{\mathrm{g}}_0\exp \left(-\frac{\mathrm{t}}{\uptau_2}\right)}{1+\exp \left(-\frac{\mathrm{t}-\upmu}{\uptau_1}\right)}$, with maximal conductance g₀ = 5 nS, and dynamical parameters μ = 0.52 ms, τ₁ = 0.11 and τ₂ = 3.95 ms) in 4 different spine geometries. Diffusion coefficient D⁻ of negative ions ranges from 0.2 D⁺ to 1.0 D⁺, with D⁺fixed equal to D (see Table 1)

To finish, we speculate that part of the reason that spine neck resistance measurements have been at odds with each other could be due to the fact that changes in ion concentration in the spine dynamically alters its resistance, an effect which critically depends on the morphology which varies in different spine. Therefore, in addition to the voltage dynamics in the spine head, the net current through the neck could be influenced by the net ion concentration inside the spine nanodomain, and care must be taken to measure those in order to properly interpret the electrical function of spines. The potential effect of ionic concentration on spine electrical properties is something which is not of purely academic interest, as the extent to which spines implement electrical compartments and shape the dynamics and amplitudes of EPSPs is of fundamental importance to neuroscience, because they serve to mediate most excitatory transmission in the vertebrate central nervous system.