1 Introduction

Absence epilepsy, a chronic neurological disorder with petit mal seizures, commonly occurs in the children (Panayiotopoulos 1997). Epileptic absence seizures in humans are characterized by the transient deprivation of consciousness accompanied by well structured bilaterally synchronous periodic (~ 2-4Hz) spike-wave discharges (SWD) (Fong et al. 1998). However, rodent models for absence seizures can generate SWD in a relatively fast frequency (5-10 Hz) (Destexhe 1999). Thalamocortical interaction is shown to be critical for the generation of SWD in both the rodent models (Liu et al. 1991) and humans (Moeller et al. 2013). Recurrent ~ 2-4Hz SWD of absence seizure can also induce the cognitive, linguistic and behavioral disorders (Barnes & Paolicchi 2008; Caplan et al. 2008). Because of chronic nature of these disorders, patients with long term anti-epileptic drug treatment may suffer from drug side-effects (Chen et al. 2017; Loring and Meador 2004). Also, invasive surgery is typically not recommended due to the absence of neuroradiological abnormalities for absence epilepsy. Potentially alternative therapies to control or suppress the SWD of absence seizure are yet fully explored. Electric stimulus, which can suppress epileptic seizures by aborting the SWD of epileptic brain activities (Taylor et al. 2014; Salem et al. 2016; Blik 2015; Schiller and Bankirer 2007; Su et al. 2008), is considered as a potential supplemental treatment to antiepileptic drugs. However, the dynamic mechanism underlying the spatiotemporal evolutions and abatements of SWD to other firing states, are not well understood.

Spindles are the non-rapid eye movement (NREM) sleep EEG rhythms, i.e., 7-14 Hz in cats (Steriade 2003; Contreras et al. 1997) and 12-15Hz in humans (Rosanova and Ulrich 2005; Steriade 2003), that can occur independently and being correlated to the slow oscillations of 0.6-0.8 Hz (Rosanova & Ulrich 2005) or 0.1-0.2 Hz (Steriade 2003; Steriade et al. 1987). The slow oscillation in human brain is a traveling wave which can periodically sweep the cortex and can form a wave train to trigger the thalamic spindles (Rosanova and Ulrich 2005). Sleep EEG spindling rhythms can also be slow (< 13Hz) or fast (> 13Hz) spindles, respectively (Molle et al. 2011; Chatburn et al. 2013). Also, spindles in deep sleep are common brain waves that can be observed in both the normal and abnormal persons. As the normal cortical firing states, spindling activities can be found in the deep sleeping state of the normal persons, but also can be detected in the persons with various typical disorders, such as schizophrenia (Wamsley et al. 2011; Tsekou et al. 2015; Ferrarelli 2015), Parkinson’s disease (Christensen et al. 2014; Latreille 2015) and epilepsy (Boly et al. 2017). In addition, both in vivo (Lee et al. 2013; Steriade et al. 1985, 1987) and vitro (Krosigk et al. 1993) recordings suggest that thalamic reticular nucleus (TRN) neurons are spindle pacemakers where the sleep spindles can be abolished after disconnecting SRN (specific relay nucleus) and TRN neurons. Lewis et al. (2015) recently found that TRN can coordinate the slow-wave oscillations of different brain regions to consolidate the new memories and facilitate sharing information. In particular, the spectral power density of NREM sleep EEG slow-wave activity is usually in the range of 0.75-4.5 Hz (Achermann and Borbely 1997; Amzica and Steriade 1997). For example, sleep slow-wave can exhibit characteristic UP-DOWN state with dominant low frequency component (< 2 Hz) (Zhao et al. 2015), through the observations for the local field measurement in the slow-wave sleep state of cortex (Sanchez-Vives and Mccormick 2000). Neurophysiologically, the cortical neurons are excessively depolarized in the UP state while the DOWN state involves strong inhibition of cortical neurons.

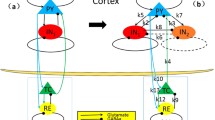
It has been revealed that the two low-frequency (i.e., < 15Hz) conspicuous brain rhythms, SWD and spindle oscillations share the common thalamocortical mechanism (Veggiotti et al. 1999; Tamaki et al. 2008; van Luijtelaar 1997; Traub et al. 2005). They are induced by the interplays between the GABAergic TRN and the corticopetal SRN, i.e., the thalamic SRN-TRN circuit (Kandel & Buzski 1997; Tamaki et al. 2008; van Luijtelaar 1997; Kostopoulos et al. 1981; Kostopoulos 2000; Da Silva et al. 2003; Shouse et al. 2000; Steriade et al. 1993). Experimental findings based on a genetic WAG/Rij rat model of absence epilepsy (Meeren et al. 2009; Sitnikova et al. 2010, 2014a, b) also demonstrated that unilateral destructions of both the TRN and its inhibitory projecting target, SRN, can bilaterally abolish the SWD and ipsilaterally abolish the sleep spindles. In particular, absence seizures might inherit some intrinsic properties of sleep spindles, and also sleep spindles can be transformed into the SWD (Kostopoulos et al. 1981; Kostopoulos 2000; Da Silva et al. 2003; Shouse et al 2000), as shown in Fig. 1a, where the ’spike’ component of SWD is originated from the merging of spindle waves (Kostopoulos 2000). However, the connection between non-REM sleep rhythms and SWD is complex and does not seem to point to a simple mechanism. In Fig. 1b we provide ictal recordings of 3 temporal scalp electrodes’ EEG from an epileptic patient during sleep, where we can observe the coexistence of spindles and slow-wave oscillations (Upper panel), the recurrence of spindles oscillations (Middle panel) and the alternative paroxysmal behavior between SWD and spindling activities (Lower panel). In addition, the propagation dynamics of SWD and sleep waves are observed in the EEG, MEG and slice models (Golomb et al. 1996; Pinault & O’Brien 2005; Shouse et al. 2000; Westmijse et al. 2009; Evangelista et al. 2015).

Fig. 1
figure 1

(Color online) a Experimental electrophysiology modified from Kostopoulos et al. (1981) and Kostopoulos (2000). Upper panel: EEG samples from the middle suprasylvian gyrus of a cat before and after intramuscular injection of penicillin at the times indicated. Triangles indicate the times of single stimuli to nucleus centralis medialis (NCM). Bottom panel: Representative EEG samples from five successive periods of recording before and after the intramuscular injection of penicillin. b Ictal recordings of 3 temporal scalp electrodes’ EEG during the epileptic seizures in sleep. Upper panel: 10 s of 3 EEG recordings of an epileptic patient simultaneously show the spindle and slow wave oscillations. Middle panel: 60 s of 3 EEG recordings of an epileptic patient show the reoccurrences of spindling oscillations. Lower panel: 20 s of 3 EEG recordings of an epileptic patient show the alternative occurrences between spindling oscillations and SWD

Full size image

Computational models provide a potential way to explore the mechanisms underlying the typical 2-4 Hz SWD of epileptic absence seizures and its precusor, spindle oscillations, which have been investigated in numerous previous neural population models (Breakspear et al. 2006; Goodfellow et al. 2011; Taylor et al. 2014; Taylor and Baier 2011; Suffczynski et al. 2004; Sargsyan et al. 2007; Steyn-Ross et al. 2005a, b; Steyn-Ross et al. 2010; Wilson et al. 2005; Yousif and Denham 2005; Drover et al. 2010; Destexhe et al. 1998; O’reilly et al. 2015; Sinha et al. 2014). However, the effect of brain network topology on the emergence of SWD and spindles, as well as the spatiotemporal evolutions between them, have not been well understood. In addition, Taylor et al. (2013, 2014, 2015) developed a thalamocortical neural field model, as shown in Fig. 2a, to investigate the effects of stimulation on spike-wave discharges (SWD), thereby guiding studies about the initiations and abatements of epileptic absence seizure. Hence, using this single-compartment neural field model (Taylor et al. 2014) we first investigate the transitional dynamics and mechanism between SWD and slow-wave oscillations with the modulation of TRN due to its pacemaker role (Lewis et al. 2015). Next, we will expand the single-compartment thalamocortical neural field model into a coupled thalamocortical model, using 3 thalamocortical compartments with 2 unidirectionally connective configurations, linear and circular structures (Fig. 6a and b), respectively, to explore the spatiotemporal evolutions of the wave states in the different compartments. Finally, in order to demonstrate the qualitative stability of activity evolutions, i.e., independent of the number of nodes and topological structures of neural network, we further expand the 3-compartment coupled thalamocortical model into the 10-compartment coupled one, with the linear and circular structures (Fig. 6c and d), and the nearest-neighbor (NN) coupled network (Fig. 6e) as well as its realization of small-world (SW) topology via random rewiring (Fig. 6f), respectively. This approach allows to investigate the robustness of SWD spatiotemporal evolutions for network topology.

Fig. 2
figure 2

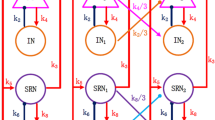
(Color online) Schematic diagrams of the computational models. a Single-compartment thalamocortical neural field model proposed by Taylor et al. (2014), which is composed of the cortical subnetwork consisting of the excitatory pyramidal neuronal population PY and the inhibitory interneuronal population IN, and the subcortical SRN-TRN circuit model which mainly consists of the specific relay nuclei (SRN) and the thalamic reticular nucleus(TRN) cells (Taylor et al. 2015). b A portion of coupled 3 compartments thalamocortical network. The connective mode is the same as the work of Yan and Li (2011). The lines with arrows indicate the excitatory synaptic functions, and the lines with the closed or open circles represent the inhibitory synaptic functions and the control inputs, respectively. The functions k 1, k 2,..., k 9 are the quantitative descriptions of the coupling among the different neuronal populations, PY, IN, SRN and TRN, respectively. The specific parametric values follow the previous works of Taylor et al. (2014, 2015). The function k 6 describes the inhibitory synaptic action from TRN to SRN, which is the critical bifurcation parameter to be considered in this paper

Full size image

2 Model description and method

2.1 Network structure and neural field model

2.1.1 A single-compartment of Taylor model

Neural field model was initially proposed to characterize the macroscopic dynamics of neuronal populations in a low computational cost. Absence seizure are known to arise in the thalamocortical circuit (Evangelista et al. 2015; Liu et al. 1991; Moeller et al. 2013).

Taylor et al. (2014) developed a thalamocortical model (see Fig. 2a for detail), which is based on the thalamocortical loop (Breakspear et al. 2006; Robinson et al. 2002), to investigate the stimulation in spike-wave discharges (SWD). As shown in Fig. 2(a), the minimal thalamocortical model is composed of the cortical excitatory pyramidal (PY) neuronal population and inhibitory interneuronal (IN) population in cortex area, as well as the subcortical SRN-TRN circuit model consisting of neuron populations of the specific relay nucleus (SRN) and thalamic reticular nucleus (TRN) (Taylor et al. 2014, 2015). The lines with arrows represent the excitatory projections mediated by glutamate. The lines with closed circles denote the G A B A A − mediated inhibitory projections. Specifically, a single-compartment Taylor model can be described as follows,

$$\begin{array}{@{}rcl@{}} \frac{\text{dPY}}{\text{dt}}&=& (\varepsilon_{\text{py}}-\text{PY}+\kappa_{1}\mathrm{F}[\text{PY}]-\kappa_{2}\mathrm{F}[\text{IN}]\\ &&+ \kappa_{3}\mathrm{F}[\text{SRN}])\tau_{1}+\mathrm{u}_{1}(\mathrm{t}), \end{array} $$
(1)
$$\begin{array}{@{}rcl@{}} \frac{\text{dIN}}{\text{dt}}&=& (\varepsilon_{\text{in}}-\text{IN}+\kappa_{4}\mathrm{F}[\text{PY}])\tau_{2}+ \mathrm{u}_{2}(\mathrm{t}), \end{array} $$
(2)
$$\begin{array}{@{}rcl@{}} \frac{\text{dSRN}}{\text{dt}} &=& (\varepsilon_{\text{srn}}-\text{SRN}+\kappa_{5}\mathrm{F}[\text{PY}]\\ &-& \kappa_{6}\mathrm{G}[\text{TRN}])\tau_{3}+\mathrm{u}_{3}(\mathrm{t}), \end{array} $$
(3)
$$\begin{array}{@{}rcl@{}} \frac{\text{dTRN}}{\text{dt}}&=& (\varepsilon_{\text{trn}}-\text{TRN}+\kappa_{7}\mathrm{F}[\text{PY}]+\kappa_{8}\mathrm{G}[\text{SRN}]\\ &-& \kappa_{9}\mathrm{G}[\text{TRN}])\tau_{4}+\mathrm{u}_{4}(\mathrm{t}) \end{array} $$
(4)

where PY represents the excitatory pyramidal neuronal population and IN represents the inhibitory interneuronal population, respectively. The parameters ε p y , ε i n , ε s r n and ε t r n are additive constants as used in the original version of Taylor model. The coefficients κ 1, κ 2,..., κ 9 are the connectivity strengths within different neuronal populations whose linking rules are in agreement with the experimentally known connection values (Pinault and O’Brien 2005) (also see Fig. 2(a)). F(x) = 1/(1 + υ −x) is the sigmoid transition function as used in model of Taylor (2014, 2015), where υ determines the steepness and x = PY,IN, SRN, TRN in Eqs. (1)–(4).

In particular, in order to simplify the analysis without qualitatively impacting the related dynamics, we simplified the thalamic subsystem by approximating the sigmoid function F(x) = 1/(1 + υ −x) with a linear activation term G(x) = α x + β, where x = SRN and TRN. This approximation is justified because the thalamic compartment is mainly operating in the linear range of the sigmoid for the SWD. Taylor et al. (2014) shows the qualitative agreement between the two versions of the model with sigmoidal and linear activation functions for the thalamic compartment including the existence of bistable SWD upon perturbation. This also follows the connection schematic as shown in the previous models of Taylor et al. (2014, 2015) and Pinault and O’Brien (2005). In addition, to mimic the effect of stimulation on SWD, we added a stimulus control u(t), i.e., a perturbation, on the cortical variables, PY and IN, in the state space.

2.1.2 The coupled thalamocortical model network

Spatially-extended networks have also been simulated to study the homogeneous or heterogeneous mode of SWD in cortex (Goodfellow et al. 2011; Taylor & Baier 2011; Fan et al. 2015; Jansen & Rit 1995; Ursino et al. 2010; Sotero et al. 2007). However, these model networks mainly focused on the macroscopic models of SWD which only incorporate cortico-cortical connectivities. However, subcortical structure, especially thalamus, has modulation role in the rhythmic generation mechanisms during absence seizures (Liu et al. 1991; Moeller et al. 2013). Therefore, there is a need for macroscopic models incorporating thalamocortico-thalamocortical connectivities. Further, spike-wave discharges (SWD) and sleep spindles are known to share common thalamo-cortical mechanism (Sitnikova et al. 2014a, b; Tamaki et al. 2008, van Luijtelaar et al. 1997). Thus, in this study, we introduce extensions to the original Taylor model by spatially expanding Taylor’s model into multi-compartment coupled network (see Fig. 6). Generally, 2 coupled compartments can be modeled as follows (also see Fig. 2b),

$$\begin{array}{@{}rcl@{}} \frac{\text{dPY}_{\mathrm{j}}}{\text{dt}} &=& (\varepsilon_{\text{py}}-\text{PY}_{\mathrm{j}}+\kappa_{1}\mathrm{F}[\text{PY}_{\mathrm{j}}]-\kappa_{2}\mathrm{F}[\text{IN}_{\mathrm{j}}]\\ &+&\kappa_{3}\mathrm{F}[\text{SRN}_{\mathrm{j}}])\tau_{1}+ {\mathrm{u}_{1}^{\mathrm{j}}}(\mathrm{t})+\frac{\kappa_{1}}{\mathrm{m}_{1}}\mathrm{F}\left[\mathrm{P}{\mathrm{Y}_{\mathrm{i}}^{\mathrm{S}}}\right]\\ &-&\frac{\kappa_{2}}{\mathrm{m}_{1}}\mathrm{F}\left[\mathrm{I}{\mathrm{N}_{\mathrm{i}}^{\mathrm{S}}}\right]+\frac{\kappa_{1}}{\mathrm{m}_{2}}\mathrm{F}\left[\mathrm{P}{\mathrm{Y}_{\mathrm{k}}^{\mathrm{L}}}\right]+ \frac{\kappa_{1}}{\mathrm{m}_{3}}\mathrm{F}\left[\mathrm{P}{\mathrm{Y}_{\mathrm{l}}^{\mathrm{D}}}\right], \end{array} $$
(5)
$$\begin{array}{@{}rcl@{}} \frac{\text{dIN}_{\mathrm{j}}}{\text{dt}} &=&(\varepsilon_{\text{in}}-\text{IN}_{\mathrm{j}}+\kappa_{4}\mathrm{F}[\text{PY}_{\mathrm{j}}])\tau_{2}\\ &+& {\mathrm{u}_{2}^{\mathrm{j}}}(\mathrm{t})+\frac{\kappa_{4}}{\mathrm{m}_{1}}\mathrm{F}\left[\mathrm{P}{\mathrm{Y}_{\mathrm{i}}^{\mathrm{S}}}\right], \end{array} $$
(6)
$$\begin{array}{@{}rcl@{}} \frac{\text{dSRN}_{\mathrm{j}}}{\text{dt}}&=&(\varepsilon_{\text{srn}}-\text{SRN}_{\mathrm{j}}+\kappa_{5}\mathrm{F}[\text{PY}_{\mathrm{j}}]-\kappa_{6}\mathrm{G}[\text{TRN}_{\mathrm{j}}])\tau_{3}\\ &+& {\mathrm{u}_{3}^{\mathrm{j}}}(\mathrm{t})+\frac{\kappa_{6}}{\mathrm{m}_{1}}\mathrm{G}\left[\text{TR}{\mathrm{N}_{\mathrm{i}}^{\mathrm{S}}}\right], \end{array} $$
(7)
$$\begin{array}{@{}rcl@{}} \frac{\text{dTRN}_{\mathrm{j}}}{\text{dt}}&=&(\varepsilon_{\text{trn}}-\text{TRN}_{\mathrm{j}}+\kappa_{7}\mathrm{F}[\text{PY}_{\mathrm{j}}]+\kappa_{8}\mathrm{G}[\text{SRN}_{\mathrm{j}}]\\ &-&\kappa_{9}\mathrm{G}[\text{TRN}_{\mathrm{j}}])\tau_{4}+ {\mathrm{u}_{4}^{\mathrm{j}}}(\mathrm{t})+\frac{\kappa_{8}}{\mathrm{m}_{1}}\mathrm{G}\left[\text{SR}{\mathrm{N}_{\mathrm{i}}^{\mathrm{S}}}\right]\\ &-&\frac{\kappa_{9}}{\mathrm{m}_{1}}\mathrm{G}\left[\text{TR}{\mathrm{N}_{\mathrm{i}}^{\mathrm{S}}}\right] \end{array} $$
(8)

where the subscripts i, j, k, l ∈{1, 2, ...,10} and i, k, l < j representing the unidirectional connectivity from the pre-compartment i, k, l to the post-compartment j.

In addition, it is believed that cortical excitatory pyramidal neurons have sufficiently long axons which can produce significant propagation effect on the distant neuronal populations, while other neural populations can only influence their adjacent areas due to the too short axons. Hereby, three types of inter-minicolumn connections are applied (see Fig. 6g), i.e., S: Short-range connective configurations as shown in Fig. 2b, L: Long-range excitatory connections from pyramidal neuronal populations, D: Distant excitatory connection from pyramidal neuronal populations at some distance. The connective strength, k i , is divided by m 1=3, m 2=6 and m 3=9 to respectively describe the effect of S-/L-/D-type of inter-minicolumn connectivities.

2.2 Model parameters

Most parameters in the model in this paper are from literature (Taylor et al. 2013, 2014, 2015; Baier et al. 2012, 2017; Taylor and Baier 2011; Fan et al. 2015; Wang et al. 2012) (see also the Tables 1 and 2) which were originally estimated from experimental data. However, due to lack of data, in inter-compartment connectivities, the parameters are estimated in numerical studies. In addition, in order to mimic the effect of stimulus-induced SWD, we performed a stimulus control ui(t) on the cortical variables, PY and IN, respectively, where u1(t) and u2(t) take the values in Table 1, and (u3(t),u4(t)) = (0, 0). The control parameters are the same as those used in Taylor et al. (2014). During the simulations, k 6 is the bifurcation parameter which varies in the physiologically reasonable range, while the other parameter values are kept the same as the Taylor model.

Table 1 Model parameters for the neuronal populations, PY, IN, SRN and TRN
Full size table
Table 2 In simulation results depicted in Figs. 3-12, coupling strengths, k 1, k 2,..., k 9, among the four different neuronal populations, PY, IN, TRN and SRN, are as follows
Full size table

2.3 Simulation method and data analysis

The MATLAB (MathWorks, USA) simulating environment is used to perform the numerical calculations. During the numerical simulations for both the single-compartment model or 3 coupled compartments networks, differential equations are solved by a standard fourth-order Runge-Kutta solver. Typically models are calculated for more than 20 s, we have the fixed temporal step of 1 ms. The simulation data of a stable state after 10 s are used for the steady state. The bifurcation (Zhao and Robinson 2015; Chen et al. 2014, 2015; Fan et al. 2015) and power spectrum analysis (Zhao et al. 2015; Zhao and Robinson 2015; Chen et al. 2014; Fan et al. 2015) are utilized to describe the occurrences, propagations and transformations of various critical dynamical features generated by our simulation and affected by the stimulations. Firstly, to explore the transitions between various dynamical states, the bifurcation and time frequency analysis are performed for the critical thalamic parameters, k 6. Therein, the bifurcation diagram is plotted by calculating the stable local minimum and maximum values of the average for the cortical excitatory and inhibitory neuronal populations. To evaluate the dominant frequency of neural oscillations, the spectrograms are estimated using the fast Fourier transform (FFT) for the time series of the average for the cortical excitatory and inhibitory neuronal populations. The maximum peak frequency of power spectral density (PSD) is defined as the dominant frequency. In particular, by combining techniques of both bifurcation and spectrogram analysis, the parametric regions corresponding to typical 2-4 Hz SWD oscillations can be outlined as well as propagations and evolutions of SWD can be observed at these regions.

3 Results

Based upon the Taylor model, we first focus on the effects of k 6, i.e., the coupling strength from TRN to SRN, on the occurrence of the SWD oscillation and its transition dynamics, with the introduction of stimulations or perturbations on the steady state. Next, we use the 3 compartments of thalamocortical field networks to investigate the propagations and evolutions of stimulus-induced epileptic SWD within the different compartments at different k 6 modulation. Finally, we investigate the evolution stability of SWD and spindling oscillations in complex topology of multimodule neural network with 10 compartments.

3.1 Single-compartment neural field model

3.1.1 Thalamic reticular nucleus (TRN)-induced transition from SWD to slow-wave oscillation

In this section, we investigate the transitions of SWD into other firing states induced by the inhibitory synaptic coupling strength of TRN projected into the SRN, as well as the effects of stimulations on the transitions of SWD.

Results in Fig. 3 show that without (Fig. 3a) and with (Fig. 3b) single-pulse stimulations onto the single-compartment system, the model can both display rich dynamics by varying the coupling strength, k 6, i.e., the inhibitory synaptic function from TRN to SRN, in [0, 4]. In particular, as shown in the upper panel of Fig. 3a, without stimulation the single-compartment model transits from the high saturated state in ‘I’ (Fig. 3c) to the periodic 1/2-spike and wave discharges in ‘II’ as the parameter k 6 changes in [0, 0.49]. Successively, transition to the low saturated state (‘III’) occurs when k 6 increases in the region of [0.49, 1.17]. Afterwards, with k 6 further increasing, the system transits between the bistable low saturated state and SWD in ‘IV’. Finally, for the large value of k 6, the system transits from low saturated state in ‘V’ into the slow-wave oscillations in ‘VI’, which occurs after around k 6 = 1.75. In the lower panel of Fig. 3a we present the variation of dominant frequency corresponding to the various firing states within the upper panel of Fig. 3a. From the evolutions of dominant frequencies, we observe several sudden jumps and dives which correspond to the critical transitions of different firing states. Compared the upper panel of Fig. 3a to the low panel of Fig. 3a, we see that the periodic 1/2-spike and wave discharges before left green bar is with at frequency of 2-4Hz, a hallmark of human epileptic absence seizures. While the periodic spike-wave discharge, i.e., SWD, after the right green bar has a relatively faster frequency of 4-10Hz except some single-points. Interestingly, as k 6 further increases, the system can subsequently transit into a low saturated state again. Next, as the value of k 6 passes around k 6 = 1.75, the system transits into slow-wave oscillations. This is consistent with observed experimental evidences that the increasing synaptic inhibition from TRN to SRN can gradually induce the slow-wave oscillations of deep sleep (Lee et al. 2013; Steriade et al. 1985; Krosigk et al. 1993; Rosanova and Ulrich 2005). Also, with the increasing k 6, the frequency of simple slow-wave oscillations is gradually increasing in the step-like fashion.

Fig. 3
figure 3

(Color online) a, b Bifurcation diagrams (upper panels) and corresponding dominant frequencies (lower panels) for a single-compartment model without single-pulse stimulations in (a) and with stimulation in (b), as the coupling strength, k 6, increases in [0, 4]. c The time series corresponding to the different states in (a). The corresponding parameters are set as: (I) k 6 = 0.1 (high saturated state), (II) k 6 = 0.4 (periodic 2-spike and wave discharges), (III) k 6 = 1 (low saturated state), (IV) k 6 = 1.3 (SWD) and (VI) k 6 = 3 (slow-wave oscillations). d shows the stimulus-induced periodical SWD at k 6 = 0.6. The close-ups of (d) are 2-4 Hz SWD, i.e., characteristic of epileptic absence seizure. The left black arrow in (a, b) indicates the parameter values where the 2-spike and wave discharges can be terminated by a single-pulse stimulation, while within the values of k 6 indicated by the right black arrow the SWD can be terminated by a single-pulse stimulation, e.g., e shows the stimulus-induced terminations of SWD at k 6 = 1.185. The parametric interval indicated by the two vertical green dashed lines is the interval where stimulations can induce the occurrences of SWD. (f) shows the time series as k 6 increasing in a step fashion with time. (f1) Synaptic function TRN → SRN, is a step function, increasing for t ∈ [4.3, 29] (unit: sec). Time series (upper panels) and the corresponding dynamic power spectrums (lower panels) are depicted in (f2) without stimulations, and the same activities under stimulations are in (f3). Zoom-in panels in (f2) and (f3) show ∼ 4Hz spike-wave discharges (SWD) and ~ 5Hz simple slow-wave oscillation, respectively

Full size image

However, after introducing the stimulation, as shown in Fig. 3b, periodic SWD can be induced by the stimulation or perturbation in the parametric region of [0.49, 1], indicated by the two green vertical dashed lines. Physiologically, this means that stimulation may lead to the occurrence of epileptic absence seizures characterized by 2-4Hz SWD, from the background state (i.e., low saturated state). For example, in the Fig. 3d we observe that as k 6 is taken at 0.6, the system initially lies in the background state before t = 20s. Then, we introduce the single-pulse stimulation at t = 20s with U(t) = (u1(t),u2(t),u3(t),u4(t))=(-0.3,-0.3,0,0), which represents the small negative perturbations on the system in the background state. After the introduction of stimulation, rhythmic SWD activities can be induced by the single-pulse stimulation indicated by the red vertical bar. Furthermore, the stimulation can also terminate the SWD back into the background low saturated state in the parametric region around [1.18, 1.195] (see also the red circle in the lower panel of Fig. 3b corresponding to the right black arrow in the upper panel). As shown in the Fig. 3e, when k 6 is taken at a larger value, e.g., k 6 = 1.185, the system displays SWD before introducing the stimulation. However, after we add a single-pulse stimulation, i.e., U(t) = (-0.3,-0.3,0,0) indicated by the red vertical bar, on the system, the SWD is terminated by the stimulation and the system transits from the SWD into the background state.

Compared Fig. 3d to e, it can be inferred that the effect of stimulation on the epileptic SWD can be modulated by the synaptic strength of TRN, i.e., k 6. In particular, Fig. 3f shows activity changes with assuming that the inhibitory synaptic coupling strength from TRN to SRN, k 6, is time-dependent and step-wise increasing for 0s ≤ t ≤ 30s, as shown in Fig. 3(f1). Along with the temporally increasing k 6= k 6(t), without the stimulation, the single-compartment neural field model system displays SWD with the basically decreasing amplitude but the increasing frequencies (Fig. 3(f2)). Particularly, as k 6 is increasing into around k 6 = 1.6 with t = 22s, the amplitudes SWD are damped into the background state. However, as the single-pulse stimulation indicated by the red bar (upper panel of Fig. 3(f3)) is introduced at around t = 25s, the simple slow-wave oscillations (close-up in the upper panel of Fig. 3(f3)) with the frequency of ~ 5Hz (lower panel of Fig. 3(f3)) can be induced. Hence, single-pulse stimulations can induce transitions from SWD to slow-wave oscillations.

3.1.2 The dynamical mechanisms underlying the stimulus-induced spike-wave discharges and slow-wave oscillations

In the last section, we have observed rich dynamical behaviors induced by TRN in the modified model. However, the dynamical bifurcation mechanisms underlying these activity transitions are still missing. Hence, in this section, we will elaborate the mechanistic explanations for the bifurcation mechanisms of these transitional behaviors. In particular, we will consider Fig. 3a as instance to mechanistically illustrate various dynamical transitions.

In Fig. 4b, the extrema of the model output for different values of k 6 are shown. Compared Fig. 4a to b, we can see that for the much small values (k 6 <≈0.2066) there is only one stable fixed point representing the high saturated state of the system. This follows a fold of cycles bifurcation (LPC1, Fig. 4b) at k 6 ≈0.2066 with giving birth to one stable limit cycle and one unstable, which results in a bistable region, 0.2066 <≈ k 6 <≈0.2308. That is the area of Fig. 4a indicated by the left first black rectangle, with the coexistence of a stable fixed point and a stable limit cycle. Accordingly, the system transits from the high saturated firings to the bistable states between the non-seizure state and SWD oscillations. Then the system enter into a monostable region (i.e., 0.2308 <≈ k 6 <≈0.3532, indicated by the green rectangle) following a subcritical Hopf bifurcation (HB1, Fig. 4b), where the stability of fixed points switches. However, the system can restore into the bistable state due to another subcritical Hopf bifurcation (HB2, Fig. 4b) at k 6 ≈0.3532, which accompanies the switch of fixed points from unstability to stability. Particularly, when k 6 ≈> 0.3968, a tristable region (i.e., 0.3968 <≈ k 6 <≈0.5094, indicated by pink rectangle) with two stable limit cycles and one stable focus arises following the second LPC bifurcation (LPC2) at k 6 ≈0.3968. Consecutively, the system can enter into the bistable region again due to the third LPC bifurcation (LPC3) at k 6 ≈0.5094. Further, when k 6 ≈> 1.336 but lower than k 6 ≈1.665, the bistable region disappears following the fourth LPC bifurcation (LPC4) at k 6 ≈1.336. The system transits into the background low saturated state. However, as k 6 ≈> 1.665, a bistable region reappears due to the fifth LPC bifurcation (LPC5). Compared Fig. 4b to a, we can see that the system then transits from the background low saturated state to simple slow waves (clonic) oscillations. Beyond the reappearance of unstable focus due to the supercritical Hopf bifurcation (HB3, Fig. 4b), another bistable region indicated by the last black rectangle (Fig. 4a) and composed of two stable limit cycles with different oscillation amplitudes (Fig. 4b) occurs. In addition, for much large values of k 6 (e.g., k 6 ≈> 4.926), the limit cycles with smaller oscillation amplitude disappears due to another LPC bifurcation (LPC6). Then the system transits into the monostable states again.

Fig. 4
figure 4

a Minima and maxima of time series for different values of k 6, corresponding to Fig. 3a. Colored rectangles represent the multi-stable parameter regions, where green rectangle indicates the monostability, black rectangles represent the bistable regions between non-seizure and SWD states, and pink rectangle corresponds to the tristable region, respectively. The green points indicated by L i (i = 1,2,...,6) correspond to the fold of cycles bifurcations (LPC), and the black points indicated by H j (j = 1,2,3) correspond to the Hopf bifurcation points (HB). The horizontal double arrows represent the potential spike wave discharges (SWD) of absence seizures and slow-wave oscillations of clonic epileptic seizures. Therein, the region indicated by the green rectangle represents the spontaneous SWDs. b Dynamical bifurcation diagram corresponding to the various state transitions in (a). As k 6 increasing, the system undergoes six LPC bifurcations indicated by green points and three Hopf bifurcations (HB) indicated by black points, respectively. LPC bifurcations occur at the transition between bistability and excitability. The stabilities of fixed points can be switched around HB bifurcations. Overall, the parameter regions consist of stable fixed point, stable limit cycles, bistable regions composed of stable limit cycle and stable fixed point (or two stable limit cycles with different amplitudes) and tristable region composed of stable fixed point and two stable limit cycles, respectively

Full size image

Overall, as k 6 increasing, the system can successively transits from high saturated state, SWD and low saturated state to the slow-wave oscillations. However, for the typical values of k 6 within the multistable regions, the system status will be eventually dependent on both the initial values of the four state variables and the applied stimulation perturbations. From the mathematical standpoint, in the bistable region of the four dimensional state space there exists a separating manifold, i.e., separatrix, similar to the blue lines shown in Fig. 4b, even though this manifold of system is structurally complex. In particular, when the initial values for the four state variables are close to the side of separatrix near the stable focus, the system will converge to the steady states, while the system will show the SWD or simple slow-wave oscillations when the initial values are close to the side of separatrix near the stable limit cycle. In addition, stimulation perturbations can change the time phase of system, which may drive the system beyond the separatrix and hence finally change the states of system. Thereby, as shown in Figs. 3a and b, the system presents rich dynamical transition behaviors, where all the initial values of the four state variables during the simulations are set to [0.1724, 0.1803, -0.0818, 0.2775]. By contrast, the monostable regions correspond to the spontaneous firing states of the system including the spontaneous SWD (see the region indicated by the green rectangle in Fig. 4a) and slow-wave oscillations.

3.1.3 The choice of stimulation parameter

As mentioned above, different activity states can transit between each other by typical single-pulse stimulations that drive the system from one basin of attraction to another. The pulse input, for example, can move a trajectory beyond a separatrix of a saddle point, into the basin of attraction of a steady state. Here, the basin of attraction of background state serves as the target for seizure abating stimuli. In general, a basic of attraction is non spatial-temporally uniform, even for background state. Efficient seizure abating stimuli typically depend on the amplitude and phase of the SWD cycle at the moment of stimulation, as well as the direction of the stimulus in state space. However, it has been demonstrated by the work of Taylor et al. (2014) that fixing the stimulation direction does not restrict the generality of the investigation, we thereby fix the stimulation direction to point to the PY and IN variables in state space and allow stimulation timing and amplitude to vary.

Figure 5a and b show the numerically reconstructed basin of the background state. In Fig. 5a, the basin appears to be closer the SWD attractor, hence SWD can be easily initiated and terminated by typical stimulation perturbations. By contrast, in Fig. 5b, slow-wave attractor appears to surround the basin, thus typical stimulation can induce the slow-wave oscillation from background state. However, the slow wave is not easily terminated into the background state. Figure 5c shows a time series for SWD at k6=1.185, where a stimulus of fixed amplitude with U(t) = (-0.3,- 0.3,0,0) was applied at different phases/time points. Stimulation outcome are labeled as successful and unsuccessful, colored in pink and cyan when the system can go and not go to background activity, respectively. Here, we observe that during the ascending phase of slow wave component in SWD, the stimulus to the cortical populations can terminate SWD. During the descending phase of slow wave component and the almost whole spike component in SWD, this particular single pulse stimulus can not stop the seizures. Figure 5d is a time series for one deterministic SWD cycle from Fig. 5c. In Fig. 5e, we simultaneously scanning the stimulation time points and stimulation amplitude during the same SWD cycle as Fig. 5d. The scan result is plotted depending on the two scanned parameters. The same color code as in (c) has been used. Yellow dashed line in (e) indicates the stimulation amplitude used in Fig. 5c. We can observe from Fig. 5e that for the majority of the time series, only weaker stimulations stop SWD seizures. This underlines that stronger stimulation does not necessarily lead to better success. There exists a phase in the later part of slow wave component in SWD where only moderate stimulations can not stop SWD oscillations. However, for the ending phase in slow wave component of SWD, termination can always not be achieved by the single-pulse stimulation. However, it is, in essence, the geometry of the basin of attraction that determines the outcome of a stimulation. The success depends on if the stimulus pushed the trajectory to reach over the basin of attraction.

Fig. 5
figure 5

(color online) Basin of attraction of the background state in the three dimensional state space corresponding to k 6 = 0.6 (a) and k 6 = 1.8 (b), respectively. Red lines indicate the SWD (a) and slow wave (b) attractors. Black dots indicate the background state. Colored dots are located in the basin of attraction of the background state. The SWD basin of attraction is not specifically shown, as it is simply the part in state space that is not the background basin. Stars show the stimulation timings, t=20s and 25s, respectively. c SWD firing series at k 6 = 1.185, where pink sections indicate the stimulation timings when SWD can be successfully terminated by single-pulse stimulations, while stimulation applied in the cyan sections can not successfully terminate the SWD. d Color coded time series of one cycle of SWD. The pink color indicates a return to the background fixed point if stimulated at the color-coded position using a fixed stimulus amplitude U(t) = (-0.3,-0.3,0,0). e Color coded map of stimulation amplitude and timing in the same SWD cycle corresponding to (d). The particular amplitude used for (d) has been outlined in a yellow line

Full size image

3.2 Stimulus-induced propagations and evolutions of SWD to the sleep-like UP-DOWN and spindle oscillations

In the last section, we mainly investigate the transitions of SWD into the slow-wave oscillations at different levels of k 6, i.e., the synaptic coupling strength from TRN to SRN, and induced by the inhibitory weak single-pulse stimulation or small perturbations. Electrophysiological experiments have long demonstrated transitions between SWD and deep sleep-like slow-wave oscillations including the UP-DOWN and spindle activities (Kostopoulos et al. 1981; Sanchez-Vives & Mccormick 2000; Crunelli et al. 2015; Eschenko et al. 2012). In this section, we explore the propagations, evolutions and transformations of SWD into the sleep-like UP-DOWN and spindle states in our network model. Specifically, we consider the 3 compartments of thalamocortical neural field model networks with the open (Fig. 6a) and closed (Fig. 6b) connective configurations. We focus on if these spatially-extended networks provide new dynamical routes to the spontaneous transitions and abatements of epileptic seizure activities.

Fig. 6
figure 6

(Color online) The unidirectional connective configurations of model network. a, c open-ended (or linear) connections; b, d close-ended (circular) connections; e Nearest neighbor coupled network characterized by p = 0. Each vertex is connected to its k =2 nearest neighbors; f Realization of small-world topology via random rewiring of a certain fraction p of links (in this case 2 out of all 20 were rewired, hence p = 0.1); g Three connective types of the model network, i.e., S: Short-range connections (see also Fig. 2b), L: Long-range excitatory connection, and D: Distant excitatory connection

Full size image

Connections in 3 coupled compartments are parameterized by connection strengths shown in Table 2. Using this extended network, we have chosen several data points from the connective and stimulating parameter spaces to produce previous experimental findings with the propagations and transitions from the epileptic SWD to the UP-DOWN and spindles states. The time series for different compartments are generated from stimulation perturbations to the background state of the first compartment. The power spectra derived from the time series and calculated by the fast Fourier transform (FFT) are also used to illustrate the oscillating frequencies.

3.2.1 Linearly-extended model network

We first consider the case of open connective model network, as shown in Fig. 6a. In Fig. 7a, we show the time series for the 3 coupled compartments with k 6 = 0.6 (a1) and introducing the stimulation perturbations of U1(t) = (−0.3,−0.3,0,0), indicated by the red vertical bar in Fig. 7(a 1) and (b1), onto the first compartment. Similarly, to Taylor model, without the stimulation (see Fig. 3a), each single-compartment displays the low saturated state as k 6 = 0.6. Whereas, a single-pulse stimulation can induce SWD as shown in Fig. 3b. In Fig. 7(a1), the stimulation is performed onto the first compartment in the background state at t = 20s. We provide a close-up showing the resulted ~ 3Hz SWD in epileptic absence seizures. In addition, Figs. 7(a2) and (a3) show the time series for the second and third compartments, respectively, displaying the background low-amplitude and high-frequency oscillations. However, compared the Fig. 7(a1) with Fig. 7(a2) and (a3), due to the successively synaptic propagating effects, different firing states have been induced in the second and third compartments. In particular, when the stimulus-induced SWD in the first compartment propagates into the third compartment, the SWD has transited into the slow UP-DOWN state in the deep sleep, as shown in the zoom-in panel of Fig. 7(a3). This may represent the propagations and transitions from epileptic SWD to the sleep UP-DOWN state.

Fig. 7
figure 7

(Color online) Simulation results for 3-compartment coupled model network with open connective configuration at k 6 = 0.6 (a) and k 6 = 0.8 (b), respectively. Time series of the average of the excitatory pyramidal neurons and inhibitory interneurons, i.e., (a1,b1): \(\frac {\text {PY}_{1}+\text {IN}_{1}}{2}\), (a2,b2): \(\frac {\text {PY}_{2}+\text {IN}_{2}}{2}\) and (a3,b3): \(\frac {\text {PY}_{3}+\text {IN}_{3}}{2}\), respectively. The synaptic stimulation perturbations are U1(t) = (\( u_{1}^{1} \)(t), \( u_{2}^{1} \)(t), \( u_{3}^{1} \)(t), \( u_{4}^{1} \)(t)) = (-0.3, -0.3, 0, 0), U2(t) = U 3(t)=0, beginning at the red vertical bars. The zoom-in panels in (a1) and (a3) show the periodic ~ 3Hz spike-wave discharges (SWD) and ~ 3Hz UP-DOWN slow-wave oscillations which are typical in the epileptic absence seizures and deep sleep, respectively. The zoom-in panels in (b1), (b2) and (b3) show the periodic ~ 3Hz spike-wave discharges (SWD), the spindles, i.e., ~ 13Hz waves grouped in sequences that recur with a rhythm of 0.6Hz, and the tonic oscillations with varying amplitude, respectively

Full size image

As the inhibitory synaptic function from TRN to SRN, i.e., k 6, increases into a larger value at k 6 = 0.8, each single-compartment also intrinsically remains in the background low saturated states without the stimulation perturbations. However, under the larger value of k 6 = 0.8, and a stimulation strength, U1(t) = (−0.3,−0.3,0,0), indicated by the red vertical bar and performed onto the first compartment, the system can not only induce the occurrence of ~ 3Hz SWD (see Fig. 7(b1)), but also induce the generations of deep sleep spindles (see Fig. 7(b2)) in the second compartment. The spindle oscillation is characterized by the ~ 13Hz waves grouped in sequences with a rhythm of ~ 0.6Hz. In addition, the synaptic function from the second compartment can induce the tonic oscillations of the third compartment.

3.2.2 Circularly-extended model network

In this section, we consider the closed (or circular) connective model network of the 3 compartments of neural field models. The connective configuration is shown in Fig. 6b.

As shown in Fig. 3a, when k 6 = 0.6 and without stimulation each compartment displays the background resting states. However, as we introduce the relatively weaker stimulation (e.g., U1(t) = (−0.01,−0.01,0,0) ) at t = 20s, this stimulation can induce the periodic spindles which can also be consistently observed on the whole 3 coupled compartments with the circular coupling, as shown in all Figs. 8(a1- a3). The spectrograms corresponding to the 3 compartments are given in Fig. 8(a4), where the two peaks of ~ 0.2Hz and ~ 13Hz represent the dominant frequencies between spindle-spindle and oscillations within the single spindle. As shown in the zoom-in panel of Fig. 8(a1) the spindles show ~ 13Hz oscillations grouped in sequences that repeats with a frequency of ~ 0.2Hz. Compare this to the outcome of the clinical situation displayed in the middle panel of Fig. 1b, periodic spindles is qualitatively comparable to the real spindling oscillations, even though in sleep the recurrence of spindles is separated by irregular intervals of arrhythmic dynamic for some seconds.

Fig. 8
figure 8

(Color online) The simulated results in 3-compartment coupled model network with circularly connective configuration, at k 6 = 0.6 and U1(t) = (\( u_{1}^{1} \) (t), \( u_{2}^{1} \)(t), \( u_{3}^{1} \)(t), \( u_{4}^{1} \)(t)) = (-0.01, -0.01, 0, 0), U2(t) =U3(t)=0. The stimulation is performed at the red vertical bar. The zoom-in panel in (a) shows the periodic ~ 0.2Hz spindles with the rhythmic waves of ~ 13Hz. (d): Power spectrums corresponding to the time series show 13Hz and 0.2Hz peaks of the spindle waves

Full size image

In order to examine the effect of periodic stimulations on the occurrences and transitions of SWD and spindles, we perform the periodical stimulations indicated by the red vertical bars in Fig. 8(b1) onto the first compartment with k 6 = 0.6, U1(t) = (−0.3,−0.3,0,0) and the interstimulus interval T = 20s. We observe in Fig. 8(b1) that periodic single-pulse stimulations initiated at t = 20s induce the periodic transitions from SWD to spindles illustrated by the zoom-in panels in Fig. 8(b1).

The power spectrums corresponding to the time series show the 0.025Hz, 0.2Hz, 3Hz and 13Hz peaks of the mixed mode oscillations in the system, including the SWD and spindles. The frequency of periodic transitions between SWD and spindles is ~ 0.025Hz, the frequency of SWD is ~ 3Hz, and the periodic ~ 0.2Hz spindles is with the rhythmic waves of ~ 13Hz. In addition, under the circularly connective network, the second and third compartments display the periodic transitions between simple tonic oscillations and spindles, hence the effects of periodic stimulations performed on the first compartments can also be found in the second and third ones.

It is noted that Fig. 8(b3) shows a transient. This is because when the stimulation effect performed on the first compartment propagates into the third one, it can only induce the transient insufficient initiations. However, we still can observe the evolution effects of multi-rhythmic activities among different compartments. In addition, it can be seen that this alternative mode of transitions between SWD and spindle is qualitatively comparable to the real seizure event shown in the lower panel of Fig. 1b.

3.2.3 New dynamics arising from the network model

We begin with coupled network composed of 3 identical thalamocortical subsystems or 3 compartments. As displayed above, the network model can produce the spindling oscillations in addition to the background state and SWD, even though spindling oscillations were not observed in the single-compartment model. In order to understand the spatialtemporal evolution of these activity states within the various compartments of coupled network, we look into the attractors of the system’s behavior and their basins of attraction.

From Figs. 7 and 8, we can infer that the coupled thalamocortical model network dynamics is mainly composed of seizure attractor, sleeping attractor (UP-DOWN and spindles) and background state attractor. In addition, interactions among the different compartments can be considered as perturbation inputs between each other, which can essentially affect activity states of each subsystem. We use unidirectional connectivity in our model. For each compartment, computational results indicated that the perturbation inputs (coupling strength) received from precompartment is stronger than its perturbation inputs to the postcompartment. Network’s strong oscillatory behavior can be spontaneously abated in finite time by impulse inputs.

Figure 9 shows the subsystem slices through the twelve dimensional basin structure of three subsystems by keeping eight model variables constant. Figure 9a and b show the UP-DOWN attractor and spindle attractor corresponding to the Fig. 7(a3) and (b2), respectively. This is because the high-amplitude SWD induced by the single-pulse stimulation applied on the first compartment can only make the following compartments reach the basin of the low-amplitude sleeping oscillation or background state attractors, with successively interactive perturbation inputs became weakening along the path. Figure 9c shows the coexistence of three attractors, i.e., SWD attractor, spindle attractor and background state attractor, corresponding to Fig. 8b. Figure 9d is the close-up of Fig. 9(c) showing the basin of attraction of the spindle and background states for the first compartment of circularly coupled network, where the values of the other two subsystems were chosen from the background tonic attractor in order to reduce the impacts of them to first subsystem. It was observed from Fig. 9d that spindle attractor and background tonic attractor are in close vicinity to each other, such that relatively weaker stimulation perturbation can induce the transitions from background to spindles. Therefore, for the circular network, weak stimulation can induce the spindles within the whole 3-compartment coupled network (see Fig. 8a) by means of the interactive perturbation inputs between different subsystems. Detailed investigations reveal that only the stimulation strength larger than 0.255 can induce SWD from the background state. Particularly, periodic strong stimulations can drive the system to recurrently shift between the basins of SWD attractor and spindle attractor, hence inducing the periodic transitions between seizure activity and spindling oscillations. Green, red, black and blue stars indicate the typical stimulation positions at t=20s, 40s, 60s and 80s. However, the scenario in first compartment can be weakened when it propagates into the following compartments due to the weak downstream perturbation inputs.

Fig. 9
figure 9

(Color online) Phase portrait spanned by the 3 fields TRN1,2,3, S R N 1,2,3 and Mean(PY1,2,3,IN1,2,3). a, b show the UP-DOWN attractor and spindle attractor, corresponding to the lower panel of Fig. 7a and middle panel of Fig. 7b, respectively. c show the SWD attractor, spindle (chaotic) attractors and background tonic (limit cycle) attractor. d is the partial close-up of (c), where red shows the spindle attractor and black shows the tonic attractor. Stars in (c) and (d) represent the stimulation timings in Fig. 8, where green, red, black and blue stars correspond to t=20s, 40s, 60s and 80s, respectively. Colored dots in (d) show the basin of attraction of the spindle and background states. The part in the state space that is not the spindle and background basin is the SWD basin of attraction

Full size image

3.3 Evolution stability of SWD and spindling oscillations in topology of multimodule neural network

Finally, in order to demonstrate the spatiotemporal evolution robustness of SWD and spindles obtained above, we further expand the 3-compartment coupled thalamocortical model network into the 10-compartment coupled one, with linear and circular structures, and nearest-neighbor (NN) coupled network as well as its realization of small-world (SW) topology via random rewiring, respectively (see Fig. 6).

Figure 10 shows the results of linearly coupled 10-compartment model network. It is seen from Fig. 10 that SWD (Fig. 10a) induced by single-pulse stimulation applied in the first compartment at t = 20s can first transit into the spindling oscillations of second compartment (Fig. 10b). After that, the system evolves into the simple tonic oscillations (Fig. 10c). However, as the network activities spread into the distant compartments, the system displays the spindle-like oscillations (Fig. 10d), and eventually the consistent irregular spindling oscillations (Fig. 10e). Next, we investigate the evolution effect of SWD within the circularly coupled 10-compartment model network. Similar to the case of 3-compartment model, the first step is to apply weak single-pulse stimulations into the first compartment, i.e., U1(t) = (-0.01, -0.01, 0, 0), as shown in Fig. 11(a1). Consequently, we can see from Fig. 11 that the whole system shows the irregular spindling oscillations, which are qualitatively consistent with those obtained by the 3-compartment models. In particular, when we applied the periodical stronger single-pulse stimulations into the first compartment, as shown in Fig. 11b, we observe the periodical transitions between SWD and irregular spindling oscillations (Fig. 11(b1)), which eventually evolve into the consistent irregular spindling oscillations.

Fig. 10
figure 10

(Color online) The simulation results of 10-compartment model network with linearly connective configuration at k 6 = 0.8 and U1(t) = (\( u_{1}^{1} \) (t), \( u_{2}^{1} \)(t), \( u_{3}^{1} \)(t), \( u_{4}^{1} \)(t)) = (-0.3, -0.3, 0, 0), Ui(t)=0 (i=2,3,...,10), the single-pulse stimulation at t=20s is indicated by the red vertical bars in (a)

Full size image
Fig. 11
figure 11

(Color online) The simulation results of 10-compartment coupled model network at k 6 = 0.6 with circularly connective configuration. a The single-pulse stimulation applied on the first compartment at t=20s are indicated by the red vertical bars (a1), i.e., U1(t) = (\( u_{1}^{1} \) (t), \( u_{2}^{1} \)(t), \( u_{3}^{1} \)(t), \( u_{4}^{1} \)(t)) = (-0.01, -0.01, 0, 0). b Periodic stimulations applied on the first compartment are indicated by the red vertical bars in (b1), i.e., U1(t) = (\( u_{1}^{1} \) (t), \( u_{2}^{1} \)(t), \( u_{3}^{1} \)(t), \( u_{4}^{1} \)(t)) = (-0.3, -0.3, 0, 0), the period of which is 20s. Ui(t)=0 (i=2,3,...,10)

Full size image

To observe the evolutions of SWD within the multi-compartment coupled network with complex topological structures, we consider two topological forms, i.e., nearest-neighbor (NN) coupled network (Fig. 6e) and the realization of small-world (SW) topology via random rewiring of a certain fraction of links (Fig. 6f). Figure 12 shows the results of NN-/SW-type coupled 10-compartment model network. As a whole, it can be seen from Fig. 12 that with SWD spreading from first compartment to other ones, both the activity wave amplitudes within the two type of coupled networks are gradually decreased. In particular, for the case of NN-type network, SWD firstly transits into the simple tonic oscillations (see Fig. 12(a2 −a5)). As the activity wave propagates into the sixth compartment spindle-like oscillations are induced (Fig. 12(a6)), which eventually evolves into the irregular spindling oscillations (Fig. 12(a7 −a10)). In contrast to the NN-type network, SWD eventually evolves into the consistent background tonic oscillations within SW-type network, except for the transient spindling oscillations in the fifth compartment (Fig. 12(b5)). This suggests the evolutions of SWD is sensitive to the network topology, given the lower rewiring probability, p = 0.01, of SW-type network with respect to NN-type network. However, the epileptic SWD can be ultimately transformed into the normal brain activities (spindles and background tonic oscillations), preventing the disease from spreading, which physiologically means the self-regulations of neural system.

Fig. 12
figure 12

(Color online)The simulation results of 10-compartment coupled model network at k 6 = 0.6 with two topological connectivities: a Nearest-Neighbor Coupled Network: U1(t) = (\( u_{1}^{1} \) (t), \( u_{2}^{1} \)(t), \( u_{3}^{1} \)(t), \( u_{4}^{1} \)(t)) = (-0.3, -0.3, 0, 0), Ui(t)=0, (i=2,3,...,10); b Small-world Network: U1(t) = (-0.25, -0.25, 0, 0) and Ui(t)=0, (i=2,3,...,10). The single-pulse stimulations applied on the first compartment at t=20s are indicated by the red vertical bars (a1, b1). The zoom-in panels show the SWD, tonic and spindling oscillations

Full size image

4 Conclusion and discussion

In this paper, based on the recent experimental findings that thalamic reticular nucleus (TRN) can be the pacemaker of the slow sleep waves (Lee et al. 2013; Lewis et al. 2015; Ferrarelli and Tononi 2017), we began with a minimal single-compartment thalamocortical neural field model to study the effect of TRN on the generations, transitions and propagations of SWD and sleep-like waves including the UP-DOWN and spindle states. It was found that with increasing of the inhibition from TRN to SRN the system can lead to the transitions from SWD to slow-wave oscillation. Particularly, it was shown that stimulation can induce the occurrences of both the SWD and slow-wave oscillation in a specific parametric intervals of TRN, hence leading to the evolutions from SWD to slow-wave oscillations. Then, we considered an extended model networks composed of 3 compartments with the linearly and circularly connective configurations, respectively, to explore propagations among different compartments. It was shown that, for the case of linear connections, stimulation can induce the extended network system to show slow-wave states of brain, especially the UP-DOWN and spindles states. However, for the case of circular connection, weak stimulations can induce the consistent spindle waves, while the stronger periodic single-pulse stimulations can induce the periodic transitions between SWD and spindles. Overall, the cortical close-ended connectivity benefits the rich waveform transformations in electronic activities, but the cortical open-ended connectivity facilitates the propagation of activity waves. Furthermore, to demonstrate the evolution robustness of wave activity with respect to the topological structures of neural network, we further expand the 3-compartment coupled network into the larger 10-compartment coupled one, with the linear and circular structures, and the nearest-neighbor (NN) coupled network as well as its realization of small-world (SW) topology via random rewiring, respectively. Interestingly, qualitatively similar results were obtained for the cases of linear and circular connectivities, while NN and SW networks can suppress the brain activity wave into the low-amplitude oscillations.

Slow wave between 0.75 Hz to 4.5 Hz commonly associated with sleeping rhythms of normal human is well known to researchers (Achermann and Borbely 1997; Amzica & Steriade 1997), it can be detected through in-vivo EEG human study. There are also several modeling studies to capture this important feature of sleeping rhythms and implore other transition features (Goodfellow et al. 2011; Taylor et al. 2014; Taylor and Baier 2011, among others). Slow wave is very important for sleeping rhythm study and is a hallmark for classifying sleeping periods (awake, shallow sleep, deep sleep, etc) of a normal human subject. However, our model study focuses on seizure patients, and is on the transition mechanism from SWD to spindle for the specific time period before and after the onset of seizures. In the seizure model, the kind of slow wave 0.75-4.5Hz of normal human cannot be materialized, at least to the extend of this model. In single compartment Taylor model of seizure patient, the slow wave is indeed clonic slow wave, as seen in Fig 3a. The frequency is in the range of 5-10 Hz. Since the type of slow wave observed by (Achermann and Borbely 1997) in-vivo EEG of normal person, we have also looked at network model computed results for comparison with normal sleeping rhythm slow wave. We did not observe any typical sleeping slow waves in our network model, but we have observed a mixed mode oscillation of spindles, and the dominant frequency is at 0.2 Hz and a high frequency tonic oscillations of 13Hz (Fig. 8). Thus the seizure patient model reflects a mix of sleeping rhythm and clonic onset. There is a significant difference between normal vs seizure subject.

Neural population models can be used to describe the macroscopic neural activity which can be clinically recorded by EEG. These models provide an effective way to examine the effect of control simulation strategies (Breakspear et al. 2006). In this study, spatially-extended model networks composed of multiple compartments are used to replicate spatiotemporal patterns commonly observed in both the experimental electrophysiology and human EEG during generalized seizures. Exactly, it is compared to traces from different EEG electrodes. In particular, our results that the epileptic SWD can be ultimately transformed into the normal brain activities, i.e., low-amplitude spindles and background tonic oscillations, can be considered as the self-terminations of epileptic seizures preventing the disease from spreading, which physiologically means the self-regulations of neural system.

However, the connection between non-REM sleep rhythms and epileptic SWD is complex and seems to point to a number of dynamic mechanisms. For example, information transmission delays are inherent to the nervous system (Guo et al. 2016a, b; Wang et al. 2009), which has been widely found to perform key roles in taming neurodynamics, thus inducing transitions between different dynamical patterns. Therefore, more sufficient dynamical mechanisms underlying the transitions between SWD and sleeping UP-DOWN and spindle oscillations still need to be further explored. We hope that our results will inspire testable hypotheses for electrophysiological experiments in the near future.