1 Introduction

In materials science and engineering, alloy formation is used to control various physical properties of semiconductors, especially the magnitude of the bandgap and hence the optoelectronic properties, to achieve the requirements for certain applications of semiconductor devices. Although this may be achievable through the formation of ternary alloys, the possibility of the formation of quaternary alloys opens a further avenue and represents an enhanced technique to tune various physical properties of semiconductors more precisely and hence widen their applications.

Group IIB–VIA semiconductors such as ZnSe, ZnTe, CdSe, and CdTe are well-known materials for use in microelectronic and optoelectronic applications. The ambient phases of both ZnSe and ZnTe [1] as well as CdSe and CdTe [2] include cubic zincblende (B3) and wurtzite (B4). CdSe and CdTe are widely used as efficient optical materials in the manufacture of visual displays, solid-state laser devices, photodetectors and sensors, light-emitting diodes, blue–green laser diodes [3,4,5], photovoltaic devices and solar cells [6,7,8,9], high-quality quantum rods and their heterostructures [10], nanocrystals [11,12,13], nanowires [14, 15], quantum dots [16, 17], CdTe nanorod arrays for efficient solar energy conversion [18], etc. On the other hand, both ZnSe and ZnTe are widely used in the manufacture of blue–green laser diodes [19], optical waveguides [20], and wide-bandgap heterostructure lasers [21].

The potential of such materials for use in different application areas has been established based on experimental studies of the electronic structure [22,23,24,25], optical properties [26, 27], and elastic properties [28, 29] of bulk CdSe, CdTe, ZnSe, and ZnTe. Experimentally, growth and optical characterization of CdSe thin films [30], characterization of the photosensitivity of CdSe thin films [31], photovoltaic applications of CdTe thin films [32], optical characterization of nanocrystalline CdTe thin films for solar cell applications [33], optical characterization of ZnSe thin films [34], deposition as well as structural and electrical characterization of ZnTe thin films [35], photoluminescence study of ZnTe thin films [36], structural and optical characterization of ZnTe epilayers [37], etc. have been performed for use in different potential applications.

In the case of bulk group II–VI ternary alloys, as well as their thin films and nanostructures, experiments have identified n-CdSe0.7Te0.3/p-CdSe0.15Te0.85 alloys as efficient materials for use in solar cells [38], CdSexTe1−x nanocrystal solar cells as a highly efficient and cost-effective alternative to conventional silicon-based photovoltaic cells [39], and CdSexTe1−x alloy nanocrystals as an efficient materials for use in graded-bandgap solar cells [40]. In addition, the synthesis of rod-shaped/irregular dot-shaped CdSexTe1−x semiconductor nanocrystals for the fabrication of solar cells [41], the synthesis of colloidal ZnTe1−xSex quantum dot (QD) semiconductor alloys as well as the study of the composition and size dependence of their optical gaps [42], the solution-phase synthesis of ZnSexTe1−x ternary alloy nanowires as well as the study of their bandgap bowing [43], the synthesis, optical characterization, and application-oriented studies of ZnSexTe1−x ternary alloy nanowires [44], etc. have been performed. Growth and characterization of zincblende ZnxCd1−xSe single-crystal films [30], ZnCdSe heterostructures [45], ZnCdSe∕ZnSe quantum well (QW) structures [46], and ZnCdSe-ZnSSe multiple quantum well (MQW) structures [47] have been performed due to their versatile optoelectronic and photovoltaic applications. Also, the growth and characterization of CdZnTe thin films have been performed for their photovoltaic applications [48] as well as for photoinduced electrical data storage [49]. Moreover, close-spaced vacuum sublimation deposition of thick polycrystalline Cd1−xZnxTe films and their structural and optical characterization were performed by Znamenshchykov and coworkers [50]. Wang and coworkers prepared promising materials to design more cost-effective solar cells by manipulating the depletion region of CdxZn1–xTe nanocrystal solar cells [51]. Levy and coworkers showed that compositional tuning of the optical bandgap, electronic states, and electrochemical potential of ternary Zn1−xCdxTe quantum dots (QDs) can endow them with the ability to address the growing threat of antimicrobial-resistant infections [52].

In the case of cadmium–zinc chalcogenide quaternary alloys, several experimental studies have been performed to date. Molecular beam epitaxial (MBE) growth of Cd1−yZnySexTe1−x quaternary alloys was performed by Chen and coworkers [53]. Moreover, ZnCdSeTe layers are efficient active layers for light-emitting diodes (LEDs) and laser diodes (LDs) emitting in the red to yellow–green range [54]. MBE-grown Zn1−yCdySexTe1−x layers on GaAs substrates are suitable for the formation of ZnSe/ZnCdSeTe heterostructures [55]. Spray pyrolysis growth of CdZnSeTe and their optical and electrical characterization were performed by Gaikwad and coworkers [56]. Cd0.9Zn0.1Te0.98Se0.02 with compositional homogeneity and reduced defects was grown by Roy and coworkers as a new gamma-ray spectroscopic material, having a wide range of applications in medical imaging, nonproliferation, high-energy physics, and astrophysics [57].

On the theoretical side, the structural, elastic, electronic, optical, and thermodynamic properties, etc., of bulk diatomic zincblende CdSe and CdTe [58,59,60,61,62,63,64,65,66,67,68,69,70,71,72], ZnSe and ZnTe [68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84], bulk pure CdSe1−xTex ternary alloys [85,86,87], and ZnSexTe1−x [88,89,90,91,92] as well as bulk mixed ternary alloys CdxZn1−xSe [93, 94] and Cd1−xZnxTe [95,96,97,98] have been studied in the framework of different DFT-based approaches, especially the FP-LAPW approach, and applying a variety of different exchange–correlation potential schemes. Theoretical studies on some other chalcogenide ternary alloys with zinc or cadmium as one of the constituents have also been performed [99, 100]. Moreover, based on first-principles calculations, Zhou proposed various possible structures for two-dimensional (2D) ZnX and CdX (X = S, Se, and Te) materials, which have applications in energy storage and conversion due to their unique electronic structure and optical properties [101].

In the case of bulk quaternary CdZnSeTe alloys, theoretical studies have been carried out on topics such as the optical properties of zincblende CdxZn1−xSeyTe1−y under the conditions of lattice matching to a ZnTe substrate using the pseudopotential approach in the virtual crystal approximation (VCA) [102] and the electronic band structure of ZnyCd1−ySexTe1−x quaternary alloy involving the effects of compositional disorder and bond relaxation using a tight-binding formalism within the VCA [103]. However, those studies covered a very limited number of compounds and properties. Therefore, a detailed theoretical study of various properties of all the compounds in the CdxZn1−xSeyTe1−y quaternary system using an appropriate exchange–correlation (XC) potential scheme is necessary across the whole range of Cd concentration (x) and Se concentration (y).

The results of the first-principles calculations of the structural, electronic, and optical properties of cubic CdxZn1−xSeyTe1−y quaternary alloys as well as the corresponding binary and ternary compositions are reported herein across the whole range of cationic (x) and anionic (y) concentrations (x, y = 0.0, 0.25, 0.50, 0.75, and 1.0) using reliable XC potential schemes. Moreover, the dependence of the said properties on the anionic (Se) concentration (y) and cationic (Cd) concentration (x) is investigated in detail. The results of these calculations suggest new experiments and that such alloys could be potential candidates for use in different optoelectronic and photovoltaic applications.

2 Computational details

Density functional theory (DFT) [104, 105] has proven to be one of the most accurate methods for the computation of the electronic structure of solids [106,107,108,109,110,111,112]. The DFT-based full-potential linearized augmented plane wave (FP-LAPW) methodology [113] has been implemented successfully in the WIEN2k code [114, 115], and is used to calculate the structural, electronic, and optical properties of binary, ternary, and quaternary materials in the CdxZn1−xSeyTe1−y quaternary system in the present study. For the structural properties, the XC potentials are calculated using the Perdew–Burke–Ernzerhof generalized gradient approximation (PBE-GGA) scheme [116], while the modified Becke–Johnson (mBJ) [117, 118] and Engel–Vosko generalized gradient approximation (EV-GGA) [119] schemes are utilized for efficient calculations of the XC potentials for the electronic and optical properties. For visualization purposes and to carry out some analyses, the graphical code XCrySDen [120] is also applied in the present study.

In the FP-LAPW approach, Kohn–Sham wavefunctions inside non-overlapping muffin-tin spheres surrounding the atomic sites are expanded in spherical harmonics with a maximum value of the angular momentum of lmax = 10. The same are expanded using a plane-wave basis set in the interstitial region of the unit cell using a cut-off value of Kmax = 8.0/RMT, where RMT is the smallest muffin-tin radius and Kmax is the magnitude of the largest K-vector in the plane wave expansion. The potential and charge density Fourier expansion parameter Gmax is taken as 16 Ry1/2. The RMT values of Cd, Zn, Se, and Te are taken as 2.4, 2.5, 2.3, and 2.5 a.u., respectively. The Brillouin zone integrations are performed using a mesh of 5000 k-points. Both the plane wave cut-off and the number of k-points are varied to ensure total energy convergence, achieved via self-consistent field (SCF) calculations, when the energy is less than a threshold value of 10−5 Ry.

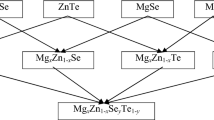
The CdxZn1−xSeyTe1−y quaternary system is surrounded by two cationic ternary systems, viz. CdxZn1−xSe and CdxZn1−xTe, as well as two anionic ternary systems, viz. ZnSeyTe1−y and CdSeyTe1−y. They are again formed from the four binary compounds ZnSe, ZnTe, CdSe, and CdTe. Therefore, the eight-atom 1 × 1 × 1 cubic zincblende unit cell of these binary compounds is designed by using the experimental lattice parameters of ZnSe, ZnTe, CdSe, and CdTe [26] in the introductory stage. The eight-atom cubic anionic ternary (pseudobinary) alloys ZnSeyTe1−y and CdSeyTe1−y with y = 0.25, 0.50, and 0.75 are designed by successive substitution of Te atom(s) with Se atom(s) in the 1 × 1 × 1 unit cell of ZnTe and CdTe, respectively. Similarly, the eight-atom cubic cationic ternary alloys CdxZn1−xSe and CdxZn1−xTe with x = 0.25, 0.50, and 0.75 are designed by successive replacement of Zn atom(s) with Cd atom(s) in the 1 × 1 × 1 unit cell of ZnSe and ZnTe, respectively. The quaternary (pseudoternary) alloys CdxZn1−xSeyTe1−y with x = 0.25, 0.50, and 0.75 are designed by using a cationic substitution process, i.e., consecutive substitution of Zn atom(s) with Cd atom(s) in the cubic unit cells of the anionic ternary alloys ZnSeyTe1−y (y = 0.25, 0.50, and 0.75), and each of the resultant nine quaternary structures is also an eight-atom cubic cell. They can also be formed from the other three ternary systems by cationic/anionic substitution. A schematic diagram of the procedure for the formation of the ternary and quaternary alloys from their basic constituent binaries [121] is shown in Fig. 1. The crystal structures of the nine newly designed quaternary materials in the Cd0.25Zn0.75SeyTe1−y, Cd0.50Zn0.50SeyTe1−y, and Cd0.75Zn0.25SeyTe1−y systems are shown in Supplementary Figs. S1(a–c), S2(a–c), and S3(a–c), respectively, for y = 0.25, 0.50, and 0.75 in the Electronic Supplementary Material.

Fig. 1
figure 1

A schematic diagram showing the formation of the ternary and quaternary alloys in the CdxZn1−xSeyTe1−y system from their basic constituent binary compounds

Full size image

In the present study, the concentration dependence of the structural, electronic, and optical properties of the CdxZn1−xSeyTe1−y quaternary system is investigated in two ways. In the first way, we consider the entire anionic concentration range with y = 0.0, 0.25, 0.50, 0.75, and 1.0 at each of five cationic concentrations, viz. x = 0.0, 0.25, 0.50, 0.75, and 1.0, and hence investigate the effects of successive anionic substitution on these properties at each of the cationic concentrations. In the second way, we consider the entire cationic concentration range with x = 0.0, 0.25, 0.50, 0.75, and 1.0 at each of five anionic concentrations y = 0.0, 0.25, 0.50, 0.75, and 1.0 and investigate the effects of successive cationic substitution on the aforesaid properties at each of the anionic concentrations. In both ways, the qualitative nature of the specimens in each subsystem, formed at either fixed x or y, is similar, as shown in matrix form in Table 1.

Table 1 A matrix presenting the qualitative nature of each specimen with different x and y values
Full size table

3 Results and discussion

3.1 Structural properties

The structural properties of the binary, ternary, and quaternary specimens in the CdxZn1−xSeyTe1−y quaternary system are computed using the structural optimization technique, where the total energy of each of the designed unit cells is minimized with respect to the cell parameters as well as the atomic positions. The total energy of each unit cell at different volumes around the equilibrium unit cell volume are calculated using the self-consistent field (SCF) technique, and the resultant parabolic variation is fit using Murnaghan’s equation of state [122], yielding the ground-state structural parameters, such as the minimum energy (\( E_{0} \)), equilibrium volume (\( V_{0} \)), equilibrium lattice parameter (\( a_{0} \)), bulk modulus (\( B_{0} \)), and first-order pressure derivative of the bulk modulus (\( B_{0}^{\prime } \)), for each sample (Table 2). Some available experimental and earlier theoretical structural data for the specimens are also included in Table 2 for comparison.

Table 2 The calculated \( a_{0} \), \( B_{0} \), and \( B^{/} \) values of the specimens in the CdxZn1−xSeyTe1−y quaternary system
Full size table

3.1.1 The lattice constant and bulk modulus of the binary, ternary, and quaternary specimens

For the binary compounds ZnSe and ZnTe, our computed structural data can be compared with some available experimental \( a_{0} \), \( B_{0} \), and \( B_{0}^{\prime } \) data [22, 23, 28]. In the case of the other pair of binary compounds, i.e., CdSe and CdTe, only experimental \( a_{0} \) and \( B_{0} \) data [22, 23] are available, while no \( B_{0}^{\prime } \) data are available for comparison. Our computed \( a_{0} \) and \( B_{0} \) values for ZnSe, ZnTe, CdSe, and CdTe are in excellent agreement with the respective experimental data. In the case of \( B_{0}^{/} \) of this pair of zinc chalcogenides, our computed data for ZnSe is overestimated by 0.271 while that for ZnTe is underestimated by 0.278, with respect to the corresponding experimental data [22, 28]. Our computed \( a_{0} \), \( B_{0} \), and \( B_{0}^{\prime } \) data for the said binary compounds can also be compared with some available earlier theoretical data for ZnSe and ZnTe [70, 71, 73, 77, 79,80,81,82,83,84, 91] as well as CdSe and CdTe [60, 61, 63,64,65,66, 68, 70, 71, 86, 87], revealing good agreement between our computed lattice constant and bulk modulus data for the binaries and several corresponding sets of earlier theoretical data.

No experimental structural data for the anionic ternary alloys ZnSeyTe1−y and CdSeyTe1−y or cationic ternary alloys CdxZn1−xSe and CdxZn1−xTe are unavailable for comparison. However, our computed \( a_{0} \) and \( B_{0} \) data for these ternary alloys can be compared with a few available earlier theoretical data for the corresponding specimens in the ZnSeyTe1−y [91], CdSeyTe1−y [86, 87], and CdxZn1−xSe [94] systems as well as earlier theoretical \( a_{0} \) data for ternary alloys in the CdxZn1−xTe system [96]. The calculated \( a_{0} \) value for each of the anionic ternary alloys ZnSeyTe1−y and CdSeyTe1−y as well as the cationic ternary alloys CdxZn1−xSe is marginally underestimated, while the \( B_{0} \) value calculated for each of them is marginally overestimated with respect to the corresponding earlier theoretical data. On the other hand, we note marginal overestimation of our calculated \( a_{0} \) value compared with the corresponding earlier theoretical data in case of each of the ternary alloys in the CdxZn1−xTe system.

In the case of the quaternary specimens in the CdxZn1−xSeyTe1−y system, we are unable to compare our computed structural data due to the lack of such experimental or earlier theoretical data in the literature.

3.1.2 The concentration dependence of the lattice constant and bulk modulus

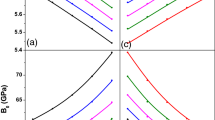
In the present study, the concentration dependence of \( a_{0} \) and \( B_{0} \) for the specimens in the CdxZn1−xSeyTe1−y quaternary system is investigated over the entire cationic and anionic concentration range with x/y = 0.0, 0.25, 0.50, 0.75, and 1.0. At each of the five specified cationic (Cd) concentrations x, it is observed that the lattice constant \( a_{0} \) decreases nonlinearly with increasing anionic (Se) concentration y, and each such variation is shown in Fig. 2a. In this case, the substitution of tellurium atom(s) of greater radius (1.23 Å) with selenium atom(s) of smaller radius (1.03 Å) decreases the volume of the cubic unit cell and thereby the lattice constant \( a_{0} \). Due to the inverse proportionality between the lattice constant and bulk modulus, a nonlinear increase in \( B_{0} \) and hence the hardness of the specimen with increasing anionic (Se) concentration y at each of the five aforesaid cationic concentrations x is shown in Fig. 2b.

Fig. 2
figure 2

The variation of the calculated a\( a_{0} \) with the Se concentration y at each of the fixed Cd concentrations x, b\( B_{0} \) with the Se concentration y at each of the fixed Cd concentrations x, c\( a_{0} \) with the Cd concentration x at each of the fixed Se concentrations y, and d\( B_{0} \) with the Cd concentration x at each of the fixed Se concentrations y for the specimens in the CdxZn1−xSeyTe1−y quaternary system

Full size image

Again, at each of the five fixed values of the anionic (Se) concentration y, the lattice constant \( a_{0} \) is observed to increase nonlinearly with increasing cationic (Cd) concentration x, with each such variation being shown in Fig. 2c. The substitution of zinc atom(s) of smaller radius (1.42 Å) with cadmium atom(s) of greater radius (1.61 Å) is responsible for the increase in the cubic unit cell volume and thereby the lattice constant \( a_{0} \). From this, we observe a nonlinear decrease in the bulk modulus \( B_{0} \) and hence the hardness of the specimen with increasing cationic (Cd) concentration x at each of the five aforesaid anionic concentrations y, as shown in Fig. 2d.

For an ideal alloy system, Vegard’s law [123] suggests a linear concentration (x/y) dependence (LCD) for the lattice constant (\( a_{0} \)), while experimental studies [124, 125] confirm a nonlinear variation in a real alloy system, having the form

$$ a(x) = \alpha_{a} + \beta_{a} x + \delta_{a} x^{2}. $$
(1)

The nonlinear coefficient \( \delta_{a} \) is known as the bowing parameter of the lattice constant versus concentration curve for any real alloy system, and can be calculated by fitting the corresponding \( a_{0} \) versus concentration (x/y) curve using Eq. 1. A similar quadratic relationship can also quantitatively explain the nonlinearity in the concentration dependence of the bulk modulus in any real alloy system, where the nonlinear coefficient \( \delta_{B} \) measures the bowing in the bulk modulus versus concentration curve.

Here, the \( a_{0} \) versus y curve at each of the cationic concentrations x as well as \( a_{0} \) versus x curve at each of the anionic concentrations y shows marginal upward bowing due to the marginal mismatch between the lattice constants of the terminal binary/ternary compounds. On the other hand, each of the \( B_{0} \) versus y as well as \( B_{0} \) versus x curves at each fixed x and y, respectively, exhibits small downward bowing due to the small mismatch between the bulk modulus of the corresponding terminal binary/ternary compounds. In the case of the lattice constant as well as the bulk modulus versus anionic/cationic concentration curves, the respective calculated bowing parameters \( \delta_{a} \) and \( \delta_{B} \) are presented in Table 3. It is observed that \( \delta_{a} \) decreases while \( \delta_{B} \) increases gradually as one proceeds from ZnSeyTe1−y to CdSeyTe1−y via consecutive replacement of Zn with Cd atom(s). In contrast, \( \delta_{a} \) increases while \( \delta_{B} \) decreases gradually as one proceeds from CdxZn1−xTe to CdxZn1−xSe via consecutive replacement of Te with Se atom(s).

Table 3 The bowing parameters calculated from the concentration dependence curves of \( a_{0} \) and \( B_{0} \)
Full size table

The calculated contour plots for \( a_{0} \) versus x and y are shown in Fig. 3a, while that for \( B_{0} \) versus x and y is shown in Fig. 3b in the case of the CdxZn1−xSeyTe1−y quaternary system, where deviations of both \( a_{0} \) and \( B_{0} \) in each system from their respective LCD can be observed again. The \( a_{0} \) or \( B_{0} \) of any ternary or quaternary specimen corresponding to any x/y composition in the range 0 ≤ x, y ≤ 1 can be evaluated from the corresponding contour plot.

Fig. 3
figure 3

The contour maps of the calculated a lattice constant \( a_{0} \) and b bulk modulus \( B_{0} \) versus the compositions x and y for the CdxZn1−xSeyTe1−y quaternary alloys

Full size image

3.2 Electronic properties

The experimental or theoretical study of the electronic properties of any semiconductor is necessary to investigate its appropriateness for the fabrication of microelectronic or optoelectronic devices. In the present work, density functional calculations of the electronic properties of the binary, ternary, and quaternary specimens in the CdxZn1−xSeyTe1−y quaternary system are performed using the mBJ and EV-GGA schemes for the computation of the necessary XC potentials. The bandgap for each of the said specimens calculated using both XC functionals is presented in Table 4. In addition, some available experimental as well as some earlier theoretical bandgap values are also presented in Table 4 for comparison. Table 4 also shows that, in the case of each of the specimens under consideration and for both XC functionals employed, the calculated bandgap follows the trend \( E_{\rm g}^{\text{mBJ}} > E_{\rm g}^{{{\text{EV-GGA}}}} \).

Table 4 The minimum bandgap (\( E_{\rm g} \)) of the specimens in the CdxZn1−xSeyTe1−y quaternary system calculated using the mBJ and EV-GGA functionals
Full size table

3.2.1 Band structure

The band structure computed for each of the binary compounds ZnSe, ZnTe, CdSe, and CdTe exhibits a direct minimum bandgap (\( \varGamma \)–\( \varGamma \)) in the zincblende phase when using both XC functionals. Some experimental observations for ZnSe and ZnTe [22, 24, 25] as well as CdS and CdSe [22, 24] also support such qualitative features of the respective calculated band structures. The ternary specimens in the ZnSeyTe1−y, CdSeyTe1−y, CdxZn1−xTe, and CdxZn1−xSe systems also indicate a direct bandgap (\( \varGamma \)–\( \varGamma \)). Although no experimental information is available regarding the qualitative features of the band structure of any of these ternary alloys, the computed results can be compared with some respective earlier theoretical findings for ZnSeyTe1−y [90], CdSeyTe1−y [86, 87], CdxZn1−xSe [94], and CdxZn1−xTe [96], revealing good agreement. In the case of the band structure of each of the nine quaternary specimens in the CdxZn1−xSeyTe1−y system, a direct fundamental bandgap (\( \varGamma \)–\( \varGamma \)) is also observed. However, we cannot find any experimental observations or earlier theoretical studies on the band structure of these quaternary specimens to compare them. Such newly designed direct-bandgap, optically active quaternary semiconductor materials may be useful for the manufacture of faster and highly efficient optoelectronic devices [126]. The band structure of the nine quaternary specimens in the Cd0.25Zn0.75SeyTe1−y, Cd0.50Zn0.50SeyTe1−y, and Cd0.75Zn0.25SeyTe1−y systems are presented in Figs. S4(a–c), S5(a-c), and S6(a-c), respectively, for y = 0.25, 0.50, and 0.75, in the Electronic Supplementary Materials.

3.2.2 The bandgap of the binary, ternary, and quaternary specimens

From Table 4, it is observed that the experimental fundamental bandgap (\( E_{\rm g} \)) for the binary compounds ZnSe and ZnTe [22, 24, 25] as well as CdSe and CdTe [22, 24] is in excellent agreement with our corresponding data calculated using the mBJ functional, while the results calculated using the EV-GGA functional are much smaller than the corresponding experimental outcomes. Only one set of earlier theoretical bandgap data for ZnSe and ZnTe [84] agree well with our corresponding data calculated using the mBJ functional, although they are 0.069 eV and 0.005 eV smaller compared with our mBJ-based data. In the case of the Cd chalcogenides, a set of earlier theoretical bandgap data for CdSe [84] and CdTe [58] agree excellently with our corresponding mBJ-based data, although they are 0.141 eV and 0.009 eV smaller compared with our respective mBJ-based results.

No experimental bandgap data for any of the anionic or cationic ternary alloys are available in the literature for comparison. In the case of all the anionic ternary specimens in the ZnSeyTe1−y and CdSeyTe1−y systems as well as the cationic ternary specimens in the CdxZn1−xSe and CdxZn1−xTe systems, both our mBJ- and EV-GGA-based calculated bandgap values for each ternary specimen are well overestimated with respect to corresponding earlier theoretical data for ZnSeyTe1−y [90] and CdSeyTe1−y [86, 87] alloys calculated using the PBE-GGA and EV-GGA functional as well as for CdxZn1−xSe [94] alloys using the PBE-GGA functional and for CdxZn1−xTe [96] alloys using the local density approximation (LDA) functional. Again, no experimental or earlier theoretical bandgap data for any of the nine quaternary specimens in the CdxZn1−xSeyTe1−y system are available in literature for comparison.

3.2.3 The concentration dependence of the bandgap

An investigation of the cationic (x) and anionic (y) concentration (x/y = 0.0, 0.25, 0.50, 0.75, and 1.0) dependence of the fundamental energy bandgap (\( E_{\rm g} \)) of the specimens in the CdxZn1−xSeyTe1−y quaternary system is presented in this subsection. At each of the five fixed cationic (Cd) concentrations x, the calculated \( E_{\rm g} \) is observed to increase nonlinearly with increasing anionic (Se) concentration (y), with each such variation being shown in Fig. 4a and b for the mBJ and EV-GGA functional, respectively. On the other hand, at each of the five fixed anionic (Se) concentrations y, the calculated \( E_{\rm g} \) is observed to decrease nonlinearly with increasing cationic (Cd) concentration (x), with each such variation calculated using the mBJ and EV-GGA functional being shown in Fig. 4c and d, respectively.

Fig. 4
figure 4

The variation of the a mBJ-calculated minimum bandgap \( E_{\rm g} \) with the Se concentration y at each of the fixed Cd concentrations x, b EV-GGA-calculated minimum bandgap \( E_{\rm g} \) with the Se concentration y at each of the fixed Cd concentrations x, c mBJ-calculated minimum bandgap \( E_{\rm g} \) with the Cd concentration x at each of the fixed Se concentrations y, and d EV-GGA-calculated minimum bandgap \( E_{\rm g} \) with the Cd concentration x at each of the fixed Se concentrations y of the specimens in the CdxZn1−xSeyTe1−y quaternary system

Full size image

For any real alloy system, the nonlinear concentration dependence of the bandgap \( (E_{\rm g} ) \) can be expressed as

$$ E_{\rm g} (x) = \alpha_{\rm g} + \beta_{\rm g} x + \delta_{\rm g} x^{2}, $$
(2)

where \( E_{\rm g} (x) \) is the concentration-dependent bandgap and the nonlinear coefficient \( \delta_{\rm g} \) is called the bandgap bowing or optical bowing parameter. For any specific XC functional, the bandgap bowing coefficient \( \delta_{\rm g} \) for each alloy system can be calculated by fitting the \( E_{\rm g} \) versus x or y curve using Eq. 2.

Here, the \( E_{\rm g} \) versus y curves at each Cd concentration (x) as well as the \( E_{\rm g} \) versus x curves at each Se concentration (y) show downward bowing when employing both XC functionals. The \( \delta_{\rm g} \) value calculated from each \( E_{\rm g} \) versus anionic/cationic concentration curve when using both XC functionals is presented in Table 5. It is clear from Table 5 that \( \delta_{\rm g} \) gradually decreases when employing both XC functionals as one proceeds from ZnSeyTe1−y to CdSeyTe1−y with consecutive replacement of Zn with Cd atom(s). On the other hand, \( \delta_{\rm g} \) gradually increases when using both XC functionals as one proceeds from CdxZn1−xTe to CdxZn1−xSe with successive replacement of Te with Se atom(s). No experimental or earlier theoretical \( \delta_{\rm g} \) data for any of these systems are available for comparison.

Table 5 The optical bowing parameters (\( \delta_{\rm g} \)) calculated from the concentration dependence curves of \( E_{\rm g} \)
Full size table

For the CdxZn1−xSeyTe1−y quaternary system, the contour map calculated for \( E_{\rm g} \) versus the compositions x/y using the mBJ and EV-GGA functionals is shown in Fig. 5a and b, respectively. From such contour plots, the \( E_{\rm g} \) value of any ternary or quaternary specimen corresponding to any x/y compositions in the range 0 ≤ x, y ≤ 1 can be evaluated.

Fig. 5
figure 5

The contour maps calculated for the minimum bandgap \( E_{\rm g} \) versus the compositions x and y for the CdxZn1−xSeyTe1−y quaternary alloys using the a mBJ or b EV-GGA functional

Full size image

3.2.4 The density of states (DOS)

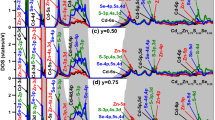
Using the density of states (DOS) of any semiconductor specimen, one can identify the atomic and orbital signature of the various electronic states present in its band structure. In the present study, although we compute the total density of states (TDOS) and partial density of states (PDOS) for each of the specimens in the CdxZn1−xSeyTe1−y quaternary system, only the TDOS (filled gray curves) and PDOS (colored lines) of the ternary and quaternary specimens in the Cd0.25Zn0.75SeyTe1−y system for the whole range of anionic (y) concentrations and those in the CdxZn1−xSe0.25Te0.75 system for the whole range of cationic (x) concentrations are presented as representatives in Figs. 6a–e and 7a–e, respectively. In both figures, the contributions of the different atomic orbitals of the constituents of each specimen in both systems in their various regions of valence and conduction bands are clearly presented. Moreover, the effects of gradual anionic (y) substitution at fixed cationic (x) concentration on the DOS (Fig. 6a–e) as well as the effects of successive cationic (x) substitution at fixed anionic (y) concentration on the DOS (Fig. 7a–e) are clearly observed.

Fig. 6
figure 6

The TDOS (filled gray curves) and PDOS (colored lines) of the specimens in the Cd0.25Zn0.75SeyTe1−y quaternary alloys with ay = 0.0, by = 0.25, cy = 0.50, dy = 0.75, and ey = 1.0 (Color figure online)

Full size image
Fig. 7
figure 7

The TDOS (filled gray curves) and PDOS (colored lines) of the specimens in the CdxZn1−xSe0.25Te0.75 quaternary alloys with ax = 0.0, bx = 0.25, cx = 0.50, dx = 0.75, and ex = 1.0 (Color figure online)

Full size image

From Figs. 6a and 7a, one can observe from the TDOS and PDOS of the ternary specimens Cd0.25Zn0.75Te and ZnSe0.25Te0.75, respectively, that the different regions of the valence and conduction bands of the former are dominated by various orbitals of the Cd, Zn, and Te atoms, while the same for the latter are dominated by various orbitals of the Zn, Se, and Te atoms. With increasing doping of Se atom in the former as well as Cd atom in the latter, Figs. 6b–d and 7b–d show that, in different regions of the valence and conduction bands of the successive quaternary specimens, the contribution of the different chalcogen orbitals now results from the combined contribution of selenium and tellurium atoms in the former set, while the contribution of different orbitals of atom(s), other than chalcogens, now comes from combined contributions of Cd and Zn atoms in the latter set. Moreover, in the different valence and conduction band regions of the said specimens, the contribution from different orbitals of Se atom(s) gradually increase while those of Te gradually decrease with increasing Se concentration in the former set, while the contribution from different orbitals of Cd atom(s) gradually increase while those of Zn gradually decrease with increasing Cd concentration in the latter set. Finally, note the complete domination of the different orbitals of Se atoms in the TDOS and PDOS of the ternary specimen Cd0.25Zn0.75Se in Fig. 6e, and those of Cd atoms in the TDOS and PDOS of the ternary specimen CdSe0.25Te0.75 in Fig. 7e. Note that, in the different valence and conduction band regions of the said specimens, the contributions of the atomic orbitals of Cd and Zn in the former set and the contributions of the atomic orbitals of Se and Te in the latter set remain unchanged due to their presence at fixed concentrations in each set.

In both cases, the most interesting part of the DOS for each specimen is the region of the valence and conduction bands closest to the Fermi level, because most of the significant dipole-allowed optical transitions take place between different orbitals in these regions. It is observed from the PDOS of all the specimens in the Cd0.25Zn0.75SeyTe1−y system in Fig. 6a–e or the PDOS of all the specimens in the CdxZn1−xSe0.25Te0.75 system in Fig. 7a–e that the contributions to the valence band closest to the Fermi level mostly come from chalcogen-p states, i.e., Te-5p or Se-4p or both. On the other hand, the conduction band of these compounds near the Fermi level is dominated almost equally by either Zn-5s or Cd-6s or both of them, as well as collectively by chalcogen-s, p, and d orbitals, i.e., either Te-5p, 6s, 5d or Se-4p, 5s, 4d or both sets of these chalcogen orbitals.

3.3 Optical properties

When an electromagnetic wave is incident on a crystal, electronic excitations take place within it, resulting in the observation of different optical features of the crystal. For any solid, such features are strongly dependent on its electronic properties. The study of the optical properties of a crystal thus provides a clear idea about the nature of its response to incident electromagnetic radiation at a particular frequency, and materials can be selected for the manufacture of optoelectronic devices based on such optical features. The optical features of materials are mainly studied in terms of the frequency-dependent complex dielectric function \( \varepsilon (\omega ) \), expressed as [127]:

$$ \varepsilon (\omega ) = \varepsilon_{1} (\omega ) + \mathrm{i}\varepsilon_{2} (\omega ), $$
(3)

where the real and imaginary parts of \( \varepsilon (\omega ) \) are \( \varepsilon_{1} (\omega ) \) and \( \varepsilon_{2} (\omega ) \), respectively. The refractive index \( n(\omega ) \), extinction coefficient \( k(\omega ) \), normal incidence reflectivity \( R(\omega ) \), optical conductivity \( \sigma (\omega ) \), optical absorption coefficient \( \alpha (\omega ) \), and energy loss function \( L(\omega ) \) of any semiconductor specimen can then be derived from its \( \varepsilon_{1} (\omega ) \) and \( \varepsilon_{2} (\omega ) \). Their expressions along with some of the ancillary optical parameters are presented as Eqs. SQ1-SQ14 in Sect. I of the Electronic Supplementary Material.

3.3.1 The frequency response curves of the different optical parameters

In the present work, we calculate the frequency response of \( \varepsilon_{1} (\omega ) \), \( \varepsilon_{2} (\omega ) \), \( n(\omega ) \), \( k(\omega ) \), \( R(\omega ) \), \( \sigma (\omega ) \), \( \alpha (\omega ) \), and \( L(\omega ) \) for the binary, ternary, and quaternary specimens in the CdxZn1−xSeyTe1−y system up to an incident energy of 30.0 eV using Eqs. SQ1-SQ14 and employing both the mBJ and EV-GGA functional. The frequency responses of \( \varepsilon_{1} (\omega ) \) and \( \varepsilon_{2} (\omega ) \) calculated using the mBJ functional are shown in Figs. 8 and 9, respectively, in the main text, while those of \( n(\omega ) \), \( k(\omega ) \), \( R(\omega ) \), \( \sigma (\omega ) \), \( \alpha (\omega ) \), and \( L(\omega ) \) calculated using the same XC functional are presented in Figs. S7–S12 in the Electronic Supplementary Material. In each of these figures, the five curves obtained for fixed cationic (Cd) concentration (x) but the five different anionic (Se) concentrations (y) are presented in each of the five left panels. On the other hand, the five curves obtained for fixed anionic (Se) concentration (y) but all five different cationic (Cd) concentrations (x) are presented in each of the five right panels.

Fig. 8
figure 8

The frequency response curves of \( \varepsilon_{1} \)(\( \omega \)) for the specimens in the CdxZn1−xSeyTe1−y quaternary system for the different Se concentrations at each of the Cd concentrations (five left panels) and for the different Cd concentrations at each of the Se concentrations (five right panels)

Full size image
Fig. 9
figure 9

The frequency response curves of \( \varepsilon_{2} \)(\( \omega \)) for the specimens in the CdxZn1−xSeyTe1−y quaternary system for the different Se concentrations at each of the Cd concentrations (five left panels) and for the different Cd concentrations at each of the Se concentrations (five right panels)

Full size image

In each of the \( \varepsilon_{1} (\omega ) \) spectra in Fig. 8, it is observed that \( \varepsilon_{1} (\omega ) \) is substantially high with prominent peak(s) up to about 6.0 eV. Then, in the mid-energy region of about 6.5–16.0 eV, the calculated \( \varepsilon_{1} (\omega ) \) in all the spectra becomes negative, while in the subsequent energy region beyond 16.0 eV, \( \varepsilon_{1} (\omega ) \) in all the spectra again achieves very low positive values. A negative value of \( \varepsilon_{1} (\omega ) \) for any of these specimens is a signature of metallic behavior, corresponding to reflection of the incident electromagnetic radiation in this spectral range. From each of the \( n(\omega ) \) spectra in Fig. S7, it is observed that \( n(\omega ) \) is significantly high and shows prominent peaks up to an incident energy of about 7.0 eV, while \( n(\omega ) \) < 1 is observed in the subsequent higher energy region for each specimen. The \( R(\omega ) \) spectra of all the specimens in Fig. S8 show that it is significantly high in the broad energy region of 2.0–14.0 eV, with \( R(\omega ) \) > 0.20, then gradually drops down to very low values in the subsequent energy region.

From the frequency response spectra of \( \varepsilon_{2} (\omega ) \) for all the specimens in the CdxZn1−xSeyTe1−y quaternary system in Fig. 9, it is observed that \( \varepsilon_{2} (\omega ) \) is significantly high in the incident energy region of 3.0–9.0 eV, while it becomes insignificant in the subsequent energy region for all the specimens. The highest occupied molecular orbital (HOMO)–lowest unoccupied molecular orbital (LUMO) electronic transitions between the different atomic orbitals of the valence and conduction band are responsible for the occurrence of the peak(s) in the \( \varepsilon_{2} (\omega ) \) spectra of each specimen in the aforesaid energy region.

The most intense peaks in the \( \varepsilon_{2} (\omega ) \) spectra of ZnSe and ZnTe at 6.14 eV and 4.99 eV are due to the strong electronic transitions Se-4p → Zn-5s and Te-5p → Zn-5s, respectively, while the comparatively much lower-intensity peaks at 7.58 eV and 6.24 eV in the \( \varepsilon_{2} (\omega ) \) spectra of ZnSe and ZnTe are due to the comparatively much weaker electronic transitions Se-4p → Zn-4p and Te-5p → Zn-4p, respectively, from the occupied valence to the unoccupied conduction band. On the other hand, the most intense peaks in the \( \varepsilon_{2} (\omega ) \) spectra of CdSe and CdTe at 5.89 eV and 4.88 eV are due to the strong electronic transitions Se-4p → Cd-6s and Te-5p → Cd-6s, respectively, while the weak-intensity peaks at 7.31 eV and 6.22 eV in the \( \varepsilon_{2} (\omega ) \) spectra of CdSe and CdTe are due to the comparatively weak electronic transitions Se-4p → Cd-5p and Te-5p → Cd-5p, respectively, from the occupied valence to the unoccupied conduction band. Note that the intensity difference between the two peaks in the \( \varepsilon_{2} (\omega ) \) spectra of each of ZnSe and ZnTe is greater compared with that between the two peaks in the \( \varepsilon_{2} (\omega ) \) spectra of each of CdSe and CdTe.

In the case of the \( \varepsilon_{2} (\omega ) \) spectra of the anionic ternary specimen ZnSe0.25Te0.75, the first intense peak at 5.26 eV is due to the combined effect of the very strong Te-5p → Zn-5s and much weaker Se-4p → Zn-5s electronic transitions, while that arising in the \( \varepsilon_{2} (\omega ) \) spectra of CdSe0.25Te0.75 at 4.97 eV is due to the combined effect of the very strong Te-5p → Cd-6s and much weaker Se-4p → Cd-6s electronic transitions from the valence to conduction band. On the other hand, the next intense peak at 6.38 eV in the \( \varepsilon_{2} (\omega ) \) spectra of ZnSe0.25Te0.75 is due to the combined effect of the strong Te-5p → Zn-4p and much weaker Se-4p → Zn-4p transitions, while that at 6.39 eV in the \( \varepsilon_{2} (\omega ) \) spectra of CdSe0.25Te0.75 is due to the combined effect of the strong Te-5p → Cd-5p and much weaker Se-4p → Cd-5p electronic transitions from the valence to conduction band. It is also observed that the intensity difference between the two peaks in the \( \varepsilon_{2} (\omega ) \) spectra of ZnSe0.25Te0.75 is greater compared with that between the two peaks in the \( \varepsilon_{2} (\omega ) \) spectra of CdSe0.25Te0.75. Note also that the intensity of the transitions originating from Se-4p gradually dominates over the transitions originating from Te-5p and the peak positions clearly exhibit a marginal blue-shift in both the ZnSeyTe1−y and CdSeyTe1−y systems with increasing Se concentration (y).

In the case of the \( \varepsilon_{2} (\omega ) \) spectra of the cationic ternary specimens Cd0.25Zn0.75Se and Cd0.25Zn0.75Te, the first intense peaks at 6.00 eV and 4.88 eV are due to the combined effect of the electronic transitions Se-4p → Zn-5s, Se-4p → Cd-6s and Te-5p → Zn-5s, Te-5p → Cd-6s, respectively, from the valence to conduction band. On the other hand, the next intense peaks at 7.52 eV and 6.24 eV are due to the electronic transitions Se-4p → Zn-4p, Se-4p → Cd-5p and Te-5p → Zn-4p, Te-5p → Cd-5p, respectively, from the valence to conduction band. Also, note the substantial intensity difference between the two peaks in the \( \varepsilon_{2} (\omega ) \) spectra of each of the said cationic ternary alloys. Note also that the intensity of the transitions terminating at Cd-6s, 5p gradually dominates over the transitions to Zn-5s, 4p with increasing Cd concentration (x) in both the CdxZn1−xSe and CdxZn1−xTe systems.

In the case of the \( \varepsilon_{2} (\omega ) \) spectra of the nine quaternary specimens Cd0.25Zn0.75SeyTe1−y, Cd0.50Zn0.50SeyTe1−y, and Cd0.75Zn0.25SeyTe1−y with y = 0.25, 0.50, and 0.75, the first intense peak in each spectra is due to the combined effect of the Te-5p → Zn-5s, Te-5p → Cd-6s, Se-4p → Zn-5s, and Se-4p → Cd-6s electronic transitions from the valence to conduction band. On the other hand, the comparatively low-intensity peak in each spectrum at the higher-energy side of the first peak is due to the Te-5p → Zn-4p, Te-5p → Cd-5p, Se-4p → Zn-4p, and Se-4p → Cd-5p electronic transitions from the valence to conduction band. Keeping the Cd concentration (x) fixed, if one gradually increases the Se concentration (y) to 0.50 then 0.75, the transitions originating from Se-4p become gradually stronger compared with the transitions originating from Te-5p in both peaks in the \( \varepsilon_{2} (\omega ) \) spectra of each corresponding quaternary specimen. On the other hand, if one gradually increases the Cd concentration (x) to 0.50 then 0.75 while keeping the Se concentration (y) fixed, the transitions terminating at Cd-6s, 5p become gradually stronger compared with the transitions terminating at Zn-5s,4p in both peaks of the \( \varepsilon_{2} (\omega ) \) spectra in each corresponding quaternary specimen.

In the frequency response spectra of \( k(\omega ) \) of each specimen in Fig. S9, \( k(\omega ) \) > 1 is observed throughout the incident energy region of 3.5–10.5 eV, with the peaks having a maximum amplitude of \( k(\omega ) \) > 2. Therefore, incident photons with energy in this specific range suffer more obstruction during their penetration through each of these specimens compared with photons having energy beyond this energy region in the \( k(\omega ) \) spectra [126].

The \( \sigma (\omega ) \) spectra of each specimen in Fig. S10 show a couple of peaks in the narrow incident energy region of 4.0–9.0 eV with peak values \( \sigma (\omega ) \) greater than at least 6000 Ω−1 cm−1, while \( \sigma (\omega ) \) becomes very low beyond this energy region. The \( \alpha (\omega ) \) spectra of each specimen in Fig. S11 show substantial optical absorption [\( \alpha (\omega ) \) > 100] in the 5.0–12.5 eV incident energy region.

The electron energy loss function \( L(\omega ) \) is used to investigate electrons inelastically scattered by atoms at lattice site and to calculate the amount of energy loss during such scattering processes. It is obvious from Eq. SQ14 that the \( L(\omega ) \) of any specimen will be strongly dependent on its \( \varepsilon_{2} (\omega ) \) [128] and that their frequency responses will be qualitatively opposite in nature. In the \( L(\omega ) \) spectra of each specimen in Fig. S12, it is observed that \( L(\omega ) \) is insignificant because of the significantly high value of \( \varepsilon_{2} (\omega ) \) in the energy region up to 10.0 eV. This indicates that inelastic scattering of only a few electrons occurs, resulting in minimum energy loss in this energy region. On the other hand,\( L(\omega ) \) gradually increases beyond an incident energy of 10.0 eV because \( \varepsilon_{2} (\omega ) \) gradually decreases beyond this energy value. As a result, the number of inelastically scattered electrons and hence the resulting energy loss gradually increase beyond 10.0 eV. It is also observed that \( L(\omega ) \) for each specimen is significantly high with multiple peaks in the incident energy region of 11.0–22.0 eV, because \( \varepsilon_{2} (\omega ) \) is significantly low (less than unity) in this region. Note that one can measure the plasma resonance frequency for any specimen from the energetic position of the most intense peak in its \( L(\omega ) \) spectra.

3.3.2 The zero-frequency limits and critical points in the different optical spectra

The zero-frequency limits \( \varepsilon_{1} (0) \), \( n(0) \), and \( R(0) \) of the \( \varepsilon_{1} (\omega ) \), \( n(\omega ) \), and \( R(\omega ) \) spectra, respectively, are calculated. For any specimen, these give the magnitude of the optical parameters \( \varepsilon_{1} (\omega ) \), \( n(\omega ) \), and \( R(\omega ) \) in the respective spectra at zero incident energy/frequency, which are known as the static dielectric constant, static refractive index, and static reflectivity, respectively. The \( \varepsilon_{1} (0) \), \( n(0) \), and \( R(0) \) values calculated for all of the specimens in the CdxZn1−xSeyTe1−y quaternary system using both the mBJ and EV-GGA functionals are presented in Table 6, along with available experimental or earlier theoretical data for a few specimens for comparison.

Table 6 The \( \varepsilon_{1} (0) \), \( n(0) \), and \( R(0) \) values of the binary, ternary, and quaternary specimens in the CdxZn1−xSeyTe1−y system calculated using the mBJ and EV-GGA functionals
Full size table

Few experimental \( \varepsilon_{1} (0) \) data for ZnSe [26], ZnTe [27], CdSe [26], and CdTe [27] are available for comparison, while no experimental \( \varepsilon_{1} (0) \) data for ternary or quaternary specimens or any experimental \( n(0) \) and \( R(0) \) data for the binary, ternary, and quaternary specimens are available for comparison. Also, some earlier theoretical \( \varepsilon_{1} (0) \) data for ZnSe and ZnTe [68, 72, 97] and CdSe and CdTe [59, 68, 69, 72, 87, 100], \( n(0) \) and \( R(0) \) data for ZnSe and ZnTe [97], \( n(0) \) data for CdSe and CdTe [67, 87, 100], and \( R(0) \) data for CdSe and CdTe are available in literature.

Our mBJ-based computed \( \varepsilon_{1} (0) \) data for the binary compounds ZnSe, ZnTe, CdSe, and CdTe are in excellent agreement with the corresponding experimental data due to the excellent match of our mBJ-based computed bandgaps with the respective experimental findings. On the other hand, our EV-GGA-based \( \varepsilon_{1} (0) \) results for each of ZnSe, ZnTe, CdSe, and CdTe are fairly overestimated with respect to the corresponding experimental data due to the fair underestimation of our EV-GGA-based computed bandgaps with respect to the corresponding experimental data. Each of our mBJ-based calculated \( n(0) \) and \( R(0) \) results for any of the binary specimens is underestimated with respect to the corresponding previously calculated data due to our higher corresponding calculated larger bandgap compared with those reported in earlier theoretical studies.

Only the earlier theoretical \( \varepsilon_{1} (0) \) data for each of the anionic ternary specimens CdSeyTe1−y calculated using the EV-GGA functional [87] and that for the cationic ternary specimen Cd0.25Zn075Se calculated using the mBJ functional [98] are substantially underestimated with respect to our corresponding data calculated using both the mBJ and EV-GGA functional. In the case of the Cd0.25Zn075Se ternary alloy, our mBJ-based computed \( n(0) \) data are underestimated with respect to earlier mBJ-based theoretical data [98] due to our higher calculated mBJ-based bandgap compared with the corresponding earlier study.

From Table 6, the following facts can be noted: The \( \varepsilon_{1} (0) \), \( n(0) \), and \( R(0) \) values calculated for any of the specimens using both XC functionals exhibit the trends \( \varepsilon_{1} (0)^{\text{EV-GGA}} \) > \( \varepsilon_{1} (0)^{\text{mBJ}} \), \( n(0)^{\text{EV-GGA}} \) > \( n(0)^{\text{mBJ}} \), and \( R(0)^{\text{EV-GGA}} \) > \( R(0)^{\text{mBJ}} \), whereas our calculated fundamental bandgaps follow the trend \( E_{\rm g}^{\text{mBJ}} \) > \( E_{\rm g}^{\text{EV-GGA}} \) in Table 4 in this situation. The aforesaid correlation between \( \varepsilon_{1} (0) \) and \( E_{\rm g} \) can be clarified by the approximate relation among them, as proposed by Penn [129]:

$$ \varepsilon_{1} (0) \approx 1 + \left( {\frac{{\hbar \omega_{p} }}{{E_{\rm g} }}} \right)^{2}. $$
(4)

Equation 4 indicates an approximate inverse proportionality between \( \varepsilon_{1} (0) \) and the square of \( E_{\rm g} \). Therefore, the \( \varepsilon_{1} (0) \) of a material increases with a decrease in the bandgap, and vice versa.

For any specimen, the approximate relationship between \( n(0) \) and \( \varepsilon_{1} (0) \) is [127]

$$ n(0) \approx \sqrt {\varepsilon_{1} (0)}. $$
(5)

One can establish all the aforesaid correlations between \( n(0) \) and \( E_{\rm g} \) using the following relation between them, obtained by combining Eqs. 4 and 5:

$$ n(0) \approx \sqrt {1 + \left( {\frac{{\hbar \omega_{p} }}{{E_{\rm g} }}} \right)^{2} }. $$
(6)

Equation 6 indicates an approximate inverse proportionality between \( n(0) \) and \( E_{\rm g} \). Therefore, an increase in \( E_{\rm g} \) results in a decrease in \( n(0) \), and vice versa, in any semiconductor.

The extinction coefficient \( k(\omega ) \) becomes zero for each specimen at zero incident frequency, so the relationship between \( n(0) \) and \( R(0) \), using Eq. SQ10, becomes

$$ R(0) = \left[ {\frac{1 - n(0)}{1 + n(0)}} \right]^{2}. $$
(7)

Finally, the aforesaid correlations between \( E_{\rm g} \) and \( R(0) \) can also be established using the following relation between them, obtained by combining Eqs. 6 and 7:

$$ R(0) = \left[ {\frac{{1 - \sqrt {1 + \left( {\frac{{\hbar \omega_{p} }}{{E_{\rm g} }}} \right)^{2} } }}{{1 + \sqrt {1 + \left( {\frac{{\hbar \omega_{p} }}{{E_{\rm g} }}} \right)^{2} } }}} \right]^{2}. $$
(8)

Clearly, Eq. 8 indicates that an increase in \( E_{\rm g} \) will result in a reduction in \( R(0) \), and vice versa, in any semiconductor.

The critical points in the \( \varepsilon_{2} (\omega ) \), \( k(\omega ) \), \( \sigma (\omega ) \), and \( \alpha (\omega ) \) spectra are the threshold incident energy \( E_{\rm c} \) (eV) at which each of these optical parameters starts responding to the incident radiation. Note that a semiconductor specimen with higher fundamental bandgap requires a higher critical point energy in its \( \varepsilon_{2} (\omega ) \) and \( k(\omega ) \) spectra, and vice versa, according to the Kramers–Kronig transformations between \( \varepsilon_{1} (\omega ) \) and \( \varepsilon_{2} (\omega ) \) [Eqs. SQ3 and SQ4] as well as between \( n(\omega ) \) and \( k(\omega ) \) [Eqs. SQ6 and SQ7], respectively. Since \( \sigma (\omega ) \) is proportional to \( \varepsilon_{2} (\omega ) \) and \( \alpha (\omega ) \) is proportional to \( k(\omega ) \) according to Eqs. SQ11 and SQ13, respectively, a similar bandgap dependence of the critical points is observed in the \( \sigma (\omega ) \) and \( \alpha (\omega ) \) spectra. The critical points in the aforesaid spectra of all the binary, ternary, and quaternary specimens in the CdxZn1−xSeyTe1−y quaternary system calculated using both the mBJ and EV-GGA functionals are presented in Table 7, but no experimental critical point data for any of these specimens are available for comparison. On the other hand, earlier calculated critical points in the \( \varepsilon_{2} (\omega ) \), \( k(\omega ) \), \( \sigma (\omega ) \), and \( \alpha (\omega ) \) spectra of only the binary specimens CdSe and CdTe are available in literature [100]. It is observed from Table 7 that each of our mBJ- and EV-GGA-based computed critical points in each of the \( \varepsilon_{2} (\omega ) \), \( k(\omega ) \), \( \sigma (\omega ) \), and \( \alpha (\omega ) \) spectra of CdSe and CdTe are much higher than the respective earlier theoretically reported critical points for CdSe and CdTe [100]. This is because our bandgaps for CdSe and CdTe calculated using both XC functionals are much higher than the respective bandgaps reported in that earlier theoretical study [100]. It is clear from Table 7 that our calculated critical point in each of the \( \varepsilon_{2} (\omega ) \), \( k(\omega ) \), \( \sigma (\omega ) \), and \( \alpha (\omega ) \) spectra of any specimen obeys the trend \( E_{\rm c}^{\text{mBJ}} \) > \( E_{\rm c}^{\text{EV-GGA}} \), since our bandgaps calculated with both XC functionals follow the trend \( E_{\rm g}^{\text{mBJ}} \) > \( E_{\rm g}^{\text{EV-GGA}} \) in Table 4.

Table 7 The critical points in the \( \varepsilon_{2} (\omega ) \), \( k(\omega ) \), \( \sigma (\omega ) \), and \( \alpha (\omega ) \) spectra of the binary, ternary, and quaternary specimens in the CdxZn1−xSeyTe1−y system calculated using the mBJ and EV-GGA functionals
Full size table

3.3.3 The concentration dependence of the zero-frequency limits and critical points

The zero-frequency limits \( \varepsilon_{1} (0) \), \( n(0) \), and \( R(0) \) as well as the critical points in the \( \varepsilon_{2} (\omega ) \), \( k(\omega ) \), \( \sigma (\omega ) \), and \( \alpha (\omega ) \) spectra of the specimens in the CdxZn1−xSeyTe1−y quaternary system are strongly dependent on the cationic (Cd) and anionic (Se) concentrations x and y, respectively. The concentration dependence of these optical constants is studied in this subsection.

At each of the five fixed values of the cationic (Cd) concentration x, each of the zero-frequency limits \( \varepsilon_{1} (0) \), \( n(0) \), and \( R(0) \) calculated using both XC functionals decreases, while the critical points in each of the \( \varepsilon_{2} (\omega ) \), \( k(\omega ) \), \( \sigma (\omega ) \), and \( \alpha (\omega ) \) spectra increase with increasing anionic (Se) concentration y, as observed from Tables 6 and 7, respectively. On the other hand, at each of the five fixed anionic (Se) concentrations y, each of the \( \varepsilon_{1} (0) \), \( n(0) \), and \( R(0) \) calculated using both XC functionals increases, while the critical points in each of the \( \varepsilon_{2} (\omega ) \), \( k(\omega ) \), \( \sigma (\omega ) \), and \( \alpha (\omega ) \) spectra decrease with increasing cationic (Cd) concentration x, as presented in Tables 6 and 7, respectively. Note that, in the former type of variation, our bandgap calculated using both the mBJ and EV-GGA functional increases, while the reverse trend is observed in the latter type of bandgap variation. Therefore, both variation trends for each of \( \varepsilon_{1} (0) \), \( n(0) \), and \( R(0) \) as well as the critical points in each of the said spectra with the cationic (x) and anionic (y) concentration are strongly related to the concentration (x/y) dependence of the bandgap. An increase in the bandgap results in a decrease in each of these zero-frequency limits and an increase in the critical points, respectively, and vice versa. Therefore, this bandgap dependence of each of \( \varepsilon_{1} (0) \), \( n(0) \), and \( R(0) \) is again well supported by Eqs. 4, 6, and 8, respectively, while that of each of the critical points in the said spectra is supported by the Kramers–Kronig transformations between \( \varepsilon_{1} (\omega ) \) and \( \varepsilon_{2} (\omega ) \) [Eqs. SQ3 and SQ4], between \( n(\omega ) \) and \( k(\omega ) \) [Eqs. SQ6 and SQ7], as well as Eqs. SQ11 and SQ13, respectively.

3.4 Substrate selection for growth of quaternary alloys

This section investigates the possibility of lattice matching between CdxZn1−xSeyTe1−y and ZnTe, InAs, GaSb, and InP, to test their acceptability as appropriate substrates for the growth of these quaternary alloys. This is due to the fact that the lattice constants of some of these quaternary alloys are very close to these substrates. ZnTe, InAs, GaSb, and InP are also direct-bandgap semiconductors in their zincblende crystallographic phase. Moreover, they are available with a high degree of purity. Therefore, they can be chosen as suitable substrates for the growth of some of the CdxZn1−xSeyTe1−y quaternary alloys. The lattice parameters of ZnTe, InAs, GaSb, and InP are taken to be 6.104 Å, 6.058 Å, 6.095 Å, and 5.868 Å, respectively.

The lattice constant \( a(x,y) \) for each quaternary alloy is determined using the modified Vegard’s rule as [130]

$$ a(x,y) = xya_{\text{CdSe}} + (1 - x)ya_{\text{ZnSe}} + x(1 - y)a_{\text{CdTe}} + (1 - x)(1 - y)a_{\text{ZnTe}}, $$
(9)

where \( a_{\text{CdSe}} \), \( a_{\text{CdTe}} \), \( a_{\text{ZnSe}} \), and \( a_{\text{ZnTe}} \) are the lattice constants of CdSe, CdTe, ZnSe, and ZnTe, respectively.

Now, substituting \( a(x,y) \) with the lattice constant of ZnTe in Eq. 9, the condition for lattice matching of CdxZn1−xSeyTe1−y with this diatomic compound is

$$ y = \frac{0.079 + 0.435x}{0.445 - 0.025x}\quad \left( {0 \, \le x \le \, 0.796} \right). $$
(10)

Meanwhile, substituting \( a(x,y) \) with the lattice constant of InAs in Eq. 9, the condition for lattice matching of CdxZn1−xSeyTe1−y with InAs is

$$ y = \frac{0.051 + 0.369x}{0.421 - 0.061x}\quad \left( {0 \, \le x \le \, 0.861} \right). $$
(11)

Also, substituting \( a(x,y) \) with the lattice constant of GaSb in Eq. 9, the condition for lattice matching of CdxZn1−xSeyTe1−y with this diatomic compound is

$$ y = \frac{0.013 + 0.369x}{0.421 - 0.061x}\quad \left( {0 \, \le x \le \, 0.948} \right). $$
(12)

Similarly, the condition for lattice matching of CdxZn1−xSeyTe1−y with InP, obtained by substituting \( a(x,y) \) with the lattice constant of InP in Eq. 9, is

$$ y = \frac{0.240 + 0.369x}{0.421 - 0.061x}\quad \left( {0 \, \le x \le \, 0.420} \right). $$
(13)

The results of this study show that five quaternaries achieve less than 5% lattice mismatch to the ZnTe substrate, corresponding to the specific concentrations x = 0.25, y = 0.25; x = 0.50, y = 0.25; x = 0.50, y = 0.50; x = 0.75, y = 0.50; x = 0.75, y = 0.75 with lattice mismatch values of 1.85%, 3.72%, 2.03%, 3.70%, and 1.87%, respectively. Again, there are five quaternaries achieving less than 5% lattice mismatch to the InAs substrate, corresponding to the specific concentrations x = 0.25, y = 0.25; x = 0.50, y = 0.25; x = 0.50, y = 0.50; x = 0.75, y = 0.50; x = 0.75, y = 0.75 with lattice mismatch values of 1.89%, 3.68%, 2.81%, 4.34%, and 2.64%, respectively.

It is observed that there are six quaternary alloys, corresponding to concentrations x = 0.25, y = 0.25; x = 0.50, y = 0.25; x = 0.50, y = 0.50; x = 0.75, y = 0.25; x = 0.75, y = 0.50; x = 0.75, y = 0.75, which achieve less than 5% lattice mismatch to the GaSb substrate, with values of 1.26%, 3.04%, 2.17%, 4.38%, 3.69%, and 2.00%, respectively. Finally, in the case of the InP substrate, it is found that there are only two quaternaries that achieve less than 5% lattice mismatch, corresponding to concentrations x = 0.25, y = 0.50; x = 0.25, y = 0.75, with corresponding lattice mismatch values of 4.15% and 2.17%, respectively.

Equation 10 provides a line of x and y concentrations along which the corresponding alloys are lattice matched to ZnTe; three different concentrations are considered along the straight line: (0.25, 0.427); (0.50, 0.685); (0.75, 0.951). Equation 11 provides a line of x and y concentrations along which the corresponding alloys are lattice matched to InAs; the corresponding three different concentrations considered along the straight line are (0.25, 0.352); (0.50, 0.602); (0.75, 0.873). Again, Eq. 12 provides another line of x and y concentrations along which the corresponding alloys are lattice matched to GaSb, and the corresponding three different concentrations considered along the straight line are (0.25, 0.259); (0.50, 0.506); (0.75, 0.772).

Figures 10, 11, and 12 show the energy bandgap as a function of the cadmium (x) concentration along the ZnTe, InAs, and GaSb matching line, respectively, as calculated using both the EV-GGA and mBJ functionals. These results reveal that one can tune the cationic (x) and anionic (y) concentrations in the quaternary alloys to achieve a range of bandgap and hence optical properties for the alloys grown on ZnTe, InAs, and GaSb substrates. It is clear from Fig. 10 that, when using the EV-GGA functional, the bandgap ranges from 1.53 to 1.74 eV, while it ranges from 2.25 to 2.42 eV with the mBJ functional in the case of the ZnTe substrate. From Fig. 11, note that the bandgap ranges from 1.52 to 1.74 eV for the EV-GGA functional, but from 2.26 to 2.40 eV for the mBJ functional in the case of the InAs substrate. Finally, from Fig. 12, it is clear that the bandgap ranges from 1.52 to 1.73 eV for the EV-GGA functional, but from 2.24 to 2.38 eV with the mBJ functional in the case of the GaSb substrate.

Fig. 10
figure 10

The energy bandgap of the CdxZn1−xSeyTe1−y quaternary alloys lattice matched to ZnTe as a function of the Cd concentration x as calculated using the mBJ (red line) and EV-GGA (blue line) functional (Color figure online)

Full size image
Fig. 11
figure 11

The energy bandgap of the CdxZn1−xSeyTe1−y quaternary alloys lattice matched to InAs as a function of the Cd concentration x as calculated using the mBJ (red line) and EV-GGA (blue line) functional (Color figure online)

Full size image
Fig. 12
figure 12

The energy bandgap of the CdxZn1−xSeyTe1−y quaternary alloys lattice matched to GaSb as a function of the Cd concentration x as calculated using the mBJ (red line) and EV-GGA (blue line) functional (Color figure online)

Full size image

4 Conclusions

The structural and optoelectronic properties of the specimens in the CdxZn1−xSeyTe1−y quaternary system are calculated as a function of the compositions x and y by employing the DFT-based FP-LAPW approach. The XC potentials are calculated using the PBE-GGA functional for the structural properties and both the mBJ and EV-GGA functionals for the optoelectronic properties. Considering the whole range of anionic concentration (y) at each of the fixed cationic concentrations (x) and vice versa, the CdxZn1−xSeyTe1−y quaternary system is divided into five binary–ternary and ternary–quaternary subsystems in each category, and the concentration dependence of the said properties is studied in detail. The dependence of the lattice constant, bulk modulus, and bandgap on the concentrations x and y exhibits nonlinear behavior. A decrease in the lattice constant and an increase in the bulk modulus are observed with increasing anionic concentration y at each cationic concentration x, while the reverse is observed with increasing cationic concentration x at each fixed anionic concentration y. A direct bandgap (Γ–Γ) is observed for each of the specimens in the CdxZn1−xSeyTe1−y quaternary system. At each of the cationic concentrations x, the bandgap increases with increasing anionic concentration y, while the opposite is observed for the variation of the bandgap with the cationic concentration x at each of the anionic concentrations y. The frequency response of different optical parameters is computed. It is observed that the zero-frequency limit in each of the \( \varepsilon_{1} (\omega ) \), \( n(\omega ) \), and \( R(\omega ) \) spectra shows the opposite trend, while the critical point in each of the \( \varepsilon_{2} (\omega ) \), \( k(\omega ) \), \( \sigma (\omega ) \), and \( \alpha (\omega ) \) spectra shows the same trend, with respect to the variation of the bandgap with the concentrations x and y. Finally, the CdxZn1−xSeyTe1−y quaternary alloys that are lattice matched to the ZnTe, InAs, GaSb, and InP substrates are investigated, revealing that these materials can act as suitable substrates for the growth of some of the said quaternary alloys. These results for the quaternary alloys should be useful for the design of optoelectronic devices for operation in the visible and ultraviolet (UV) spectral ranges, when they are lattice matched to ZnTe, InAs, GaSb, and InP as substrates.