Simplification and modification of multiple controlled Toffoli circuits for testability

Abstract

Testability dramatically enhances the operating cost in reversible logic circuits as it increases the cost metrics such as gate count, quantum cost, number of wires and garbage output. This increase also affects the utilization of resources, which further enhances overall cost of testing. This paper presents a new design for testability methodology for reversible circuits by exploring the properties of multiple controlled Toffoli and Fredkin gates, to produce online testable circuits at lower cost metrics. The method includes simplification and modification of Toffoli circuits to form parity-preserving Toffoli–Fredkin cascades. The testability in these cascades can be achieved by comparing the parity of inputs and outputs using controlled-NOT gates on an additional wire. Single-point failures in reversible logic circuits are targeted by means of detecting bit faults. In contrast to the existing work, the present model is robust, low cost and has lesser design complexity. Experiments are conducted on a set of benchmark circuits to prove the efficacy of the present work. The results show an average reduction by 15.9 % in gate cost and 11.0 % in total operating cost when compared to the most recent existing work formulated on the same platform.

1 Introduction

The upcoming technologies like trapped atoms [1], nuclear magnetic resonance [2], quantum dots [3] and superconductors [4] allow quantum communication to enable the sharing of secrets by the laws of physics. Reversible logic circuits are one of the foundations for future generation systems with its applications to quantum computation. They are theoretically proven for providing nearly energy-free computation by preventing the loss of information in the form of heat [5]. A few physical realizations of reversible and partially reversible circuits have also been reported [4, 6]. Due to the phenomenon of quantum de-coherence, quantum systems are much more fault-prone [7]. The consideration of faults and fault tolerance cannot be ignored. Testing of these circuits has also achieved a notable attention for the detection of various types of fault models. Since any kind of fault occurrence results in the change of single-/multiple-bit values at the output wires of the circuit, the detection is done by means of single-/multiple-bit faults [8]. Based on reviews and analysis of the existing work, parity checking is found the most favorable method of testing due to the property of having the same number of inputs and outputs. The parity is preserved or generated by means of testable gates [6,7,8,9] and modification principles [10,11,12,13]. These processes largely increase the hardware requirements to produce testable circuits and consume a significant time. Another solution is designing with built-in parity-preserving features [14], but it requires modification of existing synthesis algorithm which may increase design complexity. Exploiting the properties of multiple controlled Toffoli (MCT) and multiple controlled Fredkin (MCF) gates, we present a new methodology for the modification of Toffoli circuits into simplified Toffoli–Fredkin cascades to produce parity-preserving circuits. This property facilitates cursive testing with these circuits using a parity checker at the outputs which reduces hardware requirements and, consequently, reduces the cost of testing.

1.1 Related work

Numerous methodologies are available in the literature, which are based on the principles of designing using novel testable gates, designing using modification of an original circuit and designing with built-in testability features. Concentrating on modification principles, the key innovations related to the proposed work are discussed as follows:

The gates of an arbitrary circuit are modified and cascaded with an identity gate to form a respective testable reversible cell (TRC), which produces two-parity output on additional wires [13]. The original gates are then replaced by these cells to form a testable circuit. Another method is the conversion of Toffoli gates of a circuit into respective extended Toffoli gates (ETG) to preserve the parity of whole circuit on an extra wire [15]. The gate cascading approach is followed by adding another gate of same size after each gate keeping the same control input and target input on the new wire to preserve the parity of circuit [3]. In the modified gates approach, Toffoli and Peres gates are modified into a respective testable form by adding one gate of the same type and five controlled-NOT gates (CNOT-A NOT gate with a control), to preserve the parity of the input and output [16]. These gates will take the place of the original gates to form testable circuits. The methodologies consume a large amount of hardware cost in producing testable circuits for the detection of fault models by means of single-bit faults. The additional cost required in all these methods is summarized in Table 1, where N is the number of gates, n represents the number of wires present in original circuit and $k_i$ denotes the size of $i^{th}$ gate of the circuit [17].

Table 1 Testing parameters of existing methods

1.2 Simulation setup

The simulations for evaluating the efficacy of the proposed work in this paper are performed on a machine with a 64-bit Ubuntu 16.04 LTS equipped with Intel Core I7-4790, 3.60 GHz clock and 4 GB of memory. The perquisites used in different parts of this paper are listed as follows:

• The benchmark circuits description in the form of Toffoli–Fredkin cascade (TFC) and programmable logic array (PLA) files is taken from reversible logic synthesis and benchmark pages [18, 19].

• Revkit—It is an open-source tool kit for reversible circuit designs. It is a modular and extensible framework which provides a significant number of approaches and algorithms, but also easily enables the addition of new methods and ideas. Several optimization and verification methods based on existing synthesis algorithms are also incorporated within the tool kit.

• The circuits are synthesized using well-known garbage-free transformation-based synthesis algorithm [20]. The functions of given benchmarks are converted into the corresponding reversible circuit using binary decision diagram (BDD) to reversible binary decision diagram (RBDD) and synthesized into Toffoli circuits.

• RCViewer—It is an application which is intended to aid in the visualization of reversible quantum circuits made up of Toffoli and Fredkin gates in cascade format. It can calculate the quantum cost of the circuit and assist in analyzing the output of a circuit in truth table form and verifying the output of a circuit against a programmable logic array file.

2 Proposed design for testability methodology

The methodology is directed by three courses of action after obtaining reversible Toffoli specification of a given Boolean function to obtain testable multiple controlled Toffoli–Fredkin (MCTF) circuits. They are simplification of Toffoli circuits, gates cascading and parity checking in order to detect the occurrence of single-bit faults as demonstrated in Fig. 1. The predefined patterns of three MCT gates in the synthesized circuit are replaced by their equivalent MCF gates to optimize number of gates in the first stage. The gates cascading explained in the previous section will be done on non-simplified MCT gates, where another gate is cascaded using an extra wire followed by the parity checking. Detailed methodology and subsequent algorithm are explained in this section with an example.

Fig. 1

Design process

The essence of the proposed approach is based on the explored properties of MCT and MCF gates. Preposition 1 and 2 elaborate the properties of these gates, respectively.

An MCT gate has k control inputs and one target input T, as shown in Fig. 2a. The control inputs follow the same input-to-output relationship, and the output function $f(k_n,T)$ can be calculated by Eq. (1). The gate without any control is called as NOT gate, which inverts its target input.

$$\begin{aligned} f_i(k_n,T_i)=(k_1\bullet k_2\bullet \ldots k_n)\oplus T_i\quad ; \,i=\{1,2\} \end{aligned}$$

(1)

Fig. 2

MCT gate and corresponding modification

Proposition 1

If another MCT gate is cascaded with same control inputs and the target input is kept on a wire other than the place assigned for previous gate, the circuit produced is parity preserving.

Proof

Consider an MCT is cascaded with same control inputs and the target input ($T_2$) is kept on a wire other than the place assigned for $T_1$, as shown in Fig. 2b. The outputs $f(k_n,T_1)$ and $f(k_n,T_2)$ can be calculated by Eq. (3). The exclusive sum of all the inputs (I) and outputs (O) calculated in Eq. (2) is a null value. Hence, the circuit produced is parity preserving.

$$\begin{aligned} I\oplus O&= [k^*\oplus T1\oplus T_2] \oplus [k^*\oplus f_1(k_n,T_1)\oplus f_2(k_n,T_2)] \nonumber \\&=[k^*\oplus T1\oplus T_2]\oplus [k^*\oplus (k\oplus T_1)\oplus (k\oplus T_2)]=0 \end{aligned}$$

(2)

An MCF gate has k control inputs and two target inputs $T_1$ and $T_2$, as shown in Fig. 3. The control inputs follow the same relationship as that of MCT gates, and the output functions $f_1(k_n,T_1,T_2)$ and $f_2(k_n,T_1,T_2)$ can be calculated by Eq. (3). Depending upon the values of control inputs, the gate interchanges or transfers its target inputs to its output. The gate without any control is called as swap gate, which interchanges its target inputs.

$$\begin{aligned} f_j(k,T_1,T_2)=k_1 \cdot t_1+k_2 \cdot t_2 {\left\{ \begin{array}{ll} \text {for }j=1; \quad k_1=\bar{k}, \quad k_2=k\\ \text {for }j=2; \quad k_1=k,\quad k_2=\bar{k} \end{array}\right. } \end{aligned}$$

(3)

$\square$

Fig. 3

An MCF gate

Proposition 2

MCF gates themselves are parity-preserving gates.

Proof

For a gate to be parity preserving, the EXOR of all inputs and output should result a null value. Considering an MCF gate shown in Fig. 3, the EXOR of inputs (I) and output (O) calculated in Eq. (4) results a null value, where $k=$($k_1\bullet k_2\bullet \ldots k_n$) and $k^*=$($k_1\oplus k_2\oplus \ldots k_n$). Hence, MCF gates themselves are parity-preserving gates.

$$\begin{aligned} I\oplus O&=[k^*\oplus T1\oplus T_2] \oplus [k^*\oplus f_1(k_n,T_1)\oplus f_2(k_n,T_2)]\nonumber \\&=[k^*\oplus T_1\oplus T_2] \oplus [k^*\oplus (\overline{k}\cdot T_1+k\cdot T_2) \oplus (k\cdot T_1+\overline{k}\cdot T_2)] \nonumber \\&=[T_1\oplus T_2]\oplus [T_1\oplus T_2]=0 \end{aligned}$$

(4)

$\square$

2.1 Design process

(a) Simplification In this process, the combinations of gates from a synthesized MCT circuit are replaced by their equivalent MCF gates. This process is performed by searching equivalent MCF binary decision diagram (BDD) structure in reversible binary decision diagram (RBDD). For instance, the combination of three controlled-NOT (CNOT) gates shown in Fig. 4a is replaced by a swap gate, the combination of three Toffoli gates shown in Fig. 4b is replaced by a Fredkin gate, and similarly the combination of three MCT gates shown in Fig. 4c is replaced by an MCF gate. The motivation behind the transformation is to reduce the number of gates and quantum cost of the circuit, as three MCT gates can be replaced by single gate and the quantum cost of MCF gates is lesser than MCF gates which is summarized in Table 2. There are several tools available for designing reversible circuits, and the variation in the results can be seen in different tools in terms of performance metrics. We have opted RCViewer [18] to obtain the quantum costs.

Fig. 4

Transformation of MCT to a swap gate, b Fredkin gate, c MCF gate

Table 2 Quantum cost of MCF and MCF gates

(b) Gates cascading In this stage, the MCT gates which are left after transformation will be cascaded with another MCT gate of same size keeping the control input same as that of the previous gate. The target output is placed on a new constant input wire, as shown in Fig. 2b. For a NOT gate, another NOT gate is placed on the new wire after it. This process transforms Toffoli–Fredkin circuit into Toffoli–Fredkin cascades in which the MCT gates are placed in a set of two gates along with MCF gates.

Theorem 1

Circuit produced by cascading modified MCT blocks and MCF gates is parity preserving.

Proof

Consider a circuit containing N gates on n wires, in which $(I_1, I_2, \ldots I_n)$ are the input and $(O_1, O_2, \ldots O_n)$ are the output of the circuit and the intermediate stages are $(O_{i1},O_{i2},\ldots O_\mathrm{in})$, where $i=(1~\text {to}~n)$.

The intermediate I/O mapping can be given by:

$$\begin{aligned} {[}O_{11},O_{12},\ldots O_{1n}]\rightarrow [O_{21},O_{22},\ldots O_{2n}]\rightarrow \ldots [O_{N1},O_{N2},\ldots O_{Nn}] \end{aligned}$$

Since intermediate stages are parity preserving, the EXOR of the previous stage ($P_s$) and the next stage ($N_s$) is given by Eq. (5)

$$\begin{aligned} P_{s}\oplus N_s=0\quad \forall {\left\{ \begin{array}{ll} P_s=O_{N1}\oplus O_{N2}\oplus \ldots O_{Nn}\\ N_s=O_{(N+1)1}\oplus O_{(N+1)2}\oplus \ldots O_{(N+1)n} \end{array}\right. } \end{aligned}$$

(5)

For $N_s=(O_{11}\oplus O_{12}\oplus \ldots O_{1n})$, $P_s=(I_{1}\oplus I_{2}\oplus \ldots I_n)$

If $P_{s}\oplus N_{s}=0 \,\,\forall \,\, i=(1\,to \,N),$

then $(I_{1}\oplus I_{2}\oplus \ldots I_{n})\oplus (O_{1}\oplus O_{2}\oplus \ldots O_{n})=0$

Hence, the circuit produced will be parity preserving which provides the ease of testing at lower costs. The parity (P) of the circuit can be given by Eq. (6), where $I_i$ are the input to the circuit, $O_i$ are the output of the circuit and $\sum$ denotes EXOR sum of inputs and outputs.

$$\begin{aligned} P = \left( \sum _{i=1}^{n}I_i\right) \oplus \left( \sum _{i=1}^{n}O_i\right) \end{aligned}$$

(6)

$\square$

(c) Parity checking Fault detection is achieved by generating input and output parity of the circuit. For n-wire reversible circuit, the parity checking is processed by using n CNOT gates from a wire of the circuit to a wire on which gates cascading was done. This addition is done before and after the whole circuit as explained with gates cascading method shown in Fig. 5. The output of the new wire (${T_\mathrm{out}}$) can be given by Eq. (7). The input to this new wire is kept constant 0. Since the circuit is parity preserving, the test output will always result a null value for a fault-free circuit. It will result a logic value 1 due to the occurrence of any single-bit fault for its detection.

$$\begin{aligned} T_\mathrm{out}=\left( \sum _{i=1}^{n}I_i\right) \oplus \left( \sum _{i=1}^{n}O_i\right) \oplus T_\mathrm{in} \end{aligned}$$

(7)

Fig. 5

Fault detection

Consider a circuit on three wires, and assigning $T_\mathrm{in}=0$, $T_\mathrm{out}$ can be given by Eq. (8)

$$\begin{aligned} T_\mathrm{out}=[(I_1\oplus I_2 \oplus I_3)\oplus (O_1\oplus O_2 \oplus O_3)] \end{aligned}$$

(8)

Since the circuit is parity preserving, $T_\mathrm{out}=0$. Consider any fault occurred at any level of the circuit. As each block of the circuit is also parity preserving, the same parity information will be transferred to the next level. Hence, the values at the output will be inverted in odd numbers. Considering $O_1\rightarrow \overline{O_1}$, $T_\mathrm{out}$ will flip to 1 and the fault occurrence can be detected, as shown in Eq. (9).

$$\begin{aligned} T_\mathrm{out}&=[(I_1\oplus I_2 \oplus I_3)\oplus (\overline{O_1}\oplus O_2 \oplus O_3)] \nonumber \\&= [O_1\oplus \overline{O_1}]=[O_1+\overline{O_1}]=1 \end{aligned}$$

(9)

2.2 Algorithm

The proposed algorithm covers the steps for designing reversible circuits with testability. For a given programmed logic array (PLA) of an original circuit (P), Algorithm 1 produces a testable circuit ($C^T$). Initially, the registers assigned for circuit parameters such as the number of wires (n), gates (N) and gates position in $C^T$ are kept empty. In the first stage of modification, P is reformed into a binary decision diagram and then embedded in a reversible binary decision diagram for its synthesis into the reversible Toffoli circuit. The information will be stored in $C^T$ and the corresponding parameters n and N get updated. The MCT to MCF gates are transformed on the MCT gate combinations ($Xc_{T_{3}}$) basis with corresponding swap ($X_{F_{s}}$) and MCF gate ($X_{F_{t}}$) in the second stage. Since the combinations are to be checked in a set of three gates, the total number of checking positions (Chk) will be $N-2$. Starting from the first iteration (Count), if $Xc_{T_{3}}$ equivalent to $X_{F_{s}}$ is identified, a swap gate will take place for three MCT gates. Identification of $Xc_{T_{3}}$ equivalent to $X_{F_{t}}$ will result in the placement of an MCF gate with the corresponding Toffoli circuit.

After each replacement, chk will jump to $chk+3$. If the combinations do not find any equivalence, chk will jump to $chk+1$. This process will end after the last three combinations, and the respective values of n, N and $C^T$ will be updated simultaneously. The process is followed by the gates cascading process ($\psi$). The gates left after the transformation will be cascaded by another gate keeping the same control input and target input on a new constant input wire. For an MCT gate, another MCT gate is cascaded and a NOT gate is cascaded by another NOT gate on the extra wire (process $\psi _t$). Finally, the parity checker incorporation process is performed for producing a testable circuit ($C^T$) containing N gates and n wires.

2.3 An example

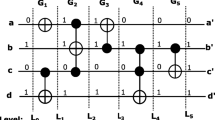
Consider a synthesized Toffoli circuit on three wires shown in Fig. 6a, containing 11 gates with input (a, b, c) and output $(a',b',c')$. The calculated quantum cost for this circuit is 37. There are three MCT gate combinations present in the circuit which can be replaced by their equivalent MCF gates for the first modification process, as shown in Fig. 6b. In the second stage of modification, the left MCT gates are cascaded with another gate to form parity-preserving Toffoli–Fredkin cascades, as shown in Fig. 6c. This circuit is then included with CNOT gates to incorporate parity checking for the detection of faults, as shown in Fig. 6d. The process transformed the original circuit into corresponding testable form on the cost of only two extra gates and single wire. Moreover, the calculated quantum cost is 27 which gets reduced due to the inclusion of MCF gates.

Fig. 6

Circuit transformation, a original circuit, b simplification, c gate cascading, d parity checker inclusion

3 Simulation and results

A set of benchmark circuits are synthesized on the basis of the proposed methodology using transformation-based synthesis algorithm on Revkit tool kit [18, 19]. Initially, the original function is implemented into corresponding reversible Toffoli circuit using BDD to RBDD conversion. This circuit is further simplified and modified in accordance with the proposed method.

Table 3 Operating costs for the proposed methodology

The synthesis report for original and corresponding testable circuits (based on the proposed algorithm) is demonstrated in terms of wires (n), gates (N), T-depth (TD), T-count (TC), logical qubits (q) and garbage output (G) of the circuit in Table 3. The operating cost is calculated by taking summation of all the measures. It is analyzed that the present method produces testable circuits at lower costs due to the incorporation of MCF gates. For instance, the testable circuits of $ex1\_226$, $ex2\_227$ and $ex3\_229$ are synthesized at lesser number of gates using the proposed method than corresponding original circuits. Due to non-availability of MCT to MCF transformations, the gate count will increase for $4gt4\_73$, $4gt11\_82$ and $4mod7-v0\_94$ circuits.

Table 4 Comparison with the existing work

Same circuits are also implemented in accordance with the Toffoli-based ESOP approach [15], gate cascading approach [3] and inbuilt testable design methodology [14]. Due to slight variation in TD, TC and q, these matrices are ignored in the comparisons listed in Table 4. The most efficient methodology is based on designing with inbuilt testability features which gives motivation to develop a new synthesis algorithm that may increase the designing complexity [14]. The wires and garbage are the same as this approach, but the proposed work has achieved a $15.9\%$ reduction in gate costs and $11.0\%$ in total operating cost, except fo the r 5mod5 circuit. As each gate will be cascaded by another gate without MCT to MCF transformation where the simplification is not possible, the proposed methodology will produce the same results as that of the gates cascading approach [3]. The modified circuits in accordance with the ESOP and gates cascading-based approach result in the same number of wires and garbage, but a large reduction in gate count can be seen. Overall, the calculations show an excellent result in producing testable circuits from their original form. The proposed work has achieved a reduction of $75.7\%$ and $66.7\%$ in total operating costs as compared to the ESOP and gate cascading approaches, respectively.

4 Conclusion and future scope

This paper presents a new method of designing reversible logic circuits with testability using multiple controlled Toffoli and Fredkin gates. The two-stage simplification and modification process produces parity-preserving circuits which can be tested using a parity checker at the outputs using CNOT gates on an extra wire. The methodology provides full coverage of single-bit faults by utilizing few gates and an extra wire, without an increase in garbage output. Diminution in the size and power requirements can be achieved as a consequence. The efficiency of the work in this area also corresponds to a large reduction in the operating cost. The quantum cost is also minimized during the conversion process, which is a key metric in quantum circuits. The reduction in operating cost by exploring new parity-preserving gates and synthesis algorithms will be the primary concern for the future foundation of this work.