Abstract
We recently designed two calculi as stepping stones towards superposition for full higher-order logic: Boolean-free \(\lambda \)-superposition and superposition for first-order logic with interpreted Booleans. Stepping on these stones, we finally reach a sound and refutationally complete calculus for higher-order logic with polymorphism, extensionality, Hilbert choice, and Henkin semantics. In addition to the complexity of combining the calculus’s two predecessors, new challenges arise from the interplay between \(\lambda \)-terms and Booleans. Our implementation in Zipperposition outperforms all other higher-order theorem provers and is on a par with an earlier, pragmatic prototype of Booleans in Zipperposition.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Superposition is a leading calculus for first-order logic with equality. We have been wondering for some years whether it would be possible to gracefully generalize it to extensional higher-order logic and use it as the basis of a strong higher-order automatic theorem prover. Towards this goal, we have, together with colleagues, designed superposition-like calculi for three intermediate logics between first-order and higher-order logic. Now we are finally ready to assemble a superposition calculus for full higher-order logic. The filiation of our new calculus from Bachmair and Ganzinger’s standard first-order superposition is as follows:

Our goal was to devise an efficient calculus for higher-order logic. To achieve it, we pursued two objectives. First, the calculus should be refutationally complete. Second, the calculus should coincide as much as possible with its predecessors \(\hbox {o}\)Sup and \(\lambda \)Sup on the respective fragments of higher-order logic (which in turn essentially coincide with Sup on first-order logic). Achieving these objectives is the main contribution of this article. We made an effort to keep the calculus simple, but often the refutational completeness proof forced our hand to add conditions or special cases.
Like \(\hbox {o}\)Sup, our calculus \(\hbox {o}\lambda \)Sup operates on clauses that can contain Boolean subterms, and it interleaves clausification with other inferences. Like \(\lambda \)Sup, \(\hbox {o}\lambda \)Sup eagerly \(\beta \eta \)-normalizes terms, employs full higher-order unification, and relies on a fluid subterm superposition rule (FluidSup) to simulate superposition inferences below applied variables—i.e., terms of the form \(y\>t_1\dots t_n\) for \(n \ge 1\).
In addition to the issues discussed previously and the complexity of combining the two approaches, we encountered the following main challenges.
First, because \(\hbox {o}\)Sup contains several superposition-like inference rules for Boolean subterms, our completeness proof requires dedicated fluid Boolean subterm hoisting rules (FluidBoolHoist, FluidLoobHoist), which simulate Boolean inferences below applied variables, in addition to FluidSup, which simulates superposition inferences.
Second, due to restrictions related to the term order that parameterizes superposition, it is difficult to handle variables bound by unclausified quantifiers if these variables occur applied or in arguments of applied variables. We solve the issue by replacing such quantified terms \(\forall y.\>t\) or \(\exists y.\>t\) by equivalent terms  or
or  in a preprocessing step. We leave all other quantified terms intact so that we can process them more efficiently.
in a preprocessing step. We leave all other quantified terms intact so that we can process them more efficiently.
Third, like other higher-order calculi that support Booleans, our calculus must include some form of primitive substitution [1, 11, 21, 34]. For example, given the clauses \({\textsf {a} } \not \approx {\textsf {b} }\) and  , it is crucial to find the substitution
, it is crucial to find the substitution  , which does not arise through unification. Primitive substitution accomplishes this by blindly substituting logical connectives and quantifiers; here it would apply
, which does not arise through unification. Primitive substitution accomplishes this by blindly substituting logical connectives and quantifiers; here it would apply  to the second clause, where y and \(y'\) are fresh variables. In the context of superposition, this is problematic because the instantiated clause is subsumed by the original clause and could be discarded. Our solution is to immediately clausify the introduced logical symbol, yielding a clause that is no longer subsumed.
to the second clause, where y and \(y'\) are fresh variables. In the context of superposition, this is problematic because the instantiated clause is subsumed by the original clause and could be discarded. Our solution is to immediately clausify the introduced logical symbol, yielding a clause that is no longer subsumed.
The core of this article is the proof of refutational completeness. To keep it manageable, we structure it in three levels. The first level proves completeness of a calculus in first-order logic with Booleans, essentially relying on the completeness of \(\hbox {o}\)Sup. The second level lifts this result to a ground version of our calculus by transforming the first-order model constructed in the first level into a higher-order model, closely following \(\lambda \)Sup. The third level lifts this result further to the nonground level by showing that each ground inference on the second level corresponds to an inference of our calculus or is redundant. This establishes refutational completeness of our calculus.
We implemented our calculus in the Zipperposition prover and evaluated it on TPTP and Sledgehammer benchmarks. The new Zipperposition outperforms all other higher-order provers and is on a par with an ad hoc implementation of Booleans in the same prover by Vukmirović and Nummelin [39].
This article is structured as follows. Section 2 introduces syntax and semantics of higher-order logic and other preliminaries of this article. Section 3 presents our calculus, proves it sound, and discusses its redundancy criterion. Section 4 contains the detailed proof of refutational completeness. Section 5 discusses our implementation in Zipperposition. Section 6 presents our evaluation results.
An earlier version of this article is contained in Bentkamp’s PhD thesis [7], and parts of it were presented at CADE-28 [9]. This article extends the conference paper with more explanations and detailed soundness and completeness proofs. We phrase the redundancy criterion in a slightly more general way to make it more convenient to use in our completeness proof. However, we are not aware of any concrete examples where this additional generality would be useful in practice. We also present a concrete term order fulfilling our abstract requirements as well as additional evaluation results.
2 Logic
Our logic is higher-order logic (simple type theory) with rank-1 polymorphism, Hilbert choice, Henkin semantics, and functional and Boolean extensionality. It closely resembles Gordon and Melham’s HOL [20] and the TPTP TH1 standard [25].
Although standard semantics is commonly considered the foundation of the HOL systems, also Henkin semantics is compatible with the notion of provability employed by the HOL systems. By admitting nonstandard models, Henkin semantics is not subject to Gödel’s first incompleteness theorem, allowing us to claim refutational completeness of our calculus.
On top of the standard higher-order terms, we install a clausal structure that allows us to formulate calculus rules in the style of first-order superposition. It does not restrict the flexibility of the logic because an arbitrary term t of Boolean type can be written as the clause  .
.
2.1 Syntax
We use the notation \(\bar{a}_n\) or \(\bar{a}\) to stand for the tuple \((a_1,\dots ,a_n)\) or product \(a_1 \times \dots \times a_n\), where \(n \ge 0\). We abuse notation by applying an operation on a tuple when it must be applied elementwise; thus, \(f(\bar{a}_n)\) can stand for \((f(a_1),\dots ,f(a_n))\), \(f(a_1) \times \dots \times f(a_n)\), or \(f(a_1, \dots , a_n)\), depending on the operation f.
As a basis for our logic’s types, we fix an infinite set  of type variables. A set \(\Sigma _{{\textsf {ty} }}\) of type constructors with associated arities is a type signature if it contains at least one nullary Boolean type constructor \(\hbox {o}\) and a binary function type constructor \(\rightarrow \). A type, usually denoted by \(\tau \) or \(\upsilon \), is inductively defined to either be a type variable
of type variables. A set \(\Sigma _{{\textsf {ty} }}\) of type constructors with associated arities is a type signature if it contains at least one nullary Boolean type constructor \(\hbox {o}\) and a binary function type constructor \(\rightarrow \). A type, usually denoted by \(\tau \) or \(\upsilon \), is inductively defined to either be a type variable  or have the form \(\kappa (\bar{\tau }_n)\) for an n-ary type constructor \(\kappa \in \Sigma _{{\textsf {ty} }}\) and types \(\bar{\tau }_n\). We write \(\kappa \) for \(\kappa ()\) and \(\tau \rightarrow \upsilon \) for \({\rightarrow }(\tau ,\upsilon )\). A type declaration is an expression
or have the form \(\kappa (\bar{\tau }_n)\) for an n-ary type constructor \(\kappa \in \Sigma _{{\textsf {ty} }}\) and types \(\bar{\tau }_n\). We write \(\kappa \) for \(\kappa ()\) and \(\tau \rightarrow \upsilon \) for \({\rightarrow }(\tau ,\upsilon )\). A type declaration is an expression  (or simply \(\tau \) if \(m = 0\)), where all type variables occurring in \(\tau \) belong to \(\bar{\alpha }_m\).
(or simply \(\tau \) if \(m = 0\)), where all type variables occurring in \(\tau \) belong to \(\bar{\alpha }_m\).
To define our logic’s terms, we fix a type signature \(\Sigma _{{\textsf {ty} }}\) and a set  of term variables with associated types, written as \({\textit{x}}:\tau \) or \({\textit{x}}\). We require that there are infinitely many variables for each type.
of term variables with associated types, written as \({\textit{x}}:\tau \) or \({\textit{x}}\). We require that there are infinitely many variables for each type.
A term signature is a set \(\Sigma \) of (function) symbols, usually denoted by \({\textsf {a} }\), \({\textsf {b} }\), \({\textsf {c} }\), \({\textsf {f} }\), \({\textsf {g} }\), \({\textsf {h} }\), each associated with a type declaration, written as  . We require the presence of the logical symbols
. We require the presence of the logical symbols  ;
;  ;
;  ;
;  ; and
; and  . Moreover, we require the presence of the Hilbert choice operator
. Moreover, we require the presence of the Hilbert choice operator  . The logical symbols are printed in bold to distinguish them from the notation used for clauses below. Although \({\varepsilon }\) is interpreted in our semantics, we do not consider it to be a logical symbol. The reason is that our calculus will enforce the semantics of \({\varepsilon }\) by an axiom, whereas the semantics of the logical symbols will be enforced by inference rules.
. The logical symbols are printed in bold to distinguish them from the notation used for clauses below. Although \({\varepsilon }\) is interpreted in our semantics, we do not consider it to be a logical symbol. The reason is that our calculus will enforce the semantics of \({\varepsilon }\) by an axiom, whereas the semantics of the logical symbols will be enforced by inference rules.
In the following, we also fix a term signature \(\Sigma \). A type signature and a term signature form a signature.
We will define terms in three layers of abstraction: raw \(\lambda \)-terms, \(\lambda \)-terms, and terms; where \(\lambda \)-terms will be \(\alpha \)-equivalence classes of raw \(\lambda \)-terms and terms will be \(\beta \eta \)-equivalence classes of \(\lambda \)-terms.
We write \(t :\tau \) for a raw lambda term t of type \(\tau \). The set of raw \(\lambda \)-terms and their associated types is defined inductively as follows. Every  is a raw \(\lambda \)-term of type \(\tau \). If
is a raw \(\lambda \)-term of type \(\tau \). If  and \(\bar{\upsilon }_m\) is a tuple of types, called type arguments, then \({\textsf {f} }{\langle \bar{\upsilon }_m\rangle }\) (or simply \({\textsf {f} }\) if \(m = 0\)) is a raw \(\lambda \)-term of type \(\tau \{\bar{\alpha }_m \mapsto \bar{\upsilon }_m\}\). If \(x:\tau \) and \(t:\upsilon \), then the \(\lambda \)-expression \(\lambda x.\> t\) is a raw \(\lambda \)-term of type \(\tau \rightarrow \upsilon \). If \(s:\tau \rightarrow \upsilon \) and \(t:\tau \), then the application \(s\>t\) is a raw \(\lambda \)-term of type \(\upsilon \). Using the spine notation [17], raw \(\lambda \)-terms can be decomposed in a unique way as a nonapplication head t applied to zero or more arguments: \(t \> s_1\dots s_n\) or \(t \> \bar{s}_n\) (abusing notation). For the symbols
and \(\bar{\upsilon }_m\) is a tuple of types, called type arguments, then \({\textsf {f} }{\langle \bar{\upsilon }_m\rangle }\) (or simply \({\textsf {f} }\) if \(m = 0\)) is a raw \(\lambda \)-term of type \(\tau \{\bar{\alpha }_m \mapsto \bar{\upsilon }_m\}\). If \(x:\tau \) and \(t:\upsilon \), then the \(\lambda \)-expression \(\lambda x.\> t\) is a raw \(\lambda \)-term of type \(\tau \rightarrow \upsilon \). If \(s:\tau \rightarrow \upsilon \) and \(t:\tau \), then the application \(s\>t\) is a raw \(\lambda \)-term of type \(\upsilon \). Using the spine notation [17], raw \(\lambda \)-terms can be decomposed in a unique way as a nonapplication head t applied to zero or more arguments: \(t \> s_1\dots s_n\) or \(t \> \bar{s}_n\) (abusing notation). For the symbols  and
and  , we will typically use infix notation and omit the type argument.
, we will typically use infix notation and omit the type argument.
A raw \(\lambda \)-term s is a subterm of a raw \(\lambda \)-term t, written \(t = t[s]\), if \(t = s\), if \(t = (\lambda x.\>u[s])\), if \(t = (u[s])\>v\), or if \(t = u\>(v[s])\) for some raw \(\lambda \)-terms u and v. A proper subterm of a raw \(\lambda \)-term t is any subterm of t that is distinct from t itself. A variable occurrence is free in a raw \(\lambda \)-term if it is not bound by a \(\lambda \)-expression. A raw \(\lambda \)-term is ground if it is built without using type variables and contains no free term variables.
The \(\alpha \)-renaming rule is defined as  , where y does not occur free in t and is not captured by a \(\lambda \)-binder in t. Two terms are \(\alpha \)-equivalent if they can be made equal by repeatedly \(\alpha \)-renaming their subterms. Raw \(\lambda \)-terms form equivalence classes modulo \(\alpha \)-equivalence, called \(\lambda \)-terms. We lift the above notions on raw \(\lambda \)-terms to \(\lambda \)-terms.
, where y does not occur free in t and is not captured by a \(\lambda \)-binder in t. Two terms are \(\alpha \)-equivalent if they can be made equal by repeatedly \(\alpha \)-renaming their subterms. Raw \(\lambda \)-terms form equivalence classes modulo \(\alpha \)-equivalence, called \(\lambda \)-terms. We lift the above notions on raw \(\lambda \)-terms to \(\lambda \)-terms.
A substitution \(\rho \) is a function from type variables to types and from term variables to \(\lambda \)-terms such that it maps all but finitely many variables to themselves. We require that it is type correct—i.e., for each  , \(x\rho \) is of type \(\tau \rho \). The letters \(\theta ,\rho ,\sigma \) are reserved for substitutions. Substitutions \(\alpha \)-rename \(\lambda \)-terms to avoid capture; for example, \((\lambda x.\> y)\{y \mapsto x\} = (\lambda x'\!.\> x)\). The composition \(\rho \sigma \) applies \(\rho \) first: \(t\rho \sigma = (t\rho )\sigma \). The notation \(\sigma [\bar{x}_n \mapsto \bar{s}_n]\) denotes the substitution that replaces each \(x_i\) by \(s_i\) and that otherwise coincides with \(\sigma \).
, \(x\rho \) is of type \(\tau \rho \). The letters \(\theta ,\rho ,\sigma \) are reserved for substitutions. Substitutions \(\alpha \)-rename \(\lambda \)-terms to avoid capture; for example, \((\lambda x.\> y)\{y \mapsto x\} = (\lambda x'\!.\> x)\). The composition \(\rho \sigma \) applies \(\rho \) first: \(t\rho \sigma = (t\rho )\sigma \). The notation \(\sigma [\bar{x}_n \mapsto \bar{s}_n]\) denotes the substitution that replaces each \(x_i\) by \(s_i\) and that otherwise coincides with \(\sigma \).
The \(\beta \)- and \(\eta \)-reduction rules are specified on \(\lambda \)-terms as  and
and  . For \(\beta \), bound variables in t are implicitly renamed to avoid capture; for \(\eta \), the variable x may not occur free in t. Two terms are \(\beta \eta \)-equivalent if they can be made equal by repeatedly \(\beta \)- and \(\eta \)-reducing their subterms. The \(\lambda \)-terms form equivalence classes modulo \(\beta \eta \)-equivalence, called \(\beta \eta \)-equivalence classes or simply terms.
. For \(\beta \), bound variables in t are implicitly renamed to avoid capture; for \(\eta \), the variable x may not occur free in t. Two terms are \(\beta \eta \)-equivalent if they can be made equal by repeatedly \(\beta \)- and \(\eta \)-reducing their subterms. The \(\lambda \)-terms form equivalence classes modulo \(\beta \eta \)-equivalence, called \(\beta \eta \)-equivalence classes or simply terms.
We use the following nonstandard normal form: The \(\beta \eta {\textsf {Q} }_{\eta }\)-normal form  of a \(\lambda \)-term t is obtained by applying
of a \(\lambda \)-term t is obtained by applying  and
and  exhaustively on all subterms and finally applying the following rewrite rule \({\textsf {Q} }_{\eta }\) exhaustively on all subterms:
exhaustively on all subterms and finally applying the following rewrite rule \({\textsf {Q} }_{\eta }\) exhaustively on all subterms:

where t is not a \(\lambda \)-expression. Here and elsewhere, \({\textsf {Q} }\) stands for either  or
or  .
.
We lift all of the notions defined on \(\lambda \)-terms to terms:
Convention 1
When defining operations that need to analyze the structure of terms, we use the \(\beta \eta {\textsf {Q} }_{\eta }\)-normal representative as the default representative of a \(\beta \eta \)-equivalence class. Nevertheless, we will sometimes write  for clarity.
for clarity.
Many authors prefer the \(\eta \)-long \(\beta \)-normal form [22, 24, 29], but in a polymorphic setting it has the drawback that instantiating a type variable with a functional type can lead to \(\eta \)-expansion. Below quantifiers, however, we prefer \(\eta \)-long form, which is enforced by the \({\textsf {Q} }_{\eta }\)-rule. The reason is that our completeness theorem requires arguments of quantifiers to be \(\lambda \)-expressions.
A literal is an equation \(s \approx t\) or a disequation \(s \not \approx t\) of terms s and t. In both cases, the order of s and t is not fixed. We write \(s \mathrel {\dot{\approx }}t\) for a literal that can be either an equation or a disequation. A clause \(L_1 \vee \dots \vee L_n\) is a finite multiset of literals \(L_{\!j}\). The empty clause is written as \(\bot \).
Our calculus does not allow nonequational literals. These must be encoded as  or
or  . We even considered excluding negative literals by encoding them as
. We even considered excluding negative literals by encoding them as  , following \(\mathrel {\leftarrow \rightarrow }\)Sup[19]. However, this approach would make the conclusion of the equality factoring rule (EFact) too large for our purposes. Regardless, the simplification machinery will allow us to reduce negative literals of the form
, following \(\mathrel {\leftarrow \rightarrow }\)Sup[19]. However, this approach would make the conclusion of the equality factoring rule (EFact) too large for our purposes. Regardless, the simplification machinery will allow us to reduce negative literals of the form  and
and  to
to  and
and  , thereby eliminating redundant representations of literals.
, thereby eliminating redundant representations of literals.
A complete set of unifiers on a set X of variables for two terms s and t is a set U of unifiers of s and t such that for every unifier \(\theta \) of s and t there exists a member \(\sigma \in U\) and a substitution \(\rho \) such that \(x\sigma \rho = x\theta \) for all \(x \in X.\) We let \({{\,\textrm{CSU}\,}}_X(s,t)\) denote an arbitrary (preferably, minimal) complete set of unifiers on X for s and t. We assume that all \(\sigma \in {{\,\textrm{CSU}\,}}_X(s,t)\) are idempotent on X—i.e., \(x\sigma \sigma = x\sigma \) for all \(x \in X.\) The set X will consist of the free variables of the clauses in which s and t occur and will be left implicit. To compute \({{\,\textrm{CSU}\,}}(s,t)\), Huet-style preunification [21] is not sufficient, and we must resort to full unification procedures [23, 38].
2.2 Semantics
A type interpretation  is defined as follows. The universe
is defined as follows. The universe  is a collection of nonempty sets, called domains. We require that
is a collection of nonempty sets, called domains. We require that  . The function
. The function  associates a function
associates a function  with each n-ary type constructor \(\kappa \), such that
with each n-ary type constructor \(\kappa \), such that  and for all domains
and for all domains  , the set
, the set  is a subset of the function space from
is a subset of the function space from  to
to  . The semantics is standard if
. The semantics is standard if  is the entire function space for all
is the entire function space for all  . A type valuation \(\xi \) is a function that maps every type variable to a domain. The denotation of a type for a type interpretation
. A type valuation \(\xi \) is a function that maps every type variable to a domain. The denotation of a type for a type interpretation  and a type valuation \(\xi \) is recursively defined by
and a type valuation \(\xi \) is recursively defined by  and
and  .
.
A type valuation \(\xi \) can be extended to be a valuation by additionally assigning an element  to each variable \(x :\tau \). An interpretation function
to each variable \(x :\tau \). An interpretation function  for a type interpretation
for a type interpretation  associates with each symbol
associates with each symbol  and domain tuple
and domain tuple  a value
a value  , where \(\xi \) is a type valuation that maps each \(\alpha _i\) to
, where \(\xi \) is a type valuation that maps each \(\alpha _i\) to  . We require that
. We require that
-
(I1)
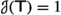
-
(I2)

-
(I3)

-
(I4)

-
(I5)

-
(I6)

-
(I7)

-
(I8)

-
(I9)

-
(I10)

-
(I11)

for all \(a,b\in \{0,1\}\),  ,
,  , and
, and  .
.
The comprehension principle states that every function designated by a \(\lambda \)-expression is contained in the corresponding domain. Loosely following Fitting [18, Sect. 2.4], we initially allow \(\lambda \)-expressions to designate arbitrary elements of the domain, to be able to define the denotation of a term. We impose restrictions afterwards using the notion of a proper interpretation, enforcing comprehension.
A \(\lambda \)-designation function  for a type interpretation
for a type interpretation  is a function that maps a valuation \(\xi \) and a \(\lambda \)-expression of type \(\tau \) to an element of
is a function that maps a valuation \(\xi \) and a \(\lambda \)-expression of type \(\tau \) to an element of  . A type interpretation, an interpretation function, and a \(\lambda \)-designation function form an interpretation
. A type interpretation, an interpretation function, and a \(\lambda \)-designation function form an interpretation  .
.
For an interpretation  and a valuation \(\xi \), the denotation of a term is defined as
and a valuation \(\xi \), the denotation of a term is defined as  , and
, and  . For ground terms t, the denotation does not depend on the choice of the valuation \(\xi \), which is why we sometimes write
. For ground terms t, the denotation does not depend on the choice of the valuation \(\xi \), which is why we sometimes write  for
for  .
.
An interpretation  is proper if
is proper if  for all \(\lambda \)-expressions \(\lambda x.\>t\) and all valuations \(\xi \). If a type interpretation
for all \(\lambda \)-expressions \(\lambda x.\>t\) and all valuations \(\xi \). If a type interpretation  and an interpretation function
and an interpretation function  can be extended by a \(\lambda \)-designation function
can be extended by a \(\lambda \)-designation function  to a proper interpretation
to a proper interpretation  , then this
, then this  is unique [18, Proposition 2.18]. Given an interpretation
is unique [18, Proposition 2.18]. Given an interpretation  and a valuation \(\xi \), an equation \(s\approx t\) is true if
and a valuation \(\xi \), an equation \(s\approx t\) is true if  and
and  are equal and it is false otherwise. A disequation \(s\not \approx t\) is true if \(s \approx t\) is false. A clause is true if at least one of its literals is true. A clause set is true if all its clauses are true. A proper interpretation
are equal and it is false otherwise. A disequation \(s\not \approx t\) is true if \(s \approx t\) is false. A clause is true if at least one of its literals is true. A clause set is true if all its clauses are true. A proper interpretation  is a model of a clause set N, written
is a model of a clause set N, written  , if N is true in
, if N is true in  for all valuations \(\xi \).
for all valuations \(\xi \).
2.3 Skolem-Aware Interpretations
Some of our calculus rules introduce Skolem symbols—i.e., symbols representing objects mandated by existential quantification. We define a Skolem-extended signature that contains all Skolem symbols that could possibly be needed by the calculus rules.
Definition 2
Given a term signature \(\Sigma \), let the Skolem-extended term signature \(\Sigma _{\textsf {sk} }\) the smallest signature that contains all symbols from \(\Sigma \) and a symbol  for all types \(\upsilon \), variables \(z:\upsilon \), terms \(t:\upsilon \rightarrow \hbox {o}\) over the signature \((\Sigma _{{\textsf {ty} }}, \Sigma _{\textsf {sk} })\), where \(\bar{\alpha }\) are the free type variables occurring in t and \(\bar{x}:\bar{\tau }\) are the free term variables occurring in t in order of first occurrence.
for all types \(\upsilon \), variables \(z:\upsilon \), terms \(t:\upsilon \rightarrow \hbox {o}\) over the signature \((\Sigma _{{\textsf {ty} }}, \Sigma _{\textsf {sk} })\), where \(\bar{\alpha }\) are the free type variables occurring in t and \(\bar{x}:\bar{\tau }\) are the free term variables occurring in t in order of first occurrence.
Interpretations as defined above can interpret the Skolem symbols arbitrarily. For example, an interpretation  does not necessarily interpret the symbol
does not necessarily interpret the symbol  as
as  . Therefore, an inference producing
. Therefore, an inference producing  from
from  is unsound w.r.t. \(\models \). As a remedy, we define Skolem-aware interpretations as follows:
is unsound w.r.t. \(\models \). As a remedy, we define Skolem-aware interpretations as follows:
Definition 3
We call a proper interpretation over a Skolem-extended signature Skolem-aware if for all Skolem symbols  , where \(\bar{\alpha }\) are the free type variables and \(\bar{x}\) are the free term variables occurring in t in order of first occurrence. An interpretation is a Skolem-aware model of a clause set N, written
, where \(\bar{\alpha }\) are the free type variables and \(\bar{x}\) are the free term variables occurring in t in order of first occurrence. An interpretation is a Skolem-aware model of a clause set N, written  , if
, if  is Skolem-aware and
is Skolem-aware and  .
.
3 The Calculus
The inference rules of our calculus \(\hbox {o}\lambda \)Sup have many complex side conditions that may appear arbitrary at first sight. They are, however, directly motivated by our completeness proof and are designed to restrict inferences as much as possible without compromising refutational completeness.
The \(\hbox {o}\lambda \)Sup calculus closely resembles \(\lambda \)Sup, augmented with rules for Boolean reasoning that are inspired by \(\hbox {o}\)Sup. As in \(\lambda \)Sup, superposition-like inferences are restricted to certain first-order-like subterms, the green subterms. Our completeness proof allows for this restriction because it is based on a reduction to first-order logic.
Definition 4
(Green subterms and positions) A green position of a \(\lambda \)-term is a finite sequence of natural numbers defined inductively as follows. For any \(\lambda \)-term t, the empty sequence \(\varepsilon \) is a green position of t. For all symbols  , types \(\bar{\tau }\), and \(\lambda \)-terms \(\bar{u}\), if p is a green position of \(u_i\), then i.p is a green position of \({\textsf {f} }{\langle \bar{\tau }\rangle }\>\bar{u}\).
, types \(\bar{\tau }\), and \(\lambda \)-terms \(\bar{u}\), if p is a green position of \(u_i\), then i.p is a green position of \({\textsf {f} }{\langle \bar{\tau }\rangle }\>\bar{u}\).
The green subterm of a \(\lambda \)-term at a given green position is defined inductively as follows. For any \(\lambda \)-term t, t itself is the green subterm of t at green position \(\varepsilon \). For all symbols  , types \(\bar{\tau }\), and \(\lambda \)-terms \(\bar{u}\), if t is a green subterm of \(u_i\) at some green position p for some i, then t is the green subterm of \({\textsf {f} }{\langle \bar{\tau }\rangle }\>\bar{u}\) at green position i.p.
, types \(\bar{\tau }\), and \(\lambda \)-terms \(\bar{u}\), if t is a green subterm of \(u_i\) at some green position p for some i, then t is the green subterm of \({\textsf {f} }{\langle \bar{\tau }\rangle }\>\bar{u}\) at green position i.p.
For positions in clauses, natural numbers are not appropriate because clauses and literals are unordered. A green position in a clause C is a tuple L.s.p where \(L = s \mathrel {\dot{\approx }}t\) is a literal in C and p is a green position in s. The green subterm of C at green position L.s.p is the green subterm of s at green position p. A green position is top level if it is of the form \(L.s.\epsilon \).
We write \(s|_p\) to denote the green subterm at position p in s. A position p is at or below a position q if q is a prefix of p. A position p is below a position q if q is a proper prefix of p.
For example, the green subterms of  are the term itself,
are the term itself,  , and \(\lambda x.\>{\textsf {h} }\>{\textsf {b} }\).
, and \(\lambda x.\>{\textsf {h} }\>{\textsf {b} }\).
Definition 5
(Green contexts) We write  to denote a \(\lambda \)-term s with the green subterm u at position p and call
to denote a \(\lambda \)-term s with the green subterm u at position p and call  a green context; We omit the subscript p if there are no ambiguities.
a green context; We omit the subscript p if there are no ambiguities.
The notions of green positions, subterms, and context are lifted to \(\beta \eta \)-equivalence classes via the \(\beta \eta {\textsf {Q} }_{\eta }\)-normal representative.
3.1 Preprocessing
Our completeness theorem requires that quantified variables do not appear in certain higher-order contexts. Quantified variables in these higher-order contexts are problematic because they have no clear counterpart in first-order logic and our completeness proof is based on a reduction to first-order logic. We use preprocessing to eliminate such problematic occurrences of quantifiers.
Definition 6
The rewrite rules  and
and  , which we collectively denote by
, which we collectively denote by  , are defined on \(\lambda \)-terms as
, are defined on \(\lambda \)-terms as

where the rewritten occurrence of \({\textsf {Q} }{\langle \tau \rangle }\) is unapplied, has an argument that is not a \(\lambda \)-expression, or has an argument of the form \(\lambda x.\>v\) such that x occurs free in a nongreen position of v.
If either of these rewrite rules can be applied to a given term, the term is  -reducible; otherwise, it is
-reducible; otherwise, it is  -normal. We lift this notion to \(\beta \eta \)-equivalence classes via the \(\beta \eta {\textsf {Q} }_{\eta }\)-normal representative. A clause or clause set is
-normal. We lift this notion to \(\beta \eta \)-equivalence classes via the \(\beta \eta {\textsf {Q} }_{\eta }\)-normal representative. A clause or clause set is  -normal if all contained terms are
-normal if all contained terms are  -normal.
-normal.
For example, the term  is
is  -normal. A term may be
-normal. A term may be  -reducible because a quantifier appears unapplied (e.g.,
-reducible because a quantifier appears unapplied (e.g.,  ); a quantified variable occurs applied (e.g.,
); a quantified variable occurs applied (e.g.,  ); a quantified variable occurs inside a nested \(\lambda \)-expression (e.g.,
); a quantified variable occurs inside a nested \(\lambda \)-expression (e.g.,  ); or a quantified variable occurs in the argument of a variable, either a free variable (e.g.,
); or a quantified variable occurs in the argument of a variable, either a free variable (e.g.,  ) or a bound variable (e.g.,
) or a bound variable (e.g.,  ).
).
We can also characterize  -normality as follows:
-normality as follows:
Lemma 7
Let t be a term with spine notation \(t = s\>\bar{u}_n\). Then t is  -normal if and only if \(\bar{u}_n\) are
-normal if and only if \(\bar{u}_n\) are  -normal and
-normal and
-
(i)
s is of the form \({\textsf {Q} }{\langle \tau \rangle }\), \(n=1\), and \(u_1\) is of the form \(\lambda y.\>u'\) such that y occurs free only in green positions of \(u'\); or
-
(ii)
s is a \(\lambda \)-expression whose body is
 -normal; or
-normal; or -
(iii)
s is neither of the form \({\textsf {Q} }{\langle \tau \rangle }\) nor a \(\lambda \)-expression.
Proof
This follows directly from Definition 6. \(\square \)
In the following lemmas, our goal is to show that  -normality is invariant under \(\beta \eta {\textsf {Q} }_{\eta }\)-normalization—i.e., if a \(\lambda \)-term t is
-normality is invariant under \(\beta \eta {\textsf {Q} }_{\eta }\)-normalization—i.e., if a \(\lambda \)-term t is  -normal, then so is
-normal, then so is  . However,
. However,  -normality is not invariant under arbitrary \(\beta \eta \)-conversions. Clearly, a \(\beta \)-expansion can easily introduce
-normality is not invariant under arbitrary \(\beta \eta \)-conversions. Clearly, a \(\beta \)-expansion can easily introduce  -reducible terms, e.g.,
-reducible terms, e.g.,  .
.
Lemma 8
If t and v are  -normal \(\lambda \)-terms, then \(t\>v\) is a
-normal \(\lambda \)-terms, then \(t\>v\) is a  -normal \(\lambda \)-term.
-normal \(\lambda \)-term.
Proof
We prove this by induction on the structure of t. Let \(s\>\bar{u}_n = t\) be the spine notation of t. By Lemma 7, \(\bar{u}_n\) are  -normal and one of the lemma’s three cases applies. Since t is of functional type and
-normal and one of the lemma’s three cases applies. Since t is of functional type and  -normal, s cannot be of the form \({\textsf {Q} }{\langle \tau \rangle }\), excluding case (i). Cases (ii) and (iii) are independent of \(\bar{u}_n\), and hence appending v to that tuple does not affect the
-normal, s cannot be of the form \({\textsf {Q} }{\langle \tau \rangle }\), excluding case (i). Cases (ii) and (iii) are independent of \(\bar{u}_n\), and hence appending v to that tuple does not affect the  -normality of t. \(\square \)
-normality of t. \(\square \)
Lemma 9
If t is a  -normal \(\lambda \)-term and \(\rho \) is a substitution such that \(x\rho \) is
-normal \(\lambda \)-term and \(\rho \) is a substitution such that \(x\rho \) is  -normal for all x, then \(t\rho \) is
-normal for all x, then \(t\rho \) is  -normal.
-normal.
Proof
We prove this by induction on the structure of t. Let \(s\>\bar{u}_n = t\) be its spine notation. Since t is  -normal, by Lemma 7, \(u_n\) are
-normal, by Lemma 7, \(u_n\) are  -normal and one of the following cases applies:
-normal and one of the following cases applies:
Case (i): s is of the form \({\textsf {Q} }{\langle \tau \rangle }\), \(n = 1\), and \(u_1\) is of the form \(\lambda y.\>u'\) such that y occurs free only in green positions of \(u'\). Since our substitutions avoid capture, \(y\rho = y\) and y does not appear in \(x\rho \) for all other variables x. It is clear from the definition of green positions (Definition 4) that since y occurs free only in green positions of \(u'\), y also occurs free only in green positions of \(u'\rho \). Moreover, by the induction hypothesis, \(u_1\rho \) is  -normal. Hence, \(t\rho = {\textsf {Q} }{\langle \tau \rho \rangle }\>(u_1\rho ) = {\textsf {Q} }{\langle \tau \rho \rangle }\>(\lambda y.\>u'\rho )\) is also
-normal. Hence, \(t\rho = {\textsf {Q} }{\langle \tau \rho \rangle }\>(u_1\rho ) = {\textsf {Q} }{\langle \tau \rho \rangle }\>(\lambda y.\>u'\rho )\) is also  -normal.
-normal.
Case (ii): s is a \(\lambda \)-expression whose body is  -normal. Then \(t\rho = (\lambda y.\>s'\rho )\>(\bar{u}_n\rho )\) for some
-normal. Then \(t\rho = (\lambda y.\>s'\rho )\>(\bar{u}_n\rho )\) for some  -normal \(\lambda \)-term \(s'\). By the induction hypothesis, \(s'\rho \) and \(\bar{u}_n\rho \) are
-normal \(\lambda \)-term \(s'\). By the induction hypothesis, \(s'\rho \) and \(\bar{u}_n\rho \) are  -normal. Therefore, \(t\rho \) is also
-normal. Therefore, \(t\rho \) is also  -normal.
-normal.
Case (iii): s is neither of the form \({\textsf {Q} }{\langle \tau \rangle }\) nor a \(\lambda \)-expression. If s is of the form \({\textsf {f} }{\langle \bar{\tau }\rangle }\) for some  , then \(t\rho = {\textsf {f} }{\langle \bar{\tau }\rho \rangle }\>(\bar{u}_n\rho )\). By the induction hypothesis, \(\bar{u}_n\rho \) are
, then \(t\rho = {\textsf {f} }{\langle \bar{\tau }\rho \rangle }\>(\bar{u}_n\rho )\). By the induction hypothesis, \(\bar{u}_n\rho \) are  -normal, and therefore \(t\rho \) is also
-normal, and therefore \(t\rho \) is also  -normal. Otherwise, s is a variable x and hence \(t\rho = x\rho \>(\bar{u}_n\rho )\). Since \(x\rho \) is
-normal. Otherwise, s is a variable x and hence \(t\rho = x\rho \>(\bar{u}_n\rho )\). Since \(x\rho \) is  -normal by assumption and \(\bar{u}_n\rho \) are
-normal by assumption and \(\bar{u}_n\rho \) are  -normal by the induction hypothesis, it follows from (repeated application of) Lemma 8 that \(t\rho \) is also
-normal by the induction hypothesis, it follows from (repeated application of) Lemma 8 that \(t\rho \) is also  -normal. \(\square \)
-normal. \(\square \)
Lemma 10
Let t be a \(\lambda \)-term of functional type that does not contain the variable x. If \(\lambda x.\>t\>x\) is  -normal, then t is
-normal, then t is  -normal.
-normal.
Proof
Since \(\lambda x.\>t\>x\) is  -normal, \(t\>x\) is also
-normal, \(t\>x\) is also  -normal. Let \(s\>\bar{u}_n = t\). Since \(t\>x\) is
-normal. Let \(s\>\bar{u}_n = t\). Since \(t\>x\) is  -normal and x is not a \(\lambda \)-expression, s cannot be a quantifier by Lemma 7. Cases (ii) and (iii) are independent of \(\bar{u}_n\), and hence removing x from that tuple does not affect
-normal and x is not a \(\lambda \)-expression, s cannot be a quantifier by Lemma 7. Cases (ii) and (iii) are independent of \(\bar{u}_n\), and hence removing x from that tuple does not affect  -normality. Thus, \(t\>x\) being
-normality. Thus, \(t\>x\) being  -normal implies that t is
-normal implies that t is  -normal. \(\square \)
-normal. \(\square \)
Lemma 11
Let t be a \(\lambda \)-term and x a variable occurring free only in green positions of t. Let \(t'\) be a term obtained via a \(\beta \eta {\textsf {Q} }_{\eta }\)-normalization step from t. Then x occurs free only in green positions of \(t'\).
Proof
By induction on the structure of t. If x does not occur free in t, the claim is obvious. If \(t = x\), there is no possible \(\beta \eta {\textsf {Q} }_{\eta }\)-normalization step because for these steps the head of the rewritten term must be either a \(\lambda \)-expression or a quantifier. So we now assume that x does occur free in t and that \(t \not = x\). Then, by the assumption that x occurs free only in green positions, t must be of the form \({\textsf {f} }{\langle \bar{\tau }\rangle }\>\bar{u}\) for some  , some types \(\bar{\tau }\) and some \(\lambda \)-terms \(\bar{u}\). The \(\beta \eta {\textsf {Q} }_{\eta }\)-normalization step must take place in one of the \(\bar{u}\), yielding \(\bar{u}'\) such that \(t'= {\textsf {f} }{\langle \bar{\tau }\rangle }\> \bar{u}'\). By the induction hypothesis, x occurs free only in green positions of \(\bar{u}'\) and therefore only in green positions of \(t'\). \(\square \)
, some types \(\bar{\tau }\) and some \(\lambda \)-terms \(\bar{u}\). The \(\beta \eta {\textsf {Q} }_{\eta }\)-normalization step must take place in one of the \(\bar{u}\), yielding \(\bar{u}'\) such that \(t'= {\textsf {f} }{\langle \bar{\tau }\rangle }\> \bar{u}'\). By the induction hypothesis, x occurs free only in green positions of \(\bar{u}'\) and therefore only in green positions of \(t'\). \(\square \)
Lemma 12
Let t be  -normal and let \(t'\) be obtained from t by a \(\beta \eta {\textsf {Q} }_{\eta }\)-normalization step. If it is an \(\eta \)-reduction step, we assume that it happens not directly below a quantifier. Then \(t'\) is also
-normal and let \(t'\) be obtained from t by a \(\beta \eta {\textsf {Q} }_{\eta }\)-normalization step. If it is an \(\eta \)-reduction step, we assume that it happens not directly below a quantifier. Then \(t'\) is also  -normal.
-normal.
Proof
By induction on the structure of t. Let \(s\>\bar{u}_n = t\). By Lemma 7, \(\bar{u}_n\) are  -normal, and one of the following cases applies:
-normal, and one of the following cases applies:
Case (i): s is of the form \({\textsf {Q} }{\langle \tau \rangle }\), \(n = 1\), and \(u_1\) is of the form \(\lambda y.\>v\) such that y occurs free only in green positions of v. Then the normalization cannot happen at t, because s is of the form \({\textsf {Q} }{\langle \tau \rangle }\) and \(u_1\) is a \(\lambda \)-expression already. It cannot happen at \(u_1\) by the assumption of this lemma. So it must happen in v, yielding some \(\lambda \)-term \(v'\). Then \(t = s \> (\lambda y.\>v')\). The \(\lambda \)-term \(v'\) is  -normal by the induction hypothesis and hence \((\lambda y.\>v')\) is
-normal by the induction hypothesis and hence \((\lambda y.\>v')\) is  -normal. Since y occurs free only in green positions of v, by Lemma 11, y occurs free only in green positions of \(v'\). Thus, \(t'\) is
-normal. Since y occurs free only in green positions of v, by Lemma 11, y occurs free only in green positions of \(v'\). Thus, \(t'\) is  -normal.
-normal.
Cases (ii) and (iii): s is a \(\lambda \)-expression whose body is  -normal; or s is neither of the form \({\textsf {Q} }{\langle \tau \rangle }\) nor a \(\lambda \)-expression.
-normal; or s is neither of the form \({\textsf {Q} }{\langle \tau \rangle }\) nor a \(\lambda \)-expression.
If the \(\beta \eta {\textsf {Q} }_{\eta }\)-normalization step happens in some \(u_i\), yielding some \(\lambda \)-term \(u_i'\), then \(u_i'\) is  -normal by the induction hypothesis. Thus, \(t' = s\>u_1\>\cdots \>u_{i-1}\>u_{i}'\>u_{i+1}\cdots \>u_n\) is also
-normal by the induction hypothesis. Thus, \(t' = s\>u_1\>\cdots \>u_{i-1}\>u_{i}'\>u_{i+1}\cdots \>u_n\) is also  -normal.
-normal.
Otherwise, if \(s = \lambda x.\>v\) and the \(\beta \eta {\textsf {Q} }_{\eta }\)-normalization step happens in v, yielding some \(\lambda \)-term \(v'\), then \(v'\) is  -normal by the induction hypothesis. Thus, \(t' = (\lambda x.\>v')\>\bar{u}_n\) is also
-normal by the induction hypothesis. Thus, \(t' = (\lambda x.\>v')\>\bar{u}_n\) is also  -normal.
-normal.
Otherwise, the \(\beta \eta {\textsf {Q} }_{\eta }\)-normalization step happens at \(s\>\bar{u}_m\) for some \(m \le n\), yielding some \(\lambda \)-term \(v'\). Then \(t' = v'\>u_{m+1}\>\cdots \>u_n\). The \(\lambda \)-terms s and \(\bar{u}_m\) are  -normal and by repeated application of Lemma 8, \(s\>\bar{u}_m\) is also
-normal and by repeated application of Lemma 8, \(s\>\bar{u}_m\) is also  -normal. The \(\lambda \)-term \(v'\) is
-normal. The \(\lambda \)-term \(v'\) is  -normal by Lemma 9 (for \(\beta \)-reductions) or Lemma 10 (for \(\eta \)-reductions). The normalization step cannot be a \({\textsf {Q} }_{\eta }\)-normalization because s is not a quantifier. Since \(\bar{u}_n\) are also
-normal by Lemma 9 (for \(\beta \)-reductions) or Lemma 10 (for \(\eta \)-reductions). The normalization step cannot be a \({\textsf {Q} }_{\eta }\)-normalization because s is not a quantifier. Since \(\bar{u}_n\) are also  -normal, by repeated application of Lemma 8, \(t[v'] = v'\>u_{m+1}\>\cdots \>u_n\) is also
-normal, by repeated application of Lemma 8, \(t[v'] = v'\>u_{m+1}\>\cdots \>u_n\) is also  -normal. \(\square \)
-normal. \(\square \)
A direct consequence of this lemma is that  -normality is invariant under \(\beta \eta {\textsf {Q} }_{\eta }\)-normalization, as we wanted to show:
-normality is invariant under \(\beta \eta {\textsf {Q} }_{\eta }\)-normalization, as we wanted to show:
Corollary 13
If t is a  -normal \(\lambda \)-term, then
-normal \(\lambda \)-term, then  is also
is also  -normal.
-normal.
As mentioned above, the converse does not hold. Therefore, following our convention,  -normality is defined on terms (i.e., \(\beta \eta \)-equivalence classes) via \(\beta \eta {\textsf {Q} }_{\eta }\)-normal forms. It follows that
-normality is defined on terms (i.e., \(\beta \eta \)-equivalence classes) via \(\beta \eta {\textsf {Q} }_{\eta }\)-normal forms. It follows that  -normality is well-behaved under applications of terms as well:
-normality is well-behaved under applications of terms as well:
Lemma 14
If t and v are  -normal terms where t is of functional type, then \(t\>v\) is also
-normal terms where t is of functional type, then \(t\>v\) is also  -normal.
-normal.
Proof
Since  -normality is defined via \(\beta \eta {\textsf {Q} }_{\eta }\)-normal forms, we must show that if
-normality is defined via \(\beta \eta {\textsf {Q} }_{\eta }\)-normal forms, we must show that if  and
and  are
are  -normal, then
-normal, then  is
is  -normal. By Lemma 8,
-normal. By Lemma 8,  is
is  -normal. By Corollary 13,
-normal. By Corollary 13,  is
is  -normal. \(\square \)
-normal. \(\square \)
A preprocessor  -normalizes the input problem. It clearly terminates because each
-normalizes the input problem. It clearly terminates because each  -step reduces the number of quantifiers. The
-step reduces the number of quantifiers. The  -normality of the initial clause set of a derivation will be a precondition of the completeness theorem. Although inferences may produce
-normality of the initial clause set of a derivation will be a precondition of the completeness theorem. Although inferences may produce  -reducible clauses, we do not
-reducible clauses, we do not  -normalize during the derivation process itself. Instead,
-normalize during the derivation process itself. Instead,  -reducible ground instances of clauses will be considered redundant by the redundancy criterion. Thus, clauses whose ground instances are all
-reducible ground instances of clauses will be considered redundant by the redundancy criterion. Thus, clauses whose ground instances are all  -reducible can be deleted. However, there are
-reducible can be deleted. However, there are  -reducible clauses, such as
-reducible clauses, such as  , that nevertheless have
, that nevertheless have  -normal ground instances. Such clauses must be kept because the completeness proof relies on their
-normal ground instances. Such clauses must be kept because the completeness proof relies on their  -normal ground instances.
-normal ground instances.
In principle, we could omit the side condition of the  -rewrite rules and eliminate all quantifiers. However, the calculus (especially, the redundancy criterion) performs better with quantifiers than with \(\lambda \)-expressions, which is why we restrict
-rewrite rules and eliminate all quantifiers. However, the calculus (especially, the redundancy criterion) performs better with quantifiers than with \(\lambda \)-expressions, which is why we restrict  -normalization as much as the completeness proof allows. Extending the preprocessing to eliminate all Boolean terms as in Kotelnikov et al. [27] does not work for higher-order logic because Boolean terms can contain variables bound by enclosing \(\lambda \)-expressions.
-normalization as much as the completeness proof allows. Extending the preprocessing to eliminate all Boolean terms as in Kotelnikov et al. [27] does not work for higher-order logic because Boolean terms can contain variables bound by enclosing \(\lambda \)-expressions.
3.2 Term Orders and Selection Functions
The calculus is parameterized by a strict and a nonstrict term order, a literal selection function, and a Boolean subterm selection function. These concepts are defined below.
Definition 15
(Strict ground term order) A well-founded strict total order \(\succ \) on ground terms is a strict ground term order if it satisfies the following criteria, where \(\succeq \) denotes the reflexive closure of \(\succ \):
-
(O1)
compatibility with green contexts: \(s' \succ s\) implies
 ;
; -
(O2)
green subterm property:
 ;
; -
(O3)
 for all terms
for all terms  ;
; -
(O4)
\({\textsf {Q} }{\langle \tau \rangle }\> t \succ t\>u\) for all types \(\tau \), terms t, and terms u such that \({\textsf {Q} }{\langle \tau \rangle }\>t\) and u are
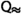 -normal and the only Boolean green subterms of u are
-normal and the only Boolean green subterms of u are  and
and  .
.
Given a strict ground term order, we extend it to literals and clauses via the multiset extensions in the standard way [2, Sect. 2.4].
Remark 16
The property \({\textsf {Q} }{\langle \tau \rangle }\> t \succ t\>u\) from (O4) cannot be achieved in general—a fact that Christoph Benzmüller made us aware about. Without further restrictions, it would imply that \({\textsf {Q} }{\langle \tau \rangle } (\lambda x.\> x) \succ (\lambda x.\> x) ({\textsf {Q} }{\langle \tau \rangle } (\lambda x.\> x)) = {\textsf {Q} }{\langle \tau \rangle } (\lambda x.\> x)\), contradicting irreflexivity of \(\succ \). Restricting the Boolean green subterms of u to be only  and
and  resolves this issue. A second issue is that (O4) without further restrictions would imply \({\textsf {Q} }{\langle \tau \rangle }\> (\lambda y.\> y {\textsf {a} }) \succ (\lambda y.\> y\>{\textsf {a} }) (\lambda x.\>{\textsf {Q} }{\langle \tau \rangle }\> (\lambda y.\> y\>{\textsf {a} })) = {\textsf {Q} }{\langle \tau \rangle }\> (\lambda y.\> y {\textsf {a} })\), again contradicting irreflexivity. The restriction on the Boolean green subterms of u does not apply here because the Boolean subterms of \(\lambda x.\>{\textsf {Q} }{\langle \tau \rangle }\> (\lambda y.\> y {\textsf {a} })\) are not green. The restriction to
resolves this issue. A second issue is that (O4) without further restrictions would imply \({\textsf {Q} }{\langle \tau \rangle }\> (\lambda y.\> y {\textsf {a} }) \succ (\lambda y.\> y\>{\textsf {a} }) (\lambda x.\>{\textsf {Q} }{\langle \tau \rangle }\> (\lambda y.\> y\>{\textsf {a} })) = {\textsf {Q} }{\langle \tau \rangle }\> (\lambda y.\> y {\textsf {a} })\), again contradicting irreflexivity. The restriction on the Boolean green subterms of u does not apply here because the Boolean subterms of \(\lambda x.\>{\textsf {Q} }{\langle \tau \rangle }\> (\lambda y.\> y {\textsf {a} })\) are not green. The restriction to  -normal terms resolves this second issue, but it forces us to preprocess the input problem.
-normal terms resolves this second issue, but it forces us to preprocess the input problem.
Definition 17
(Strict term order) A strict term order is a relation \(\succ \) on terms, literals, and clauses such that its restriction to ground entities is a strict ground term order and such that it is stable under grounding substitutions (i.e., \(t \succ s\) implies \(t\theta \succ s\theta \) for all substitutions \(\theta \) grounding the entities t and s).
Definition 18
(Nonstrict term order) Given a strict term order \(\succ \) and its reflexive closure \(\succeq \), a nonstrict term order is a relation \(\succsim \) on terms, literals, and clauses such that \(t \succsim s\) implies \(t\theta \succeq s\theta \) for all \(\theta \) grounding the entities t and s.
Although we call them orders, a strict term order \(\succ \) is not required to be transitive on nonground entities, and a nonstrict term order \(\succsim \) does not need to be transitive at all. Normally, \(t \succeq s\) should imply \(t \succsim s\), but this is not required either. A nonstrict term order \(\succsim \) allows us to be more precise than the reflexive closure \(\succeq \) of \(\succ \). For example, we cannot have \(y\>{\textsf {b} } \succeq y\>{\textsf {a} }\), because \(y\>{\textsf {b} } \not = y\>{\textsf {a} }\) and \(y\>{\textsf {b} } \not \succ y\>{\textsf {a} }\) by stability under grounding substitutions (with \(\{y \mapsto \lambda x.\>{\textsf {c} }\}\)). But we can have \(y\>{\textsf {b} } \succsim y\>{\textsf {a} }\) if \({\textsf {b} } \succ {\textsf {a} }\). In practice, the strict and the nonstrict term order should be chosen so that they can compare as many pairs of terms as possible while being computable and reasonably efficient.
Definition 19
(Maximality) An element x of a multiset M is \(\unrhd \)-maximal for some relation \(\unrhd \) if for all \(y \in M\) with \(y \unrhd x\), we have \(y = x\). It is strictly \(\unrhd \)-maximal if it is \(\unrhd \)-maximal and occurs only once in M.
Definition 20
(Literal selection function) A literal selection function is a mapping from each clause to a subset of its literals. The literals in this subset are called selected. The following restrictions apply:
-
A literal must not be selected if it is positive and neither side is
 .
. -
A literal
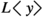 must not be selected if \(y\> \bar{u}_n\), with \(n \ge 1\), is a \(\succeq \)-maximal term of the clause.
must not be selected if \(y\> \bar{u}_n\), with \(n \ge 1\), is a \(\succeq \)-maximal term of the clause.
Definition 21
(Boolean subterm selection function) A Boolean subterm selection function is a function mapping each clause C to a subset of the green positions with Boolean subterms in C. The positions in this subset are called selected in C. Informally, we also say that the Boolean subterms at these positions are selected. The following restrictions apply:
-
A subterm
 must not be selected if \(y\> \bar{u}_n\), with \(n \ge 1\), is a \(\succeq \)-maximal term of the clause.
must not be selected if \(y\> \bar{u}_n\), with \(n \ge 1\), is a \(\succeq \)-maximal term of the clause. -
A subterm must not be selected if it is
 or
or  or a variable-headed term.
or a variable-headed term. -
A subterm must not be selected if it is at the top-level position on either side of a positive literal.
3.3 The Core Inference Rules
Let \(\succ \) be a strict term order, let \(\succsim \) be a nonstrict term order, let \(\textit{HLitSel}\) be a literal selection function, and let \(\textit{HBoolSel}\) be a Boolean subterm selection function. The calculus rules depend on the following auxiliary notions.
Definition 22
(Eligibility) A literal L is (strictly) \(\unrhd \)-eligible w.r.t. a substitution \(\sigma \) in C for some relation \(\unrhd \) if it is selected in C or there are no selected literals and no selected Boolean subterms in C and \(L\sigma \) is (strictly) \(\unrhd \)-maximal in \(C\sigma .\)
The \(\unrhd \)-eligible positions of a clause C w.r.t. a substitution \(\sigma \) are inductively defined as follows:
-
(E1)
Any selected position is \(\unrhd \)-eligible.
-
(E2)
If a literal
 is either \(\unrhd \)-eligible and negative or strictly \(\unrhd \)-eligible and positive, then \(L.s.\varepsilon \) is \(\unrhd \)-eligible.
is either \(\unrhd \)-eligible and negative or strictly \(\unrhd \)-eligible and positive, then \(L.s.\varepsilon \) is \(\unrhd \)-eligible. -
(E3)
If the position p is \(\unrhd \)-eligible and the head of \(C|_p\) is not
 or
or  , the positions of all direct green subterms are \(\unrhd \)-eligible.
, the positions of all direct green subterms are \(\unrhd \)-eligible. -
(E4)
If the position p is \(\unrhd \)-eligible and \(C|_p\) is of the form
 or
or  , then the position of s is \(\unrhd \)-eligible if
, then the position of s is \(\unrhd \)-eligible if  and the position of t is \(\unrhd \)-eligible if
and the position of t is \(\unrhd \)-eligible if  .
.
If \(\sigma \) is the identity substitution, we leave it implicit.
We define deeply occurring variables as in \(\lambda \)Sup, but exclude \(\lambda \)-expressions directly below quantifiers:
Definition 23
(Deep occurrences) A variable occurs deeply in a clause C if it occurs free inside an argument of an applied variable or inside a \(\lambda \)-expression that is not directly below a quantifier.
For example, x and z occur deeply in  , whereas y does not occur deeply. Intuitively, deep occurrences are occurrences of variables that can be caught in \(\lambda \)-expressions by grounding.
, whereas y does not occur deeply. Intuitively, deep occurrences are occurrences of variables that can be caught in \(\lambda \)-expressions by grounding.
Fluid terms are defined as in \(\lambda \)Sup, using the \(\beta \eta {\textsf {Q} }_{\eta }\)-normal form:
Definition 24
(Fluid terms) A term t is called fluid if (1)  is of the form \(y\>\bar{u}_n\) where \(n \ge 1\), or (2)
is of the form \(y\>\bar{u}_n\) where \(n \ge 1\), or (2)  is a \(\lambda \)-expression and there exists a substitution \(\sigma \) such that
is a \(\lambda \)-expression and there exists a substitution \(\sigma \) such that  is not a \(\lambda \)-expression (due to \(\eta \)-reduction).
is not a \(\lambda \)-expression (due to \(\eta \)-reduction).
Case (2) can arise only if t contains an applied variable. Intuitively, fluid terms are terms whose \(\eta \)-short \(\beta \)-normal form can change radically as a result of instantiation. For example, \(\lambda x.\> y\> {\textsf {a} }\> (z\> x)\) is fluid because applying \(\{z \mapsto \lambda x.\>x\}\) makes the \(\lambda \) vanish: \((\lambda x.\> y\> {\textsf {a} }\> x) = y\> {\textsf {a} }\). Similarly, \(\lambda x.\> {\textsf {f} }\>(y\>x)\>x\) is fluid because \((\lambda x.\> {\textsf {f} }\>(y\>x)\>x)\{y \mapsto \lambda x.\>{\textsf {a} }\} = (\lambda x.\> {\textsf {f} }\>{\textsf {a} }\>x) = {\textsf {f} }\>{\textsf {a} }\). In Sect. 5, we will discuss how fluid terms can be overapproximated in an implementation.
The rules of our calculus are stated as follows. The superposition rule strongly resembles the one of \(\lambda \)Sup but uses our new notion of eligibility, and the new conditions 9 and 10 stem from the Sup rule of \(\hbox {o}\)Sup:

-
1.
u is not fluid;2.u is not a variable deeply occurring in C;
-
3.
variable condition: if u is a variable y, there must exist a grounding substitution \(\theta \) such that \(t\sigma \theta \succ t'\sigma \theta \) and \(C\sigma \theta \prec C''\sigma \theta \), where \(C'' = C\{y\mapsto t'\}\);
-
4.
\(\sigma \in {{\,\textrm{CSU}\,}}(t,u)\);5.\(t\sigma \not \precsim t'\sigma \);6.the position of u is \(\succsim \)-eligible in C w.r.t. \(\sigma \);
-
7.
\(C\sigma \not \precsim D\sigma \);8.\(t \approx t'\) is strictly \(\succsim \)-eligible in D w.r.t. \(\sigma \);
-
9.
\(t\sigma \) is not a fully applied logical symbol;
-
10.
if
 , the position of the subterm u is at the top level of a positive literal.
, the position of the subterm u is at the top level of a positive literal.
The second rule is a variant of Sup that focuses on fluid green subterms. It stems from \(\lambda \)Sup.

with the following side conditions, in addition to Sup’s conditions 5 to 10:
-
1.
u is a variable deeply occurring in C or u is fluid;
-
2.
z is a fresh variable;3. \(\sigma \in {{\,\textrm{CSU}\,}}(z\>t{,}\;u)\);4.\((z\>t')\sigma \not = (z\>t)\sigma \).
The ERes and EFact rules are copied from \(\lambda \)Sup. As a minor optimization, we replace the \(\succsim \)-eligibility condition of \(\lambda \)Sup’s EFact by a \(\succsim \)-maximality condition and a condition that nothing is selected. The new conditions are not equivalent to the old one because positive literals of the form  can be selected.
can be selected.

For ERes: \(\sigma \in {{\,\textrm{CSU}\,}}(u,u')\) and \(u \not \approx u'\) is \(\succsim \)-eligible in C w.r.t. \(\sigma \). For EFact: \(\sigma \in {{\,\textrm{CSU}\,}}(u,u')\), \(u\sigma \not \precsim v\sigma \), \((u \approx v)\sigma \) is \(\succsim \)-maximal in \(C\sigma \), and nothing is selected in C.
Argument congruence—the property that \(t \approx s\) entails \(t\>z \approx s\>z\)—is embodied by the rule ArgCong, which is identical with the rule of \(\lambda \)Sup:

where \(n > 0\) and \(\sigma \) is the most general type substitution that ensures well-typedness of the conclusion. In particular, if s accepts k arguments, then ArgCong will yield k conclusions—one for each \(n \in \{1,\ldots , k\}\)—where \(\sigma \) is the identity substitution. If the result type of s is a type variable, ArgCong will yield infinitely many additional conclusions—one for each \(n > k\)—where \(\sigma \) instantiates the result type of s with \(\alpha _1 \rightarrow \cdots \rightarrow \alpha _{n-k} \rightarrow \beta \) for fresh \(\bar{\alpha }_{n-k}\) and \(\beta \). Moreover, the literal \(s \approx s'\) must be strictly \(\succsim \)-eligible in C w.r.t. \(\sigma \), and \(\bar{x}_n\) is a tuple of distinct fresh variables.
The following rules are concerned with Boolean reasoning and originate from \(\hbox {o}\)Sup. They have been adapted to support polymorphism and applied variables.

-
1.
\(\sigma \) is a type unifier of the type of u with the Boolean type \(\hbox {o}\) (i.e., the identity if u is Boolean or \(\alpha \mapsto \hbox {o}\) if u is of type \(\alpha \) for some type variable \(\alpha \));
-
2.
u is neither variable-headed nor a fully applied logical symbol;
-
3.
the position of u is \(\succsim \)-eligible in C;
-
4.
the occurrence of u is not at the top level of a positive literal.

1.  ; 2. \(s \approx s'\) is strictly \(\succsim \)-eligible in C w.r.t. \(\sigma \).
; 2. \(s \approx s'\) is strictly \(\succsim \)-eligible in C w.r.t. \(\sigma \).

-
1.
 , or
, or  , respectively;
, respectively; -
2.
x, y, and \(\alpha \) are fresh variables;
-
3.
the position of u is \(\succsim \)-eligible in C w.r.t. \(\sigma \);
-
4.
if the head of u is a variable, it must be applied and the affected literal must be of the form
 , or \(u \approx v\) where v is a variable-headed term.
, or \(u \approx v\) where v is a variable-headed term.

-
1.
\(\sigma \in {{\,\textrm{CSU}\,}}(t,u)\) and \((t, t')\) is one of the following pairs:

where y is a fresh variable;
-
2.
u is not a variable;
-
3.
the position of u is \(\succsim \)-eligible in C w.r.t. \(\sigma \);
-
4.
if the head of u is a variable, it must be applied and the affected literal must be of the form
 , or \(u \approx v\) where v is a variable-headed term.
, or \(u \approx v\) where v is a variable-headed term.

-
1.
 and
and  , respectively, where \(\beta \) is a fresh type variable, y is a fresh term variable, \(\bar{\alpha }\) are the free type variables and \(\bar{x}\) are the free term variables occurring in \(y\sigma \) in order of first occurrence;
, respectively, where \(\beta \) is a fresh type variable, y is a fresh term variable, \(\bar{\alpha }\) are the free type variables and \(\bar{x}\) are the free term variables occurring in \(y\sigma \) in order of first occurrence; -
2.
u is not a variable;
-
3.
the position of u is \(\succsim \)-eligible in C w.r.t. \(\sigma \);
-
4.
if the head of u is a variable, it must be applied and the affected literal must be of the form
 , or \(u \approx v\) where v is a variable-headed term;
, or \(u \approx v\) where v is a variable-headed term; -
5.
for ForallRw, the indicated occurrence of u is not in a literal
 , and for ExistsRw, the indicated occurrence of u is not in a literal
, and for ExistsRw, the indicated occurrence of u is not in a literal  .
.
In principle, the subscript of the Skolems above could be normalized using Boolean tautologies to share as many Skolem symbols as possible. This is an extension of our calculus that we did not investigate any further.
Like Sup, also the Boolean rules must be simulated in fluid terms. The following rules are Boolean counterparts of FluidSup:

-
1.
u is fluid;
-
2.
z and x are fresh variables;
-
3.
\(\sigma \in {{\,\textrm{CSU}\,}}(z\>x{,}\;u)\);
-
4.
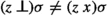 ;
; -
5.
 and
and  ;
; -
6.
the position of u is \(\succsim \)-eligible in C w.r.t. \(\sigma \).

Same conditions as FluidBoolHoist, but  is replaced by
is replaced by  in condition 4.
in condition 4.
In addition to the inference rules, our calculus relies on two axioms, below. Axiom (Ext), from \(\lambda \)Sup, embodies functional extensionality; the expression \({\textsf {diff} }{\langle \alpha ,\beta \rangle }\) abbreviates  . Axiom (Choice) characterizes the Hilbert choice operator \(\varepsilon \).
. Axiom (Choice) characterizes the Hilbert choice operator \(\varepsilon \).


3.4 Rationale for the Rules
Most of the calculus’s rules are adapted from its precursors. Sup, ERes, and EFact are already present in Sup, with slightly different side conditions. Notably, as in \(\lambda \)fSup and \(\lambda \)Sup, Sup inferences are required only into green contexts. Other subterms are accessed indirectly via ArgCong and (Ext).
The rules BoolHoist, EqHoist, NeqHoist, ForallHoist, ExistsHoist, FalseElim, BoolRw, ForallRw, and ExistsRw, concerned with Boolean reasoning, stem from \(\hbox {o}\)Sup, which was inspired by \(\mathrel {\leftarrow \rightarrow }\)Sup. Except for BoolHoist and FalseElim, these rules have a condition stating that “if the head of u is a variable, it must be applied and the affected literal must be of the form  , or \(u \approx v\) where v is a variable-headed term.” The inferences at variable-headed terms permitted by this condition are our form of primitive substitution [1, 21], a mechanism that blindly substitutes logical connectives and quantifiers for variables z with a Boolean result type.
, or \(u \approx v\) where v is a variable-headed term.” The inferences at variable-headed terms permitted by this condition are our form of primitive substitution [1, 21], a mechanism that blindly substitutes logical connectives and quantifiers for variables z with a Boolean result type.
Example 25
Our calculus can prove that Leibniz equality implies equality (i.e., if two values behave the same for all predicates, they are equal) as follows:

The clause  describes Leibniz equality of \({\textsf {a} }\) and \({\textsf {b} }\); if a predicate z holds for \({\textsf {a} }\), it also holds for \({\textsf {b} }\). The clause \({\textsf {a} } \not \approx {\textsf {b} }\) is the negated conjecture. The EqHoist inference, applied on \(z\>{\textsf {b} }\), illustrates how our calculus introduces logical symbols without a dedicated primitive substitution rule. Although
describes Leibniz equality of \({\textsf {a} }\) and \({\textsf {b} }\); if a predicate z holds for \({\textsf {a} }\), it also holds for \({\textsf {b} }\). The clause \({\textsf {a} } \not \approx {\textsf {b} }\) is the negated conjecture. The EqHoist inference, applied on \(z\>{\textsf {b} }\), illustrates how our calculus introduces logical symbols without a dedicated primitive substitution rule. Although  does not appear in the premise, we still need to apply EqHoist on \(z\>{\textsf {b} }\) with
does not appear in the premise, we still need to apply EqHoist on \(z\>{\textsf {b} }\) with  . Other calculi [1, 11, 21, 34] would apply an explicit primitive substitution rule instead, yielding essentially
. Other calculi [1, 11, 21, 34] would apply an explicit primitive substitution rule instead, yielding essentially  . However, in our approach this clause is subsumed and could be discarded immediately. By hoisting the equality to the clausal level, we bypass the redundancy criterion.
. However, in our approach this clause is subsumed and could be discarded immediately. By hoisting the equality to the clausal level, we bypass the redundancy criterion.
Next, BoolRw can be applied to  with
with  . The two FalseElim steps remove the
. The two FalseElim steps remove the  literals. Then Sup is applicable with the unifier \(\{w\mapsto \lambda x_1\, x_2\, x_3.\> x_2\}\in {{\,\textrm{CSU}\,}}({\textsf {b} }{,}\; w\>{\textsf {a} }\>{\textsf {b} }\>{\textsf {b} })\), and ERes derives the contradiction.
literals. Then Sup is applicable with the unifier \(\{w\mapsto \lambda x_1\, x_2\, x_3.\> x_2\}\in {{\,\textrm{CSU}\,}}({\textsf {b} }{,}\; w\>{\textsf {a} }\>{\textsf {b} }\>{\textsf {b} })\), and ERes derives the contradiction.
This mechanism resembling primitive substitution is not the only way our calculus can instantiate variables with logical symbols. Often, the correct instantiation can also be found by unification with a logical symbol that is already present:
Example 26
The following derivation shows that there exists a function y that is equivalent to the conjunction of \({\textsf {p} }\>x\) and \({\textsf {q} }\>x\) for all arguments x:

Here, \({\textsf {sk} }\) stands for  . First, we use the rule ExistsHoist to resolve the existential quantifier, using the unifier
. First, we use the rule ExistsHoist to resolve the existential quantifier, using the unifier  for fresh variables \(\alpha \), \(y'\), and z. Then ForallRw skolemizes the universal quantifier, using the unifier
for fresh variables \(\alpha \), \(y'\), and z. Then ForallRw skolemizes the universal quantifier, using the unifier  for fresh variables \(\beta \) and \(z'\). The Skolem symbol takes \(y'\) as argument because it occurs free in
for fresh variables \(\beta \) and \(z'\). The Skolem symbol takes \(y'\) as argument because it occurs free in  . Then BoolRw applies because the terms \(y'\>({\textsf {sk} }\>y')\) and
. Then BoolRw applies because the terms \(y'\>({\textsf {sk} }\>y')\) and  are unifiable and thus
are unifiable and thus  is unifiable with
is unifiable with  . Finally, two FalseElim inferences lead to the empty clause.
. Finally, two FalseElim inferences lead to the empty clause.
Like in \(\lambda \)Sup, the FluidSup rule is responsible for simulating superposition inferences below applied variables, other fluid terms, and deeply occurring variables. Complementarily, FluidBoolHoist and FluidLoobHoist simulate the various Boolean inference rules below fluid terms. Initially, we considered adding a fluid version of each rule that operates on Boolean subterms, but we discovered that FluidBoolHoist and FluidLoobHoist suffice to achieve refutational completeness.
Example 27
The following clause set demonstrates the need for the rules FluidBoolHoist and FluidLoobHoist:

The set is unsatisfiable because the instantiation  produces the clause
produces the clause  , which is unsatisfiable in conjunction with \({\textsf {a} }\not \approx {\textsf {b} }\).
, which is unsatisfiable in conjunction with \({\textsf {a} }\not \approx {\textsf {b} }\).
The literal selection function can select either literal in the first clause. ERes is applicable in either case, but the unifiers  and
and  do not lead to a contradiction. Instead, we need to apply FluidBoolHoist if the first literal is selected or FluidLoobHoist if the second literal is selected. In the first case, the derivation is as follows:
do not lead to a contradiction. Instead, we need to apply FluidBoolHoist if the first literal is selected or FluidLoobHoist if the second literal is selected. In the first case, the derivation is as follows:

The FluidBoolHoist inference uses the unifier \(\{y \mapsto \lambda u.\> z'\>u\>(x'\> u),\ z \mapsto \lambda u. z'\>{\textsf {b} }\>u,\ x \mapsto x'\>{\textsf {b} }\} \in {{\,\textrm{CSU}\,}}(z\>x{,}\; y\>{\textsf {b} })\). We apply ERes to the first literal of the resulting clause, with unifier  . Next, we apply EqHoist with the unifier
. Next, we apply EqHoist with the unifier  to the literal created by FluidBoolHoist, effectively performing a primitive substitution. The resulting clause can superpose into \({\textsf {a} } \not \approx {\textsf {b} }\) with the unifier \(\{x'' \mapsto \lambda u.\> u\} \in {{\,\textrm{CSU}\,}}(x''\>{\textsf {b} }{,}\; {\textsf {b} })\). The two sides of the interpreted equality in the first literal can then be unified, allowing us to apply BoolRw with the unifier
to the literal created by FluidBoolHoist, effectively performing a primitive substitution. The resulting clause can superpose into \({\textsf {a} } \not \approx {\textsf {b} }\) with the unifier \(\{x'' \mapsto \lambda u.\> u\} \in {{\,\textrm{CSU}\,}}(x''\>{\textsf {b} }{,}\; {\textsf {b} })\). The two sides of the interpreted equality in the first literal can then be unified, allowing us to apply BoolRw with the unifier  . Finally, applying ERes twice and FalseElim once yields the empty clause.
. Finally, applying ERes twice and FalseElim once yields the empty clause.
Remarkably, none of the provers that participated in the CASC-J10 competition can solve this two-clause problem within a minute. Satallax finds a proof after 72 s and LEO-II after over 7 minutes. The CASC-28 version of our new Zipperposition implementation solves it in 3 s.
3.5 Soundness
All of our inference rules and axioms are sound w.r.t.  and the ones that do not introduce Skolem symbols are also sound w.r.t. \(\models \). Any derivation using our inference rules and axioms is satisfiability-preserving w.r.t. both \(\models \) and
and the ones that do not introduce Skolem symbols are also sound w.r.t. \(\models \). Any derivation using our inference rules and axioms is satisfiability-preserving w.r.t. both \(\models \) and  if the initial clause set does not contain \({\textsf {sk} }\) symbols. The preprocessing is sound w.r.t. both \(\models \) and
if the initial clause set does not contain \({\textsf {sk} }\) symbols. The preprocessing is sound w.r.t. both \(\models \) and  :
:
Theorem 28
(Soundness and completeness of  -normalization)
-normalization)  -normalization preserves denotations of terms and truth of clauses w.r.t. proper interpretations.
-normalization preserves denotations of terms and truth of clauses w.r.t. proper interpretations.
Proof
It suffices to show that

for all types \(\tau \), proper interpretations  , and all valuations \(\xi \).
, and all valuations \(\xi \).
Let f be a function from  to \(\{0,1\}\). Then
to \(\{0,1\}\). Then

By the definition of proper interpretations (Sect. 2.2), we have

Thus, it remains to show that  if and only if f is constantly 1. This holds because by the definition of term denotation,
if and only if f is constantly 1. This holds because by the definition of term denotation,  and because
and because  by properness of the interpretation, for all
by properness of the interpretation, for all  . The case of
. The case of  is analogous. \(\square \)
is analogous. \(\square \)
To show soundness of the inferences, we need the substitution lemma for our logic:
Lemma 29
(Substitution lemma) Let  be a proper interpretation. Then
be a proper interpretation. Then

for all terms t, all types \(\tau \), and all substitutions \(\rho \), where  for all type variables \(\alpha \) and
for all type variables \(\alpha \) and  for all term variables x.
for all term variables x.
Proof
Analogous to Lemma 18 of \(\lambda \)Sup [10]. \(\square \)
It follows that a model of a clause is also a model of its instances:
Lemma 30
If  for some interpretation
for some interpretation  and some clause C, then
and some clause C, then  for all substitutions \(\rho \).
for all substitutions \(\rho \).
Proof
Analogous to Lemma 19 of \(\lambda \)Sup [10], using Lemma 29. \(\square \)
With this lemma in place, we can prove the soundness of our calculus. Some of the rules and axioms are only sound w.r.t.  .
.
Theorem 31
(Soundness) Axiom (Choice) and all of our inference rules, except for ForallRw and ExistsRw, are sound w.r.t. \(\models \). All of our axioms and inference rules are sound w.r.t.  . Both of these claims hold even without the variable condition and the side conditions on fluidity, deeply occurring variables, order, and eligibility.
. Both of these claims hold even without the variable condition and the side conditions on fluidity, deeply occurring variables, order, and eligibility.
Proof
Analogous to Lemma 20 of \(\lambda \)Sup [10]. For the Boolean rules, we make use of the special requirements on interpretations of logical symbols.
We elaborate on the soundness of ForallRw, ExistsRw, and Ext w.r.t.  .
.
For ForallRw: Let  be a Skolem-aware model of
be a Skolem-aware model of  . By Lemma 29,
. By Lemma 29,  is a model of
is a model of  as well. Since
as well. Since  , we have
, we have  . Thus, to show that
. Thus, to show that  is also a model of the conclusion
is also a model of the conclusion  , it suffices to show that
, it suffices to show that  .
.
This follows directly from the definition of Skolem-awareness (Definition 3), which states that

For ExistsRw, we can argue analogously.
For (Ext), we must show that any Skolem-aware model  is a model of axiom (Ext) \(z\>({\textsf {diff} }{\langle \alpha ,\beta \rangle }\>z\>y)\not \approx y\>({\textsf {diff} }{\langle \alpha ,\beta \rangle }\>z\>y) \mathrel \vee z\approx y\). By the definition of Skolem-awareness, we have
is a model of axiom (Ext) \(z\>({\textsf {diff} }{\langle \alpha ,\beta \rangle }\>z\>y)\not \approx y\>({\textsf {diff} }{\langle \alpha ,\beta \rangle }\>z\>y) \mathrel \vee z\approx y\). By the definition of Skolem-awareness, we have  . Thus, if the first literal of (Ext) is false in
. Thus, if the first literal of (Ext) is false in  for some valuation \(\xi \), then
for some valuation \(\xi \), then

It follows that there exists no  such that
such that  and
and  are different. Thus,
are different. Thus,  and hence the second literal of (Ext) must be true under
and hence the second literal of (Ext) must be true under  and \(\xi \). \(\square \)
and \(\xi \). \(\square \)
To prove satisfiability preservation w.r.t. \(\models \), we need the following lemma:
Lemma 32
Let  be a clause set that does not contain any \({\textsf {sk} }\) symbols. Then N is satisfiable w.r.t. \(\models \) if and only if it is satisfiable w.r.t.
be a clause set that does not contain any \({\textsf {sk} }\) symbols. Then N is satisfiable w.r.t. \(\models \) if and only if it is satisfiable w.r.t.  .
.
Proof
If N is satisfiable w.r.t.  , then it is satisfiable w.r.t. \(\models \) by definition. For the other direction, we assume that N has a model
, then it is satisfiable w.r.t. \(\models \) by definition. For the other direction, we assume that N has a model  , and we must show that there exists a Skolem-aware model
, and we must show that there exists a Skolem-aware model  of N.
of N.
To transform the model  into a skolem-aware model
into a skolem-aware model  , we redefine the interpretation of the Skolem symbol
, we redefine the interpretation of the Skolem symbol  as follows. Given some domains
as follows. Given some domains  , let
, let  . Then define
. Then define  and
and  where \(s'\) is obtained from s by replacing each occurrence of a subterm
where \(s'\) is obtained from s by replacing each occurrence of a subterm  by \((\lambda \bar{x}.\>\varepsilon {\langle \upsilon \rangle }\>t)\{\bar{\alpha }\mapsto \bar{\upsilon }\}\). This modification of
by \((\lambda \bar{x}.\>\varepsilon {\langle \upsilon \rangle }\>t)\{\bar{\alpha }\mapsto \bar{\upsilon }\}\). This modification of  yields a new interpretation
yields a new interpretation  , which is still a model of N because N does not contain any \({\textsf {sk} }\) symbols. Moreover, it is a Skolem-aware model of N because our redefinition ensures
, which is still a model of N because N does not contain any \({\textsf {sk} }\) symbols. Moreover, it is a Skolem-aware model of N because our redefinition ensures  . \(\square \)
. \(\square \)
Theorem 33
(Satisfiability preservation) Any derivation using our inference rules and axioms is satisfiability-preserving w.r.t. both \(\models \) and  if the initial clause set does not contain \({\textsf {sk} }\) symbols.
if the initial clause set does not contain \({\textsf {sk} }\) symbols.
Proof
By Theorem 31, all of our inference rules and axioms are sound w.r.t.  . Thus, they clearly preserve satisfiability w.r.t.
. Thus, they clearly preserve satisfiability w.r.t.  .
.
If the initial clause set of a derivation does not contain \({\textsf {sk} }\) symbols and is satisfiable w.r.t. \(\models \), it is also satisfiable w.r.t.  by Lemma 32. By satisfiability preservation w.r.t.
by Lemma 32. By satisfiability preservation w.r.t.  , any clauses derived from this initial clause set are then satisfiable w.r.t.
, any clauses derived from this initial clause set are then satisfiable w.r.t.  . By definition of
. By definition of  (Definition 3), the derived clauses are therefore also satisfiable w.r.t. \(\models \). This proves satisfiability preservation w.r.t. \(\models \). \(\square \)
(Definition 3), the derived clauses are therefore also satisfiable w.r.t. \(\models \). This proves satisfiability preservation w.r.t. \(\models \). \(\square \)
3.6 The Redundancy Criterion
As in \(\lambda \)fSup and \(\lambda \)Sup, the redundancy criterion and the completeness proof distinguish three levels of logics. We have a higher-order level \({\text {H} }\), a  -normal ground higher-order level \({\text {GH} }\), and a ground monomorphic first-order level \({\text {GF} }\) with an interpreted Boolean type. We use
-normal ground higher-order level \({\text {GH} }\), and a ground monomorphic first-order level \({\text {GF} }\) with an interpreted Boolean type. We use  ,
,  , and
, and  to denote the respective sets of terms,
to denote the respective sets of terms,  ,
,  , and
, and  to denote the respective sets of types, and
to denote the respective sets of types, and  ,
,  , and
, and  to denote the respective sets of clauses. We will define a grounding function
to denote the respective sets of clauses. We will define a grounding function  that connects levels \({\text {H} }\) and \({\text {GH} }\) and an encoding
that connects levels \({\text {H} }\) and \({\text {GH} }\) and an encoding  that connects levels \({\text {GH} }\) and \({\text {GF} }\). Schematically, the three levels are connected as follows:
that connects levels \({\text {GH} }\) and \({\text {GF} }\). Schematically, the three levels are connected as follows:

3.6.1 Redundancy of Clauses
In first-order superposition, a clause is considered redundant if all its ground instances are entailed by \(\prec \)-smaller ground instances of other clauses. In essence, this will also be our definition, but we will use a special grounding function  and the entailment notion of the \({\text {GF} }\) level.
and the entailment notion of the \({\text {GF} }\) level.
Let \((\Sigma _{{\textsf {ty} }},\Sigma )\) be the signature of level \({\text {H} }\). The level \({\text {GH} }\) has the same signature but is restricted to ground  -normal terms and clauses. For the \({\text {GF} }\) level, we employ the logic of \(\hbox {o}\)Sup [31]. Its signature (\(\Sigma _{{\textsf {ty} }},\Sigma _{\text {GF} })\) is defined as follows. The type constructors \(\Sigma _{{\textsf {ty} }}\) are the same in both signatures, but \({\rightarrow }\) is an uninterpreted type constructor on \({\text {GF} }\) and not to be confused with the arrow used for type declarations in the logic of \(\hbox {o}\)Sup [31], which we will avoid in this article due to the ambiguity . For each ground instance \({\textsf {f} }{\langle \bar{\upsilon }\rangle } : \tau _1\rightarrow \cdots \rightarrow \tau _n\rightarrow \tau \) of a symbol \({\textsf {f} } \in \Sigma \), we introduce a first-order symbol \(\smash {{\textsf {f} }^{\bar{\upsilon }}_{\!j}} \in \Sigma _{\text {GF} }\) with argument types \(\bar{\tau }_{\!j}\) and result type \(\tau _{\!j+1} \rightarrow \cdots \rightarrow \tau _n \rightarrow \tau \), for each j. This is done for both logical and nonlogical symbols. Moreover, for each ground term \(\lambda x.\>t\), we introduce a symbol \({\textsf {lam} }_{\lambda x.\>t} \in \Sigma _{\text {GF} }\) of the same type. The symbols
-normal terms and clauses. For the \({\text {GF} }\) level, we employ the logic of \(\hbox {o}\)Sup [31]. Its signature (\(\Sigma _{{\textsf {ty} }},\Sigma _{\text {GF} })\) is defined as follows. The type constructors \(\Sigma _{{\textsf {ty} }}\) are the same in both signatures, but \({\rightarrow }\) is an uninterpreted type constructor on \({\text {GF} }\) and not to be confused with the arrow used for type declarations in the logic of \(\hbox {o}\)Sup [31], which we will avoid in this article due to the ambiguity . For each ground instance \({\textsf {f} }{\langle \bar{\upsilon }\rangle } : \tau _1\rightarrow \cdots \rightarrow \tau _n\rightarrow \tau \) of a symbol \({\textsf {f} } \in \Sigma \), we introduce a first-order symbol \(\smash {{\textsf {f} }^{\bar{\upsilon }}_{\!j}} \in \Sigma _{\text {GF} }\) with argument types \(\bar{\tau }_{\!j}\) and result type \(\tau _{\!j+1} \rightarrow \cdots \rightarrow \tau _n \rightarrow \tau \), for each j. This is done for both logical and nonlogical symbols. Moreover, for each ground term \(\lambda x.\>t\), we introduce a symbol \({\textsf {lam} }_{\lambda x.\>t} \in \Sigma _{\text {GF} }\) of the same type. The symbols  , and
, and  are identified with the corresponding first-order logical symbols.
are identified with the corresponding first-order logical symbols.
Definition 34
(The grounding function  on terms and clauses) Given a clause
on terms and clauses) Given a clause  , let its ground instances
, let its ground instances  be the set of all clauses in
be the set of all clauses in  of the form \(C\theta \) for some grounding substitution \(\theta \) such that for all free variables x occurring in C, the only Boolean green subterms of \(x\theta \) are
of the form \(C\theta \) for some grounding substitution \(\theta \) such that for all free variables x occurring in C, the only Boolean green subterms of \(x\theta \) are  and
and  .
.
Restricting the grounding to the Boolean terms  and
and  allows condition O4 to consider only terms u with Boolean subterms
allows condition O4 to consider only terms u with Boolean subterms  and
and  . This is crucial because without the restriction no suitable term order would exist. The approach resembles basic superposition [4] where the redundancy criterion only considers ground instances that are irreducible w.r.t. an arbitrary term rewriting system. A disadvantage of basic superposition is that its redundancy criterion severely restricts the simplification machinery because the irreducible terms are unknown during a derivation. In our setting, however, we know that
. This is crucial because without the restriction no suitable term order would exist. The approach resembles basic superposition [4] where the redundancy criterion only considers ground instances that are irreducible w.r.t. an arbitrary term rewriting system. A disadvantage of basic superposition is that its redundancy criterion severely restricts the simplification machinery because the irreducible terms are unknown during a derivation. In our setting, however, we know that  and
and  will be normal forms of the term rewriting system used in the completeness proof. Thus, we can restrict grounding to the Boolean terms
will be normal forms of the term rewriting system used in the completeness proof. Thus, we can restrict grounding to the Boolean terms  and
and  without compromising the simplification machinery.
without compromising the simplification machinery.
Since we have defined all clauses in  to be
to be  -normal, the ground instances
-normal, the ground instances  of a clause are
of a clause are  -normal as well. The clauses in
-normal as well. The clauses in  being
being  -normal allow us to define the encoding
-normal allow us to define the encoding  as follows:
as follows:
Definition 35
(The encoding  on terms and clauses) The encoding
on terms and clauses) The encoding  is recursively defined by
is recursively defined by

using  representatives of terms. The encoding
representatives of terms. The encoding  is extended to map from
is extended to map from  to
to  by mapping each literal and each side of a literal individually.
by mapping each literal and each side of a literal individually.
Although we define  only on ground terms, the encoding of variables
only on ground terms, the encoding of variables  is necessary for variables bound by
is necessary for variables bound by  and
and  . Since the terms
. Since the terms  are
are  -normal, these variables occur neither applied nor inside \(\lambda \)-expressions.
-normal, these variables occur neither applied nor inside \(\lambda \)-expressions.
The mapping  is clearly bijective. Using the inverse mapping, the order \(\succ \) can be transferred from
is clearly bijective. Using the inverse mapping, the order \(\succ \) can be transferred from  to
to  and from
and from  to
to  by defining \(t \succ s\) as
by defining \(t \succ s\) as  and \(C \succ D\) as
and \(C \succ D\) as  . The property that \(\succ \) on clauses is the multiset extension of \(\succ \) on literals, which in turn is the multiset extension of \(\succ \) on terms, is maintained because
. The property that \(\succ \) on clauses is the multiset extension of \(\succ \) on literals, which in turn is the multiset extension of \(\succ \) on terms, is maintained because  maps the multiset representations elementwise.
maps the multiset representations elementwise.
A key property of  is that there is a bijection between green subterms on \({\text {GH} }\) and subterms on \({\text {GF} }\) that are not below quantifiers:
is that there is a bijection between green subterms on \({\text {GH} }\) and subterms on \({\text {GF} }\) that are not below quantifiers:
Lemma 36
Let  . If p is a green position in t or a position in
. If p is a green position in t or a position in  that is not below a quantifier, we have
that is not below a quantifier, we have  . In other words, s is a green subterm of t at position p if and only if
. In other words, s is a green subterm of t at position p if and only if  is a subterm of
is a subterm of  at position p that is not below a quantifier.
at position p that is not below a quantifier.
Proof
Analogous to Lemma 3.17 of \(\lambda \)fSup [8]. \(\square \)
Lemma 37
The relation \(\succ \) on  is a term order in the sense of \(\hbox {o}\)Sup. That is, it is a well-founded strict order \(\succ \) on ground terms such that
is a term order in the sense of \(\hbox {o}\)Sup. That is, it is a well-founded strict order \(\succ \) on ground terms such that
-
1.
compatibility with contexts holds, but not necessarily below quantifiers;
-
2.
the subterm property holds, but not necessarily below quantifiers;
-
3.
totality holds;
-
4.
 for any term
for any term 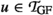 that is not
that is not  or
or  ; and
; and -
5.
 for any term
for any term  whose only Boolean subterms are
whose only Boolean subterms are  and
and  .
.
Proof
Transitivity and irreflexivity follow directly from transitivity and irreflexivity of \(\succ \) on  . Well-foundedness, compatibility with contexts, subterm property and totality can be shown analogously to Lemma 3.19 of \(\lambda \)fSup [8], using Lemma 36. That
. Well-foundedness, compatibility with contexts, subterm property and totality can be shown analogously to Lemma 3.19 of \(\lambda \)fSup [8], using Lemma 36. That  or
or  are the smallest terms follows from (O3) of Definition 15. Finally,
are the smallest terms follows from (O3) of Definition 15. Finally,  follows from (O4) of Definition 15. \(\square \)
follows from (O4) of Definition 15. \(\square \)
Each of the three levels has an entailment relation \(\models \). A clause set \(N_1\) entails a clause set \(N_2\), denoted by \(N_1 \models N_2\), if all models of \(N_1\) are also a models of \(N_2\). For \({\text {H} }\) and \({\text {GH} }\), we use higher-order models; for \({\text {GF} }\), we use first-order models with interpreted Booleans as defined by \(\hbox {o}\)Sup [31]. We write  to abbreviate
to abbreviate  and
and  to abbreviate
to abbreviate  . On the \({\text {H} }\) level, we additionally define Skolem-aware entailment, denoted by
. On the \({\text {H} }\) level, we additionally define Skolem-aware entailment, denoted by  , to hold if all Skolem-aware models of a clause set
, to hold if all Skolem-aware models of a clause set  are also models of a clause set
are also models of a clause set  .
.
We define the sets of redundant clauses w.r.t. a clause set as follows:
-
Given
 and
and  , let \(C\in \textit{GFRed}_{\text {C} }(N)\) if \(\{D \in N \mid D \prec C\}\models C\).
, let \(C\in \textit{GFRed}_{\text {C} }(N)\) if \(\{D \in N \mid D \prec C\}\models C\). -
Given
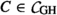 and
and  , let \(C\in {\textit{GHRed}}_{\text {C} }(N)\) if
, let \(C\in {\textit{GHRed}}_{\text {C} }(N)\) if  .
. -
Given
 and
and  , let \(C\in {\textit{HRed}_{\text {C} }}(N)\) if for every
, let \(C\in {\textit{HRed}_{\text {C} }}(N)\) if for every  , we have
, we have  or there exists \(C' \in N\) such that \(C \sqsupset C'\) and
or there exists \(C' \in N\) such that \(C \sqsupset C'\) and  .
.
The tiebreaker \(\sqsupset \) can be an arbitrary well-founded partial order on  , natural candidates being restrictions of (ill-founded) strict subsumption [10, Sect. 3.4].
, natural candidates being restrictions of (ill-founded) strict subsumption [10, Sect. 3.4].
3.6.2 Redundancy of Inferences
Standard simplification rules and most other optimizations can be justified by clause redundancy. For a few other prover optimizations (e.g., simultaneous superposition [6]), a notion of inference redundancy is required. For first-order superposition, an inference is considered redundant if for each of its ground instances, a premise is redundant or the conclusion is entailed by clauses smaller than the main premise. For most inference rules, our definition follows this idea, using specific ground instances and  for entailment; other rules need nonstandard notions of inference redundancy.
for entailment; other rules need nonstandard notions of inference redundancy.
Each of the three levels has an associated inference system \(\textit{HInf}\), \(\textit{GHInf}\), and \(\textit{GFInf}\). For \({\text {H} }\), it is the inference system \(\textit{HInf}\) consisting of the rules described above. We view axioms (Ext) and (Choice) as premiseless inference rules Ext and Choice, respectively. We fix the selection functions \(\textit{HLitSel}\) and \(\textit{HBoolSel}\) globally.
The system \(\textit{GHInf}\) is parameterized by selection functions and a witness function, which are defined as follows.
Definition 38
(\({\text {GH} }\) level selection functions) A \({\text {GH} }\) level literal selection function \(\textit{GHLitSel}\) maps each clause  to a subset of its literals. A \({\text {GH} }\) level Boolean subterm selection function \(\textit{GHBoolSel}\) maps each clause
to a subset of its literals. A \({\text {GH} }\) level Boolean subterm selection function \(\textit{GHBoolSel}\) maps each clause  to a subset of its green positions with Boolean subterms.
to a subset of its green positions with Boolean subterms.
We require these selection functions to have the property that for every  , there exists a
, there exists a  with
with  for which the selections \(\textit{HLitSel}(D)\), \(\textit{HBoolSel}(D)\) and the selections \(\textit{GHLitSel}(C)\), \(\textit{GHBoolSel}(C)\) correspond in the following sense: A literal K is selected in C if and only if there exists a selected literal L in D with \(L\theta = K\); a green position C.K.p is selected in C if and only if there exists a literal L in D with \(L\theta = K\) such that D.L.p is selected.
for which the selections \(\textit{HLitSel}(D)\), \(\textit{HBoolSel}(D)\) and the selections \(\textit{GHLitSel}(C)\), \(\textit{GHBoolSel}(C)\) correspond in the following sense: A literal K is selected in C if and only if there exists a selected literal L in D with \(L\theta = K\); a green position C.K.p is selected in C if and only if there exists a literal L in D with \(L\theta = K\) such that D.L.p is selected.
Definition 39
(Witness function) A witness function \(\textit{GHWit}\) maps a clause  and a green position of a quantifier-headed term in C to a term
and a green position of a quantifier-headed term in C to a term  such that \({\textsf {Q} }{\langle \tau \rangle }\>t \succ t\>\textit{GHWit}(C,p)\) if \(C|_p = {\textsf {Q} }{\langle \tau \rangle } \>t\).
such that \({\textsf {Q} }{\langle \tau \rangle }\>t \succ t\>\textit{GHWit}(C,p)\) if \(C|_p = {\textsf {Q} }{\langle \tau \rangle } \>t\).
The witness function will be used to provide appropriate Skolem terms that witness the existence of terms fulfilling the given predicate.
In our completeness proof, the choice of the \({\text {GH} }\) level selection and witness functions will depend on the saturated clause set in the limit of the derivation. Since we do not know this clause set during the derivation, we need to consider all possible parameters in our redundancy criterion:
Definition 40
(Set of parameter triples Q) Let Q be the set of parameters triples \((\textit{GHLitSel},\textit{GHBoolSel}, \textit{GHWit})\) where \(\textit{GHLitSel}\) and \(\textit{GHBoolSel}\) are \({\text {GH} }\) level selection functions and \(\textit{GHWit}\) is a witness function.
We write \(\textit{GHInf}~^q\) with \(q = (\textit{GHLitSel}, \textit{GHBoolSel}, \textit{GHWit})\in Q\) to specify the inference system for a given set of parameters. The rules of \(\textit{GHInf}\,^q\) include Sup, ERes, EFact, BoolHoist, FalseElim, EqHoist, NeqHoist, and BoolRw with the restriction that all references to \(\succsim \) are replaced by \(\succeq \).
In addition, \(\textit{GHInf}\,^q\) contains the rules GForallHoist, GExistsHoist, GArgCong, GExt, and GChoice, which enumerate ground terms in the conclusion where their \(\textit{HInf}\) counterparts use fresh variables. They enumerate all terms  such that the only Boolean green subterms of u are
such that the only Boolean green subterms of u are  and
and  . Let
. Let  be the set of all such terms u. Then these rules are stated as follows:
be the set of all such terms u. Then these rules are stated as follows:

where p is \(\succeq \)-eligible in C and 

where \(t \approx s\) is strictly \(\succeq \)-eligible in \(C' \mathrel \vee t \approx s\) and  .
.
The rules GExt and GChoice are premiseless and their conclusions are the infinitely many  -instances of (Ext) and (Choice), respectively.
-instances of (Ext) and (Choice), respectively.
Moreover, \(\textit{GHInf}\,^q\) contains the following two rules, which use the witness function \(\textit{GHWit}\) instead of Skolem terms:

where p is \(\succeq \)-eligible in C; for GForallRw,  is not a tautology; and for GExistsRw,
is not a tautology; and for GExistsRw,  is not a tautology.
is not a tautology.
The inference systems \(\textit{GHInf}~^{q}\) are indeed inference systems on  —i.e., if the premises are in
—i.e., if the premises are in  , the conclusions are in
, the conclusions are in  , too. The conclusions are obviously ground. They are also
, too. The conclusions are obviously ground. They are also  -normal:
-normal:
Lemma 41
If the premises of a \(\textit{GHInf}~^{q}\) inference are  -normal, then the conclusion is also
-normal, then the conclusion is also  -normal.
-normal.
Proof
The conclusions of GExt and GChoice are  -normal because
-normal because  maps into
maps into  , which is restricted to
, which is restricted to  -normal clauses.
-normal clauses.
The definition of  -normality (Definition 6) clearly only depends on the contained quantifier-headed subterms. As long as no new quantifier-headed subterms are added, a clause set cannot become
-normality (Definition 6) clearly only depends on the contained quantifier-headed subterms. As long as no new quantifier-headed subterms are added, a clause set cannot become  -reducible.
-reducible.
The inference rules ERes, EFact, and FalseElim do not introduce any subterms that were not already present in the premises. The inference rules Sup, BoolHoist, EqHoist, NeqHoist, BoolRw only introduce new subterms by replacing a green subterm of a  -normal term by another
-normal term by another  -normal term. Since green positions are never below quantifiers, these rules also do not add new quantifier-headed subterms.
-normal term. Since green positions are never below quantifiers, these rules also do not add new quantifier-headed subterms.
For the inference rules GForallHoist, GExistsHoist, GArgCong, GForallRw, and GExistsRw, we can use Lemma 14 to show that the conclusions are  -normal. \(\square \)
-normal. \(\square \)
The inference system \(\textit{GFInf}\) is parameterized by an analogous parameter triple \((\textit{GFLitSel},\textit{GFBoolSel},\textit{GFWit})\). Using the bijection  , we can translate a parameter triple q of \(\textit{GHInf}\) to a parameter triple
, we can translate a parameter triple q of \(\textit{GHInf}\) to a parameter triple  of \(\textit{GFInf}\). Let
of \(\textit{GFInf}\). Let  be the inference system containing the inferences isomorphic to \(\textit{GHInf}~^{q}\) obtained by
be the inference system containing the inferences isomorphic to \(\textit{GHInf}~^{q}\) obtained by  , except for GArgCong, GExt, and GChoice. This is essentially identical to the ground inference system of \(\hbox {o}\)Sup [31].
, except for GArgCong, GExt, and GChoice. This is essentially identical to the ground inference system of \(\hbox {o}\)Sup [31].
We extend the functions  and
and  to inferences:
to inferences:
Notation 42
Given an inference \(\iota \), we write \(\textit{prems}(\iota )\) for the tuple of premises,  for the main (i.e., rightmost) premise, and \(\textit{concl}(\iota )\) for the conclusion.
for the main (i.e., rightmost) premise, and \(\textit{concl}(\iota )\) for the conclusion.
Definition 43
(The encoding  on inferences) Given an inference \(\iota \in \textit{GHInf}\) that is not a GArgCong, GExt, or GChoice inference, let
on inferences) Given an inference \(\iota \in \textit{GHInf}\) that is not a GArgCong, GExt, or GChoice inference, let  denote the inference defined by
denote the inference defined by  and
and  .
.
Definition 44
(The grounding function  on inferences) Given a parameter triple \(q\in Q\) and an inference \(\iota \in \textit{HInf}\), we define the set
on inferences) Given a parameter triple \(q\in Q\) and an inference \(\iota \in \textit{HInf}\), we define the set  of ground instances of \(\iota \) to be all inferences \(\iota '\in \textit{GHInf}~^{q}\) such that \(\textit{prems}(\iota ') = \textit{prems}(\iota )\theta \) and \(\textit{concl}(\iota ') = \textit{concl}(\iota )\theta \) for some grounding substitution \(\theta \).
of ground instances of \(\iota \) to be all inferences \(\iota '\in \textit{GHInf}~^{q}\) such that \(\textit{prems}(\iota ') = \textit{prems}(\iota )\theta \) and \(\textit{concl}(\iota ') = \textit{concl}(\iota )\theta \) for some grounding substitution \(\theta \).
Thus,  maps FluidSup to Sup, FluidBoolHoist to BoolHoist, ForallRw to GForallRw, ExistsRw to GExistsRw, ForallHoist to GForallHoist, ExistsHoist to GExistsHoist, ArgCong to GArgCong, Ext to GExt, Choice to GChoice, and inferences of other \(\textit{HInf}\) rules to inferences of the identically named rules in \(\textit{GHInf}\). For FluidLoobHoist, which needs not be grounded to prove refutational completeness, we let
maps FluidSup to Sup, FluidBoolHoist to BoolHoist, ForallRw to GForallRw, ExistsRw to GExistsRw, ForallHoist to GForallHoist, ExistsHoist to GExistsHoist, ArgCong to GArgCong, Ext to GExt, Choice to GChoice, and inferences of other \(\textit{HInf}\) rules to inferences of the identically named rules in \(\textit{GHInf}\). For FluidLoobHoist, which needs not be grounded to prove refutational completeness, we let  . Although the rules FluidBoolHoist and FluidLoobHoist are dual to each other, their redundancy criteria are asymmetric because only FluidBoolHoist has a counterpart in \(\textit{GHInf}\), namely BoolHoist.
. Although the rules FluidBoolHoist and FluidLoobHoist are dual to each other, their redundancy criteria are asymmetric because only FluidBoolHoist has a counterpart in \(\textit{GHInf}\), namely BoolHoist.
We define the sets of redundant inferences w.r.t. a given clause set as follows:
-
Given \(\iota \in \textit{GFInf}~^q\) and
 , let \(\iota \in \textit{GFRed}_{\text {I} }^{\,q}(N)\) if \(\textit{prems}(\iota ) \cap \textit{GFRed}_{\text {C} }(N) \not = \varnothing \) or \(\{D \in N \mid D \prec \textit{mprem}(\iota )\} \models \textit{concl}(\iota )\).
, let \(\iota \in \textit{GFRed}_{\text {I} }^{\,q}(N)\) if \(\textit{prems}(\iota ) \cap \textit{GFRed}_{\text {C} }(N) \not = \varnothing \) or \(\{D \in N \mid D \prec \textit{mprem}(\iota )\} \models \textit{concl}(\iota )\). -
Given \(\iota \in \textit{GHInf}~^q\) and
 , let \(\iota \in {\textit{GHRed}}_{\,\text {I} }^{\,q}(N)\) if
, let \(\iota \in {\textit{GHRed}}_{\,\text {I} }^{\,q}(N)\) if-
\(\iota \) is GArgCong, GExt, or GChoice and \(\textit{concl}(\iota )\in N\mathrel \cup {\textit{GHRed}}_{\text {C} }(N)\); or
-
\(\iota \) is any another inference and
 .
.
-
-
Given \(\iota \in \textit{HInf}\) and
 , let \(\iota \in \textit{HRed}_{\text {I} }(N)\) if
, let \(\iota \in \textit{HRed}_{\text {I} }(N)\) if-
\(\iota \) is a FluidLoobHoist inference and
 or
or -
\(\iota \) is any other inference and
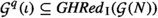 for all \(q\in Q\).
for all \(q\in Q\).
-
Some authors prefer not to define inferences with a redundant premise as redundant, but in our proof of refutational completeness, this will be crucial for the lifting lemma of \(\textsc {ForallRw} \) and \(\textsc {ExistsRw} \).
A clause set N is saturated w.r.t. an inference system and the inference component \({\textit{Red}_{\text {I} }}\) of a redundancy criterion if every inference from clauses in N is in \({\textit{Red}_{\text {I} }}(N).\)
3.7 Simplification Rules
The redundancy criterion \((\textit{HRed}_{\text {I} }, {\textit{HRed}_{\text {C} }})\) is strong enough to support most simplification rules implemented in Schulz’s first-order prover E [33, Sects. 2.3.1 and 2.3.2], although some require minor adaptions. To describe the adaptions, we introduce the notion of blue subterms, which include all green subterms but also some subterms below quantifiers.
Definition 45
(Blue subterms and positions) Blue subterms and positions are inductively defined as follows. A blue position is a tuple of natural numbers. For any \(\lambda \)-term t, the empty tuple \(\varepsilon \) is a blue position of t, and t is the blue subterm of t at position \(\varepsilon \). For all symbols  , if t is a blue subterm of \(u_i\) at position p, then i.p is a blue position of \({\textsf {f} }{\langle \bar{\tau }\rangle }\>\bar{u}\), and t is the blue subterm of \({\textsf {f} }{\langle \bar{\tau }\rangle }\>\bar{u}\) at position i.p. If t is a blue subterm of u at position p, then 1.p is a blue position of \({\textsf {Q} }{\langle \tau \rangle }\>(\lambda x.\> u)\) and t is the blue subterm of \({\textsf {Q} }{\langle \tau \rangle }\>(\lambda x.\> u)\) at position 1.p.
, if t is a blue subterm of \(u_i\) at position p, then i.p is a blue position of \({\textsf {f} }{\langle \bar{\tau }\rangle }\>\bar{u}\), and t is the blue subterm of \({\textsf {f} }{\langle \bar{\tau }\rangle }\>\bar{u}\) at position i.p. If t is a blue subterm of u at position p, then 1.p is a blue position of \({\textsf {Q} }{\langle \tau \rangle }\>(\lambda x.\> u)\) and t is the blue subterm of \({\textsf {Q} }{\langle \tau \rangle }\>(\lambda x.\> u)\) at position 1.p.
For example, the blue subterms of  are all of the green subterms and \({\textsf {q} }\). The notions of blue positions and subterms are lifted to \(\beta \eta \)-equivalence classes via the \(\beta \eta {\textsf {Q} }_{\eta }\)-normal representative.
are all of the green subterms and \({\textsf {q} }\). The notions of blue positions and subterms are lifted to \(\beta \eta \)-equivalence classes via the \(\beta \eta {\textsf {Q} }_{\eta }\)-normal representative.
Deletion of duplicated literals, deletion of resolved literals, syntactic tautology deletion, negative simplify reflect, and clause subsumption adhere to our redundancy criterion. Positive simplify-reflect and equality subsumption are supported by our criterion if they are applied on blue subterms. Semantic tautology deletion can be applied as well, but we must use the entailment relation  . Rewriting of positive and negative literals (demodulation) can only be applied on blue subterms. Moreover, for positive literals, the rewriting clause must be smaller than the rewritten clause—a condition that is also necessary with the standard first-order redundancy criterion but not always fulfilled by Schulz’s rule. As for destructive equality resolution, even in first-order logic the rule cannot be justified with the standard redundancy criterion, and it is unclear whether it preserves refutational completeness.
. Rewriting of positive and negative literals (demodulation) can only be applied on blue subterms. Moreover, for positive literals, the rewriting clause must be smaller than the rewritten clause—a condition that is also necessary with the standard first-order redundancy criterion but not always fulfilled by Schulz’s rule. As for destructive equality resolution, even in first-order logic the rule cannot be justified with the standard redundancy criterion, and it is unclear whether it preserves refutational completeness.
As a representative example, we show how demodulation into green contexts can be justified. Demodulation into blue contexts and the other simplification rules can be justified similarly.
Lemma 46
Demodulation into green contexts is a simplification:

where \(t\sigma \succ t'\sigma \) and \(C \succ (t\approx t')\sigma \). It adheres to our redundancy criterion—i.e., the deleted premise C is redundant w.r.t. the conclusions.
Proof
Let N be the set consisting of the two conclusions. We must show that \(C \in {\textit{HRed}_{\text {C} }}(N)\). Let \(C\theta \) be a ground instance of C. By the definition of \({\textit{HRed}_{\text {C} }}\), it suffices to show that  . By the definition of \({\textit{GHRed}}_{\text {C} }\), it thus suffices to show that
. By the definition of \({\textit{GHRed}}_{\text {C} }\), it thus suffices to show that  . By the definition of \(\textit{GFRed}_{\text {C} }\), this is equivalent to proving that the clauses in
. By the definition of \(\textit{GFRed}_{\text {C} }\), this is equivalent to proving that the clauses in  that are smaller than
that are smaller than  entail
entail  .
.
By compatibility with green contexts and stability under substitutions of \(\succ \), the condition \(t\sigma \succ t'\sigma \) implies that  is a clause in
is a clause in  that is smaller than
that is smaller than  . By stability under substitutions, \(C \succ (t\approx t')\sigma \) implies that
. By stability under substitutions, \(C \succ (t\approx t')\sigma \) implies that  is another clause in
is another clause in  that is smaller than
that is smaller than  . By Lemma 36, green subterms on the \({\text {GH} }\) level correspond to subterms on the \({\text {GF} }\) level. Thus,
. By Lemma 36, green subterms on the \({\text {GH} }\) level correspond to subterms on the \({\text {GF} }\) level. Thus,  by congruence. \(\square \)
by congruence. \(\square \)
All of \(\lambda \)Sup’s extensions [10, Sect. 5] can also be used in our setting. DemodExt and PruneArg are sound w.r.t. both \(\models \) and  . NegExt, ExtInst, and \(\lambda \) Sup are sound w.r.t.
. NegExt, ExtInst, and \(\lambda \) Sup are sound w.r.t.  if the appropriate \({\textsf {sk} }\) symbols are reused. As shown in the proof of Theorem 33, this implies that these rules are satisfiability-preserving w.r.t. \(\models \), provided that the initial clause set does not contain \({\textsf {sk} }\) symbols. If fresh Skolem symbols are used, the rules are satisfiability-preserving w.r.t. both \(\models \) and
if the appropriate \({\textsf {sk} }\) symbols are reused. As shown in the proof of Theorem 33, this implies that these rules are satisfiability-preserving w.r.t. \(\models \), provided that the initial clause set does not contain \({\textsf {sk} }\) symbols. If fresh Skolem symbols are used, the rules are satisfiability-preserving w.r.t. both \(\models \) and  . DupSup and FlexSup are sound w.r.t. both \(\models \) and
. DupSup and FlexSup are sound w.r.t. both \(\models \) and  .
.
Under some circumstances, certain inference rules of our calculus can be applied as simplifications—i.e., a premise can be deleted after performing them. The FalseElim and BoolRw rules can be applied as a simplification if \(\sigma \) is the identity. If the head of u is  , ForallHoist and ForallRw can both be applied and, together, serve as one simplification rule. If the head of u is
, ForallHoist and ForallRw can both be applied and, together, serve as one simplification rule. If the head of u is  and ForallRw cannot be applied due to its condition 5, ForallHoist alone serves as a simplification rule. The same holds for ExistsHoist and ExistsRw if the head of u is
and ForallRw cannot be applied due to its condition 5, ForallHoist alone serves as a simplification rule. The same holds for ExistsHoist and ExistsRw if the head of u is  . For all of these simplifications, the eligibility conditions can be ignored.
. For all of these simplifications, the eligibility conditions can be ignored.
If \(\sigma \) is the identity, the rule BoolHoist can also be applied as a simplification in combination with the following rule to the same subterm u:

Again, the eligibility condition can be ignored, and u can even be a fully applied logical symbol as long as it is not  or
or  .
.
3.8 Clausification
Like \(\hbox {o}\)Sup, our calculus does not require the input problem to be clausified during the preprocessing, and it supports higher-order analogs of the three inprocessing clausification methods introduced by Nummelin et al. Inner delayed clausification relies on our core calculus rules to destruct logical symbols. Outer delayed clausification adds the following clausification rules to the calculus:

The double bars identify simplification rules (i.e., the conclusions make the premise redundant and can replace it). The first two rules require that s has a logical symbol as its head, whereas the last two require that s and t are Boolean terms other than  and
and  . The function \({{\,\mathrm{\textit{oc}}\,}}\) distributes the logical symbols over the clause C—e.g.,
. The function \({{\,\mathrm{\textit{oc}}\,}}\) distributes the logical symbols over the clause C—e.g.,  , and
, and  . It is easy to check that our redundancy criterion allows us to replace the premise of the OuterClaus rules with their conclusion. Nonetheless, we apply EqOuterClaus and NeqOuterClaus as inferences because the premises might be useful in their original form.
. It is easy to check that our redundancy criterion allows us to replace the premise of the OuterClaus rules with their conclusion. Nonetheless, we apply EqOuterClaus and NeqOuterClaus as inferences because the premises might be useful in their original form.
Besides the two delayed clausification methods, a third inprocessing clausification method is immediate clausification. This clausifies the input problem’s outer Boolean structure in one swoop, resulting in a set of higher-order clauses. If unclausified Boolean terms rise to the top during saturation, the same algorithm is run to clausify them. This method can be made to adhere to our redundancy criterion as well, although advanced clausification techniques such as the Tseitin transformation [36] and miniscoping [30] sometimes violate the criterion. The observations described for \(\hbox {o}\)Sup [31, Sect. 6] essentially apply to our calculus as well.
Unlike delayed clausification, immediate clausification is a black box and is unaware of the proof state other than the Boolean term it is applied to. Delayed clausification, on the other hand, clausifies the term step by step, allowing us to interleave clausification with the strong simplification machinery of superposition provers. It is especially powerful in higher-order contexts: Examples such as  can be refuted directly by equality resolution, rather than via more explosive rules on the clausified form.
can be refuted directly by equality resolution, rather than via more explosive rules on the clausified form.
3.9 A Concrete Term Order
We define a concrete order  that fulfills the properties of a strict term order as defined in Definition 17 to show that the requirements can indeed be fulfilled and to provide a concrete order for implementations of our calculus.
that fulfills the properties of a strict term order as defined in Definition 17 to show that the requirements can indeed be fulfilled and to provide a concrete order for implementations of our calculus.
Given a signature \((\Sigma _{{\textsf {ty} }},\Sigma )\), we encode types and terms as terms over the untyped first-order signature  . The encoding introduces an identically named first-order (term) variable \(\alpha \) for each higher-order type variable \(\alpha \), a first-order variable \(z_x\) for each higher-order variable x, and a first-order variable \(z_t\) for each fluid higher-order term t. We define the encoding in two parts. The first part is the encoding
. The encoding introduces an identically named first-order (term) variable \(\alpha \) for each higher-order type variable \(\alpha \), a first-order variable \(z_x\) for each higher-order variable x, and a first-order variable \(z_t\) for each fluid higher-order term t. We define the encoding in two parts. The first part is the encoding  , resembling the one defined for \(\lambda \)Sup. The auxiliary function
, resembling the one defined for \(\lambda \)Sup. The auxiliary function  replaces each free occurrence of the variable x by a De Bruijn index—that is, a symbol \({\textsf {db} }^i\) where i is the number of \(\lambda \)-expressions surrounding the variable occurrence. The encoding
replaces each free occurrence of the variable x by a De Bruijn index—that is, a symbol \({\textsf {db} }^i\) where i is the number of \(\lambda \)-expressions surrounding the variable occurrence. The encoding  recursively encodes higher-order types into untyped first-order terms as follows:
recursively encodes higher-order types into untyped first-order terms as follows:  and
and  . Using \(\beta \eta {\textsf {Q} }_{\eta }\)-normal representatives, it recursively encodes higher-order terms into untyped first-order terms as follows:
. Using \(\beta \eta {\textsf {Q} }_{\eta }\)-normal representatives, it recursively encodes higher-order terms into untyped first-order terms as follows:

Via this encoding, the term order conditions (O1), (O2), and (O3) can be easily achieved. For (O4), however, we need to transform the encoded term further to ensure that the symbols  and
and  occur only as translations of fully applied quantifiers in green contexts. Then we can achieve (O4) by assigning them a large weight. The function
occur only as translations of fully applied quantifiers in green contexts. Then we can achieve (O4) by assigning them a large weight. The function  transforms the result of
transforms the result of  in this way by applying a function
in this way by applying a function  to all subterms below \({\textsf {lam} }\) symbols. It maps untyped first-order terms to untyped first-order terms as follows:
to all subterms below \({\textsf {lam} }\) symbols. It maps untyped first-order terms to untyped first-order terms as follows:

In particular, for any higher-order type \(\tau \), we have  because \(\lambda \)-expressions do not occur in types.
because \(\lambda \)-expressions do not occur in types.
The function  replaces
replaces  by
by  by
by  , and
, and  by a fresh variable
by a fresh variable  .
.

Again, for any higher-order type \(\tau \), we have  because the variables \(z_u\) and the constants
because the variables \(z_u\) and the constants  and
and  never occur in the result of applying
never occur in the result of applying  to types.
to types.
For example,  encodes the term
encodes the term  into the first-order term
into the first-order term  and
and  transforms it further into
transforms it further into  .
.
Using the encoding  and the function
and the function  , we define our term order
, we define our term order  . Let
. Let  be the transfinite Knuth–Bendix order [28] on first-order terms. The weight of
be the transfinite Knuth–Bendix order [28] on first-order terms. The weight of  and
and  must be \(\omega \), the weight of
must be \(\omega \), the weight of  and
and  must be 1, and the weights of all other symbols must be smaller than \(\omega \). The precedence > must be total and
must be 1, and the weights of all other symbols must be smaller than \(\omega \). The precedence > must be total and  must be the symbols of lowest precedence. We do not use subterm coefficients (i.e., all coefficients are 1), nor a symbol of weight 0. Let
must be the symbols of lowest precedence. We do not use subterm coefficients (i.e., all coefficients are 1), nor a symbol of weight 0. Let  be the order induced by
be the order induced by  from
from  , meaning
, meaning  if and only if
if and only if  . Let
. Let  be the order induced by
be the order induced by  from
from  , meaning
, meaning  if and only if
if and only if  . We extend
. We extend  to literals and clauses in the usual way. We will show that
to literals and clauses in the usual way. We will show that  fulfills the properties of a strict term order:
fulfills the properties of a strict term order:
Lemma 47
The restriction of  to ground terms is a strict ground term order, as defined in Definition 15.
to ground terms is a strict ground term order, as defined in Definition 15.
Proof
We follow the proof of Lemma 31 of Bentkamp et al. The transfinite Knuth–Bendix order  has been shown to enjoy irreflexivity, transitivity, well-foundedness, totality on ground terms, the subterm property, and compatibility with contexts [28]. Transitivity and irreflexivity of
has been shown to enjoy irreflexivity, transitivity, well-foundedness, totality on ground terms, the subterm property, and compatibility with contexts [28]. Transitivity and irreflexivity of  imply transitivity and irreflexivity of
imply transitivity and irreflexivity of  , respectively.
, respectively.
Well-foundedness: If there existed an infinite chain  of ground terms, there would also be the chain
of ground terms, there would also be the chain  , contradicting the well-foundedness of
, contradicting the well-foundedness of  .
.
Totality: For any ground terms t and s we have  , or
, or  by ground totality of
by ground totality of  . In the first two cases, it follows that
. In the first two cases, it follows that  or
or  respectively. In the last case, it follows that \(t = s\) because
respectively. In the last case, it follows that \(t = s\) because  and
and  are clearly injective.
are clearly injective.
(O1): By induction on the depth of the context, it suffices to show that  implies
implies  for all t, s,
for all t, s,  , \(\bar{\tau }\), \(\bar{u}\), and \(\bar{v}\). This amounts to showing that
, \(\bar{\tau }\), \(\bar{u}\), and \(\bar{v}\). This amounts to showing that  implies
implies

which follows directly from compatibility of  with contexts and the induction hypothesis.
with contexts and the induction hypothesis.
(O2): Let s be a term. We show that  by induction on p, where \(s|_p\) denotes the green subterm at position p. If \(p = \varepsilon \), this is trivial. If \(p = p'.i\), we have
by induction on p, where \(s|_p\) denotes the green subterm at position p. If \(p = \varepsilon \), this is trivial. If \(p = p'.i\), we have  by the induction hypothesis. Hence, it suffices to show that
by the induction hypothesis. Hence, it suffices to show that  . From the existence of the position \(p'.i\), we know that \(s|_{p'}\) must be of the form \(s|_{p'} = {\textsf {f} }{\langle \bar{\tau }\rangle }\>\bar{u}_k\) for some
. From the existence of the position \(p'.i\), we know that \(s|_{p'}\) must be of the form \(s|_{p'} = {\textsf {f} }{\langle \bar{\tau }\rangle }\>\bar{u}_k\) for some  . Then \(s|_{p'.i} = u_i\). The encoding yields
. Then \(s|_{p'.i} = u_i\). The encoding yields  and hence
and hence  by the subterm property of
by the subterm property of  . Hence,
. Hence,  and thus
and thus  .
.
(O3): Since we do not have a symbol of weight 0, and  and
and  have weight 1, there cannot be any term of smaller weight. Since moreover
have weight 1, there cannot be any term of smaller weight. Since moreover  and
and  have the lowest precedence, they are the smallest terms w.r.t.
have the lowest precedence, they are the smallest terms w.r.t.  . We have
. We have  because
because  has higher precedence. Since
has higher precedence. Since  and
and  , it follows that
, it follows that  and
and  are the smallest ground terms w.r.t.
are the smallest ground terms w.r.t.  and that
and that  .
.
(O4): Let \({\textsf {Q} }{\langle \tau \rangle }\>t\) and u be  -normal ground terms. We assume that the Boolean green subterms of u are
-normal ground terms. We assume that the Boolean green subterms of u are  and
and  . We must show
. We must show  , which is equivalent to
, which is equivalent to  .
.
All symbols except  and
and  have finite weight. Only
have finite weight. Only  and
and  have weight \(\omega \). Since all subterm coefficients are 1, the coefficient of \(\omega \) in the weight of a given term indicates the number of occurrences of the symbols
have weight \(\omega \). Since all subterm coefficients are 1, the coefficient of \(\omega \) in the weight of a given term indicates the number of occurrences of the symbols  and
and  in that term.
in that term.
In \(\eta \)-expanded form, we have \(t = \lambda x.\>s\) for some s. Then we have  and
and  . By
. By  -normality, x occurs free only in green positions of s. Therefore, replacing x by u in s does not trigger any \(\beta \eta {\textsf {Q} }_{\eta }\)-normalizations. Thus,
-normality, x occurs free only in green positions of s. Therefore, replacing x by u in s does not trigger any \(\beta \eta {\textsf {Q} }_{\eta }\)-normalizations. Thus,  and
and  are almost identical, except that
are almost identical, except that  contains \({\textsf {db} }^i\) where
contains \({\textsf {db} }^i\) where  contains
contains  . Since the only Boolean green subterms of u are
. Since the only Boolean green subterms of u are  and
and  ,
,  does not contain
does not contain  or
or  . So
. So  and
and  contain the same number of
contain the same number of  and
and  symbols. Hence,
symbols. Hence,  contains exactly one more of these symbols than
contains exactly one more of these symbols than  . This means that the weight of the former is larger than the weight of the latter and, thus,
. This means that the weight of the former is larger than the weight of the latter and, thus,  . \(\square \)
. \(\square \)
Lemma 48
The relation  is a strict term order as defined in Definition 17.
is a strict term order as defined in Definition 17.
Proof
Given Lemma 47, it remains to show that  is stable under grounding substitutions. Assume
is stable under grounding substitutions. Assume  for some terms s and \(s'\). Let \(\theta \) be a higher-order substitution grounding s and \(s'\). We must show
for some terms s and \(s'\). Let \(\theta \) be a higher-order substitution grounding s and \(s'\). We must show  . We will define a first-order substitution \(\rho \) grounding
. We will define a first-order substitution \(\rho \) grounding  and
and  such that
such that  and
and  . Since
. Since  , we have
, we have  . The transfinite Knuth–Bendix order
. The transfinite Knuth–Bendix order  has been shown to be stable under substitutions [28]. Hence,
has been shown to be stable under substitutions [28]. Hence,  and therefore
and therefore  and
and  .
.
We define the first-order substitution \(\rho \) as \(\alpha \rho = \alpha \theta \) for type variables \(\alpha \),  , and
, and  for terms u. Strictly speaking, the domain of a substitution must be finite, so we restrict this definition of \(\rho \) to the finitely many variables that occur in the computation of
for terms u. Strictly speaking, the domain of a substitution must be finite, so we restrict this definition of \(\rho \) to the finitely many variables that occur in the computation of  and
and  .
.
Clearly, we have  and
and  for all types \(\tau \) occurring in the computation of
for all types \(\tau \) occurring in the computation of  and
and  . Moreover,
. Moreover,  and
and  for all terms t occurring in the computation of
for all terms t occurring in the computation of  and
and  , which we show by induction on the structure of t.
, which we show by induction on the structure of t.
If \(t=x\) or if t is fluid,  .
.
If \(t = {\textsf {f} }{\langle \bar{\tau }\rangle }\>\bar{u}\) for  , then
, then

If \(t = {\textsf {Q} }{\langle \tau \rangle }\>(\lambda x.\>u)\), then

If \(t = (\lambda x\mathbin :\tau .\;u)\) and t is not fluid, then

For  , we can argue analogously, using \({\textsf {Q} }_1'\) instead of \({\textsf {Q} }_1\) and
, we can argue analogously, using \({\textsf {Q} }_1'\) instead of \({\textsf {Q} }_1\) and  instead of
instead of  . \(\square \)
. \(\square \)
4 Refutational Completeness
We present a proof of refutational completeness for our higher-order logic superposition calculus. The literature contains two different notions of refutational completeness: static and dynamic. They are defined as follows. For the precise definitions of inference systems and redundancy criteria, we refer to Waldmann et al. [40].
Definition 49
(Static refutational completeness) Let \(\models \) be an entailment relation, let \(\textit{Inf}\) be an inference system, and let \(({\textit{Red}_{\text {I} }}, {\textit{Red}_{\text {C} }})\) be a redundancy criterion. The inference system \(\textit{Inf}\) is statically refutationally complete w.r.t. \(\models \) and \(({\textit{Red}_{\text {I} }}, {\textit{Red}_{\text {C} }})\) if we have \(N \models \bot \) if and only if \(\bot \in N\) for every clause set N that is saturated w.r.t. \(\textit{Inf}\) and \({\textit{Red}_{\text {I} }}\).
Definition 50
(Dynamic refutational completeness) Let \(\models \) be an entailment relation, let \(\textit{Inf}\) be an inference system, and let \(({\textit{Red}_{\text {I} }}, {\textit{Red}_{\text {C} }})\) be a redundancy criterion. Let \((N_i)_i\) be a finite or infinite sequence over sets of clauses. Such a sequence is a derivation if \(N_i \setminus N_{i+1} \subseteq {\textit{Red}_{\text {C} }}(N_{i+1})\) for all i. It is fair if all \(\textit{Inf}\)-inferences from clauses in the limit inferior \(\bigcup _i \bigcap _{\!j \ge i} N_{\!j}\) are contained in \(\bigcup _i {\textit{Red}_{\text {I} }}(N_i)\). The inference system \(\textit{Inf}\) is dynamically refutationally complete w.r.t. \(\models \) and \(({\textit{Red}_{\text {I} }}, {\textit{Red}_{\text {C} }})\) if for every fair derivation \((N_i)_i\) such that \(N_0 \models \bot \), we have \(\bot \in N_i\) for some i.
We have introduced three different notions of entailment on the \({\text {H} }\) level:  , \(\models \), and
, \(\models \), and  . With respect to
. With respect to  , static and dynamic completeness hold unconditionally. For the other two notions of entailment, we will need to add an additional precondition that ensure that the initial clause set is
, static and dynamic completeness hold unconditionally. For the other two notions of entailment, we will need to add an additional precondition that ensure that the initial clause set is  -normal, which can only be stated for dynamic completeness. For
-normal, which can only be stated for dynamic completeness. For  , we need to require in addition that the initial clause set does not contain any \({\textsf {sk} }\) symbols.
, we need to require in addition that the initial clause set does not contain any \({\textsf {sk} }\) symbols.
4.1 Outline of the Proof
Following the completeness proof of \(\lambda \)fSup and \(\lambda \)Sup, our proof proceeds in three steps, corresponding to the three levels defined above:
-
1.
We prove static refutational completeness of \(\textit{GFInf}{}\).
-
2.
We show static refutational completeness of \(\textit{GHInf}\) by transforming the model constructed on the \({\text {GF} }\) level into a higher-order interpretation.
-
3.
We lift the result to the \({\text {H} }\) level by invoking the saturation framework of Waldmann et al. [40].
For the first step, since \(\textit{GFInf}\) is essentially identical with \(\hbox {o}\)Sup, we can rely on Nummelin et al.’s completeness theorem for \(\hbox {o}\)Sup. The refutational completeness result holds for any tuple of parameters  . In addition to the refutational completeness of \(\textit{GFInf}{}\), the subsequent steps also depend on some properties of the constructed model, which we can easily derive from lemmas proved by Nummelin et al.
. In addition to the refutational completeness of \(\textit{GFInf}{}\), the subsequent steps also depend on some properties of the constructed model, which we can easily derive from lemmas proved by Nummelin et al.
For the second step, we fix a parameter triple \(q \in Q\) and a set  saturated w.r.t. \(\textit{GHInf}^{\,q}\) and not containing the empty clause. Then the first step guarantees us a model of
saturated w.r.t. \(\textit{GHInf}^{\,q}\) and not containing the empty clause. Then the first step guarantees us a model of  . Based on this model, we construct a higher-order interpretation that we show to be a model of N. In essence, the proof is analogous to the one of \(\lambda \)Sup, but additionally, we need to consider
. Based on this model, we construct a higher-order interpretation that we show to be a model of N. In essence, the proof is analogous to the one of \(\lambda \)Sup, but additionally, we need to consider  -normality and the logical symbols.
-normality and the logical symbols.
For the third step, the main proof obligation the saturation framework leaves to us is to show that nonredundant \(\textit{GHInf}^{\,q}\) inferences can be lifted to corresponding \(\textit{HInf}\) inferences. For this lifting, we must choose a suitable parameter triple \(q \in Q\), given a clause set  saturated w.r.t. \(\textit{HInf}\) and the \({\text {H} }\) selection functions. In particular, we must specify the witness function to produce Skolem terms according to the given set N. Then the saturation framework guarantees static refutational completeness w.r.t.
saturated w.r.t. \(\textit{HInf}\) and the \({\text {H} }\) selection functions. In particular, we must specify the witness function to produce Skolem terms according to the given set N. Then the saturation framework guarantees static refutational completeness w.r.t. . We show that this implies dynamic refutational completeness w.r.t. \(\models \) for
. We show that this implies dynamic refutational completeness w.r.t. \(\models \) for  -normal initial clause sets.
-normal initial clause sets.
4.2 The Ground First-Order Level
The inference system \(\textit{GFInf}\) is essentially identical with Nummelin et al.’s ground \(\hbox {o}\)Sup calculus, with the following caveats:
-
The conditions of EFact superficially appear different but are equivalent.
-
\(\textit{GFInf}\)’s last condition of ForallRw and ExistsRw is weaker than \(\hbox {o}\)Sup’s to simplify our presentation. Where \(\hbox {o}\)Sup tests for general tautologies, \(\textit{GFInf}\) only tests for a certain form of tautological literal. Clearly, this does not compromise the refutational completeness of \(\textit{GFInf}\).
-
The redundancy criterion of \(\hbox {o}\)Sup requires that a finite subset of \(\{D \in N\mid D\prec C\}\) entails C, whereas \(\textit{GFRed}_{\text {C} }\) requires that \(\{D \in N\mid D\prec C\}\) entails C. Since first-order logic with Booleans is compact, the two criteria are equivalent.
Similar to Bachmair and Ganzinger’s construction for Sup, Nummelin et al. define the model via a term rewriting system \(R_M^*\). As they explain in Definition 16 and Lemma 17, such a term rewriting system \(R_M^*\) can be viewed as an interpretation in \({\text {GF} }\)’s logic with the property that \(t \leftrightarrow _{R_M^*} s\) if and only if \(\smash {\llbracket t\rrbracket _{R_M^*}^{}} = \smash {\llbracket s\rrbracket _{R_M^*}^{}}\) for any two ground terms t and s. The interpretation \(R_M^*\) fulfills the following property:
Lemma 51
Let  produce a rule \(s \rightarrow t \in R_M^*\) (i.e., the rule \(s \rightarrow t\) is introduced into \(R_M^*\) because of C). Then \(s \approx t\) is strictly \(\succeq \)-eligible in C and \(C'\) is false in \(R_M^*\).
produce a rule \(s \rightarrow t \in R_M^*\) (i.e., the rule \(s \rightarrow t\) is introduced into \(R_M^*\) because of C). Then \(s \approx t\) is strictly \(\succeq \)-eligible in C and \(C'\) is false in \(R_M^*\).
Proof
The literal \(s \approx t\) is \(\succeq \)-eligible in C by (C3) of \(\hbox {o}\)Sup. It is even strictly \(\succeq \)-eligible by (C6). The subclause \(C'\) is false in \(R_M^*\) by Lemma 26 of \(\hbox {o}\)Sup. \(\square \)
Since Nummelin et al. prove refutational completeness, but do not explicitly state that \(\smash {R_{N\setminus \textit{GFRed}_{\text {C} }(N)}^*}\) is the model witnessing the completeness, we retrace the last step of their completeness proof in the proof of the following theorem. This also allows us to circumvent the mismatch between the redundancy criteria. Adapted to the context of this article, their completeness theorem can be restated as follows:
Theorem 52
(Ground first-order static refutational completeness) Let  be a parameter triple. Then the inference system \(\textit{GFInf}^{\,q}\) is statically refutationally complete w.r.t. \(\models \) and \((\textit{GFRed}_{\text {I} }, \textit{GFRed}_{\text {C} })\). More precisely, if
be a parameter triple. Then the inference system \(\textit{GFInf}^{\,q}\) is statically refutationally complete w.r.t. \(\models \) and \((\textit{GFRed}_{\text {I} }, \textit{GFRed}_{\text {C} })\). More precisely, if  is a clause set saturated w.r.t. \(\textit{GFInf}~^{q}\) and \(\textit{GFRed}_{\text {I} }^{\,q}\) such that \(\bot \not \in N\), then \(R_{N\setminus \textit{GFRed}_{\text {C} }(N)}^*\) is a model of N.
is a clause set saturated w.r.t. \(\textit{GFInf}~^{q}\) and \(\textit{GFRed}_{\text {I} }^{\,q}\) such that \(\bot \not \in N\), then \(R_{N\setminus \textit{GFRed}_{\text {C} }(N)}^*\) is a model of N.
Proof
This proof is inspired by the one of Theorem 4.9 of Bachmair and Ganzinger [3].
By Lemma 31 of \(\hbox {o}\)Sup, \(\textit{GFInf}^{\,q}\) fulfills the reduction property of counterexamples w.r.t. \(\succ \). This means that for any clause set M where C is the smallest clause in M that is false in \(R_{M}^{*}\), there exists an inference from M with
-
main premise C,
-
side premises that are true in \(R_{M}^{*}\), and
-
a conclusion that is smaller than C and false in \(R_{M}^{*}\).
To derive a contradiction, we assume that \(\smash {R_{N\setminus \textit{GFRed}_{\text {C} }(N)}^*}\not \models N\). Then there must be a smallest clause in \(C\in N\) that is false in \(\smash {R_{N\setminus \textit{GFRed}_{\text {C} }(N)}^*}\). Using \(M = N\setminus \textit{GFRed}_{\text {C} }(N)\), we obtain an inference \(\iota \) with the above properties. Since N is saturated w.r.t. \(\textit{GFInf}^{\,q}\) and \(\textit{GFRed}_{\text {I} }^{\,q}\) and \(\textit{prems}(\iota ) \subseteq M \subseteq N\), we have \(\iota \in \textit{GFRed}_{\text {I} }^{\,q}(N)\). By definition, this means \(\textit{prems}(\iota ) \cap \textit{GFRed}_{\text {C} }(N) \not = \varnothing \) or \(\{D \in N \mid D \prec C\} \models \textit{concl}(\iota )\). Since \(\textit{prems}(\iota ) \subseteq M = N\setminus \textit{GFRed}_{\text {C} }(N)\), it must be the latter. Then \(R_M^* \not \models \{D \in N \mid D \prec C\}\) because \(R_{M}^{*} \not \models \textit{concl}(\iota )\). This contradicts the minimality of C. \(\square \)
4.3 The Ground Higher-Order Level
In this subsection, let \(q = (\textit{GHLitSel}, \textit{GHBoolSel}, \textit{GHWit}) \in Q\) be a parameter triple and let  . Since all terms on the \({\text {GH} }\) level are
. Since all terms on the \({\text {GH} }\) level are  -normal, in particular N is
-normal, in particular N is  -normal. We assume that N is saturated w.r.t. \(\textit{GHInf}^{\,q}\) and \({\textit{GHRed}}_{\,\text {I} }^{\,q}\), and that \(\bot \not \in N\). Clearly,
-normal. We assume that N is saturated w.r.t. \(\textit{GHInf}^{\,q}\) and \({\textit{GHRed}}_{\,\text {I} }^{\,q}\), and that \(\bot \not \in N\). Clearly,  is then saturated w.r.t.
is then saturated w.r.t.  and
and  and
and  is a model of
is a model of  by Theorem 52.
by Theorem 52.
In the following, we abbreviate  as \(R\). Given two terms
as \(R\). Given two terms  , we write \(s\sim t\) to abbreviate
, we write \(s\sim t\) to abbreviate  , which is equivalent to
, which is equivalent to  .
.
Lemma 53
For all terms \(t,s:\tau \rightarrow \upsilon \) in  , these statements are equivalent:
, these statements are equivalent:
-
1.
\(t\sim s\);
-
2.
\(t\>({\textsf {diff} }\>t\>s)\sim s\>({\textsf {diff} }\>t\>s)\);
-
3.
\(t\>u\sim s\>u\) for all
 .
.
Proof
Analogous to Lemma 38 of \(\lambda \)Sup, using Lemma 51 and the \(\beta \eta {\textsf {Q} }_{\eta }\)-normal form. \(\square \)
Lemma 54
Let  and let \(\theta \), \(\theta '\) be grounding substitutions such that \(s\theta \) and \(s\theta '\) are
and let \(\theta \), \(\theta '\) be grounding substitutions such that \(s\theta \) and \(s\theta '\) are  -normal, \(x\theta \sim x\theta '\) for all variables x, and \(\alpha \theta = \alpha \theta '\) for all type variables \(\alpha \). Then \(s\theta \sim s\theta '\).
-normal, \(x\theta \sim x\theta '\) for all variables x, and \(\alpha \theta = \alpha \theta '\) for all type variables \(\alpha \). Then \(s\theta \sim s\theta '\).
Proof
This proof is almost identical to the one of Lemma 39 of \(\lambda \)Sup [10]. The only difference lies in Case 4.1 that must deal with quantifiers. What follows is a copy of the beginning of this previous proof that introduces the notions relevant to deal with the extra case here.
In this proof, we work directly on \(\lambda \)-terms. To prove the lemma, it suffices to prove it for any \(\lambda \)-term s. Here, for \(\lambda \)-terms \(t_1\) and \(t_2\), the notation \(t_1\sim t_2\) is to be read as  because
because  is only defined on \(\beta \eta {\textsf {Q} }_{\eta }\)-normal terms.
is only defined on \(\beta \eta {\textsf {Q} }_{\eta }\)-normal terms.
Definition We extend the syntax of \(\lambda \)-terms with a new polymorphic function symbol  . We will omit its type argument. It is equipped with two reduction rules: \(\oplus \>t\>s \rightarrow t\) and \(\oplus \>t\>s \rightarrow s\). A \(\beta \oplus \)-reduction step is either a rewrite step following one of these rules or a \(\beta \)-reduction step.
. We will omit its type argument. It is equipped with two reduction rules: \(\oplus \>t\>s \rightarrow t\) and \(\oplus \>t\>s \rightarrow s\). A \(\beta \oplus \)-reduction step is either a rewrite step following one of these rules or a \(\beta \)-reduction step.
The computability path order \(\succ _{\textsf {CPO} }\) [14] guarantees that
-
\(\oplus \>t\>s \succ _{\textsf {CPO} } s\) by applying rule \(@\rhd \);
-
\(\oplus \>t\>s \succ _{\textsf {CPO} } t\) by applying rule \(@\rhd \) twice;
-
\((\lambda x.\>t)\>s \succ _{\textsf {CPO} } t[x\mapsto s]\) by applying rule \(@\beta \).
Since this order is moreover monotone, it decreases with \(\beta \oplus \)-reduction steps.
The order is also well founded; thus, \(\beta \oplus \)-reductions terminate. And since the \(\beta \oplus \)-reduction steps describe a finitely branching term rewrite system, by Kőnig’s lemma [26], there is a maximal number of \(\beta \oplus \)-reduction steps from each \(\lambda \)-term.
Definition A \(\lambda \)-term is term-ground if it does not contain free term variables. It may contain polymorphic type arguments.
Definition We introduce an auxiliary function  that essentially measures the size of a \(\lambda \)-term but assigns a size of 1 to term-ground \(\lambda \)-terms.
that essentially measures the size of a \(\lambda \)-term but assigns a size of 1 to term-ground \(\lambda \)-terms.

We prove \(s\theta \sim s\theta '\) by well-founded induction on s, \(\theta \), and \(\theta '\) using the left-to-right lexicographic order on the triple \(\bigl (n_1(s), n_2(s), n_3(s)\bigr )\in {\mathbb {N}}^3\), where
-
\(n_1(s)\) is the maximal number of \(\beta \oplus \)-reduction steps starting from \(s\sigma \), where \(\sigma \) is the substitution mapping each term variable x to \(\oplus \>x\theta \>x\theta '\);
-
\(n_2(s)\) is the number of free term variables occurring more than once in s;
-
 .
.
In Case 4.1 of the proof of Lemma 39 of \(\lambda \)Sup [10], we consider a \(\lambda \)-term s that contains exactly one free term variable that occurs exactly once in s and s is of the form \(f{\langle \bar{\tau }\rangle }\>\bar{t}\), for some symbol \({\textsf {f} }\), some types \(\bar{\tau }\), and some \(\lambda \)-terms \(\bar{t}\). For any  the proof proceeds as before, because then the definition of the encoding
the proof proceeds as before, because then the definition of the encoding  coincides with the one of \(\lambda \)Sup. The remaining case to handle is thus when s is of the form \({\textsf {Q} }{\langle \tau \rangle }\>(\lambda z.\>t)\).
coincides with the one of \(\lambda \)Sup. The remaining case to handle is thus when s is of the form \({\textsf {Q} }{\langle \tau \rangle }\>(\lambda z.\>t)\).
In that case, we have  where
where  , but \(\theta \) and \(\theta '\) are not necessarily grounding for t since t may contain the variable z that is bound in s. Thus, we cannot apply our induction hypothesis directly on t. Instead we want to apply it on \(t\{z\mapsto u\}\), which we denote \(t_u\), where
, but \(\theta \) and \(\theta '\) are not necessarily grounding for t since t may contain the variable z that is bound in s. Thus, we cannot apply our induction hypothesis directly on t. Instead we want to apply it on \(t\{z\mapsto u\}\), which we denote \(t_u\), where  .
.
It is possible to apply the induction hypothesis to obtain \(t_u\theta \sim t_u\theta '\) because
-
\(n_1(s) = n_1(t_u)\) since all \(\beta \oplus \)-reductions in s are also in \(t_u\);
-
\(n_2(s) = 0 = n_2(t_u)\) since the same unique free term variable occurs in s and in \(t_u\); and
-
\(n_3(t_u) < n_3(s)\) because
 implies \(n_3(t_u) = n_3(t)\) and hence
implies \(n_3(t_u) = n_3(t)\) and hence  .
.
Moreover, since \(\theta \) and \(\theta '\) do not capture z, and since u is  -normal, \(t_u\theta = (t\theta )\{z\mapsto u\}\) is
-normal, \(t_u\theta = (t\theta )\{z\mapsto u\}\) is  -normal by Lemma 9 and similarly for \(\theta '\). Thus, we obtain \((t\theta )\{z\mapsto u\}\sim (t\theta ')\{z\mapsto u\}\).
-normal by Lemma 9 and similarly for \(\theta '\). Thus, we obtain \((t\theta )\{z\mapsto u\}\sim (t\theta ')\{z\mapsto u\}\).
Now, let us consider the case where  : By the definition of interpretations on the \({\text {GF} }\) level, by Lemma 6 (substitution lemma) of \(\hbox {o}\)Sup, and R being term-generated, we have
: By the definition of interpretations on the \({\text {GF} }\) level, by Lemma 6 (substitution lemma) of \(\hbox {o}\)Sup, and R being term-generated, we have

The same holds for \(\theta '\). Moreover, above we deduced \((t\theta )\{z\mapsto u\}\sim (t\theta ')\{z\mapsto u\}\) from the induction hypothesis. Thus, \(s\theta \sim s\theta '\), as desired in the case  . The case
. The case  is analogous, with \(\max \) instead of \(\min \). \(\square \)
is analogous, with \(\max \) instead of \(\min \). \(\square \)
We proceed by defining a higher-order interpretation  derived from \(R\). We call this interpretation
derived from \(R\). We call this interpretation  because we use it to show refutational completeness of \(\textit{GHInf}\); it is a higher-order interpretation as defined in Sect. 2, which can interpret ground as well as nonground terms. Let
because we use it to show refutational completeness of \(\textit{GHInf}\); it is a higher-order interpretation as defined in Sect. 2, which can interpret ground as well as nonground terms. Let  , meaning that
, meaning that  is the universe of \(R\) for type \(\tau \) and
is the universe of \(R\) for type \(\tau \) and  is the interpretation function of \(R\).
is the interpretation function of \(R\).
To illustrate the construction, we will employ the following running example. Let \(\Sigma _{{\textsf {ty} }}= \{\iota , \hbox {o}, \rightarrow \}\) and let \(\Sigma \) contain \({\textsf {f} } :\iota \rightarrow \iota \) and \({\textsf {a} } :\iota \), as well as the logical symbols and the choice constant \(\varepsilon \). Then, on the \({\text {GF} }\) level, the type signature is also \(\Sigma _{{\textsf {ty} }}\), and the term signature is the set \(\Sigma _{\text {GF} }\), which contains \({\textsf {f} }_0\), \({\textsf {f} }_1\), \({\textsf {a} }_0\), subscripted versions of all logical symbols, such as  , and
, and  , as well as symbols \(\varepsilon _i^\tau \) for each
, as well as symbols \(\varepsilon _i^\tau \) for each  , and a symbol \({\textsf {lam} }_{\lambda x.\>t}\) for each
, and a symbol \({\textsf {lam} }_{\lambda x.\>t}\) for each  . We write [t] for the equivalence class of
. We write [t] for the equivalence class of  modulo \(R\). The universes
modulo \(R\). The universes  are sets of such equivalence classes; for instance
are sets of such equivalence classes; for instance  , and
, and  . We assume that R is such that \([{\textsf {a} }_0]\), \([{\textsf {f} }_1({\textsf {a} }_0)]\), \([{\textsf {f} }_1({\textsf {f} }_1({\textsf {a} }_0))]\), ... are all different from each other, and therefore that
. We assume that R is such that \([{\textsf {a} }_0]\), \([{\textsf {f} }_1({\textsf {a} }_0)]\), \([{\textsf {f} }_1({\textsf {f} }_1({\textsf {a} }_0))]\), ... are all different from each other, and therefore that  is infinite.
is infinite.
When defining the universe  of the higher-order interpretation, we need to ensure that it contains subsets of function spaces, since
of the higher-order interpretation, we need to ensure that it contains subsets of function spaces, since  must be a subset of the function space from
must be a subset of the function space from  to
to  for all
for all  . However, the first-order universes
. However, the first-order universes  consist of equivalence classes of terms from
consist of equivalence classes of terms from  w.r.t. the rewriting system \(R\), not of functions.
w.r.t. the rewriting system \(R\), not of functions.
To repair this mismatch, we will define a family of functions  that give a meaning to the elements of the first-order universes
that give a meaning to the elements of the first-order universes  . We will define a domain
. We will define a domain  for each ground type \(\tau \) and then let
for each ground type \(\tau \) and then let  be the set of all these domains
be the set of all these domains  . Thus, there will be a one-to-one correspondence between ground types and domains. Since the higher-order and first-order type signatures are identical (including \({\rightarrow }\), which is uninterpreted in \({\text {GF} }\)’s logic), we can identify higher-order and first-order types.
. Thus, there will be a one-to-one correspondence between ground types and domains. Since the higher-order and first-order type signatures are identical (including \({\rightarrow }\), which is uninterpreted in \({\text {GF} }\)’s logic), we can identify higher-order and first-order types.
We define  and
and  in a mutual recursion. To ensure well definedness, we must simultaneously show that
in a mutual recursion. To ensure well definedness, we must simultaneously show that  is bijective. We start with nonfunctional types \(\tau \): Let
is bijective. We start with nonfunctional types \(\tau \): Let  and let
and let  be the identity. Clearly, the identity is bijective. For functional types, we define
be the identity. Clearly, the identity is bijective. For functional types, we define

To verify that this equation is a valid definition of  , we must show that
, we must show that
-
every element of
 is of the form
is of the form  for some
for some  ;
; -
every element of
 is of the form
is of the form  for some
for some  ;
; -
the definition does not depend on the choice of such s and u;
-
 for all
for all  .
.
The first claim holds because R is term-generated and  is a bijection. The second claim holds because R is term-generated and
is a bijection. The second claim holds because R is term-generated and  and
and  are bijections. To prove the third claim, we assume that there are other ground terms
are bijections. To prove the third claim, we assume that there are other ground terms  and
and  such that
such that  and
and  . Since
. Since  is bijective, we have
is bijective, we have  . Using the \(\sim \)-notation, we can write this as \(u\sim v\). The terms s, t, u, and v are in
. Using the \(\sim \)-notation, we can write this as \(u\sim v\). The terms s, t, u, and v are in  , and thus
, and thus  -normal, allowing us to apply Lemma 54 to the term \(x\>y\) and the substitutions \(\{x\mapsto s, y\mapsto u\}\) and \(\{x\mapsto t, y\mapsto v\}\). Thus, we obtain \(s\>u\sim t\>v\)—i.e.,
-normal, allowing us to apply Lemma 54 to the term \(x\>y\) and the substitutions \(\{x\mapsto s, y\mapsto u\}\) and \(\{x\mapsto t, y\mapsto v\}\). Thus, we obtain \(s\>u\sim t\>v\)—i.e.,  , indicating that the definition of
, indicating that the definition of  above does not depend on the choice of s and u. The fourth claim is obvious from the definition of
above does not depend on the choice of s and u. The fourth claim is obvious from the definition of  and the third claim.
and the third claim.
It remains to show that  is bijective. For injectivity, we fix two terms
is bijective. For injectivity, we fix two terms  such that for all
such that for all  , we have
, we have  . By Lemma 53, it follows that
. By Lemma 53, it follows that  , which shows that
, which shows that  is injective. For surjectivity, we fix an element
is injective. For surjectivity, we fix an element  . By definition of
. By definition of  , there exists a term s such that
, there exists a term s such that  for all u. Hence,
for all u. Hence,  , proving surjectivity and therefore bijectivity of
, proving surjectivity and therefore bijectivity of  . Below, we will usually write
. Below, we will usually write  instead of
instead of  since the type \(\tau \) is determined by
since the type \(\tau \) is determined by  ’s first argument.
’s first argument.
In our running example, we have  and
and  is the identity
is the identity  . The function
. The function  maps \([{\textsf {lam} }_{\lambda x. x}]\) to the identity
maps \([{\textsf {lam} }_{\lambda x. x}]\) to the identity  ; it maps \([{\textsf {lam} }_{\lambda x. {\textsf {a} }}]\) to the constant function
; it maps \([{\textsf {lam} }_{\lambda x. {\textsf {a} }}]\) to the constant function  ; it maps \([{\textsf {f} }_0]\) to the function
; it maps \([{\textsf {f} }_0]\) to the function  ; and it maps
; and it maps  to the function
to the function  . There are many more functions in
. There are many more functions in  , but still
, but still  is a proper subset of the function space
is a proper subset of the function space  because the function space is uncountably infinite, whereas
because the function space is uncountably infinite, whereas  and hence
and hence  is countable. Thus, the construction works only because we allow nonstandard Henkin models.
is countable. Thus, the construction works only because we allow nonstandard Henkin models.
We define the higher-order universe as  . In particular, this implies that
. In particular, this implies that  as needed, where 0 is identified with
as needed, where 0 is identified with  and 1 with
and 1 with  . Moreover, we define
. Moreover, we define  for all \(\kappa \in \Sigma _{{\textsf {ty} }}\), completing the type interpretation of
for all \(\kappa \in \Sigma _{{\textsf {ty} }}\), completing the type interpretation of  and ensuring that
and ensuring that  .
.
We define the interpretation function  for nonquantifier symbols
for nonquantifier symbols  by
by  , and for quantifiers by
, and for quantifiers by  and
and  for all
for all  .
.
In our example, we thus have  , which is the function \([t] \mapsto [{\textsf {f} }_1(t)]\).
, which is the function \([t] \mapsto [{\textsf {f} }_1(t)]\).
We must show that this definition indeed fulfills the requirements of an interpretation function (Sect. 2.2). By definition, we have
-
(I1)
 ; and
; and -
(I2)
 .
.
Let \(a,b\in \{0,1\}\),  , and
, and  . Then
. Then
-
(I3)
 ;
; -
(I4)
 ;
; -
(I5)
 ; and
; and -
(I6)
 .
.
Let  and
and  .
.
-
(I7)
Since
 is bijective and R is term-generated, there exist ground terms u and v such that
is bijective and R is term-generated, there exist ground terms u and v such that 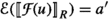 and
and  . Then
. Then 
which is 1 if \(a' = b'\) and 0 otherwise.
-
(I8)
Similarly
 if \(a' = b'\) and 1 otherwise.
if \(a' = b'\) and 1 otherwise. -
(I9)
The requirement for
 holds by definition of
holds by definition of  .
. -
(I10)
The requirement for
 holds by definition of
holds by definition of  .
. -
(I11)
Let
 and
and  . For the requirement on \(\varepsilon \), we must show that
. For the requirement on \(\varepsilon \), we must show that  .
.First, we assume that
 . We want to show that
. We want to show that  . Let
. Let  . We have
. We have  for some \(p:\tau \rightarrow \hbox {o}\) and
for some \(p:\tau \rightarrow \hbox {o}\) and  for some
for some  because
because  and
and  are bijective and R is term-generated. Since N is saturated, all conclusions of GChoice belong to N. In particular, we have
are bijective and R is term-generated. Since N is saturated, all conclusions of GChoice belong to N. In particular, we have  and hence
and hence  . Thus, we have
. Thus, we have  . Since
. Since 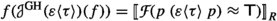 , our assumption implies that
, our assumption implies that  . Moreover,
. Moreover, 
Since our choice of a was arbitrary, this shows that
 . For the other direction, we assume that
. For the other direction, we assume that 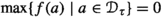 . Then, by definition of \(\max \), and since
. Then, by definition of \(\max \), and since  , we have in particular
, we have in particular  . Thus, we have
. Thus, we have  as required.
as required.
This concludes the proof that  is an interpretation function.
is an interpretation function.
Finally, we need to define the designation function  , which takes a valuation \(\xi \) and a \(\lambda \)-expression \(\lambda x.\> t\) as arguments. Given \(\xi \) and \(\lambda x.\> t\), we choose a grounding substitution \(\theta \) such that
, which takes a valuation \(\xi \) and a \(\lambda \)-expression \(\lambda x.\> t\) as arguments. Given \(\xi \) and \(\lambda x.\> t\), we choose a grounding substitution \(\theta \) such that  for all type variables \(\alpha \) and all variables y in \(\lambda x.\> t\). Such a substitution can be constructed as follows: We can fulfill the first equation in a unique way because there is a one-to-one correspondence between ground types and domains. Since
for all type variables \(\alpha \) and all variables y in \(\lambda x.\> t\). Such a substitution can be constructed as follows: We can fulfill the first equation in a unique way because there is a one-to-one correspondence between ground types and domains. Since  is an element of a first-order universe and \(R\) is term-generated, there exists a ground term s such that
is an element of a first-order universe and \(R\) is term-generated, there exists a ground term s such that  . Choosing one such s and defining
. Choosing one such s and defining  gives us a grounding substitution \(\theta \) with the desired property.
gives us a grounding substitution \(\theta \) with the desired property.
We define  if \(\lambda x.\>t\) is
if \(\lambda x.\>t\) is  -normal, and otherwise
-normal, and otherwise  . Since
. Since  is only defined on
is only defined on  -normal terms, we need to show that \((\lambda x.\> t)\theta \) is
-normal terms, we need to show that \((\lambda x.\> t)\theta \) is  -normal if \(\lambda x.\>t\) is
-normal if \(\lambda x.\>t\) is  -normal. This holds because by construction of \(\theta \) all \(y\theta \) are
-normal. This holds because by construction of \(\theta \) all \(y\theta \) are  -normal and thus so is \((\lambda x.\> t)\theta \) according to Lemma 9. Moreover we need to show that our definition does not depend on the choice of \(\theta \). We assume that there exists another substitution \(\theta '\) with the properties
-normal and thus so is \((\lambda x.\> t)\theta \) according to Lemma 9. Moreover we need to show that our definition does not depend on the choice of \(\theta \). We assume that there exists another substitution \(\theta '\) with the properties  for all \(\alpha \) and
for all \(\alpha \) and  for all variables y in \(\lambda x.\> t\). Then we have \(\alpha \theta = \alpha \theta '\) for all \(\alpha \) due to the one-to-one correspondence between domains and ground types. We have
for all variables y in \(\lambda x.\> t\). Then we have \(\alpha \theta = \alpha \theta '\) for all \(\alpha \) due to the one-to-one correspondence between domains and ground types. We have  for all free variables y in \(\lambda x.\> t\) because
for all free variables y in \(\lambda x.\> t\) because  is injective. By Lemma 54 it follows that
is injective. By Lemma 54 it follows that  , which proves that
, which proves that  is well defined.
is well defined.
In our running example, for all \(\xi \) we have  , which is the identity. If \(\xi (y) = [{\textsf {a} }_0]\), then
, which is the identity. If \(\xi (y) = [{\textsf {a} }_0]\), then  , which is the constant function \(c \mapsto [{\textsf {a} }_0]\).
, which is the constant function \(c \mapsto [{\textsf {a} }_0]\).
This concludes the definition of the interpretation  . It remains to show that
. It remains to show that  is proper. We need a lemma:
is proper. We need a lemma:
Lemma 55
Let  be an interpretation such that
be an interpretation such that  for all \(\lambda \)-terms t and all valuations \(\xi \). Then
for all \(\lambda \)-terms t and all valuations \(\xi \). Then  -normalization preserves denotations of terms and truth of clauses w.r.t.
-normalization preserves denotations of terms and truth of clauses w.r.t.  .
.
Proof
We must show  for all \(\lambda \)-terms t and all valuations \(\xi \). We cannot work with \(\beta \eta \)-equivalence classes here because that would require the interpretation to be proper and thus result in a circular argument. We proceed by induction on the structure of t.
for all \(\lambda \)-terms t and all valuations \(\xi \). We cannot work with \(\beta \eta \)-equivalence classes here because that would require the interpretation to be proper and thus result in a circular argument. We proceed by induction on the structure of t.
If \(t = \lambda x.\>u\), by applying our assumption on  twice and because
twice and because  -normalization is idempotent, we have for all a
-normalization is idempotent, we have for all a

Otherwise, if \(t = s\>\bar{u}\), where s is a head that is not of the form \({\textsf {Q} }{\langle \tau \rangle }\),

If \(t = {\textsf {Q} }{\langle \tau \rangle }\>u\), where t is not  -reducible at its head, then
-reducible at its head, then

Otherwise we have \(t = {\textsf {Q} }{\langle \tau \rangle }\) or \(t = {\textsf {Q} }{\langle \tau \rangle }\>u\) such that t is  -reducible at its head. In these cases, it suffices to show that
-reducible at its head. In these cases, it suffices to show that  and
and  for all types \(\tau \) and all valuations \(\xi \). The argument we use here resembles the proof of Lemma 28, but here we cannot assume
for all types \(\tau \) and all valuations \(\xi \). The argument we use here resembles the proof of Lemma 28, but here we cannot assume  to be proper.
to be proper.
Let f be a function from  to \(\{0,1\}\). Then
to \(\{0,1\}\). Then

By our assumption on  , we have
, we have

Thus, it remains to show that  if and only if f is constantly 1. This holds because
if and only if f is constantly 1. This holds because  and, by our assumption on
and, by our assumption on  ,
,  for all
for all  .
.
The case of  is analogous. \(\square \)
is analogous. \(\square \)
Corollary 56
Let  be an interpretation such that
be an interpretation such that  for all \(\lambda \)-terms t and all valuations \(\xi \). Then
for all \(\lambda \)-terms t and all valuations \(\xi \). Then  is proper.
is proper.
Thus, to show that  is proper, it suffices to prove that
is proper, it suffices to prove that  . For quantifiers, we have the following relation between the higher-order interpretation
. For quantifiers, we have the following relation between the higher-order interpretation  and the first-order interpretation \(R\):
and the first-order interpretation \(R\):
Lemma 57
Let  and
and  . Then, for any term p such that \({\textsf {Q} }{\langle \tau \rangle }(\lambda x.\> p)\) is
. Then, for any term p such that \({\textsf {Q} }{\langle \tau \rangle }(\lambda x.\> p)\) is  -normal and such that
-normal and such that  ,
,

Proof
Let \({\textsf {Q} }\), f, and p be as in the preconditions of the lemma. If  , then
, then

If  , the proof is analogous, but uses \(\max \) instead of \(\min \). \(\square \)
, the proof is analogous, but uses \(\max \) instead of \(\min \). \(\square \)
A similar relation holds on all  -normal terms:
-normal terms:
Lemma 58
Given a ground  -normal \(\lambda \)-term t, we have
-normal \(\lambda \)-term t, we have

Proof
The proof is analogous to that of Lemma 40 of \(\lambda \)Sup, using the \(\beta \eta {\textsf {Q} }_{\eta }\)-normal form instead of the \(\beta \eta \)-normal form and with a special case for quantifier-headed terms. We proceed by induction on t. Assume that  for all proper subterms s of t. If t is of the form \({\textsf {f} }{\langle \bar{\tau }\rangle }\), then it cannot be a quantifier since t is
for all proper subterms s of t. If t is of the form \({\textsf {f} }{\langle \bar{\tau }\rangle }\), then it cannot be a quantifier since t is  -normal. Thus,
-normal. Thus,

If t is of the form \(t = {\textsf {Q} }{\langle \tau \rangle }\>u\), then \(u = \lambda x.\> v\) since t is  -normal, and
-normal, and

If t is an application \(t = t_1\>t_2\), where \(t_1\) is of type \(\tau \rightarrow \upsilon \) and \(t_1\) is not a quantifier, then

If t is a \(\lambda \)-expression, then

where \(\theta \) is a substitution such that  and
and  . \(\square \)
. \(\square \)
We also need to employ the following lemma, which is very similar to the substitution lemma, but we must prove it here for our particular interpretation  because we have not shown that
because we have not shown that  is proper yet.
is proper yet.
Lemma 59
(Substitution lemma) We have  and
and  for all
for all  -normal \(\lambda \)-terms t, all
-normal \(\lambda \)-terms t, all  and all grounding substitutions \(\rho \), where
and all grounding substitutions \(\rho \), where  for all type variables \(\alpha \) and
for all type variables \(\alpha \) and  for all term variables x.
for all term variables x.
Proof
Analogous to Lemma 41 of \(\lambda \)Sup, using the \(\beta \eta {\textsf {Q} }_{\eta }\)-normal form instead of the \(\beta \eta \)-normal form. \(\square \)
Lemma 60
The interpretation  is proper.
is proper.
Proof
By Corollary 56, it is enough to show that  . First, we show it for all
. First, we show it for all  -normal \(\lambda \)-expressions \(\lambda x.\>t\), all valuations \(\xi \), and all values a:
-normal \(\lambda \)-expressions \(\lambda x.\>t\), all valuations \(\xi \), and all values a:

The case where \(\lambda x.\>t\) is not  -normal is reduced to the previous case because then
-normal is reduced to the previous case because then  and
and  where
where  by definition. \(\square \)
by definition. \(\square \)
Lemma 61
 is a model of N.
is a model of N.
Proof
Because all terms in N are  -normal, by Lemma 58,
-normal, by Lemma 58,  for all
for all  . Since
. Since  is a bijection, it follows that any literal
is a bijection, it follows that any literal  is true in
is true in  if and only if
if and only if  is true in \(R\). Hence, a clause
is true in \(R\). Hence, a clause  is true in
is true in  if and only if
if and only if  is true in \(R\). By Theorem 52 and the assumption that \(\bot \notin N\), \(R\) is a model of
is true in \(R\). By Theorem 52 and the assumption that \(\bot \notin N\), \(R\) is a model of  — that is, for all clauses \(C\in N\),
— that is, for all clauses \(C\in N\),  is true in \(R\). Hence, all clauses \(C\in N\) are true in
is true in \(R\). Hence, all clauses \(C\in N\) are true in  and therefore
and therefore  is a model of N. \(\square \)
is a model of N. \(\square \)
We summarize the results of this subsection in the following theorem:
Theorem 62
(Ground static completeness) Let \(q \in Q\) be some parameter triple. Then \(\textit{GHInf}^{\,q}\) is statically refutationally complete w.r.t. \(\models \) and \(({\textit{GHRed}}_{\,\text {I} }^{\,q}, {\textit{GHRed}}_{\text {C} })\). In other words, if  is a clause set saturated w.r.t. \(\textit{GHInf}^{\,q}\) and \({\textit{GHRed}}_{\,\text {I} }^{\,q}\), then \(N \models \bot \) if and only if \(\bot \in N\).
is a clause set saturated w.r.t. \(\textit{GHInf}^{\,q}\) and \({\textit{GHRed}}_{\,\text {I} }^{\,q}\), then \(N \models \bot \) if and only if \(\bot \in N\).
The construction of  relies on the specific properties of R. It would not work with an arbitrary interpretation. In the other direction, transforming a higher-order model into a first-order model with interpreted Booleans is easier, as the following lemma shows:
relies on the specific properties of R. It would not work with an arbitrary interpretation. In the other direction, transforming a higher-order model into a first-order model with interpreted Booleans is easier, as the following lemma shows:
Lemma 63
Given a proper higher-order interpretation  on \({\text {GH} }\), there exists an interpretation
on \({\text {GH} }\), there exists an interpretation  on \({\text {GF} }\) such that for any clause
on \({\text {GF} }\) such that for any clause  the truth values of C in
the truth values of C in  and of
and of  in
in  coincide.
coincide.
Proof
Let  be a proper higher-order interpretation on \({\text {GH} }\). Let
be a proper higher-order interpretation on \({\text {GH} }\). Let  be the \({\text {GF} }\) universe for the ground type \(\tau \). For a symbol \(\smash {{\textsf {f} }^{\bar{\upsilon }}_{\!j}} \in \Sigma _{\text {GF} }\), let
be the \({\text {GF} }\) universe for the ground type \(\tau \). For a symbol \(\smash {{\textsf {f} }^{\bar{\upsilon }}_{\!j}} \in \Sigma _{\text {GF} }\), let  (up to currying). For a symbol \({\textsf {lam} }_{\lambda x.\>t} \in \Sigma _{\text {GF} }\), let
(up to currying). For a symbol \({\textsf {lam} }_{\lambda x.\>t} \in \Sigma _{\text {GF} }\), let  .
.
The requirements on the \({\text {GF} }\)-interpretation of logical symbols are fulfilled because we have similar requirements on \({\text {H} }\):  ; and similarly for the other logical symbols. Thus, this defines an interpretation
; and similarly for the other logical symbols. Thus, this defines an interpretation  on \({\text {GF} }\).
on \({\text {GF} }\).
We need to show that for any  ,
,  if and only if
if and only if  . It suffices to show that
. It suffices to show that  for all terms
for all terms  . We prove this by induction on the structure of the \(\beta \eta {\textsf {Q} }_{\eta }\)-normal form of t. If t is a \(\lambda \)-expression, this is obvious. If t is of the form \({\textsf {f} }{\langle \bar{\upsilon }\rangle }\>\bar{s}_{\!j}\), then
. We prove this by induction on the structure of the \(\beta \eta {\textsf {Q} }_{\eta }\)-normal form of t. If t is a \(\lambda \)-expression, this is obvious. If t is of the form \({\textsf {f} }{\langle \bar{\upsilon }\rangle }\>\bar{s}_{\!j}\), then  and hence
and hence

If t is of the form  , then
, then  and hence
and hence

A similar argument applies for  . Since the definition of
. Since the definition of  recurses into subterms below quantifiers, we finally need to consider the case where t is a variable x. In that case, we have
recurses into subterms below quantifiers, we finally need to consider the case where t is a variable x. In that case, we have  and hence
and hence  . \(\square \)
. \(\square \)
4.4 The Nonground Higher-Order Level
To lift the result to the nonground level, we employ the saturation framework of Waldmann et al. [40]. Clearly, the entailment relation \(\models \) on \({\text {GH} }\) qualifies as a consequence relation in the sense of the framework. We need to show that our redundancy criterion on \({\text {GH} }\) qualifies as a redundancy criterion and that  qualifies as a grounding function:
qualifies as a grounding function:
Lemma 64
The pair \(({\textit{GHRed}}_{\,\text {I} }^{\,q},{\textit{GHRed}}_{\text {C} })\) is a redundancy criterion in the sense of the saturation framework.
Proof
We must prove the conditions (R1) to (R4) of the saturation framework. Adapted to our context, they state the following for all clause sets  :
:
-
(R1)
if \(N \models \bot \), then \(N \setminus {\textit{GHRed}}_{\text {C} }(N) \models \bot \);
-
(R2)
if \(N \subseteq N'\), then \({\textit{GHRed}}_{\text {C} }(N) \subseteq {\textit{GHRed}}_{\text {C} }(N')\) and \({\textit{GHRed}}_{\,\text {I} }(N) \subseteq {\textit{GHRed}}_{\,\text {I} }(N')\);
-
(R3)
if \(N' \subseteq {\textit{GHRed}}_{\text {C} }(N)\), then we have \({\textit{GHRed}}_{\text {C} }(N) \subseteq {\textit{GHRed}}_{\text {C} }(N \setminus N')\) and \({\textit{GHRed}}_{\,\text {I} }(N) \subseteq {\textit{GHRed}}_{\,\text {I} }(N \setminus N')\);
-
(R4)
if \(\iota \in \textit{GHInf}\) and \(\textit{concl}(\iota ) \in N\), then \(\iota \in {\textit{GHRed}}_{\,\text {I} }(N)\).
For (R1), it suffices to show that \(N \setminus {\textit{GHRed}}_{\text {C} }(N) \models N\). Let  be a model of \(N \setminus {\textit{GHRed}}_{\text {C} }(N)\). By Lemma 63, there exists a model
be a model of \(N \setminus {\textit{GHRed}}_{\text {C} }(N)\). By Lemma 63, there exists a model  of
of  . We show that
. We show that  for each clause
for each clause  by well-founded induction on C w.r.t. \(\succ \). If
by well-founded induction on C w.r.t. \(\succ \). If  , we have already shown that
, we have already shown that  . Otherwise,
. Otherwise,  and hence
and hence  . By the induction hypothesis, it follows that
. By the induction hypothesis, it follows that  . Thus, we have shown that
. Thus, we have shown that  . By Lemma 63, this implies
. By Lemma 63, this implies  .
.
For the first part of (R2), let \(N \subseteq N'\) and \(C \in {\textit{GHRed}}_{\text {C} }(N)\), i.e.,  . We must show that
. We must show that  . This is obvious because
. This is obvious because  .
.
For the second part of (R2), let \(N \subseteq N'\) and \(\iota \in {\textit{GHRed}}_{\,\text {I} }(N)\). We must show that \(\iota \in {\textit{GHRed}}_{\,\text {I} }(N')\). If \(\iota \) is a GArgCong, GExt, or GChoice inference, we have \(\textit{concl}(\iota ) \in N \cup {\textit{GHRed}}_{\text {C} }(N)\). Using the first part of (R2), it follows that \(N \cup {\textit{GHRed}}_{\text {C} }(N) \subseteq N' \cup {\textit{GHRed}}_{\text {C} }(N')\), which implies \(\iota \in {\textit{GHRed}}_{\,\text {I} }(N')\). If \(\iota \) is some other kind of inference, we have  or
or  . In the first case,
. In the first case,  because by the first part of (R2), we have
because by the first part of (R2), we have  . In the second case, we have
. In the second case, we have  implies
implies  .
.
For the first part of (R3), let \(N' \subseteq {\textit{GHRed}}_{\text {C} }(N)\) and \(C \in {\textit{GHRed}}_{\text {C} }(N)\), i.e.,  . We must show that
. We must show that  . Let
. Let  be a model of
be a model of  . It suffices to show that
. It suffices to show that  , meaning
, meaning  for every
for every  such that
such that  . We prove this by well-founded induction on E w.r.t. \(\succ \). If
. We prove this by well-founded induction on E w.r.t. \(\succ \). If  , the claim holds by assumption. Otherwise,
, the claim holds by assumption. Otherwise,  ; hence
; hence  and therefore
and therefore  by the induction hypothesis.
by the induction hypothesis.
For the second part of (R3), let \(N' \subseteq {\textit{GHRed}}_{\text {C} }(N)\) and \(\iota \in {\textit{GHRed}}_{\,\text {I} }(N)\). We must show that \(\iota \in {\textit{GHRed}}_{\,\text {I} }(N \setminus N')\). If \(\iota \) is a GArgCong, GExt, or GChoice inference, we have \(\textit{concl}(\iota ) \in N \cup {\textit{GHRed}}_{\text {C} }(N)\). Using \(N' \subseteq {\textit{GHRed}}_{\text {C} }(N)\), and by the first part of (R3), it follows that \(\textit{concl}(\iota ) \in N \cup {\textit{GHRed}}_{\text {C} }(N) = (N \setminus N' )\cup {\textit{GHRed}}_{\text {C} }(N) \subseteq (N \setminus N' )\cup {\textit{GHRed}}_{\text {C} }(N \setminus N')\) and therefore \(\iota \in {\textit{GHRed}}_{\,\text {I} }(N \setminus N')\). If \(\iota \) is some other kind of inference, we have  or
or  . In the first case,
. In the first case,  because by the first part of (R3), we have
because by the first part of (R3), we have  . In the second case, it suffices to show that
. In the second case, it suffices to show that  , which can be shown analogously to the induction used for the first part of (R3).
, which can be shown analogously to the induction used for the first part of (R3).
For (R4), let \(\iota \in \textit{GHInf}\) and \(\textit{concl}(\iota ) \in N\). We must show that \(\iota \in {\textit{GHRed}}_{\,\text {I} }(N)\). If \(\iota \) is a GArgCong, GExt, or GChoice inference, we must show \(\textit{concl}(\iota ) \in N \cup {\textit{GHRed}}_{\text {C} }(N)\), which obviously holds by assumption. If \(\iota \) is some other kind of inference, it suffices to show  . This holds because
. This holds because  and
and  . \(\square \)
. \(\square \)
Lemma 65
For every \(q\in Q\), the function  is a grounding function in the sense of the saturation framework.
is a grounding function in the sense of the saturation framework.
Proof
We must prove the conditions (G1), (G2), and (G3) of the saturation framework. Adapted to our context, they state the following:
-
(G1)
 ;
; -
(G2)
for every
 , if
, if 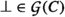 , then \(C = \bot \);
, then \(C = \bot \); -
(G3)
for every \(\iota \in \textit{HInf}\),
 .
.
Clearly, \(C = \bot \) if and only if  if and only if
if and only if  , proving (G1) and (G2). For every \(\iota \in \textit{HInf}\), by the definition of
, proving (G1) and (G2). For every \(\iota \in \textit{HInf}\), by the definition of  (Definition 44) and by Lemma 41, we have
(Definition 44) and by Lemma 41, we have  , and thus (G3) by (R4). \(\square \)
, and thus (G3) by (R4). \(\square \)
To lift the completeness result of the previous subsection to the nonground calculus \(\textit{HInf}\), we employ Theorem 14 of the saturation framework, which, adapted to our context, is stated as follows.
Theorem 66
(Lifting theorem) If, for every parameter triple \(q \in Q\), \(\textit{GHInf}^{\,q}\) is statically refutationally complete w.r.t. \(({\textit{GHRed}}_{\,\text {I} }^{\,q},{\textit{GHRed}}_{\text {C} })\), and if for every  that is saturated w.r.t. \(\textit{HInf}\) and \(\textit{HRed}_{\text {I} }\) there exists a \(q \in Q\) such that
that is saturated w.r.t. \(\textit{HInf}\) and \(\textit{HRed}_{\text {I} }\) there exists a \(q \in Q\) such that  , then also \(\textit{HInf}\) is statically refutationally complete w.r.t. \((\textit{HRed}_{\text {I} }, {\textit{HRed}_{\text {C} }})\) and
, then also \(\textit{HInf}\) is statically refutationally complete w.r.t. \((\textit{HRed}_{\text {I} }, {\textit{HRed}_{\text {C} }})\) and  .
.
Proof
This is almost an instance of Theorem 14 of the saturation framework. We take  for \({{\textbf {F}}}\),
for \({{\textbf {F}}}\),  for \({{\textbf {G}}}\). Clearly, the entailment relation \(\models \) on \({\text {GH} }\) is a consequence relation in the sense of the framework. By Lemma 64 and 65, \(({\textit{GHRed}}_{\,\text {I} }^{\,q},{\textit{GHRed}}_{\text {C} })\) is a redundancy criterion in the sense of the framework, and
for \({{\textbf {G}}}\). Clearly, the entailment relation \(\models \) on \({\text {GH} }\) is a consequence relation in the sense of the framework. By Lemma 64 and 65, \(({\textit{GHRed}}_{\,\text {I} }^{\,q},{\textit{GHRed}}_{\text {C} })\) is a redundancy criterion in the sense of the framework, and  are grounding functions in the sense of the framework, for all \(q\in Q\). The redundancy criterion \((\textit{HRed}_{\text {I} },{\textit{HRed}_{\text {C} }})\) matches exactly the intersected lifted redundancy criterion
are grounding functions in the sense of the framework, for all \(q\in Q\). The redundancy criterion \((\textit{HRed}_{\text {I} },{\textit{HRed}_{\text {C} }})\) matches exactly the intersected lifted redundancy criterion  of the saturation framework. Theorem 14 of the saturation framework applies only when \({\sqsupset } = \varnothing \). By Lemma 16 of the saturation framework, it also holds if \({\sqsupset } \not = \varnothing \). \(\square \)
of the saturation framework. Theorem 14 of the saturation framework applies only when \({\sqsupset } = \varnothing \). By Lemma 16 of the saturation framework, it also holds if \({\sqsupset } \not = \varnothing \). \(\square \)
Let  be a clause set saturated w.r.t. \(\textit{HInf}\) and \(\textit{HRed}_{\text {I} }\). For the above theorem to apply, we need to show that there exists a \(q \in Q\) such that all inferences \(\iota \in \textit{GHInf}^{\,q}\) with
be a clause set saturated w.r.t. \(\textit{HInf}\) and \(\textit{HRed}_{\text {I} }\). For the above theorem to apply, we need to show that there exists a \(q \in Q\) such that all inferences \(\iota \in \textit{GHInf}^{\,q}\) with  are liftable or redundant. Here, \(\iota \) being liftable means that \(\iota \) is a
are liftable or redundant. Here, \(\iota \) being liftable means that \(\iota \) is a  -ground instance of an \(\textit{HInf}\)-inference from N; \(\iota \) being redundant means that
-ground instance of an \(\textit{HInf}\)-inference from N; \(\iota \) being redundant means that  .
.
To choose the right \(q=(\textit{GHLitSel},\textit{GHBoolSel},\textit{GHWit})\in Q\), we observe that each ground clause  must have at least one corresponding clause \(D\in N\) such that C is a ground instance of D. We choose one of them for each
must have at least one corresponding clause \(D\in N\) such that C is a ground instance of D. We choose one of them for each  , which we denote by
, which we denote by  . Then we choose \(\textit{GHLitSel}\) and \(\textit{GHBoolSel}\) such that the selections in C correspond to those in
. Then we choose \(\textit{GHLitSel}\) and \(\textit{GHBoolSel}\) such that the selections in C correspond to those in  in the sense of Definition 38.
in the sense of Definition 38.
To choose the witness function \(\textit{GHWit}\), let  and let p be a green position of a quantifier-headed term \(C|_p = {\textsf {Q} }{\langle \tau \rangle }\>t\). Let
and let p be a green position of a quantifier-headed term \(C|_p = {\textsf {Q} }{\langle \tau \rangle }\>t\). Let  and let \(\theta \) be the grounding substitution such that \(D\theta = C\). Let \(p'\) be the green position corresponding to p in D. If there exists no such position \(p'\), we define \(\textit{GHWit}(C, p)\) to be some arbitrary term that fulfills the order requirements of a witness function. Otherwise, let \(\beta \) and y be fresh variables and we extend \(\theta \) to a substitution \(\theta '\) by defining \(\beta \theta ' = \tau \) and \(y\theta '=t\). Then \(\theta '\) is a unifier of \({\textsf {Q} }{\langle \beta \rangle }\>y\) and \(D|_{p'}\) and hence there exists an idempotent \(\sigma \in {{\,\textrm{CSU}\,}}(Q{\langle \beta \rangle }\>y{,}\;D|_{p'})\) such that for some substitution \(\rho \) and for all free variables x in D and for \(x \in \{y,\beta \}\), we have \(x\sigma \rho = x\theta '\). We let \(\textit{GHWit}(C,p)\) be
and let \(\theta \) be the grounding substitution such that \(D\theta = C\). Let \(p'\) be the green position corresponding to p in D. If there exists no such position \(p'\), we define \(\textit{GHWit}(C, p)\) to be some arbitrary term that fulfills the order requirements of a witness function. Otherwise, let \(\beta \) and y be fresh variables and we extend \(\theta \) to a substitution \(\theta '\) by defining \(\beta \theta ' = \tau \) and \(y\theta '=t\). Then \(\theta '\) is a unifier of \({\textsf {Q} }{\langle \beta \rangle }\>y\) and \(D|_{p'}\) and hence there exists an idempotent \(\sigma \in {{\,\textrm{CSU}\,}}(Q{\langle \beta \rangle }\>y{,}\;D|_{p'})\) such that for some substitution \(\rho \) and for all free variables x in D and for \(x \in \{y,\beta \}\), we have \(x\sigma \rho = x\theta '\). We let \(\textit{GHWit}(C,p)\) be  if the quantifier-headed term is a
if the quantifier-headed term is a  -term and
-term and  if the quantifier-headed term is an
if the quantifier-headed term is an  -term where \(\bar{\alpha }\) are the free type variables and \(\bar{x}\) are the free variables occurring in \(D|_{p'}\) in order of first occurrence.
-term where \(\bar{\alpha }\) are the free type variables and \(\bar{x}\) are the free variables occurring in \(D|_{p'}\) in order of first occurrence.
By definition of  (Definition 34), for all free variables x occurring in D the only Boolean green subterms of \(x\theta \) are
(Definition 34), for all free variables x occurring in D the only Boolean green subterms of \(x\theta \) are  and
and  . The term \({\textsf {Q} }{\langle \tau \rangle }\>t\) must be
. The term \({\textsf {Q} }{\langle \tau \rangle }\>t\) must be  -normal because it occurs in
-normal because it occurs in  . Hence \({\textsf {Q} }{\langle \tau \rangle }\>t \succ t\>\textit{GHWit}(C,p)\) by order condition O4.
. Hence \({\textsf {Q} }{\langle \tau \rangle }\>t \succ t\>\textit{GHWit}(C,p)\) by order condition O4.
With respect to this parameter triple \(q = (\textit{GHLitSel}, \textit{GHBoolSel}, \textit{GHWit})\), we can show that all inferences from  are liftable or redundant:
are liftable or redundant:
Lemma 67
Let  and
and  . Let \(\sigma \) and \(\rho \) be substitutions such that \(x\sigma \rho = x\theta \) for all free variables in C. (This holds for example if \(\sigma \) is an element of a CSU corresponding to a unifier \(\theta \).) If a literal in a clause \(C\theta \) is (strictly) \(\succeq \)-eligible w.r.t. \(\textit{GHLitSel}\), then a corresponding literal in C is (strictly) \(\succsim \)-eligible w.r.t. \(\sigma \) and \(\textit{HLitSel}\). If a green position in a clause \(C\theta \) is \(\succeq \)-eligible w.r.t. \(\textit{GHBoolSel}\) and there exists a corresponding green position in C, then the corresponding position in C is \(\succsim \)-eligible w.r.t. \(\sigma \) and \(\textit{HBoolSel}\).
. Let \(\sigma \) and \(\rho \) be substitutions such that \(x\sigma \rho = x\theta \) for all free variables in C. (This holds for example if \(\sigma \) is an element of a CSU corresponding to a unifier \(\theta \).) If a literal in a clause \(C\theta \) is (strictly) \(\succeq \)-eligible w.r.t. \(\textit{GHLitSel}\), then a corresponding literal in C is (strictly) \(\succsim \)-eligible w.r.t. \(\sigma \) and \(\textit{HLitSel}\). If a green position in a clause \(C\theta \) is \(\succeq \)-eligible w.r.t. \(\textit{GHBoolSel}\) and there exists a corresponding green position in C, then the corresponding position in C is \(\succsim \)-eligible w.r.t. \(\sigma \) and \(\textit{HBoolSel}\).
Proof
Literals: If the literal in \(C\theta \) is selected w.r.t. \(\textit{GHLitSel}\), then the corresponding literal is also selected in  w.r.t. \(\textit{HLitSel}\) by definition of \(\textit{GHLitSel}\) (Definition 38). If \(L\theta \) is (strictly) \(\succeq \)-maximal in \(C\theta \), then \(L\sigma \) is (strictly) \(\succsim \)-maximal in \(C\sigma \).
w.r.t. \(\textit{HLitSel}\) by definition of \(\textit{GHLitSel}\) (Definition 38). If \(L\theta \) is (strictly) \(\succeq \)-maximal in \(C\theta \), then \(L\sigma \) is (strictly) \(\succsim \)-maximal in \(C\sigma \).
Positions: Let p be the position in \(C\theta \) and let \(p'\) be the corresponding position in C. We proceed by induction over the definition of eligible positions (Definition 22). If p is selected in \(C\theta \) w.r.t. \(\textit{GHBoolSel}\), then \(p'\) is selected in  w.r.t. \(\textit{HBoolSel}\) by definition of \(\textit{GHBoolSel}\) (Definition 38). Otherwise, if p is at the top level of a literal \(L\theta = s\theta \mathrel {\dot{\approx }}t\theta \), then \(s\theta \not \preceq t\theta \) implies \(s\sigma \not \precsim t\sigma \), (strict) \(\succeq \)-eligibility of \(L\theta \) implies (strict) \(\succsim \)-eligibility of L w.r.t. \(\sigma \) (as shown above), and hence \(p'\) is eligible in C w.r.t. \(\sigma \). Otherwise, the position p is neither selected nor at the top level. Let q be the position directly above p and \(q'\) be the position directly above \(p'\). By the induction hypothesis, q and \(q'\) are eligible. If the head of \(C\theta _p\) is not
w.r.t. \(\textit{HBoolSel}\) by definition of \(\textit{GHBoolSel}\) (Definition 38). Otherwise, if p is at the top level of a literal \(L\theta = s\theta \mathrel {\dot{\approx }}t\theta \), then \(s\theta \not \preceq t\theta \) implies \(s\sigma \not \precsim t\sigma \), (strict) \(\succeq \)-eligibility of \(L\theta \) implies (strict) \(\succsim \)-eligibility of L w.r.t. \(\sigma \) (as shown above), and hence \(p'\) is eligible in C w.r.t. \(\sigma \). Otherwise, the position p is neither selected nor at the top level. Let q be the position directly above p and \(q'\) be the position directly above \(p'\). By the induction hypothesis, q and \(q'\) are eligible. If the head of \(C\theta _p\) is not  or
or  , then the head of \(C_{p'}\) cannot be
, then the head of \(C_{p'}\) cannot be  or
or  either. If the head \(C\theta _p\) is
either. If the head \(C\theta _p\) is  or
or  , then \(C_{p'}\) must also be
, then \(C_{p'}\) must also be  or
or  because the position \(p'\) is green. Hence, \(p'\) is eligible because \(s\theta \not \succeq t\theta \) implies \(s\sigma \not \succsim t\sigma \). \(\square \)
because the position \(p'\) is green. Hence, \(p'\) is eligible because \(s\theta \not \succeq t\theta \) implies \(s\sigma \not \succsim t\sigma \). \(\square \)
In some edge cases, it is ambiguous what “the corresponding” literal is. When \(C\theta \) contains multiple occurrences of a literal that correspond to different literals in C, we must choose a selected literal if available, or else a \(\succsim \)-maximal literal to make the lemma above work. In the following, we will implicitly assume that the correct literal is chosen when we refer to “the corresponding” literal.
Lemma 68
All ERes, EFact, GArgCong, GExt, GChoice, BoolHoist, and FalseElim inferences are liftable.
Proof
For ERes, EFact, GArgCong, and GExt, the proof is as in Lemma 50 of \(\lambda \)Sup [10]. For GChoice, the proof is analogous to GExt.
BoolHoist: Let \(\iota \in \textit{GHInf}\) be a BoolHoist inference with  . Then \(\iota \) is of the form
. Then \(\iota \) is of the form

where  .
.
If p corresponds to a position at or below an unapplied variable in C, u could only be  or
or  , contradicting the condition of \(\textsc {BoolHoist} \) that u is not a fully applied logical symbol.
, contradicting the condition of \(\textsc {BoolHoist} \) that u is not a fully applied logical symbol.
If p corresponds to a position at or below a fluid term in C, we will lift to a FluidBoolHoist inference. Let \(p = p_1.p_2\) such that \(p_1\) is the longest prefix of p that corresponds to a green position \(p_1'\) in C. Let \(v = \smash {C|_{p_1'}}\). Then v is fluid. Let z and x be fresh variables. Define a substitution \(\theta '\) that maps the variable z to  , the variable x to \(v\theta |_{p_2}\), and all other variables w to \(w\theta \). Then
, the variable x to \(v\theta |_{p_2}\), and all other variables w to \(w\theta \). Then  . So \(\theta '\) is a unifier of \(z\>x\) and v, and thus there exists an idempotent \(\sigma \in {{\,\textrm{CSU}\,}}(z\>x{,}\;v)\) such that for some substitution \(\rho \), for all free variables y in C, and for \(y \in \{x,z\}\), we have \(y\sigma \rho = y\theta '\). By the conditions of BoolHoist,
. So \(\theta '\) is a unifier of \(z\>x\) and v, and thus there exists an idempotent \(\sigma \in {{\,\textrm{CSU}\,}}(z\>x{,}\;v)\) such that for some substitution \(\rho \), for all free variables y in C, and for \(y \in \{x,z\}\), we have \(y\sigma \rho = y\theta '\). By the conditions of BoolHoist,  and
and  . Then
. Then  and
and  because \(u = v\theta |_{p_2} = x\theta ' = x\sigma \rho \). Hence, we have
because \(u = v\theta |_{p_2} = x\theta ' = x\sigma \rho \). Hence, we have  , and thus
, and thus  . The position \(p_1\) must be eligible in \(C\theta \) because p is eligible in \(C\theta \) and \(p_1\) is the longest prefix of p that corresponds to a green position \(p_1'\) in C. Eligibility of \(p_1\) in \(C\theta \) implies eligibility of \(p_1'\) in C by Lemma 67. Thus there exists the following FluidBoolHoist inference \(\iota '\):
. The position \(p_1\) must be eligible in \(C\theta \) because p is eligible in \(C\theta \) and \(p_1\) is the longest prefix of p that corresponds to a green position \(p_1'\) in C. Eligibility of \(p_1\) in \(C\theta \) implies eligibility of \(p_1'\) in C by Lemma 67. Thus there exists the following FluidBoolHoist inference \(\iota '\):

The inference \(\iota \) is the \(\sigma \rho \)-ground instance of \(\iota '\) and is therefore liftable.
Otherwise, we will lift to a BoolHoist inference. Since u is not at or below a variable-headed term, there is a subterm \(u'\) of C at position \(p'\) corresponding to the subterm u of \(C\theta \) at position p. Since u is a Boolean term, there is a type unifier \(\sigma \) of the type of \(u'\) with the Boolean type. Eligibility of u in \(C\theta \) implies eligibility of \(u'\) in C by Lemma 67. Since the occurrence of u in \(C\theta \) is not at the top level of a positive literal, the corresponding occurrence of \(u'\) in C is not at the top level of a positive literal either. Thus, there exists the following BoolHoist inference \(\iota '\):

Then \(\iota \) is a ground instance of \(\iota '\) and is therefore liftable.
FalseElim: Let \(\iota \in \textit{GHInf}\) be an FalseElim inference with  . Then \(\iota \) is of the form
. Then \(\iota \) is of the form

where  and the literal \(s\theta \approx s'\theta \) is strictly \(\succeq \)-eligible w.r.t. \(\textit{GHLitSel}\). Since \(s\theta \approx s'\theta \) and
and the literal \(s\theta \approx s'\theta \) is strictly \(\succeq \)-eligible w.r.t. \(\textit{GHLitSel}\). Since \(s\theta \approx s'\theta \) and  are unifiable and ground, we have
are unifiable and ground, we have  and
and  . Thus, there exists an idempotent
. Thus, there exists an idempotent  such that for some substitution \(\rho \) and for all free variables x in C, we have \(x\sigma \rho = x\theta \). Then \(s \approx s'\) is strictly \(\succsim \)-eligible in C w.r.t. \(\sigma \). Hence, the following inference \(\iota '\in \textit{HInf}\) is applicable:
such that for some substitution \(\rho \) and for all free variables x in C, we have \(x\sigma \rho = x\theta \). Then \(s \approx s'\) is strictly \(\succsim \)-eligible in C w.r.t. \(\sigma \). Hence, the following inference \(\iota '\in \textit{HInf}\) is applicable:

Then \(\iota \) is the \(\sigma \rho \)-ground instance of \(\iota '\) and is therefore liftable. \(\square \)
Lemma 69
All Sup inferences are liftable or redundant.
Proof
The proof is as for Lemmas 52 and 53 of \(\lambda \)Sup [10]. The proof works with the altered definition of deeply occurring variables (Definition 23) because congruence holds below quantifiers on the \({\text {GF} }\) level. \(\square \)
Lemma 70
All EqHoist, NeqHoist, GForallHoist, GExistsHoist, GForallRw, GEx-istsRw, and BoolRw inferences from  are liftable or redundant.
are liftable or redundant.
Proof
Let \(\iota \,{\in }\, \textit{GHInf}\) be a EqHoist, NeqHoist, GForallHoist, GExistsHoist, GForallRw, GExistsRw, or BoolRw inference from  . Let \(C\theta = \textit{prems}(\iota )\) where
. Let \(C\theta = \textit{prems}(\iota )\) where  . Let p be the position of the affected subterm in \(C\theta \).
. Let p be the position of the affected subterm in \(C\theta \).
We distinguish two cases. We will show that \(\iota \) is liftable if
-
(A)
p corresponds to a position in C that is not at or below a fluid term, or
-
(B)
p is the position of a term v in a literal
 or
or  in \(C\theta \).
in \(C\theta \).
Otherwise, we will show that \(\iota \) is redundant.
Liftable Cases: If condition A or B holds, p corresponds to some position \(p'\) in C. Let \(u = C|_{p'}\). By the definition of the grounding function  (Definition 34), for all free variables x occurring in C, the only Boolean green subterms of \(x\theta \) are
(Definition 34), for all free variables x occurring in C, the only Boolean green subterms of \(x\theta \) are  and
and  . Since \(u\theta \) is a fully applied logical symbol different from
. Since \(u\theta \) is a fully applied logical symbol different from  and
and  , the term u cannot be a variable. Eligibility of p in \(C\theta \) implies eligibility of \(p'\) in C by Lemma 67. If u is a fluid term, by conditions A and B, it must be in a literal
, the term u cannot be a variable. Eligibility of p in \(C\theta \) implies eligibility of \(p'\) in C by Lemma 67. If u is a fluid term, by conditions A and B, it must be in a literal  or
or  or \(u \approx v\) of C, for some variable-headed term v.
or \(u \approx v\) of C, for some variable-headed term v.
-
BoolRw: Let \((t,t')\) be the pair used among the ones listed for BoolRw. Then we can extend \(\theta \) to the free variables in t such that the resulting substitution \(\theta '\) is a unifier of t and u. Therefore, there exists an idempotent \(\sigma \in {{\,\textrm{CSU}\,}}(t{,}\; u)\) such that for some substitution \(\rho \) and for all free variables x in C, we have \(x\sigma \rho = x\theta '\). Thus, there is the following \(\textsc {BoolRw} \) inference \(\iota '\in \textit{HInf}\):

In this case, \(\iota \) is the \(\sigma \rho \)-ground instance of \(\iota '\) and is therefore liftable.
-
\(\textsc {GForallRw} \): Then
 and the inference \(\iota \) is of the form
and the inference \(\iota \) is of the form 
for some term v and some type \(\tau \).
Let \(\beta \) be a type variable and y a variable of type \(\beta \rightarrow \hbox {o}\). We define a substitution \(\theta '\) mapping y to v, \(\beta \) to \(\tau \), and all other variables x to \(x\theta \). Then
 and hence \(\theta '\) is a unifier of
and hence \(\theta '\) is a unifier of  and u. Hence, there exists an idempotent
and u. Hence, there exists an idempotent  such that for some substitution \(\rho \), for all free variables x in C, and for \(x \in \{\beta ,y\}\), we have \(x\sigma \rho = x\theta '\). Since the affected literal in \(C\theta \) is not of the form
such that for some substitution \(\rho \), for all free variables x in C, and for \(x \in \{\beta ,y\}\), we have \(x\sigma \rho = x\theta '\). Since the affected literal in \(C\theta \) is not of the form  , the affected literal in C cannot be of the form
, the affected literal in C cannot be of the form  . Thus, there exists the following inference \(\iota '\in \textit{HInf}\):
. Thus, there exists the following inference \(\iota '\in \textit{HInf}\): 
We have
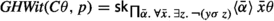 by definition of the witness function, where \(\bar{\alpha }\) are the free type variables and \(\bar{x}\) are the free variables occurring in \(y\sigma \) in order of first occurrence. Hence, \(\iota \) is the \(\sigma \rho \)-ground instance of \(\iota '\) and is therefore liftable.
by definition of the witness function, where \(\bar{\alpha }\) are the free type variables and \(\bar{x}\) are the free variables occurring in \(y\sigma \) in order of first occurrence. Hence, \(\iota \) is the \(\sigma \rho \)-ground instance of \(\iota '\) and is therefore liftable. -
\(\textsc {GExistsRw} \): Analogous to \(\textsc {GForallRw} \).
-
EqHoist: Let x and y be fresh variables. Then we can extend \(\theta \) to a x and y such that the resulting substitution \(\theta '\) is a unifier of u and
 . Thus, there exists an idempotent
. Thus, there exists an idempotent  such that for some substitution \(\rho \), for all free variables z in C, and for \(z \in \{x,y\}\), we have \(z\sigma \rho = z\theta '\). Hence, there is the following \(\textsc {EqHoist} \) inference \(\iota '\in \textit{HInf}\):
such that for some substitution \(\rho \), for all free variables z in C, and for \(z \in \{x,y\}\), we have \(z\sigma \rho = z\theta '\). Hence, there is the following \(\textsc {EqHoist} \) inference \(\iota '\in \textit{HInf}\): 
Then \(\iota \) is the \(\sigma \rho \)-ground instance of \(\iota '\) and is therefore liftable.
-
NeqHoist: Analogous to EqHoist.
-
GForallHoist: Let \(\alpha \) be a fresh type variable and y be a fresh variable. Then we can extend \(\theta \) to y such that the resulting substitution \(\theta '\) is a unifier of u and
 . Thus, there exists an idempotent
. Thus, there exists an idempotent  such that for some substitution \(\rho \), for all free variables x in C, and for \(x = y\), we have \(x\sigma \rho = x\theta '\). Thus, there is the following \(\textsc {ForallHoist} \) inference \(\iota '\in \textit{HInf}\):
such that for some substitution \(\rho \), for all free variables x in C, and for \(x = y\), we have \(x\sigma \rho = x\theta '\). Thus, there is the following \(\textsc {ForallHoist} \) inference \(\iota '\in \textit{HInf}\): 
Then \(\iota \) is the \(\sigma \rho \)-ground instance of \(\iota '\) and is therefore liftable.
-
GExistsHoist: Analogous to GForallHoist.
Redundant Case: Neither condition A nor B holds. Then p corresponds to a position in C at or below a fluid term, but p is not the position of v in a literal  or
or  . Let \(p = p_1.p_2\) such that \(p_1\) is the longest prefix of p that corresponds to a green position \(p_1'\) in C. Let \(u = \smash {C|_{p_1'}}\). Let z and x be fresh variables. Define a substitution \(\theta '\) that maps the variable z to
. Let \(p = p_1.p_2\) such that \(p_1\) is the longest prefix of p that corresponds to a green position \(p_1'\) in C. Let \(u = \smash {C|_{p_1'}}\). Let z and x be fresh variables. Define a substitution \(\theta '\) that maps the variable z to  , the variable x to \(u\theta |_{p_2}\), and all other variables w to \(w\theta \). Then
, the variable x to \(u\theta |_{p_2}\), and all other variables w to \(w\theta \). Then  . So \(\theta '\) is a unifier of \(z\>x\) and u. Thus, there exists an idempotent \(\sigma \in {{\,\textrm{CSU}\,}}(z\>x{,}\;u)\) such that for some substitution \(\rho \), for all free variables y in C, and for \(y \in \{z, x\}\), we have \(y\sigma \rho = y\theta '\). For all of the inference rules, \(C\theta |_p = u\theta |_{p_2}\) cannot be
. So \(\theta '\) is a unifier of \(z\>x\) and u. Thus, there exists an idempotent \(\sigma \in {{\,\textrm{CSU}\,}}(z\>x{,}\;u)\) such that for some substitution \(\rho \), for all free variables y in C, and for \(y \in \{z, x\}\), we have \(y\sigma \rho = y\theta '\). For all of the inference rules, \(C\theta |_p = u\theta |_{p_2}\) cannot be  or
or  . Thus,
. Thus,  and therefore
and therefore  . Hence, we have
. Hence, we have  and therefore
and therefore  . Analogously, we have
. Analogously, we have  . The position \(p_1\) must be eligible in \(C\theta \) because p is eligible in \(C\theta \) and \(p_1\) is the longest prefix of p that corresponds to a green position \(p_1'\) in C. Eligibility of \(p_1\) in \(C\theta \) implies eligibility of \(p_1'\) in C by Lemma 67. Then there are the following inferences \(\iota _\text {bool}\) and \(\iota _\text {loob}\) from C:
. The position \(p_1\) must be eligible in \(C\theta \) because p is eligible in \(C\theta \) and \(p_1\) is the longest prefix of p that corresponds to a green position \(p_1'\) in C. Eligibility of \(p_1\) in \(C\theta \) implies eligibility of \(p_1'\) in C by Lemma 67. Then there are the following inferences \(\iota _\text {bool}\) and \(\iota _\text {loob}\) from C:

Since N is saturated w.r.t. \(\textit{HInf}\) and \(\textit{HRed}_{\text {I} }\), these inferences are in \(\textit{HRed}_{\text {I} }(N)\). We have

These two clauses entail  . Since p is not the position of v in a literal
. Since p is not the position of v in a literal  or
or  , the two clauses are also smaller than
, the two clauses are also smaller than  . Since \(\iota _\text {bool} \in \textit{HRed}_{\text {I} }(N)\), we have
. Since \(\iota _\text {bool} \in \textit{HRed}_{\text {I} }(N)\), we have  and therefore the clauses
and therefore the clauses  that are smaller than
that are smaller than  entail
entail  . Similarly, since \(\iota _\text {loob} \in \textit{HRed}_{\text {I} }(N)\), we have
. Similarly, since \(\iota _\text {loob} \in \textit{HRed}_{\text {I} }(N)\), we have  . Therefore
. Therefore  is entailed by clauses in
is entailed by clauses in  that are smaller than or equal to itself. Thus, \(C\theta \) is redundant and therefore \(\iota \) is redundant. Here, it is crucial that we consider inferences with a redundant premise as redundant. \(\square \)
that are smaller than or equal to itself. Thus, \(C\theta \) is redundant and therefore \(\iota \) is redundant. Here, it is crucial that we consider inferences with a redundant premise as redundant. \(\square \)
By the above lemmas, every \(\textit{HInf}\) inference is liftable or redundant. Using these lemmas, we can apply Theorem 66 to lift ground refutational completeness to nonground refutational completeness.
Lemma 71
(Static refutational completeness w.r.t.  ) The inference system \(\textit{HInf}\) is statically refutationally complete w.r.t.
) The inference system \(\textit{HInf}\) is statically refutationally complete w.r.t.  and \((\textit{HRed}_{\text {I} }, {\textit{HRed}_{\text {C} }})\). In other words, if
and \((\textit{HRed}_{\text {I} }, {\textit{HRed}_{\text {C} }})\). In other words, if  is a clause set saturated w.r.t. \(\textit{HInf}\) and \(\textit{HRed}_{\text {I} }\), then
is a clause set saturated w.r.t. \(\textit{HInf}\) and \(\textit{HRed}_{\text {I} }\), then  if and only if \(\bot \in N\).
if and only if \(\bot \in N\).
Proof
We want to apply Theorem 66. \(\textit{GHInf}^{\,q}\) is statically refutationally complete for all \(q\in Q\) by Theorem 62. By Lemmas 68, 69, and 70, for every saturated  , there exists
, there exists  such that all inferences \(\iota \in \textit{GHInf}^{\,q}\) with
such that all inferences \(\iota \in \textit{GHInf}^{\,q}\) with  either are
either are  -ground instances of \(\textit{HInf}\)-inferences from N or belong to
-ground instances of \(\textit{HInf}\)-inferences from N or belong to  . Thus, Theorem 66 applies. \(\square \)
. Thus, Theorem 66 applies. \(\square \)
Dynamic refutational completeness is easy to derive from static refutational completeness:
Lemma 72
(Dynamic refutational completeness w.r.t.  ) The inference system \(\textit{HInf}\) is dynamically refutationally complete w.r.t.
) The inference system \(\textit{HInf}\) is dynamically refutationally complete w.r.t.  and \((\textit{HRed}_{\text {I} }, HRedC)\), as per Definition 50.
and \((\textit{HRed}_{\text {I} }, HRedC)\), as per Definition 50.
Proof
By Theorem 17 of the saturation framework, this follows from Lemma 71. \(\square \)
To derive a corresponding result for the entailment relation \(\models \), we employ the following lemma, which states equivalence of Herbrand entailment  and Tarski entailment \(\models \) on
and Tarski entailment \(\models \) on  -normal clauses.
-normal clauses.
Lemma 73
Let  be
be  -normal. Then we have
-normal. Then we have  if and only if \(N \models \bot \).
if and only if \(N \models \bot \).
Proof
By Lemma 30, any model of N is also a model of  . So
. So  implies \(N \models \bot \).
implies \(N \models \bot \).
For the other direction, let  be a model of
be a model of  . We must show that there exists a model of N. Let
. We must show that there exists a model of N. Let  be the interpretation obtained from
be the interpretation obtained from  by removing all domains that cannot be expressed as
by removing all domains that cannot be expressed as  for some ground type \(\tau \) and by removing all domain elements that cannot be expressed as
for some ground type \(\tau \) and by removing all domain elements that cannot be expressed as  for some ground term t. We restrict the type interpretation function
for some ground term t. We restrict the type interpretation function  , the interpretation function
, the interpretation function  , and the \(\lambda \)-designation function
, and the \(\lambda \)-designation function  of
of  accordingly.
accordingly.
The restriction  of
of  still maps the logical symbols correctly: For most logical symbols, this is obvious. Only
still maps the logical symbols correctly: For most logical symbols, this is obvious. Only  and
and  deserve some further explanations. For all domains
deserve some further explanations. For all domains  of
of  , we have
, we have  . For the corresponding domain
. For the corresponding domain  , if it has not been removed entirely, we have just defined
, if it has not been removed entirely, we have just defined  . We must show that
. We must show that  for all f that can be expressed as
for all f that can be expressed as  for some ground term t. This claim can only be violated if there exist
for some ground term t. This claim can only be violated if there exist  with \(f(a) = 1\) and if all of them have been removed in
with \(f(a) = 1\) and if all of them have been removed in  . But we have not removed all such elements a because one of them can be expressed as
. But we have not removed all such elements a because one of them can be expressed as  where t is the ground term such that
where t is the ground term such that  . We can argue similarly for
. We can argue similarly for  .
.
Clearly, all terms have the same denotation in  as in
as in  . Thus, the truth values of ground clauses are identical in
. Thus, the truth values of ground clauses are identical in  and
and  . Since
. Since  is proper,
is proper,  is also proper. Hence,
is also proper. Hence,  implies
implies  .
.
It remains to show that  . Let \(C \in N\) and let \(\xi \) be a valuation for
. Let \(C \in N\) and let \(\xi \) be a valuation for  . We must show that C is true in
. We must show that C is true in  under \(\xi \). By assumption, C is
under \(\xi \). By assumption, C is  -normal.
-normal.
By the construction of  , there is a grounding substitution \(\theta \) such that for all type variables \(\alpha \) and all free term variables x occurring in C, we have
, there is a grounding substitution \(\theta \) such that for all type variables \(\alpha \) and all free term variables x occurring in C, we have  and
and  . Then, by Lemma 29,
. Then, by Lemma 29,  for all subterms t of C. Moreover, we can choose \(\theta \) such that for all variables x, the only Boolean green subterms of \(x\theta \) are
for all subterms t of C. Moreover, we can choose \(\theta \) such that for all variables x, the only Boolean green subterms of \(x\theta \) are  and
and  and such that \(x\theta \) is
and such that \(x\theta \) is  -normal. If \(x\theta \) contains a Boolean green subterm different from
-normal. If \(x\theta \) contains a Boolean green subterm different from  and
and  , we can replace it by
, we can replace it by  or
or  while preserving its denotation and thus the property that
while preserving its denotation and thus the property that  for all subterms t of C. If \(x\theta \) is not
for all subterms t of C. If \(x\theta \) is not  -normal, we
-normal, we  -normalize it, which preserves the denotation of terms by Lemma 55.
-normalize it, which preserves the denotation of terms by Lemma 55.
By Lemma 9, it follows that \(C\theta \) is  -normal. Thus,
-normal. Thus,  . Since
. Since  and thus \(C\theta \) is true in
and thus \(C\theta \) is true in  , also C is true in
, also C is true in  under \(\xi \) because
under \(\xi \) because  for all subterms t of C. \(\square \)
for all subterms t of C. \(\square \)
Using this lemma, we can derive the following theorem, which is essentially dynamic refutational completeness with the caveat that the initial clause set must be  -normal, which in practice can be fulfilled by
-normal, which in practice can be fulfilled by  -normalizing the input problem in preprocessing.
-normalizing the input problem in preprocessing.
Theorem 74
(Dynamic refutational completeness w.r.t. \(\models \)) Let \((N_i)_i\) be a derivation w.r.t. \({\textit{HRed}_{\text {C} }}\), as per Definition 50, such that \(N_0\) is  -normal and \(N_0 \models \bot \). Moreover, assume that \((N_i)_i\) is fair w.r.t. \(\textit{HInf}\) and \(\textit{HRed}_{\text {I} }\). Then we have \(\bot \in N_i\) for some i.
-normal and \(N_0 \models \bot \). Moreover, assume that \((N_i)_i\) is fair w.r.t. \(\textit{HInf}\) and \(\textit{HRed}_{\text {I} }\). Then we have \(\bot \in N_i\) for some i.
Proof
This is a consequence of Lemmas 72 and 73. \(\square \)
We can derive dynamic refutational completeness for  with additional assumptions on
with additional assumptions on  -normality and the absence of \({\textsf {sk} }\)-symbols. These assumptions can be fulfilled by
-normality and the absence of \({\textsf {sk} }\)-symbols. These assumptions can be fulfilled by  -preprocessing and by making the \({\textsf {sk} }\) symbols internal such that they can not be expressed by the input language of the prover.
-preprocessing and by making the \({\textsf {sk} }\) symbols internal such that they can not be expressed by the input language of the prover.
Theorem 75
(Dynamic refutational completeness w.r.t.  ) Let \((N_i)_i\) be a derivation w.r.t. \({\textit{HRed}_{\text {C} }}\), as defined in Definition 50, such that \(N_0\) is
) Let \((N_i)_i\) be a derivation w.r.t. \({\textit{HRed}_{\text {C} }}\), as defined in Definition 50, such that \(N_0\) is  -normal, \(N_0\) does not contain any \({\textsf {sk} }\) symbols, and
-normal, \(N_0\) does not contain any \({\textsf {sk} }\) symbols, and  . Moreover, assume that \((N_i)_i\) is fair w.r.t. \(\textit{HInf}\) and \(\textit{HRed}_{\text {I} }\). Then we have \(\bot \in N_i\) for some i.
. Moreover, assume that \((N_i)_i\) is fair w.r.t. \(\textit{HInf}\) and \(\textit{HRed}_{\text {I} }\). Then we have \(\bot \in N_i\) for some i.
Proof
By Lemma 32, \(N_0 \models \bot \). Hence, Theorem 74 applies. \(\square \)
5 Implementation
We implemented our calculus in the Zipperposition prover,Footnote 1 whose OCaml source code makes it convenient to prototype calculus extensions. It has also assimilated some of E’s [33] heuristics, which helps it achieve strong performance at the CASC competition.
Like the calculus, its implementation extends the implementations of \(\lambda \)Sup and \(\hbox {o}\)Sup. From the former, we inherit the given clause loop which supports enumerating infinitely many inference conclusions [37, Sect. 5], calculus extensions, and higher-order heuristics [37]. From the latter, we inherit the encoding of negative predicate literals as  and a basis for the implementation of FalseElim, BoolRw, ForallRw, ExistsRw, and all Hoist rules.
and a basis for the implementation of FalseElim, BoolRw, ForallRw, ExistsRw, and all Hoist rules.
The implementation of \(\hbox {o}\)Sup relies heavily on BoolSimp, and we keep this rule as the basis of our Boolean simplification machinery. As a result, BoolRw can be reduced to two cases: (1) all arguments \(\bar{s}_n\) of \(u = h \, \bar{s}_n\) are variable-headed terms, and thus we must unify \(s_i\) with all combinations of  and
and  ; or (2) either
; or (2) either  or
or  , and thus we must compute the unifiers of s and t.
, and thus we must compute the unifiers of s and t.
As in the implementation of \(\lambda \)Sup, we approximate fluid terms as terms that are either nonground \(\lambda \)-expressions or terms of the form \(x\, \bar{s}_n\) with \(n>0\). Two slight, accidental discrepancies are that we also count variable occurrences below quantifiers as deep and perform EFact inferences even if the maximal literal is selected. Since we expect FluidBoolHoist and FluidLoobHoist to be highly explosive, we penalize them and all of their offspring. In addition to various \(\lambda \)Sup extensions [10, Sect. 5], we also use all the rules for Boolean reasoning described by Vukmirović and Nummelin [39] except for the BoolEF rules. The BoolEF rules have been removed from Zipperposition because they did not seem to improve the prover’s performance.
Our implementation is a graceful extension of \(\hbox {o}\)Sup. For the rules EqHoist, NeqHoist, ForallHoist, and ExistsHoist, if the subterm u is not variable-headed, there is an obvious most general unifier, which allows us to avoid invoking the unification procedure and to generate the conclusion directly, as in \(\hbox {o}\)Sup.
6 Evaluation
We evaluate our implementation and compare it with other higher-order provers. Our experiments were performed on StarExec Miami servers equipped with Intel Xeon E5-2620 v4 CPUs clocked at 2.10 GHz. We used all 2606 TH0 theorems from the TPTP 7.3.0 library [35] and 1253 “Judgment Day” problems [15] generated using Sledgehammer (SH) [32] as our benchmark set. An archive containing the benchmarks and the raw evaluation results is publicly available.Footnote 2 We divide the evaluation in two parts: evaluation of the calculus rules and comparison with other higher-order provers.
Calculus Evaluation. In this first part, we evaluate selected parameters of Zipperposition by varying only the studied parameter in a fixed well-performing configuration. This base configuration disables axioms (Choice) and (Ext) and the Fluid- rules. It uses the unification procedure of Vukmirović et al. [38] in its complete variant—i.e., the variant that produces a complete set of unifiers. It uses none of the early Boolean rules described by Vukmirović and Nummelin [39]. The preprocessor  is disabled as well. All of the completeness-preserving simplification rules described in Sect. 3.7 are enabled, except for the simplifying BoolHoist (combined with LoobHoist). The configuration uses immediate clausification. We set the CPU time limit to 30 s in all three experiments.
is disabled as well. All of the completeness-preserving simplification rules described in Sect. 3.7 are enabled, except for the simplifying BoolHoist (combined with LoobHoist). The configuration uses immediate clausification. We set the CPU time limit to 30 s in all three experiments.
In the first experiment, we assess the overhead incurred by the Fluid- rules. These rules unify with a term whose head is a fresh variable. Thus, we expected that they needed to be tightly controlled to achieve good performance. To test our hypothesis, we simultaneously modified the parameters of these three rules. In Fig. 1, the off mode simply disables the rules, the pragmatic mode uses a terminating incomplete unification algorithm (the pragmatic variant of Vukmirović et al. [38]), and the complete mode uses a complete unification algorithm. The results show that disabling Fluid- rules altogether achieves the best performance. When the complete variant of the unification algorithm is used, inferences are scheduled in a queue designed to postpone explosive inferences [10, Sect. 6]. In contrast, in the pragmatic variant, a terminating algorithm is employed, but still flooding the proof state with Fluid- rules conclusions severely hinders performance. Even though enabling Fluid- rules degrades performance overall, complete finds 35 proofs not found by off, and pragmatic finds 22 proofs not found by off. On Sledgehammer benchmarks, this effect is much weaker, likely because the Sledgehammer benchmarks require less higher-order reasoning: complete finds only one new proof over off, and pragmatic finds only four.
In the second experiment, we explore the clausification methods introduced at the end of Sect. 3: inner delayed clausification, which relies on the core calculus to reason about logical symbols; outer delayed clausification, which clausifies step by step guided by the outermost logical symbols; and immediate clausification, which eagerly applies a monolithic clausification algorithm when encountering top-level logical symbols. The modes inner and outer employ \(\hbox {o}\)Sup’s Rename rule, which renames Boolean terms headed by logical symbols using a Tseitin-like transformation if they occur at least four times in the proof state. Vukmirović and Nummelin [39] observed that outer clausification can greatly help prove higher-order problems, and we expected it to perform well for our calculus, too. The results are shown in Fig. 2. The results confirm our hypothesis: The outer mode outperforms immediate on both TPTP and Sledgehammer benchmarks. The inner mode performs worst, but on Sledgehammer benchmarks, it proves 17 problems beyond the reach of the other two. Looking at the proofs found by inner, we observed a pattern: in many cases (e.g., for the benchmarks prob_295__3252866_1, prob_296__3252872_1, prob_366__5338318_1, prob_419__5371618_1) the problems contain axioms of the form  . When such axioms are not clausified, superposition and demodulation can often reduce either \(\phi \) or \(\psi \) to
. When such axioms are not clausified, superposition and demodulation can often reduce either \(\phi \) or \(\psi \) to  or
or  . At this point, simplification rules will act on the resulting term, simplifying it enough that the proof can easily be found.
. At this point, simplification rules will act on the resulting term, simplifying it enough that the proof can easily be found.
In the third experiment, we investigate the effect of axiom (Choice), which is necessary to achieve refutational completeness. To evaluate (Choice), we either disabled it in a configuration labeled off or set the axiom’s penalty p to different values. In Zipperposition, penalties are propagated through inference and simplification rules and are used to increase the heuristic weight of clauses, postponing the selection of penalized clauses. The results are shown in Fig. 3. As expected, disabling (Choice), or at least penalizing it heavily, improves performance. Yet enabling (Choice) can be crucial: For 19 TPTP problems, the proofs are found when (Choice) is enabled and \(p=4\), but not when the rule is disabled. On Sledgehammer problems, this effect is weaker, with only two new problems proved for \(p=4\).
Prover Comparison. In this second part, we compare Zipperposition’s performance with other higher-order provers. Like at CASC-J10, the wall-clock time limit was 120 s, the CPU time limit was 960 s, and the provers were run on StarExec Miami. We used the following versions of all systems that took part in the THF division: CVC4 1.8 [5], Leo-III 1.5.2 [34], Satallax 3.5 [16], and Vampire 4.5 [13]. The developers of Vampire have informed us that its higher-order schedule is optimized for running on a single core. As a result, the prover suffers some degradation of performance when running on multiple cores. We evaluate both the version of Zipperposition that took part in CASC-J10 (Zip) and the updated version of Zipperposition that supports our new calculus (New Zip). Zip’s portfolio of prover configurations is based on \(\lambda \)Sup and techniques described by Vukmirović and Nummelin [39]. New Zip’s portfolio is specially designed for our new calculus and optimized for TPTP problems. The portfolio does not contain a complete configuration, but the combination of configurations is close to complete.
Leo-III, Satallax, and Zipperposition are cooperative theorem provers: They invoke a backend reasoner to finish the proof attempt. To test the performance of their calculi in isolation, we also invoked them in uncooperative mode. To assess the performance of Boolean reasoning, we used Sledgehammer benchmarks generated both with native Booleans (SH) and with an encoding into Boolean-free higher-order logic (\({\hbox {o}}\)fSH). For technical reasons, the encoding also performs \(\lambda \)-lifting, but this minor transformation should have little impact on results [10, Sect. 7].
The results are shown in Figure 4. The updated version of New Zip beats Zip on TPTP problems but lags behind Zip on Sledgehammer benchmarks as we have yet to further explore more general heuristics that work well with our new calculus. The Sledgehammer benchmarks fail to demonstrate the superiority of native Booleans reasoning compared with an encoding, and in fact CVC4 and Leo-III perform dramatically better on the encoded Boolean problems, suggesting that there is room for tuning.
The uncooperative versions of Zipperposition show strong performance on both benchmark sets. This suggests that, with thorough parameter tuning, higher-order superposition outperforms tableaux, which had been the state of the art in higher-order reasoning for a decade. Without backend reasoners, Zipperposition proves fewer Sledgehammer problems than Vampire. We conjecture that implementing our calculus in Vampire or E would remove the need for a backend reasoner and make the calculus even more useful in practice.
7 Conclusion
We have created a superposition calculus for higher-order logic and proved it sound and refutationally complete. Most of the key ideas have been developed in previous work by us and colleagues, but combining them in the right way has been challenging. A key idea was to  -normalize away inconvenient terms.
-normalize away inconvenient terms.
Unlike earlier refutationally complete calculi for full higher-order logic based on resolution or paramodulation, our calculus employs a term order, which restricts the proof search, and a redundancy criterion, which can be used to add various simplification rules while keeping refutational completeness. These two mechanisms are undoubtedly major factors in the success of first-order superposition, and it is very fortunate that we could incorporate both in a higher-order calculus. An alternative calculus with the same two mechanisms could be achieved by combining \(\hbox {o}\)Sup with Bhayat and Reger’s combinatory superposition [12]. The article on \(\lambda \)Sup [10, Sect. 8] discusses related work in more detail.
The evaluation results show that our calculus is an excellent basis for higher-order theorem proving. In future work, we want to experiment further with the different parameters of the calculus (for example, with Boolean subterm selection heuristics) and implement it in a state-of-the-art prover such as E.
References
Andrews, P.B.: On connections and higher-order logic. J. Autom. Reason. 5(3), 257–291 (1989)
Bachmair, L., Ganzinger, H.: Rewrite-based equational theorem proving with selection and simplification. J. Log. Comput. 4(3), 217–247 (1994)
Bachmair, L., Ganzinger, H.: Resolution theorem proving. In: Robinson, J.A., Voronkov, A. (eds.) Handbook of Automated Reasoning, vol. 1, pp. 19–99. MIT Press, Cambridge (2001)
Bachmair, L., Ganzinger, H., Lynch, C., Snyder, W.: Basic paramodulation and superposition. In: D. Kapur (ed.) CADE-11, LNCS, vol. 607, pp. 462–476. Springer (1992)
Barrett, C.W., Conway, C.L., Deters, M., Hadarean, L., Jovanovic, D., King, T., Reynolds, A., Tinelli, C.: CVC4. In: CAV, LNCS, vol. 6806, pp. 171–177. Springer (2011)
Benanav, D.: Simultaneous paramodulation. In: M.E. Stickel (ed.) CADE-10, LNCS, vol. 449, pp. 442–455. Springer (1990)
Bentkamp, A.: Superposition for higher-order logic. Ph.D. thesis, Vrije Universiteit Amsterdam (2021)
Bentkamp, A., Blanchette, J., Cruanes, S., Waldmann, U.: Superposition for lambda-free higher-order logic. Log. Meth. Comput. Sci. 17(2), 1:1-1:38 (2021)
Bentkamp, A., Blanchette, J., Tourret, S., Vukmirovic, P.: Superposition for full higher-order logic. In: A. Platzer, G. Sutcliffe (eds.) CADE-28, LNCS, vol. 12699, pp. 396–412. Springer (2021)
Bentkamp, A., Blanchette, J., Tourret, S., Vukmirović, P., Waldmann, U.: Superposition with lambdas. J. Autom. Reason. 65, 893–940 (2021)
Benzmüller, C., Paulson, L.C., Theiss, F., Fietzke, A.: LEO-II—A cooperative automatic theorem prover for higher-order logic. In: A. Armando, P. Baumgartner, G. Dowek (eds.) IJCAR 2008, LNCS, vol. 5195, pp. 162–170. Springer (2008)
Bhayat, A., Reger, G.: Set of support for higher-order reasoning. In: B. Konev, J. Urban, P. Rümmer (eds.) PAAR-2018, CEUR Workshop Proceedings, vol. 2162, pp. 2–16. CEUR-WS.org (2018)
Bhayat, A., Reger, G.: A combinator-based superposition calculus for higher-order logic. In: N. Peltier, V. Sofronie-Stokkermans (eds.) IJCAR 2020, Part I, LNCS, vol. 12166, pp. 278–296. Springer (2020)
Blanqui, F., Jouannaud, J.P., Rubio, A.: The computability path ordering. Log. Meth. Comput. Sci. 11(4), 15 (2015)
Böhme, S., Nipkow, T.: Sledgehammer: Judgement Day. In: J. Giesl, R. Hähnle (eds.) IJCAR 2010, LNCS, vol. 6173, pp. 107–121. Springer (2010)
Brown, C.E.: Satallax: An automatic higher-order prover. In: B. Gramlich, D. Miller, U. Sattler (eds.) IJCAR 2012, LNCS, vol. 7364, pp. 111–117. Springer (2012)
Cervesato, I., Pfenning, F.: A linear spine calculus. J. Log. Comput. 13(5), 639–688 (2003)
Fitting, M.: Types, Tableaus, and Gödel’s God. Kluwer (2002)
Ganzinger, H., Stuber, J.: Superposition with equivalence reasoning and delayed clause normal form transformation. Inform. Comput. 199(1–2), 3–23 (2005)
Gordon, M.J.C., Melham, T.F. (eds.): Introduction to HOL: A Theorem Proving Environment for Higher Order Logic. Cambridge University Press (1993)
Huet, G.P.: A mechanization of type theory. In: N.J. Nilsson (ed.) IJCAI-73, pp. 139–146. William Kaufmann (1973)
Huet, G.P.: A unification algorithm for typed lambda-calculus. Theor. Comput. Sci. 1(1), 27–57 (1975)
Jensen, D.C., Pietrzykowski, T.: Mechanizing \(\omega \)-order type theory through unification. Theor. Comput. Sci. 3(2), 123–171 (1976)
Jouannaud, J.P., Rubio, A.: Rewrite orderings for higher-order terms in eta-long beta-normal form and recursive path ordering. Theor. Comput. Sci. 208(1–2), 33–58 (1998)
Kaliszyk, C., Sutcliffe, G., Rabe, F.: TH1: The TPTP typed higher-order form with rank-1 polymorphism. In: P. Fontaine, S. Schulz, J. Urban (eds.) PAAR-2016, CEUR Workshop Proceedings, vol. 1635, pp. 41–55. CEUR-WS.org (2016)
Kőnig, D.: Über eine Schlussweise aus dem Endlichen ins Unendliche. Acta Sci. Math. (Szeged) 3499/2009(3:2–3), 121–130 (1927)
Kotelnikov, E., Kovács, L., Suda, M., Voronkov, A.: A clausal normal form translation for FOOL. In: C. Benzmüller, G. Sutcliffe, R. Rojas (eds.) GCAI 2016, EPiC, vol. 41, pp. 53–71. EasyChair (2016)
Ludwig, M., Waldmann, U.: An extension of the Knuth-Bendix ordering with LPO-like properties. In: N. Dershowitz, A. Voronkov (eds.) LPAR-14, LNCS, vol. 4790, pp. 348–362. Springer (2007)
Mayr, R., Nipkow, T.: Higher-order rewrite systems and their confluence. Theor. Comput. Sci. 192(1), 3–29 (1998)
Nonnengart, A., Weidenbach, C.: Computing small clause normal forms. In: Handbook of Automated Reasoning, pp. 335–367. Elsevier and MIT Press (2001)
Nummelin, V., Bentkamp, A., Tourret, S., Vukmirović, P.: Superposition with first-class Booleans and inprocessing clausification (technical report). https://matryoshka-project.github.io/pubs/boolsup_report.pdf
Paulson, L.C., Blanchette, J.C.: Three years of experience with Sledgehammer, a practical link between automatic and interactive theorem provers. In: G. Sutcliffe, S. Schulz, E. Ternovska (eds.) IWIL-2010, EPiC, vol. 2, pp. 1–11. EasyChair (2012)
Schulz, S.: E-a Brainiac theorem prover. AI Commun. 15(2–3), 111–126 (2002)
Steen, A., Benzmüller, C.: The higher-order prover Leo-III. In: D. Galmiche, S. Schulz, R. Sebastiani (eds.) IJCAR 2018, LNCS, vol. 10900, pp. 108–116. Springer (2018)
Sutcliffe, G.: The TPTP problem library and associated infrastructure—from CNF to TH0, TPTP v6.4.0. J. Autom. Reason. 59(4), 483–502 (2017)
Tseitin, G.: On the complexity of derivation in propositional calculus. In: Automation of reasoning: Classical Papers on Computational Logic, vol. 2, pp. 466–483. Springer (1983)
Vukmirović, P., Bentkamp, A., Blanchette, J., Cruanes, S., Nummelin, V., Tourret, S.: Making higher-order superposition work. In: A. Platzer, G. Sutcliffe (eds.) CADE-28, LNCS. Springer (2021)
Vukmirović, P., Bentkamp, A., Nummelin, V.: Efficient full higher-order unification. In: Z.M. Ariola (ed.) FSCD 2020, LIPIcs, vol. 167, pp. 5:1–5:17. Schloss Dagstuhl—Leibniz-Zentrum für Informatik (2020)
Vukmirović, P., Nummelin, V.: Boolean reasoning in a higher-order superposition prover. In: PAAR-2020, CEUR Workshop Proceedings, vol. 2752, pp. 148–166. CEUR-WS.org (2020)
Waldmann, U., Tourret, S., Robillard, S., Blanchette, J.: A comprehensive framework for saturation theorem proving. In: N. Peltier, V. Sofronie-Stokkermans (eds.) IJCAR 2020, Part I, LNCS, vol. 12166, pp. 316–334. Springer (2020)
Acknowledgements
Uwe Waldmann provided advice and carefully checked the completeness proof. Visa Nummelin led the design of the \(\hbox {o}\)Sup calculus, which was a crucial stepping stone for this work. Simon Cruanes helped us with the implementation. Martin Desharnais generated (and regenerated) the Sledgehammer benchmarks. Ahmed Bhayat explained the higher-order Vampire schedule and suggested textual improvements. Christoph Benzmüller provided us insight into the pitfalls of higher-order reasoning. Alexander Steen explained the details of Leo-III scheduling. Geoff Sutcliffe let us use StarExec Miami for our experiments. Simon Cruanes, Herman Geuvers, Mathias Fleury, Nicolas Peltier, Giles Reger, Mark Summerfield, and the anonymous reviewers suggested textual improvements. We thank them all.
Bentkamp, Blanchette, and Vukmirović’s research has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No. 713999, Matryoshka). Bentkamp’s research has received funding from a Chinese Academy of Sciences President’s International Fellowship for Postdoctoral Researchers (grant No. 2021PT0015). Blanchette’s research has received funding from the Netherlands Organization for Scientific Research (NWO) under the Vidi program (project No. 016.Vidi.189.037, Lean Forward).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Bentkamp, A., Blanchette, J., Tourret, S. et al. Superposition for Higher-Order Logic. J Autom Reasoning 67, 10 (2023). https://doi.org/10.1007/s10817-022-09649-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10817-022-09649-9




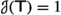










 -normal; or
-normal; or ;
; ;
; for all terms
for all terms  ;
; -normal and the only Boolean green subterms of u are
-normal and the only Boolean green subterms of u are  and
and  .
. .
. must not be selected if
must not be selected if  must not be selected if
must not be selected if  or
or  or a variable-headed term.
or a variable-headed term. is either
is either  or
or  , the positions of all direct green subterms are
, the positions of all direct green subterms are  or
or  , then the position of s is
, then the position of s is  and the position of t is
and the position of t is  .
. , the position of the subterm u is at the top level of a positive literal.
, the position of the subterm u is at the top level of a positive literal. , or
, or  , respectively;
, respectively; , or
, or 
 , or
, or  and
and  , respectively, where
, respectively, where  , or
, or  , and for
, and for  .
.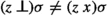 ;
; and
and  ;
; for any term
for any term 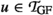 that is not
that is not  or
or 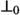 ; and
; and for any term
for any term  whose only Boolean subterms are
whose only Boolean subterms are  and
and  .
. and
and  , let
, let 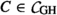 and
and  , let
, let  .
. and
and  , let
, let  , we have
, we have  or there exists
or there exists  .
. , let
, let  , let
, let  .
. , let
, let  or
or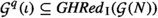 for all
for all  .
. .
. implies
implies  .
. is of the form
is of the form  for some
for some  ;
; is of the form
is of the form  for some
for some  ;
; for all
for all  .
. ; and
; and .
. ;
; ;
; ; and
; and .
. is bijective and R is term-generated, there exist ground terms u and v such that
is bijective and R is term-generated, there exist ground terms u and v such that 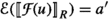 and
and  . Then
. Then 
 if
if  holds by definition of
holds by definition of  .
. holds by definition of
holds by definition of  .
. and
and  . For the requirement on
. For the requirement on  .
. . We want to show that
. We want to show that  . Let
. Let  . We have
. We have  for some
for some  for some
for some  because
because  and
and  are bijective and R is term-generated. Since N is saturated, all conclusions of
are bijective and R is term-generated. Since N is saturated, all conclusions of  and hence
and hence  . Thus, we have
. Thus, we have  . Since
. Since 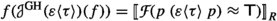 , our assumption implies that
, our assumption implies that  . Moreover,
. Moreover, 
 . For the other direction, we assume that
. For the other direction, we assume that 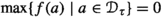 . Then, by definition of
. Then, by definition of  , we have in particular
, we have in particular  . Thus, we have
. Thus, we have  as required.
as required. ;
; , if
, if 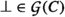 , then
, then  .
. or
or  in
in 
 and the inference
and the inference 
 and hence
and hence  and u. Hence, there exists an idempotent
and u. Hence, there exists an idempotent  such that for some substitution
such that for some substitution  , the affected literal in C cannot be of the form
, the affected literal in C cannot be of the form  . Thus, there exists the following inference
. Thus, there exists the following inference 
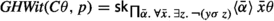 by definition of the witness function, where
by definition of the witness function, where  . Thus, there exists an idempotent
. Thus, there exists an idempotent  such that for some substitution
such that for some substitution 
 . Thus, there exists an idempotent
. Thus, there exists an idempotent  such that for some substitution
such that for some substitution 



