Abstract
The notion of a monad cannot be expressed within higher-order logic (HOL) due to type system restrictions. I show that if a monad is restricted to values of a fixed type, this notion can be formalised in HOL. Based on this idea, I develop a library of effect specifications and implementations of monads and monad transformers. Hence, I can abstract over the concrete monad in HOL definitions and thus use the same definition for different (combinations of) effects. I illustrate the usefulness of effect polymorphism with a monadic interpreter.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Monads have become a standard way to write effectful programs in pure functional languages [34]. In proof assistants, they provide a popular abstraction for modelling and reasoning about effects [4, 5, 8, 19, 22, 32, 36]. Abstractly, a monad consists of a type constructor
 and two polymorphic operations,
and two polymorphic operations,
 for embedding values and
for embedding values and
 for sequencing, with infix notation
for sequencing, with infix notation
 , satisfying three monad laws:
, satisfying three monad laws:

Yet, the notion of a monad cannot be expressed as a formula in higher-order logic (HOL) [12] as there are no type constructor variables like
 in HOL and the sequencing operation
in HOL and the sequencing operation
 occurs with three different type instances in the first law. Thus, only concrete monad instances have been used to model side effects of HOL functions. In fact, monad definitions for different effects abound in HOL, e.g., a state-error monad [4], memoization [36], non-determinism with errors and divergence [19], probabilistic choice [5], probabilistic resumptions with errors [22], and certification monads [32]. Each of these formalisations fixes
occurs with three different type instances in the first law. Thus, only concrete monad instances have been used to model side effects of HOL functions. In fact, monad definitions for different effects abound in HOL, e.g., a state-error monad [4], memoization [36], non-determinism with errors and divergence [19], probabilistic choice [5], probabilistic resumptions with errors [22], and certification monads [32]. Each of these formalisations fixes
 to a particular type (constructor) and develops its own reasoning infrastructure. This approach achieves value polymorphism, i.e., one monad can be used with varying types of values, but not effect polymorphism where one function can be used with different monads.
to a particular type (constructor) and develops its own reasoning infrastructure. This approach achieves value polymorphism, i.e., one monad can be used with varying types of values, but not effect polymorphism where one function can be used with different monads.
In this article, I give up value polymorphism in favour of effect polymorphism. The idea is to fix the type of values to some type
 . Then, the monad type constructor
. Then, the monad type constructor
 is applied only to
is applied only to
 . The resulting combination
. The resulting combination
 is represented by an ordinary HOL type variable
is represented by an ordinary HOL type variable
 . So, the monad operations have the HOL types
. So, the monad operations have the HOL types
 and
and
 This notion of a monad can be formalised within HOL. In detail, I present an Isabelle/HOL libraryFootnote 1 for different monadic effects and their algebraic specification. All effects are also implemented as value-monomorphic monads and monad transformers. Using Isabelle’s module system [2], function definitions can be made abstractly and later specialised to several concrete monads. As a running example, I formalise and reason about a monadic interpreter for a small arithmetic language. The library has been used in a larger project to define and reason about parsers and serialisers for security protocols (Sect. 6).
This notion of a monad can be formalised within HOL. In detail, I present an Isabelle/HOL libraryFootnote 1 for different monadic effects and their algebraic specification. All effects are also implemented as value-monomorphic monads and monad transformers. Using Isabelle’s module system [2], function definitions can be made abstractly and later specialised to several concrete monads. As a running example, I formalise and reason about a monadic interpreter for a small arithmetic language. The library has been used in a larger project to define and reason about parsers and serialisers for security protocols (Sect. 6).
Contributions I show the advantages of trading in value polymorphism for effect polymorphism. First, HOL functions with effects can be defined in an abstract monadic setting (Sect. 2) and reasoned about in the style of Gibbons and Hinze [7]. This preserves the level of abstraction that the monad notion provides. As the definitions need not commit to a concrete monad, they can be used in richer effect contexts too—simply by combining the modular effect specifications. When a concrete monad instance is needed, it can be easily obtained by interpretation using Isabelle’s module system.
Second, as HOL can express the notion of a value-monomorphic monad, I have also formalised several monad transformers [20, 26] in HOL (Sect. 3). Thus, there is no need to define the monad and derive the reasoning principles for each combination of effects, as is current practice with value polymorphism. Instead, it suffices to formalise every effect only once as a transformer and combine them modularly.
Third, relations between different instances can be proven using the theory of representation independence (Sect. 4) as supported by Isabelle’s Transfer package [14]. This makes it possible to switch in the middle of a bigger proof from a complicated monad to a simpler one.
In comparison to the conference version [23], this article additionally implements binary probabilistic choice from countable choice (Sect. 2.3) and presents monad transformers for non-determinism (Sect. 3.5) and a non-deterministic interpreter (Sect. 3.6).
2 Abstract Value-Monomorphic Monads in HOL
In this section, I specify value-monomorphic monads for several types of effects. A monadic interpreter for an arithmetic language will be used throughout as a running example. The language, adapted from Nipkow and Klein [27], consists of integer constants, variables, addition, and division.

I formalise the concept of a monad using Isabelle’s module system of locales [2]. The locale
 below fixes the two monad operations
below fixes the two monad operations
 and
and
 (written infix as
(written infix as
 and assumes that the monad laws hold. It will collect definitions of functions, which use the monad operations, and theorems about them, whose proofs can use the monad laws. Every locale also defines a predicate of the same name that collects all the assumptions; for example,
and assumes that the monad laws hold. It will collect definitions of functions, which use the monad operations, and theorems about them, whose proofs can use the monad laws. Every locale also defines a predicate of the same name that collects all the assumptions; for example,
 expresses that the two functions
expresses that the two functions
 and
and
 satisfy the monad laws. When a user interprets the locale with more concrete operations (e.g.,
satisfy the monad laws. When a user interprets the locale with more concrete operations (e.g.,
 and
and
 and has discharged the assumptions for these operations, every definition and theorem inside the locale context is specialised to these operations. Although the type of values is a type variable
and has discharged the assumptions for these operations, every definition and theorem inside the locale context is specialised to these operations. Although the type of values is a type variable
 ,
,
 is fixed inside the locale. Instantiations may still replace
is fixed inside the locale. Instantiations may still replace
 with any other HOL type. In other words, the locale
with any other HOL type. In other words, the locale
 formalises a monomorphic monad, but leaves the type of values unspecified. As usual,
formalises a monomorphic monad, but leaves the type of values unspecified. As usual,
 abbreviates
abbreviates
 .
.

Monads become useful only when effect-specific operations are available. In the remainder of this section, I formalise monadic operations for different types of effects and their properties. For each effect, I introduce a new locale in Isabelle that extends the locale
 , fixes the new operations, and specifies their properties. A locale extension inherits parameters and assumptions. This leads to a modular design: if several effects are needed, one merely combines the relevant locales in a multi-extension.
, fixes the new operations, and specifies their properties. A locale extension inherits parameters and assumptions. This leads to a modular design: if several effects are needed, one merely combines the relevant locales in a multi-extension.
2.1 Failure and Exception
Failures are among the simplest effects and are widely used. A failure aborts the computation immediately. The locale
 given below formalises the failure effect
given below formalises the failure effect
 . It assumes that a failure propagates from the left hand side of
. It assumes that a failure propagates from the left hand side of
 , i.e.,
, i.e.,
 aborts a computation. In contrast, there is no assumption about how
aborts a computation. In contrast, there is no assumption about how
 behaves on
behaves on
 ’s right hand side. Otherwise, if
’s right hand side. Otherwise, if
 also assumed
also assumed
 , then
, then
 would undo any effect of
would undo any effect of
 . Although the standard implementation of failures using the
. Although the standard implementation of failures using the
 type satisfies this additional law, many other monad implementations do not, e.g., state-exception monads. Note that there is no need to delay the evaluation of
type satisfies this additional law, many other monad implementations do not, e.g., state-exception monads. Note that there is no need to delay the evaluation of
 in HOL because HOL has no execution semantics.
in HOL because HOL has no execution semantics.

As a first example, I define the monadic interpreter
 for arithmetic expressions by primitive recursion using these abstract monad operations inside the locale
for arithmetic expressions by primitive recursion using these abstract monad operations inside the locale
 .Footnote 2 The first argument is an interpretation function
.Footnote 2 The first argument is an interpretation function
 for the variables. The evaluation fails when a division by zero occurs.
for the variables. The evaluation fails when a division by zero occurs.

Note that evaluating a variable can have an effect
 , which is necessary to obtain a compositional interpreter. Let
, which is necessary to obtain a compositional interpreter. Let
 be the substitution function for
be the substitution function for
 . That is,
. That is,
 replaces every
replaces every
 in
in
 with
with
 . Then, the following compositionality statement holds (proven by induction on
. Then, the following compositionality statement holds (proven by induction on
 and term rewriting with the definitions), where function composition \(\circ \) is defined as \((f \circ g)(x) = f\ (g\ x)\).
and term rewriting with the definitions), where function composition \(\circ \) is defined as \((f \circ g)(x) = f\ (g\ x)\).

I refer to failures as exceptions whenever there is an operator
 to handle them. Following Gibbons and Hinze [7], the locale
to handle them. Following Gibbons and Hinze [7], the locale
 assumes that
assumes that
 and
and
 form a monoid and that
form a monoid and that
 s are not handled. It inherits fail-bind and the monad laws by extending the locale
s are not handled. It inherits fail-bind and the monad laws by extending the locale
 . No properties about the interaction between
. No properties about the interaction between
 and
and
 are assumed because in general exception handling does not distribute over sequencing.
are assumed because in general exception handling does not distribute over sequencing.

2.2 State
Some computations rely on a state that changes over time, e.g., counters, pseudo-random number generators, and destructive updates, where old versions are no longer needed. Such stateful computations use operations to read (
 ) and replace (
) and replace (
 ) the state of type
) the state of type
 . In a value-polymorphic setting,
. In a value-polymorphic setting,
 and
and
 are usually computations that return the state or
are usually computations that return the state or
 inhabiting the singleton type
inhabiting the singleton type
 . Without value-polymorphism, these types cannot be formalised in the HOL setting because
. Without value-polymorphism, these types cannot be formalised in the HOL setting because
 cannot be applied to different value types. Instead, my operations additionally take a continuation:
cannot be applied to different value types. Instead, my operations additionally take a continuation:
 and
and
 . In a value-polymorphic setting, both signatures are equivalent. Passing the continuation
. In a value-polymorphic setting, both signatures are equivalent. Passing the continuation
 as in
as in
 and
and
 yields the conventional operations. Conversely, my operations
yields the conventional operations. Conversely, my operations
 can be implemented as
can be implemented as
 and
and
 using conventional
using conventional
 and
and
 . The locale
. The locale
 collects the properties
collects the properties
 and
and
 must satisfy:
must satisfy:

The first four assumptions adapt Gibbons’ and Hinze’s axioms for the state operations [7] to the new signature. The fifth, get-const, additionally specifies that
 can be discarded if the state is not used. The last two assumptions, bind-get and bind-put, demand that
can be discarded if the state is not used. The last two assumptions, bind-get and bind-put, demand that
 and
and
 distribute over
distribute over
 . In the conventional value-polymorphic setting, where the continuations are applied using
. In the conventional value-polymorphic setting, where the continuations are applied using
 , these two are subsumed by the monad laws. In the remainder of this paper,
, these two are subsumed by the monad laws. In the remainder of this paper,
 and
and
 always take continuations.Footnote 3
always take continuations.Footnote 3
A state update function
 can be implemented abstractly for all state monads. Like
can be implemented abstractly for all state monads. Like
 ,
,
 takes a continuation
takes a continuation
 .
.

The expected properties of
 can be derived from
can be derived from
 ’s assumptions by term rewriting. For example,
’s assumptions by term rewriting. For example,

As an example, I implement a memoisation operator
 using the state operations. To that end, the state must be refined to a lookup table, which I model as a map of type
using the state operations. To that end, the state must be refined to a lookup table, which I model as a map of type
 . The definition uses the function
. The definition uses the function
 that takes a map
that takes a map
 and updates it to associate
and updates it to associate
 with
with
 , leaving the other associations as they are; formally,
, leaving the other associations as they are; formally,
 .
.

A memoisation operator should satisfy the following three properties. First, it evaluates the memoised function at most on the given argument, not on others. This can be expressed as a congruence rule, which holds by
 ’s definition: [3]
’s definition: [3]

Second, memoisation should be idempotent, i.e., if a function is already being memoised, then there is no point in memoising it once more.

The mechanised proof of memo-idem in Isabelle needs only two steps, which are justified by term rewriting with the properties of the monad operations and the
 operator. Every assumption about
operator. Every assumption about
 and
and
 except get-put is needed. Appendix A contains a step-by-step proof that illustrates reasoning with the algebraic monad properties.
except get-put is needed. Appendix A contains a step-by-step proof that illustrates reasoning with the algebraic monad properties.
Third, the memoisation operator should indeed evaluate
 on
on
 at most once. As
at most once. As
 memoises only the result of
memoises only the result of
 , but not the effect of evaluating
, but not the effect of evaluating
 , the next lemma captures this correctness property. Its proof is similar to memo-idem’s.
, the next lemma captures this correctness property. Its proof is similar to memo-idem’s.

2.3 Probabilistic Choice
Randomised computations are built from an operation
 for probabilistic choice. The probabilities are specified using probability mass functions (type
for probabilistic choice. The probabilities are specified using probability mass functions (type
 ) [11], i.e., discrete probability distributions. Binary probabilistic choice, which is often used in the literature [6, 7, 30], is less general as it leads to finite distributions. Continuous distributions would work, too, but they would require measurability conditions everywhere.
) [11], i.e., discrete probability distributions. Binary probabilistic choice, which is often used in the literature [6, 7, 30], is less general as it leads to finite distributions. Continuous distributions would work, too, but they would require measurability conditions everywhere.
Like the state operations,
 takes a continuation to separate the type of probabilistic choices
takes a continuation to separate the type of probabilistic choices
 from the type of values. The locale
from the type of values. The locale
 assumes the following properties:
assumes the following properties:
-
sampling from the one-point distribution
 has no effect (sample-dirac),
has no effect (sample-dirac), -
sequencing
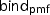 in the probability monad yields sequencing (sample-bind),
in the probability monad yields sequencing (sample-bind), -
sampling can be discarded if the result is unused (sample-const),
-
sampling from independent distributions commutes (sample-comm, independence is expressed by p and q not taking y and x as an argument, respectively.)
-
sampling is relationally parametric in the choices (sample-param), and
-
sampling distributes over both sides of
 (bind-sample1, bind-sample2).
(bind-sample1, bind-sample2).

The assumption sample-param ensures that
 does not look at the identity of the choices. This is expressed as a Reynolds-style parametricity condition [31] where
does not look at the identity of the choices. This is expressed as a Reynolds-style parametricity condition [31] where
-
 is a relation between the choices, where the condition
is a relation between the choices, where the condition
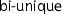 expresses that
expresses that
 relates each choice with at most one choice, i.e.,
relates each choice with at most one choice, i.e.,
 does not identify choices;Footnote 4
does not identify choices;Footnote 4 -
the relator
 lifts a relation on elementary events to probability distributions:
lifts a relation on elementary events to probability distributions:
 iff
iff
 for all
for all
 , where
, where
 denotes the probability of the event
denotes the probability of the event
 under the distribution
under the distribution
 ;
; -
the right-associative function relator
 relates two functions
relates two functions
 and
and
 iff
iff
 implies
implies
 for all
for all
 and
and
 ; and
; and -
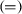 denotes the identity relation.
denotes the identity relation.
For example, consider two biased coins
 and
and
 that show heads with probabilities
that show heads with probabilities
 and
and
 , respectively. Then, it should not matter whether we flip
, respectively. Then, it should not matter whether we flip
 or
or
 provided that we switch the actions for heads and tails. Formally,
provided that we switch the actions for heads and tails. Formally,
 if
if
 and
and
 . This identity follows from sample-param using
. This identity follows from sample-param using
 .
.
Parametricity in particular ensures that
 calls the continuation
calls the continuation
 only on values in
only on values in
 ’s supportFootnote 5
’s supportFootnote 5 (take
(take
 in sample-param)Footnote 6:
in sample-param)Footnote 6:

Binary probabilistic choice
 can be defined in terms of
can be defined in terms of
 . It behaves as
. It behaves as
 with probability
with probability
 and as
and as
 with probability
with probability
 . For it to be well-behaved, we must require that the type
. For it to be well-behaved, we must require that the type
 of choices contains at least three choices, say
of choices contains at least three choices, say
 ,
,
 , and
, and
 . Let
. Let
 be the distribution that assigns probability
be the distribution that assigns probability
 to
to
 to
to
 . (The third choice
. (The third choice
 is needed to prove the associativity law below.)
is needed to prove the associativity law below.)

From the
 assumptions, I can derive Gibbons and Hinze’s specification [7]. All assumptions are used except sample-comm. Associativity crucially relies on sample-param and the existence of a third choice
assumptions, I can derive Gibbons and Hinze’s specification [7]. All assumptions are used except sample-comm. Associativity crucially relies on sample-param and the existence of a third choice
 as we must distribute the probability over three computations, not just the two of the inner choice operator.
as we must distribute the probability over three computations, not just the two of the inner choice operator.

2.4 Combining Abstract Monads
Formalising monads in this abstract way has the advantage that the different effects can be easily combined. In the running example, suppose that the variables represent independent random variables. Then, expressions are probabilistic computations and evaluation computes the joint probability distribution. For example, if
 and
and
 represent coin flips with
represent coin flips with
 representing heads and
representing heads and
 tails, then
tails, then
 represents the probability distribution of the number of heads.
represents the probability distribution of the number of heads.
Here is a first attempt. Let
 specify the distribution
specify the distribution
 for each random variable
for each random variable
 . Combining the locales for failures and probabilistic choice, we let the variable environment do the sampling, where
. Combining the locales for failures and probabilistic choice, we let the variable environment do the sampling, where
 :
:

As the name suggests,
 does not achieve what was intended. If a variable occurs multiple times in
does not achieve what was intended. If a variable occurs multiple times in
 , say
, say
 , then
, then
 samples
samples
 afresh for each occurrence. So, if
afresh for each occurrence. So, if
 , i.e.,
, i.e.,
 is a coin flip,
is a coin flip,
 computes the probability distribution given by
computes the probability distribution given by
 instead of
instead of
 . Clearly, every variable should be sampled at most once. Memoising the variable evaluation achieves that. So, we additionally need state operations.
. Clearly, every variable should be sampled at most once. Memoising the variable evaluation achieves that. So, we additionally need state operations.

The interpreter
 samples a variable only when needed. For example, in
samples a variable only when needed. For example, in
 , the division by zero makes the evaluation fail before
, the division by zero makes the evaluation fail before
 is sampled.
is sampled.
The locale
 adds an assumption that
adds an assumption that
 distributes over
distributes over
 . Such distributivity assumptions are typically needed because of the continuation parameters, which break the separation between effects and sequencing. Their format is as follows: If two operations
. Such distributivity assumptions are typically needed because of the continuation parameters, which break the separation between effects and sequencing. Their format is as follows: If two operations
 and
and
 with continuations do not interact, then we assume
with continuations do not interact, then we assume
 . Sometimes, such assumptions follow from existing assumptions. For example, sample-put follows from bind-sample2 and
. Sometimes, such assumptions follow from existing assumptions. For example, sample-put follows from bind-sample2 and
 for all
for all
 . A similar law holds for
. A similar law holds for
 .
.

In contrast, sample-get does not follow from the other assumptions due to the restriction to monomorphic values. The state of type
 , which
, which
 passes to its continuation, may carry more information than a value can hold. Indeed, in the case of
passes to its continuation, may carry more information than a value can hold. Indeed, in the case of
 , the type
, the type
 of values is countable, but the state type
of values is countable, but the state type
 is not if the type of variables is infinite. As
is not if the type of variables is infinite. As
 passes no information to its continuation,
passes no information to its continuation,
 ’s continuation can be pushed into
’s continuation can be pushed into
 as shown above. Still,
as shown above. Still,
 needs its continuation; otherwise, it would have to create a return value out of nothing, which would cause problems later (Sect. 4). Moreover, there is no need to explicitly specify how
needs its continuation; otherwise, it would have to create a return value out of nothing, which would cause problems later (Sect. 4). Moreover, there is no need to explicitly specify how
 interacts with
interacts with
 and
and
 as
as
 and
and
 are special cases of get-const and sample-const.
are special cases of get-const and sample-const.
Instead of lazy sampling, we can also sample all variables eagerly. Let
 return the (finite) set of variables in
return the (finite) set of variables in
 . Then, the interpreter
. Then, the interpreter
 with eager sampling is defined as follows (all three definitions live in the locale
with eager sampling is defined as follows (all three definitions live in the locale
 ):
):

where
 is the fold operator for finite sets [28]. The operator
is the fold operator for finite sets [28]. The operator
 requires that the folding function
requires that the folding function
 is left-commutative, i.e.,
is left-commutative, i.e.,
 for all
for all
 ,
,
 , and
, and
 . In our case,
. In our case,
 is left-commutative by the following lemma about
is left-commutative by the following lemma about
 whose assumptions hold for
whose assumptions hold for
 thanks to return-bind, bind-sample\(_{1}\), bind-sample\(_2\), and sample-get. Moreover, by correct, it is also idempotent, i.e.,
thanks to return-bind, bind-sample\(_{1}\), bind-sample\(_2\), and sample-get. Moreover, by correct, it is also idempotent, i.e.,
 .
.

This lemma and correct illustrate the typical form of monadic statements. The assumptions and conclusions take a continuation
 for the remainder of the program. This way, the statements are easier to apply because they are in normal form with respect to bind-assoc. This observation also holds in a value-polymorphic setting.
for the remainder of the program. This way, the statements are easier to apply because they are in normal form with respect to bind-assoc. This observation also holds in a value-polymorphic setting.
Now, the question is whether eager and lazy sampling are equivalent. In general, the answer is no. For example, for
 from above,
from above,
 samples and memoises the variable
samples and memoises the variable
 , but
, but
 does not. Thus, there are contexts that distinguish the two. If we extend
does not. Thus, there are contexts that distinguish the two. If we extend
 with exception handling from
with exception handling from
 such that
such that
 and
and
 never fail,
never fail,

then the two can be distinguished:

In contrast, if we assume that failures erase state updates, then the two are equivalent:

Proof
The proof consists of three steps proven by induction on
 . First, by idempotence and left-commutativity,
. First, by idempotence and left-commutativity,
 commutes with
commutes with
 for any finite
for any finite
 :
:

Here,
 ensures that all state updates are lost if a division by zero occurs. The next two steps will use (1) in the inductive cases for
ensures that all state updates are lost if a division by zero occurs. The next two steps will use (1) in the inductive cases for
 and
and
 to bring together the sampling of the variables and the evaluation of the subexpressions. Second,
to bring together the sampling of the variables and the evaluation of the subexpressions. Second,

shows that the sampling can be done first, which holds by correct. Finally,

holds for any finite set
 with
with
 . Here,
. Here,
 is the interesting case, which follows from
is the interesting case, which follows from
 and correct. Taking
and correct. Taking
 and
and
 , (2) and (3) prove the theorem. \(\square \)
, (2) and (3) prove the theorem. \(\square \)
In Sect. 3.6, I show that some monads satisfy lazy-eager’s assumption, but not all.
2.5 Abstract Monad Properties
Some monad transformer implementations require that the transformed monad satisfies additional properties. I consider three properties, which I formalise as locales:
-
A monad is commutative if independent computations can be reordered.
-
A monad is discardable if we may drop a computation whose result is not used.
-
A monad is duplicable if a computation may be duplicated.

2.6 Further Abstract Monads
Apart from exceptions, state, and probabilistic choice, I have formalised specifications for the following effects. I only present them to the level of detail needed for understanding the remainder of this paper.
Non-determinism Non-determinism is often used in specification where implementation choices are unspecified; implementations can then refine the non-determinism [1, 19]. Backtracking can also be implemented elegantly using non-deterministic choice and failure [33]. I specify two choice operators: binary
 and countable
and countable
 where the type
where the type
 consists of all countable sets over
consists of all countable sets over
 . Unbounded choice would be similar to countable choice. Their specification is similar to probabilities, but I demand less to allow more implementations in Sect. 3.5. The laws for
. Unbounded choice would be similar to countable choice. Their specification is similar to probabilities, but I demand less to allow more implementations in Sect. 3.5. The laws for
 are taken from Gibbons and Hinze [7].
are taken from Gibbons and Hinze [7].

Reader and writer monads The reader monad makes it possible to pass immutable data to (many) functions without threading the parameter through. For example, a security parameter in cryptography is typically hidden in pen-and-paper notation and a reader monad achieves the same in a formalisation. Environments, e.g., variable bindings, are also good candidates for a reader monad. The operation
 retrieves the data of type
retrieves the data of type
 .
.
The writer monad allows programs to output data in several steps using
 . Unlike updates in the state monad, outputs cannot be made undone. It is in particular suitable for logging.
. Unlike updates in the state monad, outputs cannot be made undone. It is in particular suitable for logging.
Resumption Resumptions provide a semantic domain for reactive and concurrent programs [9, 29]. The primitive operation
 interrupts a computation to output a value of type
interrupts a computation to output a value of type
 and waits for some input of type
and waits for some input of type
 before the computation resumes.
before the computation resumes.
3 Implementations of Monads and Monad Transformers
In the previous section, I specified the properties of monadic operations abstractly. Now, I provide monad implementations that satisfy these specifications. Some effects are implemented as monad transformers [20, 26], which allow me to compose implementations of different effects almost as modularly as the locales specifying them abstractly. In particular, I analyse whether the transformers preserve the specifications of the other effects. All implementations are polymorphic in the values such that they can be used with any value type, although by the value-monomorphism restriction, each usage must individually commit to one value type.
3.1 The Identity Monad
The simplest monad implementation in my library is the identity monad
 , which models the absence of all effects. It is not really useful in itself, but will be an important building block when combining monads using transformers. The datatype
, which models the absence of all effects. It is not really useful in itself, but will be an important building block when combining monads using transformers. The datatype
 is a copy of
is a copy of
 with constructor
with constructor
 and selector
and selector
 . To distinguish the abstract monad operations from their implementations, I subscript the latter with the implementation type. The lemma states that
. To distinguish the abstract monad operations from their implementations, I subscript the latter with the implementation type. The lemma states that
 satisfy the assumption of the locale
satisfy the assumption of the locale
 . Moreover, the identity monad is commutative, discardable, and duplicable.
. Moreover, the identity monad is commutative, discardable, and duplicable.

3.2 The Probability Monad
The probability monad
 is another basic building block. I use discrete probability distributions [11] and Giry’s probability monad operations
is another basic building block. I use discrete probability distributions [11] and Giry’s probability monad operations
 and
and
 , which I already used in the abstract specification in Sect. 2.3. Then, probabilistic choice
, which I already used in the abstract specification in Sect. 2.3. Then, probabilistic choice
 is just monadic sequencing on
is just monadic sequencing on
 . The probability monad is commutative and discardable.
. The probability monad is commutative and discardable.

3.3 The Failure and Exception Monad Transformer
Failures and exception handling are implemented as a monad transformer. Thus, these effects can be added to any monad
 . In the value-polymorphic setting, the failure monad transformer takes a monad
. In the value-polymorphic setting, the failure monad transformer takes a monad
 and defines a type constructor
and defines a type constructor
 such that
such that
 is isomorphic to
is isomorphic to
 . That is, the transformer specialises the value type
. That is, the transformer specialises the value type
 of the inner monad to
of the inner monad to
 . In the value-monomorphic setting, the type variable
. In the value-monomorphic setting, the type variable
 represents the application of
represents the application of
 to the value type, i.e.,
to the value type, i.e.,
 . So,
. So,
 is just a copy of
is just a copy of
 :
:

As
 ’s operations depend on the inner monad, I fix abstract operations
’s operations depend on the inner monad, I fix abstract operations
 and
and
 in an unnamed context and define
in an unnamed context and define
 ’s operations in terms of them. The line on the left indicates the scope of the context. At the end, which is marked by
’s operations in terms of them. The line on the left indicates the scope of the context. At the end, which is marked by
 , the fixed operations become additional arguments of the defined functions. Values in the inner monad now have type
, the fixed operations become additional arguments of the defined functions. Values in the inner monad now have type
 . The definitions themselves are standard [26].
. The definitions themselves are standard [26].

If
 and
and
 form a monad, so do
form a monad, so do
 and
and
 , and
, and
 and
and
 satisfy the effect specification from Sect. 2.1, too. The next lemma expresses this.
satisfy the effect specification from Sect. 2.1, too. The next lemma expresses this.

The monad
 is
is
-
commutative if the inner monad
 is commutative and discardable;
is commutative and discardable; -
duplicable if
 is duplicable and discardable; and
is duplicable and discardable; and -
not discardable, e.g.,
 .
.
Clearly, I want to keep using the existing effects of the inner monad. So, I must lift their operations to
 and prove that their specifications are preserved. The lifting is not hard; the continuations of the operations are transformed in the same way as
and prove that their specifications are preserved. The lifting is not hard; the continuations of the operations are transformed in the same way as
 transforms its continuation. Here, I only show how to lift the state operations, where the locale
transforms its continuation. Here, I only show how to lift the state operations, where the locale
 extends
extends
 and
and
 with catch-get and catch-put. Moreover,
with catch-get and catch-put. Moreover,
 also lifts
also lifts
 ,
,
 ,
,
 ,
,
 ,
,
 , and
, and
 , preserving their specifications.
, preserving their specifications.

From now on, as the context scope has ended,
 take the inner monad’s operations
take the inner monad’s operations
 and
and
 as additional arguments. For example, I obtain a plain failure monad by applying
as additional arguments. For example, I obtain a plain failure monad by applying
 to
to
 . Interpreting the locale
. Interpreting the locale
 and
and
 yields an executable version of the interpreter
yields an executable version of the interpreter
 from Sect. 2.1, which I refer to as
from Sect. 2.1, which I refer to as
 . Then, Isabelle’s code generator and simplifier both evaluate
. Then, Isabelle’s code generator and simplifier both evaluate

to
 . Given some variable environment
. Given some variable environment
 ,Footnote 7 I obtain a textbook-style interpreter [27, Sect. 3.1.2] as
,Footnote 7 I obtain a textbook-style interpreter [27, Sect. 3.1.2] as
 .
.
3.4 The State Monad Transformer
The state monad transformer adds the effects of a state monad to some inner monad. The formalisation follows the same ideas as for
 , so I only mention the important points. The state monad transformer transforms a monad
, so I only mention the important points. The state monad transformer transforms a monad
 into the type
into the type
 where
where
 is the type of states. So, in HOL, the type of values of the inner monad becomes
is the type of states. So, in HOL, the type of values of the inner monad becomes
 and
and
 represents
represents
 .
.

Like for
 , the state monad operations
, the state monad operations
 and
and
 depend on inner monad operations
depend on inner monad operations
 and
and
 . With
. With
 and
and
 defined in the obvious way, the transformer satisfies the specification
defined in the obvious way, the transformer satisfies the specification
 for state monads.
for state monads.

The state monad transformer lifts the other effect operations
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 , and
, and
 according to their specifications. But
according to their specifications. But
 cannot be lifted through
cannot be lifted through
 such that catch-get and catch-put hold. As our exceptions carry no information, the inner monad cannot pass the state updates before the failure to the handler.
such that catch-get and catch-put hold. As our exceptions carry no information, the inner monad cannot pass the state updates before the failure to the handler.
3.5 The Non-determinism Transformers
Non-determinism can be modelled by a collection type like lists, multisets, and sets. Thanks to value monomorphism, I can abstract over the collection type and provide one generic implementation. Later, I will obtain four implementations based on finite lists, finite multisets, finite sets, and countable sets by instantiation. Being finite, the first three only support binary non-deterministic choice
 , whereas countable sets additionally implement countable choice
, whereas countable sets additionally implement countable choice
 . Moreover, they all have an “empty” value—the empty list or (multi-)set—which can model failure. All implementations therefore provide a
. Moreover, they all have an “empty” value—the empty list or (multi-)set—which can model failure. All implementations therefore provide a
 operation, which is the neutral element for nondeterministic choice:
operation, which is the neutral element for nondeterministic choice:
 . As I will discuss below, the different collection types impose different requirements on the inner monad.
. As I will discuss below, the different collection types impose different requirements on the inner monad.
The generic non-determinism transformer
 changes the inner monad’s value type from
changes the inner monad’s value type from
 to a collection of
to a collection of
 , which I model by the type variable
, which I model by the type variable
 . Thus, the inner monad’s
. Thus, the inner monad’s
 operation has type
operation has type
 and
and
 has type
has type
 . Similar to the other monad transformers, the
. Similar to the other monad transformers, the
 operation must first swap the inner monad constructor with the collection type constructor such that it can use the inner monad’s
operation must first swap the inner monad constructor with the collection type constructor such that it can use the inner monad’s
 operation. In my monomorphic setting, I model the swap as a
operation. In my monomorphic setting, I model the swap as a
 operation with type
operation with type
 . It takes a collection
. It takes a collection
 of values and a family
of values and a family
 of non-deterministic computations indexed by
of non-deterministic computations indexed by
 and merges all their effects and values into one computation. Moreover, I also need operations
and merges all their effects and values into one computation. Moreover, I also need operations
 ,
,
 , and
, and
 (written infix as
(written infix as
 ) to construct collections, as I have abstracted over the concrete type. The locale
) to construct collections, as I have abstracted over the concrete type. The locale
 captures these operations and their properties:
captures these operations and their properties:
-
The inner monad must be commutative (extension of the locale
 ).
). -
The second argument to
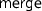 plays a role similar to the continuation arguments of other effect operations like
plays a role similar to the continuation arguments of other effect operations like
 and
and
 . Therefore,
. Therefore,
 must respect the monad laws (merge-bind and merge-return).
must respect the monad laws (merge-bind and merge-return). -
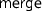 combines the effects of a computation family as expected for the collection operations (merge-empty, merge-single, merge-union).
combines the effects of a computation family as expected for the collection operations (merge-empty, merge-single, merge-union). -
The collection operations form a monoid, i.e.,
 is associative and
is associative and
 the neutral element (monoid).
the neutral element (monoid).

I can now implement the monad operations for the non-determinism transformer for binary choice. Commutativity of the inner monad is needed only for alt-bind.

Most other effect operations lift through
 as usual, except for
as usual, except for
 and
and
 . As
. As
 absorbs
absorbs
 , failures cannot be caught. For
, failures cannot be caught. For
 , bind-sample\(_2\) cannot be preserved: on the left-hand side, sampling from
, bind-sample\(_2\) cannot be preserved: on the left-hand side, sampling from
 is done independently for every possible result of
is done independently for every possible result of
 whereas on the right-hand side, the same sample
whereas on the right-hand side, the same sample
 is used for all of
is used for all of
 ’s results.
’s results.
Countable choice
 requires a bit more. Ideally, we could use
requires a bit more. Ideally, we could use
 to combine all the effects of countable choice, but the monomorphism restriction does not allow this:
to combine all the effects of countable choice, but the monomorphism restriction does not allow this:
 combines a family of computations indexed by a collection of values, whereas
combines a family of computations indexed by a collection of values, whereas
 must merge a family indexed by a countable set of choices. Like for probabilistic choices in Sect. 2.3, I do not want to unify the value type
must merge a family indexed by a countable set of choices. Like for probabilistic choices in Sect. 2.3, I do not want to unify the value type
 with the choice type
with the choice type
 . I therefore fix another operation
. I therefore fix another operation
 and its appropriate properties. Then, I get
and its appropriate properties. Then, I get

Like for probabilistic sampling in Sect. 2.3, binary choice
 can be expressed using countable choice
can be expressed using countable choice
 if the choice type
if the choice type
 contains at least three elements.
contains at least three elements.
I have instantiated the generic implementation for four collection types: finite lists, finite multisets, finite sets, and countable sets. The first three are similar: The operations
 and
and
 are obviously the empty and singleton list or (multi-)set, and
are obviously the empty and singleton list or (multi-)set, and
 is list concatenation or (multi-)set union. Since the three collection types are all finite,
is list concatenation or (multi-)set union. Since the three collection types are all finite,
 is implemented by folding binary choice over the collection, starting with
is implemented by folding binary choice over the collection, starting with
 as the neutral element. For lists, e.g., I define
as the neutral element. For lists, e.g., I define
 , where
, where
 and
and
 are the well-known functions on lists.
are the well-known functions on lists.
The requirements on the inner monad are as follows: Lists and multisets need a commutative monad, and finite sets need a commutative and duplicable monad. From a reasoning perspecitive, the list implementation is therefore inferior to multisets: they both require a commutative inner monad, but multisets satify more laws than lists. For example,
 is commutative, but
is commutative, but
 is not. Conversely, from a programming perspective, the lack of commutativity allows a programmer to specify preferences among the alternatives, which cannot be done with (multi-)sets.
is not. Conversely, from a programming perspective, the lack of commutativity allows a programmer to specify preferences among the alternatives, which cannot be done with (multi-)sets.
The finite set implementation is commutative if the inner monad is additionally discardable. Lists and multisets are not commutative for cardinality reasons. All implementations are neither discardable (because of
 ) nor duplicable (because choices need not be made consistently.)
) nor duplicable (because choices need not be made consistently.)
For countable sets, the inner monad must be commutative and duplicable. Yet, we cannot implement
 using the operations of the inner monad as there is no “limit” operation to deal with infinite sets. Instead, I treat
using the operations of the inner monad as there is no “limit” operation to deal with infinite sets. Instead, I treat
 like another effect operation that monads can implement and transformers lift. Among the implementations, only the identity monad from Sect. 3.1 and the reader and failure transformers from Sect. 3.7 and 3.3 meet the commutativity and duplicatibility requirement. I have implemented the merge operations only for the identity monad and the reader transformer. Lifting fails for the failure transformer because the failure operation from the non-determinism transformer is incompatible with failure from the failure transformer.
like another effect operation that monads can implement and transformers lift. Among the implementations, only the identity monad from Sect. 3.1 and the reader and failure transformers from Sect. 3.7 and 3.3 meet the commutativity and duplicatibility requirement. I have implemented the merge operations only for the identity monad and the reader transformer. Lifting fails for the failure transformer because the failure operation from the non-determinism transformer is incompatible with failure from the failure transformer.
3.6 Composing Monads with Transformers
Composing the two monad transformers
 and
and
 with the monad
with the monad
 , I can now instantiate the probabilistic interpreter from Sect. 2.4. As is well known, the order of composition matters. If I first apply
, I can now instantiate the probabilistic interpreter from Sect. 2.4. As is well known, the order of composition matters. If I first apply
 to
to
 and then
and then
 (
(
 for short), the resulting interpreter
for short), the resulting interpreter
 nests the result state of type
nests the result state of type
 inside the
inside the
 type for failures, i.e., failures do not return a new state. Thus, failures erase state updates, i.e.,
type for failures, i.e., failures do not return a new state. Thus, failures erase state updates, i.e.,
 , and lazy and eager sampling are equivalent (lazy-eager). Conversely, if I apply
, and lazy and eager sampling are equivalent (lazy-eager). Conversely, if I apply
 after
after
 to
to
 (
(
 for short), then
for short), then
 and failures do return a new state as only the result type
and failures do return a new state as only the result type
 sits inside
sits inside
 . In particular,
. In particular,
 in general, and lazy and eager sampling are not equivalent. I will consider the
in general, and lazy and eager sampling are not equivalent. I will consider the
 case further in Sect. 4.
case further in Sect. 4.
If we are interested in a non-deterministic rather than a probabilistic interpreter, then we can use the non-determinism monad transformer instead, say with countable choice. So let us compose countable choice
 and
and
 with the identity monad
with the identity monad
 for short; the order
for short; the order
 is not sensible as the non-determinism transformer should not be applied to a non-commutative state monad). Note that no failure transformer shows up in the composition as the non-determinism transformer already provides a failure operation. Failure therefore behaves differently from the probabilistic case. For example, I can define a lazy evaluator like in the probabilisitic case by using
is not sensible as the non-determinism transformer should not be applied to a non-commutative state monad). Note that no failure transformer shows up in the composition as the non-determinism transformer already provides a failure operation. Failure therefore behaves differently from the probabilistic case. For example, I can define a lazy evaluator like in the probabilisitic case by using
 instead of
instead of
 . Consider the expression
. Consider the expression
 . Running
. Running
 in the initial state
in the initial state
 with
with
 yields only one possible outcome
yields only one possible outcome
 , which results from choosing
, which results from choosing
 for
for
 . Choosing
. Choosing
 for
for
 results in a division by
results in a division by
 , i.e., a failure, and failures in
, i.e., a failure, and failures in
 are silently ignored. In contrast, in the
are silently ignored. In contrast, in the
 monad,
monad,
 with
with
 gives a uniform distribution over two outcomes: failure and
gives a uniform distribution over two outcomes: failure and
 . The
. The
 behaviour can be recovered by sandwiching a failure transformer between the state and non-determinism transformers (
behaviour can be recovered by sandwiching a failure transformer between the state and non-determinism transformers (
 ). Then,
). Then,
 also produces both outcomes, failure and
also produces both outcomes, failure and
 .
.
3.7 Further Monads and Monad Transformers
Apart from the monad implementations presented so far, my library provides implementations for the other types of effects mentioned in Sect. 2.6. In particular, I define a reader (
 ) and a writer monad transformer. The reader monad transformer differs from
) and a writer monad transformer. The reader monad transformer differs from
 only in that no updates are possible. Thus,
only in that no updates are possible. Thus,
 leaves the type of values of the inner monad unchanged, as no new state must be returned.
leaves the type of values of the inner monad unchanged, as no new state must be returned.

Resumptions are formalised as a plain monad using the codatatype

Unfortunately, I cannot define resumptions as a monad transformer in HOL despite the restriction to monomorphic values. The reason is that for a transformer with inner monad
 , the second argument of the constructor
, the second argument of the constructor
 would have to be of type
would have to be of type
 , i.e., the codatatype would recurse through the unspecified type constructor
, i.e., the codatatype would recurse through the unspecified type constructor
 . This is not supported by Isabelle’s codatatype package [3] and, in fact, for some choices of
. This is not supported by Isabelle’s codatatype package [3] and, in fact, for some choices of
 , e.g., unbounded nondeterminism, the resumption transformer type does not exist in HOL at all. For the same reason, we cannot have other monad transformers that have similar recursive implementation types. Therefore, I fail to modularly construct all combinations of effects. For example, probabilistic resumptions with failures [22] are out of reach and must still be constructed from scratch.
, e.g., unbounded nondeterminism, the resumption transformer type does not exist in HOL at all. For the same reason, we cannot have other monad transformers that have similar recursive implementation types. Therefore, I fail to modularly construct all combinations of effects. For example, probabilistic resumptions with failures [22] are out of reach and must still be constructed from scratch.
3.8 Overloading the Monad Operations
When several monad transformers are composed, the monad operations quickly become large HOL terms as the transformer’s operations take the inner monad’s as explicit arguments. These large terms must be handled by the inference kernel, the type checker, the parser, and the pretty-printer, even if locale interpretations hide them from the user using abbreviations. To improve readability and the processing time of Isabelle, my library also defines the operations as single constants which are overloaded for the different monad implementations using recursion on types [35]. As overloading does not need these explicit arguments, it avoids the processing times for unification, type checking, and (un)folding of abbreviations. Yet, Isabelle’s check against cyclic definitions [18] fails to see that the resulting dependencies must be acyclic (as the inner monad is always a type argument of the outer monad). So, I moved these overloaded definitions to a separate file and marked them as unchecked.Footnote 8 Overloading is just a syntactic convenience, on which the library and the examples in this paper do not rely. If users want to use it, they are responsible for not exploiting these unchecked dependencies.
4 Moving Between Monad Instances
Once all variables have been sampled eagerly, the evaluation of the expression itself is deterministic. Thus, the actual evaluation need not be done in a monad as complex as
 or
or
 . It suffices to work in a reader-failure monad with operations
. It suffices to work in a reader-failure monad with operations
 and
and
 , which I obtain by applying the monad transformers
, which I obtain by applying the monad transformers
 and
and
 to
to
 (
(
 for short). Such simpler monads have the advantage that reasoning becomes easier as more laws hold. I now explain how the theory of representation independence [25] can be used to move between different monad instances by going from
for short). Such simpler monads have the advantage that reasoning becomes easier as more laws hold. I now explain how the theory of representation independence [25] can be used to move between different monad instances by going from
 to
to
 . This ultimately yields a theorem that characterises
. This ultimately yields a theorem that characterises
 in terms of
in terms of
 . So, in general, this approach makes it possible to switch in the middle of a bigger proof from a complicated monad to a much simpler one.
. So, in general, this approach makes it possible to switch in the middle of a bigger proof from a complicated monad to a much simpler one.
Let me first deal with sampling. To go from
 to
to
 , I use a relation
, I use a relation
 between
between
 and
and
 since relations work better with higher-order functions than equations. Following Huffman and Kunčar [14], I call such a relation a correspondence relation.
since relations work better with higher-order functions than equations. Following Huffman and Kunčar [14], I call such a relation a correspondence relation.
 is parametrised by a relation
is parametrised by a relation
 between the values, which I will use later to express the differences in the values due to the monad transformers changing the value type of the inner monad. In detail,
between the values, which I will use later to express the differences in the values due to the monad transformers changing the value type of the inner monad. In detail,
 relates a value
relates a value
 to the one-point distribution
to the one-point distribution
 iff
iff
 relates
relates
 to
to
 . Then, the monad operations of
. Then, the monad operations of
 and
and
 respect this relation. Respectfulness is formalised using the function relator
respect this relation. Respectfulness is formalised using the function relator
 , which was already used in Sect. 2.3 for parametricity. The following two conditions express that the monad operations respect
, which was already used in Sect. 2.3 for parametricity. The following two conditions express that the monad operations respect
 :
:
-
 and
and -
 .
.
Note the similarity between the relations and the types of the monad operations, where
 and
and
 take the roles of the type variables for values and of the monad type constructor, respectively. As the monad transformers
take the roles of the type variables for values and of the monad type constructor, respectively. As the monad transformers
 and
and
 are relationally parametric in the inner monad and
are relationally parametric in the inner monad and
 is parametric in the monad, I prove the following relation between the evaluators automatically using Isabelle/HOL’s Transfer prover [14]
is parametric in the monad, I prove the following relation between the evaluators automatically using Isabelle/HOL’s Transfer prover [14]

where
 refers to the state-failure-identity composition of monads, and
refers to the state-failure-identity composition of monads, and
 and
and
 are the relators for the datatypes
are the relators for the datatypes
 and
and
 [3]. Formally, the relators lift relations on the inner monad to relations on the transformed monad. For example,
[3]. Formally, the relators lift relations on the inner monad to relations on the transformed monad. For example,
 iff
iff
 for all
for all
 , and
, and
 iff
iff
 . Intuitively, (4) states that in the monads SFP and SFI,
. Intuitively, (4) states that in the monads SFP and SFI,
 behaves the same with respect to states updates and failure and the results are the same; in particular, the evaluation is deterministic.
behaves the same with respect to states updates and failure and the results are the same; in particular, the evaluation is deterministic.
In the following, I use the property of a relator
 that if
that if
 is the graph
is the graph
 of a function
of a function
 , then
, then
 is the graph of the function
is the graph of the function
 , where
, where
 is the canonical map function for the relator. For example,
is the canonical map function for the relator. For example,
 , so
, so

where
 iff
iff
 . Isabelle’s datatype package automatically proves these relator-graph identities. The correspondence relation
. Isabelle’s datatype package automatically proves these relator-graph identities. The correspondence relation
 satisfies a similar law:
satisfies a similar law:
 where
where
 .
.
Having eliminated probabilities, I next switch from the state monad transformer to the reader monad transformer. I again define a correspondence relation
 between
between
 and
and
 . It takes as parameters the environment
. It takes as parameters the environment
 and the correspondence relation
and the correspondence relation
 between the inner monads. It relates the two monadic values
between the inner monads. It relates the two monadic values
 and
and
 iff
iff
 relates the results of running
relates the results of running
 and
and
 on
on
 , i.e.,
, i.e.,
 . Again, I show that the monad operations respect
. Again, I show that the monad operations respect
 as formalised below. As
as formalised below. As
 and
and
 are monad transformers, I assume that the operations of the inner monads respect
are monad transformers, I assume that the operations of the inner monads respect
 . These assumptions can be expressed using
. These assumptions can be expressed using
 since the inner operations are arguments to
since the inner operations are arguments to
 ’s and
’s and
 ’s operations. Here,
’s operations. Here,
 adapts the relation
adapts the relation
 on values to
on values to
 ’s change of the value type from
’s change of the value type from
 to
to
 ;
;
 iff
iff
 and
and
 , i.e.,
, i.e.,
 relates the results and the state is not updated.
relates the results and the state is not updated.
-
 ,
, -
 ,
, -
 , and
, and -
 ,
,
Then, by representation independence, the Transfer package automatically proves the following relation between
 and
and
 , where
, where
 uses
uses
 instead of
instead of
 , and
, and
 and
and
 are the relators for the datatypes
are the relators for the datatypes
 and
and
 .
.

This says that running
 in RFI and SFI computes the same result, has the same behaviour with respect to state queries and failures, and does not update the state.
in RFI and SFI computes the same result, has the same behaviour with respect to state queries and failures, and does not update the state.
Actually, I can go from
 directly to
directly to
 , without the monad
, without the monad
 as a stepping stone, thanks to
as a stepping stone, thanks to
 taking a relation on the value types:
taking a relation on the value types:

As
 is the graph of
is the graph of
 , using only the graph properties like (5) of
, using only the graph properties like (5) of
 and the relators, and using
and the relators, and using
 ’s definition, I derive the characterisation of
’s definition, I derive the characterisation of
 from (6):
from (6):

where
 and
and
 are the canonical map functions for
are the canonical map functions for
 and
and
 . Thus, instead of reasoning about
. Thus, instead of reasoning about
 in
in
 , I can conduct the proofs in the simpler monad
, I can conduct the proofs in the simpler monad
 . For example, as
. For example, as
 is commutative, subexpressions can be evaluated in any order. Thus, I get the following identity expressing the reversed evaluation order (and a similar one for
is commutative, subexpressions can be evaluated in any order. Thus, I get the following identity expressing the reversed evaluation order (and a similar one for
 .Footnote 9
.Footnote 9

In summary, I have demonstrated a generic approach to switch from a complicated monad to a much simpler one. Conceptually, the correspondence relations
 and
and
 just embed one monad or monad transformer (
just embed one monad or monad transformer (
 and
and
 ) in a richer one (
) in a richer one (
 and
and
 ). It is precisely this embedding that ultimately yields the
). It is precisely this embedding that ultimately yields the
 functions in the characterisation. In this functional view, the respectfulness conditions express that the embedding is a monad homomorphism. Yet, I use relations for the embedding instead of functions because only relations work for higher-order operations in a compositional way.
functions in the characterisation. In this functional view, the respectfulness conditions express that the embedding is a monad homomorphism. Yet, I use relations for the embedding instead of functions because only relations work for higher-order operations in a compositional way.
The reader may wonder why I go through all the trouble of defining correspondence relations and showing respectfulness and parametricity. Indeed, in this example, it would probably have been easier to simply perform an induction over expressions and prove the equation directly. The advantage of my approach is that it does not rely on the concrete definition of
 . It suffices to know that
. It suffices to know that
 is parametric in the monad, which Isabelle derives automatically from the definition. This automated approach therefore scales to arbitrarily complicated monadic functions whereas induction proofs do not. Moreover, note that the correspondence relations and respectfulness lemmas only depend on the monads. They can therefore be reused for other monadic functions.
is parametric in the monad, which Isabelle derives automatically from the definition. This automated approach therefore scales to arbitrarily complicated monadic functions whereas induction proofs do not. Moreover, note that the correspondence relations and respectfulness lemmas only depend on the monads. They can therefore be reused for other monadic functions.
5 Related Work
Huffman et al. [13, 15] formalise the concept of value-polymorphic monads and several monad transformers in Isabelle/HOLCF, the domain theory library of Isabelle/HOL. They circumvent HOL’s type system restrictions by projecting everything into HOLCF’s universal domain of computable values. That is, they trade in HOL’s set-theoretic model with its simple reasoning rules for a domain-theoretic model with ubiquituous \(\bot \) values and strictness side conditions. This way, they can define a resumption monad transformer (for computable continuations). Being tied to domain theory, their library cannot be used to model effects of plain HOL functions, which is my goal, the strictness assumptions make their laws and proofs more complicated than mine, and functions defined with HOLCF do not work with Isabelle’s code generator. Still, their idea of projecting everything into a universal type could also be adapted to plain HOL, albeit only for a restricted class of monads; achieving a similar level of automation and modularity would require a lot more effort than my approach, which uses only existing Isabelle features.
Gibbons and Hinze [7] axiomatize monads and effects using Haskell-style type constructor classes and use the algebraic specification to prove identities between Haskell programs, similar to my abstract locales in Sect. 2. Their specification of state effects omits get-const, but they later assume that it holds [7, Sect. 10.2]. Being value-polymorphic, their operations do not need my continuations and the laws are therefore simpler. In particular, no new assumptions are typically needed when monad specifications are combined. In contrast, my continuations sometimes require interaction assumptions like sample-get. Gibbons and Hinze only consider reasoning in the abstract setting and do not discuss the transition to concrete implementations and the relations between implementations. Also, they do not prove that monad implementations satisfy their specifications. Later, Jeuring et al. [17] showed that the implementations in Haskell do not satisfy them because of strictness issues similar to the ones in Huffman’s work.
Lobo Vesga [21] formalised some of Gibbons’ and Hinze’s examples in Agda. She does not need assumptions for the continuations like I do as value-polymorphic monads can be directly expressed in Agda. Like Gibbons and Hinze, she does not study the connection between specifications and implementations. Thanks to the good proof automation in Isabelle, my mechanised proofs are much shorter than hers, which are as detailed as Gibbons’ and Hinze’s pen-and-paper proofs.
Lochbihler and Schneider [24] implemented support for equational reasoning about applicative functors, which are more general than monads. They focus on lifting identities on values to a concrete applicative functor. Reasoning with abstract applicative functors is not supported. Like monads, the concept of an applicative functor cannot be expressed as a predicate in HOL. Moreover, the applicative operations do not admit value monomorphisation like monads do, as the type of
 contains applications of the functor type constructor
contains applications of the functor type constructor
 to
to
 ,
,
 , and
, and
 .Footnote 10 So, monads seem to be the right choice, even though I could have defined the interpreter
.Footnote 10 So, monads seem to be the right choice, even though I could have defined the interpreter
 applicatively (but not, e.g., memoisation).
applicatively (but not, e.g., memoisation).
Grimm et al. [8] model several effects and their combinations in the dependently typed logic of F* to reason about various effectful programs. They need not choose between effect and value polymorphism thanks to F*’s richer logic. Like me, they model monads for probabilities, state, exceptions, and the reader monad, and study among others the memoization problem and an interpreter. They also discuss how they can switch from a reader monad to a state monad. Yet, their definitions do not achieve my level of modularity in two respects: First, the type annotation of an F* function fixes the monad implementation whereas my approach with locales can leave the implementation abstract. Second, they define a new monad for every effect combination whereas I combine effects modularly thanks to monad transformers.
Wimmer et al. [36] propose a tool to automatically memoize pure recursive functions using a state monad similar to my
 function. They use similar ideas of relational parametricity (Sect. 4) to prove the monadification step correct. However, their memoization function only works in a concrete state monad and only for pure functions; other effects like probabilistic choice and non-determinism are not yet supported.
function. They use similar ideas of relational parametricity (Sect. 4) to prove the monadification step correct. However, their memoization function only works in a concrete state monad and only for pure functions; other effects like probabilistic choice and non-determinism are not yet supported.
6 Conclusion
I have presented a library of abstract monadic effect specifications and their implementations as monads and monad transformers in Isabelle/HOL. I illustrated its usage and the elegance of reasoning using a monadic interpreter. The type system of HOL forced me to restrict the monads to monomorphic values. Monomorphic values work well when the reasoning involves only a few monadic functions like in the running example. In larger projects, this restriction can become a limiting factor. Nevertheless, in a project on formalising computational soundness results,Footnote 11 I successfully formalised and reasoned about several complicated serialisers and parsers for symbolic messages of security protocols. In that work, reasoning abstractly about effects and being able to move from one monad instance to another were crucial. For example, the serialiser converts symbolic protocol messages into bitstrings. The challenges were similar to those of the interpreter
 . Serialisation may fail when the symbolic message is not well-formed, similar to division by zero in the interpreter. When serialisation encounters a new nonce, it randomly samples a fresh bitstring, which must also be used for serialising further occurrences of the same nonce. I formalised this similar to the memoisation of variable evaluation in the interpreter. A further challenge not present in the interpreter was that the serialiser must also record the serialisation of all subexpressions such that the parser can map bitstrings generated by the serialiser back to symbolic messages without calling a decryption oracle or inverting a cryptographic hash function. The construction relied on the invariant that the recorded values were indeed generated by the serialiser, but such an invariant cannot be expressed easily for a probabilistic, stateful function. I therefore formalised also the switch from lazy to eager sampling for the serialiser (lazy sampling was needed to push the randomisation of encryptions into an encryption oracle) and the switch to a read-only version without recording of results using techniques similar to the example in Sect. 4.
. Serialisation may fail when the symbolic message is not well-formed, similar to division by zero in the interpreter. When serialisation encounters a new nonce, it randomly samples a fresh bitstring, which must also be used for serialising further occurrences of the same nonce. I formalised this similar to the memoisation of variable evaluation in the interpreter. A further challenge not present in the interpreter was that the serialiser must also record the serialisation of all subexpressions such that the parser can map bitstrings generated by the serialiser back to symbolic messages without calling a decryption oracle or inverting a cryptographic hash function. The construction relied on the invariant that the recorded values were indeed generated by the serialiser, but such an invariant cannot be expressed easily for a probabilistic, stateful function. I therefore formalised also the switch from lazy to eager sampling for the serialiser (lazy sampling was needed to push the randomisation of encryptions into an encryption oracle) and the switch to a read-only version without recording of results using techniques similar to the example in Sect. 4.
Instead of specifying effects abstractly and composing them using monad transformers, I obviously could have formalised everything in a sufficiently rich monad that covers all the effects of interest, e.g., continuations. Then, there would be no need for abstract specifications as I could work directly with a concrete monad as usual, where my reasoning on the abstract level could be mimicked. But I would deprive myself of the option of going to a specific monad that covers precisely the effects needed. Such specialisation has two advantages: First, as shown in Sect. 4, simpler monads satisfy more laws, e.g., commutativity, which make the proofs easier. Second, concrete monads can have dedicated setups for reasoning and proof automation that are not available in the abstract setting. My library achieves the best of both worlds. I can reason abstractly and thus achieve generality. When this gets too cumbersome or impossible, I can switch to a concrete monad, continuing to use the abstract properties already proven.
In the long run, I can imagine a definitional package for monads and monad transformers that composes concrete value-polymorphic monad transformers. Similar to how Isabelle’s datatype package composes bounded natural functors [3], such a package must perform the construction and the derivation of all laws afresh for every concrete combination of monads, as value-polymorphic monads lie beyond HOL’s expressiveness. When combined with a reinterpretation framework for theories, I could model effects and reason about them abstractly and concretely without the restriction to monomorphic values.
Notes
Available in the Archive of Formal Proofs at https://www.isa-afp.org/entries/Monomorphic_Monad.html.
Type variables that appear in the signature of locale parameters are fixed for the whole locale. In particular, the value type
 cannot be instantiated inside the locale
cannot be instantiated inside the locale
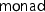 or its extension
or its extension
 . The interpreter
. The interpreter
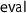 , however, returns
, however, returns
 s. For this reason,
s. For this reason,
 is defined in an extension of
is defined in an extension of
 that merely specialises
that merely specialises
 to
to
 . For readability, I usually omit this detail in this article.
. For readability, I usually omit this detail in this article.Continuation parameters like
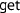 ’s and
’s and
 ’s make it possible to circumvent the restriction to monomorphic values. More generally, if we made every definition take a continuation, like in continuation-passing style, we would regain value polymorphism. In doing so, we would however lose that sequencing of computations and control flow is captured by a small number of (primitive) operations. Instead, every definition could implement arbitrary control flow, like in a continuation monad. Thus, we would need a lot more lemmas to reason about sequencing. In a commutative monad, e.g., one commutativity lemma would be needed for every pair of definitions. In contrast, my approach needs just one assumption comm to express commutativity of sequencing (Sect. 2.5), and a few assumptions about the primitive operations, e.g., sample-comm (Sect. 2.3).
’s make it possible to circumvent the restriction to monomorphic values. More generally, if we made every definition take a continuation, like in continuation-passing style, we would regain value polymorphism. In doing so, we would however lose that sequencing of computations and control flow is captured by a small number of (primitive) operations. Instead, every definition could implement arbitrary control flow, like in a continuation monad. Thus, we would need a lot more lemmas to reason about sequencing. In a commutative monad, e.g., one commutativity lemma would be needed for every pair of definitions. In contrast, my approach needs just one assumption comm to express commutativity of sequencing (Sect. 2.5), and a few assumptions about the primitive operations, e.g., sample-comm (Sect. 2.3).In my monad implementations in Sect. 3, sampling is relationally parametric for arbitrary relations
 , so I could drop the restriction
, so I could drop the restriction
 . However, this would unnecessarily exclude some other implementations as all my abstract proofs so far used only
. However, this would unnecessarily exclude some other implementations as all my abstract proofs so far used only
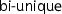 relations.
relations.The support of
 is the set of elementary events with positive probability:
is the set of elementary events with positive probability:
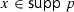 iff
iff

The conference paper [23] demanded sample-cong instead of sample-param. Parametricity is a better condition as it allows us to rename choices like in the biased coin flip example above.
Such environments can be nicely handled by adding a reader monad transformer (Sect. 4).
Isabelle’s
 feature, which resolves overloading during type checking, cannot be used either as it does not support recursive resolutions. For example, resolving
feature, which resolves overloading during type checking, cannot be used either as it does not support recursive resolutions. For example, resolving
 takes two steps: first to
takes two steps: first to
 and then to
and then to
 . The second step fails due to the intricate interleaving of type checking and resolution. Even if this is just an implementation issue, resolving overloading during type checking prevents definitions that are generic in the monad, which general overloading supports.
. The second step fails due to the intricate interleaving of type checking and resolution. Even if this is just an implementation issue, resolving overloading during type checking prevents definitions that are generic in the monad, which general overloading supports.Following the “as abstract as possible” spirit of this paper, I actually proved the identities in the locale of commutative monads and showed that
 is commutative if its inner monad is.
is commutative if its inner monad is.The alternative applicative interface [16] with the operator
 is amenable to monomorphisation if we restrict ourselves to infinite value types
is amenable to monomorphisation if we restrict ourselves to infinite value types
 as then
as then
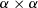 is isomorphic to
is isomorphic to
 . This interface is tailored towards a first-order language [10]. So functions must be uncurried and their arguments encoded using the isomorphism. We would thus clutter the definitions and proofs with conversions and lose the benefits of built-in higher-order unification.
. This interface is tailored towards a first-order language [10]. So functions must be uncurried and their arguments encoded using the isomorphism. We would thus clutter the definitions and proofs with conversions and lose the benefits of built-in higher-order unification.
References
Back, R.J., Wright, J.: Refinement Calculus—A Systematic Introduction. Springer, Berlin (1998)
Ballarin, C.: Locales: a module system for mathematical theories. J. Autom. Reason. 52(2), 123–153 (2014). https://doi.org/10.1007/s10817-013-9284-7
Blanchette, J.C., Hölzl, J., Lochbihler, A., Panny, L., Popescu, A., Traytel, D.: Truly modular (co)datatypes for Isabelle/HOL. In: ITP 2014. LNCS, vol. 8558, pp. 93–110. Springer (2014)
Bulwahn, L., Krauss, A., Haftmann, F., Erkök, L., Matthews, J.: Imperative functional programming with Isabelle/HOL. In: TPHOLs 2008. LNCS, vol. 5170, pp. 134–149. Springer (2008). https://doi.org/10.1007/978-3-540-71067-7_14
Eberl, M., Hölzl, J., Nipkow, T.: A verified compiler for probability density functions. In: Vitek, J. (ed.) ESOP 2015. LNCS, vol. 9032, pp. 80–104. Springer (2015). https://doi.org/10.1007/978-3-662-46669-8_4
Erwig, M., Kollmansberger, S.: Functional pearls: probabilistic functional programming in Haskell. J Funct Program 16, 21–34 (2006). https://doi.org/10.1017/S0956796805005721
Gibbons, J., Hinze, R.: Just do it: simple monadic equational reasoning. In: ICFP 2011, pp. 2–14. ACM (2011). https://doi.org/10.1145/2034773.2034777
Grimm, N., Maillard, K., Fournet, C., Hriţcu, C., Maffei, M., Protzenko, J., Ramananandro, T., Rastogi, A., Swamy, N., Zanella Béguelin, S.: A monadic framework for relational verification: applied to information security, program equivalence, and optimizations. In: CPP 2018, pp. 130–145. ACM (2018). https://doi.org/10.1145/3167090
Harrison, W.L.: The essence of multitasking. In: Johnson, M., Vene, V. (eds.) Algebraic Methodology and Software Technology (AMAST 2006). LNCS, vol. 4019, pp. 158–172. Springer (2006). https://doi.org/10.1007/11784180_14
Hinze, R.: Lifting operators and laws. http://www.cs.ox.ac.uk/ralf.hinze/Lifting.pdf. Accessed 12 June 2018 (2010)
Hölzl, J., Lochbihler, A., Traytel, D.: A formalized hierarchy of probabilistic system types. In: ITP 2015. LNCS, vol. 9236, pp. 203–220. Springer (2015). https://doi.org/10.1007/978-3-319-22102-1_13
Homeier, P.V.: The HOL-Omega logic. In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 244–259. Springer (2009). https://doi.org/10.1007/978-3-642-03359-9_18
Huffman, B.: Formal verification of monad transformers. In: ICFP 2012, pp. 15–16. ACM (2012). https://doi.org/10.1145/2364527.2364532
Huffman, B., Kunčar, O.: Lifting and Transfer: a modular design for quotients in Isabelle/HOL. In: CPP 2013. LNCS, vol. 8307, pp. 131–146. Springer (2013). https://doi.org/10.1007/978-3-319-03545-1_9
Huffman, B., Matthews, J., White, P.: Axiomatic constructor classes in Isabelle/HOLCF. In: Hurd, J., Melham, T. (eds.) TPHOLs. LNCS, vol. 3603, pp. 147–162. Springer (2005). https://doi.org/10.1007/11541868_10
Hutton, G.: Higher-order functions for parsing. J. Funct. Program. 2(3), 323–343 (1992)
Jeuring, J., Jansson, P., Amaral, C.: Testing type class laws. In: Haskell 2012, pp. 49–60. ACM (2012). https://doi.org/10.1145/2364506.2364514
Kunčar, O.: Correctness of Isabelle’s cyclicity checker: implementability of overloading in proof assistants. In: CPP 2015, pp. 85–94. ACM (2015). https://doi.org/10.1145/2676724.2693175
Lammich, P., Tuerk, T.: Applying data refinement for monadic programs to Hopcroft’s algorithm. In: ITP 2012. LNCS, vol. 7406, pp. 166–182. Springer (2012). https://doi.org/10.1007/978-3-642-32347-8_12
Liang, S., Hudak, P., Jones, M.: Monad transformers and modular interpreters. In: POPL 1995, pp. 333–343. ACM (1995). https://doi.org/10.1145/199448.199528
Lobo Vesga, E.: Hacia la formalización del razonamiento ecuacional sobre mónadas. Technical report, Universidad EAFIT (2013). http://hdl.handle.net/10784/4554
Lochbihler, A.: Probabilistic functions and cryptographic oracles in higher order logic. In: Thiemann, P. (ed.) ESOP. LNCS, vol. 9632, pp. 503–531. Springer (2016). https://doi.org/10.1007/978-3-662-49498-1_20
Lochbihler, A.: Effect polymorphism in higher-order logic (proof pearl). In: Ayala-Rincón, M., Muñoz, C.A. (eds.) Interactive Theorem Proving (ITP 2017), vol. 10499, pp. 389–409. Springer (2017). https://doi.org/10.1007/978-3-319-66107-0_25
Lochbihler, A., Schneider, J.: Equational reasoning with applicative functors. In: Blanchette, J.C., Merz, S. (eds.) ITP 2016. LNCS, vol. 9807, pp. 252–273. Springer (2016). https://doi.org/10.1007/978-3-319-43144-4_16
Mitchell, J.C.: Representation independence and data abstraction. In: POPL 1986, pp. 263–276. ACM (1986). https://doi.org/10.1145/512644.512669
Moggi, E.: An abstract view of programming languages. Technical report ECS-LFCS-90-113, LFCS, School of Informatics, University of Edinburgh (1990)
Nipkow, T., Klein, G.: Concrete semantics. Springer, Berlin (2014). https://doi.org/10.1007/978-3-319-10542-0
Nipkow, T., Paulson, L.C.: Proof pearl: defining functions over finite sets. In: Hurd, J., Melham, T. (eds.) TPHOLs 2005. LNCS, vol. 3603, pp. 385–396. Springer (2005)
Piróg, M., Gibbons, J.: The coinductive resumption monad. In: Mathematical Foundations of Programming Semantics (MFPS 2014). ENTCS, vol. 308, pp. 273–288 (2014). https://doi.org/10.1016/j.entcs.2014.10.015
Ramsey, N., Pfeffer, A.: Stochastic lambda calculus and monads of probability distributions. In: POPL 2002, pp. 154–165. ACM (2002). https://doi.org/10.1145/503272.503288
Reynolds, J.C.: Types, abstraction and parametric polymorphism. In: IFIP 1983. Information Processing, vol. 83, pp. 513–523. North-Holland/IFIP (1983)
Sternagel, C., Thiemann, R.: A framework for developing stand-alone certifiers. In: Ayala-Rincón, M., Mackie, I. (eds.) Logical and Semantic Frameworks with Applications (LSFA 2014), vol. 312, pp. 51–67. ENTCS (2015). https://doi.org/10.1016/j.entcs.2015.04.004
Wadler, P.: How to replace failure by a list of successes: a method for exception handling, backtracking, and pattern matching in lazy functional languages. In: Jouannaud, J.P. (ed.) Functional Programming Languages and Computer Architecture (FPCA 1985). LNCS, vol. 201, pp. 113–128. Springer (1985). https://doi.org/10.1007/3-540-15975-4_33
Wadler, P.: Monads for functional programming. In: Jeuring, J., Meijer, E. (eds.) Advanced Functional Programming. LNCS, vol. 925, pp. 24–52. Springer (1995). https://doi.org/10.1007/3-540-59451-5_2
Wenzel, M.: Type classes and overloading in higher-order logic. In: Gunter, E.L., Felty, A. (eds.) TPHOLs 1997. LNCS, vol. 1275, pp. 307–322. Springer (1997). https://doi.org/10.1007/BFb0028402
Wimmer, S., Hu, S., Nipkow, T.: Verified memoization and dynamic programming. In: Avigad, J., Mahboubi, A. (eds.) Interactive theorem proving. ITP 2018. LNCS, vol. 10895, pp. 579–596. Springer, Cham (2018)
Acknowledgements
I thank Dmitriy Traytel and the anonymous reviewers for suggesting many improvements to the presentation. This work is supported by the Swiss National Science Foundation Grant 153217 “Formalising Computational Soundness for Protocol Implementations”.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article extends the conference version presented at Interactive Theorem Proving 2017 [23]. Most of this work was done while the author was at the Institute of Information Security at ETH Zurich, Zurich, Switzerland.
Appendix A: Step-By-Step Proof of Lemma memo-idem
Appendix A: Step-By-Step Proof of Lemma memo-idem
Proof
First, I prove that updating the table of memoised calls is idempotent. Let
 . Then,
. Then,
 holds:
holds:

Next, let

Then,

Rights and permissions
About this article
Cite this article
Lochbihler, A. Effect Polymorphism in Higher-Order Logic (Proof Pearl). J Autom Reasoning 63, 439–462 (2019). https://doi.org/10.1007/s10817-018-9476-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10817-018-9476-2





 has no effect (sample-dirac),
has no effect (sample-dirac),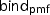 in the probability monad yields sequencing (
in the probability monad yields sequencing ( (
( is a relation between the choices, where the condition
is a relation between the choices, where the condition
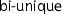 expresses that
expresses that
 relates each choice with at most one choice, i.e.,
relates each choice with at most one choice, i.e.,
 does not identify choices;
does not identify choices; lifts a relation on elementary events to probability distributions:
lifts a relation on elementary events to probability distributions:
 iff
iff
 for all
for all
 , where
, where
 denotes the probability of the event
denotes the probability of the event
 under the distribution
under the distribution
 ;
; relates two functions
relates two functions
 and
and
 iff
iff
 implies
implies
 for all
for all
 and
and
 ; and
; and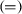 denotes the identity relation.
denotes the identity relation. is commutative and discardable;
is commutative and discardable; is duplicable and discardable; and
is duplicable and discardable; and .
. ).
).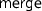 plays a role similar to the continuation arguments of other effect operations like
plays a role similar to the continuation arguments of other effect operations like
 and
and
 . Therefore,
. Therefore,
 must respect the monad laws (
must respect the monad laws (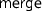 combines the effects of a computation family as expected for the collection operations (
combines the effects of a computation family as expected for the collection operations ( is associative and
is associative and
 the neutral element (
the neutral element ( and
and .
. ,
, ,
, , and
, and ,
, cannot be instantiated inside the locale
cannot be instantiated inside the locale
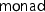 or its extension
or its extension
 . The interpreter
. The interpreter
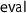 , however, returns
, however, returns
 s. For this reason,
s. For this reason,
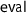 is defined in an extension of
is defined in an extension of
 that merely specialises
that merely specialises
 to
to
 . For readability, I usually omit this detail in this article.
. For readability, I usually omit this detail in this article.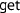 ’s and
’s and
 ’s make it possible to circumvent the restriction to monomorphic values. More generally, if we made every definition take a continuation, like in continuation-passing style, we would regain value polymorphism. In doing so, we would however lose that sequencing of computations and control flow is captured by a small number of (primitive) operations. Instead, every definition could implement arbitrary control flow, like in a continuation monad. Thus, we would need a lot more lemmas to reason about sequencing. In a commutative monad, e.g., one commutativity lemma would be needed for every pair of definitions. In contrast, my approach needs just one assumption
’s make it possible to circumvent the restriction to monomorphic values. More generally, if we made every definition take a continuation, like in continuation-passing style, we would regain value polymorphism. In doing so, we would however lose that sequencing of computations and control flow is captured by a small number of (primitive) operations. Instead, every definition could implement arbitrary control flow, like in a continuation monad. Thus, we would need a lot more lemmas to reason about sequencing. In a commutative monad, e.g., one commutativity lemma would be needed for every pair of definitions. In contrast, my approach needs just one assumption  , so I could drop the restriction
, so I could drop the restriction
 . However, this would unnecessarily exclude some other implementations as all my abstract proofs so far used only
. However, this would unnecessarily exclude some other implementations as all my abstract proofs so far used only
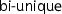 relations.
relations. is the set of elementary events with positive probability:
is the set of elementary events with positive probability:
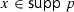 iff
iff

 feature, which resolves overloading during type checking, cannot be used either as it does not support recursive resolutions. For example, resolving
feature, which resolves overloading during type checking, cannot be used either as it does not support recursive resolutions. For example, resolving
 takes two steps: first to
takes two steps: first to
 and then to
and then to
 . The second step fails due to the intricate interleaving of type checking and resolution. Even if this is just an implementation issue, resolving overloading during type checking prevents definitions that are generic in the monad, which general overloading supports.
. The second step fails due to the intricate interleaving of type checking and resolution. Even if this is just an implementation issue, resolving overloading during type checking prevents definitions that are generic in the monad, which general overloading supports. is commutative if its inner monad is.
is commutative if its inner monad is. is amenable to monomorphisation if we restrict ourselves to infinite value types
is amenable to monomorphisation if we restrict ourselves to infinite value types
 as then
as then
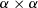 is isomorphic to
is isomorphic to
 . This interface is tailored towards a first-order language [
. This interface is tailored towards a first-order language [