Examples of unit tax superiority for a price-discriminating monopolist

Abstract

This paper compares the welfare effects of per-unit and ad valorem taxes in four pervasive price discrimination schemes: quantity discounts, two-part tariffs, bundling, and package size price discrimination. The paper shows by example that per-unit taxes may welfare dominate ad valorem tariffs in a market with a monopoly that maximizes profits by engaging in second-degree price discrimination.

1 Introduction

“No taxes can be devised which are not more or less inconvenient and unpleasant.”¹ Over 200 years later, George Washington’s words remain true. But the degree of inconvenience and unpleasantness for the citizen, the disruption to the market, and the revenue accrued by the government can and do change depending on the type of tax implemented. For this reason, the comparison of per-unit and ad valorem taxes has a long tradition in the literature.

In practice, since per-unit taxes are computed based on the quantity sold, they are recommended as ‘sin taxes’ to discourage or punish the consumption of goods like alcohol, cigarettes, or other activities with negative externalities; see, for example Dröge and Schröder (2009). Nevertheless, ad valorem taxes are more widely used because of their practical advantages over unitary taxes. Ad valorem taxes adjust automatically for inflation and do not need continual review, a feature that reduces administration costs. They also can be levied easily on all kinds of products, which is not the case for per-unit taxes. This happens, for example, when quantities are difficult to determine with certainty, or when quality differences between units of the same product make it impossible to treat them equally.

The literature has shown that, in perfectly competitive markets, both taxes are equivalent in terms of output and tax revenue. In a monopoly selling a homogeneous product at a single price for any given per-unit tax, there always exists an ad valorem tax rate which is Pareto superior, as shown for example by Skeath and Trandel (1994).

In this paper, we consider how both taxing systems compare when a monopoly uses price discrimination. Price discrimination is a prevalent practice, whenever the law authorizes it and practical considerations make it feasible, because it allows monopolies to capture a greater part of the consumer’s surplus and can also be used as an entry deterrence mechanism. The great appeal of price discrimination for the industry means that it cannot be ignored when designing taxes for monopolies. In other words, the welfare comparison of ad valorem and unitary taxes in the presence of price discrimination is an important issue because, as (Varian 1989, p. 646) affirms, “[p]rice discrimination is a ubiquitous phenomenon. Nearly all firms with market power attempt to engage in some type of price discrimination.”

In particular, we test whether the accepted superiority of ad valorem taxes holds in a partial equilibrium framework with no externalities; we consider monopolies that engage in second-degree price discrimination. Instead of looking at any theoretical price discrimination, we examine four types of discrimination which are commonly used by monopolies: bundling, two-part tariffs, bulk discounts, and package size price discrimination.

Cheung (1998) concluded that ad valorem taxation is superior to per-unit taxes regardless of the pricing policy considered in all three types of Pigouvian price discrimination. Our results lead us to a different conclusion. The reason is that he assumes a standard condition in nonlinear pricing models, namely that the individual demands of different types of agents do not cross.² In our opinion, this is a stringent assumption that excludes reasonable demand schedules. We may think of a consumer with high willingness to pay who wants only a small quantity vs another consumer with lower willingness to pay who prefers to buy a larger quantity: for instance, a high income bachelor vs a low- or middle-income family; or tourists who visit a city vs commuters. We find that, under these conditions, a per-unit tax can be welfare superior to an ad valorem tax that yields the same tax revenue.

The treatment of general optimization problems that do not satisfy the Spence–Mirrlees condition is still in its infancy [(see, for example, Araujo and Moreira (2010)] However, examples offer a tractable alternative. Besides, our paper only claims that, unless some demand structures are excluded, the superiority of the ad valorem tax over the unit tax cannot be guaranteed for monopolies engaged in some types of second-degree price discrimination. However, limited our claim is, it is undeniable that most real firms with market power engage in price discrimination.

A simple example may be illustrative. Consider a clearance sale for a product sold at 2.5 and with a cost of 1. If ad valorem taxes are 20 %, the regular retail price is 3. There are two type of potential clients. The first group is made up of a 100 clients whose willingness to pay is 2.9 for the first 2 units and 0.2 for the third one. There are 12 people in the second group whose willingness to pay is 2.9 for the first 2 units and 0 for the third one. To prevent customer churn at regular prices, the seller has two marketing strategies: “Buy two, get one free!” and “Buy one, get one 50%.” Let $R$ be revenue, $C$ cost, and $T$ taxes. The seller is better off with the first one.

$$\begin{aligned} \varPi _{3\times 2}= & {} R-C-T=6\cdot 100-300-100=200;\\ \varPi _\mathrm{BOGO}= & {} R-C-T=4.5\cdot 112-224-84=196. \end{aligned}$$

A unitary tax $t=0.5$ would change this result:

$$\begin{aligned} \varPi _{3\times 2}= & {} R-C-T=6\cdot 100-300-150=150;\\ \varPi _\mathrm{BOGO}= & {} R-C-T=4.5\cdot 112-224-112=168. \end{aligned}$$

With $t=0.5$, total welfare would increase. Government revenue would be 112 instead of 100, and although profit decreases by 32, consumer surplus would be $112(5.8-4.5)=145.6$ instead of 0.

In the following section, we provide four examples of frequently used price discrimination practices. Each of them shows how the superiority of ad valorem taxes, which has been proven under the assumption of a non-price-discriminating monopoly, does not necessarily hold under the more realistic conditions of price- discriminating monopolies.

2 Examples

In this section, we consider the welfare effects of unit and ad valorem taxes applied to price-discriminating monopolies. This scenario is of particular policy interest, because we expect that monopolies will likely use their price setting powers to maximize profits in the absence of legal restrictions. Although the welfare dominance of ad valorem taxes can be accepted as a very likely result in many situations, we show by example that it cannot be taken as granted in a monopoly with second-degree price discrimination. Our findings may be viewed as indicative of a more general phenomenon, but we claim only that they represent instances that do not fit with the accepted wisdom of ad valorem tax superiority.

The economic intuition of our result goes as follows. If a monopoly sells a homogeneous product at a uniform price, consumers will buy all units priced below or at their willingness to pay. In such a setting, per-unit taxes are inferior to ad valorem taxes because the former reduces production and, consequently, social welfare more than the latter. With second-degree price discrimination, however, it is possible that low-valued units are sold while high-valued units are not. For example, if individual A is willing to purchase only one unit of a good at price 10, and individual B is willing to buy four units at a price 8 each, with uniform pricing whenever B acquires the product so will A. However, if the product is offered at a price 7, but with a Minimum Order Quantity (i.e., the smallest quantity of the item you can buy) of 3, then B (who has a willingness to pay of 8) purchases the good, while A (who has a willingness to pay of 10) does not. In this situation, it could be possible for a per-unit tax to lead the monopolist to a different pricing scheme so that units with high value are sold instead of less valuable units. This could improve social welfare even if consumers buy less units than under an ad valorem tax.

All our examples have the same structure. We consider a demand function and, for the sake of simplicity, a monopoly with no production costs that maximizes profits and can engage in second-degree price discrimination. If the government levies an ad valorem tax, the monopoly will pay a percentage of its revenue but will not change its production levels since, under the assumption of zero costs, its revenues and profits are the same. Then, this situation is compared to the introduction of a per-unit tax that yields at least the same tax revenue. Finally, in each of the examples, we show how social welfare can be higher with unit taxation, which leads us to proposition 1.

Proposition 1

In the case of monopolies engaging in second-degree price discrimination, unitary taxes may be welfare superior to ad valorem taxes for some demand structures.

2.1 Two-part tariff

The simplest case of nonlinear pricing is probably the two-part tariff. Two-part tariffs are commonly used in utility markets, such as electricity, telephone, or gas. In this pricing scheme, consumers must pay a fixed fee $F$, regardless of the amount purchased, and a price $p$ for each unit bought.

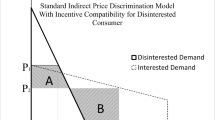
Our example goes as follows. A monopolist with no marginal costs and an unitary tax $(t)$ faces a market consisting of two (types of) consumers. Consumer 1 buys larger quantities, and her total willingness to pay is higher as well, but her willingness to pay for the last units purchased is lower than that of Consumer 2. Consumer 2 buys less units, but her willingness to pay is high and constant across all units. We suppose that the monopolist will use a two-part tariff pricing scheme in order to maximize profits. For $p>0$, the demand functions of both consumers are as follows: $Q_1=a$ if $0\le p\le 1, Q_1=0$; otherwise, $Q_2=1-p$. The graphical representation of these demand functions is given in the left panel in Fig. 1.

Fig. 1

Demand functions for consumers 1 and 2. The left panel corresponds to the two-part tariff example, and the right panel to the bulk discount one

The monopolist can sell the product to both consumers or just to one of them. If the monopolist sells only to consumer 1, the solution to the profit maximization problem can be given by $p=1$ and $F=0$, or $p=t$ and $F=a(1-t)$, or some other intermediate solutions. For any of these solutions, profits are $a(1-t)$. If the only consumer who buys the product is consumer 2, then the monopolist maximizes profits with a fixed fee $F=0.5(1-t)^2$ and a unit price $p=t$, so profits are equal to $0.5(1-t)^2$.

The profit-maximizing monopolist, if selling to one consumer only, will sell to consumer 2, when $2a+t<1\Leftrightarrow 0.5(1-t)^2>a(1-t)$. We assume $2a+t<1$.

If the monopolist wants to sell to both clients, the fixed fee $F$ must be set at a level such that both consumers are willing to pay the fixed fee and the unit price for the amount they wish to purchase. We compare $F_1=a(1-p)$ with $F_2=0.5(1-p)^2$. It can easily be proven that $F_1\le F_2\Leftrightarrow p\le 1-2a$. Two solutions are possible. First, the monopolist can choose to set a price $p\le 1-2a$ and the fixed fee $F_1$. Alternatively, the monopolist may set the uniform price at $p>1-2a$ and charge a fixed fee $F_2$. Since both clients pay the fixed fee, the profit function is given by:

$$\begin{aligned} \varPi ={\left\{ \begin{array}{ll} 2a(1-p)+(p-t)(a+1-p) &{} \text {if}\quad p\le 1-2a,\\ (1-p)^2+(p-t)(a+1-p) &{} \text {if}\quad p>1-2a. \end{array}\right. } \end{aligned}$$

(1)

The profit function given by Eq. (1) corresponds to a continuous function formed by a parabola with a maximum at $p^*=\frac{1+t-a}{2}$ (for $p\le 1-2a$), and a downward slopping line (for $p>1-2a$); $p^*$ will solve the maximization problem if $p^*<1-2a\Leftrightarrow 3a+t<1$. Assuming $3a+t<1$, the optimum will be:

$$\begin{aligned} p^*=\frac{1+t-a}{2};\;\;\;\varPi ^*=\frac{(1-t)^2+a(a+6(1-t))}{4} \end{aligned}$$

(2)

The monopolist will sell exclusively to consumer 2 when

$$\begin{aligned} \varPi ^*=\frac{(1-t)^2+a(a+6(1-t))}{4}<\frac{1}{2}(1-t)^2, \end{aligned}$$

or, since $a>0$ and $t<1$, if

$$\begin{aligned} a<\left( \sqrt{10}-3\right) (1-t). \end{aligned}$$

(3)

In contrast, the monopolist will sell to both consumers when condition (3) is reversed.

We now provide a numerical example. Consider a case where $a=0.16$ and $t=0$. Since $a=0.16<\left( \sqrt{10}-3\right)$, only consumer 2 will be served and the monopolist gets a profit of $0.5$. Now we introduce an ad valorem tax $\tau =0.1$, which results in a tax revenue level of $G_\tau =0.05$ and a social welfare level of $W_\tau =0.5$. If instead of an ad valorem tax, the government levies a per-unit tax $t=0.1$, then $a=0.16>\left( \sqrt{10}-3\right) (1-0.1)=0.146$ and now both clients will be served.

From Eq. (2), the unit price will be $p_1=0.5(1+t-a)=0.47$. Client 2 will consume $0.53$ instead of $1$; client 1 will consume $0.16$. Total consumption will be reduced from $1$ in the ad valorem case to $0.69$ with the per-unit tax, but the level of welfare will increase from $0.5$ with an ad valorem tax to $0.549$ with the unit tax.

The reason is that since there is no marginal cost, welfare can be calculated as the sum of the area under the demand function $p=1-Q$ between $Q=0$ and $Q=0.53$, which corresponds to consumer 2, and $0.16$ that corresponds to consumer 1. That is, $W_t=0.53-\frac{0.53^2}{2}+0.16=0.54955>1/2=W_\tau$. And the tax revenue is $G_t=0.069>0.05=G_\tau$.

In other words, for an ad valorem tax $\tau =0.1$, we have found a per- unit tax $t=0.1$ that simultaneously increases social welfare and government tax revenues. That means that for some demand structures a unit tax can be welfare superior to the ad valorem tax, for a profit-maximizing monopolist engaged in a two-part tariff pricing system.

2.2 Bulk discount

A bulk discount is a reduction in per-unit prices that rewards those buyers who purchase large quantities. Warehouse stores are a good example of volume discounting.

If the monopolist sets a two-block tariff to establish a bulk discount rule, purchase of low quantities (below a threshold $T$) will pay a higher price $p_\mathrm{H}$, while purchases that exceed the threshold will pay a lower price $p_\mathrm{L}$. After consumers decide how much of the good they wish to purchase, $Q$, the monopoly’s revenue function for a consumer is given by:

$$\begin{aligned} R=(p_\mathrm{H}-p_\mathrm{L})\min \{Q,T\}+p_\mathrm{L}Q. \end{aligned}$$

(4)

Two-part tariffs and bulk discounts are closely related since:

Proposition 2

• (a) If demand functions have finite reservation prices in a two-part tariff scheme, then the monopolist can earn the same profit with bulk discount.

• (b) If no consumer buys less than $T$ in the bulk discount setting, then the monopolist can earn the same profit with a two-part tariff scheme.

Proof

• (a) Let the monopolist’s two-part strategy be given by $(F,p)$ and the finite reservation prices by $p_i$. An equivalent bulk discount strategy exists when $p_\mathrm{L}=p, p_\mathrm{H}>\max \{p_i\}$ and $T<\min \{Q_i\}$, with quantity purchased given by $Q_i>0$ so that $(p_\mathrm{H}-p_\mathrm{L})T=F$.

• (b) Given a bulk discount scheme, $(p_\mathrm{H},\,p_\mathrm{L},\,T)$, the monopolist can earn the same profit with a two-part tariff if $\min \{Q_i,T\}=T$ for any $Q_i>0$, with $F=(p_\mathrm{H}-p_\mathrm{L})T$, and $p=p_\mathrm{L}$.

Our two-part tariff example cannot be used in this case, since social surplus is maximized with an ad valorem tax for $(p_\mathrm{H}=1,\,T=1/2,\,p_\mathrm{L}=0)$ and there is no inefficiency that may be corrected with unit taxes.

The following example shows a case of unit tax superiority in the presence of bulk discounts. Let the demand functions of both consumers be given by: $Q_1=a$ if $p \in [0,r]$ and $Q_1=b$ if $p\in (r,1]$; and $Q_2=1-p$, as represented in the right panel in Fig. 1.

We now consider a numerical example. Let $r=1/2, b=1/4$, and $a=2/5$, the monopolist maximizes profits with a unit tax $t$. Based on Proposition 2, we first consider the two-part tariff case. The optimum cannot be found when $p\ge r$, because then $p\ge 1-2b$ (with $b$ playing the role of $a$ in Eq. 1). With $p<r$, the fixed fee is $F_1=a(1-p)-(1-r)(a-b)$ for the first consumer and $F_2=\frac{1}{2}(1-p)^2$ for the second one. With $r=\frac{1}{2}$, $a=\frac{2}{5}, b=\frac{1}{4}$, instead of $p<1-2a$, now $F_1<F_2$, for any $p<\frac{1}{2}$. And then, using Eq. (2),we find that for any $t<2/5$, the profit-maximizing price is $p^*=\frac{3}{10}+\frac{t}{2}$, and the profit is given by.

$$\begin{aligned} \varPi _1(t)=\frac{(1-t)^2+a(a+6(1-t))}{4}-2(1-r)(a-b)=\frac{25t^2-110t+74}{100}.\qquad \end{aligned}$$

(5)

Let us consider now the bulk discount case. If $p_\mathrm{H}\le r=\frac{1}{2}$, the maximum revenue is 1/5, obtained from consumer 1, and 3/8 obtained from consumer 2. The monopolist must pay $t(2/5+1-t)$ in taxes, so that the maximum profit with $p_\mathrm{H}\le r$ cannot be any $>\varPi =23/40-t(2/5+1-t)$, which for any $t<2/5$ is always below $\varPi _1(t)$ from Eq. (5).

If $p_\mathrm{H}>1/2$, there are two possibilities. First, the monopolist sells no units with $r$ value, optimal prices are $(p_\mathrm{H}=1, T=\frac{1}{2}(1-t)^2, p_\mathrm{L}=t)$, and the monopolist extracts as much of the consumer surplus as possible. As a result, profits are:

$$\begin{aligned} \varPi _2(t)=\frac{1}{2}(1-t)^2+\frac{1}{4}(1-t)=\frac{2t^2-5t+3}{4}. \end{aligned}$$

(6)

In the second possibility, the monopolist must set $T<a$ in order to sell some units with $r$ value. If the monopolist sells $a$ to customer 1, and no more than $a$ to customer 2, profits cannot exceed $2(b+r(b-a))-4t/5=0.65-4t/5$. Again, these profits, for $t<2/5$, are below those given by Eq. (5). Hence, the monopolist must sell more than $a$ to consumer 2 to maximize profits. That is, for both consumers the condition $\min \{Q_i,T\}=T$ holds, and consequently, bulk discount and two-part tariff are equivalent, as in Proposition 2.

From Eqs. (5) and (6), $\varPi _2(0)>\varPi _1(0)$, and $\varPi _2(t)<\varPi _1(t)$, for $0.0764<t<0.52$. Either with no taxes or an ad valorem tax, the monopolist is better off with prices leading to $\varPi _2$, but for $t>0.0764$ the monopolist is better off with prices leading to $\varPi _1$.

Either with no taxes or any ad valorem tax, if prices are $(p_\mathrm{H}=1, T=\frac{1}{2}, p_\mathrm{L}=0)$, total welfare is $W_2=\frac{3}{4}$. With $p_\mathrm{L}=p^*=\frac{3}{10}+\frac{t}{2}$, for any $t<2/5$, total welfare (including consumer surplus for consumers 1 and 2) is

$$\begin{aligned} W_1=\frac{13}{40}+(1-p^*)-\frac{(1-p^*)^2}{2}=\frac{156-30t-25t^2}{200}. \end{aligned}$$

For any $t<0.17, W_1>W_2=0.75$. This shows that for any $t\in [0.0764,\,0.17]$, the monopolist reacts to the implementation of the unit tax by switching to a pricing strategy that increases total welfare.

2.3 Package size price discrimination

The supply in many consumer goods markets is composed of companies offering different sized packages of the same product. These otherwise identical products are offered at different per-unit prices, typically at volume discounts. Many examples of this price discrimination can be observed in practice, with the paper towel market providing an illustrative example.

We will proceed as in the previous cases, by providing an example where the imposition of a unit tax (but not an ad valorem tax) allows a change in the pricing scheme so that social welfare increases without decreasing government revenue.

Our example goes as follows. A monopolist has four clients. Clients 1 and 2 are willing to pay 14 monetary units for the first unit and 1 for the second. Client 3 is willing to pay 11 for the first unit and 4 for the second one. Finally, client 4 is willing to pay 10.2 for one unit.

The monopolist can sell 1-unit and 2-unit packages. By selling one 2-unit package at 15, profit obtained from clients 1, 2, and 3 will be 45 monetary units. The monopolist can increase profits only by selling to client 4. In order to do so, the monopolist offers a 1-unit package at a price $p_1$. As a result, clients 1 and 2 get a surplus of $14-p_1$ and client 3 a surplus of $11-p_1$ from buying the 1-unit package. To sell the 2-unit package, the monopolist can either $(i)$ set $p_2=p_1+1$, so that clients 1, 2 and 3 buy the 2-unit package, resulting in a total income of $4p_1+3$; or $(ii)$ set $p_2=p_1+4$, so that only client 3 buys the 2-unit package, while clients 1, 2, and 4 buy the 1-unit package, resulting in a total income of $4p_1+4$. Naturally, the monopolist chooses the latter.

Let us now consider the introduction of a unit tax $t$. The firm can (a) set $p_2=15$, sell six units, and make a profit of $\varPi =45-6t$; or (b) set $p_1=10.2$, $p_2=14.2$, sell three 1-unit packages and one 2-unit package, and make a profit of $\varPi =44.8-5t$.

With either $t=0$ or an ad valorem tax, the monopolist would choose option (a), resulting in a total welfare of 45. With a unit tax $t>0.2$, the monopolist would choose option (b), resulting in a total welfare of 53.2. For any $t>0.2$, government revenue would be $>$1.2 in scenario (a). In that same scenario, government revenue would be 1.2 with a $\tau =1.2/45=0.02\overline{6}$. That is, for these demand functions and any $\tau >0.02\overline{6}$, it is possible to find a revenue-equivalent unit tax which is also welfare superior.

2.4 Bundling

Tie-in sales are a common practice for firms. Well-known examples abound and include disparate products, such as vacation packages, season tickets for sports or cultural events, fixed-price menus in restaurants, sheet sets, and movies sold to cinemas. Mixed bundling occurs when buyers can choose between purchasing the bundle and the separate components of the package. Our model is very simple, like those found in Adams and Yellen (1976).

We analyze a situation where units of bundles and units of components can be determined, so that both ad valorem and per-unit taxations are easy to implement. Let us consider a monopolist that bundles a word processor $(W)$ and a spreadsheet $(E)$ into a single office suite $(O)$, so that clients can buy the entire bundle $(O)$ or any of the two components $(W, E)$ separately. For the sake of simplicity, marginal costs are supposed to be zero. There are four clients. Clients 1 and 2 are willing to pay  14 monetary units for  $E$ and 1 for $W$. Client 3 is willing to pay 14 for $W$ and 1 for $E$. Client 4 is only interested in purchasing  $E$, and her willingness to pay is 9.99.

Note that in this example there are two different goods; the Spence–Mirrlees condition is not violated for any of the two products, although a more general Spence–Mirrlees condition encompassing multiple goods could be violated by the preferences in our example.

By selling $O$ at 15, the monopolist will obtain a 45 monetary unit profit. The monopolist can increase profits only by selling to client 4. In order to do so, the monopolist offers $E$ at a price $p_E\le 9.99$. As a result, clients 1 and 2 get a surplus of $14-p_E$ from $E$. The firm has two options: It can allow clients 1 and 2 to only purchase $E$ or lower the price of $O$ so that they keep on buying it. The profit of the monopolist is given by $3p_E+15$ in the first scenario and by $p_E+3(15-(14-p_E))=3+4p_E$ in the second one. Naturally, profits are increasing in $p_E$.

Let us consider a unit tax $t$ on each application. The monopolist has three options:

• (a) set $p_{O}=15$, sell three $O$, and make a profit $\varPi =45-6t$,

• (b) set $p_{O}=10.99$ and $p_E=9.99$, sell three $O$ and one $E$, and make a profit $\varPi =42.96-7t$; or

• (c) set $p_{O}=15$ and $p_E=9.99$, sell one $O$ and three $E$, and make a profit $\varPi =44.97-5t$.

With either $t=0$, or an ad valorem tax, the monopolist would choose option (a), resulting in a total welfare of 45.

With a unit tax $t>0.03$, the monopolist would choose option (c), resulting in a total welfare of 52.99. For any $t>0.03$, government revenue would be $>$0.15 in scenario (a). In that same scenario, government revenue would be $>$0.15 with a $\tau >1/300=0.00\overline{3}$. That is, for these demand functions and any $\tau >0.00\overline{3}$, it is possible to find a revenue-equivalent unit tax which is also welfare superior.

3 Conclusion

In the academic literature, ad valorem taxes are widely accepted to be superior to unit taxes for monopolies without externalities. In fact, it has been proven that for monopolies that do not engage in price discrimination, ad valorem taxes are Pareto superior to unitary taxes. We show in this paper that, contrary to some generally accepted wisdom, such a result does not necessarily hold when the monopoly is able to discriminate prices.

Cheung (1998) concluded that ad valorem taxation is superior to per-unit taxes regardless of the pricing policy considered in all three types of Pigouvian price discrimination. His results are highly dependent on the (standard) condition that the individual demands of different types of agents do not cross. Our analysis can be taken as an extension, as we relax this condition to analyze partial equilibrium solutions for a profit-maximizing monopoly with no externalities in four different and widely used examples of second-degree price discrimination.

Our aim is to compare the welfare effects of per-unit and ad valorem taxes in a natural framework of price discrimination. In each of the four settings analyzed, we show that, under some plausible conditions, unit taxation can welfare dominate ad valorem taxes.

We do not claim that unitary taxes are universally preferable to ad valorem taxes. Our contention here is that, as the cases analyzed in this paper show, it is possible to find down-to-earth examples [(“exemplifying theories” as Fisher (1989) calls them] revealing the possibility of unit taxes that are welfare superior to ad valorem taxes. We believe this result to be of relevance, since policy making very often happens in situations where monopolies can and do apply price discrimination.