Entanglement and Spin Squeezing in the Evolution of a Resonant Field in a Kell-Like Medium

Abstract

We investigate entanglement and spin squeezing in the evolution of a resonant field in a Kell-like medium. With perturbation techniques, we first obtain the approximate analytical solution of the wave function, and then we further analytically and numerically calculate two mode entangled parameter and spin squeezing parameter. Its shows that the stronger entanglement and more squeezing may be achieved by increasing the coupling strength.

1 Introduction

Recently quantum entanglement [1] and spin squeezing [2,3,4,5,6,7] play significant role in quantum mechanics, as it not only holds the power for demonstration of the quantum nonlocality against local hidden variable theory, but also provides promising and wide applications in quantum information, high-precision spectroscopy [4] and atomic clocks [8]. Therefore, the generation of entanglement and spin squeezing attracted much attention. Rudner and the co-worker presented a scheme for achieving coherent spin squeezing of nuclear spin states in semiconductor quantum dots [9]. Xia and Twamley proposed a scheme to generate spin squeezing states and Greenberger-Horne-Zeilinger entanglement using a hybrid phonon-spin ensemble in diamond [10]. Eugene and Ye proposed an approach for the collective enhancement of precision for remote optical lattice clocks and a way of generating the Einstein-Podolsky-Rosen state of remote clocks [11]. Bhattacherjee and Sharma investigated spin squeezing and the quantum entanglement for the Jaynes-Cummings-Dicke model in a two component atomic Bose-Einstein condensate inside an optical cavity [12]. Abad it al. studied quantum states generated by a sequence of nearest neighbor bipartite entangling operations along a one-dimensional chain of spin qubits [13]. In this paper, we investigate entanglement and spin squeezing in the evolution of a resonant field in a Kell-like medium [14, 15]. We obtain the approximate analytical solutions of the wave function, the two-mode entangled parameter and the spin squeezing parameter by using perturbation techniques [16]. Then we analytically derive the two-mode entangled parameter and the spin squeezing parameter. Finally we numerically calculate these parameters. The paper is organized as follows. In Sec. II, we will introduce the perturbation techniques and give the approximate analytical solution of the wave function start from a product state. In Sec. III, we will give the approximate analytical solutions of the two-mode entangled parameter and the spin squeezing parameter; and then we will numerically calculate the two parameters. A conclusions will be present in Sec. IV.

2 Wave Function

We consider the propagation of a single-mode field of frequency ω₂ through a nonlinear medium, whose frequency can be modeled by ω₁, the total Hamiltonian can be described by [14, 15].

$$ H={\omega}_1{\alpha}^{+}\alpha +{\omega}_2{b}^{+}b+{k\alpha}^{+2}{\alpha}^2+g\left({b}^{+}a+{a}^{+}b\right) $$

(1)

where a and b are the annihilation operators; κ is the inter-particle interaction and g is the coupling strength between the single-mode field and the non linear medium. Although the model is important and simply, it is impossible to find the analytical solution because of the nonlinear interaction. In general, it is difficult to treat the Hamiltonian (1) in an exact way because of the presence of nonlinear interaction. Here we obtain approximate analytic solutions with perturbation techniques [16]; i.e., approximately write the wave function as|ψ(t)〉 ≈ (1 − iHt − H²t²/2)|ψ(0)〉. The perturbation techniques is valid for small dimensionless time gt. Let us assume that the initial state is|ψ(0)〉 = |N, 0〉 = |N〉_a|0〉_b, then the wave function can be approximately expressed as |ψ(t)〉 ≈ A|N, 0〉 + B|N − 1, 1〉 + Q|N − 2, 2〉 with

$$ {\displaystyle \begin{array}{c}A=1-\frac{N}{2}\left[{g}^2+{\left({\omega}_1-\kappa \right)}^2N-\left({\omega}_1-\kappa \right){N}^2+{\kappa}^2{N}^3\right]{t}^2\\ {}\kern1em + iN\left[\kappa \left(N+1\right)-{\omega}_1\right]t\end{array}} $$

(2)

$$ B=\frac{\sqrt{N}}{2}\left[\kappa g\left(2{N}^2-2N+1\right)-g\left({\omega}_1-\kappa \right)\left(2N-1\right)-g{\omega}_2\right]{t}^2- ig\sqrt{N}t $$

(3)

and $Q=-{g}^2{t}^2\sqrt{2N\left(N-1\right)}/2$. In order to investigate entanglement and spin squeezing of the model, we need further calculate some expectation values. We define the state$\left|\varphi (t)\right\rangle =\left|\psi (t)\right\rangle /\sqrt{C}$ with C = |A|² + |B|² + Q², which is normalized for all times. Thus, the usage of the normalized wave function |φ(t)〉 ensures the probabilistic interpretation of the approach [17]. Using |φ(t)〉, we may investigate the dynamics properties of the model, such as quantum entanglement, spin squeezing and so on.

3 Entangled Parameter and Spin Squeezing Parameter

Determining whether or not a state is entangled has many criteria, in general, these criteria provide only sufficient conditions for detecting entanglement. On the other hand, there are various definitions for spin squeezing [2]. Here we determine entanglement with the criteria provided by Hillery and Zubairy [18] and spin squeezing with the criteria provided by Kitagawa and Ueda, respectively.

3.1 Two Mode Entangled Parameter

Hillery and Zubairy have proven that the state is entangled if the entangled parameter

$$ \eta =\left\langle {a}^{+}a{b}^{+}b\right\rangle -{\left|\left\langle {b}^{+}a\right\rangle \right|}^2 $$

(4)

less than 0. Then by straightforward calculation, we have

$$ {\displaystyle \begin{array}{c}\eta =\frac{1}{C}\left[\left(N-1\right){\left|B\right|}^2+2\left(N-2\right){Q}^2\right]-\frac{1}{C}{\left|B\right|}^2\left[N{\left|A\right|}^2+2{Q}^2\left(N-1\right)\right]\\ {}-\frac{2}{C}\sqrt{2N\left(N-1\right)}\left(A{B}^{\ast 2}+{A}^{\ast }{B}^2\right)\end{array}} $$

(5)

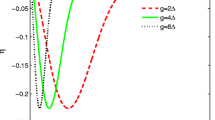
For clearly see the dependence of entangled parameter η on coupling constant g and the inter-particle interaction κ, in Fig.1 we plot η as a function of κt with various g for ω₁ = 4κ, ω₂ = 6κ and N = 10. We observe that initially there is no quantum entanglement because the initial state is a separable state. Dependent on the evolution, the system begins to be entangled state. We also observe that the larger the value of g, the smaller the value of η; which implies that the stronger coupling leads to stronger quantum entanglement.

Fig. 1

Dependence of η on κt with various g forω₁ = 4κ, ω₂ = 6κand N = 10

3.2 Spin Squeezing Parameter

Spin squeezing not only can be used as a measure of entanglement in multipartite systems, but also can be relatively easy to measure experimentally because the measurement of spin squeezing only need to measure the expectation values of the relevant mechanical quantities [7]. However, the definition of spin squeezing is not unique, it is well-known that there are several definitions of spin squeezing [3, 4]. In this paper, we employ the criteria proposed by Kitagawa and Ueda, which is defined as [2, 5].

$$ {\xi}^2=\frac{4{\left(\varDelta {J}_{n_{\perp}^m}\right)}^2}{N} $$

(6)

where ${\left(\varDelta {J}_{n_{\perp}^m}\right)}^2$ is the smallest uncertainty of an angular momentum component perpendicular to the mean spin direction and n is the optimally squeezed direction [5]. A state is said to be a spin squeezed state if the inequality ξ² < 1 is satisfied.

In order to calculate the squeezing parameter ξ², we first need to know the mean spin direction ${n}_1=\sin \theta \cos \phi \hat{x}+\sin \theta \sin \phi \hat{y}+\cos \theta \hat{z}$ determined by〈J_{x, y, z}〉. Then simple calculation gives$\left\langle {J}_x\right\rangle =\left[\sqrt{N}\operatorname{Re}\left(A{B}^{\ast}\right)+\sqrt{2\left(N-1\right)}\operatorname{Re}(BQ)\right]/C$, $\left\langle {J}_y\right\rangle =\left[\sqrt{N}\operatorname{Im}\left(A{B}^{\ast}\right)+\sqrt{2\left(N-1\right)}\operatorname{Im}\left(B\mathrm{Q}\right)\right]/C$and〈J_z〉 =  − [N|A|² + (N − 2)|B|² + (N − 4)Q²]/2C, which implies that the azimuth angle ϕ = arccos(〈J_x〉/r) with$r=\sqrt{{\left\langle {J}_x\right\rangle}^2+{\left\langle {J}_y\right\rangle}^2}$and the polar angle$\theta =\operatorname{arccos}\left(\left\langle {J}_z\right\rangle /\sqrt{r^2+{\left\langle {J}_z\right\rangle}^2}\right)$. The other two mutually orthogonal directions can be written as ${n}_2=-\sin \phi \hat{x}+\cos \phi \hat{y}$ and${n}_3=-\cos \theta \cos \phi \hat{x}-\cos \theta \sin \phi \hat{y}+\sin \theta \hat{z}$, respectively. Having known the mean spin, we obtain the smallest uncertainty of an angular momentum component [6].

$$ {\left(\varDelta {J}_{n_{\perp}^m}\right)}^2=\frac{1}{2}\left[\left\langle {J}_{n_2}^2+{J}_{n_3}^2\right\rangle -\sqrt{{\left\langle {J}_{n_2}^2-{J}_{n_3}^2\right\rangle}^2-{\left\langle {J}_{n_2}{J}_{n_3}+{J}_{n_3}{J}_{n_2}\right\rangle}^2}\right] $$

(7)

with

$$ \left\langle {J}_{n_2}^2\right\rangle =\frac{1}{2C}\left\{\frac{N}{4}\left(N+2\right)-\frac{N^2}{4}C-\sqrt{2N\left(N-1\right)}Q\left[\cos \left(2\phi \right)\operatorname{Re}A+\sin \left(2\phi \right)\operatorname{Im}A\right]\right\} $$

(8)

$$ {\displaystyle \begin{array}{c}\left\langle {J}_{n_3}^2\right\rangle =\frac{1}{2C}\left\{{\cos}^2\theta \left[\frac{N}{4}\left(N+2\right)-\frac{N^2}{4}C\right]+2{\sin}^2\theta \frac{N^2}{4}C\right\}\\ {}\kern2em +\frac{1}{2C}{\cos}^2\theta \sqrt{2N\left(N-1\right)}Q\left[\cos \left(2\phi \right)\operatorname{Re}A+\sin \left(2\phi \right)\operatorname{Im}A\right]\\ {}\kern2em +\frac{1}{2C}\sin \left(2\theta \right)\cos \phi \left[\left(N-1\right)\sqrt{N}\operatorname{Re}\left(A{B}^{\ast}\right)+\left(N-3\right)\sqrt{2\left(N-1\right)}Q\operatorname{Im}B\right]\\ {}\kern2em +\frac{1}{2C}\sin \left(2\theta \right)\sin \phi \left[\left(N-1\right)\sqrt{N}\operatorname{Re}\left(A{B}^{\ast}\right)+\left(N-3\right)\sqrt{2\left(N-1\right)}Q\operatorname{Im}B\right]\end{array}} $$

(9)

$$ {\displaystyle \begin{array}{c}\left\langle {J}_{n_2}{J}_{n_3}+{J}_{n_3}{J}_{n_2}\right\rangle =\frac{1}{C}\cos \theta \sqrt{2N\left(N-1\right)}Q\left[\sin \left(2\phi \right)\operatorname{Re}A-\cos \left(2\phi \right)\operatorname{Im}A\right]\\ {}\kern3em +\frac{1}{C}\sin \theta \sin \phi \left[N\sqrt{N}\operatorname{Re}\left(A{B}^{\ast}\right)+\left(N-2\right)\sqrt{2\left(N-1\right)}Q\operatorname{Re}B\right]\\ {}\kern3em -\frac{1}{C}\sin \theta \cos \phi \left[N\sqrt{N}\operatorname{Im}\left(A{B}^{\ast}\right)+\left(N-2\right)\sqrt{2\left(N-1\right)}Q\operatorname{Im}B\right]\end{array}} $$

(10)

Substituting Eqs.(7)–(10) into Eq.(6), we may numerically calculate spin squeezing parameter ξ². Figure 2 shows the dependence of ξ² on κt with various g. Obviously, more squeezing can be achieved by increasing the coupling strength g.

Fig. 2

Dependence of ξ² on κtwith various g for ω₁ = 4κ, ω₂ = 6κ and N = 10

4 Summary

In summary, we investigate entanglement and spin squeezing in the evolution of a resonant field in a Kell-like medium. By using the perturbation techniques, we first obtain the approximate analytical solution of the wave function, and then we further analytically and numerically calculate two mode entangled parameter and spin squeezing parameter, which are defined by Hillery and Zubairy, Kitagawa and Ueda, respectively. Its shows that the stronger entanglement and more squeezing may be achieved by increasing the coupling strength.