External Classical Field and Damping Effects on a Moving two Level atom in a Cavity Field Interaction with Kerr-like Medium

Abstract

The interaction between a moving two-level atom and squeezed coherent states in the presence of Kerr like medium and an external classical field is studied. We consider the cavity field not to be isolated, so the field suffers from a decay rate. Under the rotating wave approximation, and some certain transformations, the system is transformed to the usual Jaynes-Cummings model with Kerr medium as well as a damping term. The probability amplitude is obtained when the atomic system is prepared in its excited state. The results show that, the evolution of the atomic population inversion, the Pegg-Barnett phase, and the quasi-probability distributions are decaying in the presence of damping. While the detuning parameter delays the decay rate, also enhances a part of the phase space and decrease the rate of another part. The system is very sensitive to the Kerr like medium, where it plays a role in shortening the collapse periods, however it works to cracking and diffusing the phase space.

1 Introduction

The interaction between a two-level atom and quantized electromagnetic field is one of the important studies in quantum optics. Under the rotating wave approximation, the model of a two level atom and a single mode of the field is solvable and called Jaynes-Cummings model (JCM) [1]. This model has been studied in a huge number of theoretical and experimental papers. For example, a single two-level atom or N-level atom and one mode or N − 1 modes were studied theoretically [2, 3]. Experimentally the JCM has been realized through a superconducting cavity and Rydberg atoms [4,5,6]. The effect of Kerr-like medium and Stark Shift on JCM are studied in [7, 8]. The influence of an external classical field has been studied by many authors[9, 10]. A system of N two-level atoms in a cavity driven by a strong classical field has been examined for entanglement [9]. The fluctuations of the driven JCM by an external classical field in coherent state have been studied [10]. Also, the entanglement and the phenomenon of squeezing have been investigated [11, 12]. Influence of a damping on JCM has been discussed in many publications [13,14,15]. In most of these studies, the authors use the case of a high-Q cavity which is used to study the collapses and revivals phenomenon on JCM at resonance as well as off-resonance cases [13, 14]. Also, in a high-Q cavity the effects of damping in the off-resonance case on the degree of entanglement are studied [16]. There is a kind of damping called intrinsic damping [17], as the decay is formed within the system itself. The Jaynes-Cummings model was studied for this kind of damping and the atomic population inversion [18] and entanglement [19, 20] were discussed. Finally, there is another type of damping that depends on the non-Hermitian Hamiltonian by adding a complex term to the Hamiltonian. The effect of such damping term was discussed analytically under detuning conditions and the entropy was studied [21]. We may mention other cases [11, 22] where the same techniques were introduced, but without the classical field or Kerr-like medium. Furthermore, the purity and the phenomenon of squeezing were discussed under the influence of the intrinsic damping and the classical field for a two-level atom that interact with multi-photons [23], the results showed that the damping increase purity while washing out the squeezing phenomenon.

On the other hand, the quantum phase space is the cornerstone of the quantum optics and information [24, 25]. For instance phase distribution enabled us to visualize the format of phase space. Phase distribution of the quantized field interacting with a two-level atom in the presence of Stark effect with an additional Kerr medium are studied [8]. Also, the Hermitian phase distribution is obtained of the generalized squeezed vacuum states associated with solvable quantum systems [26]. Alternatively, the quasi probability distributions (Q-PD) play a role in study the quantum phase, where it splits into three functions, which range in preference as follows. Firstly, the Wigner function which is regular and can be negative [27]. Secondly, Husimi Q-function which is always regular and non-negative [28]. Thirdly, Glauber P-function which may be negative or singular [29]. The Q-PD have many applications in statistical mechanics, quantum optics, and quantum information processing [30]. For example, the negative values of Wigner function is usually used as an indicator to degree of entanglement [31], non-classicality [32], estimation of the efficient of quantum circuit [33]. Alternatively, the Husimi Q-function has some application in estimated the quantum variable of the quantum system by using the quantum Fisher information [34, 35], and study the quantum Wehrl entropy for atomic system [36, 37].

This article introduces the interaction between a moving two-level atom and a quantized field driven by an external classical field in the presence of Kerr-like medium and a damping term. In Section 2 we present the theoretical description of the Hamiltonian and investigate a canonical transformation to transform the Hamiltonian into a generalized JCM. We use the time-dependent Schrödinger equation to get the probability amplitudes. Section 3 examines the atomic population inversion with various values of damping and Kerr-like parameters for the cases of resonance and off-resonance. The atom is assumed initially in the excited state and the cavity field in a squeezed coherent state. The phase distribution is discussed in Section 4. Quasi probability distributions are considered in Section 5 to show that the behavior in the phase space of this system by plotting Wigner and Q Husimi functions. Finally, we present our conclusion in Section 6.

2 Description of The Physical Model and its Analytic Solution

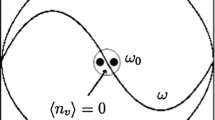
The interaction between a moving two-level atom and a quantized cavity field in the presence of a damping term, under the influence of an external classical field and the Kerr-like medium (nonlinear term) can be written in the following non-Hermitian Hamiltonian ($\hbar =1$):

$$ \hat{H}=\omega\hat{a}^{\dagger}\hat{a}+\frac{\omega_{0}}{2}\hat{\sigma}_{z}+\chi \hat{a}^{\dagger 2} \hat{a}^{2} +i\lambda(t)(\hat{a}+\hat{a}^{\dagger })(\hat{\sigma}_{+} -\hat{\sigma}_{-})+i(\xi(t)\hat{\sigma}_{+} -\xi^{*}(t)\hat{\sigma}_{-} )-i\frac{\gamma}{2} \hat{a}^{\dagger} \hat{a}, $$

(1)

where λ(t) and ξ(t) are the time dependent coupling parameter of the interactions of each atom with a quantized cavity field and with an external classical field, respectively. ω and ω₀ are the frequencies of the quantized field and atomic system respectively, σ_z and σ_± are Pauli operators so that σ_z = |e〉〈e|−|g〉〈g|, σ₊ = |e〉〈g| and σ₋ = |g〉〈e|, where |e〉 (|g〉) is the excited (ground) state of the atom, while $\hat {a^{\dagger }}$ ($\hat {a}$ ) the creation (annihilation) operators of the field, which satisfy the relation $[\hat {a},\hat {a}^{\dagger }]=1$ and χ is the dispersive part of the third-order non-linearity of the Kerr-like medium [7]. The last term in the previous equation represents the damping for the field, where the quantum electromagnetic field is dissipating with the decay coefficient γ [21, 38]. Figure 1 describes our composite system, where the cavity suffers from a decay rate γ, while the atom influenced by the classical field and the Kerr-like medium. Under this assumption the system may be considered to be an open quantum system. By using three transformations we can obtain a generalized JCM with Kerr-like medium and damping term. We consider that $\lambda (t)= 2 \lambda _{1} {\cos \nolimits } (v k t )$, where λ₁ is the coupling constant between the atom and a quantized field, v is the velocity of the atom, k is the wave number and z = vt is the direction of propagation. While $\xi (t)= \zeta \exp (i \omega _{c} t)$ where ζ is the complex parameter related to the time dependent coupling parameter of the external field and ω_c is the frequency of the external field. In this case the Hamiltonian (1) takes the form:

$$ \begin{array}{@{}rcl@{}} \hat{H}&=&\omega\hat{a}^{\dagger}\hat{a}+\frac{\omega_{0}}{2}\hat{\sigma}_{z}+\chi \hat{a}^{\dagger 2} \hat{a}^{2}+i\lambda_{1}(e^{ivkt}+e^{-ivkt})(\hat{a}+\hat{a}^{\dagger })(\hat{\sigma}_{+} -\hat{\sigma}_{-})\\ &&+i(\zeta e^{(i \omega_{c} t)}\hat{\sigma}_{+} -\zeta^{*} e^{(-i \omega_{c} t)}\hat{\sigma}_{-} )-i\frac{\gamma}{2} \hat{a}^{\dagger} \hat{a}. \end{array} $$

(2)

Fig. 1

Schematic diagram of a two-level atom interacting with a cavity field in the presence of Kerr-like medium and an external classical field has frequency ω_c, where the cavity suffers from decay rate γ

By using the operator $\hat {U}_{1}=e^{-i\omega _{c} \hat {\sigma }_{z} t/2}$ and applying a canonical transformation $\hat {H_{1}}=\hat {U}^{\dagger }_{1}\hat {H}\hat {U}_{1}-i\hat {U}^{\dagger }_{1}\frac {\partial \hat {U}_{1}}{\partial t}$ we get:

$$ \begin{array}{@{}rcl@{}} \hat{H}_{1}&=&\omega\hat{a}^{\dagger}\hat{a}+\frac{\bar{\omega}_{0}}{2}\hat{\sigma}_{z}+\chi \hat{a}^{\dagger 2} \hat{a}^{2}+i\lambda_{1}(e^{ivkt}+e^{-ivkt})(\hat{\sigma}_{+} e^{-i\omega_{c}t} -\hat{\sigma}_{-} e^{i\omega_{c}t}) (\hat{a}+\hat{a}^{\dagger })\\ &&+i(\zeta \hat{\sigma}_{+} - \zeta^{*}\hat{\sigma}_{-} )-i\frac{\gamma}{2} \hat{a}^{\dagger} \hat{a} \end{array} $$

(3)

where we have assumed that $\bar {\omega }_{0}=\omega _{0}+\omega _{c}$. The result of product of the first two brackets in the fourth term in the previous equation lead to four terms, two of them contain the factor $e^{\pm i(vk+\omega _{c})t}$, while the other two terms contain the factor $e^{\pm i(vk-\omega _{c})t}$, which are the rapidly and slowly varying terms, respectively. Therefore, in the case (ω_c = vk) discarding the rapidly oscillating terms, and assuming that $\zeta = \lambda _{2} \exp (-i \pi /2)$, we cast the Hamiltonian in the following term:

$$ \hat{H}_{1}=\omega\hat{a}^{\dagger}\hat{a}+\frac{\bar{\omega}_{0}}{2}\hat{ \sigma}_{z}+\chi \hat{a}^{\dagger 2} \hat{a}^{2}+i\lambda_{1}(\hat{\sigma}_{+} -\hat{\sigma}_{-}) (\hat{a}+\hat{a}^{\dagger })+\lambda_{2}(\hat{\sigma}_{+} + \hat{\sigma}_{-} )-i\frac{\gamma}{2} \hat{a}^{\dagger} \hat{a}. $$

(4)

Now we define the operators $\hat {S}_{z}$ and $\hat {S}_{\pm }$ with the new states |+〉 and |−〉, which represent the eigenstate of the new operators $\hat {S}_{\pm ,z}$, it related to |e〉 and |g〉 by [11, 39]:

$$ \begin{array}{@{}rcl@{}} &&|+\rangle= \cos\eta|e\rangle+\sin\eta|g\rangle ,\quad |-\rangle= \cos\eta|g\rangle-\sin\eta|g\rangle, \quad\eta =\frac{1}{2}\tan^{-1}(2 \lambda_{2}/ \bar{\omega}_{0}),\\ &&\frac{-\pi}{2}< \eta <\frac{\pi}{2}. \end{array} $$

(5)

So we can write $\hat {S}_{z,\pm }$ as:

$$ \begin{array}{@{}rcl@{}} &&\hat{S}_{z}=\cos 2\eta\hat{\sigma}_{z}+\sin 2\eta\hat{\sigma}_{+} +\sin 2\eta\hat{\sigma}_{-},\qquad \hat{S}_{+}=\frac{-1}{2}\sin 2\eta\hat{\sigma}_{z}+\cos^{2}\eta\hat{\sigma}_{+}-\sin^{2} \eta\hat{\sigma}_{-},\\ &&\hat{S}_{-}=\frac{-1}{2}\sin 2\eta\hat{\sigma}_{z}-\sin^{2}\eta\hat{\sigma}_{+}+\cos^{2}\eta\hat{\sigma}_{-}, \end{array} $$

(6)

where $\hat {S}_{\pm ,z}$ obey the following commutators $[\hat {S}_{z},\hat {S}_{\pm }]=\pm \hat {S}_{\pm }$ and $[\hat {S}_{+},\hat {S}_{-}]=\hat {S}_{z}$, we note that $\hat {S}_{\pm }^{2}=0$ and $[\hat {S}_{+},\hat {S}_{-}]_{+}=1$. After applying this transformation we get the Hamiltonian:

$$ \hat{\mathscr{H}}=\omega\hat{a}^{\dagger}\hat{a}+ \frac{\varDelta}{2} \hat{S}_{z}+\chi \hat{a}^{\dagger 2} \hat{a}^{2}+i\lambda_{1} (\hat{a}\hat{S}_{+}-\hat{a}^{\dagger }\hat{S}_{-})-i\frac{\gamma}{2} \hat{a}^{\dagger} \hat{a} $$

(7)

where $\varDelta =\sqrt {(\bar {\omega }_{0})^{2}+4{\lambda _{2}^{2}}}$. We have cast the Hamiltonian in the previous equation by removing the classical field parameter but it is included in the Δ term, which the classical field parameter only shifts the energy levels of the atomic system [11]. To obtain the dynamics of this system, suppose that the wave function |ψ(t)〉 at any time (t > 0) possesses the form:

$$ |\psi(t)\rangle=\sum\limits_{n=0}^{\infty}[\mathscr{A}_{n}(t)|n,+\rangle+\mathscr{B}_{n}(t)|n+1,-\rangle]. $$

(8)

Assuming that the initial state of the atom in superposition atomic state:

$$ |\psi\rangle_{a}=C_{e}|e\rangle+C_{g}|g\rangle \qquad\text{where} \quad|C_{e}|^{2}+|C_{g}|^{2}=1. $$

(9)

Then we can cast the initial state by, (5), in the form:

$$ \begin{array}{@{}rcl@{}} |\psi\rangle_{a}&=&(C_{e} \cos \eta + C_{g} \sin \eta )|+\rangle-(C_{e} \sin \eta - C_{g} \cos \eta ) |-\rangle\\ &=&s_{1}|+\rangle +s_{2} |-\rangle. \end{array} $$

(10)

While the radiation field initially has been prepared in the squeezed coherent state:

$$ \begin{array}{@{}rcl@{}} |\psi\rangle_{f} &=& |\beta\rangle=|\alpha,r\rangle\\ &=& (1 - |\varepsilon|^{2})^{\frac{1}{4}} \times e^{-\frac{1}{2}\left( |\beta|^{2}-\frac{|\varepsilon|}{2}(\beta^{2} e^{i \phi}+\beta^{*2} e^{-i \phi})\right)} \sum\limits_{n=0}^{\infty} \sqrt{(n!)^{-1}(-\frac{\varepsilon}{2})^{n}} \ H_{n}(\frac{\beta\sqrt{1 - |\varepsilon|^{2}}}{\sqrt{-2\varepsilon}}) |n\rangle\\& =&\sum\limits_{n=0}^{\infty} f_{n} |n\rangle, \end{array} $$

(11)

with $\varepsilon =-\frac {\nu }{\mu } =e^{-i \phi } \tanh r, \mu =\cosh r ,\nu =e^{i \phi } \sinh r$, thus |μ|² −|ν|² = 1, and β = μα + να^∗. Also H_n(.) is the Hermite polynomial of order n, which is defined by:

$$ H_{n}(q)=(-1)^{n} \exp(q^{2}) \frac{d^{n}}{d q^{n}} \exp(-q^{2}). $$

By using the time-dependent Schrödinger equation $i \frac {\partial }{\partial t}|{\varPsi }(t)\rangle =\mathscr {\hat {H}}|\psi (t)\rangle$ with the Hamiltonian (7), we obtain the probability amplitudes as two linear differential equations as follows:

$$ i\frac{\partial \mathscr{A}_{n}(t)}{\partial t}=x \mathscr{A}_{n}(t)-iz\mathscr{B}_{n}(t)\quad,\quad i\frac{\partial \mathscr{B}_{n}(t)}{\partial t}=y\mathscr{B}_{n}(t)+iz\mathscr{A}_{n}(t), $$

(12)

where (x,y,z) are defined as:

$$ x = \omega n+\chi (n^{2}-n)+ \frac{\varDelta}{2}-i \frac{\gamma}{2}n,\quad y = \omega(n+1)+\chi (n^{2}+n)- \frac{\varDelta}{2}-i \frac{\gamma}{2}(n+1)\quad, z = \lambda_{1}\sqrt{n + 1}. $$

Thus we arrive to the following forms of the probability amplitudes:

$$ \begin{array}{@{}rcl@{}} &&\mathscr{A}_{n}(t)=f_{n} e^{\frac{-1}{2}i(x+y) t}\left[s_{1} \cos(\frac{\varLambda}{2} t) +\frac{i(s_{1} R+2i s_{2} z)}{\varLambda} \sin(\frac{1}{2}\varLambda t)\right] ,\\& &\mathscr{B}_{n}(t)= f_{n}e^{\frac{-1}{2}i(x+y) t}\left[s_{2} \cos(\frac{\varLambda}{2} t)-\frac{i(s_{2} R+2i s_{1} z )}{\varLambda} \sin(\frac{1}{2}\varLambda t)\right], \end{array} $$

(13)

where R = x − y = δ − 2χn + iγ/2, $\varLambda =\sqrt {4 z^{2}+R^{2}}$ and δ =Δ −ω. The time evolution of the density matrix $\hat {\rho (t)}$ describing the system is given by:

$$ \hat{\rho}(t)=\left[\begin{array}{ll} \hat{\rho}_{11}(t) & \hat{\rho}_{12}(t)\\\hat{\rho}_{21}(t)& \hat{\rho}_{22}(t) \end{array}\right] $$

(14)

$$ \begin{array}{@{}rcl@{}} &&\hat{\rho}_{11}(t)=\sum\limits_{n,m=0}^{\infty}\mathscr{A}_{m}(t)\mathscr{A}^{*}_{n}(t)|m\rangle\langle n|, \qquad \hat{\rho}_{22}(t)=\sum\limits_{n,m=0}^{\infty}\mathscr{B}_{m}(t)\mathscr{B}^{*}_{n}(t)|m+1\rangle \langle n+1|,\\ &&\hat{\rho}_{12}(t) = \sum\limits_{n,m=0}^{\infty}\mathscr{A}_{m}(t)\mathscr{B}^{*}_{n}(t)|m\rangle\langle n + 1|,\qquad \hat{\rho}_{21}(t) = \sum\limits_{n,m=0}^{\infty}\mathscr{B}_{m}(t)\mathscr{A}^{*}_{n}(t)|m + 1\rangle\langle n|. \end{array} $$

(15)

Now we can discuss some dynamical properties of the present system, especially: the atomic inversion, the entanglement, quasi probability distribution functions and the phase probability distribution.

3 The Atomic Population Inversion

The atomic population inversion is related to the difference between the possibility of finding the atom in its excited state |e〉 or in its ground state |g〉. In fact, the atomic population inversion gives us information about the behavior of the atom during the interaction, which can be obtained by:

$$ \langle\hat{\sigma}_{z}(t)\rangle=\sum\limits_{n=0}^{\infty}(\langle n|\rho_{ee}(t)| n\rangle-\langle n|\rho_{gg}(t)| n\rangle). $$

(16)

Reversing the new state |+〉, |−〉 to the old state|e〉, |g〉 by (5) and (14) we get the atomic population inversion in the form:

$$ \langle\hat{\sigma}_{z}(t)\rangle=\sum\limits_{n=0}^{\infty}\left[\langle n|\hat{\rho}_{11}(t)|n\rangle - \langle n| \hat{\rho}_{22}(t)|n\rangle\right]\cos 2\eta -\sum\limits_{n=0}^{\infty}\left[\langle n|\hat{\rho}_{12}(t)|n\rangle - \langle n| \hat{\rho}_{21}(t)|n\rangle\right]\sin 2\eta. $$

(17)

The time evolution of the atomic population inversion $\langle \hat {\sigma }_{z}(t)\rangle$ against the scaled time λ₁t is disclosed in Fig. 2 to show the effect of damping $\frac {\gamma }{\lambda _{1}}$, external classical filed λ₂ included in the detuning parameter and the Kerr-like medium $\frac {\chi }{\lambda _{1}}$ on the system. The atomic system is initially prepared in the excited state C_e = 1,C_g = 0, meanwhile the field is prepared in the squeezed coherent state with the photon number |α|² = 16, and r = 0.7. We set the values of the damping parameter γ = 0, detuning parameter $\frac {\delta }{\lambda _{1}}=0$ and Kerr-like $\frac {\chi }{\lambda _{1}}=0$, in Fig. 2a, which represents the well-known expression for the inversion of JCM in the squeezed output [40]. If we consider the effect of the damping $\frac {\gamma }{\lambda _{1}}= 0.004$, the amplitude of revivals decreases with growing the scaled time, this means that the atom does not follow the usual interaction inside the cavity, and the atom tends eventually to a superposition state, see Fig. 2b. When we take the detuning parameter to in account $\frac {\delta }{\lambda _{1}}=2$, the function oscillates down below and up zero, see Fig. 2c. The effect of the damping parameter with the detuning parameter (i.e. $\frac {\gamma }{\lambda _{1}}= 0.004$ and $\frac {\delta }{\lambda _{1}}=2$) is displayed in Fig. 2d, where the amplitude of revivals tends to zero as the scaled time grows. For $\frac {\chi }{\lambda _{1}} =0.2$ and $\frac {\gamma }{\lambda _{1}} =0 =\frac {\delta }{\lambda _{1}}$, the time revivals are shortened, while the fluctuations and approaching to excited state. This means that the Kerr-like works on increasing the number of interactions and arrange them on short periods,see Fig. 2e. By adding the damping $\frac {\gamma }{\lambda _{1}}= 0.004$ to the previous case, the function almost dies out the scaled time develops, see Fig. 2f. Figure 2g displays the influence of the Kerr-like medium $\frac {\chi }{\lambda _{1}} =0.1$ in the off-resonance case $\frac {\delta }{\lambda _{1}} =2$ and absence of the damping. The collapses and revivals time oscillate up and down zero as the scaled time grows, meanwhile the amplitude increases. Whilst the fluctuations closer to symmetry, this means that the classical field and Kerr-like medium play an important role in magnification revivals at long periods. The influence of the three parameters is shown in Fig. 2h, the amplitude of atomic inversion tends to zero as the scaled time develops. From the above analysis we conclude that the damping parameter tends to decay the population inversion when it considers. However, the presence of an external classical field which is included in the detuning parameter works to oscillate around zero. The Kerr-like medium leads to squeeze fluctuates and decrease the amplitude of the function, when add the effect of classical field, the time revival amplifies in some periods and increases the amplitude of the inversion.

Fig. 2

The atomic inversion $\langle \hat {\protect \sigma }_{z}(t)\rangle$ against the scaled time λ₁t at α = 4, r = 0.7 and C_e = 1,C_g = 0, with different values of ($\frac {\gamma }{\lambda _{1}} ,\frac {\delta }{\lambda _{1}} ,\frac {\chi }{\lambda _{1}}$): a (0, 0, 0), b (0.004, 0, 0), c (0, 2, 0), d (0.004, 2, 0), e (0, 0, 0.1), f (0.004 ,0 ,0.1), g (0, 2,0.1 ) and h (0.004 ,2 ,0.1)

4 Phase Distribution

In this section, we study and analyze the phase distribution (P-D) in the presence of the damping, Kerr-like medium and external classical field. The hermitian phase operator has been defined by Pegg and Barnett. By the reduced density matrix of the cavity field: $\hat {\rho }_{f}(t)$, the continuum P-D P(𝜃,t) is defined as [24, 25]:

$$ P(\theta,t)=\frac{1}{2\pi}\left( \sum\limits_{n,m}^{\infty} \rho_{f}(t) e^{i(m-n)(\theta-\theta_{0})}\right). $$

(18)

By ignoring the phase angle 𝜃₀ and substituting the reduced field density matrix in our calculation, then P(𝜃,t) is written as:

$$ P(\theta,t)=\frac{1}{2\pi}\left( \left| \sum\limits_{n=0}^{\infty} \mathscr{A}_{n}(t) e^{-i n\theta}\right|^{2}+ \left| \sum\limits_{n=0}^{\infty} \mathscr{B}_{n+1}(t) e^{-i n\theta}\right|^{2}\right). $$

(19)

Figure 3 displays P(𝜃,t) with respect to scaled time λ₁t and angel 𝜃 with r = 0.7 and |α|² = 16, where the system is prepared initially in the same way as in the previous section. In resonance case and neglect of the decay parameter and Kerr-like medium ($\frac {\delta }{\lambda _{1}}=0, \frac {\gamma }{\lambda _{1}}=0,\frac {\chi }{\lambda _{1}}=0$), a single-peak at 𝜃 = 0 corresponding to the initial squeezed coherent state, as time progresses there are two peaks moving away from each other gradually until they reach 𝜃 = ±π. When the scaled time λ₁t time grows further the two peaks start converging again at 𝜃 = 0, and this is the same as in Ref. [8], see Fig. 3a. The effect of the damping parameter$\frac {\gamma }{\lambda _{1}}=0.004$ and $\frac {\chi }{\lambda _{1}}=0 ,\frac {\delta }{\lambda _{1}}=0$ is displayed in Fig. 3b, where the amplitude of the P-D decreases with the developing of the scaled time. In the case of off-resonance $\frac {\delta }{\lambda _{1}}=2$ and $\frac {\chi }{\lambda _{1}}=0 ,\frac {\gamma }{\lambda _{1}}=0$, the amplitude of P(𝜃,t) grows along two sides peaks and decreases on along the other two peaks, see Fig. 3c. While in the presence of damping for the previous case $\frac {\gamma }{\lambda _{1}}=0.004,\frac {\chi }{\lambda _{1}}=0 ,\frac {\delta }{\lambda _{1}}=2$, all peaks suffer from decay except the peak at zero, see Fig. 3d. Figure 3e exhibits the influence of Kerr-like medium on P(𝜃,t) ($\frac {\gamma }{\lambda _{1}}=0.00,\frac {\chi }{\lambda _{1}}=0.1 ,\frac {\delta }{\lambda _{1}}=0$), where the function suffers from diffusion of small peaks or so-called cracked phase. But the damping parameter causes the decay for the amplitude of these peaks, and they reduce to zero, see Fig. 3f. To visualize the effect of the Kerr-like medium with the case of off-resonance ($\frac {\gamma }{\lambda _{1}}=0.0,\frac {\chi }{\lambda _{1}}=0.1,\frac {\delta }{\lambda _{1}}=2$ ) we have plotted Fig. 3g, where the amplitude increases and there are stripes on one side of the peaks. When we add the damping to the previous case ($\frac {\gamma }{\lambda _{1}}=0.004,\frac {\chi }{\lambda _{1}}=0.1 ,\frac {\delta }{\lambda _{1}}=2$ ), Fig. 3h shows the function P(𝜃,t) to suffer from a decrease in the amplitude of the phase with the growing of the scaled time. In general, the damping plays a role in decreasing the P-D, while the detuning works to increase a portion of the phase on the expense of the other part. The Kerr-like medium leads to decrease the amplitudes and spread of a crashed phase.

Fig. 3

Phase distribution P(𝜃,t) versus the scaled time λ₁t with the same parameters in Fig. 2

5 The Quasi-Probability Distribution (Q-PD)

The analytical discussion about the behavior of the quasi-probability distribution (Q-PD) for the present system is studied in this section. The Q-PD can be defined by normal and anti-normal ordering operators through characteristic functions. Also, Q-PD may be defined by using displaced number states as series [41]:

$$ F(\varGamma,s)=\frac{2}{\pi}\sum\limits_{k=0}^{\infty}(-1)^{k}\frac{(1+s)^{k}}{(1-s)^{1+k}}\langle k,\varGamma|\hat{\rho}_{f}|\varGamma,k \rangle, $$

(20)

where Γ = x + iy. The parameter s determines the type of Q-PD function, where for W-function the parameter (s = 0), for Q-function (s = − 1), and for P-function (s = 1). In what follow we will give analytical description for W-F and Q-F.

5.1 The Wigner Function

We display the W-function (W(x,y)), where x = Re(Γ), y = Im(Γ) at fixed values of the scaled time. From the reduced density matrix for the cavity field, the W-function W(x,y) is expressed as:

$$ F(\varGamma,t) = \frac{1}{\pi}\sum\limits_{k=0}^{\infty}\sum\limits_{n,m=0}^{\infty}(- 1)^{k} \left( \mathscr{A}_{n}(t) \mathscr{A}_{m}^{*}(t)G_{k,n}({\varGamma}) G_{m,k}({\varGamma}) +\mathscr{B}_{n}(t) \mathscr{B}_{m}^{*}(t)G_{k,n+1}({\varGamma}) G_{m+1,k}({\varGamma}) \right), $$

(21)

where

$$ G_{k,l}=e^{\frac{-|\varGamma|^{2}}{2}} \sum\limits_{j=0}^{min(k,l)}\frac{(-{\varGamma})^{k-j}({\varGamma}^{*})^{l-j}\sqrt{k! l!}}{(l-j)!(k-j)! j!}. $$

(22)

Figure 4 displays the effect of the damping parameter $\frac {\gamma }{\lambda _{1}}$, detuning parameter $\frac {\delta }{\lambda _{1}}$ and Kerr-like medium $\frac {\chi }{\lambda _{1}}$ on W-function with α = 4,and r = 0.7, while the field and atom are prepared initially in the same states as the first section. In Fig. 4a we put ($\lambda _{1}t=\gamma =\delta =\frac {\chi }{\lambda _{1}} =0$), it corresponds to squeezed state [42], where a single peak at (x = 4,y = 0). At λ₁t = 4π and absence the three parameters, Fig. 4b shows that two squeezed separated peaks between them an oscillatory regime. When we increase α, the separation between peaks increases. Also, when we increase r, the oscillatory regime increases. The negative values in this figure correspond to a highly non-classical nature of squeezed coherent state. The damping parameter ($\frac {\gamma }{\lambda _{1}}=0.004$) with the previous case leads to decrease of the highest of peaks and negative values [43], see Fig. 4c. The effect of the classical field with the detuning parameter $\frac {\delta }{\lambda _{1}}=2$ is shown in Fig. 4d, where one of the separated peaks increase to almost approach to a free case (case of resonance), while negative values decrease to $\simeq -0.1$ lower than the previous damping case. When we put $\frac {\gamma }{\lambda _{1}}=0.004$, the highest of all peaks decrease, see Fig. 4e. The influence of Kerr-like medium ($\frac {\chi }{\lambda _{1}}=0.1$) on the Wigner distribution is shown in Fig. 4f, where the all peaks reduce to smaller peaks with interference between them, and the negative values increase. By adding the decay $\frac {\gamma }{\lambda _{1}}=0.004$, the non-classicality (negative values) decreases, see Fig. 4g. A remarkable behavior of the W-function in the case of off-resonance and presence of Kerr-like ($\frac {\delta }{\lambda _{1}}=2 ,\frac {\chi }{\lambda _{1}}=0.01$) where the classical field rearranges the peaks such as the fan panels, while the negative values (non-classical) increase, see Fig. 4h. If we cost the damping with Kerr-like in the off-resonance case, the peaks of W-function decrease. In general, the decay parameter leads to a decrease in the heights of peaks and the non-classicality. The detuning parameter plays a role in decreasing the non-classicality. While the Kerr-like medium plays a role in increasing the number of peaks and the non-classicality.

Fig. 4

The contour digram of the W-function against x and y at α = 4, r = 0.7 and C_e = 1,C_g = 0 with different values of ($\lambda _{1}t,\frac {\gamma }{\lambda _{1}} ,\frac {\delta }{\lambda _{1}} ,\frac {\chi }{\lambda _{1}}$): where a (0, 0, 0, 0), b (4 π, 0, 0, 0), c (4 π, 0.004, 0, 0), d (4 π, 0, 2, 0), e (4 π, 0.004, 2, 0 ), f (4 π, 0, 0, 0.1), g (4 π, 0.004, 0, 0.1), h (4 π, 0, 2, 0.1),and i (4 π, 0.004, 2, 0.1)

5.2 The Husimi Q-Function

Finally, we turn our attention to study Husimi Q-function. By using the reduced field density operator are express the Q-function as the coherent state expectation value of the operator as follows:

$$ Q(\varGamma,t)=\frac{1}{\pi}\langle\varGamma|\rho_{F}(t)|{\varGamma}\rangle, $$

(23)

where Γ = x + iy. The expression of the Q-function for the present system is written as:

$$ Q(\varGamma,t)=\frac{1}{\pi}e^{-|\varGamma|^{2}}\sum\limits_{m,n}^{\infty}\left[ \mathscr{A}_{m}(t)\mathscr{A}^{*}_{n}(t)\frac{({\varGamma}^{*})^{m}({\varGamma})^{n}}{\sqrt{n!m!}}+\mathscr{B}_{m}(t)\mathscr{B}^{*}_{n}(t)\frac{({\varGamma}^{*})^{m+1}({\varGamma})^{n+1}}{\sqrt{(n+1)!(m+1)!}}\right]. $$

(24)

Under the same conditions of Fig. 4, we have plotted Fig. 5 to discuss the behavior of the Q-function. Figure 5a displays the free case, where λ₁t = 0 and the three parameters are zero. The Q-function has one squeezed peak at point (4,0), also it has the maximum value 0.25. With the scaled time λ₁t= 4π, the one peak splits into two peaks at (0,± 4) have the maximum value $\simeq 0.125$, this is evident in Fig. 5b. We will keep the value of the scaled time without a change in the rest of the figures. The effect of decay parameter $\frac {\gamma }{\lambda _{1}}=0.004$ on the Husimi Q-function is shown in Fig. 5c, the two peaks at the same position and decay. In the case of off-resonance $\frac {\delta }{\lambda _{1}}=2$ ($\frac {\gamma }{\lambda _{1}}=0, \frac {\chi }{\lambda _{1}}=0$) one of two peaks increases in height, while the other peak decreases, see Fig. 5d. When adding the damping parameter $\frac {\gamma }{\lambda _{1}}=0.004$ for the previous case, we observe that the two peaks decrease, see Fig. 5e. The influence of the Kerr-like medium $\frac {\chi }{\lambda _{1}}=0.1$ on the function is shown in Fig. 5f, where the two peaks split into four peaks with interference. They are rotating around the center of phase space. When adding the damping $\frac {\gamma }{\lambda _{1}}=0.004$, the heights of four peaks decrease, see Fig. 5g. In the off-resonance case and the Kerr-like medium $\frac {\delta }{\lambda _{1}}=2 ,\ \frac {\chi }{\lambda _{1}}=0.1$, we note rearrangement of the four peaks where $\frac {\delta }{\lambda _{1}}$ works to reduce the interference in the phase produced by$\frac {\chi }{\lambda _{1}}$, see Fig. 5h. By adding the damping parameter for this case, we see that all peaks are decayed, this is evident in Fig. 5i. From this discussion for the Q-function, the results confirm that the phase has the same behavior under the effects of the classical field, damping, and the Kerr-like medium as the W-function.

Fig. 5

The contour digram of the Q-function against x and y with the same parameters in Fig. 4

6 Conclusion

Under some canonical transformations, we transform the system consisting of an external classical field and the Kerr-like medium interacting with a moving two-level atom in a quantized cavity field in the presence of the damping parameter of the field with a system similar to JCM with Kerr-like medium and a damping term. We have examined the effect of damping, the Kerr-like medium and the classical field on the atomic inversion, where we have prepared the atom in its excited state and the field in a squeezed coherent state. The system has shown that an increase in the value of the damping leads to a decrease in the atomic inversion, while the classical field included in detuning play role on oscillating the system around zero and decrease the amplitude of oscillation, while the Kerr-like play role in shortening the oscillations. Furthermore, we have discussed the influence of the three parameters of the present system on the phase through the Pegg and Barnett phase, W-function, and Husimi Q-function. We found a decrease in the phase when we increase the damping parameter, and the classical field plays a role in the increase of a part of the phase on the other. During the Kerr-like medium causes diffusion of the phase. Also, we are studied the non-classicality of the squeezed coherent state through the Wigner distribution. The damping as well as the classical field decreases the non-classicality, simultaneously the Kerr-like medium works to increase it.