Induced States from Coherent State via Photon-Addition Operations

Abstract

Three classes of quantum states are induced from coherent state (CS) based on three operations associated with the photon creation operator. One class is the famous photon-added coherent state (PACS) introduced by Agarwal and Tara (Phys. Rev. A 43, 492–497, 1991). The other two classes are the orthogonal states of the CS (Here we abbreviate them as OCS1 and OCS2). Indeed, the OCS1 is just the displacement Fock state, and the OCS2 is constructed by orthogonalizer proposed by Kim group (Phys. Rev. Lett. 116, 110501, 2016). In contrast to the original CS, the three induced states can exhibit their respective nonclassical properties. We study and compare some properties for these four quantum states (CS, PACS, OCS1, OCS2). The studied properties include the mean number of photons, the sub-Poissonian character, the squeezing effect in the field quadrature, and the quasi-probability distributions including the Husimi Q function and the Wigner function. Besides, their fidelities between each two of them are also discussed.

1 Introduction

Coherent states, expressed as eigenvectors of the lowering (or annihilation) operator and forming an overcomplete family, were introduced in the early papers of John R. Klauder [1]. In the quantum theory of light (quantum electrodynamics) and other bosonic quantum field theories, coherent states were also introduced by the work of Roy J. Glauber in 1963 [2]. So coherent states mark the birth of modern quantum optics and form a very useful and widely used basis in quantum physics [3, 4]. Base on the coherent states, some novel quantum states can be constructed by the different theoretical and experimental ways [5,6,7,8,9,10]. Theoretically, there are many proposals to construct quantum states in quantum state engineering [11,12,13]. Among these proposals, two typical ways of constructing new quantum states are especially common. One way is by making the superposition of the known quantum states [14,15,16,17]. For instance, the well-known Schrodinger cat state, i.e. $(1/ \sqrt {2})(\left \vert \alpha \right \rangle +\left \vert -\alpha \right \rangle )$, is just the superposition state of two coherent states (|α〉 and |−α〉) [18]. Another way to obtain quantum states is by application of the quantum operator on the known quantum state [19,20,21,22]. For instance, the squeezed coherent state can be obtained by applying the squeezing operator on the coherent state [23]. Every constructed state will exhibit its particular quantum properties, which can meet the different needs of quantum technology [24,25,26].

However, one downside for coherent states is that these states are not orthogonal to one another. Then if we give a coherent state, how can we obtain its orthogonal states? So orthogonaliztion to a known state is also a way to construct quantum state. Recently, Vanner et al introduced a general method for quantum state orthogonalization [27]. By operating an orthogonalizer on the original state, one can construct its orthogonal state. This technique can become a useful tool for quantum state engineering to produce custom-made quantum states [28, 29]. This will help us to construct the orthogonal states for the coherent state.

Inspired by the ideas of the quantum operation and the orthogonalization, we induce three classes of quantum states from the original coherent state (CS) in this paper. All the operations we used are associated with photon creation operator. One induced state is the famous photon-added coherent state (PACS) introduced by Agarwal and Tara in 1991 [30]. The other two induced states are the orthogonal states of CS. Among them, one is just the displacement Fock state, the other is constructed by orthogonalizer proposed by Kim group. We study and compare some properties for these four quantum states.

The remainder of our paper is organized as follows. In Section 2, we give the brief description of three classes of induced states from coherent state, whose normalization factors are also calculated. In addition, we also discuss the similarity for these four quantum states by virtue of the fidelities. In Section 3, we give and compare their representation in Fock state space. In Section 4, we investigate and compare some statistical properties, including mean photon number, sub-Poisson character, quadrature squeezing effect. In Section 6, we present and compare two kinds of quasi-probabilities, i.e., the Husimi Q function and the Wigner function. Conclusions and remarks are summarized in the last section.

2 Description of Three Induced States

In this section, we give a brief description for four quantum states, i.e. CS, PACS, OCS1 and OCS2.

• (I) Coherent state: CS

  The CS |α〉 is the eigenstate of the annihilation operator and is also look as the displacement vacuum state, i.e.

  $$ a\left\vert \alpha \right\rangle =\alpha \left\vert \alpha \right\rangle ,\left\vert \alpha \right\rangle =D\left( \alpha \right) \left\vert 0\right\rangle , $$

  (1)

  where D (α) = exp (αa^†− α^∗a) is the displacement operator. Based on the original CS |α〉 and by virtue of three operations associated with the photon creation operator a^†, we induce the following three classes of quantum states.

• (II) Induced state I: PACS

  By applying the operator a^†m (m is an integer) on the CS |α〉, we obtain the state

  $$ \left\vert \alpha_{a}\right\rangle =\frac{1}{\sqrt{N_{a}}}a^{\dag m}\left\vert \alpha \right\rangle $$

  (2)

  with the normalization factor $N_{a}=\partial _{\mu }^{m}\partial _{\nu }^{m}e^{\mu \alpha +\nu \alpha ^{\ast }+\mu \nu }|_{\mu =\nu = 0}=m!L_{m}(-\left \vert \alpha \right \vert ^{2})$, where L_m(x) is the Laguerre polynomial of order m. This state is just the famous photon-addition coherent state (PACS) introduced by Argawal and Tara in 1991. In their paper, they studied the mathematical and physical properties for the PACS, such as the phase squeezing effect, the sub-Poissonian character, and the quasiprobability distributions. In the limit α → 0 (m → 0) the state |α_a〉 reduced to the Fock state |m〉 (the CS |α〉), which shows that |α_a〉 occupies an intermediate position between |m〉 and |α〉.

• (III) Induced state II: OCS1

  By repeated application (m times) of the operator a^†− α^∗1 to the CS |α〉 (where 1 denotes the identity operator), we obtain the state

  $$ \left\vert \alpha_{1}^{\perp }\right\rangle =\frac{1}{\sqrt{N_{1}^{\perp }}} \left( a^{\dag }-\alpha^{\ast }\mathbf{1}\right)^{m}\left\vert \alpha \right\rangle $$

  (3)

  with the normalization factor $N_{1}^{\perp }=m!$. In essence, the state $\left \vert \alpha _{1}^{\perp }\right \rangle$ is just the displacement Fock state D (α) |m〉 according to D (α)D^†(α) = 1 and D^†(α)a^†D (α) = a^† + α^∗. However, we must notice that PACS |α_a〉 is not D (α) |m〉, because the operators D (α) and a^†m do not commute. In other perspective, $\left \vert \alpha _{1}^{\perp }\right \rangle$ (= D (α) |m〉) is an orthogonal state of the CS |α〉 (= D (α) |0〉) due to $\left \langle \alpha \right \vert \left \vert \alpha _{1}^{\perp }\right \rangle = 0$. So we call $\left \vert \alpha _{1}^{\perp }\right \rangle$ as OCS1 in this paper.

• (IV) Induced state III: OCS2

  By application of the operator a^†m − α^∗m1 to the CS |α〉, we obtain the state

  $$ \left\vert \alpha_{2}^{\perp }\right\rangle =\frac{1}{\sqrt{N_{2}^{\perp }}} \left( a^{\dag m}-\alpha^{\ast m}\mathbf{1}\right) \left\vert \alpha \right\rangle $$

  (4)

  with the normalization factor $N_{2}^{\perp }=N_{a}-\left \vert \alpha \right \vert ^{2m}=m!L_{m}(-\left \vert \alpha \right \vert ^{2})-\left \vert \alpha \right \vert ^{2m}$. It is simple to check that $\left \langle \alpha \right \vert \left \vert \alpha _{2}^{\perp }\right \rangle = 0$ as required, which means that $\left \vert \alpha _{2}^{\perp }\right \rangle$ is also an orthogonal state of the CS |α〉. So we call $\left \vert \alpha _{2}^{\perp }\right \rangle$ as OCS2 in this paper.

Recently, the research on orthogonal quantum states has aroused widespread interest of researchers. Two states, which are orthogonal to each other, are then maximally discernible. In addition, we remind reader to notice some special cases including (1) when m = 1, we know that $\left \vert \alpha _{1}^{\perp }\right \rangle =\left \vert \alpha _{2}^{\perp }\right \rangle$. (2) when α = 0, we find that |α〉 → |0〉, |α_a〉 → |m〉, $\left \vert \alpha _{1}^{\perp }\right \rangle \rightarrow \left \vert m\right \rangle$, and $\left \vert \alpha _{2}^{\perp }\right \rangle \rightarrow \left \vert m\right \rangle$. Following the steps discussed for the PACS in Argawal and Tara’s paper, we further study and compare the similarity and some statistical properties for these four quantum states.

3 Fidelity Between These Quantum States

Generally, one can discern two quantum states (|ψ₁〉 and |ψ₂〉) by seeing the overlap 〈ψ₁| |ψ₂〉 or the fidelity defined by F (|ψ₁〉 , |ψ₂〉) = |〈ψ₁| |ψ₂〉|². In essence, fidelity is a measure of the “closeness” (or similarity) of two quantum states in quantum theory [31]. In order to discern any two of these four quantum states, i.e. CS |α〉, PACS |α_a〉, OCS1 $\left \vert \alpha _{1}^{\perp }\right \rangle$ , and OCS2 $\left \vert \alpha _{2}^{\perp }\right \rangle$, we can express six fidelities as follows

$$\begin{array}{@{}rcl@{}} F_{1} &=&F\left( \left\vert \alpha \right\rangle ,\left\vert \alpha_{1}^{\perp }\right\rangle \right) = 0, F_{2}=F\left( \left\vert \alpha \right\rangle ,\left\vert \alpha_{2}^{\perp }\right\rangle \right) = 0, \\ F_{3} &=&F\left( \left\vert \alpha \right\rangle ,\left\vert \alpha_{a}\right\rangle \right) =\frac{\left\vert \alpha \right\vert^{2m}}{N_{a}}, F_{4}=F\left( \left\vert \alpha_{a}\right\rangle ,\left\vert \alpha_{2}^{\perp }\right\rangle \right) =\frac{N_{2}^{\perp }}{N_{a}}, \\ F_{5} &=&F\left( \left\vert \alpha_{a}\right\rangle ,\left\vert \alpha_{1}^{\perp }\right\rangle \right) =\frac{m!}{N_{a}}, F_{6}=F\left( \left\vert \alpha_{1}^{\perp }\right\rangle ,\left\vert \alpha_{2}^{\perp }\right\rangle \right) =\frac{m!}{N_{2}^{\perp }}. \end{array} $$

(5)

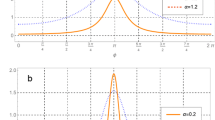
The fact is that $\left \vert \alpha _{1}^{\perp }\right \rangle$ and $\left \vert \alpha _{2}^{\perp }\right \rangle$ are always orthogonal to |α〉, which lead to F₁ = F₂ = 0 for all cases with different values of m. While all other fidelities (F₃, F₄, F₅, and F₆) depend on the relative parameters m and α. In Fig. 1, we plot the variation of Fidelities F₃, F₄, F₅, and F₆ as a function of the amplitude |α| with different values of m.

Fig. 1

(Color online) Fidelities F₃ (black solid), F₄ (blue dashed), F₅ (red dotted), and F₆ (green dotdashed) as a function of the amplitude $\left \vert \protect \alpha \right \vert$ with am = 1; bm = 2; cm = 3; dm = 4

A noteworthy feature is that the identity F₃ + F₄ = 1 is always hold, which means that PACS |α_a〉 is an intermediate state between CS |α〉 and OCS2 $\left \vert \alpha _{2}^{\perp }\right \rangle$. In the limit case, when |α| → 0, F₃ → 0 and F₄ → 1; when |α| →∞ , F₃ → 1 and F₄ → 0. Moreover, the intersecting point F₃ = F₄ = 0.5 is found at the condition (m, |α|) with (1,1), (2,2.10938), (3,3.27562), (4,4.45756), ⋯. Because $\left \vert \alpha _{1}^{\perp }\right \rangle$ is just $\left \vert \alpha _{2}^{\perp }\right \rangle$ for the case m = 1, which lead to F₃ = |α|²(1 + |α|²)^− 1, F₄ = F₅ = (1 + |α|²)^− 1, and F₆ = 1 (see Fig. 1a). In Fig. 2, we plot the difference F₆ − F₅ as the function of |α| for m = 1,2,3,4. The results show that (1) the difference between F₅ and F₆ is changing bigger for case m = 1; (2) the value of F₅ is smaller than but very close to that of F₆ for cases m > 1. The maximum values of difference (F₆ − F₅) are found at (m; |α|, (F₆ − F₅)_max), which correspond to (2;1.48806,0.0573086), (3;1.47475,0.00717978), (4;1.5808,0.000969541), ⋯. This means that the similarity of |α_a〉 and $\left \vert \alpha _{1}^{\perp }\right \rangle$ is very close to that of $\left \vert \alpha _{1}^{\perp }\right \rangle$ and $\left \vert \alpha _{2}^{\perp }\right \rangle$ as m increasing.

Fig. 2

The difference F₆ − F₅ as a function of the amplitude $\left \vert \protect \alpha \right \vert$ with am = 1; bm = 2; cm = 3; dm = 4

4 Representation of These Quantum States in Fock Space

Next we study the number distributions of the fields in CS |α〉, PACS |α_a〉, OCS1 $\left \vert \alpha _{1}^{\perp }\right \rangle$ , and OCS2 $\left \vert \alpha _{2}^{\perp }\right \rangle$. Different quantum states have different photon components [32]. Therefore we expand these four quantum states in Fock state basis.

• (I) The SC |α〉 in terms of Fock states can be written as

  $$ \left\vert \alpha \right\rangle =\sum\limits_{n = 0}^{\infty }c_{n,\left\vert \alpha \right\rangle }\left\vert n\right\rangle $$

  (6)

  with the coefficient

  $$ c_{n,\left\vert \alpha \right\rangle }=e^{-\frac{\left\vert \alpha \right\vert^{2}}{2}}\frac{\alpha^{n}}{\sqrt{n!}}, $$

  (7)

  which include all Fock components in Poisson distribution.

• (II) The PACS |α_a〉 in terms of Fock states can be written as

  $$ \left\vert \alpha_{a}\right\rangle =\sum\limits_{n=m}^{\infty }c_{n,\left\vert \alpha_{a}\right\rangle }\left\vert n\right\rangle $$

  (8)

  with the coefficient

  $$ c_{n,\left\vert \alpha_{a}\right\rangle }=e^{-\frac{\left\vert \alpha \right\vert^{2}}{2}}\frac{\alpha^{n-m}\sqrt{n!}}{\left( n-m\right) ! \sqrt{N_{a}}}. $$

  (9)

  Thus |α_a〉 amounts to a truncation of |α〉, i.e. all the Fock states |0〉, |1〉, |2〉, ⋯ , |m − 1〉 are removed in a particular fashion.

• (III) The OCS1 $\left \vert \alpha _{1}^{\perp }\right \rangle$ in terms of Fock states can be written as

  $$ \left\vert \alpha_{1}^{\perp }\right\rangle =\sum\limits_{n = 0}^{\infty }c_{n,\left\vert \alpha_{1}^{\perp }\right\rangle }\left\vert n\right\rangle $$

  (10)

  with the coefficient

  $$ c_{n,\left\vert \alpha_{1}^{\perp }\right\rangle }=\frac{e^{-\frac{ \left\vert \alpha \right\vert^{2}}{2}}}{\sqrt{n!m!}}\partial_{s}^{n}{\partial_{h}^{m}}e^{s\alpha -h\alpha^{\ast }+hs}|_{s=h = 0}. $$

  (11)

  Noting that $m!=N_{1}^{\perp }$.

• (IV) The OCS2 $\left \vert \alpha _{2}^{\perp }\right \rangle$ in terms of Fock states can be written as two sections in the following form

  $$ \left\vert \alpha_{2}^{\perp }\right\rangle =\sum\limits_{n = 0}^{m-1}c_{n,\left\vert \alpha_{2}^{\perp }\right\rangle }^{\left( 1\right) }\left\vert n\right\rangle +\sum\limits_{n=m}^{\infty }c_{n,\left\vert \alpha_{2}^{\perp }\right\rangle }^{\left( 2\right) }\left\vert n\right\rangle $$

  (12)

with the coefficient

$$\begin{array}{@{}rcl@{}} c_{n,\left\vert \alpha_{2}^{\perp }\right\rangle }^{\left( 1\right) } &=&-e^{-\frac{\left\vert \alpha \right\vert^{2}}{2}}\frac{\alpha^{\ast m}\alpha^{n}}{\sqrt{n!N_{2}^{\perp }}}, \\ c_{n,\left\vert \alpha_{2}^{\perp }\right\rangle }^{\left( 2\right) } &=&c_{n,\left\vert \alpha_{2}^{\perp }\right\rangle }^{\left( 1\right) }+e^{-\frac{\left\vert \alpha \right\vert^{2}}{2}}\frac{\alpha^{n-m}\sqrt{ n!}}{\left( n-m\right) !\sqrt{N_{2}^{\perp }}}. \end{array} $$

(13)

Obviously, the orthogonal state $\left \vert \alpha _{2}^{\perp }\right \rangle$ has repaired the truncated components of |α_a〉 and has all Fock components like |α〉 (but the distribution is not poisson distribution).

The photon number distribution for the optical field can be defined as P (n) = |C_n|², where C_n is the coefficient of the component |n〉 in its expansion in the Fock space. Photon number distributions for some CS |α〉, PACS |α_a〉, OCS1 $\left \vert \alpha _{1}^{\perp }\right \rangle$, and OCS2 $\left \vert \alpha _{2}^{\perp }\right \rangle$ with α = 1 + i and different values of m are plotted in Fig. 3.

Fig. 3

(Color online) Photon number distribution for CS (column1), PACS (column 2), OCS1 (column 3), and OCS2 (column 4) with fixed α = 1 + i for m = 1 (row 1), m = 2 (row 2), m = 3 (row 3), and m = 4 (row 4)

5 Quantum Statistical Properties

In order to study the quantum statistical properties for CS |α〉, PACS |α_a〉, OCS1 $\left \vert \alpha _{1}^{\perp }\right \rangle$ , and OCS2 $\left \vert \alpha _{2}^{\perp }\right \rangle$, we firstly give the general expressions of the expectation value 〈a^†ka^l〉 (k and l are integers) for them.

• (I) For CS |α〉, we have

  $$ \left\langle a^{\dag k}a^{l}\right\rangle_{\left\vert \alpha \right\rangle }=\alpha^{\ast k}\alpha^{l}. $$

  (14)

• (II) For PACS |α_a〉, we have

  $$ \left\langle a^{\dag k}a^{l}\right\rangle_{\left\vert \alpha_{a}\right\rangle }=\frac{\left\langle a^{m}a^{\dag k}a^{l}a^{\dag m}\right\rangle_{\left\vert \alpha \right\rangle }}{N_{a}}. $$

  (15)

• (III) For OCS1 $\left \vert \alpha _{1}^{\perp }\right \rangle$, we have

  $$ \left\langle a^{\dag k}a^{l}\right\rangle_{\left\vert \alpha_{1}^{\perp }\right\rangle }=\frac{1}{m!}{\partial_{h}^{m}}{\partial_{s}^{m}}\partial_{\mu }^{k}\partial_{\nu }^{l}e^{hs+\mu \left( h+\alpha^{\ast }\right) +\nu \left( s+\alpha \right) }|_{h=s=\mu =\nu = 0}. $$

  (16)

• (IV) For OCS2 $\left \vert \alpha _{2}^{\perp }\right \rangle$, we have

  $$\begin{array}{@{}rcl@{}} \left\langle a^{\dag k}a^{l}\right\rangle_{\left\vert \alpha_{2}^{\perp }\right\rangle } &=&\frac{\left\langle a^{m}a^{\dag k}a^{l}a^{\dag m}\right\rangle_{\left\vert \alpha \right\rangle }}{N_{2}^{\perp }}+\frac{ \left\vert \alpha \right\vert^{2m}\left\langle a^{\dag k}a^{l}\right\rangle_{\left\vert \alpha \right\rangle }}{N_{2}^{\perp }} \\ &&-\frac{\alpha^{\ast m}\left\langle a^{m}a^{\dag k}a^{l}\right\rangle_{\left\vert \alpha \right\rangle }}{N_{2}^{\perp }}-\frac{\alpha^{m}\left\langle a^{\dag k}a^{l}a^{\dag m}\right\rangle_{\left\vert \alpha \right\rangle }}{N_{2}^{\perp }}. \end{array} $$

  (17)

Here, we give the the general expression of $\left \langle a^{m_{1}}a^{\dag k}a^{l}a^{\dag m_{2}}\right \rangle _{\left \vert \alpha \right \rangle }$ with the form

$$ \left\langle a^{m_{1}}a^{\dag k}a^{l}a^{\dag m_{2}}\right\rangle_{\left\vert \alpha \right\rangle }=\partial_{\mu }^{m_{1}}\partial_{g}^{k}{\partial_{h}^{l}}\partial_{\nu }^{m_{2}}e^{h\nu + g\mu +\mu \nu +\left( h+\mu \right) \alpha +\left( g+ \nu \right) \alpha^{\ast }}|_{g=h=\mu =\nu = 0}. $$

(18)

By choosing the proper values of (m₁, k, l, m₂) from (18), one can obtain (14), (15) and (17).

5.1 Mean Number of Photons

The mean number of photons is given by

$$ \bar{n}=\left\langle a^{\dag }a\right\rangle . $$

(19)

From their respective 〈a^†ka^l〉 with k = l = 1 in (14), (15), (16) and (17), we obtain

$$ \bar{n}_{\left\vert \alpha \right\rangle }=\left\vert \alpha \right\vert^{2}, $$

(20)

$$ \bar{n}_{\left\vert \alpha_{a}\right\rangle }=\frac{\left( m + 1\right) L_{m + 1}(-\left\vert \alpha \right\vert^{2})}{L_{m}(-\left\vert \alpha \right\vert^{2})}-1, $$

(21)

$$ \bar{n}_{\left\vert \alpha_{1}^{\perp }\right\rangle }=m+\left\vert \alpha \right\vert^{2}, $$

(22)

and

$$ \bar{n}_{\left\vert \alpha_{2}^{\perp }\right\rangle }=\frac{\left( m + 1\right) !L_{m + 1}(-\left\vert \alpha \right\vert^{2})}{ m!L_{m}(-\left\vert \alpha \right\vert^{2})-\left\vert \alpha \right\vert^{2m}}-\frac{\left( 2m + 1\right) \left\vert \alpha \right\vert^{2m}+\left\vert \alpha \right\vert^{2\left( m + 1\right) }}{ m!L_{m}(-\left\vert \alpha \right\vert^{2})-\left\vert \alpha \right\vert^{2m}}-1 $$

(23)

for CS |α〉, PACS |α_a〉, OCS1 $\left \vert \alpha _{1}^{\perp }\right \rangle$, and OCS2 $\left \vert \alpha _{2}^{\perp }\right \rangle$, respectively. In particular, when m = 1, we have

$$\begin{array}{@{}rcl@{}} \bar{n}_{\left\vert \alpha_{a}\right\rangle ,m = 1} &=&2+\left\vert \alpha \right\vert^{2}-\frac{1}{1+\left\vert \alpha \right\vert^{2}}, \\ \bar{n}_{\left\vert \alpha_{1}^{\perp }\right\rangle ,m = 1} &=&\bar{n}_{\left\vert \alpha_{2}^{\perp }\right\rangle ,m = 1}= 1+\left\vert \alpha \right\vert^{2}. \end{array} $$

(24)

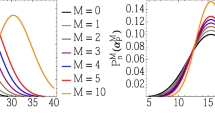
In Figs. 4 and 5, we show the mean number of photons as the function of |α|² for CS |α〉, PACS |α_a〉, OCS1 $\left \vert \alpha _{1}^{\perp }\right \rangle$, and OCS2 $\left \vert \alpha _{2}^{\perp }\right \rangle$ with different m. Obviously, the mean number of photons for |α〉 and $\left \vert \alpha _{1}^{\perp }\right \rangle$ is linearly proportional to |α|². Moreover, there exists a general trend, i.e., $\bar {n}_{\left \vert \alpha _{a}\right \rangle }>\bar {n}_{\left \vert \alpha _{2}^{\perp }\right \rangle }>\bar {n}_{\left \vert \alpha _{1}^{\perp }\right \rangle }$, for small value of m. As m increases, the difference between $\bar {n}_{\left \vert \alpha _{a}\right \rangle }$ and $\bar {n}_{\left \vert \alpha _{2}^{\perp }\right \rangle }$ change small. The fact is that the mean number of photons for |α_a〉 is nearly equal to that for $\left \vert \alpha _{2}^{\perp }\right \rangle$, that is $\bar {n}_{\left \vert \alpha _{a}\right \rangle }\approx \bar {n}_{\left \vert \alpha _{2}^{\perp }\right \rangle }$. In order to further verify this fact, we numerate some values of $(\left \vert \alpha \right \vert ^{2}, m; \bar {n}_{\left \vert \alpha \right \rangle }, \bar {n}_{\left \vert \alpha _{a}\right \rangle }, \bar {n}_{\left \vert \alpha _{1}^{\perp }\right \rangle }, \bar {n}_{\left \vert \alpha _{2}^{\perp }\right \rangle })$ as example in Table 1.

Fig. 4

(Color online) Mean number of photons $\bar {n}$ for CS (black solid), PACS (blue dashed), OCS1 (red dotted), and OCS2 (green dotdashed) as a function of the intensity $\left \vert \protect \alpha \right \vert ^{2}$ with am = 1; bm = 2; cm = 3; dm = 4

Fig. 5

(Color online) Mean number of photons $\bar {n}$ for CS (black line), PACS (blue line), OCS1 (red line), and OCS2 (green line) as a function of the intensity $\left \vert \protect \alpha \right \vert ^{2}$. The solid, dashed, dotted, dotdashed lines are corresponding to m = 1,2,3,4 in left figure and m = 5,10,15,20 in right figure

Table 1 Some values of $(\left \vert \protect \alpha \right \vert ^{2}, m; \bar {n }_{\left \vert \protect \alpha \right \rangle }, \bar {n}_{\left \vert \protect \alpha _{a}\right \rangle }, \bar {n}_{\left \vert \protect \alpha _{1}^{\perp }\right \rangle }, \bar {n}_{\left \vert \protect \alpha _{2}^{\perp }\right \rangle })$

5.2 Sub-Poissonian Statistics

The Mandel Q parameter measures the departure of the occupation number distribution from Poissonian statistics. It was introduced in quantum optics by L. Mandel [33]. It is a convenient way to characterize non-classical states with negative values indicating a sub-Poissonian statistics, which have no classical analog. In this subsection, we examine the Mandel Q parameter defined by

$$ Q_{M}=\frac{\left\langle a^{\dagger 2}a^{2}\right\rangle }{\left\langle a^{\dagger }a\right\rangle }-\left\langle a^{\dagger }a\right\rangle $$

(25)

for CS |α〉, PACS |α_a〉, OCS1 $\left \vert \alpha _{1}^{\perp }\right \rangle$, and OCS2 $\left \vert \alpha _{2}^{\perp }\right \rangle$. The distribution is Poissonian when Q_M = 0, and super- (sub-) Poissonian if Q_M > 0 (Q_M < 0). In particular, when m = 1, we know

$$\begin{array}{@{}rcl@{}} Q_{M}|_{\left\vert \alpha_{a}\right\rangle ,m = 1} &=&-\frac{1 + 2\left\vert \alpha \right\vert^{2}+ 2\left\vert \alpha \right\vert^{4}}{1 + 4\left\vert \alpha \right\vert^{2}+ 4\left\vert \alpha \right\vert^{4}+\left\vert \alpha \right\vert^{6}}, \\ Q_{M}|_{\left\vert \alpha_{1}^{\perp }\right\rangle ,m = 1} &=&Q_{M}|_{\left\vert \alpha_{2}^{\perp }\right\rangle ,m = 1}= 2-\frac{3}{ 1+\left\vert \alpha \right\vert^{2}}. \end{array} $$

(26)

In Figs. 6 and 7, we display the variations of Q_M as the function of |α| for CS |α〉, PACS |α_a〉, OCS1 $\left \vert \alpha _{1}^{\perp }\right \rangle$, and OCS2 $\left \vert \alpha _{2}^{\perp }\right \rangle$ with different values of m. The values of Q_M less than zero signify the sub-Poissonian statistics of the field. For the CS |α〉, needless to say, we always have Q_M = 0, which shows the Poissonian statistics of the CS |α〉. For the PACS |α_a〉, we see that the field always exhibits a significant amount of sub-Poissonian statistics. While for OCS1 $\left \vert \alpha _{1}^{\perp }\right \rangle$ and OCS2 $\left \vert \alpha _{2}^{\perp }\right \rangle$, there exists alway a cut-off point, which turn from sub-Poissonian to super-Poissonian character. These cut-off points fasten on the point |α| = 0.71 for OCS1 $\left \vert \alpha _{1}^{\perp }\right \rangle$ with different values of m. In other word, the OCS1 with |α| ∈ [0, 0.71) will exhibit sub-Poissonian character. But the cut-off points |α|_c are decentralized for OCS2 $\left \vert \alpha _{2}^{\perp }\right \rangle$ with different values of m, where the sub-Poissonian character is in the interval of [0, |α|_c). The parameters (m, |α|_c) related with the cut-off points for OCS2 $\left \vert \alpha _{2}^{\perp }\right \rangle$ are taken for (1, 0.71), (2, 1.30), (3, 1.87), (4, 2.42), (5, 2.95), ⋯, (10, 5.54), ⋯, (15, 8.02), ⋯, (20, 10.42),⋯, respectively. In addition, we have the following interesting limits, i.e., $\lim _{\left \vert \alpha \right \vert \rightarrow 0}Q_{M}|_{\left \vert \alpha _{a}\right \rangle }=\lim _{\left \vert \alpha \right \vert \rightarrow 0}Q_{M}|_{\left \vert \alpha _{1}^{\perp }\right \rangle }=\lim _{\left \vert \alpha \right \vert \rightarrow 0}Q_{M}|_{\left \vert \alpha _{2}^{\perp }\right \rangle }=-1$, $\lim _{\left \vert \alpha \right \vert \rightarrow \infty }Q_{M}|_{\left \vert \alpha _{a}\right \rangle }= 0$, $\lim _{\left \vert \alpha \right \vert \rightarrow \infty }Q_{M}|_{\left \vert \alpha _{1}^{\perp }\right \rangle }= 2m$, and $\lim _{\left \vert \alpha \right \vert \rightarrow \infty }Q_{M}|_{\left \vert \alpha _{2}^{\perp }\right \rangle }= 2$.

Fig. 6

(Color online) Mandel parameter Q_M for CS (black solid), PACS (blue dashed), OCS1 (red dotted), and OCS2 (green dotdashed) as a function of the amplitude $\left \vert \protect \alpha \right \vert$ with am = 1; bm = 2; cm = 3; dm = 4

Fig. 7

(Color online) Mandel parameter Q_M for CS (black line), PACS (blue line), OCS1 (red line), and OCS2 (green line) as a function of the amplitude |α|. The solid, dashed, dotted, dotdashed lines are corresponding to m = 1,2,3,4 in left figure and m = 5,10,15,20 in right figure

5.3 Squeezing Effect in the Field Quadrature X

The CS is a minimum uncertainty state but not a squeezing state because the standard deviation equal for position and momentum. In order to discuss the squeezing effect for other three induced states, let us consider the field quadrature X defined by $X=\left (a+a^{\dag }\right ) /\sqrt {2}$. Its variance can expressed as [34, 35]

$$ \begin{array}{@{}rcl@{}} \left( {\Delta} X\right)^{2} &=&+\frac{\left\langle a^{\dag 2}\right\rangle -\left\langle a^{\dag }\right\rangle^{2}}{2}+\frac{\left\langle a^{2}\right\rangle -\left\langle a\right\rangle^{2}}{2} \end{array} $$

$$ \begin{array}{@{}rcl@{}} &&+\left\langle a^{\dag }a\right\rangle -\left\vert \left\langle a^{\dag }\right\rangle \right\vert^{2}+\frac{1}{2}. \end{array} $$

(27)

Obviously, the variance for CS |α〉 is 1/2, i.e. (ΔX)²|_|α〉 = 1/2. In particular, when m = 1, we have

$$ \begin{array}{@{}rcl@{}} \left( {\varDelta} X\right)_{\left\vert \alpha_{a}\right\rangle ,m = 1}^{2} &=& \frac{3-2\left\vert \alpha \right\vert^{2}-\left( \alpha^{2}+\alpha^{\ast 2}\right) +\left\vert \alpha \right\vert^{4}}{2(1+\left\vert \alpha \right\vert^{2})^{2}}, \end{array} $$

(28)

$$ \begin{array}{@{}rcl@{}} \left( {\varDelta} X\right)_{\left\vert \alpha_{1}^{\perp }\right\rangle ,m = 1}^{2} &=&\left( {\varDelta} X\right)_{\left\vert \alpha_{2}^{\perp }\right\rangle ,m = 1}^{2}=\frac{3}{2}. \end{array} $$

(29)

The variance (ΔX)² less than 1/2 implies that the quadrature X of the field is squeezed. Using the general expressions of 〈a^†ka^l〉 in (15), (16), and (17), we can obtain the value of (ΔX)² for PACS |α_a〉 , OCS1 $\left \vert \alpha _{1}^{\perp }\right \rangle$ , and OCS2 $\left \vert \alpha _{2}^{\perp }\right \rangle$, whose variations are shown in Figs. 8 and 9 as a function of the parameter |α|.

Fig. 8

(Color online) Variance $\left ({\Delta } X\right )^{2}$ for CS (black solid), PACS (blue dashed), OCS1 (red dotted), and OCS2 (green dotdashed) as a function of the amplitude $\left \vert \protect \alpha \right \vert$ with am = 1; bm = 2; cm = 3; dm = 4

Fig. 9

(Color online) Variance (ΔX)² for CS (black line), PACS (blue line), OCS1 (red line), and OCS2 (green line) as a function of the amplitude |α|. The solid, dashed, dotted, dotdashed lines are corresponding to m = 1,2,3,4 in left figure and m = 5,10,15,20 in right figure

Needless to say, (ΔX)² for CS |α〉 is always 1/2. For the PACS |α_a〉, the squeezing effect is found in the interval of [|α|_s, ∞), where the parameters (m, |α|_s) = (1, 1), (2, 0.94), (3, 0.90), (4, 0.87), (5, 0.85), ⋯, (10, 0.80), ⋯, (15, 0.78), ⋯, (20, 0.77). For the OCS1 $\left \vert \alpha _{1}^{\perp }\right \rangle$, we have $\left ({\Delta } X\right )_{\left \vert \alpha _{1}^{\perp }\right \rangle ,m}^{2}=(2m + 1)/2$, which is independent of |α| and always bigger than 1/2. For the OCS1 $\left \vert \alpha _{2}^{\perp }\right \rangle$, if m = 1, 2, 3, there is no squeezing effect. The squeezing effect is exhibited only for m > 3 and at the interval [|α|_min, |α|_max], where the parameters (m;[|α|_min, |α|_max]) = (4; [0.89, 1.71]), (5; [0.86, 2.30]), ⋯, (10; [0.80, 4.97]), ⋯, (15; [0.78, 7.47]), ⋯, (20; [0.77, 9.89]), ⋯.

6 Quasi-Probability Distribution

In this section, we study and compare two quasi-probability functions, including the Husimi Q function and the Wigner function for these four quantum states.

6.1 Husimi Q Function

The Husimi Q distribution [36] (called Q-function in the context of quantum optics) is one of the simplest distributions of quasiprobability in phase space. The Husimi Q distribution of a pure state ρ = |ψ〉 〈ψ| can be calculated through the formula

$$ Q_{\left\vert \psi \right\rangle }\left( \zeta \right) =\frac{1}{\pi } \text{Tr}[\left\vert \zeta \right\rangle \left\langle \zeta \right\vert \rho ]=\frac{1}{\pi }\left\vert \left\langle \zeta \right\vert \left\vert \psi \right\rangle \right\vert^{2}, $$

(30)

which is effectively a trace of the density matrix over the basis of coherent states |ζ〉 with ζ = x + iy.

• (I) For CS |α〉, we have

  $$ Q_{\left\vert \alpha \right\rangle }\left( \zeta \right) =\frac{1}{\pi }\exp \left( -\left\vert \zeta -\alpha \right\vert^{2}\right). $$

  (31)

• (II) For PACS |α_a〉, we have

  $$ Q_{\left\vert \alpha_{a}\right\rangle }\left( \zeta \right) =\frac{1}{\pi N_{a}}\left\vert \zeta \right\vert^{2m}\exp \left( -\left\vert \zeta -\alpha \right\vert^{2}\right) . $$

  (32)

• (III) For OCS1 $\left \vert \alpha _{1}^{\perp }\right \rangle$, we have

  $$ Q_{\left\vert \alpha_{1}^{\perp }\right\rangle }\left( \zeta \right) =\frac{ 1}{\pi N_{1}^{\perp }}\left\vert \zeta -\alpha \right\vert^{2m}\exp \left( -\left\vert \zeta -\alpha \right\vert^{2}\right). $$

  (33)

• (IV) For OCS2 $\left \vert \alpha _{2}^{\perp }\right \rangle$, we have

  $$ Q_{\left\vert \alpha_{2}^{\perp }\right\rangle }\left( \zeta \right) =\frac{ 1}{\pi N_{2}^{\perp }}\left\vert \zeta^{m}-\alpha^{m}\right\vert^{2}\exp \left( -\left\vert \zeta -\alpha \right\vert^{2}\right). $$

  (34)

In Fig. 10, we plot some Husimi Q functions for CS |α〉, PACS |α_a〉, OCS1 $\left \vert \alpha _{1}^{\perp }\right \rangle$, and OCS2 $\left \vert \alpha _{2}^{\perp }\right \rangle$, with α = 1 + i and different values of m . Husimi Q function is normalized to unity, $\int d^{2}\zeta Q_{\left \vert \psi \right \rangle }\left (\zeta \right ) = 1$ and is non-negative definite and bounded.

Fig. 10

(Color online) Husimi Q functions as a function of ζ = x + iy ($x,y\in \left [ -4,4\right ]$) for CS (column1), PACS (column 2), OCS1 (column 3), and OCS2 (column 4) with fixed α = 1 + i for m = 1 (row 1), m = 2 (row 2), m = 3 (row 3), and m = 4 (row 4)

6.2 Wigner Function

The Wigner quasiprobability distribution (also called the Wigner function) is another quasiprobability distribution [37, 38]. Through a combination of coherent displacements and parity measurement, the Wigner function W (ζ) for a pure state ρ = |ψ〉 〈ψ| can be measured by

$$ W_{\left\vert \psi \right\rangle }\left( \zeta \right) =\frac{2}{\pi } \text{Tr}[D\left( \zeta \right) \hat{\Pi}D^{\dag }\left( \zeta \right) \rho ]=\left\langle \psi \right\vert \hat{M}\left\vert \psi \right\rangle $$

(35)

with $M=\frac {2}{\pi }D\left (\zeta \right ) \hat {\Pi }D^{\dag }\left (\zeta \right )$, where $\hat {\Pi }=\left (-1\right )^{a^{\dag }a}$ is the parity operator, and D (ζ) = exp (ζa^†− ζ^∗a) is the usual displacement operator with ζ = x + iy.

• (I) For CS |α〉, we have

  $$ W_{\left\vert \alpha \right\rangle }\left( \zeta \right) =\frac{2}{\pi }\exp \left( -2\left\vert \zeta -\alpha \right\vert^{2}\right). $$

  (36)

• (II) For PACS |α_a〉, we have

  $$ W_{\left\vert \alpha_{a}\right\rangle }\left( \zeta \right) =\frac{2m!}{\pi N_{a}}(-1)^{m}\exp \left( -2\left\vert \zeta -\alpha \right\vert^{2}\right) L_{m}\left( \left\vert 2\zeta -\alpha \right\vert^{2}\right). $$

  (37)

• (III) For OCS1 $\left \vert \alpha _{1}^{\perp }\right \rangle$, we have

  $$ W_{\left\vert \alpha_{1}^{\perp }\right\rangle }\left( \zeta \right) =\frac{ 2}{\pi }(-1)^{m}\exp \left( -2\left\vert \zeta -\alpha \right\vert^{2}\right) L_{m}\left( 4\left\vert \zeta -\alpha \right\vert^{2}\right) . $$

  (38)

• (IV) For OCS2 $\left \vert \alpha _{2}^{\perp }\right \rangle$, we have

  $$\begin{array}{@{}rcl@{}} W_{\left\vert \alpha_{2}^{\perp }\right\rangle }\left( \zeta \right) &=& \frac{ 1}{N_{2}^{\perp }}(\left\langle a^{m}\hat{M}a^{\dag m}\right\rangle_{\left\vert \alpha \right\rangle }+\left\vert \alpha \right\vert^{2m}\left\langle \hat{M}\right\rangle_{\left\vert \alpha \right\rangle } \\ &&-\alpha^{\ast m}\left\langle a^{m}\hat{M}\right\rangle_{\left\vert \alpha \right\rangle }-\alpha^{m}\left\langle \hat{M}a^{\dag m}\right\rangle_{\left\vert \alpha \right\rangle }) \end{array} $$

  (39)

with

$$ \left\langle a^{m_{1}}\hat{M}a^{\dag m_{2}}\right\rangle_{\left\vert \alpha \right\rangle }=\frac{2}{\pi }e^{-2\left\vert \zeta -\alpha \right\vert^{2}}\partial_{\mu }^{m_{1}}\partial_{\nu }^{m_{2}}e^{\left( 2\zeta -\alpha \right) \mu +\left( 2\zeta^{\ast }- \alpha^{\ast }\right) \nu -\mu \nu }|_{\mu =\nu = 0}. $$

(40)

By choosing properly (m₁, m₂) in (40), we can obtain the expression of $W_{\left \vert \alpha _{2}^{\perp }\right \rangle }\left (\zeta \right )$ in (39).

In Fig. 11, we plot some Wigner functions for CS |α〉, PACS |α_a〉, OCS1 $\left \vert \alpha _{1}^{\perp }\right \rangle$, and OCS2 $\left \vert \alpha _{2}^{\perp }\right \rangle$, with α = 1 + i and different values of m . It is well known that the negativity of the Wigner function of any state of light indicates that the state is nonclassical [39, 40]. In addition, we present W (x, y = 0) in Fig. 12 and marginal distribution

$$ P\left( x\right) =\int W\left( x+iy\right) dy $$

(41)

in Fig. 13 as a function of x for quantum states CS |α〉, PACS |α_a〉, OCS1 $\left \vert \alpha _{1}^{\perp }\right \rangle$, and OCS2 $\left \vert \alpha _{2}^{\perp }\right \rangle$ with α = 1 + i and different values of m. Here the integral in P (x) can be evaluated numerically. Obviously, it is easily to see that the Wigner function for CS |α〉 is always Gaussian and has no negativity. The negativity of Wigner function and the non-Gaussian character have be exhibited for PACS |α_a〉, OCS1 $\left \vert \alpha _{1}^{\perp }\right \rangle$, and OCS2 $\left \vert \alpha _{2}^{\perp }\right \rangle$ . In addition, we see that the oscillation of the distribution for OCS1 $\left \vert \alpha _{1}^{\perp }\right \rangle$ and OCS2 $\left \vert \alpha _{2}^{\perp }\right \rangle$ is stronger than that for CS |α〉 and PACS |α_a〉 with the same value of m.

Fig. 11

(Color online) Wigner functions as a function of ζ = x + iy ($x,y\in \left [ -4,4\right ]$) for CS (column1), PACS (column 2), OCS1 (column 3), and OCS2 (column 4) with fixed α = 1 + i for m = 1 (row 1), m = 2 (row 2), m = 3 (row 3), and m = 4 (row 4)

Fig. 12

(Color online) Wigner functions W (x, y = 0) for CS (black solid), PACS (blue dashed), OCS1 (red dotted), and OCS2 (green dotdashed) as a function of x with α = 1 + i and am = 1; bm = 2; cm = 3; dm = 4

Fig. 13

(Color online) Marginal distribution $P\left (x\right )$ for CS (black solid), PACS (blue dashed), OCS1 (red dotted), and OCS2 (green dotdashed) as a function of x with α = 1 + i and am = 1; bm = 2; cm = 3; dm = 4

7 Conclusion

To summarize, we study and compare some properties of four kinds of quantum states, that is, the CS and its three induced states including PACS, OCS1, and OCS2 via the photon-addition operations. The similarities of each two of them are also discussed by the fidelities. The results show that the PACS is the intermediate state of the CS and OCS2. The similarity of the PACS and the OCS1 is nearly equal to the similarity of the OCS1 and the OCS2. The mean number of photons for the CS and the OCS1 are linear to the intensity of the original CS. For enough large m, the mean number of photons for the PACS is nearly equal to that for the OCS2. The CS is always Poissonian. The PACS is always sub-Poissonian. While for the OCS1 and the OCS2, they shall exhibit sub-Poissonian character in the small amplitude interval and super-Poissonian character in the large amplitude interval. The CS and the OCS1 have no squeezing effect. The PACS will exhibit squeezing effect when the amplitude is bigger than a certain value. The OCS2 will exhibit squeezing effect when the amplitude is in a proper interval. In addition, we study in detail two kinds of quasiprobability function for these quantum states, where the marginal distributions are also discussed.