1 Introduction

Quantum states have wide applications in optical communications, gravitational detection, quantum teleportation [1,2,3]. The construction and preparation of the quantum state of light field, as well as the investigation of its non-classical properties have been one of the most promising research subjects in the field of quantum optics. In the construction of the quantum state, in 1991 Agarwal and Tara constructed the excitation coherent states by repeated application of the photon creation operator on the coherent state firstly and investigated non-classical properties in such states [4]. They pioneered the use of the optical field operator (creation operator and annihilation operator) acting on the reference state to construct an ideal quantum state. From then on, this method is widely used in the construction of quantum states [5,6,7,8,9,10,11,12,13]. For example, Ma et al introduced photon-added and photon subtracted squeezed vacuum state, and studied their non-classical properties [5]. Wang et al discussed statistical properties of photon-added two-mode squeezed coherent states [6]. In the experiment, the photon addition and photon subtraction have been performed [14]. With the deepening, the individual excitation of the creation operator or the annihilation operator is generalized to the case of the superposition excitation of light field operators [15,16,17]. For example, Lee et al studied a coherent superposition ta + ra+ of field annihilation and creation operators acting on continuous variable systems and proposed its application for quantum state engineering [15]. Cai et al investigated non-classical properties of the optical field when photon subtraction and addition coherent operation ta+ + ra acts on an odd superposition of coherent states [16]. Inspired by the above references, we construct SPSAESVT by operation of superposition of annihilation operator and creation operator ta+ 2 + sa2 on two modes squeezed vacuum state and study its non-classical properties. The influence of the squeezing parameter and that of the superposition coefficient of operators on the quantum properties of the state is discussed.

This paper is arranged as follows: In Section 2, we introduce SPSAESVT. In Sections 3, 4, 5 and 6, the non-classical properties are investigated in terms of the squeezing, antibunching effect, violation of Cauchy-Schwartze inequality and entanglement property between two modes. The main results are summarized in Section 7.

2 The Construction of SPSAESVT

The two-mode squeezing operator with real squeezing parameter λ can be written as

$$ S_{2} (\lambda )=\exp (a^{+}b^{+}\tanh \lambda )\times \exp [(a^{+}a+b^{+}b + 1)\ln \sec h\lambda ]\times \exp (-ab\tanh \lambda )=\exp [\lambda (a^{+}b^{+}-ab)], $$
(1)

where a+ and b+(a,b) denote creation operators (annihilation operator ) of two-mode light field, respectively. In quantum optics and quantum information processing, squeezed vacuum state is widely used because of its non-classicality. The two-mode squeezing vacuum state is generalized by the two-mode squeezing operator acting on a two-mode vacuum state. It can be written as

$$ \vert \varphi (0)\rangle =S_{2} (\lambda ))\vert 00\rangle =\sec h\lambda \exp (a^{+}b^{+}\tanh \lambda )\vert 00\rangle , $$
(2)

where |00〉 is a two-mode vacuum state. We consider the SPSAESVT obtained by application of the superposition operator ta+ 2 + sa2 on |φ(0)〉, i.e.,

$$ \vert \varphi \rangle =N(ta^{+ 2}+sa^{2})\exp (a^{+}b^{+}\tanh \lambda) \vert 00\rangle , $$
(3)

where t and s are two superposition coefficients, they satisfy s2 + t2 = 1. For simplicity, let’s assume they are real, N is the normalization constant. By demanding trρ = 1, N can be obtained in an compact form:

$$ N^{-2}= 2(t^{2}+r^{2})\cosh^{6}\lambda , $$
(4)

where r = s tanh2λ, the symbol tr denotes tracing, ρ is the density operator of SPSAESVT.

3 The Squeezing Properties of SPSAESVT

Squeezing is a well-known non-classical effect. A state is squeezed when one of its quadrature components is less than it would be in a coherent state. The use of squeezed states is necessary to perform quantum information tasks. In this section, we study the squeezing properties of SPSAESVT. In order to describe the quantum fluctuations of the light field state, we define two two-mode quadrature operators

$$\begin{array}{@{}rcl@{}} F_{1} =\frac{1}{2\sqrt 2} (a+b+a^{+}+b^{+}),\\ F_{2} =\frac{1}{2\sqrt {2i}} (a+b-a^{+}-b^{+}). \end{array} $$
(5)

They satisfy the commutation relation

$$ [F_{1} ,F_{2} ]=\frac{i}{2}, $$
(6)

Their fluctuations satisfy uncertainty relation

$$ {\Delta} {F_{1}^{2}} {\Delta} {F_{2}^{2}} \ge \frac{1}{16}. $$
(7)

When the variance of Fi(i = 1,2) satisfies the inequality

$$ {\Delta} {F_{i}^{2}} =\langle {F_{i}^{2}} \rangle =\langle F_{i} \rangle^{2}<\frac{1}{4}, $$
(8)

we can say that a state is squeezed in Fi(i = 1,2) direction. In order to describe the compression degree of i-th component of the light field, we define squeezing parameter as follow

$$ Q_{i} ={\Delta} {F_{i}^{2}} -\frac{1}{4},\;\;(i = 1,2). $$
(9)

Then, if Qi < 0, the state is squeezed in Fi(i = 1,2) direction. Combination (5), (8) and (9), we rewrite (9) in terms of creation and annihilation operators of two mode as

$$\begin{array}{@{}rcl@{}} Q_{1} &=&\frac{1}{8}[2\langle a^{+}a\rangle + 2\langle b^{+}b\rangle + 2\langle a^{+}b\rangle + 2\langle ab^{+}\rangle +\langle a^{2}+a^{+ 2}\rangle +\langle b^{2}+b^{+ 2}\rangle \\ && + 2\langle ab+a^{+}b^{+}\rangle] -\frac{1}{8}[\langle a+a^{+}\rangle +\langle b+b^{+}\rangle ]^{2},\\ Q_{2} &=&\frac{1}{8}[2\langle a^{+}a\rangle + 2\langle b^{+}b\rangle + 2\langle a^{+}b\rangle + 2\langle ab^{+}\rangle -\langle a^{2}+a^{+ 2}\rangle -\langle b^{2}+b^{+ 2}\rangle \\ && -2\langle ab+a^{+}b^{+}\rangle ]+\frac{1}{8}[\langle a-a^{+}\rangle +\langle b-b^{+}\rangle ]^{2} \end{array} $$
(10)

From (3), we derive

$$\begin{array}{@{}rcl@{}} &&\langle a\rangle =\langle a^{+}\rangle =\langle b\rangle =\langle b^{+}\rangle = 0,\\ &&\langle a^{+}a\rangle =N^{2}[4t^{2}\cosh^{4}\lambda + 10t^{2}\cosh^{6}\lambda \tanh^{2}\lambda + 6t^{2}\cosh^{8}\lambda \tanh^{4}\lambda + 6r^{2}\cosh^{8}\lambda \tanh^{2}\lambda ],\\ &&\langle b^{+}b\rangle =N^{2}[4r^{2}\cosh^{4}\lambda + 10r^{2}\cosh^{6}\lambda \tanh^{2}\lambda + 6r^{2}\cosh^{8}\lambda \tanh^{4}\lambda + 6t^{2}\cosh^{8}\lambda \tanh^{2}\lambda ],\\ &&\langle a^{2}\rangle =\langle a^{+ 2}\rangle =\langle b^{2}\rangle =\langle b^{+ 2}\rangle = 0,\\ &&\langle ab\rangle =\langle a^{+}b^{+}\rangle = 6N^{2}(t^{2}+r^{2})\tanh \lambda \cosh^{8}\lambda,\langle ab^{+}\rangle =\langle a^{+}b\rangle = 0,\\ &&Q_{1} =\frac{1}{4\cosh^{2}\lambda} (2 + 5\tanh^{2}\lambda \cosh^{2}\lambda + 3\tanh^{4}\lambda \cosh^{4}\lambda+ 3\tanh^{2}\lambda \cosh^{4}\lambda + 6\tanh \lambda \cosh^{4}\lambda ),\\ &&Q_{2} \,=\,\frac{1}{4\cosh^{2}\lambda} (2\,+\,5\tanh^{2}\lambda \cosh^{2}\lambda \,+\,3\tanh^{4}\lambda \cosh^{4}\lambda\,+\,3\tanh^{2}\lambda \cosh^{4}\lambda \,-\,6\tanh \lambda \cosh^{4}\lambda ). \end{array} $$
(11)

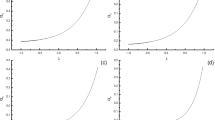
In (11), it is clear that Q1 and Q2 do not contain the superposition coefficient t. It indicates that the superposition coefficient has no effect on the squeezing effect of the state. Further, numerical results show that Q1 is greater than zero. This shows that there is not squeezing in F1 direction. In order to illustrate the squeezing properties in F2 direction, the evolution curves of Q2 with the squeezing parameter λ is plotted in Fig. 1 when t equals \(\frac {\sqrt {2}} {2}\). Figure 1 shows that Q2 decreases gradually with the increasing of the squeezing parameter λ. When the squeezing parameter λ is larger than a certain value, Q2 is less than zero, which means that SPSAESVT displays squeezing effect. The results also show that the squeezing effect of SPSAESVT is strengthened with the increasing of the squeezing parameter λ.

Fig. 1
figure 1

The evolution of Q2 with squeezing parameter λ when \(t=\frac {\sqrt {2}} {2}\)

Full size image

4 Antibunching Effect of SPSAESVT

In this section, we analyze the antibunching effect of SPSAESVT. The antibunching effect of light field can be described by the second-order correlation function. In two-mode light field, the second-order correlation function is defined as

$$ G=\frac{\langle a^{+ 2}a^{2}\rangle +\langle b^{+ 2}b^{2}\rangle} {2\langle a^{+}ab^{+}b\rangle^{2}}-1. $$
(12)

It is well known that G < 0 for antibunching and G > 0 for bunching of photons in the research state. From (3), after lengthy calculations we obtain

$$\begin{array}{@{}rcl@{}} &&\langle a^{+ 2}a^{2}\rangle =N^{2}(4t^{2}\cosh^{2}\lambda + 32t^{2}\tanh^{2}\lambda \cosh^{4}\lambda + 74t^{2}\tanh^{4}\lambda \cosh^{6}\lambda + 48t^{2}\tanh^{5}\lambda \cosh^{8}\lambda\\&& + 24t^{2}\tanh^{6}\lambda \cosh^{10}\lambda + 24r^{2}\tanh^{4}\lambda \cosh^{10}\lambda ), \\ &&\langle b^{+ 2}b^{2}\rangle =N^{2}(4r^{2}\cosh^{2}\lambda + 32r^{2}\tanh^{2}\lambda \cosh^{4}\lambda + 74r^{2}\tanh^{4}\lambda \cosh^{6}\lambda = 48r^{2}\tanh^{5}\lambda \cosh^{8}\lambda\\&& + 24r^{2}\tanh^{6}\lambda \cosh^{10}\lambda + 24t^{2}\tanh^{4}\lambda \cosh^{10}\lambda ), \\ &&\langle a^{+ 2}a^{2}\rangle +\langle b^{+ 2}b^{2}\rangle \,=\,\frac{1}{2\cosh^{6}\lambda} (4\cosh^{2}\lambda + 32\tanh^{2}\lambda \cosh^{4}\lambda + 74\tanh^{4}\lambda \cosh^{6}\lambda = 48\tanh^{5}\lambda \cosh^{8}\lambda \\&&+ 24\tanh^{6}\lambda \cosh^{10}\lambda + 24\tanh^{4}\lambda \cosh^{10}\lambda ), \\ &&\langle a^{+}ab^{+}b\rangle =\frac{\tanh \lambda} {2\cosh^{6}\lambda} (18\cosh^{6}\lambda + 42\tanh^{2}\lambda \cosh^{8}\lambda + 24\tanh^{4}\lambda \cosh^{8}\lambda ). \\ \end{array} $$
(13)

After substituting (13) into (12), we find that the second-order correlation function of SPSAESVT is independent of the superposition coefficient. This indicates that the superposition coefficient has no effect on its antibunching effect. Setting \(t=\frac {\sqrt {2}} {2}\), we plot the graph of G as the function of λ in Fig. 2. It is shown that G is always larger than zero. Thus SPSAESVT does not display the antibunching effect.

Fig. 2
figure 2

The evolution of G with squeezing parameter λ when \(t=\frac {\sqrt {2}} {2}\)

Full size image

5 Cauchy-Schwartze Inequality

The correlation between two modes in light field is described by Cauchy-Schwartze inequality. It is defined as

$$ \langle a^{+}ab^{+}b\rangle^{2}\le \langle a^{+ 2}a^{2}\rangle \langle b^{+ 2}b^{2}\rangle . $$
(14)

In order to describe the degree of violation of Cauchy-Schwartze inequality, we define

$$ I=\frac{[\langle a^{+ 2}a^{2}\rangle \langle b^{+ 2}b^{2}\rangle ]^{\frac{1}{2}}}{\vert \langle a^{+}ab^{+}b\rangle \vert} -1. $$
(15)

Thus the correlation between two modes in light field is classical as I > 0, and it is non-classical as I < 0.

Combining (13) and (15), letting λ = 1.0, we plot the evolution curve of I with t in Fig. 3. It is found that I is always less than zero. This shows that the correlation between two modes in SPSAESVT is non-classical. In addition, as the superposition coefficient t increases, the negative depth of I decreases gradually in the beginning; then it gradually increases when the superposition coefficient t is larger than a certain value. It is implied that there is a nonlinear relationship between I and the superposition coefficient t.

Fig. 3
figure 3

The evolution of I with superposition coefficient t when λ = 1.0

Full size image

On the other hand, we investigate the influence of the squeezing parameter λ on the correlation between two modes in SPSAESVT. Setting \(t=\frac {\sqrt {2}} {2}\), we plot I as the function of λ in Fig. 4. As depicted in Fig. 4, we find that the non-classical correlation property between two modes is weakened until it disappears with increase of the squeezing parameter λ.

Fig. 4
figure 4

The evolution of I with squeezing parameter λ when \(t=\frac {\sqrt {2}} {2}\)

Full size image

6 Entanglement Between Two Modes in SPSAESVT

In order to describe the entanglement between two modes in the light field, Hillery and Zubairy introduced the entanglement measurement [18]. It is defined as

$$ E=\langle a^{+}a\rangle \langle b^{+}b\rangle -\vert \langle ab\rangle \vert^{2}. $$
(16)

If E < 0, then there is an entanglement between two modes. Combining (11) and (12), we can perform numerical calculations on E. Figure 5 shows the evolution of E with superposition coefficient t, there λ = 1.0. As can be seen in Fig. 5, E is always less than zero. This means that there is an entanglement between two modes. In addition, the evolution of E with t is similar to that of I with t in Fig. 3. This also shows that there is a nonlinear relationship between the entanglement E and the superposition coefficient t.

Fig. 5
figure 5

The evolution of E with superposition coefficient t when λ = 1.0

Full size image

Same, letting \(t=\frac {\sqrt {2}} {2}\), in Fig. 6 the entanglement E is plotted as the function of λ. From Fig. 6, we can see that the entanglement property between two modes in SPSAESVT is strengthened with the increase of squeezing parameter λ.

Fig. 6
figure 6

The evolution of E with squeezing parameter λ when \(t=\frac {\sqrt {2}} {2}\)

Full size image

7 Conclusion

In the present paper, we have constructed SPSAESVT by operation of superposition of photon subtraction two times and photon addition two times ta+ 2 + sa2 on two modes squeezed vacuum state. Its quantum properties are investigated in terms of squeezing, antibunching effect, violation of Cauchy-Schwartze inequality and entanglement property between two modes. The influences of the squeezing parameter λ and that of the superposition coefficient t on its quantum properties are discussed. The numerical results indicate: (1) SMSTMSVT displays bunching effect; (2) the superposition coefficient t of the operators has no effect on the squeezing of SMSTMSVT, but its squeezing effect is strengthened as the squeezing parameter λ increases; (3) The evolution of the correlation function between two modes I with the superposition coefficient t is similar to that of the entanglement E between two modes, there is a nonlinear relationship between I and t, so is there between E and t; (4) the violation of Cauchy-Schwartze inequality is weakened with increasing of the squeezing parameter λ; (5) The negative of the entanglement measurement E is strengthened with increasing of the squeezing parameter λ. It indicates that entanglement property between two modes is strengthened with increasing of the squeezing parameter λ.