1 Introduction

The interaction between a two-level atom and a radiation light field had been widely researched, ranging from condensed matter to quantum optics and applications to quantum information. The Jaynes-Cummings model (JCM) [1] has been treated various interactions between atoms and photons, which include multi-level atoms interact with quantized fields, and various multi-photon transition processes in quantum optics [2]. It gives many quantum phenomena that can not be explained in classical terms, such as the collapses and revivals of the atomic population inversion [3], atom-cavity entanglement [4] and squeezing of the field [5].

We know that entanglement plays a central role in quantum information, quantum communication, computation and quantum cryptography. There are a lot of schemes for many-particle entanglement generation, the simplest scheme of the atom-field entanglement is the JCM describing an interaction of a two-level atom with a radiation field. The model predicts a variety of interesting phenomena, and the atom-field entanglement is among them. The atom-field entanglement for JCM has been initiated by Phoenix, Gea-Banacloche [6] and Knight [7]. Gea-Banacloche has found the JCM is valid when the field is initially in a coherent state with a large mean photon number [8,9,10,11].

The single photon and double photon Jaynes-Cummings model had been studied largely [12,13,14,15,16,17,18,19]. In this paper, we have studied the atom and light field quantum entanglement for the multiphoton transition in nonlinear medium, and researched the effect of the transition photon number N (N = 1,2,3,4,5,6) and the nonlinear coupling constant χ on the quantum entanglement degrees. We have given the quantum entanglement degrees curves with time evolution, and obtained some results. When the transition photon number N increases, the entanglement degrees oscillation get faster. When the nonlinear coefficient α > 0, the entanglement degrees oscillation get quickly. When the nonlinear coefficient α < 0, the entanglement degrees oscillation get slow, and stay the time of entanglement degrees E ≈ 1 more longer. It is benefit to the atom and light field entanglement. These results will have been used in the quantum communication and quantum information.

2 The Multiphoton Jaynes-Cummings Model and Entanglement Degrees

Let us consider the N-photon Jaynes-Cummings model, the Hamiltonian is [20, 21]

$$ H=\omega a^{+}a+\frac{1}{2}\omega_{0}\sigma_{z}+g({a^{+}}^{N}\sigma_{-}+a^{N}\sigma_{+})+\chi{a^{+}}^{2}a^{2},\hspace{0.2in}(\hbar= 1) $$
(1)

where a(a +) is the annihilation (creation) operator for a photon in an electromagnetic mode of frequency, is the radiative field mode frequency, (0) is the atomic frequency. , g is field-atom coupling constant and σ z = ∣a >< a∣ −∣b >< b∣, σ + = ∣a >< b∣, σ − = ∣b >< a∣. The nonlinear part χ a + 2 a 2 may be thought of as having been obtained from a quartic potential through the rotating-wave approximation, χ denotes the third-order susceptibility of Kerr medium, it is the nonlinear coupling constant of light field and nonlinear medium. This Hamiltonian, simple as it may seem, appears to lie in the center of many theoretical investigations. Drummond and Walls [22] and then Risken et al. [23] used it to examine the optical bistability in nonlinear media [24, 25].

The initial state is

$$ \mid\psi(0)>=c_{1}(0)\mid a,n>+c_{2}(0)\mid b,n+N> $$
(2)

where |c 1(0)|2 + |c 2(0)|2 = 1, the state ∣b > is atom ground state, state ∣a > is atom excited state, and the wave function at any time is

$$ \mid\psi(t)>=c_{1}(t)\mid a,n>+c_{2}(t)\mid b,n+N>, $$
(3)

substituting (1) and (3) into Schrodinger equation

$$ i\frac{\partial}{\partial t}\mid\psi(t)>=H\mid\psi(t)>, $$
(4)

we obtain

$$\begin{array}{@{}rcl@{}} &&i\frac{\partial}{\partial t}(c_{1}(t)\mid a,n>+c_{2}(t)\mid b,n+N>)\\ &&=(\omega a^{+}a+\frac{1}{2}\omega_{0}\sigma_{z}+g(a^{+N}\sigma_{-}\,+\,a^{N}\sigma_{+})\,+\,\chi{a^{+}}^{2}a^{2})(c_{1}(t)\!\mid \!a,n\!>\!+c_{2}(t)\mid b,n+N>)\\&& =(\omega nc_{1}(t)\,+\,\frac{1}{2}\omega_{0}c_{1}(t)\,+\,gc_{2}(t)\sqrt{\!(n\,+\,1)(n\,+\,2)\cdot\cdot\cdot(n\,+\,N)}+\chi n(n\,-\,1)c_{1}(t))\mid n,a>\\&& +(\omega (n+N)c_{2}(t)-\frac{1}{2}\omega_{0}c_{2}(t)+gc_{1}(t)\sqrt{(n + 1)(n + 2)\cdot\cdot\cdot(n+N)}\\ &&+\chi(n+N)(n+N-1)c_{2}(t))\mid n+N,b>), \end{array} $$
(5)

comparing the both sides of (5), we have

$$ i\frac{\partial}{\partial t}c_{1}(t)=\omega nc_{1}(t)+\frac{1}{2}\omega_{0}c_{1}(t)+gc_{2}(t)\sqrt{(n + 1)(n + 2)\cdot\cdot\cdot(n+N)}+\chi n(n-1)c_{1}(t), $$
(6)
$$\begin{array}{@{}rcl@{}} i\frac{\partial}{\partial t}c_{2}(t)&=&\omega (n+N)c_{2}(t)-\frac{1}{2}\omega_{0}c_{2}(t)+gc_{1}(t)\sqrt{(n + 2)(n + 1)\cdot\cdot\cdot(n+N)}\\&&+\chi(n+N)(n+N-1)c_{2}(t), \end{array} $$
(7)

using Laplace transforms to the both sides of (6) and (7), we get

$$\begin{array}{@{}rcl@{}} ipL_{1}(p)-ic_{1}(0)&=&\omega nL_{1}(P)+\frac{1}{2}\omega_{0}L_{1}(p)+g\sqrt{(n + 1)(n + 2)\cdot\cdot\cdot(n+N)}L_{2}(p)\\&&+\chi n(n-1)L_{1}(p), \end{array} $$
(8)
$$\begin{array}{@{}rcl@{}} ipL_{2}(p)-ic_{2}(0)&=&\omega (n\,+\,N)L_{2}(P)-\frac{1}{2}\omega_{0}L_{2}(p)+g\sqrt{\!(n\,+\,1)(n\,+\,2)\cdot\cdot\cdot(n\,+\,N)}L_{1}(p) \\&&+\chi(n+N)(n+N-1)L_{2}(p), \end{array} $$
(9)

We obtain

$$\begin{array}{@{}rcl@{}} L_{1}(p)&=&\frac{c_{1}}{p+i\omega n+\frac{i}{2}\omega_{0}+i\chi n(n-1)}\\&&-i\frac{g\sqrt{(n + 1)(n + 2)\cdot\cdot\cdot(n+N)}}{p+i\omega n+\frac{i}{2}\omega_{0}+i\chi n(n-1)}\left( \frac{D}{p+A}+\frac{E}{p+B}\right), \end{array} $$
(10)
$$ L_{2}(p)=\frac{D}{p+A}+\frac{E}{p+B}, $$
(11)

where \(L_{1}(p)={\mathcal {L}}[c_{1}(t)]\) and \(L_{2}(p)={\mathcal {L}}[c_{2}(t)]\) are Laplace transform of functions c 1(t), c 2(t), and

$$ A=\frac{i\omega(2n+N)+i\chi[2n^{2}+ 2(N-1)n+N^{2}-N]+i\sqrt{{\omega_{2}^{2}}+{\omega_{1}^{2}}}}{2}, $$
(12)
$$ B=\frac{i\omega(2n+N)+i\chi[2n^{2}+ 2(N-1)n+N^{2}-N]-i\sqrt{{\omega_{2}^{2}}+{\omega_{1}^{2}}}}{2}, $$
(13)
$$ D=\frac{\left( \sqrt{{\omega_{1}^{2}}+{\omega_{2}^{2}}}-\omega_{2}\right)c_{2}+\omega_{1} c_{1}}{2\sqrt{{\omega_{1}^{2}}+{\omega_{2}^{2}}}}, E=\frac{\left( \sqrt{{\omega_{1}^{2}}+{\omega_{2}^{2}}}-\omega_{2}\right)c_{2}-\omega_{1} c_{1}}{2\sqrt{{\omega_{1}^{2}}+{\omega_{2}^{2}}}}, $$
(14)

Using Laplace retransforms to (10) and (11), we have

$$\begin{array}{@{}rcl@{}} c_{1}(t)&=&e^{-\frac{i}{2}\omega(2n+N)t}e^{-\frac{i}{2}\chi[2n^{2}+ 2(N-1)n+N^{2}-N]t}\\&&\times\left[c_{1}\cos\left( \frac{\sqrt{{\omega_{1}^{2}}+{\omega_{2}^{2}}}}{2}t\right) -i\frac{c_{1}\omega_{2}+c_{2}\omega_{1}}{\sqrt{{\omega_{1}^{2}}+{\omega_{2}^{2}}}}\sin\left( \frac{\sqrt{{\omega_{1}^{2}}+{\omega_{2}^{2}}}}{2}t\right)\right] \end{array} $$
(15)
$$\begin{array}{@{}rcl@{}} c_{2}(t)&=&e^{-\frac{i}{2}\omega(2n+N)t}e^{-\frac{i}{2}\chi[2n^{2}+ 2(N-1)n+N^{2}-N]t}\\&&\times\left[c_{2}\cos\left( \frac{\sqrt{{\omega_{1}^{2}}+{\omega_{2}^{2}}}}{2}t\right) -i\frac{c_{1}\omega_{1}-c_{2}\omega_{2}}{\sqrt{{\omega_{1}^{2}}+{\omega_{2}^{2}}}}\sin\left( \frac{\sqrt{{\omega_{1}^{2}}+{\omega_{2}^{2}}}}{2}t\right)\right] \end{array} $$
(16)

where δ = ω 0 − N ω, \(\omega _{1}= 2g\sqrt {(n + 1)(n + 2)\cdot \cdot \cdot (n+N)}\), ω 2 = δ − N χ(2n + N − 1).

with the state (2), we can obtain the density operator of atom-photon system

$$\begin{array}{@{}rcl@{}} \hat{\rho}(t)&&=|\psi(t)><\psi(t)|\\&&=|c_{1}(t)|^{2}|n,a><a,n|+c_{1}(t)c_{2}^{*}(t)|n,a><b,n + 2| \\&&+c_{2}(t)c_{1}^{*}(t)|n + 2,b><a,n|+|c_{2}(t)|^{2}|n + 2,b><b,n + 2|, \end{array} $$
(17)

the reduce density operator of atom A is

$$\begin{array}{@{}rcl@{}} \hat{\rho}_{A}(t)&&=tr_{(a)}\hat{\rho}(t) \\&&=<n|\hat{\rho}(t)|n>+<n + 2|\hat{\rho}(t)|n + 2>\\&&=|c_{1}(t)|^{2}|a><a|+|c_{2}(t)|^{2}|b><b|, \end{array} $$
(18)

the matrix form of \(\hat {\rho }_{A}(t)\) at basis vectors |a > and |b >

$$\begin{array}{@{}rcl@{}} \hat{\rho}_{A}(t)=\left( \begin{array}{cc} <a|\hat{\rho}_{A}(t)|a>& <a|\hat{\rho}_{A}(t)|b>\\ <b|\hat{\rho}_{A}(t)|a>& <b|\hat{\rho}_{A}(t)|b>\end{array} \right)=\left( \begin{array}{cc} |c_{1}(t)|^{2}& 0 \\ 0 & |c_{2}(t)|^{2} \end{array} \right), \end{array} $$
(19)

the quantum system entanglement degrees is

$$\begin{array}{@{}rcl@{}} E(t)&&=-tr (\hat{\rho}_{A}(t)\log_{2}\hat{\rho}_{A}(t)) \\&&=-tr\left( \left( \begin{array}{cc} |c_{1}(t)|^{2}& 0 \\ 0 & |c_{2}(t)|^{2} \end{array} \right)\cdot\left( \begin{array}{cc} |\log_{2}c_{1}(t)|^{2}& 0 \\ 0 & \log_{2}|c_{2}(t)|^{2} \end{array} \right)\right), \\&&=-(|c_{1}(t)|^{2}\log_{2}c_{1}(t)|^{2}+|c_{2}(t)|^{2}\log_{2}|c_{2}(t)|^{2}), \end{array} $$
(20)

3 Numerical Result

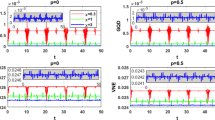
In this section, we shall calculate the quantum entanglement degrees with (15), (16) and (20). The entanglement degree E is in the range of 0 ∼ 1. In Fig. 1, we calculate the entanglement degree with linear Jaynes-Cummings model, i.e., χ = 0, the initial state superposition coefficient C 1 = 0, the entanglement degree E = 0, i.e., the atom and light field is not in entangled state at initial state, the initial photon number n = 0, the quantum discord δ 2 = 4g 2. With the time evolution, the atom and light field should be in the entangled state E ≠  0. In Fig. 1a–f, the transition photon numbers N are 1,2,3,4,5 and 6, respectively. In Fig. 1a–f, the entanglement degree 0 ≤ E ≤ 1. When the numbers of photons N increases, the entanglement degrees oscillation get faster. When N = 1,2,3, the evolution curves of entanglement degrees change slowly with time t, and stay the time of entanglement degrees E ≈ 1 more longer. When N = 4,5,6, the entanglement degree oscillate quickly, and they oscillate more quickly with N increase.

Fig. 1
figure 1

The curves of the atom and light field entanglement degrees with time evolution, the initial state superposition coefficient C 1 = 0, the initial photon number n = 0, the quantum discord δ 2 = 4g 2, the nonlinear coefficient \(\alpha =\frac {\chi }{g}= 0\)

Full size image

From Figs. 2, 3, 4, 5, 6 to 7, we calculate the entanglement degree with nonlinear Jaynes-Cummings model, i.e., χ ≠  0. The initial state superposition coefficient C 1 = 0, the initial photon number n = 0, the quantum discord δ 2 = 4g 2, and the corresponding to nonlinear coefficient are \(\alpha =\frac {\chi }{g}= 0.2\), 0.5, 0.8, − 0.2, − 0.5 and − 0.8. Comparing with Figs. 2, 3 and 4, we find when the nonlinear coefficient increase (α > 0), the entanglement degrees oscillation get quickly. Comparing with Figs. 5, 6 and 7, we find when the nonlinear coefficient decrease α < 0, the entanglement degrees oscillation get quickly. Comparing Figs. 1 with 2, we find when the nonlinear coefficient α > 0, the entanglement degrees oscillation get quickly. When the nonlinear coefficient α > 0, the nonlinear term is disadvantage of the atom and light field entanglement. Comparing Fig. 1 with 5, we find when the nonlinear coefficient α < 0, the entanglement degrees oscillation get slow. When the nonlinear coefficient α < 0, the nonlinear term is advantage of the atom and light field entanglement. These results will have been used in the quantum communication and quantum information.

Fig. 2
figure 2

The curves of the atom and light field entanglement degrees with time evolution, the initial state superposition coefficient C 1 = 0, the initial photon number n = 0, the quantum discord δ 2 = 4g 2, the nonlinear coefficient \(\alpha =\frac {\chi }{g}= 0.2\)

Full size image
Fig. 3
figure 3

The curves of the atom and light field entanglement degrees with time evolution, the initial state superposition coefficient C 1 = 0, the initial photon number n = 0, the quantum discord δ 2 = 4g 2, the nonlinear coefficient \(\alpha =\frac {\chi }{g}= 0.5\)

Full size image
Fig. 4
figure 4

The curves of the atom and light field entanglement degrees with time evolution, the initial state superposition coefficient C 1 = 0, the initial photon number n = 0, the quantum discord δ 2 = 4g 2, the nonlinear coefficient \(\alpha =\frac {\chi }{g}= 0.8\)

Full size image
Fig. 5
figure 5

The curves of the atom and light field entanglement degrees with time evolution, the initial state superposition coefficient C 1 = 0, the initial photon number n = 0, the quantum discord δ 2 = 4g 2, the nonlinear coefficient \(\alpha =\frac {\chi }{g}=-0.2\)

Full size image
Fig. 6
figure 6

The curves of the atom and light field entanglement degrees with time evolution, the initial state superposition coefficient C 1 = 0, the initial photon number n = 0, the quantum discord δ 2 = 4g 2, the nonlinear coefficient \(\alpha =\frac {\chi }{g}=-0.5\)

Full size image
Fig. 7
figure 7

The curves of the atom and light field entanglement degrees with time evolution, the initial state superposition coefficient C 1 = 0, the initial photon number n = 0, the quantum discord δ 2 = 4g 2, the nonlinear coefficient \(\alpha =\frac {\chi }{g}=-0.8\)

Full size image

4 Conclusion

In this paper, we have studied the atom and light field quantum entanglement of multiphoton transition with the Jaynes-Cummings model, and researched the effect of the transition photon number N and the nonlinear coefficient χ on the quantum entanglement degrees. We have given the quantum entanglement degrees curves with time evolution, we find when the transition photon number N increases, the entanglement degrees oscillation get faster. When the nonlinear coefficient α > 0, the entanglement degrees oscillation get quickly, the nonlinear term is disadvantage of the atom and light field entanglement, and when the nonlinear coefficient α < 0, the entanglement degrees oscillation get slow, the nonlinear term is advantage of the atom and light field entanglement. These results will have been used in the quantum communication and quantum information.