1 Introduction

Quantum entanglement is the vital resource in almost all quantum information processing and communication tasks [1], and highly entangled states are usually required in order to actually realize these tasks. However, quantum entanglement is usually fragile, and its quantity degrades exponentially due to the inevitable interaction between a quantum system and the surrounding environment. Entanglement purification provides a way for extracting a small number of relatively highly entangled states from a large number of states with less degree of entanglement. The process is known as entanglement concentration in the case of pure states, and it is known as entanglement purification or distillation in the case of mixed states. Since the primary entanglement purification protocol presented by Bennett et al. in 1996 [2], many theoretical and experimental works have been devoted to the study of entanglement concentration and purification [3,4,5,6,7,8,9,10,11,12,13,14,15,16]. For example, the scheme to concentrate the pure shared entangled states via entanglement swapping [17] has been proposed by Bose et al. [7], and recently, the scheme has been extended to the mixed shared entangled states [18]. In the latter paper, the authors showed that entanglement swapping could recover the entanglement change of a two-qubit state due to amplitude damping noises, and some initial states could be asymptotically purified into maximally entangled states by iteratively using their protocol. However, their protocol will be invalid if they don’t flip the second pair at the beginning.

Besides, many other alternatives, for example, decoherence-free subspaces [19,20,21,22,23], quantum Zeno effect with “Bang Bang” decoupling [24, 25], the weak measurement and reversal measurements [18, 26,27,28,29,30,31], have also been proposed to suppress decoherence or recover the initial entanglement. Recently, by introducing a weak measurement reversal operation, Wang et al. proposed a scheme to recover quantum states decohered by a noisy environment via environment measurement, and they showed the success probability of their scheme could be enhanced compared with the previous ones [32]. Their protocol is a probabilistic one. In Refs. [33, 34], environment measurement combined with weak measurement reversal operation or entanglement swapping is proposed to suppress the amplitude damping decoherence for entanglement distribution.

Previously, the suppression of decoherence or the recovery of the initial entanglement is almost concentrated on two-dimensional systems. Actually, high dimensional systems provide certain benefits in quantum communication [35,36,37] and computation [38]. Significant advantages for the manipulation of information carriers can be offered by high dimensional entangled systems such as qutrits [39,40,41,42,43]. For example, biphotonic qutrit-qutrit entanglement enables more efficient use of communication channels [44, 45]. More resourceful quantum information processing can be realized by using hybrid qudit quantum gates. Furthermore, higher information-density coding and greater resilience to errors than two-dimensional entangled systems can be offered by high dimensional entangled systems in quantum cryptography [46]. However, the prepared high dimensional entangled states should have sufficiently long coherence time to manipulate for practical applications of these protocols.

In this paper, we consider the entanglement purification of two-qutrit states subjected to amplitude damping (AD) channels by using entanglement swapping combined with environment measurement, and then apply our scheme to dense coding. Our scheme of entanglement purification has distinct advantage: The resultant states have much more entanglement even though entanglement swapping itself cannot purify entanglement. Our scheme can be useful for quantum information processing tasks based on quantum channels built by entanglement swapping.

The paper is organized as follows. In the subsequent section, we propose the protocol to purify entanglement of noisy two-qutrit states via environment measurement. In Section 3, the protocol is applied to dense coding. We conclude our paper in Section 4.

2 Entanglement Purification Via Environment Measurement

Two pairs of qutrits A B 1 and B 2 C are supposed to be initially prepared in the same state \(|\phi _{0}\rangle =\sqrt {\alpha }|00\rangle +\sqrt {\beta }|11\rangle +\sqrt {\gamma }|22\rangle \). Here, the state parameters α + β + γ = 1. Alice and Bob share the first pair, and the second pair is shared by Bob and Charlie. During the distribution, qutrits A and B 1 are transmitted through the local individual AD channels to Alice and Bob, and qutrits B 2 and C are transmitted through the local individual AD channels to Bob and Charlie. In this paper, the local AD channels are assumed to be same for the sake of simplicity. The AD noise is a prototype model of dissipative interaction between a quantum system and its environment [1, 47]. For example, this noise model can be used to describe the spontaneous emission of a photon by a two-level atom in a vacuum environment with zero temperature or the photon loss in an optical fiber.

There are three configurations of 3-level system to be taken into account for qutrits [48], and here, the V-configuration is considered. The lower level is denoted as |0〉, and the two upper levels are denoted as |1〉 and |2〉, respectively. The dipole transitions between levels \(|1\rangle \leftrightarrow |0\rangle \) and \(|2\rangle \leftrightarrow |0\rangle \) are allowed, while that between levels \(|2\rangle \leftrightarrow |1\rangle \) is forbidden. For the case of the environment being in the vacuum state, the AD noise, which corresponds to the spontaneous emission from the V-configuration qutrit, can be described by a unitary transformation that acts on system and environment according to Ref. [49]

$$\begin{array}{@{}rcl@{}} |0\rangle_{S}|0\rangle_{E}&\rightarrow&|0\rangle_{S}|0\rangle_{E},\\ |1\rangle_{S}|0\rangle_{E}&\rightarrow&\sqrt{1-d}|1\rangle_{S}|0\rangle_{E}+\sqrt{d}|0\rangle_{S}|1\rangle_{E},\\ |2\rangle_{S}|0\rangle_{E}&\rightarrow&\sqrt{1-D}|2\rangle_{S}|0\rangle_{E}+\sqrt{D}|0\rangle_{S}|1\rangle_{E}, \end{array} $$
(1)

where the decay rates of the upper levels |1〉, |2〉 are d, D, respectively, and d, D ∈ [0, 1]. After the qutrits transmitting through the local AD channels, the system-environment combined system will evolve as follows

$$\begin{array}{@{}rcl@{}} &&|\phi_{0}\rangle_{AB_{1}}|00\rangle_{E_{1}E_{2}}\\ &=&(\sqrt{\alpha}|00\rangle+\sqrt{\beta}|11\rangle+\sqrt{\gamma}|22\rangle)_{AB_{1}}|00\rangle_{E_{1}E_{2}}\\ &\Rightarrow&\sqrt{\alpha}|00\rangle_{AB_{1}}|00\rangle_{E_{1}E_{2}}+\sqrt{\beta}(1-d)|11\rangle_{AB_{1}}|00 \rangle_{E_{1}E_{2}}\\ &&+\sqrt{\beta}\sqrt{d(1-d)}|10\rangle_{AB_{1}}|01\rangle_{E_{1}E_{2}}\\ &&+\sqrt{\beta}\sqrt{d(1-d)}|01 \rangle_{AB_{1}}|10\rangle_{E_{1}E_{2}}\\ &&+\sqrt{\beta}d|00\rangle_{AB_{1}}|11\rangle_{E_{1}E_{2}}+\sqrt{\gamma}(1-D)|22\rangle_{AB_{1}}|00 \rangle_{E_{1}E_{2}}\\ &&+\sqrt{\gamma}\sqrt{D(1-D)}|20\rangle_{AB_{1}}|01\rangle_{E_{1}E_{2}}\\ &&+\sqrt{\gamma}\sqrt{D(1-D)}|02 \rangle_{AB_{1}}|10\rangle_{E_{1}E_{2}}\\ &&+\sqrt{\gamma}D|00\rangle_{AB_{1}}|11\rangle_{E_{1}E_{2}}. \end{array} $$
(2)

The quantum state \(|\phi _{0}\rangle _{B_{2}C}\) will undergo the same evolution as that of \(|\phi _{0}\rangle _{AB_{1}}\).

After the distribution, there are two alternatives for Bob. The first one is to trace over the freedoms of the environments, and then makes the measurement based on the two-qutrit maximally entangled states. By tracing over the freedoms of the environments, the quantum state shared by Alice and Bob is

$$\begin{array}{@{}rcl@{}} \rho_{AB_{1}}&=&(\sqrt{\beta}d+\sqrt{\gamma}D)^{2}|00\rangle\langle00|\\ &&+\beta d(1-d)(|10\rangle\langle10|+|01\rangle\langle01|)\\ &&+\sqrt{\beta\gamma dD(1-d)(1-D)}(|10\rangle\langle20|+|01\rangle\langle02|)\\ &&+\sqrt{\beta\gamma dD(1-d)(1-D)}(|20\rangle\langle10|+|02\rangle\langle01|)\\ &&+\gamma D(1-D)(|20\rangle\langle20|+|02\rangle\langle02|)\\ &&+|\psi\rangle\langle\psi|, \end{array} $$
(3)

where \(|\psi \rangle =\sqrt {\alpha }|00\rangle +\sqrt {\beta }(1-d)|11\rangle +\sqrt {\gamma }(1-D)|22\rangle \). Subsequently, Bob measures the states of the two qutrits \(B_{1}B_{2}\) in the basis

$$\begin{array}{@{}rcl@{}} |{{\Phi}_{0}^{m}}\rangle&=&\frac{1}{\sqrt{3}}(|00\rangle+e^{im\frac{2}{3}\pi}|11\rangle+e^{im\frac{4}{3}\pi}|22\rangle),\\ |{{\Phi}_{1}^{m}}\rangle&=&\frac{1}{\sqrt{3}}(|01\rangle+e^{im\frac{2}{3}\pi}|12\rangle+e^{im\frac{4}{3}\pi}|20\rangle),\\ |{{\Phi}_{2}^{m}}\rangle&=&\frac{1}{\sqrt{3}}(|02\rangle+e^{im\frac{2}{3}\pi}|10\rangle+e^{im\frac{4}{3}\pi}|21\rangle), \end{array} $$
(4)

with m = 0, 1, 2. After Bob’s measurement, the corresponding states shared by Alice and Charlie will collapse into \({\rho _{0}^{m}},\ {\rho _{1}^{m}}\) and \({\rho _{2}^{m}}\) (m = 0, 1, 2), respectively. Even though the expressions of them can be obtained with straightforward calculation, they are analytically messy so that we don’t intend to write them out explicitly. In order to compare the entanglement between \(\rho _{AB_{1}}\) and the states after entanglement swapping, negativity is introduced [50]. For a given density matrix ρ, the negativity is defined as

$$ N(\rho)=\frac{\|\rho^{T_{b}}\|-1}{2}. $$
(5)

The negativity corresponds to the sum of absolute values of negative eigenvalues of \(\rho ^{T_{b}}\), and vanishes for unentangled states. Here, \(\|\rho ^{T_{b}}\|\) means the sum of absolute values of eigenvalues of \(\rho ^{T_{b}}\), which is the partial transpose of ρ with respect to part b. If we assume the state parameters β = γ = (1 − α)/2 and the decay rates D = d for the AD noises, the quantity of entanglement for the states \({\rho _{n}^{m}}\) (m,n = 0, 1, 2) shared by Alice and Charlie after entanglement swapping is always smaller than that for the state \(\rho _{AB_{1}}\). In other words, entanglement purification cannot be achieved by entanglement swapping itself. However, it is not the case for our scheme, i.e., the state shared by Alice and Charlie has much more entanglement by using entanglement swapping combined with environment measurement.

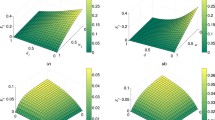
The second alternative is the scheme in this paper. Before entanglement swapping, environment measurement is implemented. Assume the results of environment measurements to be \(|00\rangle _{E_{1}E_{2}}\) and \(|00\rangle _{E_{3}E_{4}}\), respectively, the quantum state shared by Alice and Bob, and that shared by Bob and Charlie will collapse into \(|\psi \rangle _{AB_{1}}, |\psi \rangle _{B_{2}C}\). After the environment measurements, Bob makes the measurement on his two qutrits \(B_{1}B_{2}\) in the basis \(\{|{{\Phi }_{0}^{m}}\rangle ,|{{\Phi }_{1}^{m}}\rangle ,|{{\Phi }_{2}^{m}}\rangle \}\) (m = 0, 1, 2) in order to implement entanglement swapping. If Bob obtains \(|{{\Phi }_{0}^{m}}\rangle _{B_{1}B_{2}}\) as the result of measurement, Alice and Charlie will share the state \(|{\varphi _{0}^{m}}\rangle _{AC}=\alpha |00\rangle +e^{-im\frac {2}{3}\pi }\beta (1-d)^{2}|11\rangle +e^{-im\frac {4}{3}\pi }\gamma (1-D)^{2}|22\rangle \). Similarly, the shared states will be \(|{\varphi _{1}^{m}}\rangle _{AC}=\sqrt {\alpha \beta }(1-d)|01\rangle +e^{-im\frac {2}{3}\pi }\sqrt {\beta \gamma }(1-d)(1-D)|12\rangle +e^{-im\frac {4}{3}\pi }\sqrt {\alpha \gamma }(1-D)|20\rangle \), \(|{\varphi _{2}^{m}}\rangle _{AC}=\sqrt {\alpha \gamma }(1-D)|02\rangle +e^{-im\frac {2}{3}\pi }\sqrt {\alpha \beta }(1-d)|10\rangle +e^{-im\frac {4}{3}\pi }\sqrt {\beta \gamma }(1-d)(1-D)|21\rangle \) for the results of Bob’s measurement are \(|{{\Phi }_{1}^{m}}\rangle _{B_{1}B_{2}}\), \(|{{\Phi }_{2}^{m}}\rangle _{B_{1}B_{2}}\), respectively. From the expressions of \(|{\varphi _{1}^{m}}\rangle _{AC}\) and \(|{\varphi _{2}^{m}}\rangle _{AC}\), it is easy to find that the two states have the same quantity of entanglement. Moreover, as we have pointed out, the states shared by Alice and Charlie after entanglement swapping without environment measurement have less entanglement than the states after transmitting through the AD noise. Therefore, we just need to compare the quantity of entanglement for the states after entanglement swapping combined with environment measurement, i.e., \(|{\varphi _{0}^{m}}\rangle _{AC}\) and \(|{\varphi _{1}^{m}}\rangle _{AC}\), with that for the state after transmitting through the AD noise, i.e., \(\rho _{AB_{1}}\). Here, we assume the state parameters \(\beta =\gamma =\frac {1-\alpha }{2}\), and the decay rates D = d for the AD noises. The region of the parameter α and the decay rate d satisfying the inequality \(N(|{\varphi _{0}^{m}}\rangle _{AC})>N(\rho _{AB_{1}})\) is plotted in Fig. 1. From the figure, it is obviously the region is not empty. That is, the entanglement of the resultant state by using entanglement swapping combined with environment measurement is bigger than that of the state after transmitting through the AD noises when α and d are restricted in the gray shaded region. Therefore, our scheme can indeed enhance the entanglement. The result can be verified in Fig. 2, where we plot the gray shaded region in which the state parameter α and the decay rate d are restricted in order to ensure \(N(|{\varphi _{1}^{m}}\rangle _{AC})>N(\rho _{AB_{1}})\). The figure reveals that our scheme can always purify entanglement except for α and d approaching zero.

Fig. 1
figure 1

The region in which the parameter α and the decay rate d should lie in order to ensure \(N(|{\varphi _{0}^{m}}\rangle _{AC})>N(\rho _{AB_{1}})\)

Full size image
Fig. 2
figure 2

The region in which the parameter α and the decay rate d should lie in order to ensure \(N(|{\varphi _{1}^{m}}\rangle _{AC})>N(\rho _{AB_{1}})\)

Full size image

With similar analysis, it is found that entanglement swapping combined with environment measurement can also purify entanglement when two pair of qutrits A B 1 and B 2 C are initially prepared in the same state \(|\phi _{1}\rangle =\sqrt {\alpha }|01\rangle +\sqrt {\beta }|12\rangle +\sqrt {\gamma }|20\rangle \) or \(|\phi _{2}\rangle =\sqrt {\alpha }|02\rangle +\sqrt {\beta }|10\rangle +\sqrt {\gamma }|21\rangle \). That is, our scheme can be used to purify entanglement irrespective of the initial states. In Ref. [18], the author considered entanglement purification of noisy two-qubit states by using entanglement swapping with the help of weak measurement. However, the scheme does not work for some initial states and depends on the initial states.

When it comes to the physical mechanism of our scheme, it should be attributed to the probabilistic nature of our scheme. The success probability to obtain \(|00\rangle _{E_{1}E_{2}}\) as the results of environment measurements is P = 1 − β d − γ D, which is always less than 1. In other words, the state \(|\psi \rangle _{AB_{1}}\) can only be obtained probabilistically.

3 Applying the Protocol to Dense Coding

Now, let us consider the application of our scheme to dense coding. As introduced by Bennett and Wiesner [51], entanglement can be used as a resource for dense coding, and an entangled initial state that is shared between the sender and the receiver is essential to this communication protocol. During the process, there is inevitable interaction between the entangled state and its surrounding environment. In recent years, dense coding over noisy channels has attracted much attention [52,53,54,55], and the dense coding capacity is given by

$$ \chi(\rho)=\log_{2}d+S(\rho_{r})-S(\rho). $$
(6)

Here, ρ is the state shared between the sender and the receiver. d is the dimension of the sender’s system, and ρ r is the reduced density operator of the receiver’s system. S(ρ) is the von Neumann entropy.

Specific to the case of dense coding between Alice (the sender) and Charlie (the receiver), the shared state between them is assumed to be established by using entanglement swapping. The dense coding capacity for two different cases is compared. One is that only entanglement swapping is applied. The other one is the application of entanglement swapping combined with environment measurement. In other words, the dense coding capacity for the states \({\rho _{0}^{m}},\ {\rho _{1}^{m}},\ {\rho _{2}^{m}}\) and that for the states \(|{\varphi _{0}^{m}}\rangle _{AC},\ |{\varphi _{1}^{m}}\rangle _{AC},\ |{\varphi _{2}^{m}}\rangle _{AC}\) (m = 0, 1, 2) should be compared. Through straightforward calculation, the states \({\rho _{1}^{m}}\) and \({\rho _{2}^{m}}\) have the same dense coding capacity, and the dense coding capacity for the states \(|{\varphi _{1}^{m}}\rangle _{AC}\) and \(|{\varphi _{2}^{m}}\rangle _{AC}\) are equal too. Therefore, one just need to compare the dense coding capacity for the states \({\rho _{0}^{m}},\ {\rho _{1}^{m}}\) with that for states \(|{\varphi _{0}^{m}}\rangle _{AC},\ |{\varphi _{1}^{m}}\rangle _{AC}\). Henceforth, the state parameter β is assumed to be equal to γ, and the decay rate D is assumed to be same as d. It is found that \(\chi (|{\varphi _{0}^{m}}\rangle _{AC})\) is always larger than \(\chi ({\rho _{0}^{m}})\), and \(\chi (|{\varphi _{1}^{m}}\rangle _{AC})\) is always larger than \(\chi ({\rho _{1}^{m}})\). In Fig. 3, the contour plot of \(\chi (|{\varphi _{0}^{m}}\rangle _{AC})-\chi ({\rho _{1}^{m}})\) as functions of the state parameter α and the decay rate d is given. The figure indicates our scheme can improve the dense coding capacity in most of the region. The similar result can be verified when one compares the dense coding capacity for the states \( |{\varphi_{1}^{m}}\rangle _{AC} \) and \( {\rho_{0}^{m}} \) in Fig. 4, where we present the contour plot of \(\chi (|{\varphi _{1}^{m}}\rangle _{AC})-\chi ({\rho _{0}^{m}})\) versus α and d. All of these results reveal that the dense coding capacity can be improved by entanglement swapping combined with environment measurement. The physical reason underlying this result is that our scheme can purify entanglement, and dense coding depends on entanglement.

Fig. 3
figure 3

The contour plot of \(\chi (|{\varphi _{0}^{m}}\rangle _{AC})-\chi ({\rho _{1}^{m}})\) as functions of the state parameter α and the decay rate d

Full size image
Fig. 4
figure 4

The contour plot of as functions of the state parameter α and the decay \(\chi (|{\varphi _{1}^{m}}\rangle _{AC})-\chi ({\rho _{0}^{m}})\) rate d

Full size image

4 Conclusion

In this paper, we propose a scheme to purify entanglement of two-qutrit entangled states distributed through the local individual AD channels by using entanglement swapping combined with environment measurement. The quantity of entanglement of the resultant states for our scheme is bigger than that of the initial state subjected to the AD noises as well as that of the states just after application of entanglement swapping. That is, our scheme can purify entanglement under the influence of the local individual AD noises. The application of our scheme to dense coding indicates that our scheme can improve the dense coding capacity. Our scheme may have important applications in establishing high-quality entangled channels between separated participants, which is the foundation of the large-scale quantum communication and quantum computing network.