1 Introduction

The relativistic three-body wave equations have been solved for scalar particles or antiparticles interacting via a massive or massless mediating scalar field. The Hamiltonian formalism of quantum field theory in a reformulated model and variational method have been used to find approximate ground-state energy solutions for various strengths of coupling. The results contain relativistic effects such as virtual annihilation interaction or retardation effects for our three-body systems. In this work we obtain our numerical solutions for distinct cases where the relativistic effects such as retardation and virtual annihilation effects are excluded or included for different strengths of coupling.

The relativistic bound states systems in Quantum Field Theory (QFT) are usually solved by means of the Bethe and Salpeter (BS) formalism [1, 2]. However, the implementation of BS method can be a difficult task for systems containing more than two particles. Furthermore, the existence of relative-time coordinates and the perturbative treatment of interaction in BS method may complicate the calculations. Hence, the theory of relativistic bound states remains an interesting problem in recent few body conferences proceedings. For example, we can quote the investigation of the relativistic three-body bound state in three dimensions in a recent conference on few-body problems in physics [3].

A different approach from BS method is the variational method within the Hamiltonian formalism of QFT ([4,5,6]). Among its attractive characteristic is that it can appear in a form identical to the traditional Schrödinger equation in the non relativistic limit for the few body systems and that it can be applied to n-body systems where n is an arbitrary number of particles and/or antiparticles, as it has been shown in previous manuscripts ([7,8,9]). The variational method can be applicable to strongly coupled systems for which perturbation theory may not be reliable. One should note that like all variational methods, the solution may be only as good as the trial state being employed [10,11,12]. The construction of realistic and suitable trial state is a key point in the variational method.

In an earlier work introduced by Darewych [6] a transformed variational method in the Hamiltonian formalism of QFT was suggested for obtaining the relativistic wave equations. The Lagrangian of the few body systems has been reconstructed by employing Green functions in order to specify the mediating fields in terms of the particle or antiparticle field. The QFT of the system was constructed from the obtained reformulated Hamiltonian. This reformulated model has been used in this work.

The famous integral equation of Bethe and Salpeter (BS) [1] has led to the study of the two-body case. There are many papers available in the literature for the study of relativistic two-body problem (see, for examples, [13,14,15] and refs therein). After the work of BS three-body generalizations were also considered in the literature (see, for examples, [16,17,18] and refs therein). For the scalar particles or antiparticles interacting via scalar mediating field the absence of spin degrees of freedom makes the calculations rather simple compared to the QED or QCD case, and therefore investigation of such systems is popular as a model test theory.

In Ref. [14] the authors have derived relativistic two-body wave equation for scalar particle and antiparticle, termed “nucleon” and “antinucleon, interacting through a mediating scalar field (“pions”), which may be massless (μ = 0) or massive (μ/m = 0.15). The simple trial state for the two-body system (i.e. of the type \(|N{\bar {N}}{\rangle }\) ) which was considered in [14] was in reasonable agreement with other works for various coupling α. Similarly, for the three-body case (two particles and an antiparticle) [18] using simple trial state of the type \(|N{\bar {N}N}{\rangle }\) some numerical solutions have been obtained. The computations for the three-body systems in [18] have been performed without considering the virtual annihilation interaction effects.

The purpose of the present work is to study the inclusion or exclusion of virtual annihilation interaction and retardation effects for the three-body system (two particles and an antiparticle) which interact through a mediating scalar field which can be massless (μ = 0) or massive (μ/m = 0.15). The first two cases correspond to obtain the ground state energy solutions for the three-body system when both virtual annihilations and retardation effects are excluded or included, respectively. The other two cases correspond to find the ground state energy solutions when the computations are performed with virtual annihilation interaction and without retardation effects or without virtual annihilation interaction and with retardation effects.

The graphs of ground state energy solutions versus various coupling α have been plotted. The coupling for the massless case (μ = 0) is varied as follows: (0.1 ≤ α ≤ 1) or for the massive case (μ/m = 0.15 ) we have: 0.3 ≤ α ≤ 1. The coupling α close to 1 is considered strong coupling and the numbers related to α around 0.1 to 0.3 units are considered weak coupling. Over-all, the calculations show that the retardation effects or virtual annihilation interactions are relatively minor effects compared to Yukawa interactions for the three-body systems, particularly at small value of α. However, at strong coupling the magnitude of the contribution of virtual annihilation interactions and retardation effects is increasing. Even though the obtained results can not dramatically change the ground state energy solutions of the systems under study but the changes of the values of energy solutions are not negligeable, particularly at strong coupling.

From practical points of view, we can mention what follows. The observation of the three-body system (e − e − e +), consisting of two electrons and a positron, [19] paved the way for new search of other exotic three-body systems. Similarly, from experimental or theoretical point of view, one may ask the question whether bound-states of system such as π − π − π + can be formed. The study of the properties of such exotic particles and/or antiparticles is of fundamental importance. For example, the investigation of such exotic systems may help to explain why the observable universe has more matter than antimatter.

The first section is the introduction. We recall the reformulated model in Section 2 [6] or [14]. In addition, we have summarized in this section some of the previous results [18] using simple trial state of the type \(|N{\bar {N}N}{\rangle }\). These results contain the relativistic wave equations and their non-relativistic limits. In Section 3 the approximate, variational solutions for our three-body ground state energies have been presented for various cases where virtual annihilation interactions and retardations effects are included or excluded for different strengths of the coupling. Concluding remarks are given in Section 4.

2 Scalar Model and the Reformulated Theory

We quote some results from earlier works (see [6] or [14]) to make it easier to pursue the current paper. Moreover, in order to be complete and to have a self-contained manuscript it would better to recall some key points from before. We have scalar particles and antiparticles of mass m (ϕ is a complex field), interacting via a mediating real scalar field (χ). The mediating “pion” field or χ(x) can be massive (μ ≠ 0) or massless (i.e. μ = 0). A rather more simple version, in which ϕ is real, is usually studied in other works (see, for example, [13]). In that case there are only particles (with no distinct antiparticles) and their bound states are created by scalar particles ϕ, with mass m interacting through the exchange of a scalar particle χ with mass μ. In the present work ϕ(x) is the (complex) field corresponding to scalar particles and anti-particles. The Hamiltonian density in the reformulated model [6] or [14] is

$$ \mathcal{H}(x)=\mathcal{H}_{\phi }(x)+\mathcal{H}_{\chi }(x)+\mathcal{H}_{I_{1}}(x)+\mathcal{H}_{I_{2}}(x), $$
(2.1)

where \(\mathcal {H}_{\phi }(x)\) and \(\mathcal {H}_{\chi }(x)\) correspond to the Hamiltonian density of the fields ϕ and χ, respectively. \( \mathcal {H}_{I_{1}}(x)\) and \(\mathcal {H}_{I_{2}}(x)\) present the Hamiltonian density corresponding to the different type of interactions. We have

$$ \mathcal{H}_{\phi }(x)=p_{\phi^{\ast }}(x)\,p_{\phi }(x)+\nabla \phi^{\ast }(x)\cdot \nabla \phi (x)+m^{2}\,\phi^{\ast }(x)\phi (x), $$
(2.2)
$$ \mathcal{H}_{\chi }(x)={\frac{1}{{2}}}p_{\chi_{0}}^{2}+{\frac{1}{{2}}} (\nabla \chi_{0})^{2}+{\frac{1}{{2}}}\mu^{2}{\chi_{0}^{2}}, $$
(2.3)

\(\displaystyle p_{\phi ^{\ast }}=\frac {\partial \mathcal {L}}{\partial {\dot { \phi }}}={\dot {\phi }^{\ast }},~~p_{\phi }=\frac {\partial \mathcal {L}}{ \partial {\dot {\phi ^{\ast }}}}={\dot {\phi }}\) and \(\displaystyle p_{\chi _{0}}=\frac {\partial \mathcal {L}}{\partial {\dot {\chi _{0}}}}={\dot {\chi }_{0} }\) are conjugate momenta,

$$ \mathcal{H}_{I_{1}}(x)=g\,\phi^{\ast }(x)\phi (x)\chi_{0}(x), $$
(2.4)
$$ \mathcal{H}_{I_{2}}(x)=-\frac{g^{2}}{2}\int dx^{\prime }\,\phi^{\ast }(x)\phi (x)D(x-x^{\prime })\phi^{\ast }(x^{\prime })\phi (x^{\prime }), $$
(2.5)

where d x = d N x d t in N spatial plus time dimensions and

$$ D(x-x^{\prime })=\int \frac{dk}{(2\pi )^{N+1}}\,e^{-ik\cdot (x-x^{\prime })}\,\frac{1}{\mu^{2}-k^{2}+i\epsilon }\,, $$
(2.6)

where d k = d N+1 k and k 2 = k ν k ν . We use unit \(\hbar =c=1\).

One should note that χ 0(x) is a solution of the free field equation, while D(x − x ′) is a covariant Green function. g presents the coupling constant. A quantum field theory was constructed by replacing the field variables with operators. We have the Fourier decomposition of the fields as below:

$$ \phi (x)=\int \,d^{N}{q}\;\frac{1}{[(2\pi )^{N}2\omega_{q}]^{{\frac{1}{{2}}} }}\;[A(\mathbf{q})e^{-i{q\cdot x}}+B^{\dagger }(\mathbf{q})e^{i{q\cdot x}}] \text{ (and its conjugate),} $$
(2.7)
$$ \chi_{0}(x)=\int \,d^{N}{p}\frac{1}{\,[(2\pi )^{N}2{\Omega}_{p}]^{{\frac{1}{{ 2}}}}}[d(\mathbf{p})e^{-i{p\cdot x}}+d^{\dagger }(\mathbf{p})e^{i{p\cdot x}} ], $$
(2.8)

where we have \(\omega _{q}=(\mathbf {q}^{2}+m^{2})^{\frac {1}{{2}}}\), \({\Omega } _{p}=(\mathbf {p}^{2}+\mu ^{2})^{\frac {1}{{2}}}\), q ⋅ x = q ν x ν and q ν = (q 0 = ω q , q).

The momentum-space operators, A ‡, A, B ‡, B indicate the creation (A ‡, B ‡) and annihilation (A, B) of free scalar particles (or nucleons) and scalar antiparticles (or antinucleons) respectively. The d ‡, d operators designate the creation and annihilation of the free mediating-field pions. The commutation relations can be expressed as below

$$ \lbrack A(\mathbf{p}),A^{\dagger }(\mathbf{q})]=[B(\mathbf{p}),B^{\dagger }(\mathbf{q})]=\delta^{N}(\mathbf{p}-\mathbf{q}), $$
(2.9)
$$ \lbrack d(\mathbf{p}),d^{\dagger }(\mathbf{q})]=\delta^{N}(\mathbf{p}- \mathbf{q}). $$
(2.10)

The vacuum state |0〉 is described by A p |0〉 = B p |0〉 = d k |0〉 = 0. We have normal ordered the Hamiltonian (denoted by :\({\hat {H}}\):), since we are not interested in finding vacuum-energy solutions in this paper. In the Hamiltonian formalism of the QFT we wish to find solutions of the equation

$$ {\hat{P}}^{\beta }|{\Psi} {\rangle }=Q^{\beta }|{\Psi} {\rangle }, $$
(2.11)

where \({\hat {P}}^{\beta }=({\hat {H}},{\hat {\mathbf {P}}})\) is the energy-momentum operator of the quantum field theory, and Q β = (E, Q) describes the energy-momentum eigenvalue. The β = 0 component of the above equation is very difficult to solve. Hence, one may need to seek some approximation schemes. This leads us to find approximate solutions using the variational principle

$$ \delta \langle {\Psi}_{trial}|{\hat{H}}-E|{\Psi}_{trial}\rangle_{t=0}=0, $$
(2.12)

where |Ψ t r i a l 〉 is a suitable trial state that we should choose. It should contain adjustable parameters or functions.

The simplest three-body system trial state (two particles and one antiparticle) that can be taken is as follows [18]

$$ \mid \psi_{3}{\rangle }=\int d^{N}p_{1}d^{N}p_{2}d^{N}p_{3}F(\mathbf{p}_{1}, \mathbf{p}_{2},\mathbf{p}_{3})A^{\dagger }(\mathbf{p}_{1})B^{\dagger }(\mathbf{p}_{2})A^{\dagger }(\mathbf{p}_{3})|0\rangle , $$
(2.13)

where F is an adjustable function. Moreover, 〈ψ 3|ψ 3〉\(=\int d^{N}p_{1}\,d^{N}p_{2}\,d^{N}p_{3}|F\) (p 1, p 2, p 3)|2 should be finite (we shall take it to be unity). In the Appendix we have written the matrix elements needed to implement the variational principle (2.12). They contain all tree-level Feynman diagrams, namely one-pion exchange and virtual annihilation interaction.

One should note that we have \({\langle }\psi _{3}|:{\hat {H}}_{I_{1}}:|\psi _{3}{\rangle =0}\) and \({\langle }\psi _{3}|:{\hat {H}}_{\chi }:|\psi _{3}{ \rangle =0}\). This means that for the present choice of trial state, namely (2.13), we are incapable of describing process involving the absorption or emission of physical (as opposed to virtual) pions. One should also note that such process can be considered in the current formalism with inclusion of additional Fock-states in the wave function. But, we shall leave it for subsequent studies. For the wave function F(p 1, p 2, p 3) the obtained relativistic three body wave equation [18] for the coefficient function F of our trial state (2.13) is (we set t = 0):

$$\begin{array}{@{}rcl@{}} &&F(\mathbf{p}_{1},\mathbf{p}_{2},\mathbf{p}_{3})[\omega_{p_{1}}+\omega_{p_{2}}+\omega_{p_{3}}-E] \\ &=&\frac{g^{2}}{4(2\pi )^{3}}\left[ \int d^{N}p_{1}^{\prime }d^{N}p_{3}^{\prime }F(\mathbf{p}_{1}^{\prime },\mathbf{p}_{2},\mathbf{p} _{3}^{\prime })\frac{\delta^{N}(\mathbf{p}_{1}^{\prime }+\mathbf{p} _{3}^{\prime }-\mathbf{p}_{1}-\mathbf{p}_{3})}{\sqrt{\omega_{p_{1}^{\prime }}\omega_{p_{3}^{\prime }}\omega_{p_{1}}\omega_{p_{3}}}}\frac{1}{\mu^{2}-(p_{3}-p_{3}^{\prime })^{2}}\right]_{G1} \\ &&+\frac{g^{2}}{4(2\pi )^{3}}\left[ \int d^{N}p_{1}^{\prime }d^{N}p_{2}^{\prime }F(\mathbf{p}_{1}^{\prime },\mathbf{p}_{2}^{\prime }, \mathbf{p}_{3})\frac{\delta^{N}(\mathbf{p}_{1}^{\prime }+\mathbf{p} _{2}^{\prime }-\mathbf{p}_{1}-\mathbf{p}_{2})}{\sqrt{\omega_{p_{1}^{\prime }}\omega_{p_{2}^{\prime }}\omega_{p_{1}}\omega_{p2}}}\frac{1}{\mu^{2}-(p_{1}-p_{1}^{\prime })^{2}}\right]_{G2} \\ &&+\frac{g^{2}}{4(2\pi )^{3}}\left[ \int d^{N}p_{2}^{\prime }d^{N}p_{3}^{\prime }F(\mathbf{p}_{1},\mathbf{p}_{2}^{\prime },\mathbf{p} _{3}^{\prime })\frac{\delta^{N}(\mathbf{p}_{2}^{\prime }+\mathbf{p} _{3}^{\prime }-\mathbf{p}_{2}-\mathbf{p}_{3})}{\sqrt{\omega_{p_{2}^{\prime }}\omega_{p_{3}^{\prime }}\omega_{p_{2}}\omega_{p_{3}}}}\frac{1}{\mu^{2}-(p_{2}-p_{2}^{\prime })^{2}}\right]_{G3} \\ &&+\frac{g^{2}}{4(2\pi )^{3}}\left[ \int d^{N}p_{1}^{\prime }d^{N}p_{2}^{\prime }F(\mathbf{p}_{1}^{\prime },\mathbf{p}_{2}^{\prime }, \mathbf{p}_{3})\frac{\delta^{N}(\mathbf{p}_{1}^{\prime }+\mathbf{p} _{2}^{\prime }-\mathbf{p}_{1}-\mathbf{p}_{2})}{\sqrt{\omega_{p_{1}^{\prime }}\omega_{p_{2}^{\prime }}\omega_{p_{1}}\omega_{p_{2}}}}\frac{1}{\mu^{2}-(p_{2}+p_{1})^{2}}\right]_{A1} \\ &&\!+\frac{g^{2}}{4(2\pi )^{3}}\left[ \int d^{N}p_{1}^{\prime }d^{N}p_{3}^{\prime }F(\mathbf{p}_{1}^{\prime },\mathbf{p}_{2},\mathbf{p}_{3}^{\prime })\frac{\delta^{N}(\mathbf{p}_{1}^{\prime }+\mathbf{p}_{3}^{\prime }-\mathbf{p}_{1}-\mathbf{p}_{3})}{\sqrt{\omega_{p_{1}^{\prime }}\omega_{p_{3}^{\prime }}\omega_{p_{1}}\omega_{p_{3}}}}\frac{1}{\mu^{2}\!-(p_{1}^{\prime }\,+\,p_{3}^{\prime })^{2}}\right]_{A2},\\ \end{array} $$
(2.14)

where, we have \(\omega _{p}=\sqrt {\mathbf {p}^{2}+m^{2}}\).

Note that the first three terms (G1, G2, and G3) on the right side of the above equation correspond to attractive one-pion exchange interactions among the three body system (the two nucleons and the antinucleon). The last two terms (A1 and A2) are related to virtual annihilation interactions (repulsive contact potential between particle and antiparticle). One should also note that the three-body relativistic wave equation has only positive-energy solutions. The calculation have been performed in the rest frame Q = 0 where F(p 1, p 2, p 3) = f(p 1, p 2)δ 3(p 1 + p 2 + p 3), and the relativistic momentum-space wave equation is followed from the variational principle (2.12).

Because the interactions among particles or antiparticles do propagate with finite velocity (the propagation is not with infinite velocity) we are concerned with retardation effects. If we ignore the “retardation effects”, we should replace in the kernel of three-body equations the terms such as 1/[μ 2 − (p 1 − p 2)2] by 1/[μ 2 + (p 1 −p 2)2].

One should note that the statistical factors [20] should be considered in our relativistic wave equations since for the three-body problem we study (two particles and one antiparticle; all of them have the same mass) there are two identical particles with the same mass m. Hence, we should not double count the states of identical particles [20] . Therefore, for our present three-body system the statistical factor is 1/2!.

We use the Fourier transformation (coordinate space) as below

$$ {\Psi} (\mathbf{r}_{1},\mathbf{r}_{2},\mathbf{r}_{3})=\frac{1}{(2\pi )^{3N/2}} \int d^{N}p_{1}d^{N}p_{2}d^{N}p_{3}\,F(\mathbf{p}_{1},\mathbf{p}_{2},\mathbf{ p}_{3})\,e^{i(\mathbf{p}_{1}\cdot \mathbf{r}_{1}+\mathbf{p}_{2}\cdot \mathbf{ r}_{2}+\mathbf{p}_{3}\cdot \mathbf{r}_{3})}, $$
(2.15)

It is of interest to note that in the non-relativistic limit, where \(\mathbf { p}_{k}^{2}/m^{2}<<1\), (2.14) will change to the Schrödinger equation

$$ -\frac{1}{2m}\left( {\sum\limits_{i=1}^{3}{\nabla_{i}^{2}}}\right) {\Psi} (\mathbf{r} _{1},\mathbf{r}_{2},\mathbf{r}_{3})+\left( V(\mathbf{r}_{1},\mathbf{r}_{2}, \mathbf{r}_{3})-\epsilon \right){\Psi} (\mathbf{r}_{1},\mathbf{r}_{2},\mathbf{r}_{3})=0, $$
(2.16)

where 𝜖 = E − 3m.

The obtained non-relativistic potential V(r 1, r 2, r 3) is a sum of attractive Coulomb potentials (μ = 0) or Yukawa potentials (μ ≠ 0) [the corresponding terms G1, G2, and G3 in the relativistic (2.14)], due to one-pion exchange, and repulsive contact potentials (if μ < 2m) [the corresponding terms A1 and A2 in the relativistic (2.14)], because of virtual annihilation interaction between nucleon and antinucleon. The non relativistic potential V(r 1, r 2, r 3) is precisely,

$$\begin{array}{@{}rcl@{}} V(\mathbf{r}_{1},\mathbf{r}_{2},\mathbf{r}_{3}) &=&-\alpha \,\frac{e^{-\mu | \mathbf{r}_{1}-\mathbf{r}_{3}|}}{|\mathbf{r}_{1}-\mathbf{r}_{3}|}-\alpha \, \frac{e^{-\mu |\mathbf{r}_{1}-\mathbf{r}_{2}|}}{|\mathbf{r}_{1}-\mathbf{r} _{2}|}-\alpha \,\frac{e^{-\mu |\mathbf{r}_{2}-\mathbf{r}_{3}|}}{|\mathbf{r} _{2}-\mathbf{r}_{3}|} \\ &&+\,\alpha \,\frac{4\pi }{4m^{2}-\mu^{2}}\,\delta^{3}(\mathbf{r}_{1}- \mathbf{r}_{2})+\alpha \,\frac{4\pi }{4m^{2}-\mu^{2}}\,\delta^{3}(\mathbf{r }_{1}-\mathbf{r}_{3}), \end{array} $$
(2.17)

where we denote α = g 2/(16π m 2) as the effective dimensionless coupling constant.

3 The Three-body Ground State Energy Variational Solutions

It is impossible to solve analytically the relativistic (or non-relativistic) three-body wave equations. At least, we do not know how to solve them analytically. Therefore, we seek some approximate, variational solutions of the relativistic wave equations. One of the motivations behind this work is to show the validity of the present work for calculations of relativistic effects such as the effects of virtual annihilation interactions or retardation effects for strongly coupled systems. For computations of ground states energies of the three-body systems we examine relatively simple trial forms for the function F. We consider

$$ F(\mathbf{p}_{1},\mathbf{p}_{2},\mathbf{p}_{3})=f(\mathbf{p}_{1})f(\mathbf{p}_{2})\,\delta (\mathbf{p}_{1}+\mathbf{p}_{2}+\mathbf{p}_{3}), $$
(3.1)

where

$$ f(\mathbf{p}_{i})=\frac{1}{(\mathbf{p}_{i}^{2}+{p_{0}^{2}})^{\nu }}, $$
(3.2)

and p 0 and ν are parameters that can be adjusted later on. We perform our computations in the rest frame (total momentum is zero).

As pointed out before, the relativistic wave equations lead us to calculate multidimensional integrals that are impossible to solve analytically. Thereupon, we perform our numerical computations using the Monte-Carlo techniques [21]. This requires to adopt the usual Monte-Carlo procedure [21]. Self-consistency checks have been carried out by modifying the number of sample points in order to reach some acceptable convergence for the obtained ground state energy results.

We have presented our data or graphs with error bars which represents the uncertainty of the corresponding coordinate of the point. We think that our results can be accurate to at least two significant figures. The optimal values of the variational parameter p 0 have been presented for each value of the coupling constant α. One should note that in order to locate the minimum of the variational trial energy as a function of ν one can vary the parameter ν. However, changing the values of ν can not noticeably alter our numerical solutions as it can be seen for the two-body case (see Table 2 and Table 3 of [14]). Since the best values of the parameter ν mostly correspond to the case ν = 2, which is the non relativistic hydrogenic ground state value, we do not change the parameter ν and we shall fix it at ν = 2.

In Table 1 the numerical results have been presented for different cases, where retardation effects and/or virtual annihilation interaction have been included or excluded for massive-exchange case μ = 0.15m. The three-body rest energies E 3 and p 0 (wave function parameters) are given for various coupling strength α. It should be mentioned that in the literature virtual annihilation interaction is normally not included in the results. The numerical solutions have also been plotted in Fig. 1.

Table 1 Three-body bound-state mass E/m for different values of the coupling α, massive quantum exchange case μ = 0.15m , and wave function parameters p 0
Full size table
Fig. 1
figure 1

Three-body ground state energies (E/m) with and/or without virtual annihilation interactions terms and/or retardation effects, for the massive exchange case μ = 0.15 m, and different strengths of the coupling α

Full size image

As one can see from Fig. 1 the top curve corresponds to the case where virtual annihilation interactions are included and the retardation effects are excluded. The next two cases concern with rest energies E 3 (for different coupling α) that are obtained when both virtual annihilations and retardation effects are excluded and included, respectively. The lowest curve of E 3 is for the case where virtual annihilation interactions are excluded but the retardation effects are included. From these results only the last case has been studied before [18]. We did include it here for comparison purposes. Energies, E 3 and p 0 have been presented in units of m (i.e. m = 1) for different coupling strength α.

The results corresponding to the massless exchange case (μ = 0) have been presented in Table 2 and Fig. 2. It should be noted that for this case (μ = 0) the Yukawa potential becomes Coulombic in the non-relativistic limit. The numerical solutions are given for various cases where retardation effects and/or virtual annihilation interactions have been included or excluded. The three-body energies (E 3) and parameters (p 0) have been presented for different coupling strength α. E 3 and p 0 are given in units of m (i.e. m = 1) for the coupling α.

Table 2 Three-body bound-state mass E/m for different values of the coupling α, massless quantum exchange case μ = 0, and wave function parameters p 0
Full size table
Fig. 2
figure 2

Three-body ground state energies (E/m) with and/or without virtual annihilation interactions terms and/or retardation effects, for the massless exchange case μ = 0, and different strengths of the coupling α

Full size image

Binding energy of the three-body problem can be defined as B 3: B 3 = E 3 − 3 in units of m (m = 1). Therefore, one can easily see for both cases, namely, massless-exchange case (μ = 0) or massive-exchange case (μ = 0.15m) the binding energy augments with increasing α. This result can be expected since for the current scalar mediating field the dominant interactions (one-quantum exchange) are definitely attractive. Moreover, p 0 (wave-function parameter) augments while α increases, that is the wave functions become more peaked in the coordinate space at higher values of the coupling α.

Even though the qualitative behavior of E(α) for the massless-exchange case (μ = 0) is comparable to that for massive-exchange case (μ = 0.15m), the binding, for given value of α is substantially larger for the case μ = 0 than for μ/m = 0.15. It sets in at \(\alpha _{0}\rightarrow 0\).

The results presented in Tables 1 and 2 (and the graphs of Figs. 1 and 2) confirm that although the virtual annihilations or retardations effects are minor effects compared to Yukawa interactions for the systems under study but the magnitude of the contribution of virtual annihilation and retardation effects augments particularly at strong coupling.

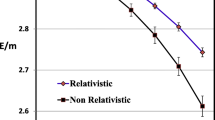
In Fig. 3 we have plotted the results obtained based on Bethe and Salpeter (BS) equation for the three-body ground-state energy (E/m) as a function of dimensionless coupling constant [22] for the case (μ/m = 0.01). In order to compare our results with BS formalism we have also included in Fig. 3 the results of the present three-body system (see Table 2, retardation effects and virtual annihilation interactions are included) for the massless exchange case (μ/m = 0). As one can see from Fig. 3, one can conclude that at relatively small coupling (0.1 ≤ α ≤ 0.3) the BS and current results are very similar. However, at strong coupling (0.4 ≤ α ≤ 1) the present results suggest a stronger binding energy compared to the BS case.

Fig. 3
figure 3

Three-body ground state energy (E/m) as a function of the coupling constant α. Curves from top to bottom: (BS) equation [22] (μ/m = 0.01), the present results (E 3) when retardation effects and virtual annihilation terms are included for the massless exchange case (μ = 0)

Full size image

4 Concluding Remarks

The variational method have been applied to study the relativistic three-body bound state systems. We have used a reformulated version of the QFT theory in which a covariant Green function has been employed. The calculations have been performed in the scalar Yukawa model, in which two scalar particles and one scalar antiparticle of mass m interact via scalar exchange field, which can be massless (μ = 0) or massive (μ/m = 0.15).

It should be mentioned that the study of renormalized QFT [23] and scalar fields or scalar perturbations [24] can be of interest as a model test theory since such work can pave the way for of the investigation of more complicated systems such as fermion particle fields and vector mediating fields.

The variational approach in this work did produce multidimensional momentum-space relativistic wave equations for the three-coefficient function F. The interaction kernels in the equations have one-meson exchange, virtual pair annihilation diagrams, and retardation effects. The resulting three-body equations are Salpeter-like (rather than Klein-Gordon-like). This means that the relativistic wave equations have only positive-energy solutions. The Monte-Carlo methods have been used to evaluate the multi-dimensional integrals.

The three-body ground state energy solutions E(α) and wave-function parameters p 0 for both the massless and massive exchange case have been determined in the domain 0.1 < α ≤ 1 and 0.3 ≤ α ≤ 1, respectively. The ground state energies are found to decrease monotonically from 3m with increasing strength of the coupling. Virtual annihilation interactions or retardations effects are small effects at low coupling and overall they can be considered minor effects compared to Yukawa interactions for the three-body systems under study. However, the magnitude of the contribution of virtual annihilations and retardation effects augments particularly at strong coupling and these effects can not be neglected.

The approach presented in this paper can be extended for n-body fermion systems [25, 26]. The resulting relativistic wave equations will be more complex and of course various calculations will be more tedious. One should note that in the case of quantum electrodynamic theory (QED) since the coupling strength of QED is small compared to the present scalar model the virtual annihilations or retardations effects would have very small contributions. One should also note that various calculations corresponding to relativistic three-quark models [27] can be of particular interest in the case of quantum chromodynamics theory (QCD).

The existence of a new scalar ”fundamental” particle, namely Higgs boson, was confirmed during the period 2011-2013. Therefore, it would be of fundamental interest to ask the question whether bound-states and related relativistic effects of, for example ”three” Higgs bosons, can be studied. The existence of two-Higgs-boson bound states has been previously investigated in [28, 29]. Even though, from theoretical point of view, the study of the bound-state of three Higgs bosons may be possible using the variational methods employed in the present work we should note that this study requires tedious calculations and is beyond the scope of the current manuscript.

Finally, it would be of interest to mention that the variational method and the Hamiltonian formalism used in the present work can be applied to QCD systems in order to study the relativistic wave equations and the corresponding relativistic effects, for example for three-body quark systems, as it has been attempted in a previous manuscript for a quark-antiquark system [30].