1 Introduction

Since the presentation of the first quantum key distribution protocol by Bennett and Brassard in 1984 [1], quantum information and quantum computation have spurred a number of theoretical and practical researches. In recent decade, researches on quantum computation and quantum information make it possible to be used in real-life world scenario applications related to information security [2–12].

In classical communication protocols, the digital signature plays an important role by offering authenticity, integrity of messages and forestalls disavowal of transmitted messages. In addition to the above mentioned requirement, in some specific applications such as electronic voting and electronic cash systems, the privacy of the message owners had to be protected. To preserve such conditions on secure communication, the concepts of blind signature and arbitrated signature schemes were proposed. Blind signature schemes provide a type of solution that the manager signs the message blindly and the voter then converts it to the signature of the original message for anyone who would probably verify it. The manager signs the message in such a way that he can neither know the content of the message nor recollect the message and the corresponding signature he has signed. In an arbitrated signature scheme, every signed message from the sender, S, to the receiver, R, goes to an arbiter, A, first. The arbitrator confirms the origin of the message and signature after subjecting them to the number of tests and sends them to the receiver.

Up to now many quantum blind signature and arbitrated quantum signature (AQS) schemes have been presented [13–22]. The AQS model by using the correlation of Greenberger-Horne-Zeilinger (GHZ) triplet states and the Leung quantum one-time pad (L-QOTP) algorithm [13] was first introduced by Zeng et al. [14]. Li et al. presented a more efficient AQS scheme by replacing GHZ states with Bell states [15]. However, Zou and Qiu [16] showed that both these two AQS schemes above were insecure because they could be disavowed by the receiver, and further proposed two improved AQS schemes. However, Hwang et al. [17] showed that the same security flaw still exists in Zou et al.’s schemes. Some other security problems and improvements were also introduced in Refs. [18–23]. Obviously, the construction and the cryptanalysis of AQS schemes are two important branches of AQS and can be mutually reinforcing.

Recently, an interesting research regarding the arbitrated quantum signature scheme based on cluster state has been done by Yang et al. [24], where the cluster states are employed for quantum key distribution and quantum signature. Motivated by this work, this paper a new arbitrated quantum signature scheme is proposed to make the original protocol not only more efficient but also more secure. The paper is organized as follows:

The next section introduces the basic preliminaries, which is involved in presenting the new improved protocol. Our improved protocol for quantum arbitrated signature is presented in Section 3. The security of the proposed protocol is analyzed in Section 4. Finally, a short discussion and a brief conclusion are given in Section 5.

2 Cluster States

In general, an N-qubit cluster state is given by [25]

$$ |C_{N}\rangle=\frac{1}{2^{\frac{N}{2}}}\otimes_{a=1}^{N}(|0\rangle_{a}\sigma_{z}^{a+1}+|1\rangle_{a}) $$
(1)

where σ z is Pauli operator. So. the four-particle cluster states can be described by

$$ |C_{4}\rangle=|\phi^{00}\rangle_{1234}=\frac{1}{2}(|0000\rangle+|0110\rangle+|1001\rangle-|1111\rangle)_{1234} $$
(2)

The four-particle cluster states were proven to be useful in many fields of quantum communication [26–29]. The usefulness of this state for arbitrated quantum signature is as follows. By performing Pauli operators on qubits 2 and 4, an orthonormal basis can be constructed as

$$ FMB=|\phi^{ij}\rangle_{1234}={\sigma_{2}^{i}}{\sigma_{4}^{j}}|\phi^{00}\rangle_{1234}|i,j=0,1,2,3 $$
(3)

Here, Pauli operators \({\sigma _{2}^{i}},{\sigma _{4}^{j}}\) act on the 2 and 4 particles in cluster states and they are one of the four Pauli operators:

$$\sigma^{0}=I=|0\rangle\langle0|+|1\rangle\langle1| , \sigma^{1}=\sigma_{z}=|0\rangle\langle0|-|1\rangle\langle1| $$
(4)
$$\sigma^{2}=\sigma_{x}=|0\rangle\langle1|+|1\rangle\langle0| , \sigma^{3}=i\sigma_{y}=|0\rangle\langle1|-|1\rangle\langle0| $$
(5)

The state |ϕ 00〉1234 can be rewritten in the following form by rearranging terms:

$$|\phi^{00}\rangle_{1234}=\frac{1}{2}\left( |0+\rangle|+0\rangle+|0-\rangle|-0\rangle+|1-\rangle|+1\rangle+|1+\rangle|-1\rangle\right)_{1234} $$
(6)
$$|\phi^{00}\rangle_{1234}=\frac{1}{2}\left( |+0\rangle|0+\rangle+|-0\rangle|0-\rangle+|-1\rangle|1+\rangle+|+1\rangle|1-\rangle\right)_{1234} $$
(7)

where |0+〉 and |+0〉 are the abbreviated expression of tensor product of |0〉 and |+〉:

$$|0+\rangle=|0\rangle\otimes|+\rangle \; \; ,\;\;|+0\rangle=|+\rangle\otimes|0\rangle$$

Thus, we have two groups of different measurement bases for the two-qubit Hilbert space:

$$AMB_{1}= { |0+\rangle,|0-\rangle,|1-\rangle|1+\rangle }$$
$$AMB_{2}= { |+0\rangle,|-0\rangle,|-1\rangle|+1\rangle }$$

Four possible measurement results |0+〉|+0〉,|0−〉|−0〉,|1−〉|+1〉,|1+〉|−1〉 can be obtained with equal probability \(\frac {1}{4}\), if one measures the qubits (1,3) in the basis AMB 1 and the qubits (2,4) in the basis AMB 2, respectively. Obviously, a similar conclusion can be derived if one measures the qubits (1,3) in the basis AMB 2 and the qubits (2,4) in the basis AMB 1, respectively. Using this property, Alice, Bob and the arbitrator can check eavesdropping in the quantum transmission.

3 High-Efficient AQS Scheme Based on the Cluster States

In this section, we introduce the new protocol for arbitrated quantum signature by using the cluster states. In this new scheme, the decoy state particle security checking is employed for guarding every eavesdropping in the first phase. Furthermore, it will be shown that the present scheme indicates more efficiency.

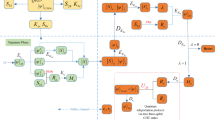
The proposed AQS scheme includes three participants, Alice is the signer, Trent is the arbitrator and Bob is the verifier. The protocol consists of three phases: the initializing, the signing and the verifying phases.

The initializing phase is accomplished as follows:

3.1 Initializing Phase

  • The arbitrator Trent prepares and sends the secret keys K AT and K BT based on |0〉,|1〉 to Alice and Bob, respectively.

  • Trent prepares a large enough number of four-qubit cluster states. He sends particles 1 and 3 for Alice and Bob, respectively and possesses particles 2 and 4 with himself.

  • Before sending particle 1 to Alice and particle 3 to Bob, Trent prepares the non-orthogonal decoy particles each randomly in one of the four-state |0〉,|1〉,|+〉,|−〉 and inserts the decoy particles into the sequence. Then, Trent sends particle 1 and decoy particles to Alice while particle 3 and decoy particles to Bob.

  • After confirming Alice and Bob have received the sequences, Trent announces publicly the positions and the states of the decoy particles. Then, Alice and Bob perform a suitable measurement on each decoy particle with the same basis as Trent chosen for preparing it. By comparing his measurement results with Alice and Bob’s announcements, Trent can then evaluate the error rate of the transmission of the sequence. If the error rate exceeds the specified threshold, they abort this communication and repeat the protocol from the beginning. Otherwise, they continue to the next step.

We denote the entangled tetrads as the sequences \( P_{i}:[{p_{i}^{1}},{p_{i}^{2}},{p_{i}^{3}},...,{p_{i}^{n}}]\;,i=1,2,3,4\). Here \(({p_{1}^{j}},{p_{2}^{j}},{p_{3}^{j}}, {p_{4}^{j}}) \) is an entangled tetrad in the same cluster state |ϕ 00〉1234 for 1≤j≤n.

The signing phase is completed as follows:

3.2 Signing Phase

  • Alice measures the particles in the sequence P 1 according to the message m = (m(1, m(2),..., m(n)), where m(i)∈{0,1}. If m(i)=0, she measures the corresponding particle \({p^{i}_{1}}\) in the |0〉,|1〉 basis otherwise, she chooses the |+〉,|−〉 basis.

  • Alice translates her measurement results into classical bits; that is, |0〉,|1〉,|+〉,|−〉 correspond to 00,01,10,11, respectively. She denotes the classical bits as R A .

  • Alice encrypts R A with her key K AT to generate her signature \(S_{A} = E_{K_{AT}}(m,R_{A})\) and sends her signature S A to Trent.

The verifying phase is performed as follows:

3.3 Verifying Phase

  • Trent decrypts S A with K AT to obtain m and R A .

  • Trent measures the corresponding particles \({p^{i}_{2}}\) and \({p^{i}_{4}}\) in P 2 and P 4 in his hand in the measurement basis corresponding to the message m;i.e., if m(i)=0, he chooses the basis AMB 2; otherwise, he chooses the basis AMB 1. Trent translates the eight states |+0〉,|−0〉,|+1〉,|−1〉,|0+〉,|0−〉,|1+〉,|1−〉 into classical bits 000,001,010,011,100,101,110,111, respectively. The encoded results can be denoted as R T .

  • Trent can deduce Alice’s measurement results \(\acute {R_{A}}\) from his own measurement results according to the correlation in (6) and (7). For example, if his measurement result is |+0〉24, Trent can infer that Alice’s measurement result should be |0〉1, and \({R^{i}_{A}}=00 \). He compares R A with \(\acute {R_{A}}\). If \(R_{A}\neq \acute {R_{A}}\) , Trent judges that Alice’s signature S A is not valid; otherwise, he accepts the signature. To ensure the data integrity during the transmission, Trent selects a proper hash function H(∙) to compute the hash function of S A . Then he encrypts m, S A , H(S A ), and R T with the key K BT , then he sends \(E_{K_{BT}}(m,S_{A},H(S_{A}),R_{T})\) to the verifier Bob.

  • Bob decrypts \(E_{K_{BT}}(m,S_{A},H(S_{A}),R_{T})\) with the key K BT and obtains m, S A , H(S A ), and R T . Then he measures the particles in the sequence P 3 with the suitable measurement basis. If m(i)=0, he measures the particle \({p^{i}_{3}}\) in the basis |+〉,|−〉; otherwise, he chooses the |0〉,|1〉 basis. He encodes the four states |0〉,|1〉,|+〉,|−〉 into classical bits 00,01,10,11, respectively, and then he denotes the encoded results as R B .

  • Bob can verify the validity of R T by checking the consistence between R B and R T according to the correlation in (6) and (7). The relationship among R A , R B , and R T is shown in Table 1. If the consistence occurs, he proceeds to step (6).

  • Bob further verifies the integrity of S A by computing the hash value of S A and comparing it with H(S A ). If the two values are equal, Bob will accept the signature S A as the valid signature for the message m, otherwise, he rejects it.

Table 1 Relationship among R A , R B , and R T
Full size table

Needless to say that, in this section Bob can ensure the data integrity and check the eavesdropping by using the classical bits R B . Since, R B and R T are related to each other according to (6) and (7), Bob simply can verify the validity of R T .

4 Efficiency and Security

In this section, the efficiency and the security of the proposed scheme are analyzed. At first, the efficiency of the proposed protocol is considered. By using Cabello’s definition of the efficiency [30], the information theoretical efficiency of a protocol is

$$ \eta=\frac{b_{s}}{q_{t}+b_{t}} $$
(8)

where b s is the expected number of secret bits received by Bob, q t is the number of qubits transmitted through the quantum channel, and b t is the number of classical bits exchanged over the public channel.

In the present arbitrated quantum signature scheme, Bob receives the signature S A containing 8n secret bits R A and n bits of the message m, while 12n classical bits R T are exchanged over the public channel and 2n qubits are transmitted among Alice, Bob and Trent during the initializing phase. Therefore, b s = 9n, q t = 2n, b t = 12n and the efficiency can be calculated as 64 %.

Now let us analyze the security of the proposed scheme. Needless to say, any secure quantum signature scheme, in addition to resistance again external attacks, which are done by an outside eavesdropper, should satisfy two the requirements: (1) The signature had not been forged by the attacker (including the malicious receiver); (2)The signature could not be disavowed by the signatory and the receiver [31–33]. Before considering the above cases it should be noted that in our scheme the arbitrator Trent shares the signing key K AT and K BT with the signer Alice and the verifying Bob. Trent as the arbitrator, is very important in two aspects, one is that he can help the receiver Bob to verify the signature; the other is that he can arbitrate some disputes between Alice and Bob. Also, Trent as the authenticated channel between Alice and Bob would avoid the vulnerability of the protocol against the distrustfulness of Trent, because Trent as an arbitrator, he must be perfectly trustworthy in our scheme. In the following discussion, we will show that the proposed scheme not only resists again an external eavesdropping, but also exhibits the above mentioned two properties.

4.1 Outside Attack

Assume an eavesdropper called Eve, who knows the procedure of our proposed quantum signature. Due to the no-cloning theorem, it is impossible for Eve to make a perfect copy of a qubit without knowing the basis, in which has initially been created. Hence, if an attacker, who is outside the protocol, wants to forge Alice’s signature, he/she needs to obtain the initial secret key K AT shared between Alice and Trent. However, it is impossible since the key is shared through unconditional secure quantum key distribution before transmitting the particles 1 and 3 to Alice and Bob. Furthermore, in the initializing phase, Trent inserts decoy particles to the sequence to guard for eavesdropping. The states and the positions of the decoy photons are unknown for Eve. Therefore, any eavesdropping done by Eve will inevitably disturb the states of the decoy particles and ultimately be detected by the two legitimate users Alice and Bob.

Also, even if the attacker obtains the key K AT , he/she still cannot forge the signature successfully since he/she cannot get the classical bits R A corresponding to Alice’s measurement result in the signing phase. In the signing phase, Alice encrypts her signature S A with classical bits R A and her key K AT . Therefore, Eve cannot forge the signature.

4.2 Forgery Attack

The signature forgery attack means that the attacker has the ability to create a fake pair of a message and a signature that the message has not been signed over the past by the legitimate signer. Suppose that the verifier Bob is malicious and tries to forge Alice’s signature.

A possible strategy is to obtain the secret key K AT and classical bits R A to generate S A in initializing phase. However, the task is impossible because the key is distributed through the quantum key distribution and if Bob wants to acquire R A , he must wield an attack strategy on particle 1, but he will be detected during the security check with decoy particles in the initializing phase, also he doesn’t know the basis measurement of Alice in the signing phase. Thus the proposed AQS scheme is secure against the forgery attack.

4.3 Disavowal Attack

Disavowal attack means that Alice signed a signature S A for a message m, and then wants to disavow that she has signed this signature. In our scheme, detecting Alice’s cheat is easy for Trent, because Alice’s signature S A encrypts with the secret key K A . Therefore, if a dispute occurs between Alice and Bob, Bob needs to take the message signature pair (m, S A ) to Trent to make a fair judgement. The signature S A has been absolutely generated by Alice, if and only if contain the secret key K A .

Moreover, in the verifying phase, the action of dishonest Alice who wants to modify S A after Trent’s action on the signature, will be found. In the check of data integrity, the hash function plays an important role. Because Alice cannot know any information about K BT , when Bob computes the hash value of S A and compares it with H(S A ), her action will be found. Therefore, a disavowal attack by the signer will not work in our scheme.

5 Conclusion and Discussion

An arbitrate quantum signature scheme based on cluster states is proposed. With the decoy photon technique in security checking, it is shown that the protocol is secure not only against the outside attack which would be done by an eavesdropper outside of the participants but also it is secure against the two types of internal attacks, i.e., the forgery attack and the disavowal attack. Furthermore by using the Cabello’s definition of the efficiency, it indicates the efficiency of 64 % confirms that the present protocol is more efficient.