Efficient Generation of Frequency-Multiplexed Entangled Single Photons

Abstract

We present two schemes to generate frequency-multiplexed entangled (FME) single photons by coherently mapping photonic entanglement into and out of a quantum memory based on Raman interactions. By splitting a single photon and performing subsequent state transfer, we separate the generation of entanglement and its frequency conversion, and find that the both progresses have the characteristic of inherent determinacy. Our theory can reproduce the prominent features of observed results including pulse shapes and the condition for deterministically generating the FME single photons. The schemes are suitable for the entangled photon pairs with a wider frequency range, and could be immune to the photon loss originating from cavity-mode damping, spontaneous emission, and the dephasing due to atomic thermal motion. The sources might have significant applications in wavelength-division-multiplexing quantum key distribution.

Frequency, as one of the most familiar degrees of freedom (DOFs) of light, has been routinely analyzed in spectroscopy for centuries and has found numerous applications in many fields [1–4]. Increasing the transmission capacity of optical fiber systems is its one of the most important applications. The wavelength division multiplexing (WDM) is a successful and typical technique for this purpose, and has had a profound impact on classical telecommunications [1, 2]. Naturally, we may use the similar method, wavelength-division-multiplexing quantum key distribution, to increase the amount of information in the quantum communication. Compared to the classical case, the different channels in quantum communication may not be independent of each other, thus the light source for the technique must be a frequency-multiplexed entangled (FME) single photon to ensure multichannel transmission and to avoid eavesdropping [5–7]. The FME single photon state has the form $\left \vert 1_{\omega _{1}, \omega _{2}} \right \rangle =c_{1}\left \vert 1\right \rangle _{\omega _{1}}\left \vert 0 \right \rangle _{\omega _{2}}+ c_{2}\left \vert 0\right \rangle _{\omega _{1}} \left \vert 1\right \rangle _{\omega _{2}}$, where $\left \vert 1\right \rangle _{\omega _{1(2)}}$ indicates the one-photon state with frequency ω ₁₍₂₎, and |0〉 indicates the vacuum state. Apparently, preparation of the above state requires coherent photonic frequency conversion, which converts photons from one frequency to another in a coherent and efficient way.

As is well known, optical frequency conversion is routinely achieved based on χ ⁽²⁾ processes [8–11] or a dark state polariton (DSP) [12–15]. In the former case, the strong driving field is a prerequisite for efficient conversion, such as the sum-frequency generation [8–10] and simulated parametric processes [11]. Recently, on the basis of the later method, the generation of two- and multi-frequency light fields has been widely studied theoretically [12–14] and experimentally [15] in multi-level atomic systems. In these systems, rich spectral features have been manifested due to constructive or destructive quantum interference between different channels. While, in the frequency degrees of freedom for quantum-based information technologies, little work has been exploited.

In this paper, We separate the processes for the generation of entanglement and for its frequency conversion, and propose two schemes to deterministically generate the FME single photons based on cavity quantum electromagnetic dynamics, which is achieved through the Raman interaction between a photon pair in cavity modes and two atomic ensembles at distance. The nature of the schemes can also be explained as the probabilistic reversible storage of entanglement, as the photonic entanglement is coherently mapped into (out of) the quantum memory, i.e., the two separated atomic ensembles, via a Raman-scattering process, the entangled AntiStokes (Stokes) photon pairs can be obtained, and may be in FME single photon state by selecting appropriate atomic energy level structure and the frequency of control fields. We find that the schemes can work in a deterministic way under certain conditions. This advance is made by introducing three key modifications over existing protocols. First, a single-photon excitation of the ensembles is employed to exclude the multiatom events in the collective spin excitation. Second, we use an ensemble of cold atoms strongly coupled to a high-finesse cavity field that maximally enhances the Stokes photon generation into the cavity mode. Third, to minimize the dissipation and the spontaneous loss from upper level and dephasing effects induced by other excited states, we consider the Raman interactions with larger single-photon detuning.

1 Generation of FME Single Photons

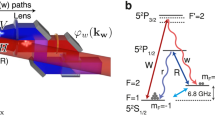
The model under consideration is shown in Fig. 1a. The single photons, generated based on Raman transitions in an optically thick caesium, are polarized at 45° from the eigen-polarizations of the beam displacer BD which splits them into entangled two optical modes to produce, in the ideal case, the following state

$$ \left\vert \psi \right\rangle_{in}=\frac{1}{\sqrt{2}}\left(\left\vert 01\right\rangle +\left\vert 10\right\rangle \right)_{\omega }. $$

(1)

Fig. 1

(Color online) a Scheme for the generation of frequency-multiplexed entangled single photons via a photon pair Raman scattering inside two distant cavities. b Schematic diagram of atom-light interaction

Then the two optical modes are respectively input into two spatially separated subsystems, which form a quantum memory (see Fig. 1a), through the left mirror without loss and excite the cavity modes of the same frequency. For each subsystem, a cold atomic ensemble, which consists of N identical Λ-type atoms distributing in space homogeneously, is trapped in a multimode optical cavity. This entangled field state is then coherently mapped to an entangled matter state for two atomic ensembles. On demand, the entanglement stored in the quantum memory can be converted back into the entanglement between two photonic modes. We will find that the reversible processes have the characteristic of inherent determinacy.

1.1 The Model of Atom-Photon Interaction

The atom-field interaction configuration under consideration is shown in Fig. 1b. The excited cavity mode with frequency ω (wave vector k) is applied to the atomic transition |g〉 ↔ |e〉, then this cavity photon is converted via spontaneous Raman scattering process into the AntiStokes photon of frequency ω′ (wave vector k′), while the atom is flipped onto the state |s〉. This AntiStokes photon is mainly forward-scattered, co-propagating with the incident photon of frequency ω and leaving the cavity through the right mirror with a transmissivity incomparably larger than that of the left mirror. This operation leads to the probabilistic storage of the incident photons in the atomic ensembles.

For the atomic ensemble where all the atoms are initially prepared in level |g〉, the collective atomic states can be defined as $\left \vert \bar {g}\right \rangle =\left \vert g^{1},g^{2},{\cdots } ,g^{N}\right \rangle$, $\left \vert \bar {s}\right \rangle =\frac {1}{\sqrt {N}} \sum \limits _{n=1}^{N}e^{i(k-k^{\prime })z_{n}}\vert g^{1},g^{2},{\cdots } ,s^{n},{\cdots } ,g^{N}\rangle$, and $\left \vert \bar {e}\right \rangle = \frac {1}{\sqrt {N}}\sum \limits _{n=1}^{N}e^{ikz_{n}}\left \vert g^{1},g^{2},{\cdots } ,e^{n},\cdots ,g^{N}\right \rangle$, etc.. In the interaction picture, under the dipole and rotating wave approximations, the Hamiltonian of the atom-cavity interaction subsystem can be obtained as follows

$$ H=\hbar {\Delta} \sigma_{ee}+\hbar \lbrack g_{\omega }a_{\omega }\sigma_{eg}+g_{\omega^{\prime }}a_{\omega^{\prime }}\sigma_{es}+h.c.], $$

(2)

where we have assumed that the system operates under the two-photon resonant condition, i.e., ω _{e g} −ω = ω _{e s} − ω′ = Δ, ω _{α β} ($\alpha ,\beta =\overline {g},\overline {s}, \overline {e}$) is the atomic transition frequency, σ _{α β} is the collective atomic flip operator defined as σ _{α β} = |α〉〈β|, a _x ($a_{x}^{\dag }$) (x = ω,ω′) is the annihilation (generation) operator for the corresponding cavity mode, and $g_{\omega (\omega ^{\prime })}$ stands for the atom-field coupling constant between the transition $\left \vert \overline {g}\right \rangle \leftrightarrow \left \vert \overline {e}\right \rangle$ ($\left \vert \overline {s} \right \rangle \leftrightarrow \left \vert \overline {e}\right \rangle$). To avoiding the effect of spontaneous emission as much as possible, we adiabatically eliminate the upper state $\left \vert \overline {e} \right \rangle$ of the atoms under the condition of the larger single-photon detuning approximation, i.e., Δ ≫ g _x [16, 17]. Then, compared to the schemes based on the adiabatic passages [18, 19], the current scheme can be used for entangled photon pairs with a wider frequency range, and the (2) reduces to

$$ H_{eff}=\hbar G\sqrt{N}S^{\dag }a_{\omega^{\prime }}^{\dag }a_{\omega }+h.c., $$

(3)

where $G=g_{\omega }g_{\omega ^{\prime }}/{\Delta }$ is the effective coupling constant for the Raman transition $\left \vert \overline {g} \right \rangle \rightarrow \left \vert \overline {e}\right \rangle \rightarrow \left \vert \overline {s}\right \rangle$ and $S^{\dag }=\left \vert \overline {s} \right \rangle \left \langle \overline {g}\right \vert$ is the corresponding collective atomic spin operator. It should be noted that, for obtaining the above effective Hamiltonian (3), the level shift has been dropped safely because it can be compensated by applying a second laser which couples the corresponding atomic levels nonresonantly with additional levels farther up in the atomic level model [16, 17].

On the basis of the effective Hamiltonian (3), we can easily see that the input photon follows the below one-to-one mappings

$$ \left(\begin{array}{c} \left\vert 1\right\rangle_{\omega }\left\vert \bar{g}\right\rangle \rightarrow \left\vert 1\right\rangle_{\omega^{\prime }}\left\vert \bar{s} \right\rangle \\ \left\vert 0\right\rangle \left\vert \bar{g}\right\rangle \rightarrow \left\vert 0\right\rangle \left\vert \bar{g}\right\rangle \end{array} \right) . $$

(4)

Thanks to the multiatomic interference effect and the cavity enhanced atom-photon interaction, the probability of the above mappings could approach unity, thus the collective atomic state and the generated AntiStokes photon will depend only on the input photon.

After the input photon is stored into the quantum memory, by applying an additional control field with frequency ω″ to the atomic transition |s〉 ↔ |e〉, the photon can be retrieved on demand. Proceeding similarly as what we have analyzed in the above discussion, we can obtain the following one-to-one mappings

$$ \left(\begin{array}{c} \left\vert 1\right\rangle_{\omega^{\prime \prime }}\left\vert \bar{s} \right\rangle \rightarrow \left\vert 1\right\rangle_{\omega_{1}}\left\vert \bar{g}\right\rangle \\ \left\vert 1\right\rangle_{\omega^{\prime \prime }}\left\vert \overline{g} \right\rangle \rightarrow \left\vert 1\right\rangle_{\omega^{\prime \prime }}\left\vert \bar{g}\right\rangle \end{array} \right) , $$

(5)

where ω ₁ ( = ω″ + ω _{g s} ) is the frequency of the retrieved photon. Based on the coherently reversible mappings of an entangled state between optical modes and atomic ensembles, we give two schemes and discuss how they can be used for generating the FME single photon in detail.

1.2 Description of the Schemes

Scheme 1

In the scheme, the atoms of ⁸⁷Rb are chosen for the quantum memory in the both subsystem, the energy level diagram is shown in Fig. 2. According to the (4), as the optical modes of a single photon entangled state, $\left \vert \psi \right \rangle _{in}=\frac {1}{\sqrt {2}}\left (\left \vert 01\right \rangle +\left \vert 10\right \rangle \right )_{\omega }$, are input into the two atomic ensembles respectively, the resulted state of the whole system will be

$$ \left\vert \psi \right\rangle_{total}=\left\vert \psi_{+}\right\rangle_{atom}\otimes \left\vert \psi_{+}\right\rangle_{photon}+\left\vert \psi_{-}\right\rangle_{atom}\otimes \left\vert \psi_{-}\right\rangle_{photon}, $$

(6)

where $\left \vert \psi _{\pm }\right \rangle _{atom}=\frac {1}{\sqrt {2}}\left (\left \vert \bar {g}\bar {s}\right \rangle \pm \left \vert \bar {s}\bar {g} \right \rangle \right )$ ($\left \vert \psi _{\pm }\right \rangle _{photon}= \frac {1}{\sqrt {2}}\left (\left \vert 01\right \rangle \pm \left \vert 10\right \rangle \right )_{\omega ^{\prime }}$) is the entangled state between the two atomic ensembles (the generated AntiStokes photons in the two subsystem). After the interaction between the entangled photon pairs and the two atomic ensembles, we can find that the entanglement exists not only between the same kinds of quantum systems, the pair of photons or the two atomic ensembles, but also between different kinds of quantum systems, the photons and the atomic ensembles. If a Bell measurement with respect to the atoms is conducted, the state of the whole system will collapse into one of the entangled photon state, |ψ ₊〉 _{p h o t o n} or |ψ ₋〉 _{p h o t o n} , with the probability 1/2. Considering the operation $\left \vert \psi _{+}\right \rangle _{photon} \stackrel {\sigma _{z}}{\longleftrightarrow } \left \vert \psi _{-} \right \rangle _{photon}$ further, where operator σ _z is 1-qubit phase gate, the target entangled photon state can be obtained deterministically. In a similar way we can get on-demanded entangled atomic state |ψ ₊〉 _{a t o m} or |ψ ₋〉 _{a t o m} . In this process, we find that the FME single photons can not be produced.

Fig. 2

(Color online) The Λ-type level structure of the D₁ transitions in ⁸⁷Rb atom for emission of Stokes or AntiStokes photon in far off-resonant Raman configuration

After a programmable storage time, we retrieve the entanglement from the atomic ensembles by applying two control lights of frequency $\omega _{1}^{\prime \prime }$ and $\omega _{2}^{\prime \prime }$ to the atomic transitions |s〉 ↔ |e〉 of the two ensembles, respectively. According to the (5), we arrive at |ψ _±〉 _{a t o m} →|ψ _±〉 _{F M E S P} ($= \frac {1}{\sqrt {2}}\left (\left \vert 0\right \rangle _{\omega _{1}}\left \vert 1\right \rangle _{\omega _{2}}\pm \left \vert 1\right \rangle _{\omega _{1}}\left \vert 0\right \rangle _{\omega _{2}}\right )$), companied by the two atomic ensembles returning to their initial state $\left \vert \bar {g} \bar {g}\right \rangle$. Compared to the incident entangled state |ψ〉 _{i n} where the two entangled optical modes have the same frequency, the frequency of the retrieved optical modes now is different. As long as the frequency of the two control lights is different, i.e., $\omega _{1}^{\prime \prime }\neq \omega _{2}^{\prime \prime }$, state |ψ _±〉 _{F M E S P} is just the FME single photon state that we are needed.

Scheme 2

In the scheme, the atoms of ⁸⁵Rb and ⁸⁷Rb are chosen for the two subsystems respectively, and their energy level diagrams are shown in Fig. 3. On the basis of the (4), after the single photon entangled state, |ψ〉 _{i n} , is stored into the quantum memory, the whole system will be in the state

$$ \left\vert \psi \right\rangle_{total}^{\prime }=\left\vert \psi_{+}\right\rangle_{atom}^{\prime }\otimes \left\vert \psi_{+}\right\rangle_{photon}^{\prime }+\left\vert \psi_{-}\right\rangle_{atom}^{\prime }\otimes \left\vert \psi_{-}\right\rangle_{photon}^{\prime }, $$

(7)

where $\left \vert \psi _{\pm }\right \rangle _{atom}^{\prime }=\frac {1}{\sqrt { 2}}\left (\left \vert \bar {g}\bar {s}^{\prime } \right \rangle \pm \left \vert \bar {s}\bar {g}^{\prime }\right \rangle \right )$, and $\left \vert \psi _{\pm }\right \rangle _{photon}^{\prime }=\frac {1}{\sqrt {2}}\left (\left \vert 0\right \rangle _{\omega _{1}^{\prime }}\left \vert 1\right \rangle _{\omega _{2}^{\prime }}\pm \left \vert 1\right \rangle _{\omega _{1}^{\prime }}\left \vert 0\right \rangle _{\omega _{2}^{\prime }}\right )$. We can see that $\left \vert \psi _{\pm }\right \rangle _{photon}^{\prime }$ is a FME single photon state, and can be obtained by conducting a Bell measurement to the atoms as discussed in the scheme 1. Of course, the state of the whole system can be collapse into one of the entangled atomic state $\left \vert \psi _{+}\right \rangle _{atom}^{\prime }$ or $\left \vert \psi _{-}\right \rangle _{atom}^{\prime }$ on demand. After a short time, we apply two control lights of frequency $\omega _{1}^{\prime \prime }$ and $\omega _{2}^{\prime \prime }$ to the atomic transitions |s〉 ↔ |e〉 and |s′〉 ↔ |e′〉 of the two atomic ensembles, respectively, then the retrieval Stokes photon will be in the state, $\left \vert \psi _{\pm }\right \rangle _{FMESP}^{\prime }=\frac {1}{\sqrt {2}}\left (\left \vert 0\right \rangle _{\omega _{1}}\left \vert 1\right \rangle _{\omega _{2}}\pm \left \vert 1\right \rangle _{\omega _{1}}\left \vert 0\right \rangle _{\omega _{2}}\right )$, which is also a FME single photon state. The frequencies of the two control fields only need to meet the condition $\omega _{1}^{\prime \prime }-\omega _{2}^{\prime \prime }\neq \omega _{g^{\prime }s^{\prime }}-\omega _{gs}$. Compared to the scheme 1, whatever in the storage or in the retrieval process, in the present one both the generated Stokes photons and the AntiStokes photons are in the FME single photon state.

Fig. 3

(Color online) The Λ-type level structure in ⁸⁷Rb (a) or ⁸⁵Rb (b) atom for emission of Stokes or AntiStokes photon in far off-resonant Raman configuration

2 Dynamics of Raman Interaction

On the basis of the reversible mapping of entanglement between optical modes and atomic ensembles, the above section provides us two schemes for the preparation of the FME single photons. We can see that, in ideal circumstances, the two schemes have the characteristic of inherent determinacy. While, in real situations, the mapping of entanglement is generally probabilistic due to some imperfect reasons. After the interaction of the atoms and the cavity photon, the output state of one subsystem can be written as

$$ \left\vert \psi \right\rangle_{out}=\sqrt{1-p}\left\vert \bar{g} \right\rangle \otimes \left\vert 1\right\rangle_{\omega }\left\vert 0\right\rangle +\sqrt{p}\left\vert \bar{s}\right\rangle \otimes \left\vert 0\right\rangle \left\vert 1\right\rangle_{\omega^{\prime }}, $$

(8)

where p is the probability of the photon emission from the atoms illuminated by, for example, the cavity photon of frequency ω. On this grounds, we can easily deduce that the generated states |ψ _±〉 _{p h o t o n} and $\left \vert \psi _{\pm }\right \rangle _{photon}^{\prime }$ based on the above two schemes is p -dependent, and the degree of entanglement for the both states according to the definition of concurrence, C, which is used to measure the entanglement admittedly [20, 21], is C = p ². Thus, for generating the FME single photons with high quality, the system arrangement with p ≃ 1 must be satisfied.

For finding the condition of the deterministic mapping of entanglement, i.e., p = 1, we treat the photon as a pulse for accurate description because a photon is actually the idealization about a weak optical pulse, and get the Heisenberg-Langevin equations for the cavity mode operators a _x (x = ω,ω′) according to the effective Hamiltonian (3)

$$\begin{array}{@{}rcl@{}} \dot{a}_{\omega }(t) &=&-iG\sqrt{N}Sa_{\omega^{\prime }}(t)-\frac{1}{2} \gamma_{\omega }a_{\omega }(t)+\sqrt{\gamma_{\omega }}a_{\omega ,in}(t), \\ \dot{a}_{\omega^{\prime }}(t) &=&-iG\sqrt{N}S^{\dag }a_{\omega }(t)-\frac{1 }{2}\gamma_{\omega^{\prime }}a_{\omega^{\prime }}(t)+\sqrt{\gamma_{\omega^{\prime }}}a_{\omega^{\prime },in}(t), \end{array} $$

(9)

where a _{x,i n} (t) stands for the operator of the photon pulse in the xth mode before entering the cavity, and satisfies the restriction $\left [ a_{x,in}(t),a_{y,in}^{\dag }(t^{^{\prime }})\right ] =\delta _{xy}\delta (t-t^{^{\prime }})$. γ _x is the damping rate of the cavity mode along its axis, which is large, and the photon loss originating from the fluorescent emission in the direction other than the cavity axis has been neglected.

If the duration (T) of the incident single-photon pulse fulfils $T\gg \gamma _{x}^{-1}$, then we can obtain the solution of the (9) after the temporal process is over [18, 19]

$$\begin{array}{@{}rcl@{}} a_{\omega }(t) &=&\frac{2}{\sqrt{\gamma }}\frac{1}{1+\eta SS^{\dag }} [a_{\omega ,in}(t)-i\sqrt{\eta }Sa_{\omega^{\prime },in}(t)], \\ a_{\omega^{\prime }}(t) &=&\frac{2}{\sqrt{\gamma }}\frac{1}{1+\eta S^{\dag }S}[a_{\omega^{\prime },in}(t)-i\sqrt{\eta }S^{\dag }a_{\omega ,in}(t)], \end{array} $$

(10)

where we have assumed that η = 4N G ²/γ ² and γ _x = γ (x = ω,ω′) for simplicity. Considering the output field a _{x,o u t} (t) related to the input field a _{x,i n} (t) and the intracavity field a _x (t) through the input-output relation $a_{x,out}(t) = \sqrt {\gamma }a_{x}(t)-a_{x,in}(t)$, the mean value of the output photon number operator $n_{x,out}(t) = \left \langle \hat {n}_{x,out}(t)\right \rangle$, where the photon number operator for the corresponding single-photon pulse is defined as $\hat {n}_{x,out}(t) = \int \nolimits _{-\infty }^{t}a_{x,out}^{\dag }(\tau )a_{x,out}(\tau )d\tau$, can be obtained and satisfies the equation

$$ \frac{dn_{x,out}(t)}{dt}=\left\langle a_{x,out}^{\dag }(t)a_{x,out}(t)\right\rangle . $$

(11)

Assuming the temporal envelope of the incident single-photon pulse has the form f(t) normalized by ${\int }_{-\infty }^{+\infty }\left \vert f(t)\right \vert ^{2}dt=1$, then we can derive

$$\begin{array}{@{}rcl@{}} \frac{dn_{\omega ,out}(t)}{dt} &=&\frac{(1-\eta )^{2}}{(1+\eta )^{2}} \left\vert f(t)\right\vert^{2}, \\ \frac{dn_{\omega^{\prime },out}(t)}{dt} &=&\frac{4\eta }{(1+\eta )^{2}} \left\vert f(t)\right\vert^{2}, \end{array} $$

(12)

where the conditions of S S ^†|ψ〉 _{i n} ≃ |ψ〉 _{i n} and $\left \langle a_{\omega ^{\prime },in}^{\dag }(t)a_{\omega ^{\prime },in}(t)\right \rangle =0$ have been used. Equation (12) indicates that the AntiStokes photon pulse obtained via the Raman scatting process has the form identical to the input one. From the definition of the probability of the AntiStokes photon generation, $p=n_{\omega ^{\prime },out}(\infty )/n_{\omega ,in}(0)$, and the conservation of the total photon number in the process, $n_{\omega ^{\prime },out}(t)+n_{\omega ,out}(t) = n_{\omega ,in}(0) = 1$, we arrive at the requirement for the deterministic mapping of entanglement, i.e.,

$$ \sqrt{N}G=\gamma /2. $$

(13)

The result indicates that the balance between the enhanced photon generation and photon loss is the requirement for the deterministic FME single photon generation. For realizing p ≃ 1 in the experiment, one can employ an optical thick atomic ensemble with appropriate shape and trap it in a high-finesse cavity along the cavity axis. In this way the coupling between the multiatom and the cavity mode could be stronger enough so that the atom-photon interaction becomes deterministic. From the present experimental technologies, there are no difficulties to realize such an arrangement.

3 Conclusions

We have presented two schemes to generate FME single photons based on the Raman interactions between a photon pair in cavity modes and two atomic ensembles at distance with the characteristic of inherent determinacy. As the balance between the coherent action and the dissipative of the system is reached, the FME single photons can be generated with near-unit probability. Our protocol alleviates the significant drawback of probabilistic protocols [22], where low preparation probabilities prevent its potential scalability [23]. The schemes also provide an alternative method for measuring level splitting of different atoms because the emitted Stokes or AntiStokes photon has imprinted on it the structure of the atomic excitation: its frequency spectrum consists of the separated lines of finite width. The schemes are robust against incoherent effects such as the cavity-mode damping, the photon loss due to spontaneous emission and the dephasing owing to inhomogeneous broadening resulting from atomic thermal motion. For the current techniques, our schemes are feasible under realistic experimental conditions. Although the generation of entanglement and the frequency conversion in our protocol is intrinsically deterministic, the two schemes may be limited by the current efficiency of single-photon source [24]. Together with the rapid improvements in sources of single-photon, our protocol will allow on demand generation of FME single photons, a powerful resource for quantum information science.