1 Introduction

As a tangible physical resource, quantum entanglement [1, 2] is one of the chief differences between quantum and classical mechanics. Without a doubt, the study of quantum entanglement is a significant problem for the development of quantum information processing [3–12]. Entanglement measures (or entanglement monotones) are utilized for quantifying the amount of entanglement in a given state. As is well-known, the concurrence [13, 14] is a popular measure for bipartite entanglements and the three-tangle [15] is used to quantify tripartite quantum correlations. Then, many axiomatic entanglement measures are extended to the multipartite systems [16–20]. Moreover, we also note that there are some experimental methods for measuring the entanglement in various different forms [21–27]. For example, in optical system, Walborn et al. [21] reported the first experimental determination of concurrence with the hyperentanglement. After that, Zhang et al. [22] described an efficient approach for measuring the concurrence of two-photon polarization-entangled states. With the help of cross-Kerr nonlinearity, the first approach of measurement of the concurrence for hyperentangled state was described [23]. In atomic system, Lee et al. [24] presented the first method for measuring the concurrence with the cavity-QED technology. Subsequently, Zhou and Sheng [25] presented an optimal way for measuring atomic entanglement. Very recently, the protocol of entanglement measurement for electronic system was proposed [26].

Bell inequality [28], as the oldest tool to detect entanglement, was designed to rule out local hidden variable models. Motivated by the Bell’s ground-breaking discovery, recent years Bell-type inequalities have been generalized from two-particle to n-particle cases, such as Clauser-Horne-Shimony-Holt inequality [29], Mermin-Ardehali-Belinskiı̆-Klyshko inequality [30–32], Werner-Wolf-żukowski-Brukner inequality [33, 34], the generalized Bell inequalities [35–39], etc. Also, we note that in the experiment, more recently, two studies of loophole-free test of local realism [40, 41] showed that one can close the main loopholes simultaneously. These results are exciting because they can convincingly support the quantum predictions. On the other hand, Bell inequalities could be used to investigate the possible connections between entanglement and quantum nonlocality for multiparticle systems. For example, based on the Svetlichny operator [42], Ghose et al. [43] investigated the relationship between tripartite entanglement and nonlocality for the Greenberger-Horne-Zeilinger (GHZ) class, and then they generalized the result to four-qubit case [44].

We here focus on four-qubit system and consider a family of the entangled states

$$\begin{array}{@{}rcl@{}} \left|\psi(\theta)\right\rangle &=&\frac{\cos{\theta}}{2}(\left| {0000} \right\rangle - \left| {0101} \right\rangle + \left| {1010} \right\rangle + \left| {1111} \right\rangle) \\ & & + \frac{\sin{\theta}}{2}(\left| {0110} \right\rangle + \left| {1001} \right\rangle - \left| {0011} \right\rangle + \left| {1100} \right\rangle) \end{array} $$
(1)

with 0≤𝜃 ≤ π/2, which belong to the states [45]

$$\begin{array}{@{}rcl@{}} \left|\psi(\theta_{1},\theta_{2})\right\rangle &=&\frac{\cos{\theta_{1}}}{2}(\left| {0000} \right\rangle + \left| {1111} \right\rangle) - \frac{\sin{\theta_{1}}}{2}(\left| {0011} \right\rangle - \left| {1100} \right\rangle) \\ & & - \frac{\cos{\theta_{2}}}{2}(\left| {0101} \right\rangle - \left| {1010} \right\rangle) + \frac{\sin{\theta_{2}}}{2}(\left| {0110} \right\rangle + \left| {1001} \right\rangle), \end{array} $$
(2)

with 0≤𝜃 1,𝜃 2≤π/2. More specifically, for 𝜃 1 = 𝜃 2 we set |ψ(𝜃 1,𝜃 2)〉=|ψ(𝜃)〉, and then for 𝜃 1 = 𝜃 2 = π/4, |ψ(π/4)〉≡|χ〉, where |χ〉 is a suitable candidate for four-qubit maximally entangled state [46]. We next calculate two kinds of four-qubit entanglement measures and discuss the violation of one of the four-qubit Bell-type inequalities, the Wu-Yeo-Kwek-Oh (WYKO) inequality [35], for the entangled states |ψ(𝜃 1,𝜃 2)〉. Noting that the WYKO inequality is optimally violated by |χ〉 but not violated by the GHZ state, here we further reveal that there exist a family of four-qubit entangled states |ψ(𝜃)〉 for which the WYKO inequality is completely violated. At last, we show a relationship between entanglement measure and quantum violation for this family of four-qubit entangled states.

2 Entanglement Measures for the States |ψ(𝜃 1,𝜃 2)〉

Now, we first consider the four-qubit entanglement measures for the entangled states |ψ(𝜃 1,𝜃 2)〉. Generally, for an n-qubit system, Wong and Christensen [16] proposed a compact measure of pure states for even n, that is,

$$ \tau_{n}(\psi)=|\langle\psi|\widetilde{\psi}\rangle|^{2}, $$
(3)

where \(|\widetilde {\psi }\rangle =\sigma ^{\otimes n}_{y}|\psi ^{*}\rangle \), σ y is a Pauli matrix. For the states |ψ(𝜃 1,𝜃 2)〉, it is easy to obtain

$$ \tau_{4}[\psi(\theta_{1},\theta_{2})]=\sin^{2}(\theta_{1}-\theta_{2})\sin^{2}(\theta_{1}+\theta_{2}). $$
(4)

Also, more recently, we note that Sharma et al. [20] defined an entanglement monotone to quantify four-qubit correlations as

$$ \tau_{(4,8)} = 4|\sqrt{12I_{(4,8)}}|, $$
(5)

where I (4,8) is a four-qubit invariant of degree 8 expressed in terms of three-qubit invariants. For the states |ψ(𝜃 1,𝜃 2)〉, we calculate τ (4,8) and find

$$\begin{array}{@{}rcl@{}} \tau_{(4,8)}[\psi(\theta_{1},\theta_{2})] & =& 8\sqrt{3}|\{ 3[\frac{1}{6}(a_{0000}a_{1111}+a_{0011}a_{1100} - a_{0101}a_{1010} - a_{0110}a_{1001})^{2} \\ & &- \frac{2}{3}(a_{0000}a_{1100}a_{0011}a_{1111} + a_{0110}a_{1010}a_{0101}a_{1001}) ]^{2} \\ & &+ 16 a_{0000}a_{1100}a_{0110}a_{1010}a_{0011}a_{1111}a_{0101}a_{1001} \}^{1/2}|\\ &=& \frac{1}{2}\sqrt{[1+\cos(2\theta_{1})\cos(2\theta_{2})]^{2}+3\sin^{2}(2\theta_{1})\sin^{2}(2\theta_{2})}, \end{array} $$
(6)

where \(a_{i_{1}i_{2}i_{3}i_{4}}\), i 1,i 2,i 3,i 4∈{0,1}, are respectively nonzero terms with the expansion of the states ψ(𝜃 1,𝜃 2) in computational basis.

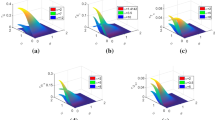
In order to gain an intuitive understanding of the two expressions, we plot the entanglement measures as a function of 𝜃 1,𝜃 2 for the states |ψ(𝜃 1,𝜃 2)〉 respectively, as shown in Figs. 1 and 2. It is easy to see that for the states |ψ(𝜃 1,𝜃 2)〉 the entanglement measures (4) and (6) are very different. Especially, for 𝜃 1 = 𝜃 2 = 𝜃, 0<𝜃<π/2, we have

$$ \tau_{4}[\psi(\theta)]=0, $$
(7)

and

$$ \tau_{(4,8)}[\psi(\theta)] = \sqrt{\cos^{4}(2\theta)+\sin^{2}(2\theta)}. $$
(8)

Thus only τ (4,8)[ψ(𝜃)] is allowed to vary with 𝜃.

Fig. 1
figure 1

Plot of the entanglement measure τ 4 as a function of 𝜃 1,𝜃 2 for the states \(\left |\psi (\theta _{1},\theta _{2})\right \rangle \)

Full size image
Fig. 2
figure 2

Plot of the entanglement measure τ (4,8) as a function of 𝜃 1,𝜃 2 for the states \(\left |\psi (\theta _{1},\theta _{2})\right \rangle \)

Full size image

3 Entanglement Measure and Quantum Violation for the States |ψ(𝜃)〉

Consider a Bell-type inequality for four-qubit systems, the WYKO inequality [35]

$$ |\langle B \rangle| \leq 2, $$
(9)

where 〈B〉 represents the expectation value of Bell operator B in some states with B = A 1 B 1 C 1 D 1 + B 1 C 2 D 2 + B 2 C 1 D 2−A 1 B 2 C 2 D 1, X 1 and X 2 are respectively measurement operators on the locations of qubit X with X∈{A,B,C,D}. If one takes an appropriate set of experimental settings [35] as A 1 = σ x ,B 1 = σ z ,C 1 = σ z ,D 1 = σ x ,B 2 = σ y ,C 2 = σ y , and D 2 = σ y , then the Bell operator B becomes

$$ B=\sigma_{x}\sigma_{z}\sigma_{z}\sigma_{x}+\sigma_{0}\sigma_{z}\sigma_{y}\sigma_{y}+\sigma_{0}\sigma_{y}\sigma_{z}\sigma_{y}-\sigma_{x}\sigma_{y}\sigma_{y}\sigma_{x}, $$
(10)

where σ 0 is identity operator and σ i (i = x,y,z) is Pauli operator.

With a straightforward calculation, one can obtain the expectation value of B in the states |ψ(𝜃 1,𝜃 2)〉, that is,

$$ \langle\psi(\theta_{1},\theta_{2})|B|\psi(\theta_{1},\theta_{2})\rangle=[1+\cos(\theta_{1}-\theta_{2})][1+\sin(\theta_{1}+\theta_{2})]. $$
(11)

In particular, for 𝜃 1 = 𝜃 2 = 𝜃, we have

$$ \langle\psi(\theta)|B|\psi(\theta)\rangle=2[1+\sin(2\theta)]. $$
(12)

Obviously, the inequality is violated by all the states |ψ(𝜃)〉. Furthermore, for 𝜃 = π/4, the inequality is maximally violated with 〈χ|B|χ〉=4.

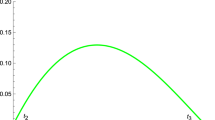
Based on our calculations for the states |ψ(𝜃)〉, we obtain a useful relationship between τ (4,8)[ψ(𝜃)] and 〈ψ(𝜃)|B|ψ(𝜃)〉. It reads

$$ \tau_{(4,8)}[\psi(\theta)] = \sqrt{1+(1-\langle\psi(\theta)|B|\psi(\theta)\rangle/2)^{4}-(1-\langle\psi(\theta)|B|\psi(\theta)\rangle/2)^{2}}, $$
(13)

as shown in Fig. 3. In comparison with the previous expressions [43, 44], our results show that the entanglement measure varies smoothly with the value of quantum violation, and as the value of quantum violation increases, τ (4,8)[ψ(𝜃)] first decreases and then increases, in the argument interval 2<〈ψ(𝜃)|B|ψ(𝜃)〉≤4. Obviously, the entanglement measure decreases to the minimum value \(\tau _{(4,8)}[\psi (\pi /8)]=\sqrt {3}/2\) as \(\langle \psi (\theta )|B|\psi (\theta )\rangle = 2+\sqrt {2}\), i.e. 𝜃 = π/8.

Fig. 3
figure 3

Plot of the relationship between τ (4,8)[ψ(𝜃)] and 〈ψ(𝜃)|B|ψ(𝜃)〉

Full size image

4 Discussion and Summary

In summary, we have calculated two kinds of four-qubit entanglement measures for the states |ψ(𝜃 1,𝜃 2)〉 and shown that τ (4,8) is a more suitable measure than τ 4 for the present states. Furthermore, the entanglement measure and the quantum violation of Bell-type inequality for a family of four-qubit entangled states |ψ(𝜃)〉 have been investigated. We revealed the relationship between entanglement measure and the amount of quantum violation of the WYKO inequality for the states |ψ(𝜃)〉 in terms of the numerical calculation. Especially for the state |χ〉 corresponding to 𝜃 = π/4, there exists an interesting result, i.e., the maximum entanglement measure τ (4,8)=1 corresponding to the maximum violation 4. Our results differ from the previous studies [43, 44]. According to the plot of the relationship between τ (4,8)[ψ(𝜃)] and 〈ψ(𝜃)|B|ψ(𝜃)〉, as the value of quantum violation increases the entanglement measure varies smoothly, ranging from the maximum 1 to the minimum \(\sqrt {3}/2\). In particular, we showed that there exist a family of four-qubit entangled states |ψ(𝜃)〉 for which the WYKO inequality is drastically violated. Thus, the WYKO inequality can be acted as a strong entanglement witness for this family of four-qubit entangled state. At last, it is worthwhile to devote some efforts to reveal the subtle relations between entanglement measures and quantum nonlocality [47, 48]. In any event, we expect that in future these discoveries will lead to a rapid progress of the quantum entanglement and its applications [49–56].