1 Introduction

With the development of quantum cryptography, there exist more and more interesting applications based on quantum cryptography since the first quantum key distribution protocol(BB84) was proposed by Benett and Brassard [1].

Secure multi-party computation (SMC), which has been extensively studied in cryptography domain, is to compute a function jointly in a distributed network where each party holds one private input, and that in the end only the evaluation result is known and other information such as their private inputs are not revealed. In theory, the general SMC problem is solvable but for some special cases of SMC, general solutions are impractical and special solutions should be developed. At present, special SMC problem is mainly researched in classical setting, but Shor pointed out [2] that SMC problems can be solved by models based on quantum setting with higher efficiency. This view point leads us to explore special SMC problem in the quantum field. Recently some special SMC problems have been solved in quantum setting, such as quantum protocol for anonymous voting and surveying [3, 4], quantum anonymous ranking [5], quantum auction [6–8], quantum protocol for millionaire problem [9], and so on.

Quantum private comparison of equality(QPCE), which was first introduced by Yao in classical cryptography [10] for the millionaires’ problem, is a fundamental special SMC problem and has become an important branch in quantum cryptography. Extended from the millionaires’ problem in which two millionaires want to know whether they are equally rich without disclosing their amount of assets, QPCE aims to achieve the goal that two parties can determine the equality of their private inputs without leaking their own information to each other, based on the unique properties of quantum mechanics. It is a pity that for active adversaries, Lo [11] shows that the equality function cannot be computed securely in a two-party scenario, even in quantum cryptography. However, if some additional assumptions(such as introducing a semi-honest third party) are made, the goal of private comparison can be obtained.

In recent years, the design and analysis of QPCE protocols have attracted much interest and attention. The first QPCE protocol was proposed by Yang et al. [12]. After that, a lot of QPCE protocols using different entangled states have been designed, such as Bell states, GHZ states, W states, and χ-type states, etc. [13–22].

In this paper, following some ideas of the protocols in Refs. [12–22], we proposed a new QPCE protocol utilizing the three-particle W-Class state and the Bell state. This protocol includes a third party TP who is assumed to be semi-honest (also called honest-but-curious), i.e., TP follows the rules of the protocol loyally (thus being honest) but in the meantime records all the information and may try to learn additional information from the protocol execution (thus being curious).

In our protocol, TP is used to prepare the initial states, do some calculations and record all intermediate computations. By comparison with the previous QPCE protocols, our protocol has the following advantages:

  • The W-Class state, which can be described as \(|W_{C}\rangle =\frac {1}{2}(|001\rangle +|010\rangle +|100\rangle +|111\rangle )\), is much more robust than the GHZ state. The maximally entangled GHZ state is also maximally fragile for it violates Bell inequalities maximally, however, the W-Class state can retain bipartite entanglement even when any qubit is traced out. This interesting property attracts us to apply entanglement swapping to it in this protocol. In addition, many quantum transmission tasks, such as quantum teleportation [23], quantum dense coding [24], etc have been presented based on the W-Class states. Thus, it is of special value to apply the W-class states in QPCE.

  • Compared with most of the previous protocols [12–22], our protocol has a higher comparison efficiency, for we use two methods to reduce the number of comparisons. First, the private inputs of two participants are divided into groups and the comparison is completed group by group. Second, in every round of comparison, two participants can compare two bits of their private information each time.

  • Unitary operations, which are used in protocols [14, 15, 19–21] to get the result, are unneeded in our protocol. The comparison result can be obtained just by doing some measurements and simple calculations, thus making our protocol easier to implement.

The structure of this paper is organized as follows: in Section 2, an efficient QPCE protocol is described in detail and the security of this protocol is analyzed in Section 3. Finally, a brief discussion and the concluding summary are given in Section 4.

2 The QPCE Protocol

In this section, a different QPCE protocol using the W-class state and the Bell state |Φ+〉 is described in steps. Before describing it, we first show the W-Class state and the entanglement swapping principle of the W-Class state and Bell state |Φ+〉:

$$\begin{array}{@{}rcl@{}} |W_{C}\rangle_{123} &=&\frac{1}{2}(|001\rangle+|010\rangle+|100\rangle+|111\rangle)_{123}\\ &=&\frac{1}{\sqrt{2}}(|0\rangle_{1}|{\Psi}^{+}\rangle_{23}+|1\rangle_{1}|{\Phi}^{+}\rangle_{23}) \end{array} $$
(1)
$$\begin{array}{@{}rcl@{}} |W_{C}\rangle_{123}\bigotimes|{\Phi}^{+}\rangle_{45} &=&\frac{1}{\sqrt{2}}(|0\rangle_{1}|{\Psi}^{+}\rangle_{23}|{\Phi}^{+}\rangle_{45}+|1\rangle_{1}|{\Phi}^{+}\rangle_{23}|{\Phi}^{+}\rangle_{45})\\ &=&\frac{1}{2\sqrt{2}}(|0\rangle_{1}|{\Phi}^{+}\rangle_{24}|{\Psi}^{+}\rangle_{35}+|0\rangle_{1}|{\Phi}^{-}\rangle_{24}|{\Psi}^{-}\rangle_{35}\\ &&+|0\rangle_{1}|{\Psi}^{+}\rangle_{24}|{\Phi}^{+}\rangle_{35}+|0\rangle_{1}|{\Psi}^{-}\rangle_{24}|{\Phi}^{-}\rangle_{35}\\ &&+|1\rangle_{1}|{\Phi}^{+}\rangle_{24}|{\Phi}^{+}\rangle_{35}+|1\rangle_{1}|{\Phi}^{-}\rangle_{24}|{\Phi}^{-}\rangle_{35}\\ &&+|1\rangle_{1}|{\Psi}^{+}\rangle_{24}|{\Psi}^{+}\rangle_{35}+|1\rangle_{1}|{\Psi}^{-}\rangle_{24}|{\Psi}^{-}\rangle_{35}) \end{array} $$
(2)

Where \(|{\Phi }^{+}\rangle =\frac {1}{\sqrt {2}}(|00\rangle +|11\rangle )\), \(|{\Phi }^{-}\rangle =\frac {1}{\sqrt {2}}(|00\rangle -|11\rangle )\), \(|{\Psi }^{+}\rangle =\frac {1}{\sqrt {2}}(|01\rangle +|10\rangle )\), \(|{\Psi }^{-}\rangle =\frac {1}{\sqrt {2}}(|01\rangle -|10\rangle )\).

The process of our protocol can be described as follows:

Input: Alice and Bob have their private integer X and Y respectively. The binary representations of X and Y in can be written as: X=(x 0,x 1,…,x N−1), Y=(y 0,y 1,…,y N−1), where x i ,y i ∈{0,1}, and \(X=\sum \limits _{i=0}^{N-1}x_{i}2^{i}\), \(Y=\sum \limits _{i=0}^{N-1}y_{i}2^{i}\), 2N−1≤m a x X,Y≤2N.

Output: Whether X=Y or not.

2.1 Preparing Step

  1. (1)

    Alice(Bob) divides the N-bit binary string X(Y) into ⌈N/2L⌉ groups, each group having 2L bits. If N mod 2 = 1, Alice(Bob) inserts one 0 at the end of the N-bit binary string X(Y), X=A ⌈N/2L⌉…A 2 A 1, Y=B ⌈N/2L⌉…B 2 B 1.

    $$ A_{j}=({x^{0}_{j}},{x^{1}_{j}},\ldots,x^{2L-1}_{j}), B_{j}=({y^{0}_{j}},{y^{1}_{j}},\ldots,y^{2L-1}_{j}) $$
    (3)
  2. (2)

    For each group A j (B j ), Alice(Bob) forms every two adjacent bits into a pair \({Q^{i}_{A}}=(x^{2i}_{j},x^{2i+1}_{j}), {Q^{i}_{B}}=(y^{2i}_{j},y^{2i+1}_{j})\).

    $$ A_{j}=({Q^{0}_{A}},{Q^{1}_{A}},\ldots,Q^{L-1}_{A}),B_{j}=({Q^{0}_{B}},{Q^{1}_{B}},\ldots,Q^{L-1}_{B}) $$
    (4)

    In order to improve the comparison efficiency and decrease the cost of the classical information, one group A j (B j ) of the private information owned by Alice(Bob) is compared in each round of comparison.

  3. (3)

    In the jth round of the comparison, TP prepares an ordered sequence S 1 which consists of L three-particle W-Class states

    $$ \left[{P^{0}_{T}}P^{0}_{A_{1}}P^{0}_{B_{1}},{P^{1}_{T}}P^{1}_{A_{1}}P^{1}_{B_{1}},\ldots,P^{L-1}_{T}P^{L-1}_{A_{1}}P^{L-1}_{B_{1}}\right] $$
    (5)

    where the subscript T, A 1, B 1 indicates the three particles in one W-Class state. Then TP prepares an ordered sequence S 2 which consists of L Bell states \(|{\Phi }^{+}\rangle =\frac {1}{\sqrt {2}}(|00\rangle +|11\rangle )\),

    $$ \left[P^{0}_{A_{2}}P^{0}_{B_{2}},P^{1}_{A_{2}}P^{1}_{B_{2}},\ldots,P^{L-1}_{A_{2}}P^{L-1}_{B_{2}}\right] $$
    (6)

    where the A 2, B 2 represent the two particles in one Bell state.

  4. (4)

    TP takes the first particles of all W-Class states in S 1 to form an ordered sequence S T

    $$ S_{T}:\left[{P^{0}_{T}},{P^{1}_{T}},\ldots,P^{L-1}_{T}\right] $$
    (7)

    TP takes the second particles of all W-Class states in S 1 and the first particles of all |Φ+〉 states in S 2 to form a new ordered sequence S A .

    $$ S_{A}:\left[P^{0}_{A_{1}}P^{0}_{A_{2}},P^{1}_{A_{1}}P^{1}_{A_{2}},\ldots,P^{L-1}_{A_{1}}P^{L-1}_{A_{2}}\right] $$
    (8)

    TP takes the third particles of all W-Class states in S 1 and the second particles of all |Φ+〉 states in S 2 to form a new ordered sequence S B .

    $$ S_{B}:\left[P^{0}_{B_{1}}P^{0}_{B_{2}},P^{1}_{B_{1}}P^{1}_{B_{2}},\ldots,P^{L-1}_{B_{1}}P^{L-1}_{B_{2}}\right] $$
    (9)
  5. (5)

    To prevent eavesdropping, TP prepares two bunches of decoy photons D A and D B randomly chosen from states {|0〉,|1〉,|+〉,|−〉}. Then TP mixes the sequences S A with D A (S B with D B ) to form two new sequences \(S_{A}^{\prime }\) and \(S_{B}^{\prime }\) and sends the sequence \(S_{A}^{\prime }\) to Alice, \(S_{B}^{\prime }\) to Bob.

2.2 Checking Step

  1. (1)

    After the two participants receive the sequences \(S_{A}^{\prime }\) and \(S_{B}^{\prime }\), TP announces the positions and the measuring bases of D A and D B .

  2. (2)

    According to the positions, Alice and Bob pick out these decoy particles from \(S_{A}^{\prime }\) and \(S_{B}^{\prime }\), and measure them in corresponding bases.

  3. (3)

    Alice and Bob send their measuring results to TP for eavesdropping detection. If the error rate exceeds a suitable threshold, TP will terminate this communication and restart from the preparing step. Otherwise, the protocol can go on to the next step.

2.3 Coding Step

  1. (1)

    After the checking step, Alice(Bob) recovers S A (S B ) by discarding the decoy photons.

  2. (2)

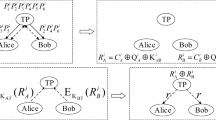
    Alice(Bob) uses Bell basis to measure the ith pair \(P^{i}_{A_{1}}P^{i}_{A_{2}}(P^{i}_{B_{1}}P^{i}_{B_{2}})\) in S A (S B ). We denote the measurement result with \({M^{i}_{A}}({M^{i}_{B}})\). After the measurement, Alice and Bob will obtain a two-bit value \({C^{i}_{A}}\) and \({C^{i}_{B}}\) respectively according to the Table 1.

    Table 1 \({C^{i}_{A}}({C^{i}_{B}})\)’s values according to \({M^{i}_{A}}({M^{i}_{B}}) \)
    Full size table
  3. (3)

    For every two-bit pair \({Q^{i}_{A}}({Q^{i}_{B}})\), Alice(Bob) calculates \({R^{i}_{A}}={Q^{i}_{A}} \oplus {C^{i}_{A}}({R^{i}_{B}}={Q^{i}_{B}} \oplus {C^{i}_{B}})\), the symbol ⊕ denotes the bit-wise exclusive-OR. Then Alice(Bob) gets a sequence \({R^{0}_{A}}{R^{1}_{A}},\ldots ,R^{L-1}_{A}({R^{0}_{B}}{R^{1}_{B}},\ldots ,R^{L-1}_{B})\).

  4. (4)

    Alice(Bob) uses quantum-one-time pad and K A (K B ) to encrypt the new sequence \({R^{0}_{A}}{R^{1}_{A}},\ldots ,R^{L-1}_{A}({R^{0}_{B}}{R^{1}_{B}},\ldots ,R^{L-1}_{B})\) and sends the encrypted sequence \(E_{K_{A}}({R^{0}_{A}}{R^{1}_{A}},\ldots ,R^{L-1}_{A})(E_{K_{B}}({R^{0}_{B}}{R^{1}_{B}},\ldots ,R^{L-1}_{B}))\) to TP.

2.4 Decoding Step

  1. (1)

    After receiving two sequences from Alice and Bob, TP uses K A ,K B to decrypt \(E_{K_{A}}({R^{0}_{A}}{R^{1}_{A}},\ldots ,R^{L-1}_{A})\), \(E_{K_{B}}({R^{0}_{B}}{R^{1}_{B}},\ldots ,R^{L-1}_{B})\).

  2. (2)

    TP calculates \(R^{i}_{AB}={R^{i}_{A}}\oplus {R^{i}_{B}}\).

  3. (3)

    TP uses the basis {|0〉,|1〉} to measure the ith particle in S T and gets \({M^{i}_{C}}\). Through calculating and summarizing for all cases, we find the following relation shown in Table 2.

    Table 2 Relation between \({Q^{i}_{A}}\) and \({Q^{i}_{B}}\) according to \({M^{i}_{C}}\) and \(R^{i}_{AB}\)
    Full size table
  4. (4)

    According to Table 2, if \({Q^{i}_{A}} = {Q^{i}_{B}}\), TP records the value r=0, else if \({Q^{i}_{A}}\neq {Q^{i}_{B}}\), r=1.

    We show two cases in the Table 3. In one round of comparison, TP obtains L cbits values in all. If all values are 0, TP records R j =0 and goes on to the next round of comparison. If there is at least one value 1, TP records R j =1,then he stops the protocol and announces the final result F=1 to indicate the inequality of their information.

    Table 3 Two cases of \({Q^{i}_{A}}\), \({Q^{i}_{B}}\)’s values
    Full size table
  5. (5)

    When j=[N/2L]+1 and all the records R j =0(j=1,2,…,[N/2L]+1), TP announces the final result F=0. Alice and Bob can simultaneously know that their inputs X and Y are equal. Through at best [N/2L]+1 rounds of comparison, Alice and Bob can prove each other whether their respective inputs X and Y are equal or not.

3 Security Analysis

In this section, attacks from all parties are analyzed, including two attack scenarios: (1) Outside eavesdropper attempts to steal two participants’ inputs X or Y. (2) Two dishonest participants and the semi-honest TP may try to obtain the private information. And we will show our protocol is secure against both the outside attack and the participant attack.

3.1 Outside Attack

Assuming an outside eavesdropper Owen, We analyze Owen’s chance of obtaining information about X and Y in every step of protocol.

In preparing step, Owen can attack the quantum channel when TP sends \(S^{\prime }_{A}(S^{\prime }_{B})\) to Alice(Bob). The Trojan horse attack can be automatically prevented since this is a one-way transmission protocol. Moreover, several other kinds of attacks, such as the intercept-resend attack, the entanglement-measure attack and the collective attack will be detected with nonzero probability during the checking step.

For example, we consider Owen takes the intercept-resend attack strategy on Bob as follows: Owen first intercepts the photon sequence \(S_{B}^{\prime }\) (from TP to Bob in preparing step(5)), then he measures \(S_{B}^{\prime }\) with Bell basis and gets a measurement result sequence \(M_{S_{B}^{\prime }}\). In order to prevent TP from discovering this attack in checking step(3), Owen generates a new photon sequence P B with the same photon states as \(M_{S_{B}^{\prime }}\). He resends P B to Bob. Then Owen may retrieve information from \(M_{S_{B}^{\prime }}\).

However, as Owen doesn’t know the position of decoy single photons in \(S_{B}^{\prime }\), he can’t discard the decoy photons when he measures \(S_{B}^{\prime }\) with Bell basis, thus the decoy photons will destroy the correctness of the measurement and Owen’s new photon sequence P B , which has the same states with measurement result \(M_{S_{B}^{\prime }}\), will be quite different from \(S_{B}^{\prime }\). After Bob has received the photon sequence P B , he will start the eavesdropping check process, and the attack will be easily detected for the the states of decoy photons has been damaged.

In coding step, Alice(Bob) sends \({R^{0}_{A}}{R^{1}_{A}},\ldots ,R^{L-1}_{A}({R^{0}_{B}}{R^{1}_{B}},\ldots ,R^{L-1}_{B})\) to TP. \({R^{i}_{A}}\) and \({R^{i}_{B}}\) can’t reveal the information X and Y, so the outside eavesdropper can’t get anything. In decoding step, TP announces only one cbit F for the comparison of secret messages. From this one cbit, outside eavesdropper can’t deduce information X and Y.

So, the outside attack is invalid to this protocol.

3.2 Participant Attack

Generally, a participant is easier to attack than an outside eavesdropper, because he can get and utilize partial information legally. We will consider two kinds of attacks.

Case 1

One participant attempts to eavesdrop the other’s private information.

Without loss of generality, because the role of Alice is same as that of Bob, we assume that Alice wants to learn Bob’s information. Similar to the outside eavesdropper, Alice’s several kinds of attack launched during the preparing step can be detected by adopting the decoy photon technique. Besides, there isn’t any information transfer between Alice and Bob during the whole process in this protocol.

Now the only way for Alice to infer Bob’s private information is by deriving from the measurement result \({M^{i}_{A}}\) of \(P^{i}_{A_{1}}P^{i}_{A_{2}}\) in her hand and \({R^{i}_{B}}\) which is sent from Bob to TP. Because Alice can’t get TP’s measurement result \({M^{i}_{C}}\), she can’t infer the measurement result \({M^{i}_{B}}\) of \(P^{i}_{B_{1}}P^{i}_{B_{2}}\) in Bob’s hand according to (2). \({R^{i}_{B}}\) is sent using the quantum-one-pad from Bob to TP thus Alice can’t eavesdrop any information about \({R^{i}_{B}}\). Therefore, Alice can’t infer Bob’s private information.

Case 2

TP attempts to eavesdrop the participants’ private information X and Y.

In this protocol, TP is semi-honest which means he is curious about the participants’ private information. Besides, TP takes part in the whole process of the protocol execution, including preparing quantum carriers, doing some measurement and recording intermediate results, which provides him more power to attack. However, all the intermediate data obtained by TP which relate to the participants’ private infoprmation are just \({R^{i}_{A}}\) and \({R^{i}_{B}}\), which are sent to TP from Alice and Bob in coding step. Thus, TP can only infer information from \({R^{i}_{A}}\), \({R^{i}_{B}}\), and TP’s measurement result \({M^{i}_{C}}\). As is shown in Table 3:

$$\begin{array}{@{}rcl@{}} &&P({R^{i}_{A}}=00)= P({R^{i}_{A}}=01)= P({R^{i}_{A}}=10)= P({R^{i}_{A}}=11)=\frac{1}{4} \\ &&P({R^{i}_{B}}=00)= P({R^{i}_{B}}=01)= P({R^{i}_{B}}=10)= P({R^{i}_{B}}=11)=\frac{1}{4} \\ &&P({M^{i}_{C}}=|0\rangle)=P({M^{i}_{C}}=|1\rangle)=\frac{1}{2} \end{array} $$
(10)

That is, TP obtains these measurement results with the same probability, so TP can’t determinately know the value of \({Q^{i}_{A}},{Q^{i}_{B}}\).

We have to point out that TP knows the comparison result r of \({Q^{i}_{A}}\) and \({Q^{i}_{B}}\) in each round. However, only with r, TP can’t deduce the exact value of \({Q^{i}_{A}}\) and \({Q^{i}_{B}}\) in each round. In other words, if r=0, i.e., the partial inputs \({Q^{i}_{A}}\) and \({Q^{i}_{B}}\) are equal, TP derives

$$\begin{array}{@{}rcl@{}} &&P({Q^{i}_{A}}={Q^{i}_{B}}=00)=\frac{1}{4},P({Q^{i}_{A}}={Q^{i}_{B}}=01)=\frac{1}{4}\\ &&P({Q^{i}_{A}}={Q^{i}_{B}}=10)=\frac{1}{4},P({Q^{i}_{A}}={Q^{i}_{B}}=11)=\frac{1}{4} \end{array} $$
(11)

if r=1, i.e., the partial inputs \({Q^{i}_{A}}\) and \({Q^{i}_{B}}\) are unequal, TP derives

$$\begin{array}{@{}rcl@{}} &&P({Q^{i}_{A}}=00,{Q^{i}_{B}}=01)=\frac{1}{12},P({Q^{i}_{A}}=00,{Q^{i}_{B}}=10)=\frac{1}{12}\\ &&P({Q^{i}_{A}}=00,{Q^{i}_{B}}=11)=\frac{1}{12},P({Q^{i}_{A}}=01,{Q^{i}_{B}}=00)=\frac{1}{12}\\ &&P({Q^{i}_{A}}=01,{Q^{i}_{B}}=10)=\frac{1}{12},P({Q^{i}_{A}}=01,{Q^{i}_{B}}=11)=\frac{1}{12}\\ &&P({Q^{i}_{A}}=10,{Q^{i}_{B}}=00)=\frac{1}{12},P({Q^{i}_{A}}=10,{Q^{i}_{B}}=01)=\frac{1}{12}\\ &&P({Q^{i}_{A}}=10,{Q^{i}_{B}}=11)=\frac{1}{12},P({Q^{i}_{A}}=11,{Q^{i}_{B}}=00)=\frac{1}{12}\\ &&P({Q^{i}_{A}}=11,{Q^{i}_{B}}=01)=\frac{1}{12},P({Q^{i}_{A}}=11,{Q^{i}_{B}}=10)=\frac{1}{12} \end{array} $$
(12)

Therefore, TP doesn’t have any advantage to derive any private information owned by Alice and Bob. So this protocol is secure against TP’s attack.

4 Discussion and Conclusions

Before making a conclusion, it is worthwhile to make a comparison between this protocol and some previous protocols. Different from most previous QPCE protocols [14, 15, 17, 25] in which the binary bits of the private information are compared one by one, two bits can be compared each time in our protocol by performing entanglement swapping between the W-Class state and Bell state. Other different aspects are described in Table 4. Through the comprehensive comparison, it can be seen that our protocol has a better performance on operability, efficiency and security.

Table 4 Comparison(supposing n classical bits are compared)
Full size table

In summary, we proposed a new QPCE protocol based on the three-particle W-Class state and Bell states swapping. It’s a new application of the three-particle W-Class state. With the help of a semi-honest TP, two participants can know the equality of their private input X and Y, but they can’t learn the information owned by each other and TP also can’t learn any information about X and Y. Various kinds of attacks are discussed. The protocol can withstand these attacks well, so the security of our protocol is quite high.

In our further works, the two-party protocol can be considered to extend to the case of multi-party, such as multi-party sorting problem.