1 Introduction

Quantum entanglement is a striking feature of quantum mechanics, and play an important valuable role for the development of quantum information technology [1–8], such as quantum teleportation, quantum dense coding, quantum computation, quantum key distribution, quantum information splitting, and so on. The generation of entangled states for two or more particles is fundamental to demonstrate quantum nonlocality. Great effort has been devoted to studying bipartite entanglement dynamics in different quantum systems [9–11], such as cavity QED, trapped ions, spin systems, atomic ensembles and photon pairs. The basic models of quantum optics and cavity quantum electrodynamics are the Jaynes-Cummings model, describing the interaction between a two-level atom at rest and a quantized mode of the radiation field. In the realm of atom, cavity quantum electrodynamics (QED) techniques has been proven to be a promising candidate for the physical realization of quantum information processing. Recently, many schemes have been proposed for quantum entanglement engineering and quantum information processing [12–15]. The cavity usually act as memories in quantum information processing, thus the decoherence of the cavity field becomes one of the main obstacles for the implementation of quantum information in cavity QED.

The respective field of physics, cavity quantum electrodynamics, is growing rapidly in the last two decades. In this paper, we have presented a method for faithfully prepare a two-atom bell entanglement state in driven cavity QED. The scheme in the paper overcame the difficulty of Bell state measurement, not the joint Bell-state measurement but the separate measurement is necessary in the cavity QED. Due to these advantages our scheme may open promising prospects for quantum-information manipulation.

2 Generating a Two-Qubit Entangled State

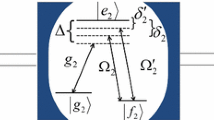
We consider two identical two-level atoms simultaneously interacting with a single-mode cavity field. The interaction between atoms and the cavity can be described as follows [16]

$$ H=\omega_{0}\sum\limits_{j=1}^{2}{S_{j}^{z}}+\omega_{a}a^{\dag}a+\sum\limits_{j=1} ^{2}g\left(a^{\dag}S_{j}^{-}+aS_{j}^{+}\right)+\varOmega\left(S_{j}^{+}e^{-i\omega_{d}t} +S_{j}^{-}e^{i\omega_{d}t}\right) $$
(1)

where ω 0, ω a and ω d are atomic transition frequency, cavity frequency and the frequency of driving field, respectively, a ‡ and a are creation and annihilation operators for the cavity mode, g is the coupling constant between atoms and cavity, atomic operators \(S_{j}^{+}=|e\rangle _{j}\langle g|\), \(S_{j}^{-}=|g\rangle _{j}\langle e|\), \({S_{j}^{z}}=\frac {1}{2}(|e\rangle _{j}\langle e|-|g\rangle _{j}\langle g|)\), Ω is the Rabi frequency of the classical field. We consider the case ω 0=ω d . In the interaction picture, the evolution operator of the system is

$$ U(t)=e^{-iH_{0}t}e^{-iH_{e}t} $$
(2)

where \(H_{0}={\sum }_{j=1}^{2}\varOmega (S_{j}^{-}+S_{j}^{+})\), H e is the effective Hamiltonian. In the large detuning \(\delta \gg \frac {1}{2}\) g and strong driving field, 2Ω≫δ,g limit, the effective Hamiltonian for this interaction can be described as follows:

$$ H_{e}=\lambda\left(\sum\limits_{j=1}^{2}\frac{1}{2}\left(|e\rangle_{j}\langle e|+|g\rangle_{j}\langle g|\right)+\sum\limits_{j,k=1,j\neq k}^{2}\left(S_{j}^{+}S_{k}^{+} +S_{j}^{+}S_{k}^{-}+H.c\right)\right) $$
(3)

where λ = g 2/2δ, δ is the detuning between ω 0 and ω a . Now we show how we can use the idea to realize quantum two atom entangled states. We let atoms 1 and 2 simultaneously enter a single mode cavity, at the same time the atoms are driven by a classical field. The state of the two atoms will undergo the following evolution:

$$\begin{array}{@{}rcl@{}} |ee\rangle_{jk} & \longrightarrow e^{-i\lambda t}\left[\cos\lambda t(\cos\varOmega t|e\rangle_{j}-i\sin\varOmega t|g\rangle_{j})\times(\cos\varOmega t|e\rangle _{k}-i\sin\varOmega t|g\rangle_{k})\right.\\ &\left. -i\sin\lambda t(\cos\varOmega t|g\rangle_{j}-i\sin\varOmega t|e\rangle_{j} )\times(\cos\varOmega t|g\rangle_{k}-i\sin\varOmega t|e\rangle_{k})\right] \end{array} $$
(4)
$$\begin{array}{@{}rcl@{}} |eg\rangle_{jk} & \longrightarrow e^{-i\lambda t}\left[\cos\lambda t(\cos\varOmega t|e\rangle_{j}-i\sin\varOmega t|g\rangle_{j})\times(\cos\varOmega t|g\rangle _{k}-i\sin\varOmega t|e\rangle_{k})\right.\\ & \left.-i\sin\lambda t(\cos\varOmega t|g\rangle_{j}-i\sin\varOmega t|e\rangle_{j} )\times(\cos\varOmega t|e\rangle_{k}-i\sin\varOmega t|g\rangle_{k})\right] \end{array} $$
(5)
$$\begin{array}{@{}rcl@{}} |ge\rangle_{jk} & \longrightarrow e^{-i\lambda t}\left[\cos\lambda t(\cos\varOmega t|g\rangle_{j}-i\sin\varOmega t|e\rangle_{j})\times(\cos\varOmega t|e\rangle _{k}-i\sin\varOmega t|g\rangle_{k})\right.\\ & -i\sin\lambda t(\cos\varOmega t|e\rangle_{j}-i\sin\varOmega t|g\rangle_{j} )\times(\cos\varOmega t|g\rangle_{k}-i\sin\varOmega t|e\rangle_{k})] \end{array} $$
(6)
$$\begin{array}{@{}rcl@{}} |gg\rangle_{jk} & \longrightarrow e^{-i\lambda t}\left[\cos\lambda t(\cos\varOmega t|g\rangle_{j}-i\sin\varOmega t|e\rangle_{j})\times(\cos\varOmega t|g\rangle _{k}-i\sin\varOmega t|e\rangle_{k})\right.\\ & \left.-i\sin\lambda t(\cos\varOmega t|e\rangle_{j}-i\sin\varOmega t|g\rangle_{j} )\times(\cos\varOmega t|e\rangle_{k}-i\sin\varOmega t|g\rangle_{k})\right] \end{array} $$
(7)

Choose the amplitudes and phases of the classical fields appropriately. Assume the state of the two atoms is initially in |g〉|e〉, we can choose \(\lambda t=\frac {1}{4}\pi \), Ω t=π by modulating the driving field appropriately, the state of the two atoms will become |ψ −〉12 \(=\frac {1}{\sqrt {2}}(|g\rangle |e\rangle -i|e\rangle |g\rangle )\). In the same way, the other three maximally two-atom entangled states can be prepared. \(\left |\left .\psi ^{+}\right .\right \rangle _{12}=\frac {1}{\sqrt {2}}(|g\rangle |e\rangle +i|e\rangle |g\rangle )\), \(\left .|\phi ^{+}\right \rangle _{12}=\frac {1}{\sqrt {2}}\left (|e\rangle |e\rangle +i|g\rangle |g\rangle \right )\), \(|\phi ^{-}\rangle _{12}=\frac {1}{\sqrt {2}}(|e\rangle |e\rangle -i|g\rangle |g\rangle )\).

Finally, it is necessary to give a brief discussion on the experimental matters. For the Rydberg atoms with principal quantum numbers 49, 50, and 51, the radiative time is about T r = 3 × 10−2 s, and the coupling constant is g = 2π × 24 kHz. The required atom-cavity-field interaction time is on the order of 10−4 s. For a normal cavity, the decay time can reach T c = 1.0 × 10−3 s. Then we get that the interaction time of atom and cavity is on the order of 10−4 s. Hence the total time for the whole system is much shorter than T r and T c so that the present scheme might be realizable based on cavity QED techniques. The present scheme opens a new prospect for quantum entanglement and quantum information processing.

3 Summary

In conclusion, we have proposed a simple scheme to realize two-atom maximally entangled states with dispersive cavity QED. Unlike previous schemes, the present one does not require the transfer of quantum information between the cavity and atom. Finally the scheme does not involve the joint Bell-state measurements and is not sensitive to both the cavity decay and the thermal field based on current cavity QED technology. Therefore, our scheme might be realizable in a not long future and may be widely useful to the future quantum communication and experiment.