1 Introduction

Loop tiling is one of the key code transformations in optimizing data locality and it is one of the most performance critical optimizations for data dominant loop kernels [1]. The selection of an efficient tile size is a critical parameter as tiles of different sizes can lead to significant variations in performance [2].

The two main strategies to address the tile size selection problem are analytical [2] and empirical [3]. The former refers to static approaches in which the tile size is selected based on static code analysis of the loop kernel and the processor memory configuration (number of caches, cache sizes, associativity, line size). Typically, the analytical loop tiling methods output the number of cache misses as a function of the tile sizes, input size (of the executed kernel), and cache characteristics, normally for single-threaded affine loop kernels. The second strategy refers to empirical (experimental-based) approaches that rely on auto-tuning. In auto-tuning, the input program is executed multiple times assuming different tile sizes, until the best solution is found. The input program is considered as a black-box and no information of the source code is extracted. A well-known auto-tuning library for linear algebra is ATLAS [4].

To the best of our knowledge, current analytical methods fail to identify optimal tile sizes across a wide range of programs and target platforms [3]. As a result, the gap between the performance delivered by the best known tile sizes (which are found manually) and those selected by current analytical methods, is high. The main reason for which current analytical methods are not that successful lies in the fact that modelling the complex and deep modern memory hierarchies and the diverse arrays’ memory access patterns and data reuse, is a very hard and complex task.

In this paper, we first demonstrate two important inefficiencies of current analytical methods and provide insight on how current methods can address these inefficiencies. Second, we propose a new loop tiling method, for single-threaded programs. The first drawback of current analytical methods is that they poorly calculate the tiles sizes; in fact, the actual tiles sizes are usually larger than the calculated sizes and as a consequence additional unforeseen cache misses occur (not captured by the method). The second drawback is that the tiles cannot remain in the cache in most cases due to the cache modulo effect. This is because the cache line size, cache associativity and data reuse of tiles, are not efficiently taken into account. Therefore, current methods cannot accurately calculate the number of cache misses for each tile size, leading to sub-optimal tile sizes.

The aim of our loop tiling method is to find the tile sizes (tile set) that minimize the number of cache misses. Although the number of cache misses does not always align with performance (execution time), it is the key performance indicator for loop tiling [2, 5]. First, the proposed method discards all the tile sets that cannot fit or remain into the cache. They considered as inefficient, as they give high cache misses values. Then, the remaining tile sets are processed and their number of cache misses is estimated by using a simple and lightweight model. Last, the tile set that offers the minimum number of cache misses is selected.

Our experimental results depict that by using our method the tiles indeed fit and remain into the cache and it is also possible to estimate the number of cache misses with a maximum error of \(1\%\) using simulation and \(3.2\%\) and \(5.9\%\) by using the processor’s hardware counters on L1 data cache and L3 cache, respectively, leading to more efficient tile sizes. Our method offers high cache misses gains and significant speedups over a related method, icc and gcc compilers and Pluto tool [1] (for a fair comparison only the loop tiling feature of Pluto is enabled).

This research work has resulted in three contributions.

  • A research work demonstrating two important inefficiencies of current analytical loop tiling methods.

  • A research work providing the theoretical background on how current methods can tackle the aforementioned inefficiencies.

  • A new loop tiling method that better exploits the cache size, cache line size and cache associativity.

The remainder of this paper is organized as follows. In Sect. 2, the related work is reviewed. The proposed methodology is presented in Sect. 3 while experimental results are discussed in Sect. 4. Finally, Sect. 5 is dedicated to conclusions.

2 Related Work

As noted, the problem of the optimum tile size selection is addressed by using two main approaches, analytical methods and empirical methods. The analytical methods refer to static approaches, where the tile size is selected based on static analysis of the loop kernel and the memory’s hardware characteristics. In this case, the tile sizes are fixed at compile time and cannot change at runtime.

In [5], an analytical model for loop tile selection is proposed for estimating the memory cost of a loop kernel and for identifying a good tile size. However, cache associativity is not taken into account in this model. In [6], authors use Presburger formulas to express cache misses, but they fail to accommodate the high set associativity values of modern caches. In [2], an improved analytical model is proposed where associativity value is taken into account, but the cache line size, cache associativity and data reuse, are not efficiently utilized compared to our method. [7] well considers temporal and spatial reuse, but the cache associativity and cache line size are not taken into account. In [8], an accurate analytical model is proposed but for tensor contractions only; tensor contraction is a higher-dimensional generalization of Matrix–Matrix Multiplication (MMM). This method works well for this family of applications, as array copying is applied to all the arrays and as a consequence the problem of cache misses estimation is simplified. Note that when using array copying each tile is copied into a contiguous buffer and the elements are ordered based on the order in which they are accessed by the kernel. Also note that array copying introduces a significant overhead, which normally degrades the overall program performance in non MMM-based applications. In [9], the authors combine loop tiling with array padding in order to improve the tile size selection process for specific array sizes (a techniques so-called pathological array sizes).

So far no analytical method has been shown to be effective in finding optimal tile sizes across a wide range of programs and target platforms [3].

Due to the problem of finding the optimum tile size is very complex and includes a vast exploration space, in addition to general methods, a large number of algorithm-specific analytical methods also exist for Matrix–Matrix Multiplication (MMM) [10] [11], Matrix-Vector Multiplication (MVM) [12], tensor contractions [8], Fast Fourier Transform (FFT) [13], stencil [14] and other algorithms, but the proposed approaches are limited in nature and cannot be generalized for different kernels. In particular, regarding stencil applications, there has been a long thread of research and development tackling data locality and parallelism, where many loop tiling strategies have been proposed such as overlapped tiling [15, 16], diamond tiling [17] and others. [18] propose an MMM-based, write efficient tiling method, for non-volatile main memories.

Although the aforementioned application specific methods take into account some or all of the following: cache size, cache associativity and cache line size, we will show that there is ample room for improvement, as the cache line size, cache associativity and the arrays’ memory access patterns, are not fully exploited. As a result, they do not analyse the cache behaviour in that detail, compared to our method.

The second line of techniques for addressing the tile size selection problem relies on empirical approaches. These approaches perform empirical auto-tuning by executing the program multiple times for different tile sizes. A successful example is the ATLAS library [4] which performs empirical tuning at installation time, to find the best tile sizes for different problem sizes on a target machine. The main drawback in empirical approaches is the enormous search space that must be explored. Other self-tuning library generators suffer from the same problem of time-consuming design space exploration.

Moreover, there are several frameworks able to generate tiled code with parameterized tiles such as PrimeTile [19], PTile [20] and DynTile [21]. Parameterized tiling refers to the application of the tiling transformation without employing predefined tiles sizes, but inserting symbolic parameters that can be fixed at runtime [22]. In [20], PTile is proposed, a compile-time framework, for tiling affine nested loops whose tile sizes are handled at runtime. Par4All [23] is a source-to-source compiler for C and Fortran that generates tiled parallel code. In [3], authors propose a novel approach for generating code to enable dynamic tile size selection, based on monitoring the performance of a few loop iterations. In [22], authors present a formulation of the parameterized tiled loop generation problem using a polyhedral set called the outset. In [24], a comparative study of PrimeTile, DynTile and PTile is presented. Pluto [1] is a popular polyhedral code generator including many additional optimizations such as parallelization and register blocking. A comparison of these tools is provided in [25]. The authors in [25] conclude their paper by pointing out that exploiting the target hardware architecture is one of the interesting points remain to be studied.

In [26], tile size selection models are created using machine learning techniques. In [27], authors use an autotuning method to find the tile sizes, when the outermost loop is parallelised. In [28, 29], authors use genetic algorithms to search the solution space.

Finally, in [30] and [31], hybrid models are proposed by combining an analytical model with empirical search to manage the search space. In [30], authors introduced a framework that combines the use of compiler models and search heuristics to perform auto-tuning. In [31], a model to determine the upper and lower bounds on the search space and consider data reuse in multiple cache levels is proposed. However, this model ignores the impact of set associativity in caches.

In [32], authors present defensive tiling, a technique to minimize cache misses in inclusion shared caches, when multiple programs run simultaneously. In [33], loop tiling is combined with cache partitioning to improve performance in shared caches.

3 Proposed Method

This section is partitioned into two subsections. In Subsect. 3.1, we demonstrate and discuss the inefficiencies of current analytical models/methods. In Subsect. 3.2, we propose an improved loop tiling method overcoming the inefficiencies found in Subsect. 3.1.

3.1 Inefficiencies of Current Analytical Methods

The two main inefficiencies of the current loop tiling analytical methods are described in detail, in Subsects. 3.1.1 and 3.1.2.

3.1.1 Current Analytical Methods Do Not Accurately Calculate the Tiles Sizes

As noted, the main idea of loop tiling optimization is to partition the arrays into smaller ones (a.k.a. tiles), so as they can fit and remain into the cache. This way, the number of accesses to the slow and energy demanding main memory is minimized. The memory size needed for a tile should be measured in cache lines and not in bytes, as data are loaded/stored from/to memory hierarchy in cache lines.

Current methods, such as [2, 5], calculate the number of cache lines occupied by a tile, by using the following formula:

$$\begin{aligned} number.lines = \lceil \frac{tile.size.in.bytes}{line.size.in.bytes} \rceil \end{aligned}$$
(1)

A ceiling function is required in Eq. 1 as even just one element of a cache line is needed, the entire cache line is loaded into L1 data cache.

Equation 1 is not accurate as different tiles (of the same size) occupy a varied number of cache lines. Let us give an example (Fig. 1). Consider an one-dimensional (1-d) array of 200 elements and non-overapping tiles consisting of 25 elements each. Also consider that each array element uses 4 bytes and the cache line size is 64 bytes. The array elements are stored into consecutive main memory locations and as a consequence they are loaded into consecutive cache locations. Current methods assume that each tile occupies two cache lines (\(\lceil \frac{25 \times 4}{64} \rceil = 2\)) (Eq. 1), therefore just two cache misses are assumed when loading the tile into the cache. However, as it can be shown in Fig. 1, half of the tiles occupy two cache lines and the other half occupy three cache lines.

Fig. 1
figure 1

An 1-d array is partitioned into tiles. 25 element tiles occupy a varied number of cache lines

Full size image

The maximum and the minimum number of cache lines occupied by a tile is given by Eqs. 2a and 2b.

$$\begin{aligned} max.number.cache.lines= & {} \lceil \frac{tile.size.in.bytes}{line.size.in.bytes} \rceil +1 \end{aligned}$$
(2a)
$$\begin{aligned} min.number.cache.lines= & {} \lceil \frac{tile.size.in.bytes}{line.size.in.bytes} \rceil \end{aligned}$$
(2b)

There are cases where the tiles occupy a varied number of cache lines (e.g., in Fig. 1, both Eqs. 2a and  2b hold) and cases where the tiles occupy a constant number of cache lines given either by Eqs. 2a or 2b; it depends on the tile size and cache line size values, as well as on the (tile.size/line.size) value. Note that tiles are normally accessed many times from memory and therefore Eqs. 1 and 2 can give significant disparities in terms of cache misses.

In Subsect. 3.2, we show that the cache size allocated for a tile, must equal to its largest size; thus, we ascertain that all the tiles fit and remain in the cache.

To conclude, current models do not accurately calculate the tiles sizes and normally, the actual tiles size is bigger than the calculated tile size. This means that less cache memory size is allocated for the tiles and as a consequence, additional unforeseen cache misses might occur. In fact the number of unforeseen cache misses is not insignificant, as the tiles are normally accessed many times.

3.1.2 The Tiles Proposed by Current Methods Cannot Remain in the Cache

The main idea behind loop tiling is to access the tiles as many times as possible from the fast cache memory rather than the slow and energy demanding main memory (or lower level cache). Therefore the reused tiles (the tiles accessed more than once) must fit and remain into the cache. However, this is not always true in current methods, where normally only part of the tiles (and not the entire tiles) remain into the cache.

Related works such as [5, 7] assume that if the aggregated size of the tiles is smaller than the cache size, then the reused tiles will remain into the cache. However, this is rarely true due to the cache modulo effect [2]. An improved model is proposed in [2], where the cache associativity value is taken into account, but still the tiles cannot remain in the cache in many cases, leading to a significant number of unforeseen cache misses.

Let us showcase the above problem with another example, the well-known MMM algorithm (Fig. 2). Although different tiles of A and B are multiplied by each other, the tile of C is reused N/Tilek times (data reuse), where Tilek is the tile size and N is the arrays size in each dimension (Fig. 2). The current analytical models, such as [2], will well consider data reuse in this case and therefore they will include this information to their cache misses calculation model; therefore, current methods do assume that the tile of C is loaded just once in the cache, not N/Tilek times, which is accurate. However, the tile of C cannot remain in the cache unless all the following three bullets hold (note that in current analytical methods only the first condition or none is satisfied):

Fig. 2
figure 2

An example. Loop tiling for MMM algorithm

Full size image

  • Each tile must contain consecutive memory locations The sub-rows of tile of C are not stored into consecutive main memory locations and as a consequence they are not loaded into consecutive cache locations; thus, cache conflicts occur due to the cache modulo effect. Note that the array’s rows (and not the tile’s sub-rows) are stored into consecutive main memory locations. A solution to this problem is array copying transformation, where the tiles of an array are copied into a new array in the order in which they are accessed by the kernel. Thus, an extra loop kernel is added prior to the studied loop kernel that copies the input array to a new one, in a tile-wise format (all the elements are stored into the new array with the exact order they are loaded in the tiled-version). Then, the tiled loop kernel uses the new array instead, and thus the tile elements are loaded in consecutive cache locations. However, array copying introduces an overhead, as the new array must be stored and loaded to/from memory and this is why it is not always performance efficient.

  • A cache way must not contain more than one tile, unless they are stored into consecutive memory locations Assume an 8-way associative L1 data cache of size 32 kB and an MMM tiling implementation with the following tile sizes: \((Tilei, Tilej, Tilek)=(112,32,32)\); also assume that the three tiles contain consecutive memory locations (the previous bullet holds). The accumulated size of the three tiles equals to the cache size (the size of tile of C, A and B is 14,336, 14,336 and 4096 bytes, respectively, 32,768 bytes in total), and the tiles’ occupy cache size which equals to (3.5, 3.5, 1) cache ways, respectively (each way is 4096 bytes). An illustration of how the tiles might be allocated to the cache in this case is shown on the top of Fig. 3. The tile of C is shown in green. The tile of C occupies 14,336 bytes and thus it requires four cache ways, one of which is used to store part of the tile of C and A (e.g., Way-0 on the top figure of Fig. 3). Note that multiple tiles of A and B are loaded and multiplied, but the tile of C must remain in the cache. When the next tiles of A and B are loaded into the cache, the part of the C tile which belongs to way-0 will be replaced by the tiles of A, B, as there is no other cache line available to hold the new tiles of A and B. This problem is mitigated (but not solved) when \((Tilei, Tilej, Tilek)=(64,64,32)\), as the tiles occupy (4, 2, 2) cache ways, respectively (bottom figure in Fig. 3). In this case, there is a non-C-Tile cache line available to hold the tiles of A and B (a cache line is available for each different modulo of the tiles memory addresses). For the remainder of this paper, we will be writing that a tile is written in a separate cache way if an empty cache line is always granted for each different modulo (with respect to the size of the cache) of the tile memory addresses, e.g., in the bottom figure of Fig. 3, the tile in red is written in two (and not three) ‘separate’ cache ways as an empty cache line is always granted for each different cache modulo value.

  • Extra cache space must be granted for the non-reused tiles Even if the two aforementioned bullets hold, it is false to assume that all the elements of C tile will remain in the cache. This is because there is no cache space allocated for the next tiles of A and B; therefore, when the next tiles of A and B are loaded into the cache they might evict cache lines from the tile of C (LRU cache replacement policy is assumed). However, if \((Tilei, Tilej, Tilek)=(64,64,16)\) is selected instead of \((Tilei, Tilej, Tilek)=(64,64,32)\), then cache space for two tiles of A and B is allocated and therefore the Tile of C will definitely remain in the cache. Note that granting extra cache space for the non-reused tiles leads to smaller tile sizes and as a consequence to more L/S and arithmetical instructions, which might degrade performance in rare cases. However, if extra cache space is not granted for the next tiles, unforeseen cache misses occur and therefore the number of cache misses cannot be accurately estimated.

Fig. 3
figure 3

An illustration of how tiles might be allocated to the cache, for the example shown in Fig. 2. On the top, \((Tilei, Tilej, Tilek)=(112,32,32)\) is shown, while in the bottom \((Tilei, Tilej, Tilek)=(64,64,32)\). Each tile is shown in a different colour (Colour figure online)

Full size image

3.1.3 Motivation Example

We evaluated the above assumptions on the dL1 cache of two host PCs, an Intel i5-7500 CPU at 3.40 GHz running Ubuntu 20.04 (PC1) and an Intel i7-4790 CPU at 3.60 GHz running Ubuntu 18.04 (PC2). Both PCs support a 32 kB 8-way associative dL1. Three different tile sets are used, one satisfying just the first bullet above (112, 32, 32), one satisfying only the first two bullets (64, 64, 32) and another satisfying all the bullets above (64, 64, 16). All the codes are manually written and compiled with gcc 9.4.0 on PC1 and gcc 7.4.0 on PC2, and ‘-O2’ optimization option. We have not used ‘-O3’ option here as in this case auto-vectorization is applied and adds ‘noise’ to our experimental results, e.g., small tile sizes along the vectorized iterator normally lead to lower performance [7]. Note that in the experimental results section (Sect. 4), vectorization is used.

The following tile sets (Tilei, Tilej, Tilek) = (112, 32, 32), (64, 64, 32), (64, 64, 16) give (10.2, 9.8, 5.2) million dL1 misses and (3.3, 3.4, 4.3)/(3.1, 3.3, 7.4) Gflops, on PC1/PC2 respectively (square matrices of type float are used). For a fair comparison, we have chosen an input size that is multiple of all the tile sizes (\(N=1344\)). The non-tiled code gives 2470 million dL1 misses and 1.53/0.35 Gflops, on PC1/PC2 respectively. The number of dL1 misses is measured by using Cachegrind tool [34] (simulation). We can conclude that the tile of C array cannot remain into dL1 unless all the three aforementioned bullets hold.

To conclude, current methods fail to provide accurate cache miss estimation for the following reasons. Firstly, the actual tile size might be bigger than the calculated tile size. This means that less cache memory is allocated for the tiles and as a consequence, additional unforeseen cache misses might occur. Secondly, the tiles cannot remain in the cache in most cases and therefore the cache misses calculation process might omit a significant number of cache misses, leading to inefficient tile sizes.

3.2 Proposed Loop Tiling Method

In this subsection, the proposed loop tiling method is provided. The aim of our loop tiling method is to find the tile sizes (tile set) that minimize the number of cache misses. Although the number of cache misses does not always align with performance, it is the key performance indicator for loop tiling [2, 5]. This is further explained in Subsect. 3.3 (Discussion) and Sect. 4.

Our method takes as input the cache hardware architecture details (cache size, associativity and cache line size) and the the loop kernel’s information (loops and their bounds, the array references and their subscripts), and generates the tile sizes (tile set) and the iterators’ nesting level values. The inputs are manually provided to our tool. After the tile set is found, the process of generating loop tiling source code is easy and straightforward by using well known tools such as Pluto. Pluto is a powerful tool able to generate source code for loop tiling with the specified tile sizes. Furthermore, Pluto applies dependence analysis and thus the output tiled code is always safe (it does not violate data dependencies).

The basic idea behind our method is first, to find all different tile sets whose tiles fit and remain into the cache, and then select the tile set achieving the minimum number of cache misses. The tile sets whose tiles do not remain into the cache are discarded as they are considered inefficient. For the remaining tile sets, a simple and lightweight method to estimate the number of cache misses for each tile set, is proposed. Note that this method can estimate the number of cache misses only when the tiles remain into the cache.

Although more accurate methods exist for calculating the number of cache misses for affine loop kernels, such as [35, 36], higher accuracy comes with computationally expensive cache models, where the cache misses calculation process normally takes some seconds. These models are not feasible in our case, as the cache misses of multiple tile sets need to be estimated (they can even be some millions) and this would take many days of simulations.

Our approach is illustrated in Algorithm 1. All the tile sets that fit and remain into the cache are given by a mathematical inequality (Step 3). All the tile sets in this inequality satisfy the three bullets in Subsect. 3.1.2. In Sect. 4.1, we will prove experimentally that these tiles indeed fit and remain into the cache. The steps of Algorithm 1 are explained in detail hereafter.

figure a

  • Step 1: In this step the iterators that loop tiling is applicable to, are manually provided; not all the loops are eligible to loop tiling mainly because of data dependencies in the code. Note that Pluto applies dependence analysis and thus generates tiled source code that yields correct behaviour.

  • Step 2: The first loop in Algorithm 1 specifies the number of the iterators to be tiled, e.g., just one iterator is tiled when i = 1, two iterators are tiled when i = 2, etc. Then, all different nesting level values are considered so as not to exclude any efficient tiling solutions. For example, in a loop kernel with three iterators (i, j, k) eligible to loop tiling, such as the original (non-tiled) version of MMM in Fig. 2, the following 15 loop tiling implementations will be generated: (i), (j), (k), (i, j), (i, k), (j, i), (j, k), (k, i), (k, j), (i, j, k), (i, k, j), (j, i, k), (j, k, i), (k, i, j), (k, j, i). The first three loop tiling implementations refer to loop tiling to one loop only, the next six implementations to two loops and the rest to three loops.

  • Step 3: All the tile sets that fit and remain into the cache are expressed by a mathematical inequality (Eq. 3). The tile sets that satisfy Eq. 3 fit and remain into the cache and therefore they are further processed, while all the others are discarded as inefficient. Equation 3, which overcomes all the inefficiencies discussed in Subsect. 3.1, is shown below:

    $$\begin{aligned} m \le \lceil \frac{Tile_1}{L_j/assoc} \rceil + \lceil \frac{Tile_{1\_next}}{L_j/assoc} \rceil + ... + \lceil \frac{Tile_n}{L_j/assoc} \rceil + \lceil \frac{Tile_{n\_next}}{L_j/assoc} \rceil \le assoc \end{aligned}$$
    (3)

    where \(Tile_{i}\) is the tile size in bytes of the ith array reference (the number of tiles equals to the number of different array references), \(L_j\) is the cache size in bytes, assoc is the \(L_j\) associativity and m defines the lower bound of Eq. 3 and it equals to the number of different array references in the loop kernel. The special case where \(m \succ assoc\) is not discussed in this paper. In Eq. 3, there is one tile for each different array reference (in the loop kernel) and thus an array might have multiple tiles.

    To address the first bullet in Subsect. 3.1.2, all the tiles must contain consecutive memory locations. The tile sets that give tiles with non-consecutive memory locations are discarded (this is further explained Step 4), e.g., 2D tiles of shape \(T1 \times T2\), where \(T2 \prec upper.bound\) do not contain consecutive memory locations.

    Equation 3 addresses the second bullet in Subsect. 3.1.2 too. The value of (\(\lceil \frac{Tile_1}{L_j/assoc} \rceil\)) is a positive integer representing the number of \(L_j\) cache ways used by Tile1, or equivalently, is a positive integer representing the number of \(L_j\) cache lines with identical cache addresses used for Tile1. Equation 3 satisfies that the array tiles directed to the same cache subregions do not conflict with each other as the number of cache lines with identical addresses needed for the tiles is not larger than the assoc value (addressing the second bullet in Sect. 3.1.2).

    To address the third bullet in Subsect. 3.1.2, for each tile in Eq. 3, we grant cache space for its next tile too, i.e., \(Tile_{n\_next}\). In case where the next tile is the same as the current tile, then the \(Tile_{i\_next}\) term is removed from Eq. 3, e.g., in Fig. 2, there are no next tiles for C array. Furthermore, if the next tile is stored in memory just after the currect tile, then just one term is inserted in Eq. 3, that is \(\lceil \frac{Tile_1 + Tile_{1\_next}}{L_j/assoc} \rceil\).

    To address the inefficiency studied in Subsect. 3.1.1, \(Tile_{i}\), which contains consecutive memory locations, is given by Eq. 4:

    $$\begin{aligned} Tile_{i} = max.number.cache.lines \times cache.line.size \times element.size \end{aligned}$$
    (4)

    where cache.line.size is the size of the cache line in elements, element.size is the size of the array’s elements in bytes and the max.number.cache.lines gives the maximum number of cache lines occupied by the tile (Eqs. 2a, 2b).

    As it was mentioned above, for each tile in Eq. 3, we grant cache space for its next tile too; however, these tiles might overlap and this is why Eq. 3 must be appropriately updated. The overlapping tiles are merged to one, bigger tile, which consists of their union (if the tiles match, then the new tile will be of the same size). In this case, the number of terms in Eq. 3 is reduced by one. This step is needed so as there are no tile duplicates in the cache. Two tiles overlap, if their memory locations overlap. Consider the example where the following two array references exist in the loop body \(A[i][j-2]\), \(A[i][j+2]\) and j loop spans from 2 to N − 2. By applying loop tiling to j loop with tile size T, the 1st tile of the 1st array reference spans within (0,T) and the 1st tile of the 2nd array reference spans within (4,T + 4). These tiles are merged and a single bigger tile is created of size (\(T+4\)).

  • Step 4 in Algorithm 1: It is common practice to apply array copying transformation before loop tiling in order all the tiles to contain consecutive memory locations. In array copying, an extra loop kernel is added prior to the studied loop kernel, where it copies the input array to a new array, in a tile-wise format; it loads the elements of the input array with the exact order they are used in the main loop kernel and stores them in the new array in-order. Then the main loop kernel uses the new array instead. Array copying adds an extra overhead in terms of memory accesses and arithmetical instructions and therefore it is not always performance efficient.

    In Step 4, all the tile sets giving tiles with no consecutive memory locations are either discarded as they cannot remain into the cache, or array copying transformation must be applied to create new tiles with consecutive memory locations. Given that array copying introduces a significant overhead and thus it is not always efficient, the user can specify whether array copying is enabled or not. If array copying option is enabled, then two tile sets are extracted by Algorithm 1, the best tile set that uses array copying and the best tile set that does not use array copying.

    Note that there is a special case where tiles of no consecutive memory locations can be further processed, without applying array copying; a tile with no consecutive memory locations can be faced as multiple tiles of consecutive memory locations, e.g., a tile of size \(2 \times T\) can be faced as two tiles of size \(1 \times T\). In this case, Eq. 3 must be appropriately updated with an extra (\(\lceil \frac{Tile_i}{L_i/assoc} \rceil\)) term, as an extra tile is inserted now. Given that the associativity value is always a small number, this special case normally holds for tiles of size \(b \times T\), where \(b \le 3\) only.

  • Step 5 in Algorithm 1: In Step 5, the number of cache misses is approximated theoretically, considering the cache hardware details, the array memory access patterns of each loop kernel and the problem’s input size. To do so, we calculate how many times the selected tiles (whose dimensions and sizes are known) are loaded/stored from/to the cache.

    We are capable of approximating the number of cache misses because the number of unforeseen misses has been minimised (the reused tiles fit and remain in the cache). This is because only the proposed tiles reside in the cache, the tiles are written in consecutive memory locations, an empty cache line is always granted for each different modulo and we use cache space for two consecutive tiles and not one (when needed). Additionally,we refer to CPUs with an instruction cache; in this case, the program code typically fits in L1 instruction cache; thus, it is assumed that the shared cache or unified cache (if any) is dominated by data.

    The number of cache misses is estimated by Eq. 5.

    $$\begin{aligned} { Num\_Cache\_Misses = \sum \nolimits _{i=1}^{i=sizeof(Tiles.List)} (repetition\_i \times cache.lines\_i) } \end{aligned}$$
    (5)

    where \(cache.lines\_i\) is the number of cache lines accessed when this tile traverses the array (given by Eq. 6), \(repetition\_i\) gives how many times the entire array (of this tile) is loaded/stored from/to this cache memory (given by Eq. 7), and Tiles.List contains all the tiles that contribute to Eq. 5 (further explained below).

    The cache.lines value in Eq. 5 is given by

    $$cache.lines = \left\{ {\begin{array}{*{20}l} {\frac{N}{{Ty}} \times \sum\limits_{{j = 1}}^{{j = M/Tx}} {\left( {\left\lceil {\frac{{j \times Tx}}{{line}}} \right\rceil - \left\lfloor {\frac{{(j - 1) \times Tx}}{{line}}} \right\rfloor } \right)} ,{\text{row - wise data array layout}}} \hfill \\ {\sum\limits_{{j = 1}}^{{j = tiles}} {\left( {\left\lceil {\frac{{j \times (Tx \times Ty)}}{{line}}} \right\rceil - \left\lfloor {\frac{{(j - 1) \times (Tx \times Ty)}}{{line}}} \right\rfloor } \right)} ,{\text{tile - wise }}} \hfill \\ \end{array} } \right.$$
    (6)

    where (Tx, Ty) are the tile sizes of the iterators in the (x,y) dimension of the array’s subscript, respectively, (N, M) are the corresponding iterators’ upper bounds (for 1D arrays \(Ty=1\)), line is the cache line size in elements, tiles is the total number of the array’s tiles and \((tiles=N/Ty \times M/Tx)\) or \((tiles=M/Tx)\) whether for 2D/1D arrays, respectively. The second branch in Eq. 6 is when array copying has been applied and therefore the array is stored into memory tile-wise.

    Let us give an example for the first branch of Eq. 6, consider a 2D array and a tile of size \((10 \times 10)\) traversing the array in the x-axis. Also consider that \((line=16)\) array elements. The first tile occupies \(10 \times (\lceil \frac{10}{16} \rceil - \lfloor \frac{0}{16} \rfloor )=10\) cache lines while the second tile occupies \(10 \times (\lceil \frac{20}{16} \rceil - \lfloor \frac{10}{16} \rfloor )=20\) cache lines. Although the array’s tiles are of equal size, they occupy a different number of cache lines and this is why a sum is used in Eq. 6. If array copying has been applied and therefore the array is written tile-wise in memory, the first tile lies between (0, 100), the second between (100, 200) etc.

    The repetition value in Eq. 5 is given by Eq. 7. Equation 7 gives how many times the entire array is accessed from memory; an array is accessed more than once when the loop kernel contains iterators than are not included in the array’s subscript, e.g., in Fig. 2, B[k][j] does not include ‘ii’ and ‘i’ iterators and therefore these iterators force B array to be accessed several times.

    $$\begin{aligned} {repetition = \mathop {\prod }\nolimits _{j=1}^{j=D} \frac{(up_j-low_j)}{T_j} \times \mathop {\prod }\nolimits _{k=1}^{k=W} \frac{(up_k-low_k)}{T_k} } \end{aligned}$$
    (7)

    where D is the number of new/extra iterators (generated by loop tiling) that (a) do not exist in the corresponding array’s subscript and (b) exist above of the iterators of the corresponding array, e.g., regarding the B tile in Fig. 2, this is the ii iterator. W is the number of new/extra iterators that (a) do not exist in the array and (b) exist between of the iterators of the array, e.g., regarding the A tile in Fig. 2, this is the jj iterator. The ii iterator forces the whole array of B to be loaded N/Tilei times, while the jj iterator forces the whole array of A to be loaded N/Tilej times.

    The Tiles.List includes all the tiles included in Eq. 3 (the ‘next’ tiles are not included; the only reason they exist in Eq. 3 is to grant extra cache space). There is a special case where not all the tiles contribute to Eq. 5 and this is why these tiles must be deleted from the Tiles.List. This is likely only when an array has multiple (different) array references and therefore multiple tiles. In this case, different tiles of the same array might access memory locations that have already been accessed just before and thus the tile resides in the cache; in this case, accessing the tile will lead to a cache hit, not a miss. This special case is not further discussed here because the aforementioned equations become complex.

3.3 Discussion

3.3.1 Multiple Levels of Tiling

Modern processors support multiple levels of cache and therefore loop tiling is normally applied to more than one cache memories (multiple levels of tiling), to further reduce the overall number of cache misses in memory hierarchy. Normally, up to k levels of tiling are applied, where k is the number of cache memories. Prior to applying loop tiling to multiple cache memories, we should consider the following questions. How many levels of tiling should be applied, to which memories (e.g., on L1 and L3 or on L1 and L2) and on what order (e.g., first apply tiling on L1 or L3)? To the best of our knowledge there is no general formal method or theoretical work that answers to these questions and therefore all different combinations must be evaluated in order to find the most efficient solution. The answers to the questions above depend on the target loop kernel, its input size and hardware architecture. Note that the more the levels of tiling applied, the higher the number of arithmetical instructions being inserted. Furthermore, different orders of tiling (e.g., first apply tiling to L1 and then to L2, or vice versa) give different binaries, as these optimizations are interdependent.

The proposed loop tiling algorithm (Algorithm 1) can be applied to each cache memory separately.

3.3.2 Loop Tiling and Vectorization

Small tile sizes along the vectorized iterator can diminish the benefits of vectorization and hardware prefetching [7]. Therefore, it is common practice that the tile size of the vectorized iterator is large enough and power of 2. In this work, we select the tile size (let Tile) of the iterator corresponding to the vectorized loop to be \(Tile \ge 64\) and multiple of k, where k is the length of the vectorization technology by the length of the arrays’ data type, e.g., for float elements and AVX technology k = 256/32 = 8.

3.3.3 Cache Misses and Execution Time

Although the execution time of data intensive loop kernels mainly depends on the time needed to load/store the data from/to memory hierarchy, the tile set that provides the minimum number of cache misses for a specific memory (or more) does not always provide the best performance. This is because the hardware architecture of modern processors is complex and thus the execution time depends on many parameters, e.g., vectorization and hardware prefetching. Furthermore, loop tiling increases the number of program instructions.

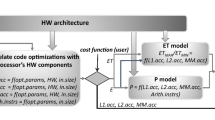
Correlating the number of cache misses with Execution Time (ET) on modern processors is a hard problem, mainly because modern memory systems support concurrent data accesses, e.g., multi-port, multi-banked and non-blocking caches. This is the reason the well-known but simplified AMAT [37] ET model fails to provide an accurate ET estimation on modern processors. The AMAT model is described by the following formula \(T_{data}=T_{L1}+T_{L2}+T_{L3}+T_{MM}\), where \(T_{data}\) is the overall time needed to load/store the data from/to memory hierarchy, \(T_{L1/2/3}\) is the time needed to load/store the data from/to L1/2/3 cache and \(T_{MM}\) is the time needed to load/store the data from/to main memory. Note that \(T_{Li}=Li.accesses \times Li.Latency\) and \(L(i+1).accesses=Li.misses\). Also, we can assume that \(T_{overall} \approx T_{data}\) for memory bound loop kernels.

Steps 5 and 6 of Algorithm 1 can be extended by using the AMAT model and therefore, the tile set achieving the minimum ET value can be selected instead of the tile set achieving the minimum number of misses. The extension is trivial when loop tiling is applied to all the cache memories, as the proposed method (in its current form) can approximate the number of Li cache misses, only when loop tiling is applied to the i memory. Estimating the number of cache misses for the cache memories that loop tiling is not applied to, is more complicated. Let us give an example. Consider that loop tiling has been applied only to dL1, for the example shown in Fig. 2; in this case, the number of L3 misses depends on whether the block row of A remains into the cache or whether the entire A array remains into the cache, and as consequence the number of L3 misses depends on the cache size, dL1 tile sizes and input size. However, the proposed method can be extended to estimate the number of Li cache misses, when loop tiling is not applied to the i memory, but with a lower accuracy.

An extension of AMAT model is C-AMAT [37], where the notions of cache hit concurrency and cache miss concurrency are introduced, but its application in this context is not trivial. In our future work, we are planning to extend C-AMAT model to correlate the number of cache misses with execution time. A starting point would be extending the AMAT model to \(T_{data}=T_{L1}/c1+T_{L2}/c2+T_{L3}/c3+T_{MM}/c4\), where c1, c2, c3, c4 introduce cache hit and miss concurrency (\(ci \ge 1\)). c1–c4 vary depending on both the memory hardware architecture and loop kernel characteristics. The first step of our future work includes a training step that estimates the (c1–c4) values for the target hardware architecture; although this step assumes that only the hardware architecture affects the (c1–c4) values (and not the loop kernel characteristics), we expect that it will be more accurate than the simplified AMAT model.

3.3.4 Cache Misses and Energy Consumption

The energy consumed by memory hierarchy accounts for a significant amount of the total energy consumed by modern processors. By reducing the number of Li cache misses, the number of \(L(i+1)\) memory accesses is reduced and as a consequence the dynamic energy consumption of \(L(i+1)\) memory is reduced. Thus, the proposed method can be used as a solution to reduce energy consumption.

3.3.5 Loop Tiling for Multi-threaded Programs

Besides optimizing for data locality, loop tiling is also used to exploit parallelism. In this case, loop tiling partitions the iteration space into tiles that are executed concurrently on different processors or CPU cores. Regarding multi-threaded programs, OpenMP programming framework is normally used to parallelize a data parallel loop into multiple threads which they all share the same last level cache. The current design trend in multi-core CPUs includes a last level cache memory which is shared amongst all the CPU cores, while all the other upper level cache memories are private. As it was explained above, tiling can be applied to all the cache memories.

Algorithm 1 can be applied to the upper level (private) cache memories of multi-threaded programs, but not to the last level shared cache (in its current form), e.g., on x86-64 processors, Algorithm 1 can be used to apply loop tiling to dL1 and/or L2 but not to L3. However, we are planning to extend the proposed method to the shared cache in our future work. In this case, multiple threads and thus multiple tiles use the last level cache, some of which are shared by all the threads. The proposed equations must take all the tiles into account as all the tiles must fit and remain into the cache. Furthermore, the tile size selection affects the workload of each thread which must be high enough to exploit parallelism.

4 Experimental Results

This section is divided into three parts. In Subsect. 4.1, the proposed method is validated. In Subsect. 4.2, our approach is evaluated in terms of cache misses and execution time over [7], icc and gcc compilers and Pluto [1]. In Subsect. 4.3, we evaluate the simulation time required to generate the tile sizes.

The experimental results are performed in two host PCs, an Intel i5-7500 CPU at 3.40 GHz running Ubuntu 20.04 (PC1), an Intel i7-4790 CPU at 3.60 GHz running Ubuntu 18.04 (PC2), and in a Zybo Zynq-7000 FPGA platform with ARM Cortex-A9 hard processor running petalinux Operating System (OS). PC1 and PC2 support three levels of cache, while Arm supports two levels of cache. PC1 supports 32 kB 8-way dL1, 256 kB 4-way L2 cache and 6 MB 12-way L3 cache. PC2 supports 32 kB 8-way dL1, 256 kB 8-way L2 cache and 8 MB 16-way L3 cache. Arm processor supports 32 kB 4-way dL1 and a 512 kB 8-way L2 cache.

The benchmarks used in this study consist of eleven popular linear algebra loop kernels taken from 4.1 PolyBench/C suite [38] (Table 1). The input size of the loop kernels is specified with letter ‘N’ (square matrices are taken of size \(N \times N\)). PolyBench supports different input sizes, a.k.a., mini, small, standard, large and extra large. The first two input sizes are not the appropriate to evaluate loop tiling as the arrays are small and fit into the cache in most cases. The extra large input size exceeds our DDR memory in some cases and it is not used. Thus, we have used the large and the standard sizes. We have also used their in-between values as a third input size. To sum up, three different input sizes are used and the average gain values are reported. The results shown in the next subsections include the initialization of the arrays.

Table 1 Loop kernels studied (taken from 4.1 PolyBench/C suite [38])
Full size table

We define ‘Re-usage ratio’ the number of array elements accessed more than once by the number of the overall array elements, e.g., in Fig. 2 (gemm), \(Reusage\_ratio = (3 \times N^2) / (3 \times N^2) = 1\). The re-usage ratios of the studied kernels are shown in Table 1. In Subsect. 4.2, we show that loop tiling cannot provide significant performance gains for kernels with low re-usage ratios.

Pluto tool is used to generate the tiled source code for the studied loop kernels (version 0.11.4). In general, Pluto takes as input C language source code and generates another optimized C source code, including loop tiling, vectorization, loop interchange and other optimizations. In this paper, only loop tiling optimization is enabled. We have used the ‘tile’ option to generate 1 level of tiling code versions and the ‘l2tile’ option to generate two levels of tiling code versions. If the tile sizes are not provided (by the user) as input to Pluto, then Pluto uses square tile sizes of fixed size ‘32’ in all cases.

For a fair comparison on the x64 processor, we have re-written the eleven tiled loop kernels (that Pluto generated) by using AVX intrinsics. By using scalar (common) C code, icc compiler becomes aggressive and applies different high level optimizations for different tile sizes and thus the performance gains we get are not related to loop tiling, e.g., vectorization is not applied for some tile sizes and register blocking might be applied to the non-tiled version, and this adds ‘noise’ to our experiments. We did not face such a problem with gcc on Arm.

4.1 Validation of the Proposed Method

The objectives of this sub-section are to showcase that (i) the tiles generated by the proposed methodo fit and remain into the cache and (ii) the proposed equations (Step 5 in Algorithm 1) can accurately estimate the number of cache misses. Note that it is not possible to accurately estimate the number of cache misses (by using the aforementioned equations) if the tiles cannot remain into the cache, as unforeseen cache misses occur in this case. Therefore, if the second objective is met then the first objective is met too.

In this subsection, we have applied loop tiling for dL1 and L3 cache memories, for the three aforementioned input sizes, and we have selected five random tile sets of each case. Then, the number of cache misses is measured in each case and the maximum error value (\(error \% = \frac{\mid experimental-theoretical \mid }{theoretical} \times 100\)) is calculated (Eq. 8).

$$\begin{aligned} error \% = \frac{\mid cache.misses.measured - Eq.~5.misses \mid }{Eq.~5.misses} \times 100 \end{aligned}$$
(8)

The maximum error value in Eq. 8 is extracted for PC2 by using (i) Cachegrind tool [34] (simulation) and (ii) Perf tool [39] using the ‘l1d.replacement’, ‘LLC-load-misses’ and ‘LLC-store-misses’ hardware counters. We used both simulation and hardware counters in order to provide a thorough experimental analysis. Cachegrind and Perf give different cache misses values (especially when the tile sizes are almost equal to the cache size) as Perf measures the number of cache misses of all the running processes, not just the process we are interested in. The number of cache misses shown by Perf is affected by any operating system process that loads/stores data from/to this memory. Thus, to get an accurate measurement, each loop kernel runs for at least 1 min (the kernel runs multiple times if needed); this way the number of cache misses due to other programs is minimized.

It is important to note that if the compiler applies high level optimizations (such as loop tiling, loop interchange or register blocking), then the arrays’ memory access patterns will change and thus Eq. 5 will not accurately estimate the number of cache misses. To make sure that the compiler does not apply any high level optimizations, we have used ‘-O2’ optimization flag and not ‘-O3’. In this subsection gcc 7.5.0 is used. In this subsection we do not evalute the execution time of the proposed method but whether the tiles remain into the cache and whether Eq. 5 can accurately estimate the number of cache misses.

The number of unforeseen cache misses in L3 is higher than in dL1. The main reasons follow. Firstly, the binary code is also loaded to L3 cache apart from the data. Secondly, the default page/frame size is smaller than the size of one cache way and therefore, multiple pages might be loaded into a cache way, introducing ‘noise’ to the cache. This problem can be alleviated by using the Operating System (OS) huge page tables (we did not do that though). Thirdly and most importantly, hardware prefetching adds extra noise to our method and this is why it has been disabled.

Each loop kernel is pinned to a specific CPU core. When using Perf, the target core must be specified so as to not measure the overall number of dL1 misses (from all dL1s) using the following command: ‘perf record -e l1d.replacement -C 2 ./executable’, where ‘-C 2’ relates to the core number.

In Table 2, we compare the number of dL1 misses as extracted from Eq. 5 against the measurements from Cachegrind and Perf. As Table 2 indicates the proposed equations provide roughly the same number of cache misses as Cachegrind. This means that first, the proposed tiles fit and remain in the cache and second, the proposed equations give a very good approximation of the number of cache misses. Five different tile sizes have been used for each loop kernel (they are shown in Table 2).

Table 2 The error in cache misses is measured for five different tile sizes using Eq. 8 and the maximum value is shown
Full size table

As it was expected, the error values are higher (about \(3\%\)) when using the dL1 hardware counter (Table 2), as other processes are loading/storing data from/to this memory too. It is important to note that Table 2 shows only the tile sizes that need roughly the size of seven out of eight cache ways, or less; the tiles that use more cache space give a much higher error value, which is up to \(20\%\). Given that this inconsistency holds only for the Perf measurements and not for Cachegrind, it is valid to assume that this is due to the fact that other processes using the dL1. In this case, each dL1 access of another process leads to an unforeseen miss.

In Table 2, we also compare the number of L3 misses as extracted from Eq. 5 against the measurements from Cachegrind and Perf. Regarding Cachegrind (simulation), the proposed method provides roughly the same number of cache misses as Cachegrind. As far as the results using the hardware counters are concerned, the noise in L3 is higher than that in dL1 for the reasons explained above. Table 2 shows only the tile sizes that need roughly the size of 9 out of 16 cache ways, or less; the tiles that use more cache space give a much higher error value, which is up to \(37\%\). This is because all the running processes use L3 cache. Note that for a fair comparison, we disabled HW prefetching. As Table 2 indicates the proposed equations give a very good approximation of the number of cache misses. mvm, doitgen, bicg, gesumv, atax and gemver give a smaller error value compared to gemm, 2 mm, 3 mm, syrk and syr2k, as the reused arrays fit and remain in L3 even without using loop tiling. This is not the case for the other kernels and this is why their error values are higher.

4.2 Performance Evaluation

In this section the proposed method is evaluated in terms of cache misses and execution time, on PC1 and Arm. The comparison is made over [7] and Pluto tool on both processors and over icc/gcc compilers on PC1/Arm, respectively. The kernels are compiled by using icc version 2021.5.0 for PC1 and by using the arm-linux-gnueabi-gcc 7.5.0 for Arm. The ‘-O3’ compiler flag is used in all cases. Each loop kernel is pinned to a specific CPU core by using the Linux kernel affinity sets (\(cpu\_set\_t\)).

The evaluation is carried out by applying first loop tiling to dL1 only (one-level of tiling), and second both to dL1 and L2 (two-levels of tiling). Note that the HW-prefetching mechanism which was disabled in the previous subsection, is now enabled. Although our method achieves significant cache miss gains in all cases, we show that execution time does not always align with the number of cache misses, especially for the loop kernels with low re-usage ratio values (Table 1).

In [7], a fast and lightweight tile size selection model is proposed that considers data reuse. In Table 3, we show the tile sizes generated by this model. This model supports both single-threaded and multi-threaded loop kernels. However, in this work we are focusing on single-threaded kernels only and thus the tile sizes shown in Table 3 refer to the single-threaded case only. According to [7], the tile size of the vectorized loop is always fixed to 256 to allow for efficient vectorization. Although [7] was evaluated by using one level of tiling only, according to [7], this model can be applied to more levels of tiling too. To do so, we have slightly amended the tile sizes found by [7] in order the L2 tiles to be multiples of the dL1 tiles (slightly smaller tiles are selected). This is common practice as it reduces the number of arithmetical instructions. Note that Pluto does not support multi-level tiling where the tile sizes of the bigger tiles are not multiples of the smaller ones, and this is another reason for this decision. The ‘–’ in the last column of Table 3 indicates that only one level of tiling is applied. This is because for these loop kernels the one level of tiling case always achieves better performance than the two levels of tiling case. Note that the tile sizes of [7] do not depend on the input size and thus they are used for all different input sizes. On the contrary, the tile sizes of the proposed method depend on the input size and are not fixed.

Table 3 Tile sizes found by the tile size selection model in [7] for PC1
Full size table

In Table 4, we show average speedup and cache misses gain values over icc compiler on PC1, when applying tiling just for dL1 and for both dL1 and L2. In Table 5, we show average speedup and cache misses gain values over gcc compiler on Arm, when applying tiling just for dL1 and for both dL1 and L2. The cache misses gain values are taken by using Cachegrind. The routine that initializes the arrays is included to the results. Pluto uses fixed tile sizes of size 32, while the tile sizes of [7] are shown in Table 3. The proposed method gives different tile sizes for each input size. The cache misses gain value is given by the number of cache misses of the un-optimized version by the number of cache misses of the evaluated tiled method.

Table 4 Comparison over icc compiler in terms of execution time and cache misses on PC1 (average values of three different input sizes are shown)
Full size table
Table 5 Comparison over gcc compiler in terms of execution time and cache misses on Arm Cortex-A9 (average values of three different input sizes are shown)
Full size table

First an analysis is provided when tiling is applied for dL1 only. The proposed method provides significant dL1 miss gains in all cases but worse execution time for the loop kernels with low re-usage ratios, i.e., mvm, gemver, bicg, gesumv, atax (Table 4). Pluto and [7] give worse execution time too, apart from the atax kernel. The main reason for this lies in the fact that most of the tile sets give a slightly higher number of L2 and L3 misses here (about \(0.1\%\)). In this case, the number of dL1 misses does not align with performance because the number of L2 and L3 misses are slighly increased. Furthermore, loop tiling introduces extra loops and thus the number of arithmetical instructions is increased too. As it was explained in Sect. 3.3.3, performance depends on many different parameters apart from the number of cache misses. It is important to note that Algorithm 1 does generate dL1 tile sets that provide performance gains (although marginal) but they are not selected by Step 6 as they do not achieve the minimum number of dL1 misses.

The dL1 miss gain is higher in gemm, doitgen, 2 mm, 3 mm, syrk and syr2k as all their arrays/tiles achieve data reuse; their tiles (which remain in dL1) are loaded (re-used) many times from dL1, highly reducing the number of dL1 misses. On the contrary, mvm, bicg, gemver, atax and gesumv loop kernels load most of their data just once from memory. For example, mvm (matrix-vector multiplication) has two 1-dimensional arrays of size N and one 2-dimensional array of size \(N \times N\) (which is loaded just once). Loop tiling transformation can reduce the number of memory accesses of the 1-dimensional arrays but not the memory accesses of the big 2-dimensional array (loaded just once); note that (\(N^2 \gg 2 \times N\)). The same holds for atax, gemver, gesumv and bicg loop kernels where most of their data are accessed just once. Therefore, loop tiling has a smaller effect in performance for these loop kernels compared to the others. Another reason that the high re-usage ratio kernels achieve higher miss and performance gains on both CPUs is that array copying transformation has been applied (Step 4 in Algorithm 1). Array copying introduces a high overhead (an extra loop kernel is added) and this is why it provides performance gains only for kernels with high re-usage ratios. The overhead of array copying is included in Tables 4 and 5.

All methods achieve higher speedup values on Arm for two main reasons. First, there is no big L3 cache on Arm and thus the effect of loop tiling (and memory management in general) has a higher impact. Second, we believe that icc compiler, which targets Intel processors only, generates faster code for Intel processors, compared to gcc compiler on Arm processors.

The proposed method provides higher cache misses gains in all cases, compared to Pluto and [7]. This is because the tiles of the proposed method remain into the cache as the cache associativity and cache line size are well considered. [7] provides cache misses gains in all cases apart from diotgen and syr2k. In these two cases the tile sizes are not well selected. Pluto’s fixed tile sizes well utilize the cache in most cases, apart from diotgen, where the bigger 3D tiles cannot fit into the cache (a 2D tile of size 32 × 32 needs 4 kB, while a 3D tile of size 32 × 32 × 32 needs 131 kB). One of the reasons Pluto does not achieve significant performance gains here is that the tile size of the vectorized loop is not large enough to take full advantage of vectorization and hardware prefetching. On the contrary, the tile size of this loop is fixed to 256 in [7].

We have also evaluated the proposed method when two levels of tiling are applied (Tables 4, 5). In this case, we first find the tile sizes for dL1 and then for L2. Note that if loop tiling is applied first to L2 and then to dL1, then the tile sets would be different (Subsect. 3.3.1). The latter order is not evaluated here.

The proposed method now provides high cache miss gains on both dL1 and L2, on both processors (Tables 4, 5), for the reasons explained above. The speedup values achieved are even higher now as both cache memories are utilized. Regarding the low re-usage ratio kernels (mvm, bicg, gemver, atax and gesumv), they do not provide any L2 miss gains as their reused arrays are small enough to fit in L2 in all cases, even for the largest input sizes used. However, performance is never degraded in this case (L2 was not well utilized when tiling just for dL1 was applied). Loop tiling cannot provide that high cache miss gains for the low data re-usage kernels as in gemm, doitgen, 2 mm, 3 mm, syrk and syr2k, and therefore the performance improvement is lower. [7] provides good tile sizes for gemm, 2 mm, 3 mm, syrk, syr2k and atax but performance is slighly degraded for mvm, diotgen, gemver, bicg and gesumv.

4.3 Tile Size Selection Overhead

In this subsection, the execution time required to generate the tile set (overhead) is evaluated on the one CPU core of PC1 (icc compiler is used). The overall number of different tile sets for the studied loop kernels can be found in Table  1. The factorial indicates different iterator orderings. According to Algorithm 1, all different tile sets are processed. The tile sets that satisfy Eq. 3 are further processed, while all the others are discarded. For the latter tile sets, only a few and simple arithmetical operations are performed, and thus, the tile size selection overhead mainly depends on the number of tile sets that satisfy Eq. 3. The more the tile sets that satisfy Eq. 3 the higher the execution time as further processing is required to estimate the number of cache misses. Although Eq. 3 includes many ceiling operations, which are time-consuming, they are implemented by using bitwise operations. \(\lceil \frac{n}{m} \rceil\) is replaced by \(((n>> log(m)) + (((n) \& (m-1))!=0))\), as m value is always a power of 2 and n, m positive integers. Furthermore, m is a constant (depends on the hardware details) and thus the logarithm can be computed just once.

The average execution time of Algorithm 1 (for the three studied input sizes) when applying loop tiling just for dL1 or just for L2 of PC1, is shown in Table 6. As it can be observed, the high re-usage ratio kernels give a higher overhead compared to the low re-usage ones, as they contain a larger search space (Table  1). In dL1 case, the overhead is low for all kernels apart from diotgen, which needs almost an hour.

Table 6 Tile size selection overhead on one CPU core of PC1
Full size table

The overhead for L2 is much higher because a higher number of tile sets satisfy Eq. 3 in this case. L2 is larger than dL1 and thus a larger number of solutions satisfy Eq. 3. Note that it is not always the case that bigger cache memories give a higher overhead than smaller cache memories. However, small memories normally include lower overheads. The overhead when applying tiling to L2 ranges between 0.5 and 5.4 h. In diotgen, the simulation time takes more than 24 h and thus we process only the even tile sizes here to speedup the process.

When loop tiling is applied to multiple cache memories, then the overhead is lower. For example, if Algorithm 1 is applied first to dL1 and then to L2, the L2 tile sizes are selected as multiples of the dL1 tile sizes and in this case the number of L2 tile sizes that satisfy Eq. 3 is many times lower, and thus the simulation time is highly reduced. Note that this common practice for multi-level tiling.

Although, the overhead shown in Table 6 can be high, there are several schemes that can be used to reduce the execution time by about one order of magnitude or even more. For example, processing the tiles that perfectly divide the iterator’s upper bound only, processing the even or odd tile sizes only, or processing less loop iterators’ orderings (Step 2 in Algorithm 1). Last, we believe that the process of finding the tile sizes can be further optimized by adopting constraint programming techniques.

5 Conclusions and Future Work

In this article, two important inefficiencies of current analytical loop tiling methods are demonstrated. We showcase that first, current methods do not accurately calculate the tiles sizes, and second, in current methods the tiles cannot remain into the cache in most cases due to the cache modulo effect. This results to inefficient tile sizes as only part of the tiles remains into the cache. Furthermore, the number of cache misses for each tile size is not accurately calculated, leading to sub-optimal tile sizes.

To address the aforementioned inefficiencies, a new loop tiling method is proposed that well considers the cache line size, cache associativity and cache size. We show that the tiles generated by our method remain into the cache and their number of cache misses can be accurately estimated. The experimental results show that it is possible to estimate the number of cache misses with a maximum error of 1% using simulation and 3.2% and 5.9% by using the processor’s hardware counters, on L1 data cache and L3 cache, respectively, leading to more efficient tile sizes, for static loop kernels.

The proposed loop tiling method achieves significant speedup values for the loop kernels with high data re-usage ratios, in all cases, over icc/gcc compilers, Pluto and other related methods. For the kernels with low data re-usage ratios, two levels of tiling are required to achieve performance gain. Last, we show that loop tiling is a transformation that cannot provide high speedup values for kernels with low data re-usage ratios.

As far as our future work is concerned, we first plan to extend the proposed method to multi-threaded loop kernels that use OpenMP framework (see Subsect. 3.3.5). In this case, the tile size selection affects the workload of each thread which must be high enough to exploit parallelism. Furthermore, as it was explained in Subsect. 3.3.3, we plan to extend C-AMAT model to correlate the number of cache misses with execution time.