On the Importance of Using Reliability Criteria in Photothermal Experiments for Accurate Thermophysical Property Measurements

Abstract

The theoretical and experimental foundations of some of the most common frequency-domain photothermal techniques for measuring thermophysical properties of materials are presented. Limitations of these methodologies when used without attention to satisfying the appropriate validity conditions are discussed and their consequences in providing inaccurate and often conflicting quantitative measurements are examined in the form of several case studies in photothermal thermophysics. The importance of adherence to experimental setup configurations and signal generation conditions consistent with photothermal theoretical models used to extract thermophysical properties (diffusivity, effusivity, optical absorption coefficient) is highlighted as an essential requirement for reliable thermophysical measurements.

1 Introduction

Since the development of theoretical models to qualitatively explain the photoacoustic effect discovered by Alexander Graham Bell in 1880, related experimental techniques, called photothermal techniques, have received much attention. To carry out a variety of qualitative and quantitative studies, various experimental setups have been developed taking advantage of the thermal and optical properties involved in photothermal signals. Obtaining the absorption spectra of materials in the condensed phase is among these first studies [1,2,3,4,5,6]. In parallel, mathematical models have also been developed to quantify various thermal and optical properties of matter. The former include thermal diffusivity and effusivity [7,8,9,10,11,12,13,14,15] and the latter include optical absorption coefficients [15,16,17,18,19,20].

In parallel, or in conjunction with the development of theoretical schemes, various experimental setups have been developed, which are suitable for measuring the thermal and optical properties of substances in various physical states.

When photothermal techniques involving modulated radiation are used, two control variables are particularly important for quantification purposes: the modulation frequency and the sample thickness. Although both can be used interchangeably to study the thermal and optical properties of substances in various phases, the nature of the sample makes it more convenient to use one of the control variables over the other, either for analytical simplicity or for ease of experimental configuration. For example, given the difficulty of having a set of identical solid samples of various thicknesses, the modulation frequency can be conveniently used as a variable to measure the thermo-optical properties of solids. On the other hand, given the ease of varying the thickness of a liquid sample, the sample thickness is the natural variable for fluids.

Similarly, photothermal transducers can be extended to include photoacoustic experimental systems (with a photoacoustic cell as a transduction medium) when appropriate, especially when the sample under study is a solid, because the sample itself can be used to seal one of the faces of the cell, allowing optimal heat exchange from the sample to the gas inside the cell, thus avoiding any other means of thermal coupling between materials, this would also be the case, if a pyroelectric or piezoelectric transducer is used. A pyroelectric or piezoelectric transducer is, however, more suitable to study liquid samples, since in this case intimate thermal contact between the fluid and the surface of the pyroelectric transducer becomes possible.

Failure to take into account the relationship between modulation frequency (thermal diffusion length) and sample thickness may result in a loss of accuracy and/or precision in the reported measurements; for example, it has been shown that measurements made using the sample thickness as a control variable are an order of magnitude more precise than those carried out using variable modulation frequency [10].

Regardless of the experimental setup used, an important factor is the quality of the information obtained: it should be obtained according to the applicable theoretical specifications, which is a critical factor in obtaining and reporting reliable experimental values. Thus, whether modulation frequency or sample thickness are used as variables, choosing a data set within an appropriate range in keeping with the control variable is of primary importance because the mathematical expressions that arise from the applied theoretical models are frequently simplified versions of more complex models which are obtained under specific limiting conditions or without taking into account all the physical phenomena involved. For instance, with some exceptions [21,22,23,24,25], the theoretical models that serve as a foundation for modulated photothermal techniques avoid the treatment of three-dimensional phenomena that occur at low frequencies [21, 22] or the radiative or thermoelastic effects that dominate at high frequencies in pyroelectric and photoacoustic techniques, respectively [23,24,25], without rigorous justification of the one-dimensionality validity.

It is therefore necessary to develop suitable experimental criteria that allow the selection of a reliable data set for an analysis that satisfies both the specific theoretical assumptions and the need for applicable boundary conditions. This is especially important when the modulation frequency is used as a variable because one must also deal with the instrumental response of the system, commonly called the transfer function.

The thermal diffusivity for solid samples and the thermal effusivity of liquids are two parameters determined with experimental setups that use modulation frequency as the control variable. On the other hand, the thermal diffusivity and the optical absorption coefficient for liquids are measured in a very simple manner using the thickness of the sample as a variable. This article describes some of the various photothermal methodologies reported for quantification of thermal diffusivity, effusivity, and optical absorption coefficient, emphasizing measurement limitations arising from ignoring validity conditions both experimental and theoretical. In addition, we also emphasize the suitability of using self-normalized photothermal techniques when the control variable is the modulation frequency and the analysis is performed on the photothermal phase, for which there are experimental validation criteria.

2 Description of Experimental Systems of Photothermal Thermophysics

2.1 Measurements of Thermal Diffusivity of Liquids and Solids Using Sample Thickness and Frequency Scans

Thermal diffusivity, effusivity, and optical absorption coefficient are usually measured with photothermal techniques using modulated radiation sources such as lasers. To emphasize the simplifications of the theoretical models usually involved in photothermal techniques, and to address their experimental limitations, below we describe the most common photothermal methodologies used to measure these properties, highlighting their advantages and comparative disadvantages. Among the most popular photothermal methods used to measure the thermal diffusivity of solid samples are photoacoustic and pyroelectric techniques that use the modulation frequency as a control variable [26,27,28,29,30].

2.1.1 Thermal Lens Spectroscopy and Thermal-Wave Resonant Cavity Methods

There are various photothermal schemes to measure the thermal diffusivity of materials in the condensed phase; some of them, such as thermal lens spectroscopy (TLS) [31,32,33,34], actively involve the optical properties of the sample. In TLS, it is assumed that the sample absorbs radiation according to the Beer-Lambert law, which makes this technique suitable only for weakly absorbing substances (at low concentrations if they are mixtures). However, the lack of experimental criteria to verify this assumption requires a study of optical properties separately from the samples.

Another methodology with increasing use is the so-called thermal wave resonator cavity (TWRC) [35,36,37,38,39,40] in which the optical properties of the liquid sample do not play any role in the analysis. This difference is fundamental and establishes a qualitative advantage of TWRC over TLS for measuring thermal diffusivities of liquid samples regardless of their optical properties. Although TLS is limited to weakly absorbing samples, in practice, this important limitation is often ignored. Thus, measurements of the thermal diffusivity of liquid samples have been reported without taking into account the technique’s limitations in terms of optical properties. This omission gives rise to systematic errors, mainly when this technique is applied to strongly absorbing samples or samples with strong optical scattering properties, such as colloidal suspensions [33, 34]. These aspects will be briefly discussed below. To provide better support for these ideas, a brief description of the techniques is also provided.

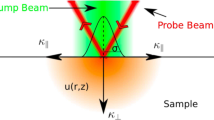
2.1.1.1 Brief Description of TLS

A general scheme of TLS is given in Fig. 1. Briefly, this technique consists of two light sources, one for excitation or heating (usually the 488-nm line of an Ar laser) and another for searching or probing (frequently the 632.8-nm beam of a He–Ne laser). The excitation beam is incident on a region located inside the liquid sample, which is contained in a glass or quartz cell. The region heated by the laser thus transfers thermal energy to its surrounding medium, giving rise to a gradient in the refractive index of the medium around it, changing the radius of the probe beam (thermal lensing effect). The temporal evolution in the luminous intensity of this light beam (i.e., the TLS signal), assuming a Gaussian test beam, is given by the expression [31, 32]

$$I(t)=I(0){\left[1-\frac{\theta }{2}{tan}^{-1}\left(\frac{2mV}{\left[{\left(1+2m\right)}^{2}+{V}^{2}\right]\frac{{t}_{c}}{2t}+1+2m+{V}^{2}}\right)\right]}^{2},$$

(1)

where the thermal diffusivity of the sample, $\alpha$, can be obtained from the fitting parameter ${t}_{c}=\frac{{\omega }_{e}^{2}}{4\alpha }$, being ${\omega }_{e}$ the radius of the Gaussian excitation beam. The other parameters involved in Eq. 1 are defined as

$$\theta =-\frac{{P}_{e}{A}_{e}{I}_{0}}{K{\lambda }_{p}}{\left(\frac{dn}{dt}\right)}_{P}, V=\frac{{Z}_{1}}{{Z}_{c}}, m={\left(\frac{{\omega }_{p}}{{\omega }_{e}}\right)}^{2},$$

where $\theta$ is the thermally induced phase shift of the probe beam after its passing through the sample, ${\omega }_{p}$ is the probe beam spot sizes at the sample, ${P}_{e}$ is the excitation laser beam power, ${A}_{e}$ is the optical absorption coefficient at the excitation beam wavelength, ${Z}_{c}$ is the confocal distance of the probe beam, ${Z}_{1}$ is the distance from the probe beam waist to the sample, ${I}_{0}$ is the sample thickness, $K$ is the thermal conductivity, ${\left(\frac{dn}{dt}\right)}_{P}$ is the temperature coefficient of the sample refractive index at the probe beam wavelength, and ${\lambda }_{p}$ is the probe beam wavelength.

Fig. 1

TLS experimental setup. M: Mirror

The theoretical expression for I(t) is obtained assuming that the excitation beam is absorbed according to the Beer-Lambert law. There are some experimental drawbacks when carrying out thermal diffusivity measurements with this technique. One of them is the implementation of the technique itself, which involves stabilized Gaussian lasers and a very special optical configuration. However, once these limitations have been overcome in the experimental system, the main limitation is that it involves the optical properties of the sample under study. This is a serious limitation for measuring thermal diffusivity as a function of concentration because, strictly speaking, a prior study is required to determine if the sample, at the given concentration, absorbs radiation according to the applicable model. Despite these limitations, thermal diffusivity values of samples such as vegetable oils [32] and colloidal suspensions of nanoparticles [33, 34] have been reported, with thermal diffusivity values that are discordant, relative to the values obtained through less demanding techniques: i.e., lower values for vegetable oils [12, 32] and values that increase anomalously with the concentration of colloidal suspensions [33, 34].

Considering that colloidal suspensions exhibit scattering properties in the visible spectrum much stronger than normal solutions (Tyndall effect), the unusual values ​​of thermal diffusivity that increase with particle concentration (measured with TLS) may be caused by the increasing scattering power of the suspensions, which generates an effect that is not taken into account in the theoretical treatment.

2.1.1.2 Brief Description of the TWRC

A suitable photothermal scheme to measure the thermal diffusivity of fluids is TWRC. This is simply a photopyroelectric technique in the transmission configuration that assumes exclusively surface absorption of radiation, in which the pyroelectric signal is obtained as a function of the thickness of the liquid sample ($L$) while maintaining a constant modulation frequency [35,36,37,38,39,40,41,42]. The surface absorption limit is guaranteed by placing a thin opaque sheet between the liquid sample and the radiation source. It should be noted that the theoretical scheme involved in TWRC is equally applicable if a photoacoustic transducer is used instead of the pyroelectric sensor [40,41,42]; comparable results are obtained using both experimental setups. Figure 2 shows the experimental setup in cross-section for a pyroelectric sensor.

Fig. 2

Schematic of a photopyroelectric spectroscopy system for measuring thermal diffusivity of liquids

The mathematical model involves the problem of heat diffusion through 3 layers immersed in semi-infinite media. Regardless of the transduction medium (i.e., a pyroelectric or a photoacoustic cell), if only the thickness of the liquid sample is taken into account as the only variable, and assuming a thermally thick limit for the liquid sample ($\left|\sigma L\right|>>1$), it can be shown that the photothermal signal can be written as [35,36,37]

$$\delta P\left(L\right)=H{e}^{-\sigma L},$$

(2)

where $H$ is a complex constant, with $\sigma =(1+i)\sqrt{\frac{\pi f}{\alpha }}$ as the complex thermal diffusion coefficient, where $\alpha$ is the thermal diffusivity of the liquid sample and $f$ is the fixed modulation frequency. It can then be observed from Eq. 2 that both the amplitude and phase of the photothermal signal have a linear behavior (the former on a semi-log scale). In both cases, the thermal diffusivity of the sample can be obtained through the slopes, $M$, of the corresponding linear fits through [35,36,37]

$$\alpha =\frac{\pi }{{M}^{2}}f$$

(3)

The linear behavior of the phase and the similarity of thermal diffusivity values ​​obtained using both amplitude and phase schemes are experimental criteria required to validate the values obtained.

It is also possible to obtain the thermal diffusivity of the liquid sample by directly measuring the so-called thermal wavelength, defined by the expression ${\lambda }_{TW}=2\sqrt{\frac{\pi \alpha }{f}}$ [37, 38].

It is important to emphasize the simplicity of the experimental configuration for this photothermal technique, which contrasts with that corresponding to TLS since the latter requires stabilized laser radiation sources with Gaussian profiles, also involving optical systems for optimal alignment. In the TWRC technique, however, any light source that can be modulated in some way can be used. Furthermore, since the signal is independent of the optical properties of the sample, this technique is appropriate for any fluid sample; the only condition is that its viscosity should allow the thickness of the liquid layer to be varied with sufficient precision and control. This independence of the optical properties of the sample makes the use of this technique very suitable for measuring the thermal diffusivity of liquid mixtures as a function of the concentration of one or some of their components, particularly colloidal suspensions [42].

2.1.2 Photoacoustic and Other Photothermal Methods Used with Solids

The photoacoustic technique has important advantages in terms of simplicity, because the sample directly seals one of the faces of the photoacoustic cell, avoiding the need for any other thermal coupling medium that would be needed for photopyroelectric techniques when used for thermophysical measurements of solids. Furthermore, the photoacoustic technique, like the photopyroelectric technique [9, 29, 30], has the flexibility to allow the easy implementation of two photothermal configurations: the frontal configuration and the transmission configuration, which are useful in the implementation of self-normalized photothermal techniques. Photothermal signal normalization schemes are required in these cases because the signal obtained is influenced by the response of the electronic devices involved in the experimental system, including the current source, lock-in amplifier, and the photothermal transducer (pyroelectric sensor or microphone). The collective signal of the associated electronics is called the transfer function and is practically impossible to model analytically. The normalized amplitude and phase can then be used for analysis following an appropriate theoretical model. Various experimental mechanisms have been proposed, including the use of a reference sample, which generally is a thin sheet of metal or other material with high thermal diffusivity and surface absorption [7].

A very suitable photothermal scheme that can eliminate the transfer function is a self-normalizing mechanism in which the photothermal signal in the frontal (back-propagation) mode is used to normalize the corresponding signal in the transmission configuration. If the experimental system is implemented properly, it is possible to obtain the signals required for the analytical self-normalization procedure with minimal modifications to the experimental system: for example, without removing the sample [29, 30]. In this manner, the influence of the transfer function can be removed leaving only the sample-related photothermal signal. This allows the corresponding theoretical predictions to be strictly satisfied assuming that there is pure thermal diffusion with no thermoelastic or thermoacoustic contributions, which can thus be used as theoretical basis to validate the experimental information obtained, leading to a reliable analysis.

Figure 3 shows a cross-section of a photoacoustic system where the experimental considerations described above can be addressed in a very simple way. In this experimental setup, it is possible to switch from the back-propagation (frontal) to the transmission configuration simply by moving the semiconductor laser beam position. A configuration using mirrors to direct the laser beam to obtain one configuration or the other can also be implemented [30].

Fig. 3

Cross-section of a photoacoustic system for implementation of transmission (a) and back-propagation (frontal) (b) configurations

When a sample is assumed to be absorbing optical radiation at the surface in the pure thermal diffusion regime, it has been shown that the self-normalized photoacoustic signal,$R\left(f\right)$, which is the quotient of photothermal signals in the transmission configuration between the photothermal signal in the frontal configuration, is given by [30]

$$R\left(f\right)=\left(1+{\gamma }_{gm}\right)\frac{{e}^{-{\sigma }_{m}l}}{\left[1+{\gamma }_{gm}{e}^{-{2\sigma }_{m}l}\right]},$$

(4)

where ${\gamma }_{gm}$ is the ratio of thermal effusivities of medium $g$ and sample $m$($g$ is the gas inside the cell),$l$ being the sample thickness. If some approximations are taken into account according to the thermal behavior of the sample, it can be shown that, in the thermally thin limit, that is $\left|{\sigma }_{m}l\right|\ll 1$, the phase tangent of this expression can be written as [30]

$${\text{tan}}\left(\Phi (f)\right)=-\left[\frac{\pi }{{\alpha }_{m}}{l}^{2}\right]f$$

(5)

In this limit, the thermal diffusivity of the sample can be obtained from the slope, $M$, of the linear least squares fit of the self-normalized phase, as a function of the modulation frequency, through Eq. 5 as [30]

$${\alpha }_{m}=\frac{\pi {l}^{2}}{M}$$

(6)

However, this approximation is only possible at achievable modulation frequencies only if sufficiently thin samples with large thermal diffusivity are available. In the region of low modulation frequencies, three-dimensional effects can be observed on the photothermal signals from a sample; avoiding them and selecting a frequency range where the one-dimensional approximation can be validated requires proper experimental criteria. These criteria consist of graphing the tangent of the self-normalized phase as a function of modulation frequency and drawing a straight line on the curve extending from the origin throughout the first set of data that follow the same trend, if this set exists, according to Eq. 5. The linear fit is then performed only on the thus selected experimental data set.

At the opposite extreme, that is, at large modulation frequencies, we have the thermally thick behavior, where analytically $\left|{\sigma }_{m}l\right|\gg 1$. In this case, the self-normalized phase exhibits a linear behavior with the square root of the modulation frequency, of the form [30]

$$\Phi \left(f\right)=-\left[\sqrt{\frac{\pi }{{\alpha }_{m}}}l\right]\sqrt{f}$$

(7)

It is then possible to obtain the thermal diffusivity in this thermal regime from the slope,$M$, of the least squares fit of the phase as a function of the square root of the modulation frequency, through the relationship [30]

$${\alpha }_{m}={\left(\frac{l}{M}\right)}^{2}\pi $$

(8)

It is very important to have a suitable experimental criterion to properly select experimental data since the signal in this thermal regime is superposed with the thermoelastic contribution of the sample. According to Eq. 7, the experimental criterion consists of drawing a straight line from the origin that overlaps the first linear data region of the self-normalized phase, plotted against the square root of the modulation frequency.

It is however possible to obtain the thermal diffusivity of the sample in an intermediate thermal regime, without resorting to any approximation other than the assumption of pure thermal diffusion, where the self-normalized relationship strictly applies, and ${\gamma }_{gm}\approx 1$. Indeed, it is possible to show that the tangent of the phase of Eq. 4 can be written as [20]

$${\text{tan}}\left(\Phi (f)\right)=-{\text{tanh}}(x){\text{tan}}(x),$$

(9)

where $x=\sqrt{\frac{\pi f}{{\alpha }_{m}}}l.$

Since the tangent function is a periodic function with period $\pi$ and discontinuities in $\frac{\pi }{2}, \frac{3\pi }{2},\dots$ as the modulation frequency increases, it is feasible to experimentally obtain these discontinuities in the plot of the tangent of the self-normalized phase as a function of the modulation frequency. This can only be feasible for self-normalized signals since the influence of the transfer function has been completely removed. The most accurate values ​​of thermal diffusivity are obtained when $x=\sqrt{\frac{\pi f}{{\alpha }_{m}}}l=\frac{\pi }{2}$, since the influence of thermoelastic behavior gradually dominates over pure thermal diffusion with increasing frequency. When the modulation frequency at which this first discontinuity occurs is obtained, the thermal diffusivity is then calculated from the expression [20]

$$\alpha =\frac{4{f}_{1}{l}^{2}}{\pi },$$

(10)

where ${f}_{1}$ is the modulation frequency where the first discontinuity is obtained graphically.

2.2 Measurement of Thermal Effusivity Using Frequency-Domain Photothermal Techniques

Thermal effusivity is a property of thermal exchange between materials. There are few photothermal methodologies for directly measuring this thermophysical property in liquids; one of them is the photoacoustic technique in the frontal configuration [13, 14]. The experimental setup is shown in Fig. 4.

Fig. 4

Cross-section of a photoacoustic spectroscopy system for measuring thermal effusivity of liquids

The radiation absorber consists of a thin sheet of highly optically absorbing material, which ensures thermally thin behavior in a wide range of modulation frequencies (up to a few kHz). The experimental setup involves using the photoacoustic signal from this material (air in the container), in a region of appropriate modulation frequencies, as a normalization signal; subsequently, the liquid sample is introduced into the container and the photoacoustic signal is taken at the same range of frequencies. It can be analytically demonstrated that, under the conditions described, the photoacoustic signal normalized in amplitude and phase (ratio of amplitudes and phase differences) is given by [14]

$$\left|R\left(f\right)\right|=\frac{1}{\sqrt{1+2\left(\frac{{b}_{sm}}{2x}\right)+2{\left(\frac{{b}_{sm}}{2x}\right)}^{2}}}$$

(11)

$$Tan\left(\Phi \left(f\right)\right)=\frac{\frac{{b}_{sm}}{2x}}{1+\frac{{b}_{sm}}{2x}},$$

(12)

where $x=\sqrt{\frac{\pi f}{{\alpha }_{m}}}l$ and ${b}_{sm}=\frac{{e}_{s}}{{e}_{m}}$, $l$ being the thickness of the light absorber and ${b}_{sm}$ the thermal effusivity ratio. Thermal effusivity is then obtained by best-fitting the normalized experimental data to the expressions described above (Eqs. 11 and 12); the thermal effusivity is obtained from the adjustment parameter ${P}_{s}=\frac{\sqrt{{\alpha }_{m}}}{2\sqrt{\pi }l}(\frac{{e}_{s}}{{e}_{m}})$, as long as the thermal properties corresponding to the reference sample are known. If this is not the case, a liquid reference sample of known thermal effusivity can be used. The thermal effusivity can then be obtained from the quotient [14]

$${e}_{s}=\frac{{P}_{S}}{{P}_{R}}{e}_{R},$$

(13)

where ${P}_{S}$ corresponds to the best-fit parameter with the liquid sample and ${P}_{R}$ is the parameter corresponding to the reference liquid sample, ${e}_{R}$ being the thermal effusivity of the reference sample (usually distilled water).

The experimental criteria for defining a range of modulation frequencies for a reliable analysis are as follows: At low frequencies, the normalized phase can be used for analysis; its graph must have upward concavity throughout the frequency range in the 1D model, which must be taken into account to eliminate data that have photoacoustic signal components influenced by three-dimensional phenomena. At high frequencies, the normalized amplitude can be used, but it must exhibit an asymptotic behavior tending to one. This latter criterion filters out data with a strong influence of thermoelastic components.

A variant of this experimental setup involves a photopyroelectric technique, which requires a thin pyroelectric sensor and sufficiently large thermal diffusivity [43, 44].

2.3 Frequency-Domain Photothermal Measurements of the Optical Absorption Coefficient of Liquid Samples

Photothermal techniques are generally used in the frequency domain for the determination of the optical absorption coefficient of liquid samples. Popular techniques are the optothermal window (OTW) [45, 46] and the photoacoustic technique [47]. The latter is just a variant of the photoacoustic experimental setup for thermal effusivity measurements (Fig. 4) but with an optical window instead of a light absorber. These two methodologies are equivalent in their theoretical analysis, differing only in replacing the photothermal transducer with a piezoelectric sensor used in OTW.

The experimental setup for the photoacoustic system to measure optical absorption coefficients using frequency as a control variable is shown in Fig. 5.

Fig. 5

Cross-section of a photoacoustic spectroscopy system for measuring the optical absorption coefficient of liquid samples

This theoretical scheme involves photothermal signals in the frequency domain in two different configurations; one of them with a highly absorbing reference sample, as a normalization signal, and the other with the sample under study. The normalized signal obtained theoretically in amplitude and phase is given, respectively, by [45, 47]

$$\left|R(f)\right|=\frac{\beta {\mu }_{s}}{\sqrt{{\left(\beta {\mu }_{s}+1\right)}^{2}+1}}$$

(14)

$$\Phi \left(f\right)=-{{\text{tan}}}^{-1}\left(\frac{1}{1+\beta {\mu }_{s}}\right),$$

(15)

where ${\mu }_{s}=\sqrt{\frac{{\alpha }_{s} }{\pi f}}$ is the thermal diffusion length and $\beta$ is the optical absorption coefficient. These equations are obtained assuming a semi-infinite medium, so there is no dependence on the thickness of the liquid sample, and also under the assumption that the optical window in the experimental system is thermally thin. The problem with this experimental setup is that it requires prior knowledge about the thermal diffusivity of the sample under study to obtain the value of the corresponding optical absorption coefficient. Furthermore, there is no certainty about which modulation frequency threshold should generate a valid scheme for a set of experimental data within the pure 1-D thermal diffusion range.

A recently introduced experimental setup to directly obtain the optical absorption coefficient of a liquid sample involves a variant of TWRC. The experimental setup involved, shown in cross-section in Fig. 6, is completely analogous to that described previously for thermal diffusivity measurements (Fig. 2), with the only difference that the opaque sheet is replaced by an optical window [20]. In the theoretical model, it is assumed that the liquid sample absorbs according to the Beer-Lambert absorption law. Under this assumption, and assuming the thickness of the liquid sample is a control variable and using the appropriate photothermal limits, it can be shown that the photothermal signal is given by [20]

$$\delta P\left(L\right)=C{e}^{-\beta L},$$

(16)

where $\beta$ is the optical absorption coefficient of the liquid sample and $C$ is a complex constant, independent of sample thickness and $\beta$. According to this equation there is a sample thickness range where photothermal phase is constant. Experimental photothermal amplitudes within this range can then be used for reliable analysis and optical absorption coefficient measurements by means of Eq. 16. This optical parameter is the slope of the best linear fit of this equation, as a function of the sample thickness, on a semi-log scale.

Fig. 6

Cross-section of a photopyroelectric spectroscopy system for direct measurement of the optical absorption coefficient of liquid samples

3 Reliable Experimental Results

Some results are presented below to illustrate some of the foregoing experimental considerations that must be taken into account for reliable analysis both when the photothermal signal is obtained as a function of the thickness of the sample, or the modulation frequency.

3.1 Measurements Using Sample Thickness Scans

Figure 7 shows photopyroelectric phase and amplitude signals, as a function of the liquid sample thickness, for distilled water. Similar thermal diffusivity measurements were carried out for two colloidal suspensions of SiO₂, in water, at two very different concentrations (column 1, Table 1). The photopyroelectric system shown in Fig. 2 was used [8]. It is worth noting the extraordinary linear behaviors of both amplitude (on a semi-log scale) and phase, and the great similarity in the thermal diffusivity values obtained in both cases. This is, as described above, a fundamental experimental criterion for choosing a range of sample thicknesses suitable for quantitative analysis.

Fig. 7

Photopyroelectric phase and amplitude signals from distilled water, as a function of the thickness of the liquid sample; for measuring thermal diffusivity. The measured values of diffusivity were $0.001458 \, {cm}^{2} \cdot s^{-1}$ and $0.001442 \, {cm}^{2} \cdot s^{-1}$ from the analysis of phase and amplitude, respectively

Table 1 Thermal diffusivity values obtained for distilled water and water-colloidal suspensions of SiO₂ (80 nm size), using pyroelectric technique. ${\alpha }_{Ph} ({\alpha }_{Amp})$ refers to the thermal diffusivity obtained from the analysis of the pyroelectric phase (pyroelectric amplitude)

Thermal diffusivity values for the three samples are summarized in Table 1, columns 2 (for pyroelectric phase) and 3 (for pyroelectric amplitude). It is worth noting that there is a slight increase in thermal diffusivity of the colloidal suspensions with the increase in concentration of SiO₂ nanoparticles. This modest increase is in contrast to similar reported values, measured using the thermal lens technique [33, 34]. Indeed, the values reported for thermal diffusivity measured using the latter photothermal methodology become very large as the concentration increases. Since the colloidal suspensions under study experience strong optical scattering properties at the wavelengths used in thermal lensing, it is evident that the reported large thermal diffusivity increases are a result of the increase in optical scattering increase with increased particle concentration.

Figures 8 and 9 show the photopyroelectric results of measuring the optical absorption coefficients of two pure liquids: glycerol and distilled water, at 1550 nm and 1310 nm, respectively. Measurements were performed using a photopyroelectric system like the one shown in Fig. 6 [8].

Fig. 8

Photopyroelectric phase and amplitude signal as a function of the thickness of a liquid glycerol sample used for measuring its optical absorption coefficient at 1550 nm. The continuous line is the best linear fit used to measure the sample´s optical absorption coefficient

Fig. 9

Photopyroelectric phase and amplitude signal as a function of the thickness of a distilled water sample used for measuring its optical absorption coefficient at 1310 nm. The continuous line is the best linear fit used to measure the sample´s optical absorption coefficient

As described above, the existence of a range of liquid sample thicknesses in these measurement results where the phase is approximately constant is clear. Within this range, it is possible to perform a reliable analysis to obtain the optical absorption coefficient. The experimental criterion of constant phase is essential because, as Figs. 8 and (especially) 9 show, there are other (narrower) regions of linear photothermal amplitude behavior; however, performing linear fits within these other regions without an associated phase constancy would result in completely different values from those obtained under the aforementioned phase behavior condition, thereby foregoing measurement reliability (although not necessarily precision).

3.2 Measurements Using Modulation Frequency Scans

As mentioned above, using modulation frequency scans there are two widely used photothermal techniques for measuring thermal effusivity and diffusivity of liquid and solid samples, respectively. To emphasize the need of taking into account proper experimental criteria that allow reliable data analysis, some experimental results are described below which also address some of the limitations described before.

3.2.1 Normalized Photoacoustic Signals for Measuring the Thermal Effusivity of Liquids

Figure 10 shows amplitude- and phase-normalized photoacoustic signals for the determination of the thermal effusivity of glycerol. The experimental system outlined in Fig. 4 [14] was used for this purpose. This figure shows that the normalized amplitude has a behavior that is in keeping with the theoretical predictions within the upper range of modulation frequencies. Instead of showing the monotonically decreasing behavior predicted by theoretical analysis and by computer simulations [14], the normalized phase exhibits increasing values at low frequencies (between 1 and 25 Hz, approximately). The increasing values obtained at low frequencies can be attributed to three-dimensional effects that result from the combination of the high thermal diffusivity of the laser radiation absorber and the small diameter of the source. A phase criterion that decreases monotonically at low frequencies can thus be used to filter out experimental data with 3D components from the amplitude analysis. A consistency criterion to be taken into account would be the similarity of the thermal effusivity values obtained from both the amplitude and phase analysis, as was established for the case of thermal diffusivity measurements using TWRC.

Fig. 10

Photoacoustic normalized amplitude and phase signals as a function of modulation frequency for measuring the thermal effusivity of glycerol. Continuous lines are the best fits to Eqs. 11 and 12, respectively

3.2.2 Self-Normalized Photoacoustic Signals for Measuring Thermal Diffusivity of Solids

Figures 11, 12, and 13 show the behavior of the self-normalized phase and its tangent, in different ranges of modulation frequency, for three materials with very different thermal diffusivities (PVDF, paper, and a metal) that illustrate the approaches described above for the case of thermal diffusivity measurements with the self-normalized photoacoustic technique.

Fig. 11

Behavior of the phase and its tangent for a PVDF sample as functions of modulation frequency and its square root, respectively. The sample was metalized on both sides to satisfy the required optical opacity limit; (a) phase tangent at low frequencies; (b) phase tangent across the entire frequency range; (c) phase at high modulation frequencies

Fig. 12

Behavior of the phase and its tangent for a paper sample as functions of modulation frequency and its square root, respectively. The sample was black painted on both sides to satisfy the required optical opacity limit; (a) phase tangent at low frequencies; (b) phase tangent across the entire frequency range; (c) phase at high modulation frequencies

Fig. 13

Behavior of the phase and its tangent for a steel sample as functions of modulation frequency and its square root, respectively. (a) phase tangent at low frequencies; (b) phase tangent across the entire frequency range; (c) phase at high modulation frequencies

The graphs corresponding to PVDF are shown in Fig. 11. Figure 11a shows the behavior of the phase tangent at low frequencies. The absence of a range of modulation frequencies that satisfy the experimental criterion described in Eq. 5 is evident here because, despite being a very thin sample, it has very low thermal diffusivity. It is useless here to experiment with frequencies below 1 Hz since the three-dimensional effects of the signal would make the analysis completely imprecise.

Figure 11b shows the phase tangent behavior in the entire frequency range under analysis. As predicted by the theoretical model, Eqs. 9 and 10, this graph presents a discontinuity at 16.5 Hz. The thermal diffusivity value of the sample can be obtained through the relationship already established, Eq. 10, which yielded α = 0.00057 cm²·s⁻¹. Finally, Fig. 11c presents the behavior of the phase as a function of the square root of the modulation frequency that allows reliable analysis in the region of the thermally thick behavior of the sample. The dotted line, drawn according to the analytical behavior described by Eq. 7, allows the selection of a subset of experimental data for obtaining the thermal diffusivity value of the sample in this range according to Eq. 8 which yielded the value α = 0.00056 cm²·s⁻¹. The agreement with the value obtained from the tangent discontinuity is remarkable and an excellent example of the necessity for satisfying strict measurement reliability criteria. It can be inferred that the precision in thermal diffusivity measurements through phase analysis with these self-normalized photoacoustic techniques can reach at least two significant figures.

Figure 12 shows similar phase and phase tangent results from for a bond paper sample, which has thermal diffusivity an order of magnitude greater than that of PVDF.

Unlike PVDF, in this case, following the criterion established in relation to Eq. 5, it was possible to select a data subset for the analysis at low modulation frequencies, as shown in Fig. 12a. As expected, a modulation frequency discontinuity in the phase tangent is shown in Fig. 12b. Finally, Fig. 14c shows the behavior of the phase as a function of the square root of the modulation frequency for high frequencies. According to Eq. 7, it is in this high-frequency range where it is possible to carry out a reliable analysis and obtain the sample thermal diffusivity by means of Eq. 8. This criterion is relevant here because, at high frequencies, the pure thermal diffusion signal becomes very weak and other photoacoustic signal generation mechanisms become relevant; for example, the thermoelastic effects, as evidenced in Fig. 12c by the deviation of the data from the dotted line. If this criterion did not exist, an inexperienced analyst would carry out the analysis in the thermoelastic range or in a range where the thermally thick condition is not satisfied: For instance, Figs. 11c and 12c exhibit regions of linear behavior that deviate from the criterion described for the thermally thick phase which can result in completely erroneous values for a given sample or in the loss of measurement accuracy. As in the case of the PVDF measurements, the agreement between the three thermal diffusivity values obtained from Fig. 12a–c (0.0019 cm²·s⁻¹, 0.0021 cm²·s⁻¹, and 0.0022 cm²·s⁻¹) is to be emphasized as an indicator and of the consistency expected under rigorous measurement reliability procedures.

Fig. 14

PVDF sample self-normalized amplitude as a function of the square root of the modulation frequency, showing linear fits over two modulation frequency sub-ranges

Finally, Fig. 13 shows the results for the phase and phase tangent from a steel sample with relatively large thermal diffusivity. Figure 13a shows that three-dimensional effects appear at very low frequencies (the experimental points outside the straight reference line), resulting from the combination of the high thermal diffusivity of the sample and the small size of the impinging laser beam. Although this could be avoided by expanding the radius of the radiation beam, the dimensions of the cell imposed a practical limit for this purpose, so the criterion established for low frequencies was essential to avoid performing analysis outside the one-dimensional regime.

The thermal diffusivity values obtained using these three analytical schemes (0.063 cm²·s⁻¹, 0.077 cm²·s⁻¹, and 0.071 cm²·s⁻¹, Fig. 13) are in good agreement, especially for the latter two. The difference with the first value could be attributed to remanent three-dimensional effects which, as explained, are difficult to eliminate and in this case prevented selecting a better set of experimental data for the analysis.

In summary, it can be concluded that with these self-normalized photoacoustic methods, it is possible to obtain the thermal diffusivity value of any material, as long as the surface opacity condition is established so as to satisfy the validity of the applicable theoretical model. The experimental criteria at low and high frequencies (thermally thin and thick limits) must be strictly followed to obtain reliable results.

Finally, it is important to point out a common practice in measurement procedures for the thermal diffusivity of materials using photoacoustic techniques with other experimental setups or normalization mechanisms. In these cases, the amplitude of the photoacoustic signal is used to perform the analysis and to obtain the thermal diffusivity value. In the self-normalized scheme described here, the amplitude of the photoacoustic signal decreases exponentially with the square root of the modulation frequency; however, the lack of proper experimental criteria for the selection of an adequate dataset may result in inaccurate analysis. Figures 14, 15, and 16 show the analysis corresponding to the self-normalized amplitude for the three photoacoustic signals obtained for PDVF, bond paper, and metal. For PVDF, the analysis was carried out in two frequency sub-ranges, as illustrated in Fig. 14a and b. In the first case, the same frequency range was used in which the phase analysis was performed (Fig. 11c). There is a large discrepancy between the values of thermal diffusivity obtained from amplitude analyses in these two modulation frequency ranges, as can be seen in Fig. 14a and b. Furthermore, they differ greatly (by one order of magnitude) from the values obtained from the previous phase analysis.

Fig. 15

Paper sample self-normalized amplitude, as a function of the square root of modulation frequency, showing linear fits over three modulation frequency sub-ranges

Fig. 16

Steel sample self-normalized amplitude, as a function of the square root of modulation frequency, showing linear fits over two modulation frequency sub-ranges

The analysis of the self-normalized amplitude for the paper sample shows similar discrepancies in thermal diffusivity values with phase analysis as was in the PVDF case. In this case, it was possible to perform the analysis of self-normalized amplitude in three modulation frequency ranges. The first of these ranges included (Fig. 15a) the amplitude corresponding to the phase used for the analysis in Fig. 12c. The last range was that in which the thermoelastic contribution dominates (Fig. 15c) and the amplitude also exhibits a linear behavior and can be used for analysis, in the absence of any other experimental criterion.

The thermal diffusivity value obtained from the analysis of the amplitude (Fig. 15a) in the range of the modulation frequencies used for the phase is higher than the value obtained from the phase (Fig. 12c). The closest value of thermal diffusivity to the ones obtained from the phase was obtained at a wider range of modulation frequencies that includes the one used for the phase analysis (Fig. 12b) but avoids the thermoelastic contribution. Finally, it can be observed that the largest thermal diffusivity value is obtained when the analysis is carried out in the region where the thermoelastic photoacoustic generation mechanism dominates. This is because the weak photoacoustic amplitude from pure heat diffusion models is affected by thermoelastic contributions which tend to yield erroneously increased diffusivity values, resulting from a lower slope. Again, as in the PVDF case, this is a pitfall of measuring the thermal diffusivity values of paper over random frequency ranges without an amplitude criterion for reliable analysis.

Finally, Fig. 16 shows the results of thermal diffusivity measurement for the steel sample obtained from the self-normalized amplitude. The analysis was carried out in two ranges of modulation frequencies, one of which (Fig. 16a) included the range used for the phase analysis, Fig. 13c. In this case, no influence of the thermoelastic generation mechanism was observed in the frequency range under analysis; however, there were higher and inconsistent thermal diffusivity values than those obtained with the phase analysis.

The results shown in Figs. 14, 15, and 16 illustrate the complexity of using the photoacoustic amplitude for reliable quantitative analysis of the thermal diffusivity of materials and lead to the conclusion that phase measurements must be used for maximum reliability and only under well-established signal trend and behavior criteria.

4 Conclusions

A broad review was presented of some of the most common photothermal methodologies used to determine thermophysical and optical properties of solid and fluid materials in their various states. A critical analysis of the use and abuse of some of these methodologies was provided, especially when the samples under study do not satisfy strict theoretical requirements. A particularly illustrative case is thermal lens spectroscopy, which has recently been applied to measure the thermal diffusivity of colloidal suspensions. Finally, we emphasized the suitability of using photothermal methods for which theoretical criteria are available for the selection of experimental data subsets suitable for reliable analysis, thereby optimizing the capabilities of photothermal techniques in terms of precision and accuracy. This is a critical aspect to be considered especially if the measured properties will be used for comparison purposes with other materials or as functions of concentration of some components, as is the case of mixtures or colloids, such as for SiO₂ colloidal suspensions described in this work.