Intermolecular Potential Model Hamiltonians for Gas–Liquid Coexistence

Abstract

A fundamental, hitherto unanswered, question in liquid-state physics is: "What is the minimum requirement of a molecular interaction Hamiltonian for the existence of a stable liquid that can coexist with its vapor phase?". It has been the subject of speculation in the thermophysical property literature since Hagen et al. (Nature 1993) reported 'no liquid phase' in a computer site–site pairwise model Hamiltonian for C₆₀. In more recent reports we have found that for simple fluids, with spherical, pairwise model Hamiltonians there exists a supercritical mesophase colloidal description of gas–liquid coexistence with a T-p density-surface critical divide being defined thermodynamically by the intersection of percolation loci. We have also reported compelling experimental evidence for the existence of a pre-freezing percolation transition whence hetero-phase fluctuations of micro-crystallites percolate equilibrium liquid state phase volume. These percolation phenomena can explain the apparent disappearance of the boiling line at finite range of attraction. As the attractive range shortens, the interception of the percolation line that define the critical-line between two-phase coexistence, and one-phase supercritical mesophase, shifts to lower T. It then intercepts with the pre-freezing percolation line, to trigger a triple point of gas, liquid and solid states, all at the same T,p-state hence also the same chemical potential. Consequently, all model pairwise classical molecular Hamiltonians with a finite size, plus attractive term, however short-range, or however weak, exhibit a triple point with a liquid–vapor coexisting state at a sufficient low temperature.

1 Introduction

Experiments on simple computer models are a valuable tool for research using the technique of Hamiltonian surgery. As the name implies, it is not what we put into the model that creates valuable scientific knowledge with new insight, it is what we leave out. The first pioneering molecular dynamics (MD) experiments on rigid spheres [1], simply discarded all attractive terms, resulting in the discovery that hard repulsive molecular Hamiltonians have coexisting fluid and crystal phases, at the same temperature and pressure, but no liquid state. If, on the other hand, we consider simple model spheres with no repulsive term, just attraction on overlap, so the spheres interpenetrate, one obtains gas and liquid phases, but no crystal state [2]. The penetrable cohesive sphere model (PCS) is the simplest molecular Hamiltonian to exhibit critical phenomena and gas–liquid coexistence. Its detailed study with more circumspection, has confirmed an alternative description of criticality where percolation lines intersect at T_c, and a supercritical mesophase of gas and liquid exists above the critical-line [3]. This begs the question, what is the definition of a 'liquid '?

Experimental studies on colloid-polymer mixtures [4] first suggested that an attractive potential of sufficiently long range is necessary for the existence of the liquid state. This phenomenon was first reported by Gast et. al. in connection with phase transitions in mixed suspensions of colloidal particles and non-adsorbing polymer molecules. In such colloid–polymer mixtures, the range and the depth of the attractive interaction can be adjusted by the size and concentration of the added polymer molecules. Experiments on model colloid-polymer mixtures have provided conclusive evidence that the topology of this phase diagram is indeed determined by the ratio of the radius of gyration of the polymer molecules to the radius of the colloidal particles [4, 5].

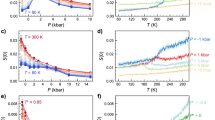
Computer modelling studies of the spherical macromolecule, C₆₀, have also suggested that below a critical range of the attractive interaction the gas–liquid transition of a given substance becomes metastable with respect to the fluid–solid transition. Girifalco [6], using computer simulations in which the C₆₀ molecules are represented by atomic spheres interacting via a multiparameter site–site Lennard–Jones potential could only study gas and crystal states. Hagen et al.[7] mapped out a phase diagram of Girifalco-C₆₀ shown in Figure l. They concluded that C₆₀ has no stable liquid phase. Cheng et al. [8], however, also with the same computer model potential, used an integral equation approach combined with MD simulations created a phase diagram of Girifalco-C₆₀ that predicted a stable liquid, albeit in a very narrow range of temperatures and densities. Subsequent studies are inconclusive and have not definitely settled the issue [9,10,11,12]. Altogether, these investigations suggest that C₆₀ could be a borderline case that may or may not have a stable liquid phase.

There are some shortcomings of Fig. 1 [7]. Not least, is the fact that neither of the computer simulation methods, used to obtain the continuous coexistence line, spanning the entire density range, are sufficiently accurate for purpose. There are inherent limitations give rise to large error bars. The computer model excludes alternative crystal structures. "Sublimation", moreover, is incorrect terminology. A gas to solid reversible transition boundary is a "deposition line". The original sinusoidal line in Fig. 1 of reference [7] contains only one data point between the densities of zero and 0.8; that is quite a stretch of imagination. The Gibbs ensemble Monte Carlo (GEMC) method is incapable of detecting crystalline states within the liquid state and completely misses any presence of alternative stable crystal structures.

Fig. 1

reproduced from computer model data from reference [7], based upon the hypotheses (i) that a critical point exists and (ii) that gas–liquid metastable critical point and coexistence envelope exist within a 2-phase fluid–solid region separated from supercritical fluid by a "sublimation line" drawn through the seven data points with the original error bounds as illustrated

"C₆₀" phase diagram schematically

Nonetheless, this model prediction for C₆₀ has led to further systematic studies, of similar models, both theoretical and computational, to establish the relationship between the range of the attractive part of the intermolecular potential and the existence of the liquid phase [8, 9]. These investigations generally appeared to confirm that below a critical range of the attraction, the liquid state becomes metastable. The general conclusion is that an attractive potential of sufficiently long range is necessary for the existence of liquid phase. Early estimates for the range-criteria of the attractions where the liquid state disappears, however, differed significantly[10,11,12,13].

The first systematic molecular simulation investigation of the necessary and sufficient condition for a given potential to give rise to a thermodynamically stable liquid is reported in the PhD Thesis of Tukur [13]. Two potential functions; Mie 12-m, with variable attractive exponent (m) from 6–10, and square-well (SW) potentials with variable width (λ) were specifically investigated using GEMC and Gibbs–Duhem Integration (GDI) methods. Tukur found the range of temperatures for which the liquid is stable shrinks as the interaction range decreases. For sufficiently short interaction ranges, both 12-m and SW fluids, revealed no stable pure liquid phase. For the Mie n-m potentials (where n is fixed at 12, and m varies), stable liquid phase disappears at m > 8. For the SW fluid. A critical range of λ/σ ~ 1.24 was obtained below which there was no liquid.

For the case of solutions of globular proteins, it was already well-known experimentally that a liquid–liquid phase separation occurs below the fluid–solid transition [14]. This liquid–liquid phase separation, however, is metastable. Curtis and Lue explained the occurrence of this metastable liquid–liquid phase separation. They argued that is because the range of attraction is small compared to the size of the protein molecule, i.e., a sticky-sphere model for globular proteins would predict no liquid state, citing the earlier results for C₆₀ [7] with a phase diagram like Fig. 1[14].

Another PhD Thesis by Magnier [15] (Chapter 8) reports extensive studies on the gas–liquid coexistence properties of SW fluids with up to 32,000 particles. These simulations, with unprecedented accuracy, confirmed the previously reported discovery of a supercritical mesophase and the absence of a critical point singularity on Gibbs p–T density-surface. Especially noteworthy in the present context is the determination from MD studies of quasi-sticky SW spheres with range λ/σ = 1.005 with a limiting high-precision critical temperature determination T_c (λ = σ) = 0.2007 ± 0.0002. This important result [15, p 176 Table 8.1] is the huge critical divide between maximum coexisting gas density (ρσ³ = 0.26) and minimum coexisting liquid density (0.47) at T_c. The critical divide widens as the range shortens. Unfortunately, Magnier did not investigate the crystal structures but, we will see below, that this gas–liquid limit of coexistence for sticky spheres (λ /σ) is a triple point.

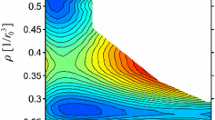
The critical divide, and supercritical mesophase, were discovered originally from computer experiments on model SW fluids, that can be understood as a perturbation of the hard-sphere (HS) fluid [16]. Although the HS fluid has a well-defined mesophase, defined by percolation transitions of excluded and accessible volume, it cannot account for gas–liquid condensation and 2-phase coexistence without an attractive potential term. The SW-model molecular Hamiltonian is defined by adding a constant energy of attraction (ε) of finite width (λ) to a HS (diameter σ) pair potential. The range must be finite, and not infinite, as implicit in the attractive term of van der Waals equation and similar mean-field theories, to give a fluid that is compliant with a thermodynamic stability over the whole range of p–T existence. It is these computer experiments that resulted in the discovery of the critical-line divide at Tc, and a supercritical mesophase bounded by percolation loci [16]. The percolation transitions are third order and defined phenomenologically by the slopes of the rigidity (dp/dρ)_T, -ve for gas, zero for mesophase, + ve for liquid [17]. This thermodynamic description of critical and supercritical states is entirely consistent with the experimental thermodynamic coexistence properties, and phase diagram, e.g., of argon, reproduced in Fig. 2 [16,17,18,19], and also of computer model Lennard–Jones fluids [20].

Fig. 2

Phase diagram of argon constructed from experimental isotherms reported in reference [17] showing the supercritical and prefreezing percolation lines that define the supercritical and prefreezing mesophases, respectively: P is the number of coexisting phases as defined by Gibbs phase rule

Comparing Fig. 2 (argon) with Fig. 1 (C₆₀) the first question is "what happens to the length of the critical dividing line (shown in Fig. 2) when the range of the attraction is reduced". When the original SW MD data in references [13,14,15,16] are re-examined with more circumspection, the flat top of the coexistence envelope becomes wider as the critical temperature (T_c) decreases, as critical temperature (T_c) and triple point (T_t) become closer, T_c T_t.

There is another relevant change, however: as the attractive range becomes shorter, the close-packed structures (e.g., FCC) become less stable relative to the metastable body-centred tetragonal (BCT) structures (which includes BCC as a special case). Figure 2 shows the phase diagram for argon drawn from equilibrium experimental equation of state isotherms that includes both the supercritical mesophase, and the pre-freezing BCT-liquid mesophase.

In the following sections we will consider the combined effect of reducing the range of attraction on the percolation lines that define these mesophases, and particularly what happens at T_c (defined by the intersection of two percolation transitions of gas in liquid (PA) and liquid in gas (PB) [16, 17], intersects with the pre-freezing percolation transition at the same pressure. First, however, we report in this context MD experiments on the simplest imaginable model molecular Hamiltonian to exhibit liquid + crystal (no gas), and gas + liquid (no crystal), given the broader definition of "liquid phase" seen in Fig. 2.

2 Computer Experiments on Simple Model Hamiltonians

2.1 Hamiltonian Surgery

A rigorous expression for the total Hamiltonian is a sum of many-body potential terms, each for a cluster of n atoms which can be defined for the total internal energy of a dynamic configuration of N atoms at a point in time is:

$$ {\text{U}}_{{({\text{N}})}} = { 1/2 }\sum_{{\text{N}}} {\text{m}}{\mathbf{v}}^{{2}} + \sum_{{{\text{i}} < {\text{j}}}} {{\phi}}_{{{\text{ij}}}} + \, \sum_{{{\text{i}} < {\text{j}} < {\text{k}}}} {{\phi}}_{{{\text{ijk}}}} + \, \sum_{{{\text{i}} < {\text{j}} < {\text{k}} < {\text{l}}}} {{\phi}}_{{{\text{ijkl}}}} \ldots . + \, \left( {{1}/{\text{n}}!} \right)\sum_{{\text{n}}} {{\phi}}_{{\text{n}}} $$

(1)

Since the earliest attempts at a theory of liquids going back 150 years to van der Waals, all the non-additive terms, n > 2, have been discarded although very little is presently known about the convergence and higher-order terms in Eq. (1). The evidence suggests, however, that two-body pair potential Hamiltonians will represent all the physical properties and phase behaviour shown in Fig. 2, for example, but this hypothesis remains to be generally verified.

For atomic liquids like argon the most common pair potential model is an inverse repulsion of short-range plus an attractive term of longer range such as the Lennard–Jones potential

$$ \phi_{{{\text{ij}}}} * \, = \left( {{\text{r}}*} \right)^{{ - {12}}} - { 2 }\left( {{\text{r}}*} \right)^{{ - {6}}} $$

(2)

where the asterisks denote reduced energy relative to the minimum at ϕ* = ϕ/ε = − 1 and r/r₀ =  + 1. It is well-known that Lennard–Jones fluids can reproduce thermodynamics properties of liquid argon with suitably fitted parameters of

ε and r₀ [19]. Extensive computer experiments of the Lennard–Jones 12–6 model fluid [20], moreover, have shown that it exhibits a critical dividing line and a supercritical mesophase.

2.2 Soft-Sphere Models

What happens to the gas–liquid coexistence states in Fig. 1 if we discard the attractive forces altogether? Then, for L-J fluids, we are simply left with

$$ \phi_{{{\text{ij}}}} * \, = \left( {{\text{r}}*} \right)^{{ - {12}}} $$

(3)

To what extent can this minimalist repulsive soft-sphere (SS) model represent the equations-of-state and phase behaviour shown for argon in Fig. 2? The short answer is not at all, the soft-sphere model misses the physics of everything we see in Fig. 2 below the Boyle temperature. The soft-sphere fluid equation of state is everywhere pV/(NkT) > 1, the known lower virial coefficients are all positive, so there is no Boyle temperature, no supercritical mesophase and percolation loci PB and PA, no gas liquid coexistence, and no triple point.

What is noteworthy, however, is that the high temperature supercritical fluid that coexists with the FCC crystal phase of argon (Fig. 2) is the same phase as the liquid, with only the liquid–crystal prefreezing and coexistence bounding it at high density. Above the Boyle temperature, moreover this single phase extends to low-density, i.e., all the way to the ideal gas. The soft-sphere model fluid is more akin to a "liquid phase"; it cannot represent any gaseous or vapor states below the Boyle temperature.

The SS model defined by Eq. (3) has been extensively investigated not only because it represents the high temperature limit of the L-J fluid (ε/kT 0), but also because it has remarkable scaling properties that explain a wide range of liquid and crystalline state properties. A more detailed summary of the soft-sphere scaling properties can be found in Chapter 2 of the PhD Thesis of Cape [21]. A single density-temperature variable defines a reduced thermodynamic state; for the present comparison with L-J fluids, we will retain the same definitions of reduced state variables.

T* = kT/ε:p* = pr₀³/ε:ρ* = Nr₀³/V (N/V is number density).

ρ* scales with T* so a single variable ρ*T* ^(−1/4) defines reduced thermodynamic density state and the fluid to crystal freezing transition scaling law is reported to be [21]

p_f* = 22.6 T_f*^(5/4). and the crystal melting density and fluid freezing densities are, respectively,

ρ_m* = 1.15 T*^(−1/4) and ρ_f* = 1.20 T*^(−1/4).

We have revisited the MD calculation of the reduced rigidity changes slope in the vicinity of the freezing transition. From p14 diagram of reference [13]we locate the BCT prefreezing percolation point, that scales to the lines in the phase diagram (Fig. 3). This is not very sharply defined by the MD data, but, guided by the similar change at prefreezing percolation (PF) from linear to exponential form for argon [17], for the percolation line PF for constant p* we obtain:

Fig. 3

Phase diagram of a repulsive two-body spherical potential: the inverse 12th power soft-sphere model in reduced pressure–temperature plane. There is no 2-phase gas–liquid coexistence or boiling line: the dashed lines are the estimate of a pre-freezing percolation transition from the thermodynamic properties reported in the PhD Thesis of Cape [13] page 14: reduced temperatures (T*) and pressures (p*) are defined in the text

τ_pf*/T_m* 1.28 and ρ_pf* = 1.28 T*^(−1/4).

The prefreezing percolation lines are also shown in the p*(T*) phase diagram (Fig. 3).

A repulsive short-range term in the model Hamiltonian is an essential ingredient for the existence of a crystalline state in coexistence with a fluid. It is of course well-known that purely repulsive models have just one fluid phase with no gas–liquid coexistence. There is now a problem with definitions, since liquid states can exist above T_c. What is the definition of gas and liquid states within supercritical fluids?

2.3 Boyle Temperatures and Gaseous States

The L-J potential is known to have a phase diagram that is quantitatively similar to argon in Fig. 2. Computer experiments on percolation loci have shown that the LJ fluid has a critical divide and a supercritical mesophase like argon [20]. We see that the Boyle temperature (defined by b₂(T) = 0, and p/ρkT = 1 as r 0), marks the onset of a gas phase as distinct from a liquid at low T,p. Another way to interpret the division of the supercritical region in Fig. 2 is that for all temperatures below T_B the low-density limit state belongs to a re-defined gaseous state. Along any isotherm there is a supercritical mesophase combination of states, and for all temperatures above the percolation line PA, all supercritical and subcritical states belong to the same phase, which we will now redefine as subcritical or supercritical quasi-'liquid' (we consider nomenclature problems in conclusion section).

Thus, we can now investigate the Boyle temperature, that does not exist for purely repulsive spheres, but is a prerequisite for gas–liquid coexistence. How does the Boyle temperature (defined by p/ρkT_B 1 as ρ 0) manifest itself as we introduce a non-zero attractive term to the soft-sphere pair potential as a function of range? Or, alternatively, we can ask what becomes of the Boyle temperature as we gradually reduce the attractive range of the pair potential from full L-J attraction, to zero? Consider next what happens to the purely repulsive n = 12 soft-sphere fluid if we add an attractive term gradually. Where does the onset of a liquid state begin, with reference to the equations-of-state in Figs. 3a and b, respectively.

The Boyle temperature is defined as that at which the 2^nd virial coefficient in the virial equation of state expansion of the pressure changes from positive to negative

$$ {\text{p }} = {\text{ Nk}}_{{\text{B}}} {\text{T}}\rho [{ 1 } + {\text{ b}}_{{2}} \left( {\text{T}} \right)\rho + {\text{b}}_{{3}} \left( {\text{T}} \right)\rho^{{2}} + \ldots ..{\text{ b}}_{{\text{n}}} \left( {\text{T}} \right)\rho^{{\left( {{\text{n}} - {1}} \right)}} \ldots .) $$

(4)

$$ {\text{b}}_{{2}} = - {2}\pi \smallint [{\text{exp}}\{ - \phi \left( {\text{r}} \right)/\left( {{\text{kT}}} \right)\} \, {-}{ 1}]{\text{ r}}^{{2}} {\text{dr}} $$

(5)

The first question we ask is what happens to the Boyle temperature when we apply Hamiltonian surgery by gradually reducing the range of attraction of the Lennard–Jones pair potential, either,

• (i) by cutting off the tail of the pair potential so that ϕ_ij = 0 for all r_ij > λ, or

• (ii) by narrowing the pair potential by increasing the attractive exponent (m = 6 for L-J) to almost 12 – the sticky-sphere limit.

Boyle temperatures are simply obtained by evaluating the integrals in Eq. (6), and the results, shown in Figs. 4a and 4b, are quite telling.

Fig. 4

(a) Reduced Boyle temperature T_B* = (k_BT_B/ε) of the truncated Lennard–Jones 12–6 model fluids with cut-off range λ/σ: (b) Boyle temperatures of the 12-m model fluid for values of the attractive exponent m between m = 6 (L-J fluid) and 12 > m > 11.9 (sticky spheres)

From Fig. 4a we see that only when the range of the attraction for the truncated L-J potential becomes zero at ϕ_ij = σ = 2^(1/6) does the Boyle temperature disappear and p/ρkT is everywhere > 1. This is then merely a truncated repulsive sphere, but without the exact scaling properties of just the inverse 12^th -power model (Eq. 3). The results for T_B from the second virial coefficient of the Mie n-m potential for m from 11.9 to 6 are plotted in Fig. 4b showing that the T_B exists as a finite constant for all sticky-sphere potentials in the limit that m 12. When m = 12 the pair potential is zero and we have an ideal gas.

Thus, all simple model Hamiltonians that have a core repulsion, however short the range of added attraction will exhibit a Boyle temperature and a range of gaseous states for which pV/NkT < 1. Does this imply a "liquid state" and a gaseous state in coexistence? If the distinction between gas and liquid is in the sign of the rigidity (dp/dρ)_T, the existence of a Boyle temperature implies that along any supercritical isotherm below the Boyle temperature there must be a higher-order thermodynamic transition from gas-like to liquid-like by the phenomenological definitions: derivatives of rigidity (d₂p/dρ²)_T, (with suggested name 'solidarity'), is -ve, zero, + ve from gas, to liquid, respectively. Solidarity is zero in the supercritical mesophase.

2.4 Zero-Repulsion Models

If we discard all repulsive terms, but just retain any, non-divergent (at r_ij = 0), attraction, we can obtain a gas–liquid coexistence state, a critical temperature, a critical-line, and a supercritical mesophase. These models are referred to as "penetrable" because without any repulsion the particles pass through one another, but as they do so, there is an attractive potential contribution to the Hamiltonian. Provided the attractive term does not diverge as r_ij 0 there exists states with thermodynamic stability. These very simple attractive classical particle models have a stable thermodynamic existence with a gas and liquid state, but, significantly, no crystal state.

The simplest such model Hamiltonian is probably the penetrable cohesive sphere (PCS) model first investigated theoretically by Widom and Rowlinson [2].

$$ {\text{U}}_{{({\text{N}})}} = { 1}/{2 }\sum_{{\text{N}}} {\text{m}}{\mathbf{v}}^{{2}} + \varepsilon [{\text{V}}_{{\text{E}}} /({4}\pi \sigma^{{3}} /{3}) \, - {\text{N}}] $$

(6)

The PCS Hamiltonian is not easily amenable to MD computer experiments, but Widom and Rowlinson [2] discovered that is has a remarkably useful exact analytic transformation scaling result with a binary system of non-additive hard spheres (N_[A] + N_[B] = N) in the limit that the non-additivity (α) of collision diameters (σ_AB) is zero.

$$ \sigma_{{{\text{AB}}}} = \alpha [(\sigma_{{{\text{AA }} + }} \sigma_{{{\text{BB}}}} )/{2}] $$

(7)

The MD simulation of the W-R C = 1 is analytically intractable, whereas the direct collisional dynamic study of W-R binary (C = 2) is very straightforward event-driven collision dynamics resulting in accurate pressure and percolation cluster statistical averages [3].

The phase diagram is shown in Fig. 5a. The percolation loci of the excluded and accessible volume determine a critical dividing line that is consistent with the experimental upper critical consulate temperatures (UCCT) literature of real binary liquids [22]. The two percolation transitions at ρ*_B = 0 are fundamental percolation properties of an ideal gas. As with the addition of square-well attraction to hard spheres, the intersection of the percolation loci triggers a critical point of constant T, p, μ, but coexisting states of two different concentrations of B, and a critical dividing line.

Fig. 5

Phase diagram of the W-R penetrable cohesive sphere (PCS) model fluid in the pressure – density projection: p*_PE and p*_PA loci are dashed blue and green, respectively; coexistence data points are red circles: the PCS liquid–gas system is obtained by transcription of W-R pressures reported in references [3, 22] using Eqs. (6,7)

The transcription equations are for the pressure of PCS (C = 1) fluid is [3, 22]

$$ {\text{p}}\sigma^{{3}} /\varepsilon = \, \left( {{\text{p}}* - {\text{ Z}}_{{\text{A}}} */{\text{V}}_{0} } \right){\text{ kT}}/\varepsilon $$

where Z_A* is the activity of a (C = 2) component defined as log_e Z_A* = μ/kT and the chemical potential μ/kT = ∫ (p-p_id) d log_e ρ_B along any isotherm. The density of the gas–liquid (C = 1) system is then equal to number density of a binary component. In effect, both systems have the same reduced number density scale.

The phase diagram resulting from exact transcription from two-component binary liquid model [3, 22] to one-component liquid + gas coexistence is shown in Fig. 5. Two coexisting states with constant T,p, μ at the percolation loci intersection in the T-p plane defines the critical point T_c-p_c, and a line of critical transitions from 2-phase coexistence (P = 2, F = 1) for T < T_c, to a single phase (P = 1, F = 2), for T > T_c. The critical gas–liquid coexisting pressure is defined by the intersection of both percolation pressure at T_c. Above T_c, the liquid percolation is the higher pressure, below T_c the (metastable) liquid percolation loci, previously known as 'spinodal', has the lower pressure. At the intersection, the two states, gas, and liquid, have the same T and p, and hence also the same μ (chemical potential), but different densities.

Therefore, we can adduce from Fig. 5, that the minimum Hamiltonian requirement for the existence of gas–liquid coexistence, and a critical point, is any finite attraction irrespective of the presence in the Hamiltonian of any repulsive terms.

3 Classical Fluid Phase Diagrams

3.1 Critical Divide Line

The experimental thermodynamic properties of a real liquids, like argon, were found to be consistent with the original thermodynamic description of liquid state limits described for square-well fluids [16]. Real simple liquids have a narrow effective width (r₀/σ = 2^1/6) and will therefore resemble the sticky-sphere limit in Fig. 1 (λ 1.0). Another noteworthy experimental result can be adduced from the historical review of Reif-Ackerman [23]. Nobody, in the history of thermodynamic measurements of fluid phase co-existence, has ever reported the direct observation or measurement of van der Waals hypothetical 'critical density' or 'critical volume'. The law of rectilinear diameters (LRD) has been invariably used to create a hypothetical "critical density" value, which, by LRD definition, is effectively the mean of the experimentally reported maximum coexisting vapour-phase density and minimum coexisting liquid phase density at the critical temperature T_c and pressure p_c. State points above this critical divide comprise a supercritical mesophase with both gaseous states and liquid states percolating the phase volume in a single Gibbs phase [24].

3.2 Phase Coexistence and Percolation Lines

The evidence for 3 distinct regions of any supercritical isotherm (below T_B) of any fluid, moreover, has been in the experimental literature since the original experiments of Thomas Andrews in 1869 [24] The p(ρ_T clearly shows the mesophase in experimental supercritical argon isotherms from Gilgen et. al. [25]. They do not report any experimental coexisting densities of either phase between the maximum coexisting gas density (10.75 mol/l) and minimum coexisting liquid density (14.9 mol/l). One can see, simply by looking however, that there are three definitive distinct regions, where the rigidity first decreases with density (gaseous), is evidently linear over a finite range (meso) to within experimental uncertainty, and then increases with increasing density (liquid-like).

The reduced phase diagrams of a classical L-J type fluid with long range (LR) attractive pair potential are show in Fig. 6. In the p–T plane the triple point is defined by intersection of any two coexistence lines whereupon crystal, liquid and gaseous phases all have the same T, p, and chemical potential. The projection in the T-r plane shows the critical divide between maximum coexisting gaseous and minimum coexisting liquid density states at the critical point on the p,T plane is defined by the intersection of the percolation transitions for available volume pockets in a liquid (PA) and the bonded clusters in the gas phase (PB). The recently reported compelling evidence for a pre-crystallisation (to FCC) of crystal (BCT)-in liquid mesophase [17, 26] is shown in both projections.

Fig. 6

Reduced temperature (T/T_t) phase diagrams of a classical L-J type fluid with long range (LR) attractive pair potential: (a) p–T plane the triple point (blue) coexistence lines (red). (b) T-ρ plane

We note that T_c/T_t is approximately equal to 2 when the full range of the pair potential, decaying as r_ij⁻⁶, is included in the Hamiltonian to determine the phase diagram. We also note that for most real molecules with dipole moments the range of the pair potential increases as also does T_c/T_t.

4 Macromolecules and Colloidal Spheres

Macromolecules like C₆₀ can have a short-range of attraction, close to one below which the boiling line will ceases to exist. As range (λ − σ) decreases, the T_c "double point" recedes to lower T, whilst BCT near T_t becomes more stable than FCC as density decreases. As T_c → T_t 0, PC will intersect the PA = PB T-p critical point, triggering a 3-state merger whence T_c = T_t and gaseous, liquid, and BCT states, can all co-exist at same T,p, and hence also μ (chemical potential), above regular FCC + gas two-phase region. This phase diagrams, shown below in Fig. 7, should describe fluids with a short-range but finite attractive potential (relative to kT), for small λ − σ values all the way to sticky spheres whence λ = σ.

Fig. 7

(a) p–T phase diagram of macromolecules with short-range attracytion showing a much shorter boiling line; (b) p–T phase diagram when the critical temperature intercepts the prefreezing percolation transition, showing a triple point incorporating the critical divide

Travis and Sadus [27] have recently obtained properties of a novel short-range potential computer model that appears to resemble molecules like C₆₀ and also colloidal spheres. This pair potential, with a more realistic softer core, is defined in reduced particle units as

$$ \begin{gathered} {\text{for r}}* \, < \, \surd {2} \;\phi_{{{\text{ij}}}} * \, = \left( {{2} - {\text{r}}*^{{2}} } \right)^{{8}} - { 2 }\left( {{2} - {\text{r}}*^{{2}} } \right)^{{4}} \hfill \\ {\text{for r}}* \, > \, \surd {2} \;\phi_{{{\text{ij}}}} * \, = 0 \hfill \\ \end{gathered} $$

(8)

Supercritical isotherms for this model show a Boyle temperature at T* 1.35 and below the Boyle temperature the pressure isotherms p(T) are consistent with a gas region (dp/dρ)_T < 0, a mesophase region (dp/dρ_T = 0, and a 'liquid' region (dp/dρ_T > 0), and, significantly, a rather wide critical divide at T_c. These results [27] from GEMC computations for the liquid–vapor coexistence, and GDI computations for the crystal-vapor coexistence are shown in Fig. 8a.

Fig. 8

(a) Original MC coexistence data supplied by K. Travis [26] for a colloidal-soft-sphere pair potential with the percolation lines drawn by interpolating the percolation points on the T = 0.7 isotherm (black crosses) between the critical divide coexisting densities and T_B. (b) Suggested reduced (T/T_t) phase diagram corresponding to that in Fig. 7b for comparison with the MC results of Travis

The pressure coexistence data points along several isotherms, but not shown here, are consistent with the supercritical mesophase and critical gas–liquid divide, and inconsistent with the hypothetical concept of a critical point singularity that disappears into metastability below a hypothetical "sublimation line".

We now know that the original Gibbs idea of a gas phase, a liquid phase, and solid phase, with supercritical continuity and indistinguishability is too simplistic and, in some respects, incorrect. Any Gibbs phase has hetero-phase fluctuations of, say, gas in liquid, that disperse at percolation transitions to percolate the phase volume in the vicinity of phase transitions. The supercritical fluid phase (F = 2) has three sub-regions separated by percolation transition loci, (i) predominantly gaseous state (with clusters), (ii) Colloidal-like meso-phase with both gas and liquid states percolating the phase volume (iii) predominantly liquid state (with holes) that can be clearly identified in T* = 0.7 supercritical isotherm shown as two crosses in Fig. 8a.

The criterion for the existence of a thermodynamic liquid state is a triple point coexistence of gas, liquid, crystal: not just liquid in coexistence with gas. A triple point is defined where two coexistence lines, crystal-fluid (gas), and crystal-fluid (liquid) intersect. There may be no gas–liquid coexistence line in p,T plane for very short-range potentials, yet there will still be a triple point. The gas + liquid states can coexist at T_c = T_t on a line above the gas-crystal 2-phase coexistence region. They also co-exist as a colloid-like dispersion, in the supercritical mesophase.

There is a value of range below which the critical temperature and the triple point temperature will coincide or intersect. Tukur [13] gives values of this for Lennard–Jones 12-n potentials for various values of n ( around 8.5), and also for the square-well potential: Tukur reported that T_c = T_t at λ/σ = 1.25 for square-well molecules of size σ and range λ. When T_c = T_t the maximum gas phase density is a dispersed liquid that percolates the predominant gas state, and the minimum coexisting liquid density contains a dispersed holes phase (gas) that percolates the phase volume. Hence the critical divide appears to be at rather a low-density in the phase diagram of the colloidal-sphere model Hamiltonian Eq. (8). Figure 8b for comparison illustrates that when the range λ is shortened until the pre-critical pre-freezing percolation transition is intersected by PA (or PE), i.e., when the critical point in the T,p plane reaches PF line. This triggers a 1^st-order phase transition with a triple point, gas, liquid, and crystal (BCT) all with the same T,p and chemical potential.

5 Conclusions

All the MD and MC results to date, are consistent with the interpretation that all pair potentials with a finite attractive component and repulsive core, including also real macro molecules e.g., C₆₀, and cohesive colloidal microspheres in thermodynamic Brownian-motion equilibrium, will exhibit a triple point, but no separate metastable critical singularity. This would be in a region, not of metastability, but of instability between the spinodals which are percolation loci in the two-phase region that define the limit of metastable existence of subcritical gas and liquid states.

The numerical methods GEMC and GDI may not be fit for purpose in the vicinity of the triple point. GEMC cannot see crystal phases, yet all the evidence suggests that the equilibrium liquid at T_t exists as a pre-freezing mesophase with up to 20% of low-density crystal structure, possibly BCT (body-centred tetragonal) percolating the phase volume. Moreover, there is evidence of large numerical uncertainties in Gibbs energies from GDI numerical integrations, when starting configurational states of small systems in 2-state phase points.

To conclude, we find that some quasi-spherical colloidal fine particles and sticky spheres, globular proteins, and macromolecules can have a range of attraction, shorter than that below which the boiling line ceases to exist. As the attractive range (λ − σ) decreases, the Tc "double point" recedes to lower T, whilst BCT at lower densities becomes more stable than FCC. When the BCT-LIQ prefreezing percolation is intersected by the receding intersection of PA and PB at Tc it will trigger a triple point, as 3 phases crystal (BCT), liquid and gas all have same T,p and chemical potential. All three density states co-exist at a uniform pressure above FCC + gas two-phase region. This phase diagram should describe fluids with a very short-range but finite attractive potential (relative to kT), for small λ − σ values to zero for sticky spheres.

Finally, we revisit the computations reported in Fig. 1, and redraw the phase diagram from the known properties of the supercritical and prefreezing mesophases. Figure 9 shows that the original GEMC data points from Hagen et al. [7] are consistent with the triple point interpretation where all thermodynamic phase-change points are defined by intersection of the percolation transition lines.

Fig. 9

A reinterpretation of the hypothetical Girifalco-C₆₀ phase diagram in Fig. 1 and Reference [7]: all the red lines, symbols, and annotations, are present interpretation; the original data with error bars is consistent a triple point below which exists the solid – gas two-phase region bounded by the gas deposition line and the solid sublimation line

The GEMC original data in Fig. 9, within the error bars as shown, is entirely consistent with the alternative interpretation we have presented in the foregoing sections. The hypothetical van der Waals point is known not to exist as such, but its removal to the region, not of metastability, but of subcritical instability is absurd. It wasn't known in 1993, but we now know that the subcritical extrapolation of the two percolation lines become the spinodals that define the limits of sub-critical gas and liquid metastability in the two-phase region.

Even for infinitely short-range i.e., sticky spheres, the existence or non-existence of a stable triple point depends only on an existence of T_t*, hence there will always exist a triple point, however, weak the Hamiltonian attraction potential term, at a sufficient low temperature.