1 Introduction

Photoacoustics and other photothermal techniques have been intensively developed for almost half a century. They have found wide application during that time in non-destructive determination of thermophysical properties of various materials, surface layers, thin films and biological tissues [1,2,3,4,5]. These methods are based on direct or indirect measurement of surface temperature variations that occur due to absorption of excitation electromagnetic energy, its conversion into heat through non-radiative deexcitation processes and heat propagation through the tested sample. The relationship between surface temperature variations and the thermophysical properties of the samples is established by solving the heat conduction equation. It means that thermophysical properties that govern dynamic heat transport can be measured by photothermal and photoacoustic experiments.

The most widespread theory of heat conduction is the classical Fourier diffusion or parabolic heat conduction (PHC) theory [6]. However, some experimentally observed phenomena, which classical theory could not explain, led to the development of generalized heat conduction theories [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26].

The phenomena observed by Peshkov in thermal measurements at very low temperatures, close to temperatures of liquid helium [7] were explained by Landau through the theory of the second sound (TSS) [27]. This theory introduced for the first time the assumption of the finite heat propagation speed, c, and explained heat propagation at very low temperature as an undamped wave process. Considering the dissipative nature of heat transport at temperatures significantly higher than liquid helium temperature and the physically justified assumption about finite heat propagation speed, the hyperbolic heat conduction (HHC) theory has been developed [28,29,30,31,32,33,34,35,36,37,38,39,40]. It describes heat conduction as a damped waves propagation with finite speed c, and introduces one additional property of a medium, thermal relaxation time, \(\tau\), defined as a phase lag between heat flux and temperature gradient, \(q\left( {r,t + \tau } \right) = - k\nabla T\left( {r,t} \right)\). In the HHC theory, thermal relaxation time,\(\tau\), is related to heat propagation speed across some medium by \(c = \sqrt {D_{T} /\tau }\), where \(D_{T}\) is thermal diffusivity of that medium. The thermal relaxation time describes the transient effects of thermal inertia associated with the thermal memory of the material medium [5, 33]. Many experimentally observed phenomena related to pulse heat excitation, which cannot be explained by PHC theory, are explained using HHC theory. Still, temperature modulated experiments with amorphous and polymeric materials were neither explained by PHC nor by HHC theory [18,19,20,21,22,23,24,25,26].

By analyzing both heat conduction theories, PHC and HHC, it can be observed that they describe the heat conduction process as an irreversible thermodynamic process via gradient of heat flux that describes heat dissipation along the temperature gradient, neglecting the irreversibility of the thermodynamic process resulting from the change in the enthalpy of the system when temperature gradient can be neglected (for example, very thin sample) [41]. In the irreversible thermodynamics developed by De Dondor, and later generalization made by Prigogine [41,42,43], it is shown that the irreversibility of the enthalpy change of the system must be taken into account when the time scale of the experiment is less than or equal to the relaxation time of the internal degrees of freedom of the system. Internal degrees of freedom and their relaxation time depend on the structural ordering of the material. In crystalline solids, structural units, atoms, molecules, or ions are interconnected by strong covalent or ionic bonds into a regular structure and can only oscillate around their equilibrium positions. Such systems have only vibrational degrees of freedom, which have a very short relaxation time. These relaxations are expected to have an influence at very high frequencies, which are much higher than the frequency scale of photothermal (PT) and photoacoustic (PA) experiments.

Polymeric materials are materials composed of long molecular chains, in which each chain consists of repeated structural units called monomers mutually related by stiff covalent bonds. These monomers are carbon compounds that make carbon backbone chains or polymers that can be linear or branched and each of them is a building block for polymeric materials [43,44,45,46]. The extremely high aspect ratio of long polymer chains inherently accommodates the bend and curvature of the macromolecule with little resistance of energy penalty. With such low-energy barriers, configurational entropy drives polymer chains to assume curvilinear shapes. The real systems consist of arrays of interacting chains, which is a significant departure from the behavior of a single chain. Polymeric materials can be pictured as a mass of intertwined worms randomly thrown into a pail. The binding forces are Van der Waals forces between molecules and mechanical entanglement between the chains.

Heat transfer phenomena may induce structural changes in these structures since monomers along the chain can oscillate around covalent bonds, long parts of the chain can oscillate around Van der Waals bonds, side chains can rotate, and so on [47]. The kinetic of such changes is related to slow relaxations and coupled with those of the heat transport processes [47] at a time and frequency scale of many experiments [22, 47]. This couple is described in theory through complex heat capacity [22, 23].

In this paper, the photothermal perturbation propagation model based on a hyperbolic heat conduction equation involving complex heat capacity is performed and discussed to explore whether photothermal experimental techniques can be employed to measure relaxation phenomena in polymeric materials. The hyperbolic equation of heat conduction is derived, including the thermal memory effect and complex heat capacity. Then, the physical meaning of imaginary heat capacity and its relation to the kinetic relaxation time in a polymer sample are discussed. Finally, the influence of kinetic relaxation time and thermal memory on the photothermal response is analyzed. In the end, the most important conclusions have been drawn.

2 Propagation of Photothermal Perturbation Across a Polymeric Sample

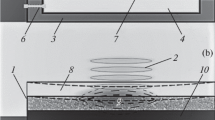
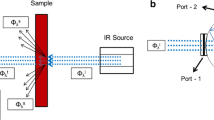
The theoretical model of a PT experiment is derived for a disk-shaped polymeric sample of thickness d and radius R, (R >> d, thin plate). The intensity-modulated monochromatic optical beam of low power (about 50 mW):

$$I = \frac{{I_{0} }}{2}(1 + \cos (\omega t)),$$
(1)

uniformly irradiates the flat surface of the sample (Fig. 1b). This enables a one-dimensional mathematical description of the problem [1, 5]. With \(I_{0}\) is designated optical incident flux [W·m−2] and with \(\omega = 2\pi f\) an angular frequency [rad·s−1], while f [Hz] is the frequency of modulation.

Fig. 1
figure 1

(a) The schematical illustration of a photothermal experiment. The intensity-modulated optical beam of low power (about 50 mW) is related to a lock-in amplifier, and the detector, situated either between optical excitation and sample (reflection configuration) or behind the sample (transmission configuration), monitors PT response proportional to surface temperature variations at each modulation frequency. (b) The geometry of the problem

Full size image

The air is considered as an optically transparent non-absorbing medium. Due to absorption by the sample, the intensity of the light decreases within the sample, and according to Beer–Lambert law can be expressed as [1, 36]:

$$I_{abs} = (1 - r)\frac{{I_{0} }}{2}e^{ - \beta x} (1 + \cos (\omega t)),$$
(2)

where \(r\) is the dimensionless optical coefficient of reflection and \(\beta\)[1/m] is the coefficient of absorption for a wavelength of the incident light. The absorbed light energy is transformed into the heat through non-radiative de-excitation and relaxation processes. Assuming instantaneous heat generation, the volumetric heat generation rate in the sample, \(P(x,t)\)[W·m−3] may be expressed as [36]:

$$P(x,t) = - \eta \frac{{\partial I_{abs} (x,t)}}{\partial x} = (1 - R)\eta \frac{{I_{0} }}{2}\beta e^{ - \beta x} (1 + \cos (\omega t)) = P_{s} (x)_{{}} + P_{d} (x,t),$$
(3)

where \(\eta\) represents the dimensionless quantum efficiency of conversion of light into heat, \(P_{s}\) is time-independent and \(P_{d}\) is time-dependent periodic density of heat power given by expressions:

$$P_{s} (x) = S_{0} \beta e^{ - \beta x} ,$$
(4)
$$P_{d} (x,t) = S_{0} \beta e^{ - \beta x} \cos (\omega t),$$
(5)

where S0 [W·m−2] is a heat flux generated at the surface of irradiated sample:

$$S_{0} = (1 - R)\eta \frac{{I_{0} }}{2}.$$
(6)

The temperature variations are obtained by solving of space one-dimensional energy balance equation (Fig. 1b)

$$\rho C_{p} \frac{\partial T(x,t)}{{\partial t}} + \frac{\partial q(x,t)}{{\partial x}} = P(x,t),$$
(7)

where are: \(\rho\)[kg·m−3] density, \(C_{p}\) [J·kg−1·K−1] heat capacity, T [K] temperature of the sample, \(\partial T(x,t)/\partial t\) heat flow, and \(q\)[W·m−2] heat flux related to temperature gradient by constitutive relations. The generalized constitutive relation that satisfies the Second Law of Thermodynamics in the frame of extended irreversible thermodynamics is given by [34]:

$$q(x,t) + \tau_{i} \frac{\partial q(x,t)}{{\partial t}} = - k\frac{\partial T(x,t)}{{\partial x}},$$
(8)

where \(\tau_{i}\) [s] is inertial relaxation time related to phase lag between temperature gradient and heat flux as well as finite heat propagation speed and thermal memory properties of a medium [5, 31, 32] and k [W·m−1·K−1] is the heat conductivity.

Considering that air is an ideal thermal insulator, the boundary conditions are given by:

$$q(0,t) = 0,$$
(9)
$$q(d,t) = 0.$$
(10)

The changes of the temperature within the sample excited by the heat source given by Eq. 3 can be described using:

$$T(x,t) = T_{amb} + \theta (x) + \vartheta (x,t),$$
(11)

where \(T_{amb}\) is the temperature of ambient (initial temperature of the system), \(\theta (x)\) is the time-independent component of the temperature change produced by the action of the time-independent heat source Eq. 5 and \(\vartheta (x,t)\) is the time-dependent component, produced by the action of the time-periodic excitation Eq. 5.

The periodic surface heat source, Eq. 4 produces periodic temperature variations within the sample and on its surfaces, the frequency of which is equal to the frequency of the source. In the reflection configuration, the amplitude and phase of periodic temperature variations on the illuminated surface are recorded, and in the transmission configuration, the amplitude and phase of periodic temperature variation on the rear surface are recorded directly or indirectly via lock-in amplifiers (Fig. 1a). The lock-in and the optical beam modulator are connected, so that lock-in always records signal at the modulation frequency, when the system is in a stationary state. Finally, the amplitude and phase characteristics of dynamic surface temperature variations are obtained, i.e. the amplitudes and phases recorded at each modulation frequency [1,2,3,4,5]. This means that only periodic temperature variations, \(\vartheta (x,t)\), are important for PT experiments. The periodic heat source, given by Eq. 5, in a complex representation becomes:

$$\tilde{P}_{d} (x,\omega ) = S_{0} \beta e^{ - \beta x} e^{ - j\omega t} ,$$
(12)

while the amplitudes and phases of periodic temperature variations can be described by introducing the Fourier transform into the model given by Eqs. 7–9:

$$\rho \tilde{C}_{p} (\omega )j\omega \tilde{\vartheta }(x,\omega ) + \frac{{d\tilde{q}(x,\omega )}}{dx} = \tilde{P}_{d} (x,\omega ),$$
(13)
$$(1 + j\omega \tau_{i} )\tilde{q}(x,\omega ) = - k\frac{{d\tilde{\vartheta }(x,\omega )}}{dx},$$
(14)

with homogeneous boundary conditions (from Eqs. 9, 10):

$$\tilde{q}(0,\omega ) = 0,$$
(15)
$$\tilde{q}(d,\omega ) = 0.$$
(16)

In the above expressions, \(\tilde{C}_{p} (\omega )\) stands for the complex heat capacity and with \(\tilde{q}(x,\omega )\) and \(\tilde{\vartheta }(x,\omega )\) are designated complex representatives of dynamic temperature variations and heat flux:

$$q(x,t) = {\text{Re}} \{ \tilde{q}(x,\omega )e^{ - j\omega t} \} ,$$
(17)
$$\vartheta (x,t) = {\text{Re}} \{ \tilde{\vartheta }(x,\omega )e^{ - j\omega t} \} .$$
(18)

In transmission PT measurements, it is very important to ensure that the tested sample is optically opaque, to protect the detector from the influence of the excitation beam [38, 48,49,50]. In both measurement configurations, transmission and reflection, the optical opacity of the sample provides a higher amount of absorbed energy, higher perturbations, and a better signal-to-noise ratio in the entire frequency range. The polymers are known to have a low coefficient of optical absorption, less than 104 m−1 so for samples whose thickness is of the order of magnitude of 100 µm or less, they are semi-transparent [50]. Therefore, in PT experiments, polymeric samples are covered with a very thin layer of a good optical absorber, whose optical absorption coefficient is 105–106 m−1, such as metal foil. In this way, the optical opacity of the measured sample is ensured (\(\beta d > 1\)) and the influence of a very thin coating on the temperature profile can be neglected [38, 48, 49].

When the optical absorption coefficient is high, all the energy is absorbed in a thin layer next to the illuminated surface [5, 49]:

$$\mathop {\lim }\limits_{{\begin{array}{*{20}c} {\beta \to \infty } \\ {} \\ \end{array} }} \tilde{P}_{d} (x,\omega ) = S_{0} \beta e^{ - \beta x} e^{ - j\omega t} = S_{0} \delta (x)e^{ - j\omega t} .$$
(19)

By replacing Eq. 19 in Eqs. 13, 14, the model is reduced to a system of homogeneous differential equations in a complex domain with inhomogeneous boundary conditions:

$$\rho \tilde{C}_{p} (\omega )j\omega \tilde{\vartheta }(x,\omega ) + \frac{{d\tilde{q}(x,\omega )}}{dx} = 0,$$
(20)
$$(1 + j\omega \tau_{i} )\tilde{q}(x,\omega ) = - k\frac{{d\tilde{\vartheta }(x,\omega )}}{dx},$$
(21)
$$\tilde{q}(0,\omega ) = S_{0} ,$$
(22)
$$\tilde{q}(d,\omega ) = 0.$$
(23)

To generalize heat conduction theory to include the kinetic degrees of freedom of the polymeric materials, let employ the thermodynamic of irreversible processes to systems with internal degrees of freedom [42, 43]. In this theory, an internal space of configuration of the system is defined, where each degree of freedom is represented by a continuing variable representing a coordinate of the internal space. During thermodynamic transformation, the diffusion along the internal coordinate, which participates in the entropy production, is supposed. Therefore, by analogy with heat conduction where heat is lost along the spatial direction defined by the hot and the cold points, in this representation, heat is lost by diffusion along the coordinate defined by the degree of freedom inside the internal space of configurations. Hence, for example, in this model, kinetic event in a thermally excited polymeric sample can be regarded as a diffusion along an internal coordinate (kinetic degree of freedom) between two stable constituents separated by a potential gap. During this diffusion effect, heat is lost (dissipated or absorbed), entropy is produced, and the mean entropy production per cycle of the oscillation is not equal to zero in difference to the preposition of reversible thermodynamic [42, 51]. This nonzero entropy change, averaged over the temperature oscillation cycle, is represented by imaginary heat capacity [22, 42]. Thus, the coefficient of proportionality between heat flow and enthalpy changes becomes a complex variable:

$$\tilde{C}_{p} = C_{p}^{^{\prime}} + jC_{p}^{^{\prime\prime}} ,$$
(24)

where the real part \(C_{p}^{^{\prime}}\) is associated with heat energy storage and the imaginary part \(C_{p}^{^{\prime\prime}}\) with heat dissipation through configurational changes i.e. through relaxation of internal degrees of freedom within the thermally induced system. A similar expression is obtained in linear response theory [18,19,20,21,22, 33], by microscopic non-equilibrium statistic physic or through pure kinetic approach but these theories didn't explain the physical meaning of imaginary heat capacity [42, 51].

If during the finite time interval ∆t, the temperature increment ∆T is not so high then thermodynamic variables of state never move far from equilibrium and their relaxations towards equilibrium are simple exponential relaxations (linear approximation). In that case, complex heat capacity can be modeled by the following expression [42]:

$$\tilde{C}_{p} = C_{p\infty } + \frac{{C_{p0} - C_{p\infty } }}{{1 + j\omega \tau_{k} }},$$
(25)

where \(C_{p}^{^{\prime}}\) and \(C_{p}^{^{\prime\prime}}\) satisfy the so-called Kramers–Kronig dispersion relations, \(\omega\) is the angular frequency of the modulated temperature, \(C_{p\infty }\) is the heat capacity related to the infinitely fast degrees of freedom of the system as compared to the frequency of temperature changes (generally vibrational modes or phonons bath), and \(C_{p0}\) is the total contribution at equilibrium (the frequency is set to zero) of the degrees of freedom, fast and slow, of the sample. The time constant \(\tau_{k}\) is the kinetic relaxation time constant associated with microstructural kinetic events.

If it is supposed that heat conduction in a photoacoustic experiment is an adiabatic process [51] (the heat cannot have time to relax towards the heat bath after one period of the temperature oscillation) then \(C_{p\infty } = 0\) and Eq. 25 is reduced to:

$$\tilde{C}_{p} = \frac{{C_{p0} }}{{1 + j\omega \tau_{k} }}.$$
(26)

By replacing Eq. 26 and Eq. 21 in Eq. 20, photothermally indssuced temperature variations are described by solving the following differential equation of heat conduction:

$$\begin{gathered} \frac{{d^{2} \tilde{\vartheta }}}{{dx^{2} }} - \sigma^{2} \tilde{\vartheta } = 0 \hfill \\ \tilde{q} = - \frac{k}{{1 + j\omega \tau_{i} }}\frac{{d\tilde{\vartheta }}}{dx}, \hfill \\ \end{gathered}$$
(27)

where the complex coefficient of heat propagation, \(\tilde{\sigma }\), is:

$$\tilde{\sigma } = \frac{1}{{\sqrt {D_{T} } }}\sqrt {\frac{{j\omega (1 + j\omega \tau_{i} )}}{{1 + j\omega \tau_{k} }}} = \alpha (\omega ) + j\frac{2\pi }{{\Lambda (\omega )}}.$$
(28)

The coefficient \(D_{T}\) represents thermal diffusivity, \(D_{T} = \frac{k}{{C_{p0} }} = \frac{k}{{\rho C_{p} }}\), \(\rho\) is the density of the sample and \(C_{p}\) is specific heat capacity, \(\alpha (\omega )\) is coefficient of attenuation of heat waves and it is inverse proportional to diffusion length and \(\Lambda (\omega )\) is the wavelength of heat waves [5, 36].

With \(\tilde{Z}_{c}\) is designated thermal impedance of the sample defined by [5, 36, 37]:

$$\tilde{Z}_{c} = \frac{{\sqrt {D_{T} } }}{k}\sqrt {\frac{{(1 + j\omega \tau_{i} )(1 + j\omega \tau_{k} )}}{j\omega }} ,$$
(29)

The heat propagation model given by Eqs. 27–29 coincides with the dual-phase-lag (DPL) of the heat propagation model proposed in [52, 53] and is widely used in explaining heat transfer in biological tissues [54,55,56].

The solutions of Eqs. 27 are given by:

$$\tilde{\vartheta }(x) = A_{1} \exp ( - \tilde{\sigma }x) + A_{2} \exp (\tilde{\sigma }x),$$
(30)
$$\tilde{q}(x) = \frac{{A_{1} }}{{\tilde{Z}_{c} }}\exp ( - \tilde{\sigma }x) - \frac{{A_{2} }}{{\tilde{Z}_{c} }}\exp (\tilde{\sigma }x).$$
(31)

Substituting Eq. 31 into boundary conditions Eqs. 22, 23 yields constants A1 and A2:

$$A_{1} = S_{0} \tilde{Z}_{c} \frac{{\exp (\tilde{\sigma }d)}}{{2sh(\tilde{\sigma }d)}}\;{\text{and}}\;A_{2} = S_{0} \tilde{Z}_{c} \frac{{\exp ( - \tilde{\sigma }d)}}{{2sh(\tilde{\sigma }d)}}.$$
(32)

By substituting Eq. 32 into Eq. 20, the surface temperature variations have been calculated:

$$\tilde{\vartheta }(0,\omega ) = S_{0} \tilde{Z}_{c} \frac{{ch(\tilde{\sigma }d)}}{{sh(\tilde{\sigma }d)}},$$
(33)
$$\tilde{\vartheta }(d,\omega ) = S_{0} \tilde{Z}_{c} \frac{1}{{sh(\tilde{\sigma }d)}}.$$
(34)

The photothermal response is obtained by direct or indirect measurement surface temperature variations [1,2,3,4,5].

3 Analyses and Discussion of a Polymeric Sample Photothermal Response

The model derived in this paper and given by Eqs. 33, 34 can be reduced to the most widely used classical Rosencwaig-Gersho (RG) model of PT response [1,2,3,4,5], assuming that \(\tau_{i} = \tau_{k} = \tau = 0\). For \(\tau_{k} = 0\) and \(\tau_{i} \ne 0\), the derived model gives a generalized hyperbolic model of PT response [5, 36]. This confirms the accuracy of the derived model.

In further analysis, all calculations were performed for a polymer sample with thickness of \(d = 20\,{\mu m}\) whose thermal properties \(D_{T} = 2x10^{ - 5} {\text{m}}^{2} \cdot {\text{s}}^{ - 1}\) and \(k = 0.45\,{\text{W}} \cdot {\text{mK}}^{ - 1}\) correspond to high density polyethylene [57] for two experimental configurations, reflection Eq. 33 and transmission Eq. 34 (Fig. 1). It is considered that S0 = 1.

Inertial and kinetic relaxation times have not been measured so far for any material, including polymeric materials, except for proceeding meat [14] used in the consideration of heat conduction in biological tissues [54,55,56]. Relaxation times of cooperative and non-cooperative processes have been studied in polymeric materials, and they change in a wide range, from 10–14 s to 100 s [22]. In this paper, it was considered that kinetic relaxations are a consequence of non-cooperative processes and that their relaxation time ranges between 1 s and 10 ns at room temperature. The assessment was performed based on dielectric loss analyzes of polyolefins [58, 59] and temperature modulated calorimetry measurement of various polymers [22]. The inertial relaxation time was estimated at 10 microseconds based on the assumption that the speed of sound propagation in polymeric materials is 1000 times higher than the speed of heat propagation [36].

Figure 2 shows the amplitudes and phases of surface temperature variations vs. the modulation frequency of excitation optical beam for the classical model [1] (\(\tau_{i} = \tau_{k} = \tau = 0\)) by green lines, hyperbolic model [5, 36] (\(\tau_{k} = 0\) and \(\tau_{i} = 10\,{\mu s}\)) by blue lines, and for derived model (\(\tau_{i} = \tau_{k} = \tau = 10\,\mu s\), red lines), for reflection (Fig. 2a and b) and transmission experimental configuration (Fig. 2c and d).

Fig. 2
figure 2

The amplitudes (a, c) and phases (b, d) of surface temperature variations vs. modulation frequencies of excitation optical beam for classic (\(\tau_{i} = \tau_{k} = \tau = 0\)—green lines), hyperbolic (\(\tau_{k} = 0\),\(\tau_{i} = 10\,{\mu s}\)—blue lines), and derived model (\(\tau_{i} = \tau_{k} = \tau = 10\,{\mu s}\)—red lines) (Color figure online)

Full size image

As can be seen from Fig. 2a and c, the amplitudes of the surface temperature variations predicted by the derived model coincide at low frequencies, less than \(1/(2\pi \tau )\), with the amplitudes predicted by the classical model (green line) and by the hyperbolic model (blue lines), for both experimental configurations, reflection and transmission. Also, the phases predicted by the derived model coincide with the phases arriving from the other two models at frequencies for the order of magnitude less than \(1/(2\pi \tau )\), for both reflection and transmission configuration (Fig. 2b and d). This confirms the expectations based on the physics of the problem, that relaxation phenomena affect the time scale of the experiment which is of the same order of magnitude as the relaxation time of these phenomena or less than it, i.e. in the frequency domain of the experiment which is larger than the inverse relaxation time [23, 42].

Comparing the results of the derived model and the results of the hyperbolic model that takes into account only inertial relaxations (blue and red lines in Fig. 2), at higher modulation frequencies, \(f > 1/(2\pi \tau )\), it can be seen that the amplitudes and phases predicted by these two models differ significantly, what can be attributed to the influence of kinetic relaxations.

As discussed in the literature [5, 36], periodic changes in amplitudes and phases of surface temperature variations, predicted by the hyperbolic model, are a consequence of the action of inertial relaxations on the wavelength and diffusion length of heat waves. When the thickness of the sample is greater than or equal to half the wavelength of heat waves, thermal resonances and antiresonances will occur in the sample. They will be noticeable only if the attenuation of heat waves is small enough, which depends on the thermal diffusivity and the thickness of the sample [5, 36]. As the derived model for a sample of the same thickness and with the same thermal diffusivity does not predict such a phenomenon (red lines in Fig. 2), it can be concluded that kinetic relaxations increase the wavelength of heat waves and prevent the manifestation of the wave nature of heat propagation.

To examine in more detail the influence of kinetic relaxations on the PT response, Fig. 3 shows the amplitudes and phases of surface temperature variations calculated based on the derived model, for \(\tau_{i} = 0\) and for three values of \(\tau_{k}\), \(\tau_{k} = 1\,{\text{ms}}\), \(\tau_{k} = 10\,{\mu s}\), and \(\tau_{k} = 0.1\,{\mu s}\). In that case, the hyperbolic model is reduced to classic and the predictions of these two models are illustrated in Fig. 3 by green lines.

Fig. 3
figure 3

The amplitudes and phases of surface temperature variations vs modulation frequency calculated on the basis of the derived model, for \(\tau_{i} = 0\) and for three different values of \(\tau_{k}\). The results of classic and hyperbolic models are illustrated by green lines (Color figure online)

Full size image

As can be seen from Fig. 3a and c, at low frequencies, \(f < 1/(2\pi \tau_{k} )\), the amplitudes of the derived model coincide with the amplitudes of the classic model for both experimental configurations. The same applies to phases (Fig. 3b and d) only for the frequency range that is an order of magnitude less than \(1/(2\pi \tau_{k} )\). As \(\tau_{k}\) increases, the frequency range in which the classical and derived models coincide decreases. At frequencies \(f > 1/(2\pi \tau_{k} )\), the derived model predicts the decreasing of amplitudes characteristic slope (Fig. 3a and c) and increasing of phases (Fig. 3b and d). In reflection experimental configuration, phases predicted by derived model increase faster (Fig. 3b), while in transmission configuration phases increase in difference to the prediction of the classical model (Fig. 3d). This can be explained by the analysis of expressions given by Eqs. 28, 29 and 33. The kinetic relaxations affect the thermal impedance by changing its frequency dependence. At high frequencies, the thermal impedance decreases inversely proportional to the modulation frequency, and its phase increases sharply. On the other hand, kinetic relaxations increase the diffusion length of heat waves almost exponentially. Therefore, the derived model predicts much larger amplitudes and phases of temperature variations than the classical one, although they prevent the occurrence of thermal resonances due to the kinetic relaxations increase the wavelength of heat waves (Eq. 28).

To analyze how the ratio of inertial and kinetic relaxations affects the PT signal, let us analyze the amplitudes and phases of surface temperature variations, for \(\tau_{i} = 10\,{\mu s}\) and for both cases: when \(p = \tau_{i} /\tau_{k} < 1\) (Fig. 4) and for the case when \(p = \tau_{i} /\tau_{k} > 1\) (Fig. 5).

Fig. 4
figure 4

The amplitudes and phases of surface temperature variations vs. modulation frequency calculated on the basis of the derived model, for \(\tau_{i} = 10\,{\mu s}\) and for \(p = \tau_{i} /\tau_{k} < 1\). The results of classic and hyperbolic models are illustrated by green and blue lines, respectively (Color figure online)

Full size image
Fig. 5
figure 5

The amplitudes and phases of surface temperature variations vs modulation frequency calculated on the basis of the derived model, for \(\tau_{i} = 10\,{\mu s}\) and for \(p = \tau_{i} /\tau_{k} > 1\). The results of classic and hyperbolic models are illustrated by green and blue lines, respectively (Color figure online)

Full size image

In Fig. 4, it can be seen that for \(p < 1\) and in the frequency range \(1/(2\pi \tau_{k} ) < f < 1/(2\pi \tau_{i} )\) the kinetic relaxations increase the amplitudes and phases of surface temperature variations compared to the classical and hyperbolic model and keep them at constant values in a wide frequency range, completely changing the appearance of amplitude and phase characteristics in relation to the classical and hyperbolic model. As p decreases, i.e. \(\tau_{k}\) approaches \(\tau_{i}\), the influence of kinetic relaxations on the increase of the thermal impedance of the sample disappears, but they affect the decrease of attenuation and increase of a wavelength of thermal waves. In this case, p < 1, the results of the derived model will not coincide with the hyperbolic one in the high-frequency range. Also, completely different behavior of the measured amplitudes and phases is expected in relation to what the classical model predicts at frequencies higher than \(1/(2\pi \tau_{k} )\).

Finally, kinetic relaxations (\(\tau_{k} > 0\)) increase of thermal impedance and heat diffusion length of the sample and consequently increase the amplitudes and phases of surface temperature variations compared to the classical and hyperbolic model (\(\tau_{k} = 0\)) at frequencies higher than \(1/(2\pi \tau_{k} )\) (Figs. 2a, b, 3 and 4). Besides, kinetic relaxations increase the wavelength of thermal waves preventing thermal resonances and antiresonances i.e. periodic changes of amplitudes and phases of surface temperature variations (Figs. 2, 3 and 4).

As can be seen from Fig. 5, if the influence of inertial relaxations is manifested at lower frequencies than the influence of kinetic relaxations (\(p > 1\)) the results of the derived model coincide in a wider frequency range with the results of the hyperbolic model. If \(p > > 1\) the results of the derived model completely coincide with the results of the hyperbolic model in the frequency range of the measurement, especially for reflection configuration (Fig. 5a and b). The position of local maxima in amplitude and phase characteristics can be calculated from Eq. 33, 34 and 28 [5, 36]:

$$f_{\max } \approx \frac{n + 1}{{2d}}\sqrt {\frac{{D_{T} }}{{\tau_{i} }}} ,\,n \in N^{0} ,$$
(35)

and local maxima desrease proportional to \(f^{ - s}\), \(s \in (1,0)\) [5, 36].

If \(1/(2\pi \tau_{i} ) < f < 1/(2\pi \tau_{k} )\), the influence of kinetic relaxations is seen through the attenuation of amplitude and phase peaks in comparison to the hyperbolic model (\(s > 1\)). At frequencies \(f > 1/(2\pi \tau_{k} )\), the kinetic relaxations disable periodic changes of amplitudes and phases of surface temperature variations due to their influence on the increase of wavelength of a heat wave. If p increases, the attenuation of the peaks is smaller. When \(p \to 1\) the effect of kinetic relaxations can be observed in transmission configuration (Fig. 5c, d) through a much steeper drop in both amplitude and phase characteristics than in the classical model.

The inertial relaxations (\(\tau_{i} > 0\)) are the cause of thermal resonances and antiresonances i.e. oscillatory changes of amplitude and phase characteristics at frequencies \(f > 1/(2\pi \tau_{i} )\) due to their influence on decreasing of the wavelength of thermal waves. The influence of inertial relaxations can be observed only if \(\tau_{k} \le \tau_{i}\) (Figs. 2, 5).

Our experimental measurements of different polyethylene samples (LDPE, LLDPE, and HDPE, prepared following procedure described in [57]) by transmission photoacoustic (Fig. 6) show periodic changes of PA amplitudes and phases that could not be explained by a classic model. In addition, the maxima of periodic changes in amplitudes fall sharply, which cannot be explained by the hyperbolic model. These results are similar to the predictions of the derived model illustrated in Fig. 5c and d. Based on the derived model and analyses of Fig. 5, one can conclude that inertial relaxation phenomena in semi-crystalline PE samples produce peaks in PA amplitudes and phases and that kinetic relaxations cause their attenuation. As it has been discussed in the analysis of Fig. 5, kinetic relaxation times in PE samples are close but shorter than inertial times. By comparing the amplitude and phase characteristics of the PA signal for LDPE, LLDPE, and HDPE (Fig. 6), it can be seen that the local maxima in the amplitude and phase characteristics appear at lower frequencies for the HDPE sample. Based on Eq. 35, it can be concluded that inertial relaxations in HDPE are less than inertial relaxation in the other two polyethylenes. In addition, the attenuation of periodic changes is less for HDPE. Based on the discussion conducted below the Fig. 5, it can be concluded that the ratio of inertial and kinetic relaxations is higher in the HDPE sample than in LDPE and LLDPE. Additional research is needed for detailed estimation of relaxation times and relating of morphology and crystallinity of polyethylenes to relaxation processes and it is subject of our further investigations.

Fig. 6
figure 6

Photoacoustic amplitudes and phases of photoacoustic signals measured on three polyethylene samples in transmission PA configuration with minimal volume cell. The samples are disk-shaped with diameter of 9 mm and thickness of 200 μm

Full size image

4 Conclusions

Based on the analysis of the generalized heat conduction model, which takes into account heat dissipation within the polymer sample due to non-equilibrium thermodynamic transformation of the heat excited sample as well as the thermal memory of the material, a PT response model of the polymeric sample has been derived. The analysis of the model shows that the derived model can be reduced to the classical one only in the case when the transient relaxations in the material are neglected.

It is shown that oscillatory changes in measured PT signals result from inertial relaxations (thermal memory of a polymeric sample). They can be observed in thin polymer samples, thinner than thermal diffusion length (\(d \le 1/\alpha\)) at high frequencies, \(f > 1/(2\pi \tau_{i} )\), and if the kinetic relaxation time is less than an inertial relaxation time, \(\tau_{k} < \tau_{i}\).

The kinetic relaxations influence to attenuation of thermal resonances, increase the slope of decreasing of the amplitude characteristic of the PT response, and cause decreasing of amplitudes and phases at high frequencies if \(\tau_{i} \ge \tau_{k}\) due to their influence on the wavelength of thermal waves. Otherwise, these relaxations change the shape of the amplitude and phase characteristics and cause the appearance of larger amplitudes and phases of the PT signal in comparison to classical and hyperbolic models due to their influence on increase thermal diffusion length and the thermal impedance.

The influence of thermal relaxation times depends on the frequency scale of the experiment. If the frequency scale of the experiment is less than \(min\left( {1/(2\pi \tau_{i} ),1/(2\pi \tau_{k} )} \right)\) their influence can be neglected. In all other cases, the influence of thermal relaxation must be considered. Theoretical analyzes combined with presented experimental investigations show that some of the relaxation phenomena can be observed by PT measurements at room temperature.