Abstract
Density and speed of sound of methane + n-heptane binary mixtures were measured at a temperature equal to 303.15 K and at pressures ranging from 10 MPa to 70 MPa. The measurements were performed in pure n-heptane and eight different mixtures with methane molar percentage ranging from 20 % to 95 %. Speed of sound data was obtained by a pulse-echo technique working at 3 MHz whereas density data were acquired from a vibrating U-tube densimeter. Isothermal and isentropic compressibilities were derived from both measurements in the same conditions. Finally, partial molar volumes, excess molar volume, excess isothermal compressibility as well as excess speed of sound and excess isentropic compressibility were estimated at the same conditions and the relative excess properties were represented as a function of methane content. From these measurements, it was observed that the large difference in compressibility of pure components provoked significant deviations to ideal behavior with relative excess values that can reach − 20 %, − 100 % and 200 % of the ideal properties for molar volume, isothermal compressibility and speed of sound, respectively. Moreover, a small clustering effect at high dilution of n-heptane at 30 MPa was brought forth to light by evaluating the partial molar volumes.
Graphic Abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Reservoir fluids mainly contain short- and long-chain n-alkanes. These unbranched saturated hydrocarbons are non-polar and simply linear. The molecules belonging to this family are only composed of three functional groups, namely, methane, methyl and methylene groups and their intermolecular interactions can be well represented by a United-Atom Description [1] in which alkanes molecules are described by a chain of pseudo-atoms to represent the functional groups whose mutual interactions are characterized by a simple pairwise Lennard–Jones potential. Despite the simplicity of these compounds, mixtures containing different alkanes may exhibit significant deviations from ideality. These non-ideal behaviors, arising mostly from asymmetry in molecular size, are particularly obvious in methane + higher n-alkane mixtures in which liquid–liquid immiscibility may appear at certain conditions of pressure, temperature and composition [2, 3]. Furthermore, significant negative excess volumes have been observed in such asymmetric methane + heavy n-alkanes binary mixtures [4]. As an example, by comparing the excess volumes reported by Dymond et al. [5] for n-hexane + n-hexadecane at elevated pressure with the excess values measured by Regueira et al. [6] in methane + n-decane system, it can be noticed that excess volumes are greater by one order of magnitude in C1 + n-C10 system than in n-C6 + n-C16 mixture in the same conditions of pressure temperature and composition although both systems have nearly the same discrepancy in chain length.
This non-ideality is strongly marked for derivative properties such as isothermal and isentropic compressibilities as well as for speed of sound, making the prediction of these properties in reservoir fluids difficult to achieve using equation of states [7]. Speed of sound was extensively investigated in binary mixtures involving “liquids”, i.e., n-alkanes higher than pentane, at atmospheric pressure [8,9,10,11,12,13] and even at high pressure [14,15,16,17,18,19,20,21], whereas experimental data of this type are particularly limited for “gas” + “liquid” n-alkanes binary mixtures [15, 22]. A literature survey reveals that excess isentropic compressibility and excess speed of sound for asymmetric binary systems composed of methane and n-alkanes higher than pentane data are so far inexistent in the open literature. Consequently, keeping in mind both the industrial and scientific interest for studying the volumetric and acoustic properties of binary systems characterized by a significant asymmetry in the compressibility of their components, our research group has initiated a broad project on the experimental determination of density, isothermal compressibility, speed of sound, isentropic compressibility as well as their related excess properties in such light–heavy alkanes asymmetric systems.
At the initial phase of this program, which is the object of this article, it was chosen to investigate the methane + n-heptane system at different pressures ranging from 10 MPa to 70 MPa along an isotherm at T = 303.15 K. For that purpose, density and speed of sound measurements were carried out in eight different mixtures ranging from 20 % to 95 % of methane content (in mol%). From these measurements, derivative properties such as isothermal and isentropic compressibilities were obtained in the same conditions. From all these data and additional measurements performed for pure components, excess molar volume, excess isothermal compressibility, excess isentropic compressibility and excess speed of sound were determined. Finally, the partial molar volume was derived from the volumetric data to explore, by extrapolation, the partial molar volume at infinite dilution of n-heptane in methane at different pressures as it exhibits an interesting behavior.
2 Materials and Methods
2.1 Chemicals
Both the gas (methane) and liquid (n-heptane) employed for preparing the mixtures were used without any further purification. The information of the supplier, as well as on the purity of component used, is displayed in Table 1.
2.2 Measurements
Density measurements were carried out with a vibrating tube density meter. The core of the apparatus is a commercial U-shaped-tube density meter (Anton Paar HP). However, the study of asymmetric mixtures composed of gas and liquid components requires the addition of several pieces of equipment for preparing, stirring and transferring the samples. A high volume–high pressure cylinder with a floating piston and a stirring ball is used for preparing the mixture in large quantity while minimizing the uncertainty in composition. A hydro-pneumatic pump is used to control the floating piston via a hydraulic fluid. A volumetric pump is connected to the upstream of the density meter so as to regulate the pressure of the fluid at the outlet during high-pressure injection of the sample fluid in the U-shaped tube. Two high weight/high precision balances with an uncertainty of 10−3 g are used for weighing both gas and liquid. An aluminum tank with a high capacity (1 dm3–40 MPa) is employed for storing gas during its weighing. The complete experimental assembly is shown in Fig. 1.
Schematic diagram of experimental setup used for density measurements. (1) gas tank fixed on high weight/high precision balance; (2) temperature sensor; (3) pressure sensor; (4) high-pressure discharge pump; (5) density matter; liquid balance; (6) liquid tank; (7) high volume–high pressure cylinder with a floating piston; (8) hydro-pneumatic pump
The experimental procedure consists in first preparing the mixture into the high-pressure cylinder by successive weighing of liquid and gas loading. The system is then pressurized above the saturation pressure and stirred to mix both components so as to obtain a homogenous mixture. After 24 h of mixing, a sample part is transferred to the measuring cell at constant pressure through the action of both pumps. During this operation more than three times the volume of the measuring cell is displaced from the feeding cylinder to the output volumetric pump in such a way as to guarantee the composition of the mixture loaded in the density meter. The standard uncertainties in mass introduced by this procedure were estimated to be better than 0.01 g for liquid component and 0.005 g for gas. The resulting combined standard uncertainty in the mole faction \(x_{c1}\) of methane was estimated for each studied sample by the following relation:
The temperature of the measuring cell is regulated by an external heat circulation thermostat and is measured with an Anton-Paar MKT 50 thermometer with an uncertainty of 0.05 K. The pressure is measured, for the full pressure range, with a Presens manometer yielding an uncertainty of 0.02 %.
The principle of the vibrating tube density meter consists of measuring the resonance period τ of the tube and relating it to the density of the fluid sample inside the tube according to the following working equation:
where A and B are two parameters specific to the vibrating tube and function of both temperature and pressure. The density meter working in a relative method, the determination of the sample density requires first the evaluation of apparatus parameters through a calibration that properly accounts for the effects of pressure on apparatus parameters [23,24,25,26]. From a physical basis, May et al. [25, 26] obtained the following relations to account for temperature and pressure impact on the apparatus parameters:
where \(T_{0 }\) is a reference temperature, \(\tau_{vac,0}^{{}}\) is the resonance period of the tube under vacuum at the reference temperature and \(\rho_{M} ,S_{vac,0} ,\beta_{\tau } , \beta_{V} ,\varepsilon_{1} , \varepsilon_{1} ,\alpha_{V}\) are material and apparatus parameters. At a given temperature \(T_{0}\), Eqs. 3 and 4 can be simplified. Thus, the working equation becomes:
where \(\tau_{r}^{{}} = \tau /\tau_{vac,0}^{{}}\) corresponds to the relative vibration period with respect to vacuum period, and \(C_{0}\), \(\beta_{\tau }\), and \(\beta_{V}\) are three parameters that must be determined by calibration using one or several reference fluids. Since the density interval covered by the investigated system is large (70–800 kg·m−3), two reference fluids were used in this work: nitrogen for the lower density range and water for the higher density range. The three apparatus parameters, appearing in Eq. 5, were determined by a nonlinear regression of experimental densities obtained from measurements of resonance periods \(\tau_{vac,0}^{{}} , \tau_{{H_{2} O}}^{{}} , \tau_{N2}^{{}}\) to reference data of water [27] and nitrogen [28] in the same pressure range for the temperature of investigation, T0 = 303.15 K.
In this calibration method, the nonlinear regression makes difficult to quantify uncertainty in density measurement by applying the conventional law of propagation of uncertainty. Therefore, a Monte Carlo method with M = 104 trials was considered to determine density \(\rho\) and its associated standard uncertainty according to the guide to the expression of uncertainty in measurement [29]. To do so, a discrete pseudo-random normal distribution having M points with a standard deviation equivalent to the combined standard uncertainty is assigned to each of the input quantities corresponding to the reference densities (\(\rho_{H2O}^{{}}\), \(\rho_{N2}^{{}}\)), the measured periods of the tube under vacuum as well as those of the tube filled with both the reference fluids and the studied fluids, i.e., \(\tau_{vac,0}^{{}}\), \(\tau_{{H_{2} O}}^{{}}\), \(\tau_{N2}^{{}}\), and \(\tau\). As the density data obtained from U-tube density meter result from four independent measurements of the resonance period, uncertainties in temperature and pressure were taken into account in each measurement by considering the following combined standard uncertainty for the resonance period:
where the subscript i refers to either vacuum or nitrogen or water or even the studied fluid.
For each of the M trials, parameters C, \(\kappa_{\tau }\), and \(\kappa_{V}\) are determined by nonlinear regression of the perturbed data considered for calibration. From the obtained set of parameters, the fluid density is calculated from Eq. 5 using the perturbed period measure with the studied sample. Finally, the average and the standard deviation of the output distribution are taken as the density \(\rho\) and its standard uncertainty in measurement \(u_{M} \left( \rho \right)\) respectively. This uncertainty is combined to the uncertainty in mixture composition and component purities xsp to obtain the combined standard uncertainty \(u_{c}^{{}} \left( \rho \right)\) of density data:
where \(\xi\) is the fractional density difference between the pure compounds and their impurities. This quantity is arbitrary set to 20 % for both components.
The method used to measure speed of sound is based on a pulse-echo technique operating with a single 3-MHz transducer. The apparatus is similar to that described previously by Bazile et al. [30]. It is mainly composed of an acoustic probe made up of a PZT piezoelectric disc embedded between two hollow cylindrical holders of different lengths so as to get a long- and a short-path length for the acoustic waves. Two reflectors facing the transducer are fixed at each end of the holder. The speed of sound is determined from the measurement of the time delay between echoes coming from the different reflectors using a digital overlap method described in a previous paper [31]. The path length difference needed for converting time delay measurement in speed of sound is obtained by calibration with water [32,33,34,35]. The entire acoustic sensor is immerged in the studied fluid enclosed in a variable volume cell equipped with a magnetically coupled stirrer that ensures an efficient stirring of the mixture inside the acoustic sensor. The temperature of the cell is regulated by heating cartridges embedded in a jacket that surrounds the full cell body. A temperature sensor in contact with the fluid is used to measure the temperature of the fluid with an uncertainty of 0.1 K. The pressure is measured using a pressure transducer accommodated in the cell wall so as to reduce fluid dead volume. This sensor is calibrated as a function of temperature against a primary standard pressure sensor with an uncertainty better than 0.02 % on the full scale. Because of the complex shape of the acoustic probe, the mixtures are prepared inside the measurement cell by first loading liquid and then the gas. As for density measurements, feed quantities are determined by weighing the injected mass using high weight/high precision balances and the resulting uncertainty for mole fractions was determined by Eq. 1.
3 Results and Discussion
Mixtures were first prepared in the speed of sound apparatus and then duplicated in the density meter. Table 2 lists the composition of the different mixtures investigated along with their expanded uncertainty \(U\left( {x_{c1} } \right)\) obtained by multiplying by the conventional coverage factor kP = 2 (P = 95 %) with the combined standard uncertainty \(u_{c} \left( {x_{c1} } \right)\) calculated from Eq. 1. Comparison of the different compositions reported in Table 2 reveals a good agreement between mixtures prepared for both measurements. The difference is always lower than the expanded uncertainty. This condition is a prerequisite for the determination of isentropic compressibility as well as excess isentropic compressibility and excess speed of sound.
3.1 Density and Molar Volume
Table 3 presents the density data obtained in the eight mixtures investigated at 303.15 K from 10 MPa to 70 MPa. The density measured in both pure components was added in this table for comparison with literature data. The densities of both pure components have been measured many times in the literature and accurate correlations have been developed [36, 37]. The present experimental results show a good consistency with the values given by the correlation of Setzmann and Wagner [36] for methane. An average absolute deviation (AAD) of 0.1 kg·m−3 and a maximum deviation (MD) of 0.22 kg·m−3 are observed with this correlation. Similarly, a good agreement is observed with the correlation of Span and Wagner [37] for n-heptane with an AAD of 0.43 kg·m−3 and an MD of 0.51 kg·m−3. All these deviations are consistent with the estimated uncertainties of both the measurements and the correlations, thereby confirming the capability of the calibration procedure for working in an extended density range.
The volumetric behavior of methane + n-heptane binary system has been previously investigated by Reamer et al. [38] from 10 mol to 90 mol% in an extended range of pressure and temperature and by Robertson and Clark [39] for one composition (95 % of methane). However, due to the difference in both mixture compositions and experimental p, T conditions, it was not possible to compare them to the present measurements. Figure 2 illustrates the experimental density data as a function of mole percent of methane at various pressures. As shown in this figure, the density of mixtures decreases monotonically from n-heptane toward pure methane density. However, this monotonicity is lost when molar volume \(V_{m}^{{}}\) is represented, instead of density, as a function of mole percent. More precisely, as can be observed in Fig. 3, at pressures below 50 MPa, the isobaric curves of \(V_{m}^{{}}\) first decrease with the mole percentage of methane and then increase for the highest content of methane (i.e., low content of n-heptane). This trend can only be explicitly observed on 30 and 40 MPa isobars, as for 10 and 20 MPa isobars, bubble points limit the curves to low methane contents only (60 % and 20 %, in mole, respectively).
This non-monotonic variation in \(V_{m}^{{}}\) with \(x_{C1}\) means a sign change in \(\left( {\partial V_{m}^{{}} /\partial x_{C1} } \right)_{p,T}\) that is given from the thermodynamic relation as
This equation indicates that the composition \(x_{C1,min}\) at which the mole volume \(V_{m}^{{}}\) is minimum corresponds to the condition where the molar volume \(V_{m}^{{}}\) is equal to both partial molar volumes \(V_{C1}^{{}}\) and \(V_{C7}^{{}}\). Below \(x_{C1,min}\), \(V_{m}^{{}}\) decreases with respect to \(x_{C1}\) meaning that \(V_{C7}^{{}} > V_{m}^{{}} > V_{C1}^{{}}\) whereas the opposite trend, i.e., \(V_{C7}^{{}} < V_{m}^{{}} < V_{C1}^{{}}\), is observed for methane compositions higher than \(x_{C1,min}\). This result implies the intersection of the curves representing the partial molar volumes \(V_{C7}^{{}}\) and \(V_{C1}^{{}}\) as a function of methane mole fraction. To confirm this behavior, the partial molar volumes of both components were numerically computed from measurements according to the following relations:
In these relations, the derivatives of molar volume with respect to methane mole fraction were estimated by first fitting the molar volume data by a Padé approximant of order 2/3. Due to the numerical derivation, the uncertainty in the determination of \(V_{C1}^{{}}\) and \(V_{C7}^{{}}\) is particularly significant at the limits of the mole fraction interval (0 and 1) which correspond to the infinite dilution of methane \(V_{C1}^{\infty }\) and heptane \(V_{C7}^{\infty }\), respectively. Nevertheless, the method is sufficiently robust for a qualitative exploration of the change in partial molar volume with respect to composition, as shown graphically in Figs. 4 and 5. It can be seen in these figures that \(V_{C1}^{{}}\) is monotonically increasing whereas \(V_{C7}^{{}}\) is monotonically decreasing with respect to \(x_{C1}^{{}}\), meaning that both partial molar volumes are always lower than pure components molar volumes \(V_{C1}^{*}\) and \(V_{C7}^{*}\), leading to a negative excess volume at any condition.
It can be noticed in Fig. 5 that \(V_{C7}^{{}}\) remains equal to \(V_{C7}^{*}\) up to 40% of methane and then it drastically decreases with the addition of methane. The lower the pressure, the higher the drop in the n-heptane partial molar volume leading to a crossover point of different isobars around 60% of methane. Such a crossover of the isobaric curves of \(V_{C7}^{{}}\), already observed by Reamer and Sage [40], spotlights a change in the pressure effect on isopleth curves of \(V_{C7}^{{}}\). Indeed, as shown in Fig. 6 which presents the effect of pressure on \(V_{C7}^{{}}\) at fixed methane composition, for mixtures with low methane content \(V_{C7}^{{}}\) decreases with respect to pressure as it would normally be the case for the molar volume of pure components. However, for higher methane content, an increase of this partial molar volume with pressure is observed.
Partial molar volume of n-heptane \(V_{C7}^{{}}\) in the binary system methane + n-heptane as a function of pressure for different isopleths at temperature T = 303.15 K.  , \(x_{c1}\) = 0 %;
, \(x_{c1}\) = 0 %;  , \(x_{c1}\) = 40 %;
, \(x_{c1}\) = 40 %;  , \(x_{c1}\) = 60 %;
, \(x_{c1}\) = 60 %;  , \(x_{c1}\) = 70 %;
, \(x_{c1}\) = 70 %;  , \(x_{c1}\) = 80 %;
, \(x_{c1}\) = 80 %;  , \(x_{c1}\) = 85 %;
, \(x_{c1}\) = 85 %;  , \(x_{c1}\) = 90 %;
, \(x_{c1}\) = 90 %;  , \(x_{c1}\) = 95 %;
, \(x_{c1}\) = 95 %;  , \(V_{C7}^{\infty }\) (Color figure online)
, \(V_{C7}^{\infty }\) (Color figure online)
The results for \(V_{C1}^{{}}\) and \(V_{C7}^{{}}\) at 30 MPa are plotted as a function of \(x_{C1 }\) on the same graph in Fig. 7. As expected by Eq. 8, a crossover between both curves is observed (around 90 % of methane for this pressure). In agreement with Eq. 8, it can be seen that the crossover point between partial molar curves also intersects the \(V_{m}^{{}}\) curve at its minimum. The fall in n-heptane partial molar volume is so pronounced at this pressure that \(V_{C7}^{{}}\) reaches a negative value at infinite dilution in this condition of temperature and pressure. Such a negative solute molar volume leads to a contraction of the system and a decrease in pressure by addition of nC7 molecules in pure C1 at fixed total volume V according to the following thermodynamic relation:
Thus, the mixture in these supercritical conditions has a lower overall volume than methane alone, see Fig. 3. Such a negative value of the nC7 partial molar volume was already noticed at infinite dilution of heptane in supercritical carbon dioxide [30]. This behavior observed in diluted solutions formed by a solvent with a very large compressibility and a solute of low volatility is often qualified as a clustering effect [41, 42]. It has been interpreted as a local structuring of solvent molecules around solute molecules [43,44,45], a picture which is fully supported by molecular simulations [46].
In this clustering regime, the number of solvent molecules (methane) surrounding a solute molecule (n-heptane) is larger than the bulk. The excess number of solvent molecules surrounding a solute molecule with respect to a uniform distribution can be quantified by means of the “cluster size” \(\xi_{cluster}^{{}}\) [43] which is related to solute–solvent fluctuation integral according to the following relation:
where \(g_{C1 - nC7}^{\infty }\) is the pair correlation function at infinite dilution of nC7 in the C1 solvent. According to the statistical mechanical theory of solutions of Kirkwood and Buff [47], the cluster size can also be related to volumetric data [43]:
From this relation and using volumetric measurements carried out at 303.15 K and 30 MPa, a value equal to 1.2 is obtained, thereby confirming an excess number of methane molecules around n-heptane at infinite dilution for this thermodynamic condition.
The deviations of molar volume from ideality have been calculated to complete the volumetric study of the system. From the experimental density, the excess molar volume \(V_{m}^{E}\) was calculated for each composition and pressure using the following expression:
with
The results are listed in Table 4 and plotted as a function of methane mol% in Fig. 8. To highlight the importance of excess volume in comparison to the ideal volume, the relative excess volume \(V_{m}^{RE}\) is plotted in Fig. 8 instead of \(V_{m}^{E}\). As proposed by Balankina [48] this quantity is defined by the ratio between excess volume and ideal molar volume:
Figure 8 shows that the excess volume caused by the asymmetry in molecular size is largely negative for all the pressure investigated indicating a substantial contraction of system during mixing compared to an ideal behavior. The lower the pressure, the larger the differences in pure component compressibility and the more significant the excess molar volume. At the lower pressures of investigation, the deviation with respect to the mole fraction additivity rule Eq. 15 can be higher than 20 %, which represents a very significant value for that excess property.
3.2 Isothermal Compressibility
The experimental observation of the large negative excess volume as well as the significant decrease in partial molar volume of nC7 solute at high dilution in methane solvent is a result of large asymmetry in the compressibility of pure components. Thus, it appears useful to study the excess isothermal compressibility of such light–heavy binary system. To this end, the isothermal compressibility was first determined by numerical derivation of density measurements carried out in pure components and in the different binary mixtures. The derivation of density data was achieved by a computation technique based on a Monte Carlo method [49] which makes possible to obtain both the isothermal compressibility \(\kappa_{T}\) and its expanded uncertainty \(U\left( {\kappa_{T} } \right)\).
The method consists in randomly disturbing the data according to their combined standard uncertainties so as to obtain M (5000) set of perturbed density data. Each of them is fitted with an equation of state and derived so as to calculate the compressibility for each of the 5000 Monte Carlo trials. Finally, the mean and the standard deviation of the resulting compressibility distribution are calculated to obtain both the compressibility and its standard uncertainty. The method which was originally developed for weakly compressible liquids works with three different equations of state proposed, respectively by Hudleston [50], Murnaghan [51] and Tammann [52] for representing liquid density with respect to pressure with only three parameters. However, for mixtures containing more than 60% of methane these equations are no longer suitable to represent the high compressibility of these mixtures. For such compressible fluids a Benedict–Webb–Rubin [53] type equation was considered for representing the high compressibility of the system in these conditions. This equation expresses the compressibility factor of the mixture \(\left( {Z = PV_{m} /\left( {RT} \right)} \right)\) of the molar density \(\rho_{m}\) according to the following expression:
So as to limit oscillation risk in compressibility computation at the extremity of the investigated pressure domain, 3 additional density measurements were added above the upper bound (at p = 75 MPa, 80 MPa and 90 MPa) and below the lower bound (7 MPa, 8 MPa and 9 MPa for a lower bound at 10 MPa). These additional densities were measured only to reduce the uncertainty in the compressibility determination and therefore were not included in Table 3. Both the isothermal compressibility and its expanded standard uncertainties \(U\left( {\kappa_{T} } \right)\) obtained in this way are listed in Table 5. This expanded uncertainty accounts for the uncertainty caused by mixture preparation and sample purities in addition to the uncertainty in isothermal compressibility computation.
As for density, the compressibility data for pure methane and n-heptane have been compared with the calculation of Setzmann and Wagner [36] and Span and Wagner [37], respectively. An average absolute deviation (AAD) of 0.14 % and a maximum deviation (MD) of 0.40 % are observed for methane whereas for n-heptane an AAD of 0.47 % and an MD of 1.2% are found. All these deviations are in good agreement with the estimated uncertainties of both the measurements and the correlations, thereby confirming the capability of the proposed computation procedure for working in an extended compressibility range.
The change in isothermal compressibility with addition of methane is shown in Fig. 9. It can be seen in this figure that \(\kappa_{T}\) increases with methane mole fraction with an exponential shape. In particular, at high content of methane, the compressibility of methane solvent drastically decreases by addition of n-heptane. This significant decrease in compressibility at high methane content is related to the positive slope of the molar volume with respect to pressure as observed in Fig. 6 for mixture with a methane content higher than 60 %. Indeed, for such conditions, the isothermal compressibility of the system is related to the difference of two positive contributions:
with
By comparing the real compression behavior with the ideal one defined by the following combination rule:
where \(\emptyset_{C1}\) stands for the volume fraction of the light component:
It can be observed in Fig. 10 that the real compressibility is much lower than the ideal one. To emphasize this difference, excess isothermal compressibility \(\kappa_{T}^{E} \left( {\kappa_{T}^{{}} - \kappa_{T}^{id} } \right)\) was calculated. The results are listed in Table 6 and the relative excess isothermal compressibility \(\kappa_{T}^{RE}\) corresponding to the ratio between excess isothermal compressibility and the ideal isothermal compressibility \(\kappa_{T}^{E} /\kappa_{T}^{id}\) is plotted along different isobars in Fig. 11. An observation of this figure reveals a large deviation of compressibility data from ideality for all investigated pressures. The excess isothermal compressibilities are much lower than those expected for an ideal solution whatever the composition. By comparing the relative excess compressibility and the relative excess volume, it can be noticed that the effect of non-ideality caused by size asymmetry is magnified on such derivative property.
3.3 Speed of Sound and Isentropic Compressibility
Measurements of speed of sound w were performed for pure n-heptane and eight different mixtures ranging from 20 mol to 95 mol% methane as for density. The data of pure methane were obtained from the reference equation of state developed by Setzmann and Wagner [36] with a maximum uncertainty of 0.15 % (level of confidence = 0.95, k = 2) in the experimental range. The full set of data is summarized in Table 7. Pure heptane data were compared with previously measured values [54,55,56,57] in the same range through the deviations with the interpolation of the literature data. Comparison with data from Boelhouwer [54] shows a very good agreement with a maximum deviation of 0.09 %. Comparison with Daridon et al. [55] yields again a good match of both sets of data with an average deviation of 0.03 % with a maximum of 0.11 %. Data from Yebra et al. [57] are also in good agreement with an average of 0.11 % and maximum deviation of 0.25 %. A slightly higher deviation is observed with the data of Dzida and Ernst [56] with an average value of 0.13 % and a maximum of 0.40 %.
The influence of composition on speed of sound is graphically presented in Fig. 12. An examination of this figure shows that the speed of sound does not follow a monotonous decrease with addition of methane. A minimum is observable in the isobaric curves whatever the pressure. To analyze the presence of this minimum, the isentropic compressibility \(\kappa_{S}^{{}}\) was calculated from speed of sound and density data using the Newton–Laplace equation:
The result is plotted in Fig. 13 for one pressure (30 MPa). The isentropic compressibility \(\kappa_{S}^{id}\) corresponding to ideal behavior is added in this figure. Because \(\kappa_{S}^{id}\) cannot be calculated by a simple combination of isentropic compressibility of pure components, the ideal isentropic compressibility is determined from the thermodynamic equation that relates it to the isothermal compressibility:
where \(\Delta \kappa^{id}\) is the ideal non-isothermal compressibility correction:
In this expression, the ideal isobaric expansion \(\alpha_{p}^{id}\) and ideal molar heat capacity \(C_{pm}^{id}\) were obtained from the following ideal combination rules:
This set of equations requires, in addition to density, isothermal compressibility and speed of sound data given in Tables 3, 5 and 7, the isobaric expansion of both pure components. It was obtained by derivation of density data with respect to temperature using the same method than the one proposed for computing isothermal compressibility. In this case polynomial functions \(\rho \left( T \right)\) and \(Z\left( T \right)\) were considered for fitting isobaric density data of pure n-heptane and methane, respectively. For that purpose, additional density data (not reported here) were used to extend the temperature range around 303.15 K. The values of isobaric expansion obtained in this way are reported in Table 8 for both components. They deviate of 0.1 % and 2.1 % on average from the correlations of Setzmann and Wagner [36] and Span and Wagner [37] for methane and n-heptane, respectively.
Observation of Fig. 13 shows that the experimental data are always lower than the ideal isentropic compressibility as already observed for isothermal compressibility. The experimental data monotonously increase with methane content whereas ideal behavior exhibits a maximum around 94 % of methane. This maximum is related to the difference in the shape of the curves \(\kappa_{T}^{id}\) and \(\Delta \kappa^{id}\), from which \(\kappa_{S}^{id}\) is deduced thanks to Eq. 24. One increases linearly with methane volume fraction \(\emptyset_{C1}\) whereas the other one exhibits a nearly parabolic shape as shown in Fig. 14. The result is a maximum in their difference and consequently a change of sign of the derivative of \(\kappa_{S}^{id}\) with respect to methane content.
Comparison between idea isothermal and isentropic compressibilities as a function of volume fraction \(\emptyset_{C1}\) at temperature T = 303.15 K and pressure p = 30 MPa.  , ideal isothermal compressibility \(\kappa_{T}^{id}\);
, ideal isothermal compressibility \(\kappa_{T}^{id}\);  , ideal non-isothermal compressibility correction \(\Delta \kappa^{id}\);
, ideal non-isothermal compressibility correction \(\Delta \kappa^{id}\);  , ideal isentropic compressibility \(\kappa_{S}^{id}\) (Color figure online)
, ideal isentropic compressibility \(\kappa_{S}^{id}\) (Color figure online)
The equation of Newton–Laplace (Eq. 23) implies that twice the logarithmic derivative of speed of sound with respect to mole fraction is equal to the sum of two contributions: \(- \left( {\partial \rho /\partial x_{C1} } \right)/\rho\) and \(- \left( {\partial \kappa_{S} /\partial x_{C1} } \right)/\kappa_{S}\). The logarithmic derivative of \(\rho\) is positive whereas the logarithmic derivative of \(\kappa_{S}\) with respect to \(x_{C1}\) can be either positive or negative. In case of an ideal solution, the logarithmic derivative of \(\kappa_{S}^{id}\) decreases with \(x_{C1}\) to reach a negative value at high methane content due to the maximum observed in Fig. 13. Consequently, the curve representing this logarithmic derivative intersects the curve of the opposite of logarithmic derivative of \(\rho_{{}}^{id}\) that monotonically increases with \(x_{C1}\) as shown in Fig. 15. At this point (around 70 % of methane) the ideal speed of sound \(w_{{}}^{id}\) (calculated from Eq. 23 with \(\rho_{{}}^{id}\) and \(\kappa_{S}^{id}\)) presents a minimum as observed in Fig. 16. A maximum is not observed in Fig. 13 for \(\kappa_{S}^{{}}\) but only in its logarithmic derivative, as shown in in Fig. 15. This leads to an intersection with the opposite of the logarithmic derivative of \(\rho\) around 95 % of methane and therefore a minimum in the speed of sound isobaric curve as shown in Fig. 16. Consequently, the existence of the extremum in the speed of sound isobaric curves is not related to the non-ideality of the binary system but rather to the definition of the speed of sound which depends both on density and isentropic compressibility according to the Newton–Laplace equation, Eq. 23.
Comparison of the change of the logarithmic derivatives with respect to methane mol% \(x_{C1}\) at T = 303.15 K and p = 30 MPa for the real and ideal solutions.  , \(\left( {\partial \kappa_{S}^{id} /\partial x_{C1} } \right)/\kappa_{S}^{id}\);
, \(\left( {\partial \kappa_{S}^{id} /\partial x_{C1} } \right)/\kappa_{S}^{id}\);  , \(- \left( {\partial \rho_{{}}^{id} /\partial x_{C1} } \right)/\rho_{{}}^{id}\);
, \(- \left( {\partial \rho_{{}}^{id} /\partial x_{C1} } \right)/\rho_{{}}^{id}\);  , \(\left( {\partial \kappa_{S} /\partial x_{C1} } \right)/\kappa_{S}\);
, \(\left( {\partial \kappa_{S} /\partial x_{C1} } \right)/\kappa_{S}\);  ,\(- \left( {\partial \rho /\partial x_{C1} } \right)/\rho\) (Color figure online)
,\(- \left( {\partial \rho /\partial x_{C1} } \right)/\rho\) (Color figure online)
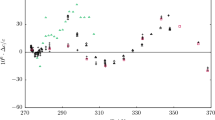
Finally, the excess isentropic compressibility \(\left( {\kappa_{S}^{E} = \kappa_{S}^{{}} - \kappa_{S}^{id} } \right)\) and the excess speed of sound \(w_{{}}^{E} = w - w_{{}}^{id}\) were calculated. Both properties are compiled in Tables 9 and 10. The relative excess properties \(\left( {\kappa_{S}^{RE} = \kappa_{S}^{E} /\kappa_{S}^{id} } \right)\) and (\(w_{{}}^{RE} = w_{{}}^{E} /w_{{}}^{id}\)) are plotted in Figs. 17 and 18 respectively. It can be noticed from these figures that \(\kappa_{S}^{RE}\) is of the same order of magnitude than \(\kappa_{T}^{RE}\) reported in Fig. 11, meaning that the deviation to ideality observed on isentropic compressibility, and consequently in speed of sound, is mainly caused by the asymmetry in isothermal compressibilities between the pure components. This asymmetry has a huge impact on speed of sound that deviates from ideal expectation by more than 200 % at low pressure.
4 Conclusion
Using two different high-pressure devices, density and speed of sound were measured in a binary asymmetric system (in terms of compressibility) composed of methane and n-heptane. The experimental data gathered at 303.15 K and at different conditions of pressure and composition have led to the determination of the isothermal and isentropic compressibilities.
In this system, the large difference in the compressibility of pure components provoked a significant negative excess values in the molar volumes with relative excess values that can reach − 20 % of the ideal molar volume. In addition, a clustering effect at p = 30 MPa was brought forth to light by evaluating the partial volume of n-heptane at infinite dilution.
Furthermore, the examination of the change of the partial molar volume of n-heptane with respect to pressure has shown an unconventional behavior with the observation of an increase of \(V_{C7}^{{}}\) with pressure for high methane content mixtures. As a result of this positive slope of the molar volume with respect to pressure, the compressibility of mixture with high methane content drastically decreases by addition of n-heptane. Relative excess volume decreases with increasing pressure but remains significant (5 %) at the highest pressure of investigation (70 MPa).
The non-ideal behavior is further reflected through the derivative properties and in particular through the relative excess isothermal compressibility that exhibits values up to 100 %. Finally, a non-monotonous change of speed of sound with respect to the addition of methane in n-heptane was found, with the presence of a minimum in the isobaric speed of sound curves plotted as a function of methane mole fraction. This extremum is not attributable to a non-ideal behavior as it is obtained, and even more significantly, with an ideal solution. It is indeed simply caused by the competition between two antagonistic effects which appear in the definition of speed of sound through the Newton–Laplace equation.
Availability of Data and Materials
All the data are given in the manuscript.
References
M.G. Martin, J.I. Siepmann, J. Phys. Chem. B 102, 2569 (1998)
E. Flöter, T.W. de Loos, J. de Swaan Arons, Int. J. Thermophys. 16, 185 (1995)
H. Quinteros-Lama, F. Llovell, J. Supercrit. Fluids 111, 151 (2016)
J.F. Arnaud, P. Ungerer, E. Behar, G. Moracchini, J. Sanchez, Fluid Phase Equilib. 124, 177 (1996)
J.H. Dymond, K.J. Young, J.D. Isdale, J. Chem. Thermodyn. 11, 887 (1979)
T. Regueira, G. Pantelide, W. Yan, E.H. Stenby, Fluid Phase Equilib. 428, 48 (2016)
J.L. Daridon, B. Lagourette, P. Xans, F. Montel, J. Pet. Sci. Eng. 19, 281 (1998)
E. Aicart, N.K. Kumaran, C.J. Halpin, G.C. Benson, J. Chem. Thermodyn. 15, 919 (1983)
G.C. Benson, C.J. Halpin, N.K. Kumaran, J. Chem. Thermodyn. 18, 1147 (1986)
G.C. Benson, C.J. Halpin, Can. J. Chem. 65, 322 (1987)
J.D. Pandey, P. Jain, V. Vyas, Can. J. Chem. 72, 2486 (1994)
A. Tourino, M. Hervello, V. Moreno, M. Iglesias, G. Marino, Phys. Chem. Liq. 42, 37 (2004)
M. Gepert, S. Ernst, J. Solut. Chem. 32, 831 (2003)
T. Takagi, H. Teranishi, Fluid Phase Equilib. 20, 315 (1985)
S. Ye, B. Lagourette, J. Alliez, H. Saint-Guirons, P. Xans, F. Montel, Fluid Phase Equilib. 74, 177 (1992)
M. Dzida, M. Cempa, J. Chem. Thermodyn. 40, 1531 (2008)
T.S. Khasanshin, V.S. Samuilov, A.P. Shchemelev, High Temp. 47, 527 (2009)
T.S. Khasanshin, V.S. Samuilov, A.P. Shchamialiou, High Temp. High Press. 39, 321 (2010)
T.S. Khasanshin, V.S. Samuilov, A.P. Shchemelev, F.M. Mosbach, J. Eng. Phys. Thermophys. 83, 1043 (2010)
T.S. Khasanshin, V.S. Samuilov, A.P. Shchemelev, High Temp. 48, 665 (2010)
T.S. Khasanshin, N.V. Golubeva, V.S. Samuilov, A.P. Shchemelev, J. Eng. Phys. Thermophys. 87, 213 (2014)
B. Lagourette, J.L. Daridon, J.F. Gaubert, P. Xans, J. Chem. Thermodyn. 26, 1051–1061 (1994)
C.D. Holcomb, S.L. Outcalt, Fluid Phase Equilib. 150–151, 815 (1998)
C. Bouchot, D. Richon, Fluid Phase Equilib. 191, 189 (2001)
E.F. May, W.J. Tay, M. Nania, A. Aleji, S. Al-Ghafri, J.P.M. Trusler, Rev. Sci. Instrum. 85, 095111 (2014)
E.F. May, W.J. Tay, M. Nania, A. Aleji, S. Al-Ghafri, J.P.M. Trusler, Rev. Sci. Instrum. 86, 049902 (2015)
W. Wagner, A. Pruß, J. Phys. Chem. Ref. Data 31, 387 (2002)
R. Span, E.W. Lemmon, R.T. Jacobsen, W. Wagner, A. Yokozeki, J. Phys. Chem. Ref. Data 29, 1361 (2000)
JCGM 101:2008. Evaluation of measurement data—Supplement 1 to the “Guide to the expression of uncertainty in measurement”—Propagation of distributions using a Monte Carlo method
J.P. Bazile, D. Nasri, A.W. Saley Hamani, G. Galliero, J.L. Daridon, J. Supercrit. Fluids. 140, 218 (2018)
J.P. Bazile, D. Nasri, J.L. Daridon, J. Chem. Eng. Data 62, 1708 (2017)
V.A. Del Grosso, C.W. Mader, J. Acoust. Soc. Am. 52, 1442 (1972)
W. Marczak, J. Acoust. Soc. Am. 102, 2776 (1997)
W.D. Wilson, J. Acoust. Soc. Am. 31, 1067 (1959)
S. Vance, J.M. Brown, J. Acoust. Soc. Am. 127, 174 (2010)
U. Setzmann, W. Wagner, J. Phys. Chem. Ref. Data 20, 1061 (1991)
R. Span, W. Wagner, Int. J. Thermophys. 24, 41 (2003)
H.H. Reamer, B.H. Sage, W.N. Lacey, Chem. Eng. Data Ser. 1, 29 (1956)
D.S. Robertson, C.R. Clark, G. Swift, Soc. Pet. Eng. J. 9, 338 (1969)
H.H. Reamer, B.H. Sage, J. Chem. Eng. Data 4, 98 (1959)
C.A. Eckert, D.H. Ziger, K.P. Johnston, T.K. Ellison, Fluid Phase Equilib. 14, 167 (1983)
C.A. Eckert, D.H. Ziger, K.P. Johnston, S. Kim, J. Phys. Chem. 90, 2738 (1986)
P.G. Debenedetti, Chem. Eng. Sci. 42, 2203 (1987)
D.B. McGuigan, P.A. Monson, Fluid Phase Equilib. 57, 227 (1990)
R.S. Wu, L.L. Lee, H.D. Cochrant, Ind. Eng. Chem. Res. 29, 977 (1990)
A.W. Saley Hamani, H. Hoang, T.Q. Quoc Viet, J.L. Daridon, G. Galliero, J. Supercrit. Fluids. 164, 104890 (2020)
J.G. Kirkwood, F.P. Buff, Fluid Phase Equilib. 52, 347 (1989)
E.S. Balankina, High Temp. 47, 56 (2009)
J.L. Daridon, J.P. Bazile, J. Chem. Eng. Data 63, 2162 (2018)
L.J. Hudleston, Trans. Faraday Soc. 33, 97 (1937)
F.D. Murnaghan, Proc Natl Acad Sci USA. 30, 244 (1944)
G.Z. Tammann, Phys. Chem. 17, 620–636 (1895)
M. Benedict, G. Webb, L.C. Rubin, J. Chem. Phys. 10, 747 (1942)
J.W.M. Boelhouwer, Phys. A 34, 484 (1967)
J.L. Daridon, B. Lagourette, A. Lagrabette, Phys. Chem. Liq. 37, 137 (1999)
M. Dzida, S.S. Ernst, J. Chem. Eng. Data 48, 1453 (2003)
F. Yebra, J. Troncoso, L. Romaní, J. Chem. Thermodyn. 104, 102 (2017)
Funding
Not applicable.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that they have no conflict of interest.
Code Availability
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Bazile, JP., Nasri, D., Hoang, H. et al. Density, Speed of Sound, Compressibility and Related Excess Properties of Methane + n-Heptane at T = 303.15 K and p = 10 to 70 MPa. Int J Thermophys 41, 115 (2020). https://doi.org/10.1007/s10765-020-02694-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10765-020-02694-9



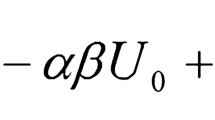


 , 10 MPa;
, 10 MPa;  , 30 MPa;
, 30 MPa;  , 50 MPa;
, 50 MPa;  , 70 MPa (Color figure online)
, 70 MPa (Color figure online)
 , 20 MPa;
, 20 MPa;  , 40 MPa;
, 40 MPa;  , 60 MPa;
, 60 MPa; 



 ,
,  ,
, 









