1 Introduction

The International Temperature Scale of 1990 (ITS-90) between 13.8033 K and 1234.93 K is realized by calibrating a standard platinum resistance thermometer (SPRT) at certain defining fixed points of the ITS-90. The triple point of Hg (\(T_{\mathrm{TP,Hg}}\), 234.3156 K) is one of such fixed points, and is indispensable for the realization of the temperature scale in all subranges of the ITS-90 between 13.8033 K and 273.16 K [1, 2]. The triple point of Hg (TPHg) is usually realized using large cells containing approximately 2 kg of Hg [3,4,5,6,7,8,9]. The TPHg is realized in such a large cell by maintaining a heat balance between the enthalpy of the transition of the sample and the heat flow from the liquid bath during continuous heating or cooling, using the same method as for other metal fixed points [10]. These systems are suitable for calibrating long-stem SPRTs, which are normally used at temperatures above 77 K. On the other hand, cryogenic fixed points below \(T_{\mathrm{TP,Hg}}\) are usually realized using an adiabatic calorimeter optimized for precise calibration of capsule-type SPRTs for use at low temperatures [11]. The adiabatic calorimeter with its small sample cell makes it possible to calibrate capsule-type SPRTs with smaller uncertainty because the influence of heat flux, the hydrostatic effect, and the distribution of temperature in the cell can all be minimized compared with larger cells.

Several attempts to develop an adiabatic calorimeter with a small Hg cell for the calibration of capsule-type SPRTs at the TPHg with low uncertainty have been reported [12,13,14,15]. The National Metrology Institute of Japan (NMIJ/AIST) has developed an adiabatic calorimeter using a pulse-tube refrigerator instead of liquid refrigerant, and succeeded in maintaining the TPHg within \(10\, \upmu \mathrm {W}\) of heat flux for a long time [14]. In this paper, we report the calibration of a capsule-type SPRT using the adiabatic system with a high-purity Hg sample (99.999 99 %, 7N) contained within a small glass cell at NMIJ/AIST and evaluate calibration uncertainty in detail. The standard combined uncertainty of the realization of TPHg using the adiabatic system was estimated to be 0.12 mK and that in calibrating a capsule-type SPRT is estimated to be 0.19 mK which included the propagation of the uncertainty from the triple point of water (TPW). It was much less than that using a conventional system based on large cells at NMIJ/AIST. The TPHg temperature realized using the adiabatic system is consistent (within the uncertainty) with that achieved by a traditional calibration system using large cells at NMIJ/AIST.

Moreover, we studied a degree of the supercooling during the realization of the TPHg. A degree of the supercooling of Hg was reported as 0.1 K to 0.3 K in a large stainless cell, up to 6 K in large glass cell, about 0.5 K in a small stainless cell, and about 3 K in a glass cell, respectively, even though high-purity Hg (within 99.999 995 %) sample was used [3, 4, 15]. However, using our small glass cell, we observed a very large supercooling, about as large as 20 K, through the realization of the TPHg. Since degree of the supercooling is known to be promoted by rapid cooling which is used for producing the large supercooling in the study of the supercooled liquid metal [16], we observed the degree of the supercooling by changing the cooling rate and evaluated the degree of the supercooling of Hg preciously. As a result, we find that degree of the supercooling is stabilized at 18.2 K even at a slow cooling rate of less than 1\(0^{-7}\,\mathrm { K}/\mathrm {s}\) by using the small glass cell.

Fig. 1
figure 1

Schematic illustration of the adiabatic calorimeter using a small glass Hg cell for calibrating a capsule-type standard platinum resistance thermometer at the triple point of Hg

Full size image

2 Experiment and Measurement

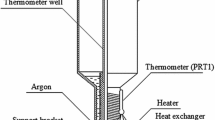
Figure 1 shows a schematic illustration of the adiabatic calorimeter with a small Hg cell. The small Hg cell was made of cylindrical borosilicate glass and had a volume of \(0.6\,\mathrm { cm}^3\). It contained about 80 mmol of mercury with a purity of 7N under its own vapor pressure. The small Hg cell and a capsule-type SPRT were installed inside an aluminum block 3 cm in diameter and 6 cm in length. To reduce the temperature distribution caused by hydrostatic pressure, we placed the small Hg cell horizontally, resulting in 3.5 mm of hydrostatic height. As a result, the temperature distribution due to the hydrostatic pressure is estimated to be approximately 0.025 mK.

The aluminum block was suspended by nylon strings and completely covered by the adiabatic shield and a dual radiation shield. We attached this system to the 2nd stage of a pulse-tube refrigerator and placed the assembly in vacuum. In order to control the adiabatic conditions, we measured the temperature difference between the adiabatic shield and the aluminum block using the multiple of the type-T thermocouples and controlled the temperature of the adiabatic shield by adjusting the current to the heater attached to the adiabatic shield using a PID controller.

On the other hand, the traditional large Hg cell was made of stainless steel and its hydrostatic height from the bottom of the thermometer well to liquid surface was 182 mm, which corresponds to approximately 1.3 mK of temperature depression. Therefore, it is necessary to correct for hydrostatic height during SPRT calibration. Such a cell is installed inside a isothermal bath and covered by thermal insulation, but the heat flux from the bath to the large Hg cell was approximately 0.7 W at \(T_{\mathrm{TP,Hg}}\), which is much larger than that of the adiabatic system. A detailed description of this cell and the method of realizing the TPHg were reported in [7].

We measured the resistance of an SPRT using a high-accuracy dc resistance bridge with a \(10\, {\Omega }\) standard resistor. To correct for the influence of self-heating caused by the measurement current, we used two measurement currents: \(I=1.0\) mA and 1.414 mA, and refered to the resistance at \(I=0\) mA by extrapolation. All data shown in this study are obtained by using the corrected resistance at \(I=0\) mA.

The measurement procedures employed to realize the TPHg using the adiabatic system were as follows. First, the system inside the vacuum jacket cooled down and temperature of the adiabatic shield was controlled by the heater attached to the adiabatic shield. In order to obtain an optimal setting for the adiabatic control, we measured the temperature drift as a function of the temperature of the adiabatic shield near \(T_{\mathrm{TP,Hg}}\). As a result, the influence of heat flux into the sample can be reduced to within \(10\, \upmu \mathrm {W}\) at \(T_{\mathrm{TP,Hg}}\). And then, the liquid sample was re-cooled until the entire sample was frozen. In this process, we observed the supercooling of the Hg in the small glass cell to be approximately 18 K which is much larger than values previously reported for both large and small cells [3, 4, 15]. This effect is described in more detail in a later section.

Second, about half of the solidified Hg was melted to reduce lattice defects of solid Hg caused by recovering from the large supercooling. After this, the liquid Hg sample was re-solidified by cooling the aluminum block down to approximately 0.5 K below \(T_{\mathrm{TP,Hg}}\).

Third, we realized the TPHg by the heat pulse method using a heater on the aluminum block. Generally, the triple point temperature of a cryogenic fixed point using an adiabatic calorimeter is determined at a melted fraction of \(F=1\) (F is the fraction of liquid phase) by extrapolating the temperature plotted against \(1/{}F\) [11]. Here, F is calculated as \(F=\sum Q_{i}/Q_{\mathrm{total}}\), where \(Q_{i}\) is an amount of heat applied during each heat pulse while on plateau, and \(Q_{\mathrm{total}}\) is the total heat of fusion of the Hg sample. In this measurement, \(Q_{\mathrm{total}}\) is approximately 190 J. After each heat pulse with the sample returned to thermal equilibrium, we obtained the F-dependent resistance of the SPRT at the TPHg.

The ITS-90 for SPRTs is defined in terms of the resistance ratio \(W=r/r_{\mathrm{TPW}}\), where r is resistance of SPRT and \(r_{\mathrm{TPW}}\) is the resistance of SPRT at the TPW. Therefore, we calibrated the SPRT at the TPW before and after the measurement at TPHg, and determined \(r_{\mathrm{TPW}}\) as the average of these results.

3 Results and Discussion

Fig. 2
figure 2

Resistance ratio \(W(=r/r_{\mathrm{TPW}}\)) vs. time t around the TPHg using a small glass cell, where r is the resistance of the standard platinum resistance thermometer and \(r_{\mathrm{TPW}}\) is resistance of the standard platinum resistance thermometer at the triple point of water. Inset shows typical data of one of the pulse heating, which is an enlargement of the main panel. The solid line of inset is fit of the data to a simple exponential function

Full size image
Fig. 3
figure 3

The melted fraction F dependences of the relaxation time \(\tau \) from 3 measurements. Inset shows the same data plotted on a log–log scale. The dot line is fit to power law divergence toward \(F=1\)

Full size image

3.1 Realization of the Triple Point of Hg

Figure 2 shows some melting curves of the TPHg obtained with the small glass cell. The plateau of the melting curve indicates the realization of the TPHg (horizontal dotted line), lasting over 100 h. The temperature of the SPRT rose during heat pulse, and then decayed exponentially toward the thermal equilibrium state after each heat pulse. The inset of Fig. 2 shows typical resistance ratio data for one heating pulse. The solid line in the inset of Fig. 2 is a simple exponential fitting function: \(W(t)= \exp {-\mathrm{t}/\mathrm{T}}\) is the resistance ratio W at thermal steady state after a heat pulse, \(W_{0}\) is W at the heat pulse stopped, and \(\tau \) is a characteristic relaxation time. From the melting curve at each heat pulse, we obtained \(\tau \) by fitting the data using the least squares method and plotting against the melted fraction F, as shown in Fig. 3. The relaxation time \(\tau \) becomes longer as the melted fraction F increases, and indicates a power law response toward \(F = 1\) as shown in the inset of Fig. 3. Resistance was measured after 1 h at \(F<0.5\) and after 2 h at \(F>0.5\), respectively. Because we used the \(F<0.85\) data to determine the liquidus point of the TPHg by extrapolation, it should be sufficient time to reduce \(W(t)-W_{\infty }\), which is the so-called dynamic temperature measurement error [11].

Fig. 4
figure 4

The resistance ratio W plotted against the inverse of the melted fraction F at TPHg using the small glass cell taken from 3 measurements. The dot line is a linear fit with 1/F in Run 1. One division in W corresponds to \(250\, \upmu \mathrm {K}\)

Full size image

Figure 4 shows the resistance ratio W of the SPRT obtained at the steady state after each pulse plotted against 1 / F. As shown in Fig. 4, W is almost flat against 1 / F well within \(250\, \upmu \mathrm {K}\) (1 scale division), which is consistent with the high purity of the sample [8, 9]. Then, we determined W at the liquidus point of the TPHg by extrapolating W against 1 / F in the range of \(0.45<F<0.85\).

Table 1 Uncertainty budget (\(k=1\)) for the realization of the TPHg using the adiabatic calorimeter with the small glass cell
Full size table

3.2 Results of the Calibration

We evaluated the uncertainty of the realization of the TPHg using the adiabatic calorimeter. The estimated uncertainty budget is shown in Table 1. The individual uncertainty components were estimated as follows.

The uncertainty from the resistance bridge and standard resistor were calculated in the same manner as in a previous report from NMIJ/AIST to be 0.011 mK and 0.02 mK, respectively [17]. In addition, we evaluated 0.05 mK of uncertainty from the resistance measurement as the standard deviation of the resistance measurement. The uncertainty of the liquidus point determination for TPHg was estimated to be 0.087 mK, as calculated from the 95 % confidence interval of the melting curve fits for \(F=0.45\)–0.85. This value caused by the distribution of the W at thermal equilibrium state is much larger than that of the previous report [17]. Furthermore, a 0.005 mK uncertainty due to repeatability of the TP realization was estimated from the standard deviation of the determined value of W at \(F=1\) taken from 3 measurements. A 0.032 mK uncertainty related to the self-heating correction was calculated from two resistance measurements with measurement currents of 1.0 mA and 1.414 mA.

When no detailed analysis is available, the uncertainty from chemical impurities \(u_\mathrm{imp}\) is calculated based on the overall maximum estimated (OME) value as \(u_{\mathrm{imp}}=xRT_{\mathrm{TP}}^2/\sqrt{3}\varDelta {H}\), where x is the nominal impurity, R is the molar gas constant, and \(\varDelta {H}\) is the molar enthalpy of fusion for Hg at \(T_{\mathrm{TP,Hg}}\), as 2301 J/mol [18]. Since the nominal purity of the Hg in the small glass cell was 99.999 99 % or higher, \(u_{\mathrm{imp}}\) was calculated to be 0.011 mK.

The temperature difference of the Hg from the bottom to surface caused by hydrostatic pressure was calculated as \({\varDelta }T=hg\rho (dT/dp)\), where h is the hydrostatic height of the Hg, g is the acceleration of gravity, and \(\rho \) is the density of liquid Hg. The value of temperature with pressure dT / dp at the TPHg is listed in Ref. [1], as \(dT/dp = 5.4 \times 10^{-8}\, \mathrm{K}\cdot {\mathrm{Pa}}^{-1} \). Since h was 3.5 mm for this sample, which corresponds 0.025 mK, we estimated a 0.007 mK uncertainty from hydrostatic effects as a rectangular distribution.

The uncertainty from adiabatic control includes both static and dynamic temperature errors. The static temperature error is caused by heat flux at the TPHg, and is evaluated as \(\varDelta T_{\mathrm{e}}=R_{\mathrm{CS}}C_{\mathrm{total}}\)(dT / dt), where \(\varDelta T_{\mathrm{e}}\) is the temperature difference caused by heat flux into the Hg cell, \(R_{\mathrm{CS}}\) is the thermal resistance between the Hg and the cell, \(C_{\mathrm{total}}\) is the total heat capacity of the Hg and the aluminum block, and dT / dt is the rate of the temperature drift near TPHg caused by heat flux [19]. In this system, \(C_{\mathrm{total}}\)(dT / dt) is below \(10\, \upmu \mathrm {W}\), as obtained from heat capacitance measurements and temperature drift measurements near TPHg.

Fig. 5
figure 5

Thermal resistance \(R_{\mathrm{CS}}\) vs. melted fraction F

Full size image

Here, we measured \(\varDelta T_{\mathrm{e}}\) for different \(C_{\mathrm{total}}(dT/dt)\) values at \(F=0.3\), 0.5, 0.6, 0.7, 0.8, 0.85, 0.9 to obtain \(R_{\mathrm{CS}}\). Figure 5 shows that \(R_{\mathrm{CS}}\) tends to increase with increasing F, which is similar to the behavior of F-dependent \(\tau \). These behaviors agree approximately with a simple resistance–capacitance model, \(\tau = R_{\mathrm{CS}}C_{\mathrm{total}}\) [19]. Since the heat flux of this measurement was less than \(10\, \upmu \mathrm {W}\), we calculated the uncertainty from static temperature error as a rectangular distribution with a maximum value of \(\varDelta T_{\mathrm{e}}\) at \(F=0.45\)–0.85. Meanwhile, the dynamic temperature error caused by the thermal equilibrium state after a heat pulse was evaluated by subtracting \(W_{\infty }\) from W at \(F=0.45\)–0.85, where \(W_{\infty }\) was determined from the exponential fitting shown in the inset of Fig. 2 and W is the measured resistance ratio, as shown in Fig. 5. Consequently, the uncertainty from static and dynamic temperature errors were 0.038 mK and 0.04 mK, respectively. The uncertainty from the adiabatic control is 0.055 mK as combined uncertainty from static temperature error and dynamic temperature error.

As shown in Table 1, the combined standard uncertainty for the realization of TPHg using the adiabatic system is 0.12 mK. When a SPRT is calibrated, it is necessary to evaluate the resistance of SPRT at the TPW and its uncertainty. Since the uncertainty from propagation from TPW was 0.14 mK, the uncertainty for calibrating SPRT using the adiabatic system at TPHg was estimated to be 0.19 mK. On the other hand, the uncertainty of a conventional system with a large cell at NMIJ/AIST is approximately 0.4 mK, as reported in [20]. The largest uncertainty contribution for a large cell stems from heat flux from the environment, resulting in a larger melting range. Moreover, the hydrostatic effect in the small cell is negligible, and does not require a correction. Consequently, using the developed adiabatic system with a small Hg cell, we can calibrate a capsule-type SPRT with much smaller uncertainty compared with a conventional system with a large Hg cell.

Furthermore, we compared the temperature of the TPHg in the adiabatic system with that in a traditional system with a large Hg cell using an SPRT. The value of the triple point temperature in the traditional system is confirmed by international comparison CCT-K3 [20]. The difference in TPHg temperatures in the small cell and the large cell was 0.13 mK, well with the combined uncertainty of the two realization. Therefore, we confirm the consistency of the triple point temperature of both mercury cells within their uncertainty.

Fig. 6
figure 6

(a) The cooling curves of Hg in small glass cell and large stainless cell. horizontal dot line indicates the \(T_{\mathrm{TP,Hg}}\) (= 234.3156 K), (b) cooling rate dependences of \(\varDelta T_{\mathrm{r}}\), (c) cooling rate dependences of \(\varDelta T_{\mathrm{SC}}\) in small glass cell (closed circle) and large stainless cell (open circle). Horizontal dot lines in (a) and (b) indicate each saturated value at low cooling rate

Full size image

3.3 Observation of Large Supercooling

This section focuses on the large supercooling, which has not been reported for similar calibrations for SPRTs using Hg cells. Figure 6a displays typical freezing curves of mercury in both large stainless and small glass cells plotted against time. As the liquid Hg in the large stainless cell was cooled, the temperature deceased below \(T_{\mathrm{TP,Hg}}\), then suddenly increased by 1 K, finally saturating at the TPHg. On the other hand, the case of the small glass cell was significantly different. As the Hg sample in the small glass cell was cooled, the temperature of the small cell decreased, reaching approximately 18 K below \(T_{\mathrm{TP,Hg}}\). Then, the temperature rose suddenly (indicating recalescence) before cooling back.

Here, we focus on the temperature increase just after recovery from supercool of Hg \(\varDelta T_{\mathrm{r}}\) for the small cell. In order to investigate the influence of different cooling rates on the supercooling, we performed temperature measurements for different cooling rates between \(3\times 10^{-8}\,\mathrm { K}{/}\mathrm {s}\) and \(1\times 10^{-3}\,\mathrm { K}{/}\mathrm {s}\) which are calculated from the average over 1 h just before the temperature increased. As shown in Fig. 6b, the temperature increase \(\varDelta T_{\mathrm{r}}\) is stable around at about 3.5 K below \(10^{-5}\,\mathrm {K}/\mathrm {s}\) of cooling rate. Since the total heat capacity of Hg and aluminum block measured by heat capacity measurement was 55 J/K, the total heat quantity caused by \(\varDelta T_{\mathrm{r}}\) was calculated to be 192 J. This value is consistent with the total heat of fusion of the sample \(Q_{\mathrm{total}}\) of 190 J. This result confirms that the temperature increase is caused by solidification of supercooled Hg in the small cell.

Next, we determined the degree of supercooling \(\varDelta T_{\mathrm{SC}}\) as the temperature difference between \(T_{\mathrm{TP,Hg}}\) and the temperature just before recalescence. As shown in Fig. 6c, \(\varDelta T_{\mathrm{SC}}\) is 18.2 K in the small cell and 1 K in the large cell regardless of the cooling rates, respectively. Previous studies reported supercooling of 0.1 to 0.3 K for large stainless Hg cells [3], so the present behavior of the large stainless cell is consistent with these results. On the other hand, previous studies reported supercooling of approximately 3 K in a small glass cell and 0.5 K in a small stainless cell, respectively [15]. \(\varDelta T_{\mathrm{SC}}\) is much larger than the results in the previous report. At present, the reasons for such a large \(\varDelta T_{\mathrm{SC}}\) for our systems are not obvious, but the following aspects maybe related to the large supercooling for Hg. Our cell was placed horizontally, so the hydrostatic pressure is much lower than that of previous report. Furthermore, the contact states of glass and stainless are different. The low wettability restricted the possibility for nucleation, so the supercooling can be expected to be deeper. In addition, the purity of Hg is sufficiently high to suppress the nucleation of supercooling.

Although the large supercooling in a small glass Hg cell is an obstacle to triple point realization for calibration purposes, it might offer a suitable system for studying the properties of supercooling liquids, which are related to the fundamental physics of nucleation and solidification [21].

4 Conclusion

We have developed an adiabatic calorimeter for calibrating a capsule-type SPRT with a small glass Hg cell. The combined standard uncertainty for the realization of the TPHg is estimated to be 0.12 mK, much less than that of a large Hg cell at NMIJ/AIST. The realized temperature at the TPHg obtained by the adiabatic system and a capsule-type SPRT is consistent with that obtained using a traditional Hg cell within the uncertainty. Moreover, we confirmed a large supercooling of 18.2 K in a small glass cell by different cooling rate measurements. The results suggest that the large supercooling is related to the small hydrostatic height of Hg, the surface contact between Hg and cell, and/or the high purity of the Hg sample.