1 Introduction

Drying is a complex process where heat and mass transfer are simultaneously involved, with coupled effects as well.

Drying has important applications, such as:

  1. (a)

    Suitable conservation of cereal grains and some other foodstuffs to get better conditions for safe storage.

  2. (b)

    Transportation costs reduction in high-moisture-absorbing materials.

  3. (c)

    Cracks prevention in wood-made furniture and also materials related to construction.

  4. (d)

    Prevention that chemical active substances of pharmaceutical products become affected by moisture.

  5. (e)

    Prevention of flowing problems due to moisture excess when processing flours, sugar, salt and others.

Besides the above applications, drying is widely used for moisture measurement of solid materials where a considerable amount of materials (some of them with complex solid matrices) require to be measured and whose drying conditions are unknown.

The measurement of moisture content in solid materials by the gravimetric method is based on the weighing of the material, before and after drying samples into an oven. For its application, it is required to know the drying conditions such as time and temperature, whose determination in many cases is carried out by experimentation which usually requires long periods of time and large amounts of energy. In addition, this determination requires continuous monitoring by an operator to opportunely stop the drying.

The fundamental transport laws of mass, energy and momentum are useful to describe the behavior of drying. Therefore, it is possible to develop models that allow to get information about the drying conditions. Several of them describe the drying behavior of a solid material but with advantages and disadvantages. Among the most used models are the following: Philip and DeVries [1], Whitaker [2], Kowalski [3,4,5], Luikov [6] and Warren [7]. Each of them satisfactorily describes the drying processes for a restricted set of materials involving unknown thermophysical properties that are difficult to measure. Also, in some cases it is difficult to find an analytical or numerical solution.

From the cited models, Luikov’s is one of the most widely used because it has application to different types of materials and it is possible to find its analytical solution for known geometries [8].

In this paper, the analytical solution of the Luikov’s model for a one-dimensional flat plate is described. It was useful for the determination of the moisture profiles for ceramic, gypsum, wood and red brick, which allowed the determination of their drying conditions (time and temperature) and the moisture content of such materials as well. There was not found any application in which the Luikov’s model was applied in the determination of the moisture content value of a solid material.

Besides to predict the moisture content value for the above-mentioned materials, the Luikov’s model was validated experimentally in samples of wood and brick and the uncertainty of predicted moisture content value was estimated.

2 Luikov’s Model for a One-Dimensional Flat Plate

Luikov’s model assumptions:

  • The capillarity of a solid material is non-deformable,

  • Only liquid water, water vapor and dry air exist inside the capillaries,

  • The pores of the solid materials are considered open,

  • The phase changes only occur between the liquid and vapor interfaces,

  • There are no chemical reactions between the moisture substances and the solid material,

  • The mass flow in the solid body is small, in such a way that the fluid and solid temperatures are locally the same, i.e., they are in thermodynamic equilibrium.

  • The dry air and water vapor masses are small with respect to that of the liquid water, in such way that they are negligible.

  • The solid material forms only one layer,

  • The solid material is isotropic.

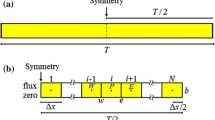
Luikov’s model equations for a flat plate (Fig. 1) are [6]:

$$ \rho C_{\text{q}} \frac{\partial T(x,t)}{\partial t} = K_{\text{q}} \frac{{\partial^{2} T(x,t)}}{{\partial x^{2} }} + \varepsilon \lambda C_{\text{m}} \rho \frac{\partial U(x,t)}{\partial t} $$
(1)
$$ \rho C_{\text{m}} \frac{\partial U(x,t)}{\partial t} = K_{\text{m}} \delta \frac{{\partial^{2} T(x,t)}}{{\partial x^{2} }} + K_{\text{m}} \frac{{\partial^{2} U(x,t)}}{{\partial x^{2} }}, $$
(2)

where T is the temperature potential; U, moisture potential; t, time; Kq, the thermal conductivity; Km, moisture conductivity; Cq, specific heat; Cm, specific moisture; ε, ratio between the vapor diffusion and the total moisture diffusion; λ, heat phase change coefficient; δ, thermogradient coefficient; and ρ, density.

Fig. 1
figure 1

Flat plate of a solid material

Full size image

Equation 1 describes the heat transfer by conduction within a body and includes a term for the heat transfer due to phase changes under total balance of energy. Equation 2 describes the moisture transfer by diffusion and includes a term that expresses the moisture transfer affected by temperature gradients.

Equations 1 and 2 are derived from the thermodynamic theory of the irreversible processes and the conservation laws of mass and energy, but in this case, the conservation law of momentum was not taken into account.

Boundary conditions at x = ±L

Boundary conditions (type 3) take into account the heat and mass flows at x = ±L, which can be written as:

$$ K_{\text{q}} \frac{\partial T(x,t)}{\partial x} + \alpha_{\text{q}} \left[ {T(x,t) - T_{\text{a}} } \right] + (1 - \varepsilon )\lambda \alpha_{\text{m}} \left[ {U(x,t) - U_{\text{a}} } \right] = 0 $$
(3)
$$ K_{\text{m}} \frac{\partial U(x,t)}{\partial x} + K_{\text{m}} \delta \frac{\partial T(x,t)}{\partial x} + \alpha_{\text{m}} \left[ {U(x,t) - U_{\text{a}} } \right] = 0. $$
(4)

At x = 0

$$ \frac{\partial T(0,t)}{\partial x} = 0 $$
(5)
$$ \frac{\partial U(0,t)}{\partial x} = 0. $$
(6)

Equation 3 describes the energy balance, assuming that heat conduction occurs into the material and convection at the boundaries. Also, it includes a term that takes into account the moisture effect due to phase change in the energy balance.

Equation 4 describes the mass balance at the boundary, assuming moisture conduction into the material and convection outside. Also, this regards the effect of the temperature gradient in the moisture balance.

Partial differential Eqs. 5 and 6 indicate that there is no heat flow, nor moisture flow in the material’s center.

The initial conditions of Luikov’s model are:

$$ T(x,0) = T_{0} $$
(7)
$$ U(x,0) = U_{0} . $$
(8)

Equations 7 and 8 indicate that at time t = 0, the material is at temperature T0 and moisture U0.

In order to solve the Luikov’s model given by Eqs. 1–8, the methodology proposed by Liu and Sheng was applied [9, 10]. In this methodology, the first step is to transform the nonhomogeneous equation system to a homogeneous one by means of a linear transformation. Then, with the help of a potential function (proposed by Liu et al. [9]), the coupled system of two partial differential equations was decoupled and transformed to a fourth-order partial differential equation. The resulting equation was solved by the separation of variables method, obtaining the following solutions:

$$ T_{1} (x,t) = \sum\limits_{n = 1}^{\infty } {A_{n} \xi_{n}^{2} e^{{ - \xi^{2} t}} \left[ {\left( { - K_{\text{m}} D_{1}^{2} + \rho C_{\text{m}} } \right)\cos D_{1} \xi_{n} x + ( - K_{\text{m}} D_{2}^{2} + \rho c_{\text{m}} )g(\xi_{n} )\cos D_{2} \xi_{n} x} \right]} $$
(9)
$$ U_{1} (x,t) = \sum\limits_{n = 1}^{\infty } {K_{\text{m}} \delta \xi_{n}^{2} e^{{ - \xi^{2} t}} A_{n} \left[ {D_{1}^{2} \cos D_{1} \xi_{n} x + g(\xi_{n} )D_{2}^{2} g(\xi_{n} )\cos D_{2} \xi_{n} x} \right]} , $$
(10)

where ξn are eigenvalues of the transcendental equation; An are coefficients depending on eigenvalues and other model’s properties; D1 and D2 are coefficients that depend on the model’s properties; g(ξn) are depending eigenvalues coefficients; x is the depth at which the heat and moisture are required to be calculated; and Km, ρ, and Cm are the coefficients described above.

2.1 Model Evaluation

In order to calculate the temperature and moisture profiles from the Luikov’s model solution, the eigenvalues of transcendental equation are calculated first, whose equation is obtained from the evaluation of the boundary conditions (Eqs. 9 and 10). Then, the coefficients An are calculated by applying the initial conditions. Finally, the temperature and moisture profiles are calculated [9,10,11].

The transcendental equation is nonlinear and has an infinite number of eigenvalues ξn (real or complex) that can be calculated by numerical methods [12, 13]. In references [9, 10, 14], complex eigenvalues were found for ceramic, wood, gypsum and brick, whose effects in the drying curve are important during first minutes, but they decrease in the falling rate period of drying. Therefore, for the purposes of this work, it is enough to take into account only the real values, because we are only concerned in the material’s dry mass.

In order to evaluate the obtained solution, materials with known thermophysical properties were selected, such as ceramic, wood, gypsum and brick, that can be found in [9, 10]. Table 1 shows the coefficients of mentioned materials and their boundary and initial conditions.

Table 1 Required thermophysical properties for Luikov’s model for ceramic, gypsum, wood and brick (L0 = 0.025 m, T0 = 20 °C, Ta = 80 °C, U0 = 20 %, Ua = 0.2 %)
Full size table

Figure 2 shows drying curves for materials described in Table 2 calculated from the Luikov’s model (obtained with Eq. 10). According to this figure, drying times at the material’s surface depend on the materials’ properties. For example, wood requires about 90 h, while gypsum and brick require about 30 h and 24 h for ceramic.

Fig. 2
figure 2

Comparison of drying curves for wood, ceramic, gypsum and brick, at x = L of the surface

Full size image
Table 2 Comparison of drying times for samples with 25 mm thickness
Full size table

The longer time for drying wood, with respect to other kind of materials, is due to the amount of bound water, which needs large amounts of energy to be evaporated. Also, wood is a highly hygroscopic material as reported in its sorption isotherm [15]. In addition, according to findings reported in [11, 16], the drying time depends on the specific moisture coefficient, which is higher for wood compared with of the other materials.

Also, the drying curve in the center of material was obtained with satisfactory results by the use of the Luikov’s model, i.e., at x = 0. In this case, the drying time is longer than that obtained for the surface. In Table 2, the obtained results are given for both cases (Table 2).

At t = 0, discrepancies among the drying curves of ceramic and gypsum are observed due to the existence of complex roots in the transcendental equations. These complex roots have effects during the first minutes of drying [9, 10, 14].

3 Experimental Setup

The experimental setup is conformed by a convective drying oven, a temperature measuring system, an ambient conditioning system and an analytical balance. In Fig. 3, some of the instruments of the experimental setup are shown.

Fig. 3
figure 3

Instruments of the experimental setup used to verify the Luikov’s model

Full size image

The convective drying oven operates from 40 °C to 325 °C with a uniformity of 0.5 °C at 100 °C (according to the manufacturer’s specifications). The working volume of the drying oven was characterized to evaluate its stability and temperature gradients. The temperature measurement system is comprised of 11 thermocouples, 10 of them are fixed and one is free of movement. Thermocouples’ electromotive forces (EMF) were measured with a digital multimeter and communicated to a PC for the data acquisition.

The ambient conditions’ measurements (relative humidity and temperature) were taken with a relative humidity capacitive sensor and an industrial platinum resistance thermometer.

The analytic balance covers the range from 0 g to 3100 g with a resolution of 0.1 g and an uncertainty of 0.09 g (k = 2).

3.1 Procedure for the Experimental Verification of Model

Samples of red brick and wood were used to verify the model.

Before the start of measurements, samples of brick were conditioned at several levels of moisture content by immersing them in liquid water for different periods. Later, they were placed at ambient conditions of the laboratory for their stabilization.

The determination of the moisture content of the samples consisted in weighing the wet mass (mh) of each one and then placing it into the drying oven.

Each sample was kept for periods of 1 h. After this, it was removed from the oven and weighed in the analytic balance immediately after (by not more than 30 s). The process was repeated until no mass changes were observed (constant mass).

4 Comparison Between the Calculated and the Experimental Drying Curves

The experimental drying curves for wood and red brick were obtained by drying the samples at 80 °C, whose results are shown in Figs. 4 and 5. The type of wood was pine with dimensions of 30 cm × 30 cm × 2 cm. For brick, samples with dimensions of 19.2 cm × 26.5 cm × 1.8 cm were used.

Fig. 4
figure 4

Comparison of experimental and calculated drying curves with Luikov’s model in samples of wood, 2.0 cm thick

Full size image
Fig. 5
figure 5

Experimental verification of Luikov’s model in samples of brick, 1.8 cm thick

Full size image

According to Fig. 4, the predicted results for wood after 8 h of drying are in a reasonable good agreement with those experimentally obtained. However, calculated drying curve (Eq. 9) is deviated from the initial condition during the first minutes due to the presence of complex eigenvalues (ξ) in the transcendental equation which, according to some authors [9, 10, 14], gives rise to nonrealistic moisture profiles when exist complex eigenvalues that are neglected. In the falling rate period of drying is expected that the solution satisfied the boundary conditions.

In Fig. 5, experimental results and predicted values for red brick are shown. The experiment was repeated with four samples whose results were similar. A good agreement between calculated values and experimental results was observed.

For both materials (wood and brick), drying conditions with Luikov’s model were predicted satisfactorily; i.e., it is required 30 h for drying a sample of wood at 80 °C, while 4 h for red brick with the dimensions above described.

4.1 Prediction of Moisture Content Values with Luikov’s Model

Predicted values of moisture content by the Luikov’s model are calculated by taking into account the measured value of mh and the calculated value of ms (Luikov), given by:

$$ m_{\text{s(Luikov)}} = \frac{{100 \cdot m_{h} }}{{\left( {U_{\text{Luikov}}^{\prime } + 100} \right)}}, $$
(11)

where \( U_{\text{Luikov}}^{\prime } \) is the moisture content of the drying curve for Luikov’s model.

In order to calculate ms(Luikov), the assumption that \( U_{\text{Luikov}}^{\prime } \)= Ua ≠ 0 should be made. This consideration is important in the calculation of ms, because it is not possible to get Ua= 0 in practice and it is not mathematically possible to calculate \( U_{\text{Luikov}}^{\prime } \).

In Table 3, results for twelve samples of red brick are shown with values of ms calculated with Eq. 11, including the experimentally measured dry mass values and those calculated from the drying curves of Luikov’s model. With calculated values of dry mass is possible to calculate the moisture content predicted by this model.

Table 3 Comparison of experimental and calculated values of dry mass for red brick samples
Full size table

In Fig. 6 are shown the differences between the calculated (by Luikov’s model) and measured values for twelve samples of brick. In addition, in this figure the uncertainty estimation of the difference for both values is included.

Fig. 6
figure 6

Uncertainty estimation of deviation between the predicted values (by Luikov model) and experimental values of moisture content for samples of brick

Full size image

The uncertainty of the difference was estimated as indicated by the guide to the expression of uncertainty in measurement (GUM [17]) assuming a uniform distribution.

According to the obtained results, the moisture content values calculated with the Luikov’s model agree in about 0.5 % with respect to the measured values, with an uncertainty of less than 1.0 % of the dry basis moisture content.

5 Conclusions

The solution of Luikov’s model for a flat one-dimensional plate was presented, which was applied to obtain the drying curves of porous solid materials such as ceramic, wood, gypsum and brick, oriented to determine their drying conditions. From the calculated curves, it was found that wood, under the same drying conditions, is one of the materials which requires longer periods to dry because of its high specific moisture coefficient.

To validate the solution, samples of wood and brick were used and were dried in a convective oven which was characterized for such purpose. The experimental drying process consisted in subsequent periods of about 1 h in order to weight the samples before and after drying for such specific time and then repeat it up to get the constant mass condition. The drying time (experimental and calculated) for each material was similar in both cases. However, the experimental results for brick have shown a better agreement with the calculated values when compared to those obtained for wood.

Finally, the moisture content of several samples of brick was determined with the drying curves obtained. The obtained results were compared with the values obtained with the Luikov’s model; small differences between them were found. From the moisture content values, the estimated uncertainty was less than 1 % of moisture content for those predicted values with the Luikov’s model.

The obtained results show that the Luikov’s model allows predict the drying time, and under some conditions, it could be used to determine the moisture content with reasonable accuracy.