Ratios, proportions, and proportional reasoning constitute a fundamental area of school mathematics that is essential for students to learn but difficult for teachers to teach (Lamon, 2007; Lobato & Ellis, 2010). These concepts are also important in understanding many situations in science and daily life (Cramer & Post, 1993). Being a special form of multiplicative reasoning (Lesh, Post & Behr, 1988), proportional reasoning plays a vital role in students’ mathematical development, and it is an essential concept in their elementary school arithmetic and in higher mathematics (Kilpatrick, Swafford & Findell, 2001; National Council of Teachers of Mathematics, 2000). Lamon (2007) defined proportional reasoning as “detecting, expressing, analyzing, explaining, and providing evidence in support of assertions about proportional relationships” (p. 647). Therefore, proportional reasoning necessitates detecting and expressing proportional relationships between two covarying quantities (Common Core State Standards Initiative, 2010).

Two types of proportional relationship problems have been used in literature: missing-value and comparison problems (Lamon, 2007). In missing-value problems, a student is typically presented with three of the four values and asked to determine the missing-value (Lamon, 2007). On the other hand, in comparison problems, two ratios are compared to determine whether they are equal, or if one is larger or smaller (Lobato & Ellis, 2010). In this study, missing-value word problems were used in investigating the PSTs’ proportional reasoning because past studies have reported PSTs’ difficulties determining proportional and nonproportional relationships and differentiating these two from each other, especially presented in missing-value word problems (Izsák & Jacobson, 2017).

This study was conducted in a mathematics education course, which was specifically designed for developing the PSTs’ proportional reasoning. The purpose of the study was to investigate the PSTs’ understanding of proportional and nonproportional relationships and abilities to differentiate these two from each other. In addition, the PSTs’ abilities to interpret and represent proportional and nonproportional situations, solution strategies that they use when solving proportion problems, and the development of their understanding of proportional and nonproportional relationships were also investigated. Thus, the following research questions are addressed:

  1. 1.

    How do preservice middle school mathematics teachers determine proportional and nonproportional relationships and differentiate these two from each other?

  2. 2.

    How do they interpret and represent proportional and nonproportional situations, and what strategies do they use when solving proportion problems?

  3. 3.

    How does their understanding of proportional and nonproportional relationships develop during a mathematics education course on ratios and proportions?

Background

Although enough attention was given to ratios and proportions in schools, many studies (e.g. Clark, 2008; De Bock, Verschaffel & Janssens, 1998; Modestou & Gagatsis, 2007) reported students’ difficulties with and weak performances in these concepts. Some researchers (e.g. Ben-Chaim, Keret & Ilany, 2007; Hull, 2000; Simon & Blume, 1994) noted that PSTs’ difficulties with proportions were often similar to students’ difficulties. One of the persistent issues in teaching and learning proportions is that students and PSTs often tend to judge nonproportional relationships as proportional and use proportional strategies for solving these problems (Atabas & Oner, 2017; Degrande, Van Hoof, Verschaffel & Van Dooren, 2017; Modestou & Gagatsis, 2007; Riley, 2010; Van Dooren, De Bock, Janssens & Verschaffel, 2007). Furthermore, some researchers (e.g. Degrande et al., 2017; Lim, 2009; Van Dooren, De Bock, Hessels, Janssens & Verschaffel, 2005) have also reported the inverse tendency—assuming nonproportional relationships to be proportional.

The ability to differentiate proportional relationships from nonproportional relationships has been considered as a sign of an individual’s competency in proportional reasoning (Lim, 2009). In the literature, different explanations for students’ and PSTs’ incorrect tendencies have been reported. Siemon, Breed and Virgona (2005) claimed the transition from additive reasoning to multiplicative reasoning as the main reason for students’ incorrect tendencies. By the same token, De Bock et al. (1998) and Van Dooren, Bock, Janssens and Verschaffel (2008) blamed superficial reasoning rooted in schooling for students’ incorrect tendencies. Furthermore, in recent years, some researchers (e.g. Boyer, Levine & Huttenlocher, 2008; Jeong, Levine & Huttenlocher, 2007) have started to question these incorrect tendencies in terms of lacking abilities. However, researchers like Degrande et al. (2017) and Van Dooren, De Bock and Verschaffel (2010) refused to assert that these incorrect tendencies depend on students’ ability to reason multiplicatively or additively, claiming that their preference for proportional relationships or nonproportional relationships depends on the features of the mathematical tasks used.

The traditional instruction on fractions, ratios, and proportions usually relies on rule memorization and rote computations (Arican, 2018; Misailadou & Williams, 2003; Riley, 2010). Moreover, very little research (e.g. Izsák & Jacobson, 2017; Lim, 2009; Livy & Herbert, 2013) has been conducted on PSTs’ proportional reasoning. In particular, only a small number of researchers (e.g. Arican, 2018; Ben-Chaim et al., 2007; Lim, 2009; Riley, 2010) studied PSTs’ proportional reasoning regarding inverse proportions, and even fewer researchers studied multiple proportions (e.g. Vergnaud, 1983, 1988), which is formed using three or more quantities. The studies on ratios and proportions generally used single proportion problems when examining students’ and PSTs’ proportional reasoning. In addition, these studies examined the current state of students’ or PSTs’ knowledge of proportional and nonproportional relationships rather than monitoring the development of this knowledge over a course on ratios and proportions. Therefore, this current study extends our knowledge of PSTs’ proportional reasoning by investigating their understanding of proportional and nonproportional relationships that were presented in single and multiple proportions problems and in graphical forms. Besides, the development of the PSTs’ proportional reasoning was monitored during a mathematics education course by conducting semi-structured interviews with selected PSTs and testing 18 PSTs on the same problems.

Conceptual Framework

The conceptual framework of this study is developed drawing on Vergnaud’s (1983, 1988, 2009) multiplicative conceptual field theory, and Beckmann and Izsák’s (2015) analysis of ratios and proportional relationships. According to Vergnaud (1983, 1988, 2009), multiplication, division, fractions, ratios, and rational numbers are not mathematically independent. Therefore, developing a larger context, the multiplicative conceptual field, he gathered all these concepts under this new framework. For Vergnaud (1988), a conceptual field is “a set of situations, the mastering of which requires mastery of several concepts of different natures” (p. 141). There are two types of conceptual fields: additive and multiplicative. Additive conceptual field includes a set of problems involving addition, subtraction, difference, interval, and translation; and multiplicative conceptual field includes problems involving multiplication, division, fraction, ratio, and similarity.

Within the multiplicative conceptual field theory, Vergnaud (1983, 1988) discussed three types of multiplicative structures: isomorphism of measures, product of measures, and multiple proportion other than product. In the isomorphism of measures structure, there is a single direct proportion between quantities compared. Whereas, in the product of measures structure, the product of two quantities is equal to a constant, so it presents an inversely proportional relationship. Finally, in the multiple proportion other than product structure, which presents multiple proportional relationships, one quantity is directly proportional to two inversely proportional quantities (e.g. Distance = Time × Speed).

Framing their study within the multiplicative conceptual field theory, Beckmann and Izsák (2015) combined models of multiplication, division, and proportional relationships by the equation M × N = P, in which M, N, and P stand for known constants. In the equation, the multiplier, M, is interpreted as the number of groups, the multiplicand, N, is interpreted as the number of units in each group, and the product, P, is interpreted as the number of total units in M groups. According to Beckmann and Izsák (2015), a directly proportional relationship is “a collection of pairs of values for x and y” that either satisfy the equation x × N = y or M × x = y (p. 20). Whereas, an inversely proportional relationship is “a collection of pairs of values for x and y” that satisfy the equation x × y = P (p. 20). In all three equations, N, M, and P are known constants, and x and y are either unknown variable amounts or two covarying values.

Methods

Research Design

A case-study methodology best suited the scope of the study because the purpose of this study was to examine the PSTs’ understanding of proportional and nonproportional relationships conducting in-depth analysis. The data of this qualitative study included the PSTs’ written responses to four open-ended problems and brief semi-structured video interviews conducted with six of the PSTs. The study was implemented in a mathematics education course that aimed at developing the PSTs’ understanding of proportional and nonproportional relationships. Moreover, the course intended to develop the PSTs’ abilities to detect, interpret, and represent multiplicative relationships between quantities. I taught the course and followed Beckmann and Izsák’s (2015) analysis of ratios and proportional relationships when teaching the course content. During the course, the PSTs were instructed about multiplicative relationships and various representation techniques (i.e. a ratio table, a strip diagram, double number lines, and graphs) for displaying these relationships.

Although the PSTs studied proportions in middle and high school, they learned these topics from a traditional perspective, which emphasized cross-multiplication and across-multiplication strategies when solving proportion problems. In both strategies, students write the information side-by-side and determine the relationship between quantities as either direct or inverse by attending to the qualitative relationships (i.e. simultaneous increases and/or decreases). If corresponding values increase or decrease together, they determine a direct relationship. On the other hand, if the value of the first quantity increases and the value of the second quantity decreases, they determine an inverse relationship. After determining the correct relationship, in the direct relationship, they draw a cross and multiply the values on two sides of this cross (Fig. 1a). Whereas, in the inverse relationship, they draw two horizontal lines and multiply the values across these lines (Fig. 1b). Although the cross and horizontal lines refer to a constant ratio and a constant product relationships, respectively, students use these lines with little understanding of these relationships.

Fig. 1
figure 1

a A PST’s solution using the cross-multiplication in the Gear I problem; b A PST’s solution using the across-multiplication in the Gear II problem

Full size image

Participants and Recruitment Procedure

During spring 2017 semester, 40 (30 females and 10 males) of the 43 PSTs, who had been attending the course, volunteered to participate in the study. The PSTs were enrolled in the middle school mathematics program of a Turkish university. I purposefully recruited these PSTs, because they were in the last year of their programs and expected to teach middle school mathematics after graduation. Working with this group of PSTs was effective in terms of collecting diversely rich answers for the research questions because they had different instructional backgrounds and were coming from various regions of Turkey. Therefore, the purposive sampling technique (e.g. Patton, 2005) was followed in recruiting the participants.

Data Collection and Analysis

In the second week of the semester, the PSTs were given a paper-pencil test that included four open-ended problems to gauge their understanding of proportional and nonproportional relationships. They were given 40 min to complete this test, and they did not have any explicit instructions on proportional and nonproportional relationships before their participation in the study. Hence, the PSTs answered problems using their prior knowledge on these concepts. The test included three real-world problems, Gear I, Gear II, and Bakery (Table 1), and an item that included two linear graphs both presenting additive relationships (Fig. 2). The two gear problems were adopted from Arican (2018), the Bakery problem from Beckmann (2013), and the two linear graphs from Arican (2015). I decided to use these four problems because they included real-world contexts, were challenging enough for the PSTs to answer, and were appropriate for studying proportional and nonproportional relationships. Before using these problems, I analyzed them for their contents and suitability for answering the research questions. Thus, I made all necessary changes to these problems to maintain the content validity.

Table 1 Description of the problems
Full size table
Fig. 2
figure 2

Graph I (a) and Graph II (b) both representing nonproportional relationships

Full size image

The content analysis method (e.g. Hsieh & Shannon, 2005) was used in analyzing the PSTs’ responses to the open-ended problems. To analyze the PSTs’ responses for each problem and tabulate findings, I generated an Excel file and recorded summaries of each PST’s responses in this file. Next, I analyzed the PSTs’ responses using these summaries and considering the research questions. I reported findings using descriptive statistics (i.e. frequencies and percentages). Moreover, I selected six PSTs (5 females and 1 male) and conducted semi-structured interviews with them to understand their reasoning in details. In my selection, I attended to the correctness of solutions and relationships identified, appropriateness of representations provided, relevance of mathematical interpretations offered, and strategies utilized in answering problems. Based on my analysis, I identified that none of the PSTs exhibited a solid understanding of these relationships. Hence, I selected three PSTs who exhibited little understanding and three PSTs who exhibited some understanding of these relationships. Each interview took between 15 and 30 min, and the PSTs’ responses were transcribed verbatim for analysis. Finally, 18 PSTs (13 females and 5 males) volunteered to take the same problems again at the end of the semester. The purpose of testing these PSTs on the same problems was to determine the development of their proportional reasoning over the course.

Problems

The gear problems were appropriate for investigating the PSTs’ reasoning on direct and inverse proportions. In both problems, two gears, Gear A and Gear B, were intertwined, so that they could revolve together (Fig. 3). In the Gear I problem, there was a directly proportional relationship between the number of notches of a gear and its radius. The multiplicative relationship between the number of notches (N) and radius (r) could be expressed with the following formula: r (cm) × \( \frac{\boldsymbol{N}}{\boldsymbol{r}} \)(notches/cm) = N (notches). From Beckmann and Izsák’s (2015) perspective, this formula could be interpreted as follows: There are a total of N notches on a gear with r cm radius in which \( \frac{\mathbf{N}}{\mathbf{r}} \) notches are placed per 1 cm. In the Gear II problem, there was an inversely proportional relationship between the number of notches (N) and number of revolutions (R). This multiplicative relationship could be expressed with the following formula: R (revolutions) × N (notches/revolution) = R × N (notches). Similar to previous equation, this formula can be interpreted as follows: a total of R × N notches rotate in R groups of revolutions in which N notches rotate per one revolution.

Fig. 3
figure 3

An illustration of two intertwined gears (The figure is taken from http://engineeronadisk.com/notes_mechanic/mechanica4.html)

Full size image

In the Bakery problem, which included multiple proportions (e.g. Arican, 2018; Vergnaud, 1983, 1988), there were two directly proportional relationships (between the number of people [P] and number of cupcakes [C] and between the number of cupcakes and number of minutes [T]) and an inversely proportional relationship (between the number of people and number of minutes). The multiplicative relationships among three quantities could be expressed by the formula P (people) × T (minutes) = C (cupcakes) × \( \frac{\boldsymbol{P}\ast \boldsymbol{T}}{\boldsymbol{C}} \) (number of person-minutes per cupcake), where “number of person-minutes per cupcake” represents the constant of proportionality. In addition to these problems, the PSTs determined relationships presented in Graph I and Graph II (see Fig. 2). In Graphs I and II, there were an additive decreasing and an additive increasing relationships between x and y that could be expressed by the equations x+y= 5 and y−x= 2, respectively.

Findings

Analysis of the First Test Results

In the Gear I problem, the PSTs calculated the number of notches of Gear B with 3-cm radius given that Gear A had 4-cm radius and 12 notches. One could calculate the correct answer, nine notches, by either forming a proportion using within ratios (\( \frac{3\kern0.35mm cm}{4\kern0.35mm cm}=\frac{x\kern0.35mm notches}{12\kern0.35mm notches} \)) or between ratios (\( \frac{3\kern0.35mm cm}{x\kern0.35mm notches}=\frac{4\kern0.35mm cm}{12\kern0.35mm notches} \)) (e.g. Vergnaud, 1983, 1988). The analysis showed that only 17 PSTs calculated the correct answer, and 21 PSTs calculated an incorrect answer (Table 2). Therefore, the PSTs’ low correct answer rate (i.e. 42.5%) suggested constraints in their understanding of the directly proportional relationship between the number of notches and radius.

Table 2 The distribution of the PSTs’ solutions
Full size table

In the Gear II problem, the product of the number of revolutions and number of notches was yielding a constant. Gear B had nine notches around, and so in 12 revolutions, a total of 108 notches were revolving around it. Since the two gears were intertwined, Gear A with 12 notches had to revolve the same total number of notches. Hence, using this constant product relationship, the number of revolutions of Gear A could be calculated dividing 108 notches by 12 notches per one revolution, which yields nine revolutions as the correct answer. As showed in Table 2, 28 PSTs solved this problem correctly. In the Bakery problem, there was an inversely proportional relationship between the number of people and number of minutes because the number of cupcakes was taken as constant. Hence, using this inversely proportional relationship, the time needed by four people to frost N cupcakes could be calculated as \( \frac{3T}{4} \) minutes. Although the inverse (i.e. Gear II) and multiple proportions (i.e. Bakery) problems were expected to be challenging for the PSTs to answer, they were able to obtain higher correct answer rates in these two problems than the Gear I problem.

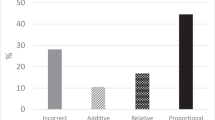
In terms of the PSTs’ abilities to determine proportional and nonproportional relationships, as indicated by Table 3, the PSTs had difficulty determining those relationships. For instance, only six PSTs determined the directly proportional relationship between the number of notches and radius. Fifteen PSTs assumed the relationship between the number of notches and radius to be inversely proportional, and 18 PSTs did not provide an answer. The analysis showed that the PSTs who identified the correct directly proportional relationship usually attended to the simultaneous increases and decreases in the values of number of notches and radius. Although many of these PSTs did not write a reason for their determination of a directly proportional relationship, some of them noted that “When the radius increases, the number of notches also increases.” Furthermore, Table 3 showed that 20 PSTs identified the inversely proportional relationship between the number of revolutions and radius, and 20 of them did not provide an answer. The PSTs who found the correct answer usually explained the inverse relationship by writing “When the radius increases, the number of revolutions decreases” or the other way around. However, very few of them were able to recognize that the product of the number of revolutions and radius (or notches) was yielding a constant.

Table 3 The PSTs’ determinations of the relationships
Full size table

In Graph I, only six PSTs were able to identify the correct nonproportional relationship between x and y. It appeared that because of the linearity of the line and the fact that when the value of x-axis increased, the value of y-axis decreased, 24 PSTs assumed an inversely proportional relationship. Furthermore, only 11 PSTs correctly identified the relationship depicted in Graph II as nonproportional. Twenty three PSTs expected a directly proportional relationship in Graph II because the line was straight and the fact that when the value of x-axis increased, the value of y-axis also increased.

The PSTs’ representations of the relationships presented in the Gear I, Gear II, and Bakery problems were showed in Table 4. Table 4 showed that only six PSTs were able to draw the correct directly proportional graph for the relationship presented in the Gear I problem, and 14 PSTs just marked two points and so did not complete their graphs. Seven of the 15 PSTs who expected an inversely proportional relationship drew their graphs as in Fig. 4a. In the Gear II problem, only two PSTs drew the correct inversely proportion graph. Fifteen PSTs’ graphs were counted as incomplete since they just marked two points. In addition, 11 PSTs drew linear graphs that indicated a decreasing additive relationship between the number of notches and number of revolutions (Fig. 4b).

Table 4 The PSTs’ representations
Full size table
Fig. 4
figure 4

a A PSTs’ incorrect graph for the relationship between the number of notches and radius; b A PSTs’ incorrect graph for the relationship between the number of revolutions and radius

Full size image

In the Bakery problem, there was an inversely proportional relationship between the number of people and number of minutes. None of the PSTs were able to draw a complete inversely proportional graph. Only one PST provided a correct representation of the problem situation using pie charts (Fig. 5). In her representation, the PST wrote that each person frosted \( \frac{N}{3} \) cupcakes in T minutes. Next, sharing N cupcakes between four people and using the cross-multiplication strategy, she calculated that \( \frac{N}{4} \) cupcakes frosted in \( \frac{3T}{4} \) minutes. Moreover, 12 PSTs provided representations that were partially complete, 20 PSTs did not provide a representation, and seven PSTs provided incorrect representations. The PSTs’ responses showed that when sharing N cupcakes between three people, some of these PSTs shared T minutes between three people too. Therefore, these PSTs calculated the time needed by one person to frost \( \frac{N}{3} \) cupcakes as \( \frac{T}{3} \) minutes rather than T minutes.

Fig. 5
figure 5

A PST’s correct representation of the problem situation in the Bakery item

Full size image

Regarding the PSTs’ solution strategies, in the Gear I problem, they mostly relied on the cross-multiplication and across-multiplication strategies when calculating their solutions. Among the 17 PSTs who calculated the correct answer, 15 of them used the cross-multiplication strategy (see Fig. 1a); one PST used the numerical multiplicative relationship between the number of notches and radius (i.e. 12 [notches] was 3 times 4 [cm]) in calculating the correct answer; and one PST calculated the correct answer considering the equity of ratio formed between circumference and number of notches ratio in both gears (i.e. \( \frac{8\pi }{12\kern0.35mm notches}=\frac{6\pi }{x\kern0.35mm notches} \)). On the other hand, 19 PSTs calculated an incorrect answer using the across-multiplication strategy (see Fig. 1b). This finding was consistent with the fact that 15 PSTs assumed an inverse relationship between the number of notches and radius. Moreover, one PST stated that there was not a relationship between the number of notches and radius, so both gears required to have 12 notches. Finally, one PST calculated the answer as \( \frac{64}{3} \) notches by assuming an inverse relationship between the number of notches of a gear and the area covered by this gear.

In the Gear II problem, the analysis showed that after determining the inverse relationship between the number of revolutions and number of notches (or radius), the PSTs tended to use the across-multiplication strategy in solving this problem. Among the 28 PSTs who solved this problem correctly, 17 of them used this strategy in calculating the answer. Moreover, the remaining 11 PSTs calculated the correct answer by multiplying the corresponding values of the number of notches and revolutions in Gear A and equating this product with the product of the number of notches and revolutions in Gear B and not necessarily writing the corresponding values side-by-side. The PSTs’ utilization of this strategy suggested their understanding of the constant product relationship between the number of notches and revolutions. On the other hand, the PSTs who calculated an incorrect solution appeared to rely on their false solutions (i.e. Gear B had 16 notches) that they provided for the Gear I problem.

In the Bakery problem, among the 23 PSTs, who calculated the correct solution, 10 of them used the across-multiplication strategy taking number of cupcakes constant (Fig. 6a). Seven PSTs equated 3 × N × T with 4 × N × X, not necessarily using the across-multiplication strategy, and calculated X as \( \frac{3T}{4} \) minutes. Only two of these seven PSTs attributed the 3 × N × T = 4 × N × X equation to the fact that the total work done by three and four people was equal. Moreover, four PSTs used the equality of \( \frac{N}{3T} \) and \( \frac{N}{4X} \) ratios in calculating the correct answer (Fig. 6b), and two PSTs used the unit ratio strategy in which they calculated the time need by one person to frost N cupcakes as 3T minutes and then divided 3T minutes by 4 to obtain the time needed by four people. On the other hand, eight of the nine PSTs, who provided an incorrect answer, assumed a directly proportional relationship between the number of people and number of minutes and calculated the answer as \( \frac{4T}{3} \) minutes using the cross-multiplication strategy. The remaining PST considered T as 120 min and obtained \( \frac{120}{3}+\frac{120x}{4}=60 \) equation. Using this equation, she calculated the answer as \( \frac{2T}{3} \) minutes.

Fig. 6
figure 6

a The across-multiplication strategy; b Equity of two ratios

Full size image

Analysis of the Semi-structured Interviews

During the semester, I conducted brief video-taped semi-structured interviews with six PSTs to investigate their understanding of proportional and nonproportional relationships and changes in their reasoning. I followed the multiplicative conceptual field theory and Beckmann and Izsák’s (2015) analysis of fractions, ratios, and proportions in designing the course content. As I explained earlier, during the course, the PSTs solved proportion problems using ratio tables, double number lines, strip diagrams, and graphs. Hence, I expected improvements in their understanding of proportional and nonproportional relationships and abilities to interpret and represent these relationships. In the following paragraphs, I presented three PSTs’ responses to the interview questions. To maintain confidentiality, all real names were replaced with pseudonyms, pauses were shown with ellipses, and actions were described within square brackets.

Feyza correctly answered the Gear I, Gear II, and Bakery problems and successfully identified the relationships presented in these problems. In addition, she wrote that the relationships depicted in Graph I and Graph II were nonproportional. However, she did not provide complete graphs in the Gear I, Gear II, and Bakery problems. In the Gear I problem, she equated\( \frac{12}{4} \) and\( \frac{x}{3} \), without their units, and calculated the number of notches on Gear B as nine. In her graph, she just marked (3 cm, 9 notches) and (4 cm, 12 notches) and drew a line segment between them (Fig. 7a). When I asked to her what would look like the whole graph, she responded as follows:

Fig. 7
figure 7

a Feyza’s response to the Gear I problem; b Feyza’s identification of the relationships in Graphs I and II

Full size image

Feyza: If I drew the whole graph, it would proceed this way [drawing a linear line upwards].

Int: Where would it pass?

Feyza: Where would it pass?…the next step, 5 and 15 and then…6 and 18.

Int: Then, is it always 3 times the ….?

Feyza: I set up a direct proportion and determined the constant of proportionality from this [pointing at \( \frac{12}{4}=\frac{x}{3} \)] as three. So, we can easily find the points that the graph passes using this number.

Int: If you continued drawing your graph downwards, would it pass through the origin?

Feyza: According to what I said earlier, when I give zero to radius there is nothing. When I give one then there must be three notches. However, if the number of notches is zero, then we cannot talk about the gear. There is not a gear then.

In her response, Feyza stated a directly proportional relationship between the number of notches and radius and identified the constant of proportionality as three. Using this constant, she easily identified the points that the directly proportional graph were passing. However, the idea that the graph was passing through the origin did not make sense for her because as she explained there would not be a gear in the zero cm and zero notches case.

In the Gear II problem, Feyza stated that the product of the values of the number of revolutions and number of notches was yielding a constant number. Hence, using a slightly different example, a gear with eight notches revolved 12 times and the second gear had 12 notches, I asked the number of revolutions of this second gear. She correctly calculated the number of revolutions as eight and explained her solution as follows:

Feyza: The product of these two [pointing at 8 notches and 12 revolutions] gives 96. The product of these two [pointing at 12 notches and 8 revolutions] also gives 96.

Int: For you, what is this 96?

Feyza: I consider it as a constant such as three in the previous problem.

Int: Do you consider like the constant of proportionality?

Feyza: Yes, but it is not responding to the constant of proportionality. Actually, there should be a mathematical explanation of this number, but I do not know how to explain it right now.

Feyza’s responses indicated her initial understanding of the constant product relationship between the number of revolutions and number of notches. However, as presented above, she had difficulty making sense of this constant product relationship mathematically.

Entering the corresponding values in Graph I and Graph II into two separate tables and considering relationships among numbers, Feyza represented the relationship between x and y in Graph I as y = 5 − x and the relationship in Graph II as y = x +2 (Fig. 7b). Next, she wrote that these two relationships were nonproportional. When I asked to her why she wrote the relationships in Graph I and Graph II as nonproportional, she explained as follows:

Feyza: This graph is proportional [pointing at Graph I].

Int: Which one did you decide as nonproportional? I assumed you wrote both of them are nonproportional.

Feyza: I wrote nonprorportional comparing these two [pointing at Graphs I and II].

Int: What do you mean by comparing these two?

Feyza: I mean, there is not a proportional relationship between these two [pointing at Graph I and Graph II], but both of them increase and decrease proportionally.

Int: I asked you guys to consider relationships in these two graphs separately.

Feyza: I wrote that there is not a proportional relationship between Graph I and Graph II. This is proportional [pointing at Graph I].

Int: Why do you think it is proportional?

Feyza: Because it increases and decreases in a certain rate. In this graph [pointing at Graph I], since the values of the increase and decrease is one, the values increases and decreases by one. If it increased or decreased by 2 or 3 each time, then the values [referring to the x and y values] would be different, but the equation [referring at y = 5 − x] would have stayed the same.

Int: What do you think about Graph II?

Feyza: I generated an equation in this one too. In this one, x minus y equals to negative two. When I gave one to x then y becomes three, and when x is two then y is four. Hence, when x increases by 1, y increases by 2. Graph II increases constantly, and this one [pointing at Graph II] was constantly decreasing. Therefore, this one [pointing at Graph II] is proportional too. Both of them are proportional because the increase and decrease are constant.

Int: I wonder, if it was okay for you to start Graph II at two. Did you consider this in the second graph?

Feyza: I think it is not an issue. If I continued drawing this graph until x-axis and gave negative two value to x, then y would take zero.

My initial analysis of Feyza’s written responses suggested some understanding on her side about nonproportional relationships presented in Graphs I and II. However, during the interview, although she found the correct additive relationships presented in Graphs I and II and instructed on the necessity of having a multiplicative relationship (i.e. constant ratio and product) between quantities when determining a relationship as proportional, she determined relationships in Graphs I and II as proportional. Thus, her attention to the simultaneous increases and decreases and constancy of the rate of change misguided her to an incorrect conclusion.

Similar to Feyza, Ece provided correct solutions to the Gear I and Gear II problems. In the Gear I problem, she used the cross-multiplication strategy in calculating the correct answer and represented the relationship between the number of notches and radius drawing a complete directly proportional graph. In the Gear II problem, she used the across-multiplication strategy to solve the problem (Fig. 8a). Next, she determined an inversely proportional relationship between the number of revolutions and radius and represented this relationship drawing the linear graph in Fig. 8a. During the interview, I asked to Ece if she could draw a new graph since she did not clearly mark the points on her graph. Hence, she drew the graph in Fig. 8b. Some exchanges later, I pointed that she had a straight line in her first graph, but a curved line in the second graph. She explained the reason as follows:

Fig. 8
figure 8

a Ece’s initial drawing of the inversely proportional graph; b Ece’s second drawing of the inversely proportional graph

Full size image

Ece: It should be straight in this one [pointing the graph in Fig. 8b] too. The reason for this is that when radius increases by 1 cm….no it should not be straight. When this one [pointing at 36 notches] decreases by half, this one [pointing at 18 notches] decreases by two-thirds. Hence, the increase in this one [referring to the increase from 1 cm to 2 cm] and this one [referring to the decrease from 36 notches to 18 notches] are not the same. [Thinking] No…no this is not [referring to the line in Fig. 8a] straight.

Int: Do you think it should be curved like this [pointing at the graph in Fig. 8b]?

Ece: Yes.

Ece’s responses showed that my point of attention to the straightness of lines precipitated a perturbation in her understanding of the inversely proportional graph. Therefore, to investigate her reasoning, I asked her understanding of an inversely proportional graph:

Int: For you, what does an inversely proportional graph look like?

Ece: For me, an inversely proportional graph looks like…so, when a variable increases, the other one decreases [drawing a graph]. It should looks like this one.

Int: Do you think, it intercepts the axes? Your previous graphs did not intercept the axes too.

Ece: I do not think it intercepts the axes because when it is 0 cm, we cannot talk about the number of revolutions.

When I asked Ece what an inversely proportional graph looks like, she drew the small linear graph, which is in the right upper corner of Fig. 8b. Similar to Feyza, she attended to the simultaneous increases and decreases in values when drawing her graph. Since Ece drew a curved graph earlier, she responded as follows to eliminate the perturbation in her understanding of an inversely proportional graph:

Ece: I am only confused about whether the line in this graph [pointing at the big curved graph in Fig. 8b] is straight or curved…this an inverse proportion too. This one [pointing at the small linear graph in Fig. 8b] is a linear inverse proportion. This one [drawing the small curved graph in Fig. 8b]…decreasing right? So, there is an inverse proportion in this one too because when one [quantity] increases, the other [quantity] decreases. So, I think there is an inverse proportion.

According to Ece, an inversely proportional graph could be linear or curved. Although she was able to obtain the correct graph by marking each point on the x and y-axes, her attention to the simultaneous increases and decreases precipitated to an inappropriate conclusion about the graph of an inversely proportional relationship. Some exchanges later, Ece decided that Graph I was representing an inverse proportion because when x increased by 1, y decreased by 1 too. However, she noted that since Graph II started at two, it was not a directly a proportional graph. In her explanation, she stated her expectation of a directly proportional graph starting from the origin. Finally, she concluded that both direct and inverse proportion graphs should have straight lines.

In addition to Feyza and Ece, I interviewed Esma for her response on the Gear I problem. Esma incorrectly solved this problem using the across-multiplication strategy and provided a graph similar to the one in Fig. 4a since she assumed an inversely proportional relationship. She explained her solution as follows:

Esma: Both gears have to travel the same distance because they were intertwined.

Int: What do you mean by the distance?

Esma: I considered the gears as the wheels of a tractor. When the tractor moves, both wheels rotate and travel the same distance. The small wheel should rotate more than the large wheel because in each rotation these wheels move a distance, which is determined by their circumferences. So, to compensate its small circumference, it [the small gear] should have more notches around.

Int: Can you explain a little bit more?

Esma: I mean…Gear A has 12 notches around. So, in one rotation of Gear A, 12 notches move. More notches rotates around Gear B because it rotates more than Gear A. So, it should have more notches around it. For example, when one notch moves on Gear A, more than one notches should move around Gear B to travel the same distance.

Int: Do you assume the notches on these two gears to have the same size or different sizes?

Esma: Gear B has smaller notches around. So, when one notch moves on Gear A, more than one notches move around Gear B.

Esma’s responses suggested that she did not understand the idea of intertwining two gears. She expected Gear B to have more notches around than Gear A because it completed more revolutions than Gear A. Although Esma drew Gear B smaller in size than Gear A, she placed respectively smaller-sized notches around it. Hence, she rationalized her incorrect solution of 16 notches.

Analysis of the Second Test Results

Eighteen PSTs volunteered to take the same test at the end of the semester. Findings were presented in Tables 5, 6, and 7. In all tables, the PSTs’ first test responses were provided besides their second test responses. Table 5 showed increments in percentages of the PSTs’ correct solutions. Although Table 5 indicated increments in the correct response rates from the overall sample and particularly for 18 PSTs, their determinations of the correct relationships only slightly increased (Table 6). Table 6 showed the PSTs’ hesitations in identifying a relationship as directly proportional or inversely proportional in the Gear I and Gear II problems. In the Gear I problem, only six PSTs identified the directly proportional relationship, and 12 PSTs did not provide an answer. Similarly, in the Gear II problem, eight PSTs identified the inversely proportional relationship, and 10 PSTs did not provide an answer. In Graphs I and II, 11 PSTs identified nonproportional relationships as inversely proportional and directly proportional, respectively.

Table 5 The Distribution of the PSTs’ solutions in the first and second tests
Full size table
Table 6 The PSTs’ determinations of the relationships in the first and second tests
Full size table
Table 7 The PSTs’ representations in the first and second tests
Full size table

In terms of the PSTs’ representations, in the Gear I problem, only seven PSTs drew a correct directly proportional graph, six PSTs provided incomplete graphs that did not start from the origin, and five PSTs did not provide an answer (Table 7). In the Gear II problem, only two PSTs drew a correct inversely proportional graph, four PSTs just marked two points and did not complete their graphs, five PSTs drew a linear additive graph as in Fig. 4b, and five PSTs did not provide an answer. In the Bakery problem, only one PST was able to draw a correct inversely proportional graph between the number of people and number of minutes, and nine PSTs did not provide a response.

Regarding the PSTs’ solution strategies, in the Gear I problem, among 17 PSTs, who calculated the correct answer, nine used the cross-multiplication strategy. Whereas four PSTs used double number line strategy (e.g. Arican, 2018); however, only one of these four PSTs was able to draw almost accurate double number lines (Fig. 9a), in which three PSTs inappropriately showed radius and number of notches on the same line. Moreover, two PSTs used directly proportional graphs that they drew in calculating the answer, and one PST used \( \frac{4 cm}{12\kern0.35mm notches}=\frac{3 cm}{x\kern0.35mm notches} \) equity to calculate the answer. In addition, one PST calculated the circumference of Gear A as 8π and obtained a 2π to 3 notches relationship. Next, he calculated the answer as nine notches because he knew that Gear B must have the same relationship.

Fig. 9
figure 9

a A PSTs’ double number line strategy in the Gear I problem; b A PSTs’ ratio table strategy in the Gear II problem

Full size image

In the Gear II problem, seven of the 16 PSTs, who calculated the correct answer, used the across-multiplication strategy, and seven PSTs calculated the correct answer showing the equity of the number of revolutions and notches (or radius) product in both gears. Moreover, two PSTs calculated the correct answer entering the information in a ratio table (Fig. 9b) and considering the constancy of products. However, among 16 correct responses, only two PSTs tried to obtain a mathematical formula to represent the relationship between the number of revolutions and radius (see Fig. 9b). These PSTs recognized that the product of the number of revolutions and radius was equal to 36. The PST who provided an incorrect answer used the cross-multiplication strategy assuming a directly proportional relationship.

In the Bakery problem, seven of the 14 PSTs, who calculated the correct answer, equated 3 × N × T with 4 × N × X, not necessarily using the across-multiplication strategy, and calculated X as \( \frac{3T}{4} \) minutes. Whereas six PSTs used the across-multiplication strategy, and one PST used the ratio table strategy. Among the three PSTs, who calculated an incorrect answer assuming a directly proportional relationship, two used the cross-multiplication strategy, and one used the double number lines strategy, which is used in presenting directly proportional relationships. Hence, in this case, the inappropriate use of double number lines yielded an incorrect answer.

Discussion and Conclusions

The present work aims to extend our knowledge of PSTs’ proportional reasoning by investigating their understanding of proportional and nonproportional relationships; their abilities to differentiate these two relationships from each other; their interpretations and representations of proportional and nonproportional situations; solution strategies that they used when solving the given problems; and the development in their understanding of proportional and nonproportional relationships during a course on ratios and proportions.

In terms of the first research question, analysis suggested that the PSTs very often attended to the qualitative relationships between two quantities when determining relationships. The PSTs inferred a directly proportional relationship between quantities if the values of two corresponding quantities were increasing or decreasing simultaneously. On the other hand, they inferred an inversely proportional relationship when the value of a quantity increased and the value of the corresponding quantity decreased. Although the PSTs’ attention to the qualitative relationships facilitated their determination of the directly and inversely proportional relationships in the Gear I, Gear II, and Bakery problems, many of them identified the nonproportional relationships presented in Graph I and Graph II as inversely and directly proportional, respectively. As stated by Arican (2015) and Izsák and Jacobson (2017), PSTs attend a variety of knowledge resources (e.g. Wagner, 2006) when determining directly and inversely proportional relationships. In this current study, some of the knowledge resources such as attention to the qualitative relationships, constancy of the rate of change, and textual features supported the PSTs’ determination of the directly and inversely proportional relationships, they were not sufficient to differentiate proportional relationships from nonproportional relationships.

During the course, the PSTs’ attention was directed to the constant ratio and constant product relationships when determining directly and inversely proportional relationships. In the Gear I problem, there was a “3 notches per 1 cm” constant ratio relationship. On the other hand, in the Gear II problem, the product of the number notches and number of revolutions was yielding a constant [12 (revolutions) × 9 (notches per 1 revolution) = 108 notches]. The analysis showed that only very few PSTs were able to recognize these relationships. During the interviews, some of the PSTs stated their difficulty working with gears and noted that they only had little experience on gears in high school Physics course. Therefore, the PSTs’ difficulties recognizing constant ratio and product relationships suggested that their limited understanding of gears might have constrained recognition of these relationships. Moreover, very few PSTs were able to recognize additive relationships presented in Graphs I and II. As in Feyza’s case, even the ones who recognized these additive relationships inferred a directly relationship or an inversely proportional relationship by attending to the qualitative relationships, constancy of the rate of change, or linearity of the lines in graphs. This finding suggested that the PSTs’ incorrect tendencies were not exclusively depended on their ability to reason additively or multiplicatively. Therefore, this finding contradicts with that of Boyer et al. (2008) and Jeong et al. (2007) who explained students’ incorrect tendencies in terms of lacking abilities. On the other hand, this finding aligns with that of Arican (2015) who suggested that PSTs may attend some knowledge resources more than others when determining directly and inversely proportional relationships.

The studies on students’ and PSTs’ understanding of proportional relationships (e.g. Atabas & Oner, 2017; Degrande et al., 2017; Lim, 2009; Riley, 2010; Van Dooren et al., 2007, 2010) reported their incorrect tendencies when determining proportional and nonproportional relationships. In the Gear II problem, none of the PSTs identified the inversely proportional relationship between the number of revolutions and radius as directly proportional. However, 20 PSTs could not provide an answer for this relationship. Whereas, in the Gear I problem, 15 PSTs identified the directly proportional relationship between the number of notches and radius as inversely proportional, and 18 PSTs could not provide an answer. This finding suggested that, as in Esma’s case, the PSTs, who inferred an inversely proportional relationship, did not understand the consequences of intertwining two gears or might have been confused by the information provided in the Gear I and Gear II problems. Some PSTs even rationalized their incorrect solution of 16 notches by drawing smaller-sized notches around Gear B. Therefore, this finding agrees with that of Degrande et al. (2017) who stated that students’ preference for proportional relationship or nonproportional relationship is affected by the features, which formed their knowledge resources, of the mathematical tasks used. On the other hand, in this study, I observed that the PSTs’ over attention to these specific features was stemmed from the traditional instruction, which they received in middle and high school.

Regarding the second research question, the PSTs’ representations of the directly and inversely proportional relationships suggested some issues in their understanding of these relationships. When representing a directly proportional relationship, many PSTs provided incomplete graphs (marking only two points) or, as in Feyza’s case, they hesitated to draw the directly proportional graph starting from the origin. Similarly, many PSTs presented the inversely proportional relationship between two quantities drawing an additive decreasing graph. As Arican (2015) also reported, the PSTs’ incorrect inversely proportional graphs suggested their inclination towards linearity when drawing an inversely proportional graph. The PSTs’ incorrect or incomplete graphs appeared to be consistent with their understanding of these relationships because they usually attended to the simultaneous increases and decreases or constancy of the rate of change when determining directly and inversely proportional relationships. In the Bakery problem, only one PST was able to provide a correct representation. This result showed the PSTs’ difficulty with coordinating relationships in problems that involve more than two quantities.

Consistent with previous research (e.g. Arican, 2018; Misailadou & Williams, 2003; Riley, 2010), the PSTs mostly relied on cross-multiplication and across-multiplication strategies when solving the direct and inverse proportion problems, respectively. Although the PSTs were instructed on the unit ratio, ratio table, double number lines, and strip diagram strategies (e.g. Arican, 2018), they still preferred cross-multiplication and across-multiplication strategies. Therefore, the PSTs’ over reliance on these strategies constrained their recognition of the multiplicative relationships. Similar to the previous conclusion, their over reliance on these strategies might have stemmed from the traditional instruction on proportions, which heavily relies on rule memorization and rote computations.

In terms of the last research question, testing 18 PSTs with the same problems showed increments in their number of correct solutions. However, the PSTs’ determination of the proportional and nonproportional relationships, abilities to differentiate these two relationships from each other, abilities to provide correct interpretations and representations of these relationships, and their solution skills increased slightly. These findings suggested that although the PSTs gained practical skills on solving proportion problems, their depth of understanding of the proportional and nonproportional relationships has improved less.

Implications for Teaching

The findings obtained from this study showed the PSTs’ incorrect tendencies about proportional and nonproportional relationships, over reliance on cross-multiplication and across-multiplication strategies, and difficulties with interpreting and representing mathematical relationships. All these difficulties appeared to be related with the traditional instruction that they received on fractions, ratios, and proportions. As presented in this study, correcting PSTs’ incorrect tendencies and developing their proportional reasoning can be a very difficult, overwhelming, and time-consuming process. These difficulties can be best handled by providing meaningful mathematics to each and every students that can achieved by training preservice and in-service teachers in accordance with the needs of students. Hence, there is a need for a reform in mathematics education in schools, in particular for the instruction on fractions, ratios, and proportions. Using real-world activities together with hands-on materials can facilitate students’ understanding of these topics. Thus, this study contributes this reformation by documenting the PSTs’ understanding of and difficulties with proportional and nonproportional relationships.