Introduction

Comparative studies about mathematics textbooks have been a prominent area of research since the results of the Third International Mathematics and Science Study (TIMSS) were released by Valverde, Bianchi, Wolfe, Schmidt and Houang (2002). Recently, Fan (2013) proposed a framework for mathematics textbooks research encompassing three areas: (1) as the subject of research (textbooks themselves, i.e. what are their features); (2) as a dependent variable (how textbooks are affected by other factors, i.e. how to choose textbooks if not mandatory); and (3) as an independent variable (how they affect other factors, i.e. students’ learning outcomes). This framework can be used to identify the following perspectives on textbook research: (1) the different approaches to handling a certain topic as embodied by the textbooks; (2) what might influence textbooks’ writers to present mathematical concepts in a certain way with regards to features of curricula; and (3) how these approaches influence students’ performance, and which approach would be more effective for students’ understanding development. In meeting the requirements of subject content in national curricula around the world, different textbooks might provide different approaches to dealing with a given topic (Jones & Fujita, 2013). The aim of the present study is to contribute to the first perspective: to investigate the approaches taken by textbooks in two different regions to a given mathematical topic. This study is part of a wider study looking at all three perspectives in the context of the teaching and learning of linear function in England and Shanghai. This paper will however focus solely on this first perspective.

Textbooks largely influence how teachers portray a mathematical topic and implement their understanding of students’ learning trajectories in a classroom, there being a “statistically significant” relationship between textbooks and classroom instruction (Valverde et al., 2002, p. 10). Many researchers have revealed that textbooks are closer to the classroom than national curricula, for example embodied in teaching strategies or activities (Fan, 2013; Fan, Zhu & Miao, 2013; Johansson, 2003; Leung, 1995; Son & Senk, 2010). In terms of textbook use in English classrooms, initial reports from TIMSS revealed that, through the key stages, the use of textbooks increased considerably from 66 % for Year 5 pupils to 84 % in Year 9 students, when teachers use textbook schemes over half of their teaching time (Foxman, 1999). However, Howson (2013, p. 652) noted that England textbooks are written “not by experienced teachers, but by experienced examiners”. The English teachers might not follow the textbooks in their entirety, but their approach to topics, students’ performance expectations, instructional features and their perspectives, would not be different to what examples in textbooks describe. On the other side, Chinese teachers study textbooks very carefully and classrooms are textbook-based (Ma, 1999). Therefore, this paper particularly analyses the nature of examples proposed in textbooks, given their role in predicting the development of students’ understanding of basic mathematical knowledge.

The present study focuses on the specific mathematical topic of linear function. Many see function as a key mathematical topic at the secondary school level (Brenner et al., 1997; Llinares, 2000). Others suggest that it represents the foundation for the whole subject of mathematics (Hitt, 1998; Oehrtman, Carlson & Thompson, 2008). We chose linear function as a fair comparable topic because the learning goals associated with the topic were similar between England and Shanghai as discussed later in the section “Linear Function in Curricula” in the Results part of the paper. We censored the requirements related to the concept of function and certain types of function in the two regions’ curricula. The overlap of types of function occurs for linear, quadratic and reciprocal functions.

The linear function is the appropriate type for the comparative topic because it is the first type of function students would encounter (Leinhardt, Zaslavsky & Stein, 1990). Therefore, depiction of the initial understanding of function can serve as an example of how the important mathematical concepts are expected to be handled within the two regions, as linear function is the paradigm case compared with the two other types: reciprocal and quadratic function. The reciprocal function is taught as a standard form in Shanghai but as a specific form in England, and is therefore not considered an appropriate topic to draw comparisons between the two regions. In terms of the quadratic function, the Shanghai curriculum introduces more properties, such as symmetry, and heavily emphasises links with other knowledge areas of both algebra and geometry. Comparing with the KS4 statutory guidance in England and Wales related to the quadratic function, e.g. “roots, intercepts and turning points of quadratic functions” (Department for Education, December 2, 2013, p. 8) as the properties to consider, it appears harder to measure or evaluate the similarity or dissimilarity between the two regions in quadratic function.

In terms of why we focus on England and Shanghai, in the area of comparative education, the consistent higher performance of Chinese students has been of growing interest especially in the UK. English educators refer to this as the England-East Asia gap in mathematics (Jerrim & Choi, 2014). Mathematics achievement has become entangled in urgent national issues in England. Particularly, Shanghai students have maintained the top position in the league table in the Programme for International Student Assessment (PISA) 2012, which has gained the interest of education authorities in England. In February 2014, Elizabeth Truss, Parliamentary Under-Secretary of State for Education and Childcare at that time, visited Shanghai to learn how maths was being taught there (Howse, February 18, 2014), and then an announcement that Shanghai maths teachers would be flown to England as part of an exchange project was released (Coughlan, March 12, 2014). Therefore, how Shanghai teachers work in the classroom has gained a great deal of interest in England. However, teaching and learning mathematics in Shanghai heavily relies on textbooks. It is worthwhile to investigate the strengths and weaknesses of the learning trajectories contained within the Shanghai textbook. However, Clarke (2003, p. 180) appealed that international comparative research “embodied in the metaphor of the mirror rather than the blueprint should underlie the function of all such studies”. Therefore, through the comparison of selected textbooks’ expectations for understanding mathematical concepts, this study will provide the key assumptions and insights into textbook-based routines, and how perceived deficiencies caused by the routines might be corrected.

Literature Review

Textbook Research

One trend of textbook comparative studies aims to discover what mathematics textbooks actually looks like, for example the layout. Compared with French and German textbooks, the layout of English textbooks has fewer questions and the structure is relatively brief (Pepin & Haggarty, 2001). That is, English textbooks are much more concise on structure and the number of questions.

Secondly, textbook studies have investigated what kind of knowledge is prioritised. Eastern textbooks have focused on pure mathematics knowledge, while Western textbooks emphasise real-life situations. For example, Park and Leung (2006) compared the Grade 8 textbooks of Eastern countries (including China, Japan and Korea) and Western countries (including England and the USA). The study found the Eastern textbooks would be more beneficial for students when conveying an idea, but less successful in motivating students, while the Western textbooks are effective in expressing the importance of mathematics in real-life, but unclear about the link between real-life situations and the mathematical concepts. Furthermore, focusing on characteristics of problems presented in textbooks, Zhu and Fan (2006, p. 614) argued that Chinese textbooks should present more authentic application problems (AAP) “whose conditions and data are, indeed, from real-life situations or collected by students themselves from their daily lives”; whereas USA textbooks should consider more challenging problems for students involving more steps in the solution, as China does. From another side, USA textbooks also include more visual information than Chinese ones.

Thirdly, how to present the content is highlighted in studies. After comparing the content presentation of the addition and subtraction of integers between American and Chinese mathematics textbooks, the Chinese textbooks were found to contain “more problems with high level mathematics content” (Li, 2000, p. 239). Researchers examined the difference between England and Japan regarding the solution of quadratic equations in junior secondary schools (Whitburn, 1995). The results showed that in England, the approach to this topic is too limited, while in Japan it would be taught both algebraically and graphically.

Fourthly, the solution strategies in examples of Eastern textbooks such as from China and Singapore are also less in number than in Western textbooks such as in the USA. Fan and Zhu (2007) compared China, Singapore and USA mathematics textbooks for problem-solving procedures in terms of two layers: general strategies referring to Polya’s four-stage problem-solving model (understanding the problem; devising a plan; carrying out the plan; and looking back) and specific strategies. The Chinese and Singapore textbook series merely presented the carrying out the plan, while more than two thirds of problem-solving procedure presented in USA textbooks adopted at least two stages. This finding may partly explain why American students perform better than Chinese pupils in open-ended problem-solving, as observed by Cai (1995).

In summary, the features of English textbooks contain more questions linking with real-world situations, while Chinese textbooks have more emphases on knowledge depth. However, little research in textbooks research focuses on the formatting of understanding development and how the depth of examples that textbooks provide or support abstract understanding, especially in comparative education area. This will be the focus of this paper, concentrating on the topic of linear function.

The Concept of Function in Lower Secondary School Textbooks

Sfard (1991) argued that the concept of function has two aspects: operational and structural, in line with the dual nature of mathematical concepts. The structural aspect is more abstract than the operational one. The concept of function is described as a flow diagram in England’s textbooks (see Fig. 1), following the idea of a function machine in primary schools. On the other hand, the concept of variable is introduced in English textbooks as “this is what the letters used to represent numbers are called” and “the variables are treated just like a set of (x, y) coordinates”. There are no terms such as independent variable or dependent variable offered.

Fig. 1
figure 1

The definition of function in GCSE Maths 2 tier-foundation for AQA A

Full size image

The view of linear function for Shanghai secondary school students is from a variable view in the lower secondary school (age 11–15), and a mapping view in the upper secondary school (age 16–18). The concept of function which appears first at Grade 8 (approx. age 14) in lower secondary school is defined as a rule-based relationship:

There are two variables, for example x and y; within the range of values allowed for x, variable y changes once x changes as they have a certain dependent relationship. Variable y is referred to the function of variable x. x is referred to the independent variable.

This definition is in line with Dirichlet’s one. In 1837, Dirichlet developed the accurate definitions of function by considering “an arbitrary nature of function” (Kleiner, 2009, p. 20):

y is a function of a variable x, defined on the interval a < x < b, if to every value of the variable x in this interval there corresponds a definite value of the variable y. Also, it is irrelevant in what way this correspondence is established.

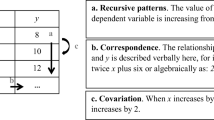
The variable view of function in lower secondary school aims to focus on the relationship between variables. According to Doorman, Drijvers, Gravemeijer, Boon and Reed (2012), the aspect of the dynamic process of co-variation is shown in the Shanghai lower secondary school textbook.

Understanding the Concept of Function

Ronda (2009) states directly that to describe students’ understanding, efforts should be made to examine its properties and representations. The concept of function has multiple representations that present this idea (Habre & Abboud, 2006). The three main representations—graphs, tables and formulae (algebraic expression), can be wrongly viewed by students as separate static entities (Schwarz & Dreyfus, 1995). That is, students can regard different representations as different tasks, instead of different means of representing the same idea (Gagatsis & Shiakalli, 2004). Four current studies have explored how students handle different representations within the concept of function. First, Ronda (2009) especially paid attention to how Grade 8, 9 and 10 secondary students understood one main representation, algebraic expression (equation), in terms of four growth points: (1) procedures for generating values; (2) representations of relationships; (3) describing properties of relationships; and (4) objects that can be manipulated and transformed. Secondly, although the concept of function has three main representations, DeMarois and Tall (1996) argued that the connections amongst representations should also include representations that are written, verbal (spoken), kinesthetic (enactive), colloquial (informal or idiomatic) and notational conventions. These eight representations were investigated within five layers of understanding: pre-action, action, process, object and proceptual. The first layer, pre-action, indicated “a ground floor” for making preparation. Three of these, action, process- and object, were similar to the first three stages of APOS theory proposed by Dubinsky and McDonald (2002). In the last layer, proceptual, students can demonstrate flexibility in shifting between different processes and object layers. Thirdly, Zachariades, Christou and Papageorgiou (2002) proposed three cognitive development levels for first year mathematics undergraduate students when they connected two main representations: algebraic expressions and the graphical representation. At Level 1, students identify typical types of function representations, and students are enabled to recognise these representations individually. At Level 2, students connected the corresponding representations, from graphical to algebraic expression, and from algebraic expression to graphs. Level 3 demonstrated the degree of accuracy of translation. Fourthly, Hitt (1998) identified teachers’ difficulties with representations and compared it with the previous literature about students’ difficulties. He suggests five levels of understanding the mathematical concepts. At Level 1, teachers showed their imprecise ideas in the graphical representation when they were required to discern if a certain curve corresponded to a function. At Level 2, the different ways of presenting the algebraic expression for the same function influenced the identification. Level 3 required the ability to connect different representations. Within Level 4, based on the connection established, learners should know that the different representations describe the same concept. When putting graphical representations in a real context at Level 5, teachers were supposed to articulate the relationship between representations and real-world situations.

There were two models depicting Shanghai secondary school (age 11–18) students’ understanding of linear function proposed by Zeng (2002) and Jia (2004), with the Jia (2004) model being developed from Zeng (2002). In the lower secondary school stage, Jia (2004) demonstrated three stages: understanding variable, stressing relations and employing formula.

Based on the different views of understanding the concept of function in the two regions, we established a theoretical framework to examine how these differences possibly shaped understanding development in the case of linear function from the textbook perspective.

Theoretical Framework

Sfard and Linchevski (1994) pointed out that mathematics is a hierarchical structure in which some strata cannot be built before another had been completed. Based on the previous literature outlined above, in this study the development of understanding of linear function is illustrated by the following processes: at the beginning, students recognise that there are different representations to present the dependent relationship between two variables, x and y; then they connect these representations by plotting the graph from the algebraic expression or finding out the rule from the graph; during the connection process, local properties, linking the parameters in the algebraic expression with the meaning of the graph, will be identified; and student now can treat the concept as a whole, with not only the different representations being understood to offer the same mathematical knowledge but also having a view of the structural aspect towards the concept; finally students can work out complex problems that link with other knowledge. Therefore, this view of understanding was framed as five hierarchical levels from the lower level to the higher level which we termed: Level 1, Dependent Relationship; Level 2, Connecting Representations; Level 3, Local Properties Noticing; Level 4, Object Analysis; and Level 5, Inventising.

Examining these levels further, the concept of linear function is initially based on mastering the representations of function. Students should know the three main representations for the concept of function: algebraic expression, tabular and graphic representation. This means that as students start to study linear function, they have achieved the first level—Dependent Relationship—already.

The concept of linear function is presented straightforwardly either as an algebraic expression such as

$$ y=2x+1 $$
(1)

or a straight line graph in the Cartesian plane. Students are initially required to individually identify these representations, as in the Level 1 proposed by Zachariades et al. (2002). Subsequently, to construct the concept of linear function, students require the understanding that these representations represent the same concept by Connecting Representations, as reflected in the first two growth points proposed by Ronda (2009). Through connecting, students can make sense of the relationship between the different representations and the concept of linear function as stressing relations, the second stage of Jia (2004). At this level, the letter x can be replaced by concrete numbers so that a link is made between the input-output view to variables view. This is also exemplified in Hitt’s (1998) study in which connecting representations is one of the levels. But at this stage of understanding, the process of connecting representations would not be related with any properties of linear function which would be involved in the next level of understanding.

Zachariades et al. (2002) proposed that students connected the corresponding representations, from graphical to algebraic expression and from algebraic expression to graphs using the tabular representation. Translating from graphical representation to algebraic expression in linear function consists of two approaches. One way is to solve the simultaneous equations through plotting two points, without indicating properties. However, if they start to identify the links between the properties of the graphs and the equations, then this makes it at the next level.

This third level we term Local Properties Noticing, where the different representations are recognised and connected. We emphasise here that common functional properties can have two categorises: local and global. We identify the local properties at this level where students work out the properties by using individual pairs of points, such as the intercept and the gradient, while the global properties move away from individual points and focus on “the entire function”, for example monotonicity (Slavit, 1997, p. 264). At this level, students will still look for pairs of variable values instead of regarding the function as an object and having a structural view.

Moving onto the next level, what we term Object Analysis, at this level students are required to regard functions as a whole, identifying the global properties described above, such as parallel and perpendicular properties and monotonicity in linear function. In turn, students can deal with the transformation of the straight line of

$$ y=f(x) $$
(2)

by a vector \( \left(\begin{array}{c}0\\ {}a\end{array}\right) \). Functions being thought of as an object or a set of ordered number pairs which can be manipulated and transformed is the last growth point proposed by Ronda (2009).

At the last level, Inventising, the learners can link to other mathematical knowledge. This was the same term used in Pirie and Kieren’s model (Pirie & Kieren, 1994) as the outermost layer, which presented a fully structured understanding of a given mathematical concept. It could be seen as using a functional view to re-examine other concepts, such as equations, inequalities and algebraic expressions, stated as employing formula by Jia (2004).

Research Questions

In this study, the aim of the research is to compare the expectation of understanding linear function as exemplified in selected mathematics textbooks in Shanghai and in England, focusing on pure mathematical knowledge rather than the application of knowledge. To do so, we applied the model of understanding function described above solely to the examples used in the textbooks. The reason why we chose worked examples will be explained in the “The Analytical Framework” section. More specifically then, the research questions we asked were as follows:

  1. 1.

    What emphases do the examples in selected textbooks place in terms of levels of understanding linear function?

  2. 2.

    At each level, are there any differences in the expression of examples as well as the suggested solution?

Methods

Selection of Textbooks

Each English textbook series has two levels of textbooks developed for two types of student abilities (Foundation Level and Higher Level), though both of them follow the national guidance for England. We collected the used textbooks from three secondary schools located in the North East of England who volunteered to take part in this study. Table 1 shows the details of the sample schools from the latest school inspection report by Ofsted (The Office for Standards in Education, children’s Services and Skills). The sample schools are referred as School SEN1, SEN2 and SEN3. To some extent, the three schools present which kind of textbooks well-performed state schools have chosen for their students. Although the selected textbooks in these schools seemed typical of those used in schools more widely, we acknowledge that they are a convenience and not a representative sample of books used in all English schools. The chapter or sections in these textbooks related to linear function were selected for this study.

Table 1 The details of the English sample schools
Full size table

On the contrary, textbook choice is not flexible in Shanghai. Since the late 1980s, Shanghai has had its own municipal curriculum: Shanghai City Primary and Secondary Mathematics Curriculum Standard (Shanghai City Education Committee, 2004). The uniform textbooks were developed based on this curriculum instead of the national ones. It also remains a centralised education system in Shanghai. Therefore, textbooks are widely used by all the lower secondary school students at state schools as well as at private schools during the compulsory schooling stage (from age 7 to 16). Each term in the school year has one separate mathematics textbook. Linear function is presented in the second term of Grade 8 (age 14), and therefore the one appropriate Shanghai textbook was included in the present study.

Therefore, the following textbooks containing linear function were examined:

England:

  1. 1.

    Collins New GCSE Maths for Edexcel Modular (Foundation 1), published by Collins;

  2. 2.

    Collins New GCSE Maths for Edexcel Modular (Higher 1), published by Collins;

  3. 3.

    Collins GCSE Maths 2 tier-foundation for AQA A, published by Collins;

  4. 4.

    Collins GCSE Maths 2 tier-higher for AQA A, published by Collins;

  5. 5.

    Foundation GCSE Mathematics: Revision and Practice, published by OXFORD University Press;

  6. 6.

    Higher GCSE Mathematics: Revision and Practice, published by OXFORD University Press;

    Shanghai:

  7. 7.

    Shanghai nine-year compulsory education textbook: Mathematics Grade 8 (Vol. 2).

The Analytical Framework

The analytical framework for this study was initially drawn from the TIMSS framework. TIMSS used “blocks” instead of sections in characterising textbooks. There were a total of ten blocks including narrative blocks, graphic blocks, exercise and question sets, activities, worked examples and an “other” block (Valverde et al., 2002). Love and Pimm (1996, p. 386) suggested that the most frequently used organisation in textbooks was the “exposition–examples–exercises” model. The different choices for “exposition” however represented what learning theory the textbooks’ authors took. This study was therefore carried out on examples which were clearly marked as “Example” in the selected textbooks.

The worked examples indicated the detailed solution strategy to a problem where they “presuppose that students will follow the flow of that pursuit” (Valverde et al., 2002, p. 142). However, the exercise block cannot indicate in which way students will be expected to solve the problems. Only the example blocks are thus highlighted in this study. In addition, we chose examples which appeared for the pure mathematical knowledge related with linear function, excluding examples relating to the application of knowledge in a real-world situation because the model of understanding function does not specifically include the application of knowledge.

The average percentage of worked examples from textbooks will be categorised within the four understanding levels (Levels 2 to 5) according to the model discussed in the theoretical framework section, and from the proposed solutions to the examples, the distinct approaches towards the same mathematical knowledge will also be investigated.

Data Coding

In accordance with the levels of understanding linear function, each example was located in one of the understanding levels. All the selected textbooks in England started with drawing the graphs from algebraic expressions which would be located at Level 2.

The first section of the Shanghai textbook was about the definition of linear function, which the English textbooks did not have, so that examples from this first section in the Shanghai textbook were not included in the study.

Data coding of understanding levels contained two steps. The first step involved identifying the number of examples at each level and the second involved calculating the percentage of these examples amongst the sum of examples in this topic. Here, each example was designated at a certain level. If an example included a set of questions, the highest level of understanding conveyed within the example was assigned.

Key words were used to level the examples. If the example requires finding the gradient, the key word “gradient” will be highlighted and coded to the corresponding level, Local Properties Noticing (see Table 2). The data coding was completed by the first author because the coding approach is plain and clear to deal with. For example, if the example question merely requires drawing the straight line from algebraic expression and the provided solution is exactly the straight line, the understanding level would be coded as Level 2. Main key words at each level were listed in Table 2. At the highest level, besides identifying the key words, the examples normally are listed at the last section of the chapter; the solution is not merely related with linear function; and the reasoning process will be offered to explain how the other knowledge links with linear function.

Table 2 Key words in each level
Full size table

Numbers at each understanding level in the three Higher Level textbooks were put together and calculated as a whole. Then, the percentage of these examples at each level could be calculated and compared. The same procedure was also undertaken for the three Foundation textbooks. Hence, the seven selected textbooks are divided into three types: Higher Level, Foundation Level and Shanghai.

Results

The Differences of the Selected English Textbooks

How to Introduce the Topic

The initial presentation of linear function in two series of English textbooks (New GCSE Maths Edexcel Modular and Collins GCSE Maths for AQA) was related to real-life graphs. Here, the linear graph was built upon the straight-line distance-time graphs which present how far someone or something has travelled over a given time period. For example, in travel graphs, the formula of average speed implies the meaning of gradient. Another series, GCSE Mathematics Revision and Practice (Foundation), started with straight-line graphs, horizontal and vertical lines, and then related lines with x and y, the coordinates. These two sub-sections paved the way towards drawing graphs. The Higher one of this series also puts linear graphs after sequences.

The Basic Knowledge in the English Textbooks

In two series, Edexcel Modular and Collins GCSE Maths for AQA, examples cover all the requirements in the curricula, while GCSE Mathematics Revision and Practice (Higher) does not introduce the parallel and perpendicular properties which are located at Level 4 in the examples. This is one objective gap between the requirements between commercial textbooks and the national curriculum, besides the used terms discussed in the next section.

Linear Function in the Curricula

Referring to how the topic is introduced in the two regions, two different approaches take place in the intended curriculum. The two English curricula (KS3 and KS4) arrange the subject content in a spiral pattern, while the Shanghai compulsory curriculum shows a non-repeated approach. In England, the topic of linear function is separated into different years and becomes more complicated as students are allowed to progress and accumulate knowledge from year to year. Topics in KS3 are further explored and extended in KS4, although KS4 also introduces new topics. In the case of linear function, Year 8 (approx. age 13) students start at drawing the graphic representation from algebraic expression; the property gradient might be introduced at Year 9 (approx. age 14); and at Year 10 (approx. age 15), students are expected to achieve all the requirements of the curricula. Conversely, the feature of the Shanghai curriculum has a narrow yet deeper scope. Linear function is introduced at Grade 8 (approx. age 14). Students are expected to learn it during a 2-week (10 consecutive classes) teaching schedule.

The topic of linear function proposed in England’s curriculum is connected to linear graph in the English textbooks. There is a disparity between England’s curricula which propose the term “linear function”, and commercial textbooks which interpret it as “linear graph”. Technically, these are two slightly different concepts. Linear graph refers to a straight line which, in addition to graphs of linear function, also includes two other kinds of graphs: the vertical lines such as

$$ \mathrm{x}=2 $$
(3)

which does not belong to the family of function, and the constant function, such as

$$ \mathrm{y}=2 $$
(4)

These two linear graphs are not associated with the concept of linear function according to the definition in the Shanghai textbook. In other words, linear function in the Cartesian plane is presented as a straight line, but not every straight line in the Cartesian plane is assigned to the concept of linear function. In this study, these two extreme example graphs will be excluded, as it will not affect the purposes of this study. At the same time, this definition of linear function illustrates that England considers linear function in a more graphical way, while Shanghai examines it using an algebraic method.

Doorman et al. (2012, p. 1246) suggested that there are “three interrelated aspects of function”: as an input-output assignment, as a dynamic process of co-variation and as a mathematical object. We use these three aspects to identify which main aspect the textbooks in each region took to present the concept of function. The selected English textbooks emphasise the input-output assignment aspect, in line with the requirement of the KS4 curriculum: “interpret simple expressions as functions with inputs and outputs” (Department for Education, December 2, 2013, p. 7). The English textbooks do not develop the variable view of function. On the other side, the dynamic process of co-variation view of function dominates in the Shanghai textbook.

Overall Distributions of Levels

Table 3 shows the percentage of examples used in the textbooks at each level of understanding function. Both the Shanghai textbook and selected Higher level textbooks covered Levels 2 to 5 of the understanding model. For the more abstract understanding levels, namely Level 4 Object Analysis and Level 5 Inventising, the Shanghai textbook provided double the percentage of examples compared to the English Higher level textbooks, with particular emphasis on Level 4. The examples from the selected Foundation level textbooks, however, evidently placed emphasis on Level 3, without presenting any examples for both Level 4 and Level 5. All the English textbooks emphasised Level 3 Local Properties Noticing. Lower down, at Level 2 Connecting Representations, the Shanghai textbook contained a greater percentages of examples than the English Higher level textbooks, but fewer than the Foundation level ones.

Table 3 The percentage of examples used at each level
Full size table

Approaches Towards Each Level

Level 2

Both regions’ textbooks started with a concrete example, using an algebraic expression, such as

$$ y=\frac{2}{3}x-2 $$
(5)

in the Shanghai textbook, and

$$ y=4x-5 $$
(6)

for values of x from 0 to 5 in English textbooks. Here, the difference was the domain (value of x) that English textbooks specified while Shanghai did not. The graph in the Shanghai textbook therefore was a straight line, while a part of a line between two points (segment) was presented in England. Therefore, the initial expectation of drawing a linear graph/function differed. The solution shown in the Shanghai textbook was to find out two pairs located in the axes so as to draw the straight line, the graphic representation.

Level 3

Particularly in the Shanghai textbook, the analysis from Table 3 suggests a big jump from Level 2 to Level 4. The percentage of examples at Level 3 was lower than that of any of the English textbooks due to only one local property, y-intercept, being introduced here. The meaning of gradient in the Shanghai textbook was simply explained as how steep the straight line was, while there was only one example provided by the textbook that indicated how to calculate the gradient using a purely algebraic approach of solving simultaneous equations. For example, the straight line \( y=kx+b \) passes through points A (−20, 5), B (10, 20), find out (1) the value of k and b; (2) the points that this straight line cut the axes (of a Cartesian coordinate system). The solution of the first question was related to the pure algebraic method to work out the gradient; because the straight line \( y=kx+b \) passes through points A (−20, 5), B (10, 20), so

$$ \left\{\begin{array}{c}\hfill -20k+b=5\hfill \\ {}\hfill 10k+b=20\hfill \end{array}\right. $$
(7)

Solving the simultaneous equations,

$$ \left\{\begin{array}{c}\hfill k=\frac{1}{2}\hfill \\ {}\hfill b=15\hfill \end{array}\right. $$
(8)

Without detailed introduction to the graphical meaning of gradient, Shanghai textbooks quickly moved on to how to apply this concept in order to identify parallel lines, and focused on the higher level of understanding, Level 4 Object Analysis, which was the most prominent understanding level in Shanghai.

By contrast, the English textbooks provided two methods of drawing a graph to make sense of the gradient; the gradient-intercept method and drawing a line with a certain gradient. Gradient is calculated by constructing a right triangle from a graph as \( \mathrm{Gradient}=\frac{\mathrm{Differences}\kern0.2em \mathrm{in}\kern0.2em y}{\mathrm{Differences}\kern0.2em \mathrm{in}\kern0.2em x}=\frac{AC}{BC} \) (see Fig. 2).

Fig. 2
figure 2

The graphic explanation of gradient

Full size image

Using the geometry approach towards gradient, the English textbooks have to explain the difference between positive gradient and negative gradient of the straight line: a line which slopes upwards to the right has a positive gradient as shown in Fig. 2, while if upwards to the left, the line has a negative gradient. This judgement for positive or negative value of gradient drawn from geometry method would not be required if using the algebraic method.

Both regions’ textbooks illustrate the meaning of gradient as the steepness of the line. From this perspective, the algebraic approach cannot explain how this method links with the meaning of steepness. This property therefore is presented as a rule-based procedure for instrumental understanding in the Shanghai textbook. The English textbooks are one step closer to greater conceptual knowledge for relational understanding because the steepness rooted in the graph is determined by the degree of angle ABC in Fig. 2. As the angle increases, the steeper the line is.

Level 4

The Foundation Level textbooks did not introduce the property of parallel lines in worked examples which was listed in the statutory guidance in the England’s curricula, while the selected Higher Level textbooks followed the statutory guidance to introduce parallel and perpendicular lines in two of the three series of textbooks.

The common global property introduced by England and Shanghai was parallel. However, differing approaches towards this property was taken as well. In the Shanghai textbook, an example required one to draw two straight lines,

$$ y=-\frac{1}{2}x+2 $$
(9)

and

$$ y=-\frac{1}{2}x $$
(10)

and then describe the geometrical relationship between the lines. The algebraic expression was offered, and the solution was obtained by observing the two lines in the Cartesian coordinate system where these two lines are parallel.

In the selected Higher Level English textbooks, the two lines were presented in the graphical representations (see Fig. 3), and the example required the following: (i) find the equation of each line; (ii) describe the geometrical relationship between the lines; (iii) describe the numerical relationships between their gradients.

Fig. 3
figure 3

An example in the English textbook

Full size image

In summary, moving from the algebraic to the graphical was emphasised in the Shanghai textbook, while the opposite way was taken in the selected English textbooks. Examples in the Shanghai textbook normally do not have a graph while the selected English textbooks display examples with the aid of graphs.

Level 5

The Shanghai textbook showed the link between linear function and inequalities from both an algebraic and a graphical approach. In the case of one example, namely for the given linear function

$$ y=\frac{2}{3}x+1 $$
(11)

(i) when \( y=5 \), find the value of x; (ii) when \( y>5 \), find the value of x; (iii) in the Cartesian plane, there are some points located in this straight line, as well as under the x-axis, find the range of abscissa for these points. The textbook gives two approaches of solution using the algebraic method first: the solution for sub-question (i)

$$ \frac{2}{3}x+1=5,\mathrm{then}\kern0.5em x=6 $$
(12)

The solution for sub-question (ii)

$$ \frac{2}{3}x+1>5,\mathrm{then}\kern0.5em x>6 $$
(13)

The solution for sub-question (iii)

$$ \frac{2}{3}x+1<0,\kern0.5em \mathrm{then}\kern0.5em x<-\frac{3}{2} $$
(14)

Following this solution, the textbook presents the graphical representation of Eq. (11), explaining the solution using the graphic method.

Conversely, the Higher Level textbooks in England merely linked to the geometrical knowledge of the midpoint of a given line. For example, with a graph of AB in the Cartesian plane, the point A is (2, −1) and the point B is (4, 5); (a) find the equation of the line parallel to AB and passing through (2, 8); (b) find the equation of the line perpendicular to the midpoint of AB. The solutions for this example provide the reason using words: (a) The gradient of AB is 3, so the new equation is of the form

$$ y=3x+c $$
(15)

The new line passes through (2,8), so

$$ 8=3\times 2+c\Rightarrow c=2 $$
(16)

Hence, the line is

$$ y=3x+2 $$
(17)

The solution of the second question (b) first pointed out that the midpoint of AB was (3, 2), and then linked to the meaning of the gradient of the perpendicular line.

The solutions at the Shanghai textbook are shown by two approaches, while the selected English textbooks tend to use words to describe the underlying reason.

Discussion

With a focus on the topic of linear function, this study examined mathematics knowledge in a total of seven mathematics textbooks from England and Shanghai in detail from a worked example perspective. We address two issues from this study in this discussion. First, the two research questions will be answered. Secondly, from the mathematical concept development perspective, the different approaches shown in the two regions will be compared. These approaches are rooted in a much broader background of how each region views mathematical understanding.

To answer Research Question 1, different emphases on understanding levels in each region were found in the examples. It has been argued that the requirements of the mathematics curricula in East Asian countries are much more difficult than those in Western countries, in terms of mastering the complexity of mathematics knowledge (Bao, 2002). Textbooks largely embody the “student performance expectations presented in content standards” (Valverde et al., 2002, p. 10). The distribution of the four levels of understanding of linear function in Table 3 indicated how deep the understanding development was going. Meanwhile, it demonstrated that a more abstract understanding for linear function, Object Analysis, was indeed highlighted in the Shanghai textbook compared to the English textbooks, along with Local Properties Noticing, as one level higher. That means the predominant understanding level in English textbooks remains in the process stage, while the Shanghai textbook promotes a structural perspective.

Furthermore, it is reasonable to speculate that the Shanghai students might be encouraged to move towards more abstract levels of understanding linear function or be given much more opportunities to work on questions located at higher levels of understanding. This potential deeper understanding of mathematics of Shanghai students might lead to better performance. On the other hand, this finding argues that English students might not have enough experience of a deeper understanding of mathematical knowledge which could possibly indicate one reason for their disappointing performance in international assessments. Their understanding development is constrained by the requirement of the curriculum and/or textbooks in general for Higher Level and Foundation Level.

In terms of Research Question 2, the algebraic solution for the lower levels of understanding, for example Level 4 Local Properties Noticing, was mainly expected in Shanghai. The strong algebraic approach in Shanghai particularly affected how the textbook introduced the concept first and the local property of gradient. A potential drawback to this algebraic approach is its abstraction because it is suggested that only children between 11 and 14 years old can understand the algebraic concept at the formal operations stage (Dreyfus & Eisenberg, 1982), though Grade 8 students in Shanghai are normally approximately 14 years old. Lue (2013) concluded that the algebraic expression is the most challenging representation to be handled, even by Grade 10 students in Taiwan, after having examined the translations between representations within six kinds of elementary functions including linear function.

Although according to Sfard the operational process is the first step towards a new notion of concepts (Kieran, 1997), there is also a possible tendency for students to remember the procedure, computed as a coefficient in the analytic approach, instead of having insight into the meaning of the concept. Indeed, as for the manipulation of algebraic expressions more generally, some students could be in control of this manipulation while some could appear to be controlled by it (Cottrill et al., 1996). That is, students could tackle the question in a mechanical or algorithmic way, namely devoid of meaning or relational understanding in the Shanghai case. One concern is that the overuse of these rules in learning function may contribute to “structurally weak” understanding for students (Stein, Baxter & Leinhardt, 1990, p. 660), as Healy and Hoyles (1999, p. 83) have pointed out that only using the symbolic aspect would miss the opportunity to “exploit the visual to explain or justify their symbolic constructions or to develop the capacity to move flexibly between representations”.

The Shanghai textbook offered two fundamental different solutions in the highest level of understanding. This effort might accelerate students’ good understanding. In mathematics education, “to understand” often means to “understand well” (Sierpinska, 1994, p. 117). Researchers proposed good understanding from two theoretical perspectives: schema and connection. From a schema perspective, Skemp (1971, p. 40) suggested that “the more other schemas we have available, the better our chance of coping with the unexpected”. The highest level of understanding in the examples provided the possible rich schema of linear function for Shanghai students. From the related networks view, Hiebert and Carpenter (1992) considered stronger and more numerous connections in existing networks as a way of determining whether students had a more thorough comprehension. Two types of solutions in the Shanghai textbook offered different ways to connect knowledge. More well-organised schemas or specifically more strengthened connections shown in the highest level of understanding examples might denote better understanding in Shanghai situation.

Limitation

Although this study has clearly revealed the different approaches towards linear function in Eastern and Western cultural contexts, there are restrictions which will be identified as follows.

Firstly, Table 3 which showed the percentage of examples in each understanding level does not imply the equivalent proportion of teaching and learning time. The findings only suggest the possibility of how teachers would do or how much students are allowed to explore these levels. According to different abilities of students, teaching time will be re-allocated by teachers.

Secondly, textbook use in the two regions has very different roles in the teaching and learning process. It is notable that teachers in England are amongst the lowest users of textbooks in TIMSS 2003 (Mullis, Martin, Gonzalez & Chrostowski, 2004). In schools, other resources, for example its own scheme of work, are also important. Although it is reasonable to speculate that other resources have the similar way to presenting this topic as the textbooks do, the findings cannot be extended to them.

Thirdly, this research focuses on specific content, linear function. The findings regarding the different approaches in which each region possibly handles the teaching of the topic cannot be generalised to other mathematical contents.

Conclusions

From this textbook analysis, it has been shown that the two regions have different approaches to understanding linear function. In fact, from the literature, it was also found that the USA curricula were categorised by two approaches to understanding mathematics: “algebra graph concept” and “algebra equation concept” (Stein, Remillard & Smith, 2007). These two opposing approaches were also related to the curriculum materials’ presentation of the concept of linear function. The English curricula and textbooks used at the sample schools preferred the “algebra graph concept” approach, which means graphs were used to form the concept in the algebra area. In contrast, the Shanghai curriculum and corresponding textbook took the “algebra equation concept” approach, namely symbolic equations is used to summarise the changes between two variables.

When probing into how the two regions explain the concept of linear function, namely from a mathematics concept development perspective, Shanghai handles linear function using a more algebraic method based on the dynamic process of co-variation view of function, while England treats linear function as a form of graph based on the input-output view of the concept. From a theoretical perspective, as in Sfard’s model (Sfard, 1991), the process or operational view of function is the first step in understanding function. Both regions’ approaches fitted with this process view. In the next step, acquiring the meaning of symbolic representation as well as a proficiency of manipulation helps the Shanghai students to move towards a more abstract level of understanding function, namely a more structural view. The symbolic representation and algebraic approach fits with the main aspect of the definition of function in the Shanghai textbook, the dynamic process with variables. It is reasonable to speculate regarding the benefits of the Shanghai approach; this coherence fits with the concept learning trajectory based on the model of understanding function as the concept of function is eventually developed towards a more structural aspect. However, Sfard and Linchevski (1994) warned that in moving quickly to the symbolic representations, there does exist the danger that students could easily just focus on automatic symbolic manipulations with the result that they cannot explain why they did that the manipulation. Therefore, a conclusion that we could draw from the present study is that Shanghai teachers or textbook writers should add more of the graphical representation for properties (e.g. gradient) to gain more of a balance between the two approaches towards understanding the property. Although at the highest level of understanding, it is recognised the Shanghai textbook does introduce the two approaches.

Looking at the development of understanding more broadly, the ways in which knowledge is thought to develop is importantly different in the two regions: through the use of representations in England, and through deeper, more abstract understanding in Shanghai. In other words, there are different ways in which each education system expects students’ learning and their understanding to develop in mathematics. This reflects the different views of understanding in the two regions. Zhang and Yu (2013) indicated some differences between Western and Eastern views regarding understanding. In the case of the addition of fractions, if students could use visual methods to solve the problem, this kind of solution is regarded as understanding in the Western. Zhang argued, however, that students could spend too much time on using a visual method, compared with a pure algebraic approach. The visual method is therefore not enough for showing understanding. Western educators regard the visual method to be a significant part of understanding. Eastern educationalists, however, consider the visual method to be a facilitator of understanding but students’ understanding should be shown without this facility by using the more abstract methods.

Finally, in examining potential implications from this study for future research, the present study’s findings suggest that in terms of comparing students’ performance in mathematics, we need to be cautious in how to structure the assessments to be used in terms of ways of presenting problems. The differences in how textbooks show example problems and their solutions have showed that English students might have more experience of graphical representations. This study therefore suggests that if students’ performance is to be compared with each other, a visual approach might positively influence English students’ academic performance in the assessment, while negatively affecting Shanghai students. As Cai (1995, p. 106) recommends the use of “a wide array of mathematical tasks” in comparative studies, the questions to be used should be selected by considering students’ familiarity with certain ways of expressing from the textbooks, ensuring that the approach towards the solution is in line with questions students are familiar in class. Therefore, the features of examples in textbooks should be considered not only when making the international assessments but also to explain the students’ performance.