Designing schedule configuration of a hybrid appointment system for a two-stage outpatient clinic with multiple servers

Abstract

Even though several clinics serve patients in more than one stage (e.g., visit nurse and then visit doctor) and employ multiple providers in each stage, most of the previous work on appointment system design considers a simplified single-stage single-server clinic. Motivated by a real-life clinic setting, this paper aims to determine the schedule configuration of a hybrid appointment system (i.e., the number of pre-booking and same-day time slots reserved for a physician along with their positions in the schedule) for a two-stage multi-server clinic. A stochastic optimization model is developed to obtain a schedule configuration that minimizes the expected total cost - a weighted sum of excessive patient waiting time, resource idle time, resource overtime, and denied appointment requests. Owing to its computational complexity, we estimate the expected total cost using the sample average approximation method. The proposed model is verified and validated using small test instances and subject matter experts. A case study of a family medicine clinic in Pennsylvania is used to illustrate the proposed approach. The schedule generated by the proposed model results in a significantly lower expected cost compared to the approximated single-stage system’s best schedule configuration and clinic’s existing configuration. Further, sensitivity analysis is conducted to assess the impacts of no-show rate, service time variation, and cost ratios on the schedule configuration. Our findings demonstrate that the schedule configuration is sensitive to changes in the average no-show rate and cost ratios but is not significantly impacted by service time variation. Several managerial insights are also drawn from our analysis. Finally, we provide directions for future research that also highlights the potential to use the revenue management approach to address the problem under study.

1 Introduction

Outpatient visits in the US have increased by 80% between 1995 and 2016, and are expected to rise for the forthcoming years due to the aging population, shift from inpatient to outpatient care, and a decrease in the number of uninsured customers [1]. For example, the Affordable Care Act (ACA) reduced the number of Americans without health insurance by 8.8 million in 2014, thereby increasing outpatient visits [2]. As a result, outpatient departments experience an average appointment delay (i.e., the time between appointment request and patient care) of 24 days, and average waiting time (i.e., total time a patient waits to be served by a medical professional) of 23 minutes [4]. On the other hand, the US is expected to have a shortage of 35,000 - 44,000 primary care doctors by 2025 [3]. This suggests that fewer resources will be available to meet the growing demand. Considering all these factors, it would appear that optimal use of doctor’s time and timely access to healthcare are critical to improving the quality of outpatient care.

Outpatient clinics use an appointment system to distribute the workload (demand) throughout their operating hours by assigning patients to smaller defined time intervals called slots. A well-designed appointment system has the potential to improve resource utilization and patient satisfaction, and plays a crucial role in managing the increasing patient demand in the future. Most outpatient clinics work close to capacity and use a pre-booking appointment system to schedule patients to a future date, weeks in advance [5]. Consequently, patients experience long appointment delays resulting in an increased likelihood of no-shows, which, in turn, contributes to inefficient resource utilization and revenue loss [6, 7]. To overcome this issue, patients are given same-day appointments under the open access appointment system [6,7,8]. However, open access is difficult to implement, reduces the continuity of care, and increases the chance of supply-demand mismatch [9]. Thus, it is challenging to design an appointment system that is patient-centered, as well as profitable.

Recent research focuses on hybrid appointment systems because of their potential to achieve the advantages of more than one appointment type [8, 10,11,12,13]. If a clinic accepts both open access and pre-booking requests, then same-day appointments can facilitate timely access to care resulting in higher patient satisfaction, and pre-booking can provide steady patient flow leading to better resource utilization. However, to achieve the best outcome, it is essential to determine the best schedule configuration (i.e., number of slots reserved for each appointment type and their position) for each physician. Overestimating the number of slots reserved for open access appointments increases resource idle time, whereas underestimating it leads to patient dissatisfaction due to capacity shortage. Further, the uncertainty associated with the consultation time, no-show rate, and number of appointment requests complicate the task of determining a good schedule configuration.

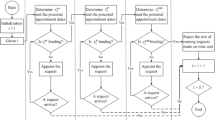
Apart from these factors, the nature of patient flow (total stages or service stops during a visit) along with the number of resources per stage, have a substantial impact on the schedule configuration and its outcomes (e.g., patient waiting time and resource idle time). As shown in Fig. 1, a clinic may adopt a single-stage or multi-stage patient flow setting with either one or multiple servers in each stage. Given the same schedule configuration, an arriving patient may wait for service at most once in a single-stage setting, and more than once in a multi-stage environment resulting in different waiting times. Therefore, to obtain an acceptable estimate for the performance of a schedule configuration, it is crucial to integrate the clinic environment in the appointment system design.

Fig. 1

Outpatient Clinic Environments: a Single-Stage Single Server b Multi-Stage Single-Server c Single-Stage Multi-Server d Multi-Stage Multi-Server

The motivation for this research stems from a real-life clinic setting that has more than one stage (namely, nurse and physician stages) with multiple servers in each stage, experiences patient no-shows, and uncertainty in the number of advance and same-day appointment requests. Given such a clinic setting, the objective of this paper is to determine the number and position of same-day and pre-booking slots reserved for each physician such that the expected total cost (weighted sum of excessive patient waiting time, resource idle time, resource overtime, and denied appointment requests) is minimized. We formulate the problem as a stochastic optimization model and use the sample average approximation method to estimate the expected total cost. Since this research approximates a real-life problem with a mathematical model, it is difficult for a clinician, who does not have the relevant quantitative background, to verify and validate the model. Therefore, we use small test instances and subject matter experts, who are familiar with the scheduling process at the clinic and have extensive operations research knowledge, to verify and validate the proposed model.

The remainder of the paper is structured as follows. In Section 2, a detailed review of relevant prior research is presented, along with gaps in the existing literature and contributions of this paper. The system description and problem statement are discussed in Sections 3 and 4, respectively. The stochastic model formulation for designing the schedule configuration and the solution approach are described in Section 5. In Section 6, a case study using real patient and clinic data is presented, and the numerical results obtained using the proposed model are reported. Finally, conclusions, managerial insights, limitations of this research, and scope for future work are discussed in Section 7.

2 Literature review

In the last 60 years, there has been extensive research that focuses on scheduling patients in an outpatient department or clinic [14, 15]. Cayirli et al. [14] provided a comprehensive review of the factors considered in the literature for modeling an outpatient clinic and designing an appointment system. The authors discussed the complications involved at each stage of the patient flow process and classified the methods used in the literature as analytical (studying the appointment system using queuing theory and mathematical modeling approaches), simulation-based (using discrete event simulation to model, evaluate and analyze complex systems) and case study (analyzing specific outpatient clinic to improve its existing operations). Also, they briefly discussed various appointment rules (e.g., Single Block rule - schedule all patients to arrive at the beginning of the day, Individual Block Fixed Interval rule - schedule one patient per slot of constant duration) used to schedule patients in an outpatient clinic. Gupta and Denton [15] provided a comprehensive review of different appointment system environments (such as primary care and specialty clinic) and factors that complicate the scheduling decisions.

Recent studies on hybrid appointment systems have addressed several challenges regarding the configuration/design of the appointment system [7, 17, 18]. Qu and Shi [19] proposed a closed-form solution to determine the optimal number of open access appointments to match the daily demand, and concluded that it is dependent on the number of appointment requests, provider capacity, and no-show rates. Liu et al. [20] considered open access and pre-booking methods to determine the day on which a patient could be scheduled such that the long-run net reward for the clinic is maximized. To compensate for no-shows in a hybrid appointment system, many studies also investigated the impact of overbooking. Kopach et al. [5] examined the effects of continuity of care and clinic throughput on double-booking for an appointment system that accepts both open access and pre-booking requests. A simulation analysis was conducted, and the results suggested that double-booking improved continuity of care and did not affect clinic throughput. A detailed configuration of a hybrid schedule using a genetic algorithm was proposed by Peng et al. [18]. The authors considered different cases (e.g., high demand, high no-show rate) and determined the schedule configuration for each of these cases. Hoseini et al. [10] determined the schedule configuration for a carve-out appointment system considering a single-stage single-server clinic setting. They assumed constant service time and accounted for demand uncertainty by formulating a mathematical model to minimize the expected cost of physician utilization, patient waiting time, and lost sales. Based on their analysis, it was evident that the position of open slots had a significant impact on physician utilization and patient waiting time.

While most research assumed homogeneous patient no-show probability, some of the previous work used patient-specific values for overbooking decisions and appointment system design [23, 24]. Muthuraman and Lawley [23] considered a hybrid appointment system and proposed a stochastic overbooking model to determine the appointment time for each patient. Their model scheduled patients in a sequential fashion (i.e., the schedule is built incrementally patient-by-patient) to improve patient waiting time, resource overtime, and revenue. Chen and Robinson [24] studied appointment sequencing for a single-stage single-server clinic that accepts both pre-booking and urgent (same-day) requests. The authors found that grouping all routine appointments together resulted in better performance, and concluded that the combination of same-day and pre-booking appointment types had a substantial impact on the appointment system design.

Based on the review of previous research, we have identified the following gaps in the literature. First, research on outpatient scheduling rarely focuses on strategic (long-term) decisions, such as the appointment system design, as almost all the studies assumed it to be known or set in advance [25]. Second, studies that focused on designing the schedule configuration of hybrid appointment systems considered a single-stage system [7, 18], whereas, in practice, healthcare systems may involve the flow of patients through multiple stages or steps [8, 26]. Since the best schedule configuration for a clinic changes depending on the number of stages, the recommendations proposed in the literature for a single-stage system might not be directly applicable to a multi-stage clinic [30]. Third, most of the prior work on designing schedule configuration restricted their model to a single provider clinic (one doctor only) [7, 8, 10, 11, 18]. While some studies have attempted to circumvent this limitation and considered a multi-provider setting, they mostly focus on sequencing patients using appointment rules as opposed to designing the schedule configuration [28, 29]. To the best of our knowledge, this study is the first to develop a mathematical approach for designing the hybrid schedule configuration under demand and service time uncertainty for a clinic with more than one-stage, where each stage has multiple providers [10, 11, 17, 23].

The contributions of this paper are as follows. First, a stochastic mixed integer linear programming (MILP) model that integrates the two-stage patient flow and multi-server setting is proposed for designing a hybrid appointment system. Second, a heuristic is developed and used in conjunction with the sample average approximation method for solving the mathematical model. Third, the proposed approach simultaneously provides the capacity and sequencing decisions for the appointment system. Finally, a case study, using real patient data from a clinic in central Pennsylvania, USA, is used to illustrate the applicability of the research methodology.

3 System description and model assumptions

In this paper, we consider an outpatient clinic that accepts same-day and advance appointment requests, where the schedule for a given day has a fixed number of equal-duration slots. Patients requesting same-day booking always show up for consultation, while patients scheduling appointments ahead of time (advance request) sometimes miss their appointments. The clinic always single-books a same-day request and may double-book certain advance requests to compensate for no-shows. This is because patients with same-day appointments always show-up, and double-booking this patient type with another request increases the risk of both patients coming for the appointment at the same time. This, in turn, increases the patient waiting time and overburdens the resources. For this reason, similar studies in the literature also refrain from combining these requests in the same slot [10, 18]. Thus, a slot can be classified as either single-advance booking (1A), double-advance booking (2A), or open access/same-day single-booking (O) depending on their capacity and appointment requests they accommodate. If a slot is double-booked with two advance requests, then it is assumed that the patient who first called for an appointment is served first. The clinic experiences fluctuating demand for both same-day and advance bookings. If the total request for a particular type exceeds the capacity reserved for it in the schedule configuration, then the clinic cannot accommodate the excess demand on the day under consideration. Moreover, the clinic provides outpatient consultation and accepts appointments only for the afternoon session as the mornings are set aside for surgical procedures. Therefore, it is assumed that all patient calls are received before the first slot of the afternoon session.

The patients are expected to arrive according to the schedule and are served in two stages (see the nurse and then see the doctor). Nearly all patients, who show up, checked-in on-time or a few minutes earlier. Therefore, similar to most previous research, patients are assumed to be punctual if they show up [8, 10, 11, 18, 29]. Further, an arriving patient is assumed to visit each stage exactly once in a sequential manner. The clinic employs a fixed number of nurses ($n \in \mathcal {N}$) and doctors ($d \in \mathcal {D}$) for providing treatment in the first and second stage, respectively. Each doctor has his/her schedule, and one doctor does not serve the patients scheduled to another doctor. However, nurses are not dedicated to a specific doctor and can serve the patients scheduled to any doctor. Patients do not have a specific preference and accept any appointment time slot with any doctor. For clinic planning purposes, each slot’s duration is divided into smaller time duration among all the stages in the clinic. The time allotted for each stage is assumed to be equal to the average service time of that stage. For example, a two-stage clinic with a 30-minute slot duration may assign 10 minutes for Stage 1 and 20 minutes for Stage 2. Hence, each stage has an earliest start time and end time. However, the clinic only communicates the appointment time (i.e., slot beginning time) and the doctor assigned to a scheduled patient. It is assumed that if there is any time available between two slots, then the resources use that time-window for administrative duties, such as updating medical records, and these times are not considered for evaluating the schedule configuration. Even though the time allocated for each stage is constant, the patient’s service time can be longer or shorter than expected, and the resources must treat the patient for the entire duration. Further, the service time for each stage is assumed to be independent because the nurse usually performs the same pre-screening check (height, weight, blood pressure, medication history, etc.) for all patients, while the doctor provides treatments that are personalized to the needs of the patient. Therefore, there is no correlation between the nurse and physician service times for the clinic under study.

4 Problem statement

The clinic under consideration experiences different scenarios (ω ∈Ω) for a particular day of the week, where a scenario represents one realization of the following random (uncertain) parameters.

• Number of same-day requests

• Number of advance requests

• For each request:

  • No-show status (0 - arrives, 1 - no-show)

  • Actual service time with nurse and doctor

As a result of these uncertainties and two-stage patient flow characteristics, the clinic is faced with two important decisions regarding the design of the appointment system - capacity and sequencing decisions. For a given day, capacity decisions deal with the problem of determining the number of slots to reserve for O, 1A, and 2A. The sequencing decision focuses on the position of the three slot types for the day under consideration. Therefore, given a set of possible scenarios for a particular day of the week, the objective is to determine the best schedule configuration for each doctor on that day, such that the expected total cost is minimized.

Unlike a dynamic scheduling problem, which incrementally builds the schedule based on the sequential arrival of appointment requests, we consider a strategic decision of designing the schedule configuration, where the realization of the scenarios under consideration is known in advance. These scenarios are typically generated based on the historical patterns observed by the clinic for a particular day of the week. In other words, we assume the probability distribution governing the uncertain parameters can be estimated using historical data, where the realization of a scenario is randomly sampled from these probability distributions. For example, if the clinic’s average no-show rate for pre-booked patients follow Bernoulli distribution and is estimated to be 20% from historical data, then the no-show status for an advance request in a scenario is 1 with probability 0.20 and 0 otherwise. As shown in Fig. 2, given the values for a representative set of scenarios, the problem is to identify the best configuration that should be implemented in the future.

Fig. 2

Overview of research problem

Since each slot ($s \in \mathcal {S}$) of a doctor ($d \in \mathcal {D}$) can take one of the three possibilities (O, 1A, 2A), the search space to find the optimal schedule configuration is exponential (i.e., $3^{(|\mathcal {S}|\times |\mathcal {D}|)}$). To determine the best schedule configuration in a reasonable time, we mathematically formulate the problem under consideration as a stochastic MILP model and adopt a Monte Carlo simulation-based approach to solve it.

5 Stochastic model for two-stage clinic with multiple servers

In most real-life cases, a stochastic system involves decisions that are constant (scenario-independent) and varying (scenario-specific) across scenarios [31]. Typically, the former category of decisions is taken before the realization of uncertain parameters, while the latter is made once these random events unfold. Similarly, for the stochastic problem under consideration, it is necessary to fix the slots reserved for each appointment type and their position in the schedule before the occurrence of random parameters (e.g., patient call for appointments). The decision to schedule the patient to a particular slot and resource, determining resource start and end time, and evaluating schedule performance (idle time, overtime, waiting time, and denied requests) are made after the occurrence of a scenario.

While there are different ways to model the stochastic problem under consideration, we have adopted the scenario-based formulation illustrated by Higle [32]. Therefore, the problem is modeled for each possible scenario and additional constraints are added to ensure the same information structure of scenario-independent variables across all scenarios. To facilitate an understanding of the optimization model, we first formulate the model with the non-linear terms. Later, we present the linear transformation of all the non-linear constraints using the three techniques discussed in Appendix A. We adopt the guidelines presented by Teter et al. [33] to define the following notations that represent the parameters and variables involved in this problem so that it can be formulated as an optimization model.

Indices and Sets

• ω ∈ Ω Set of scenarios, indexed by ω

• $t \in \mathcal {T}$ Set of patient types $\mathcal {T}$, indexed by t, $\mathcal {T} =$ {O, A}

• $p \in \mathcal {P}_{t}(\omega )$ Set of patient requests of type t in scenario ω, indexed by p

• $s \in \mathcal {S}$ Set of slots in a day, indexed by s

• $n \in \mathcal {N}$ Set of nurses, indexed by n

• $d \in \mathcal {D}$ Set of doctors, indexed by d

Deterministic Parameters

• $b_{sn}^{N}$ Appointment start time of nurse n in slot s

• $f_{sn}^{N}$ Appointment end time of nurse n in slot s

• $b_{sd}^{D}$ Appointment start time of doctor d in slot s

• $f_{sd}^{D}$ Appointment end time of doctor d in slot s

• k_t Threshold limit on the total number of patients of type t scheduled to a slot

• κ Threshold limit (in minutes) beyond which a patient is dissatisfied with the wait

• M Very large positive number

• c^NIT Nurse idle time cost ($/time)

• c^DIT Doctor idle time cost ($/time)

• c^NOT Nurse overtime cost ($/time)

• c^DOT Doctor overtime cost ($/time)

• c^WT Patient waiting time cost($/time)

• c^OC Cost of denied appointment ($/patient)

Stochastic Parameters

• σ_pt (ω) No-show status of patient p of type t in scenario ω

• η_pt (ω) Nurse service time of patient p of type t in scenario ω

• ρ_pt (ω) Doctor service time of patient p of type t in scenario ω

• Pr(ω) Probability of scenario ω

Scenario-Independent Decision Variables

• R_sd 0 if slot s of doctor d is reserved for single-booking a same-day request in all scenarios;

  1 if slot s of doctor d is reserved for single-booking an advance request in all scenarios;

  2 if slot s of doctor d is reserved for double-booking an advance request in all scenarios

Scenario-Dependent Decision Variables

• R_sd (ω) 0 if slot s of doctor d is reserved for single-booking a same-day request in scenario ω;

  1 if slot s of doctor d is reserved for single-booking an advance request in scenario ω;

  2 if slot s of doctor d is reserved for double-booking an advance request in scenario ω

• X_ptsnd (ω) 1 if patient p of type t is assigned in slot s to nurse n and doctor d in scenario ω;

  0 otherwise

• $Y_{sd}^{A}(\omega )$ 1 if slot s of doctor d accommodates only advance requests in scenario ω;

  0 otherwise

• $Y_{sd}^{O}(\omega )$ 1 if slot s of doctor d accommodates only same-day requests in scenario ω;

  0 otherwise

• $S_{ptsn}^{N}(\omega )$ Start time for patient p of type t assigned to slot s and nurse n in scenario ω

• $C_{ptsn}^{N}(\omega )$ Completion time for patient p of type t assigned to slot s and nurse n in scenario ω

• $S_{ptsd}^{D}(\omega )$ Start time for patient p of type t scheduled to slot s and doctor d in scenario ω

• $C_{ptsd}^{D}(\omega )$ Completion time for patient p of type t scheduled to slot s and doctor d in scenario ω

• $E_{sn}^{N}(\omega )$ Earliest nurse start time for nurse n in slot s under scenario ω

• $E_{sd}^{D}(\omega )$ Earliest physician start time for doctor d in slot s under scenario ω

• $L_{sn}^{N}(\omega )$ Latest completion time for nurse n in slot s under scenario ω

• $L_{sd}^{D}(\omega )$ Latest completion time for doctor d in slot s under scenario ω

• $I_{sn}^{NA}(\omega )$ Idle time of nurse n after completing service in slot s under scenario ω

• $I_{sn}^{NB}(\omega )$ Idle time of nurse n before beginning service in slot s under scenario ω

• $I_{sd}^{DA}(\omega )$ Idle time of doctor d after completing service in slot s under scenario ω

• $I_{sd}^{DB}(\omega )$ Idle time of doctor d before beginning service in slot s under scenario ω

• W_pt (ω) Waiting time of patient p of type t under scenario ω

• $\hat {W}_{pt}(\omega )$ Amount of excessive waiting time (beyond κ) of patient p of type t under scenario ω

• ${O_{n}^{N}}(\omega )$ Overtime for nurse n in scenario ω

• ${O_{d}^{D}}(\omega )$ Overtime for doctor d in scenario ω

• Z Expected total cost

Mathematical formulation

The objective function (1) seeks to minimize the expected weighted sum of excessive patient waiting time, resource idle time, resource overtime, and denied appointment requests, where the weights are the respective costs.

$$ \begin{array}{@{}rcl@{}} \text{Minimize} & Z =& \displaystyle\sum\limits_{\omega \in {\Omega}} Pr(\omega) \times \left( \begin{array}{lllllll} \displaystyle{ c^{WT} \Big[ \sum\limits_{t \in \mathcal{T}}\sum\limits_{p \in \mathcal{P}_{t}(\omega) }\hat{W}_{pt}(\omega) \Big] + c^{NIT} \Big[ \sum\limits_{s \in \mathcal{S}} \sum\limits_{n \in \mathcal{N}} \Big(I_{sn}^{NB}(\omega) + I_{sn}^{NA}(\omega)\Big) \Big] +} \\ \displaystyle{ c^{NOT} \Big [ \sum\limits_{s \in \mathcal{S}} \sum\limits_{n \in \mathcal{N}} O_{sn}^{N}(\omega) \Big ] + c^{DIT} \Big [ \sum\limits_{s \in \mathcal{S}} \sum\limits_{d \in \mathcal{D}} \Big(I_{sd}^{DB}(\omega) + I_{sd}^{DA}(\omega)\Big) \Big ] +} \\{c^{DOT} \Big [ \sum\limits_{s \in \mathcal{S}} \sum\limits_{d \in \mathcal{D}} O_{sd}^{D}(\omega) \Big ]+ c^{OC} \Big[\sum\limits_{t \in \mathcal{T}}\sum\limits_{p \in \mathcal{P}_{t}(\omega) }\Big(1- \sum\limits_{s \in \mathcal{S}}^{}\sum\limits_{n \in \mathcal{N}}^{}\sum\limits_{d \in \mathcal{D}}^{}X_{ptsnd}(\omega)\Big) \Big]} \end{array}\right) \end{array} $$

(1)

Constraint (2) ensures that a patient is scheduled to at most one slot. Constraints (3) and (4) indicate the type of request that a slot can accommodate. Constraint (3) forces the binary variable, $Y_{sd}^{A}(\omega )$, to be one if slot s of doctor d is reserved for advance requests. Likewise, constraint (4) ensures the binary variable, $Y_{sd}^{O}(\omega )$, to be one if slot s of doctor d is set aside for same-day requests. Constraint (5) ensures that each time slot of a doctor can either accommodate advance or same-day requests, but not both. Constraint (6) restricts the total number of patients per slot for each doctor to a specified upper limit. In this research, a slot reserved for an advance request can accommodate up to two patients (k_A = 2), but a slot left open for a same-day request is restricted to only one patient (k_O = 1). Note that the set of patients who are scheduled to a specific doctor may be assigned to different nurses.

$$ \begin{array}{@{}rcl@{}} \displaystyle\sum\limits_{d \in \mathcal{D}}^{}\sum\limits_{n \in \mathcal{N}}^{}\sum\limits_{s \in \mathcal{S}}^{}X_{ptsnd}(\omega) \leq 1 \qquad \qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega) , \omega \in {\Omega} \end{array} $$

(2)

$$ \begin{array}{@{}rcl@{}} \displaystyle\sum\limits_{n \in \mathcal{N}}^{}X_{ptsnd}(\omega) \leq MY_{sd}^{A}(\omega)\qquad\qquad\qquad\forall t = \{A\}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(3)

$$ \begin{array}{@{}rcl@{}} \displaystyle\sum\limits_{n \in \mathcal{N}}^{}X_{ptsnd}(\omega) \leq MY_{sd}^{O}(\omega)\qquad\qquad\qquad\forall t = \{O\}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(4)

$$ \begin{array}{@{}rcl@{}} \displaystyle Y_{sd}^{A}(\omega) + Y_{sd}^{O}(\omega) \leq 1 \qquad\qquad\qquad\qquad\qquad\forall s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(5)

$$ \begin{array}{@{}rcl@{}} \displaystyle\sum\limits_{p \in \mathcal{P}_{t}(\omega) } \sum\limits_{n \in \mathcal{N}} X_{ptsnd}(\omega) \leq k_{t}\qquad\qquad\qquad \forall {t \in {T}}, d \in \mathcal{D}, s \in {S}, \omega \in {\Omega} \end{array} $$

(6)

Constraint (7) establishes each slot in a scenario as either open access (R_sd(ω) = 0), single-advance booking (R_sd(ω) = 1), or double-advance booking (R_sd(ω) = 2). If slot s is reserved for an advance request (i.e., t = {A}), then the right hand side of Constraint (7) is one for single-booked appointments and two for double-booked appointments. If a slot is not reserved for an advance request (i.e., t≠{A}), then the right-hand side of Constraint (7) is zero, thereby indicating that the slot is open for same-day requests.

$$ \begin{array}{@{}rcl@{}} \displaystyle R_{sd}(\omega) = \sum\limits_{n \in \mathcal{N}}^{}\sum\limits_{p \in \mathcal{P}_{t}(\omega) }^{}X_{ptsnd}(\omega) \qquad\qquad\qquad\forall t = \{A\}, d \in \mathcal{D} s \in \mathcal{S}, \omega \in {\Omega} \end{array} $$

(7)

If an arriving patient finds the nurse (Stage I) busy, then the patient has to wait. Thus, the nurse start time for patient p will be the maximum time of the following three events, namely, appointment start time ($b_{sn}^{N}$), latest completion time of the nurse in the previous slot ($L_{s-1,n}^{N}(\omega )$), nurse completion time of overbooked patient ($p^{\prime }$) in the same slot ($C_{p'tsn}^{N}(\omega )$), and is given by Eq. 8. To avoid non-linearity, we replace Eq. 8 with the linear Constraints (53)–(58) as shown in Appendix B. However, if patient p is not assigned to a nurse in a slot, then Constraint (9) forces the start time of patient p by that nurse in that slot to zero, and becomes inactive otherwise (i.e., if patient p is assigned to that nurse). Note that patient p may still be assigned to a different slot, another nurse, or denied an appointment for the day under consideration. In such situations, constraints (8) and (9) will yield the appropriate start time for that patient.

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsn}^{N}(\omega) &=& \max \Big\{ \Big(\sum\limits_{s \in \mathcal{S}}b_{sn}^{N} \times X_{ptsnd}(\omega)\Big), \\ &&\Big(L_{s-1,n}^{N}(\omega) \times \sum\limits_{d \in \mathcal{D}}X_{ptsnd}(\omega) : s\in \mathcal{S} \ni s>1 \Big), \qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega) , n \in \mathcal{N}, \omega \in {\Omega} \\ &&\Big(C_{p'tsn}^{N}(\omega) \times \sum\limits_{d \in \mathcal{D}}X_{ptsnd}(\omega): p^{\prime} \in \mathcal{P}_{t}(\omega) \ni p^{\prime} \leq p-1, s \in \mathcal{S}\Big) \Big\} \end{array} $$

(8)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsn}^{N}(\omega) \leq M\sum\limits_{d \in \mathcal{D}}^{} X_{ptsnd}(\omega)\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, n \in \mathcal{N}, \omega \in {\Omega} \end{array} $$

(9)

The nurse completion time (10) for a scheduled patient is the sum of nurse start time and the service time for that patient. However, if the patient is not assigned to a nurse, then the completion time is zero. This condition leads to a constraint with a non-linear term, as shown in Eq. 10. The non-linearity in Constraint (10) can be avoided by replacing it with Constraints (57)–(62) in Appendix B.

$$ \begin{array}{@{}rcl@{}} \displaystyle C_{ptsn}^{N}(\omega) = \Big(S_{ptsn}^{N}(\omega) + \eta_{pt}(\omega) \times (1 - \sigma_{pt}(\omega))\Big) \times \sum\limits_{d \in \mathcal{D}}^{} X_{ptsnd}(\omega) \quad\quad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, n \in \mathcal{N}, \omega \in {\Omega} \end{array} $$

(10)

A patient is treated by the physician (Stage II) only after nurse pre-processing (Stage I). Thus, the actual physician start time for a scheduled patient is the maximum time of four events, namely, appointment start time of the physician ($b_{sd}^{D}$), nurse completion time of the patient ($\sum \limits _{n \in \mathcal {N}}C_{ptsn}^{N}(\omega )$), physician completion time in the previous slot ($L_{s-1,d}^{D}(\omega )$), or physician completion time of an overbooked patient in the same slot ($C_{p'tsd}^{D}(\omega )$), and is given by Eq. 11. Similar to Eq. 8, the non-linearity in Constraint (11) is linearized using Constraints (60)–(68). Constraint (12) ensures the service start time of patient p by doctor d in slot s to be zero when a patient is not assigned to that physician in that slot. Constraint (13) determines the physician completion time for patients and is linearized using Constraints (72)–(74).

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsd}^{D}(\omega) &=& \max \Big\{ \Big(\sum\limits_{s \in \mathcal{S}}b_{sd}^{D} \times \sum\limits_{s \in \mathcal{S}}\sum\limits_{n \in \mathcal{N}} X_{ptsnd}(\omega)\Big), \\ \ &&\Big(\sum\limits_{n \in \mathcal{N}}C_{ptsn}^{N}(\omega) \times \sum\limits_{s \in \mathcal{S}}\sum\limits_{n \in \mathcal{N}} X_{ptsnd}(\omega)\Big), \\ \ &&\Big(L_{s-1,d}^{D}(\omega) \times \sum\limits_{n \in \mathcal{N}} X_{ptsnd}(\omega) : s\in \mathcal{S} \ni s>1 \Big),\qquad \qquad\qquad \forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), d \in \mathcal{D}, \omega \in {\Omega} \\ &&\Big(C_{p'tsd}^{D}(\omega) \times \sum\limits_{n \in \mathcal{N}} X_{ptsnd}(\omega): p^{\prime} \in \mathcal{P}_{t}(\omega) \ni p^{\prime} \leq p-1, s \in \mathcal{S}\Big) \Big\} \end{array} $$

(11)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsd}^{D}(\omega) \leq M\sum\limits_{n \in \mathcal{N}}^{} X_{ptsnd}(\omega)\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(12)

$$ \begin{array}{@{}rcl@{}} \displaystyle C_{ptsd}^{D}(\omega) = \Big(S_{ptsd}^{D}(\omega) + \rho_{pt}(\omega) \times (1 - \sigma_{pt}(\omega))\Big) \times \sum\limits_{n \in \mathcal{N}}^{} X_{ptsnd}(\omega) \quad\quad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(13)

A slot can be double-booked, and both the patients can be assigned to the same resource. In such situations, a resource must first serve the patients in the current slot before processing a patient from the next time slot. The total expected service time of the patient(s) scheduled in a slot may be longer or shorter than the slot duration. These factors impact the latest time at which a resource completes the service and the earliest time at which a resource can begin service in a slot. The latest nurse completion time and latest physician completion time for a slot (given by Constraints (14) and (15), respectively) is the service completion time of the last patient scheduled to that slot. The non-linear Constraint (14) is replaced with linear Constraints (75)–(77), and non-linearity in Eq. 15 is avoided by replacing it with Constraints (78)–(80).

$$ \begin{array}{@{}rcl@{}} \displaystyle L_{sn}^{N}(\omega) = \max \Big(C_{ptsn}^{N}(\omega) \times \sum\limits_{d \in \mathcal{D}}X_{ptsnd}(\omega) : t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega)\Big) \qquad\qquad\qquad\forall s \in \mathcal{S}, n \in \mathcal{N}, \omega \in {\Omega} \end{array} $$

(14)

$$ \begin{array}{@{}rcl@{}} \displaystyle L_{sd}^{D}(\omega) = \max \Big(C_{ptsd}^{D}(\omega) \times \sum\limits_{n \in \mathcal{N}}X_{ptsnd}(\omega) : t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega)\Big) \qquad\qquad\qquad\forall s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(15)

The earliest nurse start time and earliest physician start time for the first slot is the expected start time of the nurse and physician, respectively (Constraints (16) and (17)). The earliest nurse start time (Constraint (18)) for all the other slots is the maximum of two times, namely, latest completion time of the nurse in the previous slot and the expected start time of the current slot. Similarly, the earliest start time for the doctor (Constraint (19)) is the maximum of latest completion time of the doctor in the previous slot or the expected start time of the doctor. The non-linearity in Constraint (18) is linearized by Constraints (81)–(84), and the non-linearity in Constraint (19) is linearized by Constraints (85)–(88).

$$ \begin{array}{@{}rcl@{}} \displaystyle E_{sn}^{N}(\omega) = b_{sn}^{N}\qquad\qquad\qquad\forall s \in \mathcal{S} \ni s = 1, n \in \mathcal{N}, \omega \in {\Omega} \end{array} $$

(16)

$$ \begin{array}{@{}rcl@{}} \displaystyle E_{sd}^{D}(\omega) = b_{sd}^{D} \qquad\qquad\qquad\forall s \in \mathcal{S} \ni s = 1, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(17)

$$ \begin{array}{@{}rcl@{}} \displaystyle E_{sn}^{N}(\omega) = \max \Big(b_{sn}^{N}, L_{s-1,n}^{N}(\omega)\Big)\qquad\qquad\qquad\forall s \in \mathcal{S} \ni s > 1, n \in \mathcal{N}, \omega \in {\Omega} \end{array} $$

(18)

$$ \begin{array}{@{}rcl@{}} \displaystyle E_{sd}^{D}(\omega) = \max \Big(b_{sd}^{D}, L_{s-1,d}^{D}(\omega)\Big)\qquad\qquad\qquad\forall s \in \mathcal{S} \ni s > 1, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(19)

At a given slot, the resources (nurse and doctor) can be idle under two situations: (i) before starting the service if the resource waits for the patient to arrive (Constraints (20) and (21)), and (ii) after completing the service if the latest completion time of a resource is earlier than the expected completion time (Constraints (22) and (25)). Further, if the latest service completion time of the resource in the last slot exceeds the clinic operating hours, then an overtime penalty is incurred. The nurse and physician overtime is estimated by Constraints (24) and (25), respectively.

$$ \begin{array}{@{}rcl@{}} \displaystyle I_{sn}^{NB}(\omega) \geq L_{sn}^{N}(\omega) - E_{sn}^{N}(\omega) - \sum\limits_{t \in \mathcal{T}}\sum\limits_{p \in \mathcal{P}_{t}(\omega)}\sum\limits_{d \in \mathcal{D}}^{}\eta_{pt}(\omega) \times (1-\sigma_{pt}(\omega)) \times X_{ptsnd}(\omega)\qquad\qquad\qquad\forall s \in \mathcal{S}, n \in \mathcal{N}, \omega \in {\Omega} \end{array} $$

(20)

$$ \begin{array}{@{}rcl@{}} \displaystyle I_{sd}^{DB}(\omega) \geq L_{sd}^{D}(\omega) - E_{sd}^{D}(\omega) - \sum\limits_{t \in \mathcal{T}}\sum\limits_{p \in \mathcal{P}_{t}(\omega)}\sum\limits_{n \in \mathcal{N}}^{}\rho_{pt}(\omega) \times (1-\sigma_{pt}(\omega)) \times X_{ptsnd}(\omega)\qquad\qquad\qquad\forall s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(21)

$$ \begin{array}{@{}rcl@{}} \displaystyle I_{sn}^{NA}(\omega) \geq f_{sn}^{N} - L_{sn}^{N}(\omega)\qquad\qquad\qquad\forall s \in \mathcal{S}, n \in \mathcal{N}, \omega \in {\Omega} \end{array} $$

(22)

$$ \begin{array}{@{}rcl@{}} \displaystyle I_{sd}^{DA}(\omega) - O_{sd}^{D}(\omega) \geq f_{sd}^{D} - L_{sd}^{D}(\omega)\qquad\qquad\qquad\forall s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(23)

$$ \begin{array}{@{}rcl@{}} \displaystyle {O_{n}^{N}}(\omega) \geq L_{sn}^{N}(\omega) - f_{sn}^{N}\qquad\qquad\qquad\forall s \in \mathcal{S} \ni s = |\mathcal{S}|, n \in \mathcal{N}, \omega \in {\Omega} \end{array} $$

(24)

$$ \begin{array}{@{}rcl@{}} \displaystyle {O_{d}^{D}}(\omega) = L_{sd}^{D}(\omega) - f_{sd}^{D}\qquad\qquad\qquad\forall s \in \mathcal{S}\ni s = |\mathcal{S}|, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(25)

The waiting time of a patient, who showed up for the appointment, is determined by Constraint (26). Moreover, a patient considers the visit to be a negative experience if he/she waits beyond a certain period (κ). This additional time spent waiting in the clinic (or excessive waiting time) is obtained using Constraint (27).

$$ \begin{array}{@{}rcl@{}} \displaystyle W_{pt}(\omega) = (1-\sigma_{pt}(\omega))\times\Bigg(\sum\limits_{s \in \mathcal{S}}^{}\sum\limits_{n \in \mathcal{N}}^{}\Big(S_{ptsn}^{N}(\omega) - b_{sn}^{N} \times X_{ptsnd}(\omega)\Big) + \\ {\kern4cm}\Big(\sum\limits_{s \in \mathcal{S}}^{}\sum\limits_{d \in \mathcal{D}}^{}S_{ptsd}^{D}(\omega)- \sum\limits_{s \in \mathcal{S}}^{}\sum\limits_{n \in \mathcal{N}}C_{ptsn}^{N}(\omega)\Big)\Bigg) \qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), \omega \in {\Omega} \end{array} $$

(26)

$$ \begin{array}{@{}rcl@{}} \displaystyle \hat{W}_{pt}(\omega) \geq W_{pt}(\omega) - \kappa\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), \omega \in {\Omega} \end{array} $$

(27)

Since slot types and their positions are scenario-independent, we introduce the nonanticipativity constraint (28), which ensures the slots reserved for open access, single-advance booking, and double-advance booking to be at the same position across all scenarios.

$$ \begin{array}{@{}rcl@{}} \displaystyle R_{sd}(\omega) - R_{sd} = 0\qquad\qquad\qquad\forall d \in \mathcal{D}, s \in \mathcal{S}, \omega \in {\Omega} \end{array} $$

(28)

The non-negativity and binary restrictions on the decision variables are ensured using Constraint (29) and Constraint (30), respectively.

$$ \begin{array}{@{}rcl@{}} &&S_{ptsn}^{N}(\omega),C_{ptsn}^{N}(\omega),S_{ptsd}^{D}(\omega),C_{ptsd}^{D}(\omega),L_{sn}^{N}(\omega),\\ &&I_{sn}^{NB}(\omega), I_{sn}^{NA}(\omega), O_{sn}^{N}(\omega),L_{sd}^{D}(\omega),DIT_{sd}^{\omega}, \qquad\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D}, n \in \mathcal{N}, \omega \in {\Omega} \\ &&I_{sd}^{DB}(\omega) , I_{sd}^{DA}(\omega), O_{sd}^{D}(\omega),W_{pt}(\omega),\hat{W}_{pt}(\omega) \geq 0 \end{array} $$

(29)

$$ \begin{array}{@{}rcl@{}} X_{ptsnd}(\omega) \in \{0, 1\}\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D}, n \in \mathcal{N}, \omega \in {\Omega} \end{array} $$

(30)

Therefore, in the stochastic MILP model, the objective function (1) will be subject to constraints (2)–(6), (9), (12), (16), (17), (20)–(30) and (53)–(88). While the mathematical model is based on the problem description and assumptions in Section 3, it can be easily extended to different clinic settings as well. For example, a clinic may wish to develop a template for the morning session and may not want to reserve the first slot for same-day requests as these patients are calling throughout the morning. In such situations, the mathematical model can be easily adapted by including a constraint that restricts the first few slots to be reserved for same-day requests. Similarly, in certain clinics, the doctor schedules may vary, where there is only a minimum overlap between the two doctor’s schedules. The proposed mathematical model can be adapted to include this real-life constraint as the decision variable tracks the doctor’s availability in each slot. Therefore, we should set the decision variable to 0 for the slots in which a doctor is not available. Also, if unpunctual arrivals are prevalent at an outpatient clinic, the proposed model can be readily extended to design the best schedule configuration by incorporating another parameter, patient arrival time, in constraints pertaining to nurse and physician start time. Moreover, the mathematical model can be easily adapted to identify the schedule configuration of a single-stage system, as shown in Appendix C.

5.1 Solution scheme

There are many ways to incorporate clinical uncertainties (demand, service time, no-shows) when formulating a mathematical model for designing a schedule configuration. The traditional scenario analysis considers three situations (worst, average, and best cases), and may not be very informative for decision-making. However, for a particular day of the week, the clinic can experience a very large (or infinite) number of scenarios. A realization of the uncertain parameters associated with each scenario is denoted by ξ, which is assumed to be modeled using known probability distributions.

Given the set of possible scenario realizations (ξ ∈Ξ) and their associated probability distribution, the stochastic optimization problem is to minimize the expected value as shown in Eq. 31, where it is a function (f ) of the decision variables x and random vector ξ.

$$ \begin{array}{@{}rcl@{}} Z^{*} = \displaystyle \min_{x } E[f(x, \xi)] \end{array} $$

(31)

For the problem under study, E[f(x, ξ)] is equivalent to the objective function given in Eq. 1. Since the computational time and complexity is enormous for solving a large number of scenarios, the stochastic MILP model discussed in Section 5 is solved repeatedly for a smaller set of finite scenarios using the sample average approximation (SAA) approach. SAA is a Monte-Carlo simulation-based method, which involves the iterative process of generating random samples resulting in a sample average estimate of the expected objective function of the stochastic problem [34]. Suppose if a typical day of the week experiences a very large number of scenarios (say, |Ω|), then using the SAA method, the expected value function is approximated by solving Q independent samples, where each sample has a finite reduced set of ν < |Ω| scenario realizations. Also, the solution obtained using the SAA method converges to the expected objective function (true optimum) value of the stochastic model with probability one as ν becomes sufficiently large [31]. Since obtaining the true optimum is also computationally expensive (as a large number of scenarios are required), we use the SAA method to obtain a feasible solution that is within a certain tolerance of the actual objective function. A step-by-step procedure for the SAA approach is given in Schütz et al. [35], and is summarized here with respect to our problem.

• Step 1: Obtain unbiased estimates of the objective function: Generate Q independent samples, each with ν scenarios. Solve the associated stochastic model to optimality for each of the Q samples. Let Z¹(ν), Z²(ν),⋯ , Z^Q(ν) denote the optimal objective function value (i.e., optimal expected total cost) and x¹(ν), x²(ν),⋯ , x^Q(ν) represent the optimal solutions for the model corresponding to Q samples. According to Shapiro and Philpott [31], Eq. 32 gives an unbiased estimator of Z^∗, and its variance is given by Eq. 33.

  $$ \begin{array}{@{}rcl@{}} \bar{Z}_{\nu} = \frac{1}{Q} \sum\limits_{j = 1}^{Q} Z^{j}(\nu) \end{array} $$

  (32)
  $$ \begin{array}{@{}rcl@{}} \displaystyle \hat{\sigma}^{2}(\nu) = \frac{1}{Q(Q-1)} \sum\limits_{j = 1}^{Q} (Z^{j}(\nu) - \bar{Z}(\nu) )^{2} \end{array} $$

  (33)

• Step 2: Compute the statistical lower bound of the objective function: An approximate lower bound for Z^∗ is obtained using the estimates computed in Step 1 and is given by Eq. 34, where t_{α, Q− 1} is the critical value of t-distribution with Q − 1 degrees of freedom.

  $$ \begin{array}{@{}rcl@{}} \displaystyle \hat{Z}_{LB} = \bar{Z}({\nu}) - t_{\alpha, Q-1} \times \hat{\sigma}({\nu}) \end{array} $$

  (34)

• Step 3: Estimate the upper bound of the objective function: To determine the upper bound, it is necessary to obtain a feasible schedule configuration (i.e., values of scenario-independent decision variables) for the problem under study and evaluate that configuration for $\nu ^{\prime }$ independent scenarios (where $\nu ^{\prime }>> \nu$). Most prior research adopts a simple heuristic (or algorithm) to obtain a good feasible solution as it can accelerate the SAA procedure by reducing the estimated optimality gap (i.e., difference between lower and upper bounds) [35, 36]. Frequency heuristic is one such approach for fixing scenario-independent binary variables [35]. According to the heuristic, if the optimal value of the binary variable is 1 for a majority of the Q samples, then that binary variable is fixed to 1 in the feasible solution and 0 otherwise. Since all the scenario-independent variables are binary in this research, we adapt the frequency heuristic used by Schütz et al. [35] to fix their values. The number and position of O, 1A, and 2A slots reserved for a doctor are determined based on their frequency of occurrence in the optimal schedule configuration of the Q samples obtained in Step 1. For each doctor, the number of open access slots in the feasible configuration is the mode of the number of open access slots reserved for that doctor in the optimal schedule configuration of the Q samples, while the remaining number of slots in the schedule are reserved for advance requests. Once the number of open access slots is fixed, their position in the schedule is determined by analyzing each slot independently. If a slot position achieves a relative majority of being open access in the optimal schedule configuration corresponding to Q samples, then that position is reserved for open access appointments (O). This procedure is repeated until the position of all the open access slots is determined. The remaining slot positions, which are reserved for advance requests, can either be single-booked (1A) or double-booked (2A). This is again determined based on the frequency of their occurrence. Given Q optimal configurations, if a slot is 2A in a majority of the cases, then it is reserved for double-booking in the feasible configuration. Otherwise, it is assigned as 1A. This approach of obtaining the feasible solution may not be suitable for all problems as it may produce weak upper bounds, thereby increasing the number of repetitions required. However, for our problem instances, it finds good feasible solutions. Upon fixing the schedule configuration obtained using the frequency heuristic, we solve the stochastic model for $\nu ^{\prime }$ independent scenarios (where $\nu ^{\prime }>> \nu$) and compute the upper bound (expected total cost) and its variance using Eqs. 35 and 36, respectively.

  $$ \begin{array}{@{}rcl@{}} \displaystyle \bar{Z}_{UB} = \frac{1}{\nu^{\prime}} \sum\limits_{j = 1}^{\nu^{\prime}} Z^{j} \end{array} $$

  (35)
  $$ \begin{array}{@{}rcl@{}} \displaystyle \hat{\sigma}^{2}(\nu^{\prime}) = \frac{1}{\nu^{\prime}(\nu^{\prime}-1)} \sum\limits_{j = 1}^{\nu^{\prime}} (Z^{j}(\nu^{\prime}) - \bar{Z}_{UB} )^{2} \end{array} $$

  (36)

• Step 4: Compute estimated optimality gap: The estimated optimality gap is the difference between the upper and lower bounds and cannot be negative ($\hat \mu _{gap} = \max \limits \{0, \bar {Z}_{UB} - \hat {Z}_{LB}$)}. The variance of the estimated gap is the sum of variance of the upper and lower bounds ($\hat {\sigma }_{gap}^{2} = \hat {\sigma }^{2}(\nu ) + \hat {\sigma }^{2}(\nu ^{\prime })$). A 100(1 - α)% confidence interval (CI) for the optimality gap is calculated as $\hat \mu _{gap} \pm z_{\alpha }({ \hat \sigma }_{gap})$.

• Step 5: Evaluate stopping criterion: As suggested in Kleywegt et al. [34], the stopping criteria is based on the optimality gap estimate. If the relative gap estimate ($\frac {\hat \mu _{gap} }{{Z}_{LB}}$) is less than a specified threshold parameter (ε), then we stop the SAA procedure. Otherwise, the sample size (ν) is increased and the procedure is repeated until the stopping criterion is achieved (i.e., when $\frac {\hat \mu _{gap} }{{Z}_{LB}} < \varepsilon$).

5.2 Practical implementation of hybrid appointment system

Since most clinics experience a weekly demand pattern, the procedure outlined in this research should be repeated to obtain the best schedule configuration for a typical workweek. Figure 3 presents an example of a hypothetical schedule configuration.

Fig. 3

Hypothetical schedule configuration for practical implementation

Upon finalizing the schedule configuration using the proposed approach, it is provided to the front desk staff (or clinical scheduler) for adoption and operational decision-making. For example, if a patient calls for a same-day appointment, then the clinical scheduler assigns the patient to one of the available open access slots (i.e., an O slot which currently has no one scheduled to it) on the day of the patient call. So, if the day under consideration is a Thursday and if all the open access slots are available, then the patient is assigned to one of the following positions - slots 1, 4, 5 of Doctor 1 or slots 1, 3, 6, 7 of Doctor 2.

Nevertheless, if a patient calls for an appointment in the future, then the scheduler must assign the patient to one of the available pre-book slots (1A or 2A) on any day starting with the next day of the patient call. In addition to adopting the proposed configuration, the clinic must also establish other policies for operational decision-making. For example, the clinic must provide a guideline on when the scheduler can begin double-booking. Typically, clinics double-book after exhausting all the pre-book slots with at least one patient. Therefore, the proposed approach provides the clinic with capacity and sequencing decisions for the appointment system, and enables the clinic to schedule patients effectively.

6 Case study

6.1 Background

The proposed methodology is demonstrated using a case study with real data. The patient-level data is obtained from a family medicine clinic in Pennsylvania and includes call records (patient call date for an appointment, appointment date and time), no-show status, entry and exit timestamps of the patient’s visit.

The clinic operates five days a week and 8 hours per day, where the morning session (8 am - noon) is primarily set aside for surgical procedures, and the afternoon session (1 pm - 5 pm) is used for outpatient consultation. The case study focuses on developing the schedule configuration only for the afternoon session. The clinic employs two nurses and six physicians to provide service. However, on any given day, there are only two full-time equivalent (FTE) nurses (or two resources in Stage 1) and two FTE physicians (or two resources in Stage 2) present. The afternoon session has a capacity of eight 30-minute slots, where the first 10 minutes is slotted for pre-screening/pre-assessment by the nurse, and the remaining 20 minutes is slotted for the physician. Note that the time reserved for nurse and physician in each slot is based on the historical average of the time taken by these resources. Currently, the clinic adopts a template where they cluster similar patient types together for ease of scheduling (Fig. 4). The advance requests are single booked in slots 2 and 4 and are double-booked in slots 1, 3 and 5. The last three slots of each doctor are reserved for same-day appointments. Moreover, the clinic does not accept a request for same-day appointments beyond noon. Thus, all the calls typically occur before the first time slot. Even though the clinic adopts this configuration on an average, it does not always strictly adhere to it and may adjust it based on the doctor’s request.

Fig. 4

Current schedule configuration of clinic under study

6.2 Parameter estimation for baseline analysis

The analysis of the demand data (patient calls) indicated that the total appointment request for a given day was similar at mid-week (Tuesdays, Wednesdays, and Thursdays) throughout the year. However, Mondays and Fridays experienced 15% higher demand on average compared to other working days. To illustrate the feasibility of the proposed approach, we chose to develop the schedule configuration for a typical Monday and used the one-year historical data for every Monday to generate the scenarios. The analysis of past patient calls indicated a Poisson distribution with a mean of 8 and 13 calls per day to be a good fit for same-day and advance requests, respectively.

The analysis of patient satisfaction survey indicated that patients who wait less than 5 minutes were highly satisfied with their visit, and the satisfaction lowered as they waited longer. Similarly, in a different study, Darivemula et al. [38] reported that patient satisfaction significantly decreases when the waiting time is longer than 5 minutes. Therefore, in this research, the threshold limit beyond which a waiting time penalty is incurred is set as 5 minutes (κ = 5). Note that the threshold value is a parameter and can be set to suit the needs of any clinic. The mathematical model will still be able to yield the best configuration for the chosen parameter. Further, based on the historical data, the average no-show rate of pre-booked patients was 30%, while the open access patients always showed up. Even though the timestamp data provided the total time spent by a patient during the visit, it does not provide the service time for each stage. Moreover, this information is often inaccurate because it is usually entered manually by a medical assistant who often forgets to record them or enters a delayed event occurrence time. Therefore, we interacted with the clinical care team and learned that the patient service time was relatively constant with a mean of 10 minutes in Stage 1 (nurse) and 20 minutes in Stage 2 (doctor). To allow some randomness, we assume the service time to be a discrete uniform distribution over the interval (9,11) for Stage 1 and (17, 23) for Stage 2. Nevertheless, a higher variation in service times is also evaluated in Section 6.4.2.

The idle time cost per hour for the nurse and doctor is approximated to their hourly wage information provided by the clinic administrators, which were $30 and $90, respectively. Since most patients visiting the clinic were residents of Elizabethtown in Pennsylvania, we used the median income in that city to estimate the penalty for excessive patient waiting time as $30 per hour [39]. It is to be noted that nurses and physicians are exempt from overtime pay in the US [40]. Nevertheless, working beyond regular operating hours is not preferred as they result in fatigue-related medical errors and burnout [41, 42]. Thus, to ensure that the resources are not overworked for a prolonged period, we penalize their overtime operation in our model. Similar to prior research, we assume the cost of resource overtime to be 1.5 times the cost of resource idle time [11, 13]. Based on the interaction with the clinic’s administrative staff, the cost associated with a denied request is set at $40. The patient is denied appointment for the particular day under consideration with the fact that the denied request can be accommodated sometime later in the scheduling horizon. Therefore, when a patient calls for an appointment, the patient is almost always given an appointment. However, that appointment date/time might be different from the day under consideration. Thus, we consider this cost as a penalty for causing a slight inconvenience to the patient as the patient is not completely turned away during their call for an appointment.

The value of M in the mathematical model should be large enough to satisfy the constraints. Although an excessively large value for M will eventually result in the optimal solution for the mathematical model, it could increase the solution time [43]. In this research, M is always used to satisfy a constraint involving the start or completion time of a resource (e.g., completion time of nurse in Constraint (62), earliest start time of doctor in Constraint (87)). Since the total scheduling period is 240 minutes (8 slots × 30 minutes/slot), the value of M is set to 400. This ensures that it is large enough to satisfy the constraints involving M and small enough to avoid unnecessary computational complexity.

Consistent with previous research [35], the SAA procedure is stopped when the relative optimality gap is less than 5% (i.e., ε = 5%). The number of scenarios (ν) for each run is increased from 10 in increments of 5 until the stopping criterion is reached. Further, we choose to solve all cases for 20 samples (i.e., Q = 20). The reference scenarios ($\nu ^{\prime }$) to determine the upper bound and evaluate the feasible schedule configuration is set to 500. Moreover, the scenarios generated are validated by comparing their values to the actual system. A t-test (at α = 0.05) confirms that the demand generated for the mathematical model is not statistically different from the actual system (i.e., p-value > 0.05 for both same-day and advance requests).

6.3 Results

The mathematical model is coded in GAMS and solved to optimality using ILOG CPLEX 12.4. The Q samples, where each sample has ν scenario realizations, are independently solved in parallel in approximately 30 minutes. The high-performance computing setup included 20 nodes, each with 512 GB RAM and 24 cores. Before conducting a detailed computational analysis, it is necessary to verify and validate the proposed mathematical model. Since the model is yet to be adopted at the outpatient clinic under study, we are unable to obtain the data on the real-world outcomes for validation by results. However, if a model cannot be proved incorrect, then that increases the confidence in the model and its result, thereby satisfying the goal of verification and validation [37]. Therefore, similar to Troy et al. [27], we attempt to identify errors or flaws in the model. If our efforts fail to prove model incorrectness, then we consider having achieved the goal of verification and validation.

First, we created many small test instances with only two scenarios and executed the model for each of these instances to obtain the optimal schedule and the associated decision variables. For the same schedule, we manually computed the values of these decision variables to check the correctness and accuracy of the model. As expected, the scenario-independent variables obtained by solving the model were the same across all scenarios. Besides, the model outputs were in complete agreement to the manually computed values for all test instances. Second, we considered certain extreme conditions to see if the model generates results that were expected. For a parameter setting with extremely high no-show rate (set almost close to 1), we expect most of the slots to be double-booked with advance requests. Likewise, if all patients are expected to come for their appointment, and if the cost of denying a request is low, then we anticipate most slots to be single-booked with an advance or same-day request. Our proposed model performed as expected for these extreme conditions. Finally, the proposed model, along with the assumptions, were presented to the healthcare professionals at the outpatient clinic, and there were no issues raised regarding the validity of the model. Moreover, the model and the associated GAMS code were also reviewed and validated by the subject matter experts, who are familiar with the clinic’s scheduling process and operations research techniques such as linear programming. As none of these attempts discredit the proposed model, they reinforced our confidence in the model’s ability to determine the best schedule configuration.

Upon verification and validation, the model is executed for the baseline setting discussed in Section 6.2. Table 1 presents the results of the baseline clinic setting for different values of sample size. The estimated lower bound for the optimization problem increases with an increase in sample size, and the relative gap falls below the threshold parameter of 5% when the sample size is set to 20 scenarios.

Table 1 Statistical lower and upper bounds of the SAA problems for Q = 20 and $\nu ^{\prime } =$ 500

To demonstrate the significance of considering the number of patient flow stages when designing an appointment system, we have also generated the best schedule configuration of an approximated single-stage (only doctor stage) system by solving the model in Appendix C using the SAA approach discussed in Section 5.1. Note that the baseline clinic settings will remain the same for the single-stage model. However, the average patient service time for the single-stage system is assumed to be the sum of nurse and doctor service time in the two-stage system. In addition, to asses the performance of the current practice, we have fixed the schedule configuration (decision variable R_sd) in the proposed model to the existing configuration (Fig. 4), and have evaluated the expected total cost over 500 scenarios. Figure 5 presents a comparison of the best schedule configuration for the single-stage and two-stage system for the same baseline clinic setting along with the current configuration adopted by the clinic.

Fig. 5

Comparison of Schedule Configuration among (a) Current System (b) Single- Stage System (c) Two-Stage System

Upon solving the mathematical model, the clinic’s current configuration yields an expected total cost of $235.04, while the configuration for the single-stage and two-stage systems results in an expected total cost of $220.43 and $186.65, respectively. Besides, the results indicate that, on average, 9.94%, 7.72%, and 6.07% of the patients are denied appointment under the current, approximated single-stage and proposed schedule configurations, respectively. Further, a t-test (at α = 0.05) confirms the expected total cost of the two-stage system to be significantly lower than the single-stage system and current configuration (i.e., p-value < 0.05).

Given the same call volume and other baseline settings, the schedule configuration is drastically different for the current setting, single-stage, and two-stage systems. Based on the configuration obtained from the SAA approach, Doctors 1 and 2 can each serve 11 patients (3 double-booked slots) in the current configuration and single-stage system. Whereas, Doctor 1 can treat 11 patients (3 double-booked slots), and Doctor 2 can serve 12 patients (4 double-booked slots) in a two-stage system. Moreover, the best configuration for a single-stage system reserves more slots for same-day requests compared to the best configuration of a clinic with two-stages. Unlike the two-stage system, the 2A slot is always separated by an O slot in the single-stage system and a 1A slot in the current configuration. However, certain aspects of the schedule configuration are common for both the single-stage and two-stage systems. The first few slots are either left open for same-day appointments or double-booked with advance requests, while the last slot is always reserved for same-day single-booking. Since both open access and double-booked slots increase the likelihood of at least one patient arriving for the appointment, reserving them for the beginning of the clinic session will prevent the clinic from starving for patients, especially when the no-show rates for advance requests are high. Also, single-booking the last slot could avoid unnecessary clinic overtime, which is likely to occur otherwise.

To quantify the negative impact of approximating a two-stage patient flow to a single-stage system, we have fixed the scenario-independent decision variable (R_sd) in the mathematical model presented in Section 5 to the best configuration of the single-stage system. After solving it for 500 scenarios, it is observed that the expected total cost obtained by fixing the configuration is 19% more than the best configuration obtained by considering the number of stages in patient flow. Therefore, the need for including the number of stages is evident from our analysis. Since the focus of this research is to design the schedule configuration for a system with two-stages, we do not consider the approximated single-stage system for further analysis.

6.4 Sensitivity Analysis

The baseline setting (average no-show rate = 30%, coefficient of variation of service time = 0.10, cost ratios - c^WT : c^NIT : c^NOT : c^DIT : c^DOT : c^OC = 30 : 30 : 45 : 90 : 135 : 40) is determined based on historical data of the clinic under study. To evaluate the impact of these key parameters on the schedule configuration, different values of average no-show rates, service time variation, and cost settings are tested.

6.4.1 Impact of No-show Rate

In our prior analysis, the scenarios are generated based on a clinic experiencing an average no-show rate of 30% for advance requests and 0% for same-day appointments. For most clinics, the average no-show rate of open access appointments is meager (less than 5%). However, it varies substantially for pre-booked appointments. To study the impact of pre-booked patient’s average no-show rate on the schedule configuration, its value is varied between 10% and 40% in increments of 10%, while fixing the service time distribution and cost ratios to the baseline setting.

Table 2 provides the schedule configuration, statistical bounds, relative gap, and denied requests for different no-show rates. It is observed that the total number of double-booked slots increases from five to eight when the no-show rate increases from 10% to 40%. This is because when more pre-booked patients are expected to miss their appointments, double-booking a majority of those requests and leaving the remaining slots open for same-day appointments (i.e., patients who have very low no-show rate) is likely to reduce the number of denied requests and resource idle time. On the contrary, when a higher proportion of pre-booked patients are expected to show up, then fewer double-booked slots are likely to reduce patient waiting time.

Table 2 Schedule Configuration, statistical bounds, relative gap and denied requests for different no-show rates

On analyzing the schedule configuration, it is evident that the first two slots are either single-booked with same-day request or double-booked with advance requests under high no-show rates (30% and 40%), but is always single-booked (with either same-day or advance request) under low no-show rates (10% and 20%). In other words, for clinics experiencing high no-show rates, it is practical to schedule same-day requests (i.e., patient who will definitely come for the appointment) or double-book advance requests in the beginning to increase the likelihood of at least one patient visit per slot, which in turn, lowers the chance of an idle system earlier in the schedule. On the contrary, clinics experiencing fewer missed appointments cannot double-book the first two slots as the probability of both the patients arriving is high, which may lead to longer waiting times. For this same reason, double-booked slots are never positioned next to each other under low no-show rates. However, under high no-show rates, two double-booked slots may be placed next to each other rather than being separated by one or more single-booked slots. Such a configuration could match the capacity with demand and avoid any major disruption. Nevertheless, the last slot is always single-booked with same-day requests regardless of the no-show rate to mitigate clinic overtime.

Thus, given the clinic settings under study, when the average no-show rates increase from 10% to 40%, the best schedule template is configured to balance capacity and demand while accommodating more patients. Since the total appointment requests and other parameters are the same for different no-show rates, the average denied requests decreases from 9.10% to 5.26%, when the no-show rate increases from 10% to 40%. Thus, the total cost of denied appointments in the objective function also decreases for increasing no-show rates. Since this is a substantial cost component in the objective function, the expected total cost also reduces as the no-show rate increases from 10% to 40%.

6.4.2 Impact of Service Time Variation

One of the biggest obstacles to appointment scheduling is service time uncertainty, which arises due to various reasons such as patient’s characteristics (e.g., age, new vs. established patient, marital status), physician characteristics (e.g., competence, motivation), appointment characteristics (e.g., type of visit), etc. Even though the variation in nurse and doctor service time is observed to be low for the clinic under study, this is subject to change due to the aforementioned characteristics. Therefore, in this section, we fix the mean service time for each resource type and consider two levels of service time variations (low and high) to analyze the impact of all possible combinations of the two levels on the schedule configuration. The baseline service time distribution along with its parameter (i.e., U(9, 11) for nurse and U(17, 23) for physician) is considered to be the low-level variation. For high-level variation in service time, we consider a uniform distribution over the interval (4, 16) for the nurse stage and (7, 33) for the physician stage. Besides, all the other parameters, clinic settings and assumptions remain the same as discussed in Sections 6.1 and 6.2. Table 3 presents the results of the analysis for all possible combinations of the two levels of service time variation associated with the nurse and physician stage. Similar to our previous findings, the last slot is always single-booked for all cases of service time variation under consideration.

Table 3 Schedule Configuration, statistical bounds, relative gap and denied requests for different service time variations

It is also observed that the number of slots reserved for each appointment type remains unchanged from the baseline setting even when the service time variation is altered. However, the position of the double-booked slots varies depending on the service time variation of the resource types. Most of the double-booked slots are positioned next to each other when the service time variation is low for both nurse and physician. Since the no-show rate for the clinic is high, such a configuration could reduce the resource idle time at the expense of a slight increase in patient waiting time.

On the contrary, double-booked slots are separated by single booked slots when the variation is high for both the resource types. If both no-show rate and service time variation are high, then placing two double-booked slots next to each other could drastically affect the patient waiting time throughout the schedule. Therefore, to avoid such a situation, the model could have spaced the double-booked slots evenly throughout the schedule configuration.

Unsurprisingly, the total cost is lowest when both the resource types have low service time variation and highest when they have high variation in service times. Besides, the variability of time spent with the doctor appears to be more disruptive than the variability of nurse service time as the cost is comparatively high when the doctor’s service time variation is high.

6.4.3 Impact of cost ratios

The baseline cost setting gives equal importance to patient’s and nurse’s time, and extrapolates the overtime cost (c^WT : c^NIT : c^NOT : c^DIT : c^DOT : c^OC = 30 : 30 : 45 : 90 : 135 : 40). In this section, we evaluate the impact of three different cost settings, CS1 - CS3, on the schedule configuration. Cost setting 1 (CS1) considers patient waiting time to be twice as important as nurse idle time, while all the other settings remain unchanged. Likewise, cost setting 2 (CS2) considers resource utilization to be paramount, and cost setting 3 (CS3) evaluates the impact of clinic accessibility. Table 4 presents the results of different cost settings.

Table 4 Schedule Configuration, statistical bounds, relative gap and denied requests for different cost ratios

When patient waiting time cost is doubled (CS1), the total number of 2A slots (and total patients served) remains the same as the baseline schedule configuration. However, unlike the baseline setting, the 2A slots are never placed next to each other. Perhaps, this is because the best configuration is trying to mitigate the risk of congestion and the effect of service delay propagating throughout the schedule.

Increasing the costs associated with resource idle time and overtime (CS2) results in more double-booked slots than the baseline setting. Further, none of the advance requests are single-booked. This is because a single-booked advance request has a higher chance of missing the appointment, which would eventually lead to resource idle time. Whereas, double-booking the advance requests increases the likelihood of at least one patient showing up for that slot, and ensures resource occupancy. The last two slots are never double-booked to avoid any potential clinic overtime. Thus, this schedule configuration aims to engage resources to the fullest and prevent unnecessary clinic overtime, despite the high no-show rate (30%).

When clinic accessibility is given more importance (CS3), the schedule is configured to include more double-booked slots, compared to all the other clinic settings evaluated. This is expected as increasing the double-booked slots provides better access to the clinic. Moreover, the double-booked slots are distributed in the first as well as the second half of the schedule configuration. While the configuration improves clinic access, it is achieved at the expense of higher patient waiting times.

7 Managerial insights and conclusions

Most of the existing research focuses on determining the schedule configuration of a single-provider system without integrating the nature of patient flow (i.e., number of stages). In this paper, we address the aforementioned gaps in the literature and propose a scenario-based approach to aid clinic administrators in designing a hybrid appointment system. A stochastic MILP model for a two-stage multi-provider setting is formulated to determine the optimal schedule configuration of a hybrid appointment system. Due to its computational complexity, we use SAA in combination with a frequency heuristic to estimate the expected total cost. The proposed model and solution approach can be adapted for any clinic that consists of two stages. The output obtained provides both capacity and sequencing decisions simultaneously, and includes the number and position of same-day single-booking, single-advance booking, and double-advance booking slots reserved for each doctor.

Real data from a family medicine clinic located in Pennsylvania is used for evaluating the feasibility of the proposed approach. In addition, several managerial insights are also drawn from our analytical results. The first slot is never single-booked with advance requests due to the risk of the resources being idle earlier in the schedule. For this same reason, clinics experiencing high no-show rates should double-book advance requests or single-book same-day appointments at the beginning of a clinic session. Whereas, if patients are less likely to miss an appointment, then the clinic should avoid double-booking earlier in the session, and single-book those slots with same-day requests to reduce patient waiting time. The optimal schedule demonstrates that the last slot should be single-booked for all settings to avoid unnecessary overtime operation of the clinic. As far as double-booking is concerned, its proportion in the schedule is mainly affected by the no-show rate and cost ratios. Besides, the double-booked slots are not positioned continuously in the presence of low no-show rates or high service time variation.

In certain situations, the schedule configuration obtained from the proposed model is counter-intuitive. For example, the best schedule configuration for a low no-show rate setting of 10% includes a double-booked slot in the penultimate position even if it would increase the chance of clinic overtime considerably. This may be because of two reasons. First, there may exist many alternate optimal solutions, and the proposed model identifies one among them. Second, the proposed model is trying to achieve a trade-off between the performance measures and decides to position the double-booked slot later in the schedule. For example, if the double-booked slot is placed in the beginning for a clinic with a 10% no-show rate, then it increases the risk of both the patients showing up for their appointment earlier in the clinic session. This, in turn, delays the start time of subsequently scheduled patients throughout the schedule. However, positioning a double-booked slot later in the schedule could avoid such a situation but increases the risk of clinic overtime. On the other hand, avoiding double-booking for a no-show rate of 10% could increase the rejection rate, which, in turn, increases the total cost (i.e., objective function). Thus, in an attempt to balance the performance measures for the given cost settings, the best configuration could have positioned a double-booked slot in the second to last position.

In the era of skyrocketing healthcare costs, the proposed approach and the insights drawn from our analysis will aid healthcare practitioners in designing an effective appointment system for a given clinic setting. Moreover, the solution obtained from our mathematical model can be used as a benchmark to evaluate the effectiveness of other approaches, such as heuristics. While the proposed approach is used to assess different clinic settings, the schedule configuration may change even for a small variation in other environmental parameters. Therefore, it is essential to develop the configuration by taking into account the parameters that are specific to a clinic. Also, after the implementation of the hybrid appointment configuration, the demand for same-day and advance requests may change over time. Hence, it is necessary to observe the demand patterns periodically and update the configuration when needed.

While the proposed mathematical model provides a schedule configuration that minimizes the expected cost for a set of possible scenarios, it also has certain limitations. First, the appointment configuration obtained from the MILP model is static for the day under consideration. Therefore, the schedule configuration does not adapt or react differently to the parameters corresponding to one specific day (i.e., one particular scenario). For instance, consider a situation in which the demand for advance requests is low for a given day, where some pre-book slots do not have any patients booked at the beginning of the day. Under such circumstances, the proposed approach does not adapt and leaves the slot empty. However, these slots may be opened for same-day appointments or left empty to recover from the delays that occurred earlier in the day. To overcome this drawback, future research could adapt yield management-based dynamic appointment policies (e.g., [21, 22]) to adjust the static configuration based on the demand for pre-book and same-day requests. Second, a request denied for a specific day becomes a demand for another day in the future. This is not considered in this research since we focus on constructing the schedule configuration for one day instead of the entire scheduling horizon. Future research could address these drawbacks by considering a weekly scheduling horizon and determining the best strategy to update the schedule configuration dynamically as more information becomes available. Third, we associate the patient’s and resource’s time to a cost by using their median income. However, numerous other factors could impact the cost per unit time. For instance, most patients may expect to wait at a physician’s office and may be prepared to stay productive (or occupied) while they wait. Therefore, depending on the clinic setting and the patient’s expectation, the waiting time cost could be lower than the hourly median wage of the patients.

Even though the correctness of the proposed model is evaluated using small test instances and subject matter experts, we could not verify and validate the model in the context of the real-world clinic as it has not yet been implemented. As a result, future work should evaluate the robustness of the model upon clinical adoption. While the configurations are obtained using the SAA method for a two-stage system with two resources per stage, it becomes computationally challenging to solve the model for more complex systems. Further, the complexity of the real-life constraints represented as a mathematical model can make it difficult to understand, especially for individuals with a non-mathematical background. Therefore, for future research, the results or feasible solutions obtained from the mathematical model could be leveraged to develop a heuristic or meta-heuristic procedure for obtaining the best schedule configuration. Moreover, the patient’s availability and patient’s provider preference can be incorporated into the model instead of assuming that they will accept any doctor and slot assigned to him/her. Alternatively, designing hybrid appointment systems can also be treated as a revenue management problem by considering a distribution of non-linear cost functions such as clinic’s revenue per patient visit, service cost for treating a patient, and waiting time cost. Also, upon implementation of the schedule configuration, an algorithm or heuristic could be designed to allow the clinicians to assign benefits (scores or points) for each visit. This would allow us to understand the distribution of those benefits between pre-booked and same-day booked appointments. Finally, the proposed model can be extended to study a clinic with three or more stages, and the impact of walk-ins on the hybrid configuration can also be considered.

Appendices

Appendix A: linearization techniques

In this section, three different linearization techniques are proposed to transform the non-linear constraints to equivalent linear constraints. These linearization techniques are used to avoid non-linearity and formulate stochastic MILP model for designing the hybrid appointment system.

1.1 A.1 Linearization technique - 1

To illustrate Linearization Technique - 1, let us consider the non-negative continuous decision variables, y and x_j, where j = 1, 2..., n. In addition, let us consider the following binary decision variables, ${{\Delta }_{i}^{j}}$ where j = 1, 2,..., n and i = 1, 2,..., I_j. If the optimization model seeks to minimizey and if y is equal to the maximum of n non-linear terms, where each non-linear term is the product of one continuous variable and one or more binary decision variables as shown in constraint (37), then the non-linear constraint can be linearized by introducing a binary variable 𝜃^j for each x_j as shown in Eqs. 38–44

$$ \begin{array}{@{}rcl@{}} \text{Non-Linear Constraint:} \displaystyle y = \max\Big(x_{1} \times \prod\limits_{i=1}^{I_{1}} {{\Delta}_{i}^{1}}, x_{2} \times \prod\limits_{i=1}^{I_{2}} {{\Delta}_{i}^{2}}, ..., x_{n} \times \prod\limits_{i=1}^{I_{n}} {{\Delta}_{i}^{n}} \Big) \end{array} $$

(37)

$$ \begin{array}{@{}rcl@{}} \text{Equivalent Linear Constraints:}&& \displaystyle y \geq x_{1} - M (I_{1} - \sum\limits_{i=1}^{I_{1}} {{\Delta}_{i}^{1}}) \end{array} $$

(38)

$$ \begin{array}{@{}rcl@{}} &&\displaystyle y \geq x_{2} - M (I_{2} - \sum\limits_{i=1}^{I_{2}} {{\Delta}_{i}^{2}}) \end{array} $$

(39)

$$ \begin{array}{@{}rcl@{}} && \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots\\ & & \displaystyle y \geq x_{n} - M (I_{n} - \sum\limits_{i=1}^{I_{n}} {{\Delta}_{i}^{n}}) \end{array} $$

(40)

$$ \begin{array}{@{}rcl@{}} && \displaystyle y \leq x_{1} + M (1 - \theta^{1}) \end{array} $$

(41)

$$ \begin{array}{@{}rcl@{}} && \displaystyle y \leq x_{2} + M (1 - \theta^{2}) \end{array} $$

(42)

$$ \begin{array}{@{}rcl@{}} & & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots\\ & & \displaystyle y \leq x_{n} + M (1 - \theta^{n}) \end{array} $$

(43)

$$ \begin{array}{@{}rcl@{}} & & \displaystyle \sum\limits_{j=1}^{n} \theta^{j} = 1 \end{array} $$

(44)

Constraints (38)–(40) becomes active if all the binary variable associated with that constraint is 1 and becomes inactive even if one of the binary variable is 0. For example, if all the ${{\Delta }_{i}^{1}}$’s are 1, then Constraint (38) becomes y ≥ x₁. Even if one of the ${{\Delta }_{i}^{1}}$’s is equal to 0 then Constraint (38) becomes y ≥ x₁ − M. Since M is a large positive number, the constraint is equivalent to y ≥−M and hence inactive. Constraint (44), forces exactly one of the 𝜃^j, j = 1, 2,..., n to be active, which in turn forces one of the Constraints (41)–(43) to be active. To ensure feasibility, the 𝜃^j, j = 1, 2,..., n corresponding to the maximum value of x_jj = 1, 2..., n becomes 1, and ensures that y takes the maximum value of x_j. This technique is used to linearize Eqs. (8), (11), (14), and (15).

1.2 A.2 Linearization technique - 2

To illustrate Linearization Technique - 2, let us consider two non-negative continuous decision variables, x and y and I binary decision variables, Δ_i, where i = 1, 2,..., I. If y is exactly equal to a non-linear term that is characterized by the product of x and Δ_i, where i = 1, 2,..., I as shown in Eq. 45, then it can be linearized using Eqs. 46–48. The condition represented by this constraint is that the variable y = x, if all the Δ_i’s are equal to one and y = 0 even if one of the Δ_i is zero.

$$ \begin{array}{@{}rcl@{}} && \text{Non-Linear Constraint:} \displaystyle y = x \times \prod\limits_{i=1}^{I} {\Delta}_{i} \end{array} $$

(45)

$$ \begin{array}{@{}rcl@{}} && \text{Equivalent Linear Constraints:} \displaystyle y \geq x - M (I- \sum\limits_{i=1}^{I} {\Delta}_{i}) \end{array} $$

(46)

$$ \begin{array}{@{}rcl@{}} && \displaystyle y \leq x + M (I- \sum\limits_{i=1}^{I} {\Delta}_{i}) \end{array} $$

(47)

$$ \begin{array}{@{}rcl@{}} && \displaystyle y \leq M ({\Delta}_{i} )\qquad\qquad\forall i \end{array} $$

(48)

If all the Δ_i’s are equal to one, then Constraints (46) and (47) will force y to be exactly equal to x and Constraint (48) becomes inactive. However, even if one of the Δ_i’s is equal to 1, then Constraints (46) and (47) will become inactive and Constraint (48) will force y to be equal to 0. This technique is used to linearize Constraints (10), (72)–(74).

In Eq. 45, if we have greater than or equal to (i.e., i.e., $y \geq x \times \prod \limits _{i=1}^{I} {\Delta }_{i}$) instead of strict equality, then the non-linear constraint can be linearized just by using Constraint (46).

1.3 A.3 Linearization technique - 3

To illustrate Linearization Technique - 3, let us consider non-negative continuous decision variables, y and x_i, where i = 1, 2..., I. If the objective function seeks to maximizey and if y is the maximum of x_i, as shown in Eq. 49, then it can be linearized using Eqs. 49–52. To linearize, we introduce a binary variable, δ_i, where i = 1, 2,..., I.

$$ \begin{array}{@{}rcl@{}} && \text{Non-Linear Constraint:} \displaystyle y = \max (x_{i} : i = 1,2,...,I) \end{array} $$

(49)

$$ \begin{array}{@{}rcl@{}} && \text{Equivalent Linear Constraints:} \displaystyle y \geq x_{i}\qquad\qquad\qquad\forall i \end{array} $$

(50)

$$ \begin{array}{@{}rcl@{}} && \displaystyle y \leq x_{i} + M(1-\delta_{i}) \qquad \qquad\forall i \end{array} $$

(51)

$$ \begin{array}{@{}rcl@{}} & & \displaystyle \sum\limits_{i=1}^{I} \delta_{i} = 1 \end{array} $$

(52)

Constraint (50) ensures that y is greater than or equal to the all the x_i’s. In other words, y must be greater than or equal to maximum of x_i, where i = 1, 2,..., I. Further, Constraint (51) is active (i.e., y ≤ x_i) only when the binary variable, δ_i, is 1 and Constraint (52) forces exactly one of the binary variables (δ_i’s) to take a value 1. Therefore, to ensure feasibility of Constraints (50) and (52), Constraint (51) will be active only for the maximum of x_i. Thus, Constraints (50) and (51) will force y to be exactly equal to the maximum of x_i’s. In this research, we use this procedure to linearize Constraints (18) and (19)

Appendix B: Linearization of the stochastic model

In this section, we present the equivalent linear equations for the non-linear constraints in the stochastic MILP model discussed in Section 5. To linearize Constraints (18) and (19), we introduce two binary variables, namely, δ_sn and Δ_sd. The variable δ_sn takes the value 1 if $L_{s-1,n}^{N}(\omega ) > b_{sn}^{N}$ and is 0 otherwise. Similarly, Δ_sd is 1 if $L_{s-1,d}^{D}(\omega ) > b_{sd}^{D}$ and 0 otherwise. In addition, we also introduce the binary variables $\theta ^{1}_{ptsn}(\omega )$, $\theta ^{2}_{ptsn}(\omega )$, $\theta ^{3}_{ptsn}(\omega )$, $\theta ^{4}_{ptsn}(\omega )$, ${\Theta }^{1}_{ptsd}(\omega )$, ${\Theta }^{2}_{ptsd}(\omega )$, ${\Theta }^{3}_{ptsd}(\omega )$, ${\Theta }^{4}_{ptsd}(\omega )$, α_ptsn(ω), and β_ptsd(ω) to determine the exact maximum for start time and latest completion times of the resources.

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsn}^{N}(\omega) \geq C_{p't^{\prime},s-1,n}^{N}(\omega) - M\big(1 - \sum\limits_{d \in \mathcal{D}}^{} X_{ptsnd}(\omega)\big)\qquad\qquad\qquad\forall t,t^{\prime} \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), p^{\prime} \in \mathcal{P}_{t^{\prime}}(\omega), s\in \mathcal{S} \ni s>1, n \in \mathcal{N} \end{array} $$

(53)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsn}^{N}(\omega) \geq C_{p'tsn}^{N}(\omega) - M\big(1 - \sum\limits_{d \in \mathcal{D}}^{} X_{ptsnd}(\omega)\big)\qquad\qquad \forall t \in \mathcal{T}, p, p^{\prime} \in \mathcal{P}_{t}(\omega), p^{\prime} = 1,2,..,p-1, s \in \mathcal{S}, n \in \mathcal{N} \end{array} $$

(54)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsn}^{N}(\omega) \geq b_{sn}^{N} - M\big(1 - \sum\limits_{d \in \mathcal{D}}^{} X_{ptsnd}(\omega)\big)\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, n \in \mathcal{N} \end{array} $$

(55)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsn}^{N}(\omega) \leq C_{p't^{\prime},s-1,n}^{N}(\omega) + M\big(1 - \theta^{1}_{ptsn}(\omega)\big)\qquad\qquad\qquad\forall t,t^{\prime} \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), p^{\prime} \in \mathcal{P}_{t^{\prime}}(\omega), s\in \mathcal{S} \ni s>1, n \in \mathcal{N} \end{array} $$

(56)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsn}^{N}(\omega) \leq C_{p'tsn}^{N}(\omega) + M\big(1 - \theta^{2}_{ptsn}(\omega)\big)\qquad\qquad \forall t \in \mathcal{T}, p, p^{\prime} \in \mathcal{P}_{t}(\omega), p^{\prime} = 1,2,..,p-1, s \in \mathcal{S}, n \in \mathcal{N} \end{array} $$

(57)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsn}^{N}(\omega) \leq b_{sn}^{N} + M\big(1 - \theta^{3}_{ptsn}(\omega)\big)\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, n \in \mathcal{N} \end{array} $$

(58)

$$ \begin{array}{@{}rcl@{}} \displaystyle \theta^{1}_{ptsd}(\omega)+\theta^{2}_{ptsd}(\omega)+\theta^{3}_{ptsd}(\omega)+\theta^{4}_{ptsn}(\omega) = \sum\limits_{n \in \mathcal{D}}^{} X_{ptsnd}(\omega)\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(59)

$$ \begin{array}{@{}rcl@{}} \displaystyle C_{ptsn}^{N}(\omega) \leq S_{ptsn}^{N}(\omega) + \eta_{pt}(\omega) \times (1 - \sigma_{pt}(\omega)) + M\big(1 - \sum\limits_{d \in \mathcal{D}}^{} X_{ptsnd}(\omega)\big) \qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, n \in \mathcal{N} \end{array} $$

(60)

$$ \begin{array}{@{}rcl@{}} \displaystyle C_{ptsn}^{N}(\omega) \geq S_{ptsn}^{N}(\omega) + \eta_{pt}(\omega) \times (1-\sigma_{pt}(\omega)) - M\big(1 - \sum\limits_{d \in \mathcal{D}}^{} X_{ptsnd}(\omega)\big) \qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, n \in \mathcal{N} \end{array} $$

(61)

$$ \begin{array}{@{}rcl@{}} \displaystyle C_{ptsn}^{N}(\omega) \leq M\sum\limits_{d \in \mathcal{D}}^{} X_{ptsnd}(\omega)\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, n \in \mathcal{N} \end{array} $$

(62)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsd}^{D}(\omega) \geq C_{p't^{\prime},s-1,d}^{D}(\omega) - M\big(1 - \sum\limits_{n \in \mathcal{N}}^{} X_{ptsnd}(\omega)\big)\qquad\qquad\qquad\forall t,t^{\prime}\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), p^{\prime} \in \mathcal{P}_{t^{\prime}}(\omega), s \in \mathcal{S} \ni s > 1, d \in \mathcal{D} \end{array} $$

(63)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsd}^{D}(\omega) \geq C_{p'tsd}^{D}(\omega) - M\big(1 - \sum\limits_{n \in \mathcal{N}}^{} X_{ptsnd}(\omega)\big)\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), p^{\prime} = 1,2,..,p-1, s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(64)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsd}^{D}(\omega) \geq \sum\limits_{n \in \mathcal{N}}^{} C_{ptsn}^{N}(\omega) - M\big(1 - \sum\limits_{n \in \mathcal{N}}^{} X_{ptsnd}(\omega)\big)\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(65)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsd}^{D}(\omega) \geq PAT_{sd}^{B} - M\big(1 - \sum\limits_{n \in \mathcal{N}}^{} X_{ptsnd}(\omega)\big)\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(66)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsd}^{D}(\omega) \leq C_{p't^{\prime},s-1,d}^{D}(\omega) + M\big(1 - {\Theta}^{1}_{ptsd}(\omega)\big)\qquad\qquad\qquad\forall t,t^{\prime}\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), p^{\prime} \in \mathcal{P}_{t^{\prime}}(\omega), s \in \mathcal{S} \ni s > 1, d \in \mathcal{D} \end{array} $$

(67)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsd}^{D}(\omega) \leq C_{p'tsd}^{D}(\omega) + M\big(1 - {\Theta}^{2}_{ptsd}(\omega)\big)\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), p^{\prime} = 1,2,..,p-1, s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(68)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsd}^{D}(\omega) \leq \sum\limits_{n \in \mathcal{N}}^{} C_{ptsn}^{N}(\omega) + M\big(1 - {\Theta}^{3}_{ptsd}(\omega)\big)\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(69)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsd}^{D}(\omega) \leq PAT_{sd}^{B} + M\big(1 - {\Theta}^{4}_{ptsd}(\omega)\big)\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(70)

$$ \begin{array}{@{}rcl@{}} \displaystyle {\Theta}^{1}_{ptsd}(\omega)+{\Theta}^{2}_{ptsd}(\omega)+{\Theta}^{3}_{ptsd}(\omega)+{\Theta}^{4}_{ptsd}(\omega) = \sum\limits_{n \in \mathcal{N}}^{} X_{ptsnd}(\omega)\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(71)

$$ \begin{array}{@{}rcl@{}} \displaystyle C_{ptsd}^{D}(\omega) \leq S_{ptsd}^{D}(\omega) + \rho_{pt}(\omega) \times (1-\sigma_{pt}(\omega)) + M\big(1 - \sum\limits_{n \in \mathcal{N}}^{} X_{ptsnd}(\omega)\big) \qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(72)

$$ \begin{array}{@{}rcl@{}} \displaystyle C_{ptsd}^{D}(\omega) \geq S_{ptsd}^{D}(\omega) + \rho_{pt}(\omega) \times (1-\sigma_{pt}(\omega)) - M\big(1 - \sum\limits_{n \in \mathcal{N}}^{}X_{ptsnd}(\omega)\big) \qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(73)

$$ \begin{array}{@{}rcl@{}} \displaystyle C_{ptsd}^{D}(\omega) \leq M\sum\limits_{n \in \mathcal{N}}^{} X_{ptsnd}(\omega)\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(74)

$$ \begin{array}{@{}rcl@{}} \displaystyle L_{sn}^{N}(\omega) \geq C_{ptsn}^{N}(\omega) - M\big(1 - \sum\limits_{n \in \mathcal{D}}^{} X_{ptsnd}(\omega)\big)\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, n \in \mathcal{N} \end{array} $$

(75)

$$ \begin{array}{@{}rcl@{}} \displaystyle L_{sn}^{N}(\omega) \leq C_{ptsn}^{N}(\omega) + M\big(1 - \alpha_{ptsn}\big)\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, n \in \mathcal{N} \end{array} $$

(76)

$$ \begin{array}{@{}rcl@{}} \displaystyle \sum\limits_{p\in\mathcal{P}_{t}(\omega)}\alpha_{ptsn} = 1\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, n \in \mathcal{N}\end{array} $$

(77)

$$ \begin{array}{@{}rcl@{}} \displaystyle L_{sd}^{D}(\omega) \geq C_{ptsd}^{D}(\omega) - M\big(1 - \sum\limits_{n \in \mathcal{N}}^{} X_{ptsnd}(\omega)\big)\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(78)

$$ \begin{array}{@{}rcl@{}} \displaystyle L_{sd}^{D}(\omega) \leq C_{ptsd}^{D}(\omega) + M\big(1 - \beta_{ptsn}\big)\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(79)

$$ \begin{array}{@{}rcl@{}} \displaystyle \sum\limits_{p\in\mathcal{P}}\beta_{ptsn} = 1\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D} \end{array} $$

(80)

$$ \begin{array}{@{}rcl@{}} \displaystyle L_{s-1,n}^{N}(\omega) \leq b_{sn}^{N} + M(1- \delta_{sn}) \qquad\qquad\qquad\forall s\in \mathcal{S}\ni s > 1, n \in \mathcal{N} \end{array} $$

(81)

$$ \begin{array}{@{}rcl@{}} \displaystyle L_{s-1,n}^{N}(\omega) \geq b_{sn}^{N} - M\delta_{sn} \qquad\qquad\qquad\forall s\in \mathcal{S}\ni s > 1, n \in \mathcal{N} \end{array} $$

(82)

$$ \begin{array}{@{}rcl@{}} \displaystyle E_{sn}^{N}(\omega) \leq b_{sn}^{N} + M(1-\delta_{sn}) \qquad\qquad\qquad\forall s\in \mathcal{S}\ni s > 1, n \in \mathcal{N} \end{array} $$

(83)

$$ \begin{array}{@{}rcl@{}} \displaystyle E_{sn}^{N}(\omega) \leq L_{s-1,n}^{N}(\omega) + M\delta_{sn}\qquad\qquad\qquad\forall s\in \mathcal{S}\ni s > 1, n \in \mathcal{N} \end{array} $$

(84)

$$ \begin{array}{@{}rcl@{}} \displaystyle L_{s-1,d}^{D}(\omega)\leq b_{sd}^{D} + M(1- {\Delta}_{sd}) \qquad\qquad\qquad\forall s\in \mathcal{S}\ni s > 1, d \in \mathcal{D} \end{array} $$

(85)

$$ \begin{array}{@{}rcl@{}} \displaystyle L_{s-1,d}^{D}(\omega) \geq b_{sd}^{D} - M{\Delta}_{sd} \qquad\qquad\qquad\forall s\in \mathcal{S}\ni s > 1, d \in \mathcal{D} \end{array} $$

(86)

$$ \begin{array}{@{}rcl@{}} \displaystyle E_{sd}^{D}(\omega) \leq b_{sd}^{D} + M(1-{\Delta}_{sd}) \qquad\qquad\qquad\forall s\in \mathcal{S}\ni s > 1, d \in \mathcal{D} \end{array} $$

(87)

$$ \begin{array}{@{}rcl@{}} \displaystyle E_{sd}^{D}(\omega) \leq L_{s-1,d}^{D}(\omega) + M{\Delta}_{sd} \qquad\qquad\qquad\forall s\in \mathcal{S}\ni s > 1, d \in \mathcal{D} \end{array} $$

(88)

Appendix C: Stochastic programming model for a single stage system

In this section, we present the stochastic program model to determine the best schedule configuration of an outpatient clinic with only one stage (doctor). The mathematical model presented in Section 5 can be easily adapted for a single-stage system by eliminating the variables and constraints involving the nurse stage. Therefore, to ensure consistency, we will use the notations presented in Section 5 but without the indices and sets representing the nurse stage. Thus, for the single stage system, the key decision variable is X_ptsd(ω) instead of X_ptsnd(ω). The objective function (89) is subject to Constraints (90)–(107).

$$ \begin{array}{@{}rcl@{}} &&\text{Minimize}, Z = \displaystyle\sum\limits_{\omega \in {\Omega}} \Bigg(p(\omega) \times \displaystyle{ c^{WT} \Big[ \sum\limits_{t \in \mathcal{T}}\sum\limits_{p \in \mathcal{P}_{t}(\omega) }W_{pt}(\omega) \Big] + c^{DIT} \Big [ \sum\limits_{s \in \mathcal{S}} \sum\limits_{d \in \mathcal{D}} \Big(I_{sd}^{DB}(\omega) + I_{sd}^{DA}(\omega)\Big) \Big ] +} \\&&{ c^{DOT} \Big [ \sum\limits_{s \in \mathcal{S}} \sum\limits_{d \in \mathcal{D}} O_{sd}^{D}(\omega) \Big ]+ c^{OC} \Big[\sum\limits_{t \in \mathcal{T}}\sum\limits_{p \in \mathcal{P}_{t}(\omega)}\Big(1- \sum\limits_{s \in \mathcal{S}}^{}\sum\limits_{d \in \mathcal{D}}^{}X_{ptsd}(\omega)\Big) \Big]} \Bigg ) \end{array} $$

(89)

$$ \begin{array}{@{}rcl@{}} \displaystyle\sum\limits_{d \in \mathcal{D}}^{}\sum\limits_{s \in \mathcal{S}}^{}X_{ptsd}(\omega) \leq 1\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), \omega \in {\Omega} \end{array} $$

(90)

$$ \begin{array}{@{}rcl@{}} \displaystyle X_{ptsd}(\omega) + X_{p't'sd}(\omega) \leq 1\qquad\qquad\qquad\forall t = {A}, t^{\prime} = {O}, p \in \mathcal{P}_{t}(\omega), p^{\prime} \in \mathcal{P}_{t^{\prime}}(\omega), s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(91)

$$ \begin{array}{@{}rcl@{}} \displaystyle \sum\limits_{t \in {T}} \sum\limits_{p \in \mathcal{P}_{t}(\omega) } X_{ptsd}(\omega) \leq \tau\qquad\qquad \forall d \in \mathcal{D}, s \in {S}, \omega \in {\Omega} \end{array} $$

(92)

$$ \begin{array}{@{}rcl@{}} \displaystyle R_{s}(\omega) = \sum\limits_{d \in \mathcal{D}}^{}\sum\limits_{p \in \mathcal{P}_{t}(\omega)}^{}X_{ptsd}(\omega) \qquad\qquad\forall t = \{A\}, s \in \mathcal{S}, \omega \in {\Omega} \end{array} $$

(93)

$$ \begin{array}{@{}rcl@{}} \displaystyle &&S_{ptsd}^{D}(\omega) = \max \Bigg\{ \Big(\sum\limits_{s \in \mathcal{S}}b_{sd}^{D} \times \sum\limits_{s \in \mathcal{S}}\sum\limits_{n \in \mathcal{N}} X_{ptsd}(\omega)\Big), \\ \ &&\Big(L_{s-1,d}^{D}(\omega) \times \sum\limits_{n \in \mathcal{N}} X_{ptsd}(\omega) : s\in \mathcal{S} \ni s>1 \Big), \\ &&\Big(C_{p'tsd}^{D}(\omega) \times X_{ptsd}(\omega): p^{\prime} \in \mathcal{P}_{t}(\omega) \ni p^{\prime} \leq p-1, s \in \mathcal{S}\Big) \Bigg\} \qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(94)

$$ \begin{array}{@{}rcl@{}} \displaystyle S_{ptsd}^{D}(\omega) \leq M X_{ptsd}(\omega)\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(95)

$$ \begin{array}{@{}rcl@{}} \displaystyle C_{ptsd}^{D}(\omega) = \Big(S_{ptsd}^{D}(\omega) + \rho_{pt}(\omega) \times (1 - \sigma_{pt}(\omega))\Big) \times X_{ptsd}(\omega) \qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(96)

$$ \begin{array}{@{}rcl@{}} \displaystyle L_{sd}^{D}(\omega) = \max \Big(C_{ptsd}^{D}(\omega) \times X_{ptsd}(\omega) : t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega)\Big) \qquad\qquad\qquad\forall s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(97)

$$ \begin{array}{@{}rcl@{}} \displaystyle E_{sd}^{D}(\omega) = b_{sd}^{D} \qquad\qquad\qquad\forall s \in \mathcal{S} \ni s = 1, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(98)

$$ \begin{array}{@{}rcl@{}} \displaystyle E_{sd}^{D}(\omega) = \max \Big(b_{sd}^{D}, L_{s-1,d}^{D}(\omega)\Big)\qquad\qquad\qquad\forall s \in \mathcal{S} \ni s > 1, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(99)

$$ \begin{array}{@{}rcl@{}} \displaystyle I_{sd}^{DB}(\omega) \geq L_{sd}^{D}(\omega) - E_{sd}^{D}(\omega) - \sum\limits_{t \in \mathcal{T}}\sum\limits_{p \in \mathcal{P}_{t}(\omega)}\rho_{pt}(\omega) \times (1-\sigma_{pt}(\omega)) \times X_{ptsd}(\omega)\qquad\qquad\qquad\forall s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(100)

$$ \begin{array}{@{}rcl@{}} \displaystyle I_{sd}^{DA}(\omega) - O_{sd}^{D}(\omega) \geq f_{sd}^{D} - L_{sd}^{D}(\omega)\qquad\qquad\qquad\forall s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(101)

$$ \begin{array}{@{}rcl@{}} \displaystyle {O_{d}^{D}}(\omega) = L_{sd}^{D}(\omega) - f_{sd}^{D}\qquad\qquad\qquad\forall s \in \mathcal{S}\ni s = |\mathcal{S}|, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(102)

$$ \begin{array}{@{}rcl@{}} \displaystyle W_{pt}(\omega) = (1-\sigma_{pt}(\omega))\times\Bigg(\sum\limits_{s \in \mathcal{S}}^{}\sum\limits_{d \in \mathcal{D}}^{}\Big(S_{ptsd}^{D}(\omega) - b_{sd}^{D} \times X_{ptsd}(\omega)\Big)\Bigg) \qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), \omega \in {\Omega} \end{array} $$

(103)

$$ \begin{array}{@{}rcl@{}} \displaystyle \hat{W}_{pt}(\omega) \geq W_{pt}(\omega) - \kappa\qquad\qquad\qquad\forall t \in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), \omega \in {\Omega} \end{array} $$

(104)

$$ \begin{array}{@{}rcl@{}} \displaystyle R_{s}(\omega) - R_{s} = 0\qquad\qquad\qquad\forall s \in \mathcal{S}, \omega \in {\Omega} \end{array} $$

(105)

$$ \begin{array}{@{}rcl@{}} &&S_{ptsd}^{D}(\omega),C_{ptsd}^{D}(\omega), L_{sd}^{D}(\omega),DIT_{sd}^{\omega}, \\ &&I_{sd}^{DB}(\omega) , I_{sd}^{DA}(\omega), O_{sd}^{D}(\omega),W_{pt}^{}(\omega) \geq 0\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(106)

$$ \begin{array}{@{}rcl@{}} &&X_{ptsd}(\omega) \in \{0, 1\}\qquad\qquad\qquad\forall t\in \mathcal{T}, p \in \mathcal{P}_{t}(\omega), s \in \mathcal{S}, d \in \mathcal{D}, \omega \in {\Omega} \end{array} $$

(107)