Abstract
We make use of the Hamilton–Jacobi and Parikh-Wilczek methods to investigate the Hawking radiation from the event horizon of a new charged anti-de Sitter black hole in four-dimensional Gauss-Bonnet gravity space–time. Both the tunneling rate of charged particles and the Bekenstein-Hawking entropy are evaluated. The emission spectrum is an impure thermal one and consistent with an underlying unitary theory. There is no difference between the emission rate of massive particle and that of massless one. The entropy is modified by a logarithmic term so that the area law of the black hole entropy is violated. It satisfies the first law of black hole thermodynamics and has the same expression as that calculated by Loop Quantum Gravity and String Theory. When the Gauss-Bonnet coupling coefficient is equal to zero, the logarithmic correction vanishes and the Bekenstein-Hawking relation in general relativity is recovered. So our results show the effects of the Gauss-Bonnet modified gravity on the Bekenstein-Hawking entropy and Hawking radiation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Since Bekenstein [1] and Hawking [2] proved that the entropy of a black hole is proportional to the area of its event horizon, black hole thermodynamics has become one of the most attractive topics in theoretical physics. Recently, a new black hole solution was proposed in four dimensional Gauss-Bonnet gravity [3] and generalized to the case including electric charge in anti-de Sitter space [4]. It has shed new light on the gravity theories [5, 6], the AdS-CFT correspondence and astropysics. For example, novel features have been discovered in holographic superconductors [7], black hole shadow[8], black hole microstructure [9]. Some other thermodynamic properties such as horizons, phase transition and Joule Thomson Expansion were also studied [4, 9, 10]. So it is natural to expect that the study of Hawking radiation of this black hole in this paper would give rise to new findings.
Black hole radiation was originally considered to be pure thermal [2], but the property does not support underlying unitary theory in quantum mechanics and violates the conservation of information. In 1995, Kraus, Parikh and Wilczek suggested that Hawking radiation should be treated as a quantum tunneling effect and self-gravitation and energy conservation taken into account. They used the method to investigate the modification to radiation spectra of the Schwarzschild and Reissner-Nordstrom black holes [11,12,13] and obtained an impurely thermal spectrum. Since then, several familiar methods including the Parikh-Wilczek, Hamilton–Jacobi method and Damour- Ruffini methods have been used to study the non-pure thermal radiation of various black holes in general relativity [14,15,16,17,18,19,20,21,22,23,24,25,26]. Later, the Parikh-Wilczek method was extended to black holes in various modified gravities [27,28,29,30,31,32] and not only the corrected radiation spectra but also various forms of Bekenstein-Hawking entropy were obtained.
In this paper, we employ the Parikh-Wilczek and Hamilton–Jacobi methods to calculate the corrected radiation spectrum of particles from the novel four-dimensional charged anti-de Sitter black hole in Gauss-Bonnet gravity. The paper is organised as follows. In the next section we start from the metric and use the relativistic Hamilton–Jacobi equation to evalate the corrected emission spectrum of the black hole. In section III we utilize the Parikh-Wilczek method to disscuss the correction to the radiation spectrum. In section IV the Bekenstein-Hawking entropy is calculated. Then we discuss the results and conclude the paper in section V.
2 Black hole metric, Hamilton–Jacobi method and emission rate
Charged anti-de Sitter solution in four-demension Gauss-Bonnet gravity spacetime was obtained in Ref. [4]. The metric reads
where M and Q are the mass and electric charge of the black hole, \(\alpha\) is the coupling constant of the Gauss-Bonnet term in the action and Λ < 0 is the cosmological constant.
Let \(r_{{\text{H}}}\) denote the outer event horizon radius, which is determined by \(f(r) = 0,\) we can factorize \(f(r)\) into
Obviously, \(f^{\prime}(r_{{\text{H}}} ) = \eta (r_{{\text{H}}} )\) exists, where the prime denotes a radial derivative.
On the other hand, the mass and Hawking temperature of the black hole can be expressed as
The classical action I of a particle emitting from the black hole horizon satisfies the relativistic Hamilton–Jacobi equation
with the electromagnetic vector potential \(A_{\mu } = \left( { - \frac{Q}{r},0,0,0} \right)\), where m and q are the rest mass and charge of the emitted radiation particle, and \(g^{\mu \nu }\) is the inverse metric of the black hole. Making use of the line element (1), we obtain
Now that the black hole is spherically symmetric, one may write the action as the form of separated variables, i.e.
where \(\omega\) is the energy of the radiation particle and \(J_{\theta } ,J_{\phi }\) are constants corresponding to angular momentums of angular coordinates \(\theta \, and \, \phi\). Simplifying the Eq. (7) yields
Solving the equation, we have
where + and − correspond to outgoing and incoming solutions, respectively. Obviously, in non-extreme cases, \(r = r_{{\text{H}}}\) is a first order singularity of the integrand, so we take advantage of the integral method of complex variable function to calculate the integral. We do the integral and obtain
Assuming that the radiation of the particle is a continuous process and taking the self-gravitation interaction and conservation of energy and charge into account, the emission of a particle decreases the black hole mass and charge and changes the horizon radius, Hawking temperature and so on. Therefore, M should be replaced by \(M - \omega\) and Q by \(Q - q\) when the equations related with M and Q are used. Thus, we write the differential of the imaginary part of the action as
Because \({\text{d}}\omega = - {\text{d}}M,{\text{d}}q = - {\text{d}}Q\), the imaginary part reads
Making use of the first law of thermodynamics for black holes \({\text{d}}M = T_{{\text{H}}} {\text{d}}S + \varphi_{{\text{H}}} {\text{d}}Q\) and the electromagnetic vector potential at the horizon \(\varphi_{{\text{H}}} = - \left. {A_{t} } \right|_{{r = r_{{\text{H}}} }} = \frac{Q}{{r_{{\text{H}}} }}\) yields
where \(\Delta S_{{{\text{BH}}}} = S_{{{\text{BH}}}} (M - \omega ,Q - q) - S_{{{\text{BH}}}} (M,Q)\) is the increment of the Bekenstein-Hawking entropy before and after the particle emission.
To ensure that the probabilities are correctly normalized so that any incoming particles crossing the horizon have a 100% chance of entering the black hole, the probability of a particle tunnelling from inside to outside the horizon will be [33]
This is consistent with an underlying unitary theory and shows that the radiation spectrum is not purely thermal.
3 Parikh-Wilczek method and emission rate
Employing the Parikh-Wilczek method, we need make a transformation
Substituting Eq. (16) into Eq. (1) yields
If \(f^{ - 1} (r) - f(r)g^{2} (r) = 1\) is satisfied, we gain a Painleve–Gullstrand line element as
The metric is not singular at the horizon and is flat Euclidean space in radial in constant-time slices. Setting \({\text{d}}s^{2} = {\text{d}}\theta = {\text{d}}\phi = 0\), we have the motion equation of the outgoing particle
where the dot denotes derivative to \(\tau\).
Of course, Eq. (19) is radial-lightlike and only true for massless particles. While the massive quanta ‘s world-line is timelike, so Eq. (19) doesn't apply to massive particles. In order to get the motion equation of a massive outgoing particle, it can be treated as a de Broglie wave. It is well-known that the phase velocity and group velocity of the de Broglie wave are not equal. If the equation of de Broglie wave is written as \(\psi (r,t) = Ce^{{i(\int {p_{r} dr} - \omega t)}}\), their definitions and the relationship between them are [14, 15]
where k is the wave number, rc is the location of the particle. The tunneling process is instantaneous, so one can think that the particle tunneling into the barrier and out it occur simultaneously. According to the coordinate clock synchronization theory of Laudau, the difference of the coordinate times of the two simultaneous events is
When \(d\theta = d\phi = 0\), Eq. (22) can be simplified to
Then the group velocity is
And the phase velocity is
From the line element (18) and Eq. (20), we have
To investigate the emission of charged particles from a black hole, the effects of the self-gravitation reaction and the electromagnetic field outside the black hole need to be considered. Because the metric is of spherical symmetry, thinking of the outgoing charged particle as a shell of energy and electric charge is reasonable. When the energy and charge conservation is taken into account, we can calculate the imaginary part of the action for a charged particle crossing the horizon outwards as [23]
where \(p_{r}\) and \(p_{\varphi }\) are the canonical momenta conjugate corresponding to the coordinates \(r\) and \(\varphi\), \(r_{{\text{i}}}\) and \(r_{{\text{f}}}\) denote the event horizon radiuses of the black hole before and after the particle of energy \(\omega\) and charge q is emitted. Making use of the Hamilton equations
Substituting Eq. (27) into Eq. (26) yields
We exchange integral order and complete the integral of r to obtain
Obviously, this equation is in complete agreement with Eq. (13). So we can obtain the same impurely thermal spectrum (15).
4 Entropy and its logarithmic correction
Now we will derive an analytical expression of the entropy of this new 4-dimensional Gauss- Bonnet gravity black hole. From Eq. (4), we can get
Substituting Eqs. (5) and (30) into Eq. (13) or Eq. (29) yields
Comparing Eqs. (31) and (14) has
We may take
where \(A_{{\text{H}}} = 4\pi r_{{\text{H}}}^{2}\) is the horizon area and \(S_{0} = 2\pi \alpha \ln 4\pi A_{0}^{ - 1}\) is an integration constant with dimension of [length]2. The result (33) shows that the black hole entropy does not satisfy the area law S = AH/4 because of the existence of an additional logarithmic term. Meanwhile, because the logarithm exists, one cannot determine the constant S0 or A0 by considering that the entropy should vanish when the event horizon of black hole disappears. But, in String Theory it could be fixed by counting up microscopic degrees of freedom of the black hole [34, 35]. According to statistical interpretations of the black hole entropy in theory of Loop Quantum Gravity and String Theory, the correction term comes from the subleading term of statistical degrees of freedom [35,36,37].
5 Conclusions and discussions
We used both the Hamilton–Jacobi and Parikh-Wilczek method to calculate the radiation rate of the massless and massive charged particles from the new four dimensional Gauss-Bonnet gravity black hole and obtained the emission spectrum. Firstly, the results obtained by the two methods coincide. Secondly, the spectrum deviates from the purely thermal one but are in agreement with an underlying unitary theory. The deviation shows that the black hole is actually a ‘grey-body’ and some other information besides the temperature may be gained from the spectrum. Third, the spectrum is determined on the increment of the black hole entropy after and before the particle emits and keeps the completely same forms obtained earlier.
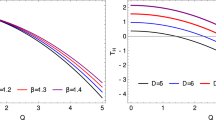
Then, we analytically derived the formula of entropy of the Gauss-Bonnet black hole. The result coincides with that obtained from the Iyer-Wald formula [5]. The entropy includes two terms. The first one is proportional to the horizon area and describes the geometric character. The second one is a logarithmic term and its presence makes that the whole entropy does not satisfy the area law. In local gravity theories even in higher derivative ones, it is unusual that the entropy is logarithmic corrective. Of course, the logarithmic correction is a well-known general result in the quantum field theory treatment of black hole entropy, which can be derived from the direct count of black hole micro-states in String Theory and Loop Quantum Gravity [38,39,40,41,42,43]. The entropy (33) obeys the first law of black hole thermodynamics, so it is just the Bekenstein-Hawking entropy, namely, \(S_{{{\text{BH}}}} = S\). When α = 0, the logarithmic term vanishes, the Bekenstein-Hawking area formula and the case in general relativity are recovered. And then the emission rate (16) can be written as \(\Gamma = \exp \left( {\Delta S_{{{\text{BH}}}} } \right)\).
In a word, the logarithmic corrective term of the Bekenstein-Hawking entropy of the Gauss- Bonnet black hole is in direct proportion to the Gauss-Bonnet coupling constant and the form of the whole entropy is just the kind expected by String Theory and Loop Quantum Gravity. While the non-pure thermal properties of Hawking radiation is due to the consideration of the self-gravitation interaction and conservation of energy (i.e. the first law of thermodynamics), namely, the back reaction of the quanta emitted. Therefore, except that the influence of the Gauss-Bonnet modification of gravity on the Hawking radiation and entropy is revealed, one can ask whether there may be a link between the result and the quantum gravity effects.
Change history
23 November 2021
A Correction to this paper has been published: https://doi.org/10.1007/s10714-021-02875-3
References
Bekenstein, J.D.: Phys. Rev. D 7, 2333 (1973)
Hawking, S.W.: Math. Phys. 43, 199 (1975)
D. Glavan and C. Lin, Phys. Rev. Lett. 124: 081301 (2020)
P. G. S. Fernandes, Phys. Lett. B 805: 135468 (2020). arXiv: gr-qc/2003.05491arXiv: gr-qc/2003.05491
H. Lu and Y. Pang, Phys. Lett.B 809: 135717 (2020). arXiv:gr qc/2003.11552
R.A.Hennigar, D. Kubizňák, R.B. Mann and C.Pollack, J. High Energy Phys. 07: 027 (2020). arXiv:gr-qc/2004.09472
X. y. Qiao, O. Y. Liang, D. Wang, Q. Y. Pan and J. L. Jing, JHEP 2020(12):192 (2020)
Guo, M.Y., Li, P.C.: Eur. Phys. J. C 80(6), 588 (2020)
S.W. Wei and Y.X. Liu. Phys. Rev. D 101: 104018 (2020). arXiv:gr-qc/2003.14275v3
K. Hegde, A. N. Kumara, C. L. A. Rizwan, K. M. Ajith and M. S. Ali, Thermodynamics, Phase Transition and Joule Thomson Expansion of novel 4-D Gauss Bonnet AdS Black Hole, arXiv: gr-qc/2003.08778
Kraus, P., Wilczek, F.: Nucl. Phys. B 433, 403 (1995)
Parikh, M.K., Wilczek, F.: Phys. Rev. Lett. 85, 5042 (2000)
Parikh, M.K.: Int. J. Mod. Phys. D 13, 2351 (2004)
Zhang, J.Y., Zhao, Z.: J. High Energy Phys. 10, 55 (2005)
Zhang, J.Y., Zhao, Z.: Nucl. Phys. B 725, 173 (2005)
Jiang, Q.Q., Yang, S.Z., Li, H.L.: Chin. Phys. 14, 1736 (2005)
Han, Y.W., Yang, S.Z.: Chin. Phys. Lett. 22, 2769 (2005)
Ren, J., Zhao, Z., Gao, C.J.: Chin. Phys. Lett. 22, 2489 (2005)
Zhang, J.Y., Zhao, Z.: Phys. Lett. B 618, 14 (2005)
Zhang, J.Y., Zhao, Z.: Mod. Phys. Lett. A 20, 1673 (2005)
Yang, S.Z., Chen, D.Y.: Chin. Phys. Lett. 24, 39 (2007)
Li, G.Q.: Europhys. Lett. 76, 203 (2006)
Zhang, J.Y., Fan, J.H.: Phys. Lett. B 648, 133 (2007)
Liu, B., Wang, G., Liu, W.B.: Mod. Phys. Lett. A 23, 281 (2008)
Niu, Z.F., Liu, W.B.: Chin. J. Phys. 46, 528 (2008)
Li, G.Q.: Mod. Phys. Lett. A 22, 209 (2007)
Li, G.Q., Zhuang, Y.W.: Turk J Phys 44, 458 (2020)
Li, G.Q., Mo, J.X.: Astrophys. Space Sci. 361, 251 (2016)
Li, G.Q., Mo, J.X.: Gen. Relativ. Gravit. 49, 57 (2017)
G. Q. Li, Chin. Phys. C 41: 045103 (2017)
Li, R.: Europhys. Lett. 96, 60014 (2011)
Li, G.Q., Ou, Y.Y., Lin, Z.T.: Lith. J. Phys. 59, 1 (2019)
R. Kerner and R. B. Mann, Phys. Lett. B 665: 277 (2008). arXiv:hep-th/0803.2246v3]
R. G. Cai, Phys. Rev. D 65, 084014 (2002). arXiv:hep-th/0109133
R. G. Cai, Phys. Lett. B 733: 183 (2014). arXiv:hep-th/1405.1246v1
R. G. Cai, L. M. Cao and N. Ohta, J. High Energy Phys. 04: 082 (2010). arXiv:hep-th/0911.4379v2
G. Cognola, R. Myrzakulov, L. Sebastiani, and S. Zerbini, Phys. Rev. D 88: 024006 (2013)
A. Strominger and C. Vafa, Phys. Lett. B 379: 99 (1996). arXiv:hep-th/9601029
S. N. Solodukhin, Phys. Rev. D 57: 2410 (1998). arXiv:hep-th/9701106
C. Rovelli, Phys. Rev. Lett. 77: 3288 (1996). arXiv:gr-qc/9603063
A. Ashtekar, J. Baez, A. Corichi and K. Krasnov, Phys. Rev. Lett. 80: 904 (1998). arXiv:gr-qc/9710007
R. K. Kaul and P. Majumdar, Phys. Rev. Lett. 84: 5255 (2000). arXiv:gr-qc/9710007
M. Arzano, A. J. M. Medved and E. C. Vagenas, J. High Energy Phys. 09:037 (2005). arXiv:hep-th/0505266v2
Acknowledgements
The research is supported by Guangdong Basic and Applied Basic Research Foundation (Grant Nos. 2021A1515010246). It is also supported by the Education Department of Guangdong Province (Grant Nos. 2017KZDXM056) and the ‘Climbing Program’ Special Funds of Guangdong (Grant Nos. pdjh2020b0362).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Li, GQ., Mo, JX. & Zhuang, YW. Corrections to Hawking radiation and Bekenstein-Hawking entropy of novel four-dimensional black holes in Gauss- Bonnet gravity. Gen Relativ Gravit 53, 97 (2021). https://doi.org/10.1007/s10714-021-02863-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10714-021-02863-7