1 Overview and motivation

In the last few decades, black hole thermodynamics has been playing an important role in order to understand quantum gravity. It is started with Hawking and Page who found that the black hole solutions in asymptotically AdS space have thermodynamic properties including a characteristic temperature and an intrinsic entropy proportional to the area of the event horizon [1]. In this connection, assuming the black hole as a thermodynamic system in equilibrium at Hawking temperature, its small statistical fluctuations around equilibrium is systematically studied diversely. These fluctuations give rise to a non-trivial multiplicative factor to the expression for the density of states. This leads to a correction to the entropy of black hole which is logarithmic, determined macroscopically from the massless particle spectrum, at the leading order [2]. These corrections are computed microscopically as well using a stringy embedding of the Kerr/CFT correspondence and found perfect agreement [3]. The first-order quantum correction to the entropy is also computed by examining the logarithmic corrections to the Cardy formula [4]. This confirms that logarithmic corrections to the entropy originated due to the statistical fluctuations around thermal equilibrium of the black hole.

The effects of thermal fluctuations on the thermodynamics of various black holes have been studied. For instance, more recently, the effect of thermal fluctuations on the thermodynamics of a massive gravity black hole in AdS space is studied [5]. From the critical points and stability analysis, it has been shown that the presence of logarithmic correction is necessary to have stable phase and critical point. On the other hand, the Van der Waals phase transitions for the massive gravity black holes is also studied and found that massive gravity theories can exhibit strikingly different thermodynamic behavior compared to that of Einstein gravity, and that the mass of the graviton can generate a range of new phase transitions that are otherwise forbidden [6]. The quantum gravity effects on Hořava–Lifshitz black hole is also investigated and discussed such effects on the black hole stability [7]. By comparing the corrected entropy to the energy fluctuations and a conformal field theory, the corrections to the thermodynamics and the phase transition of charged dilatonic black Saturn are studied [8]. Recently, the thermodynamical properties of recently proposed Schwarzschild-Beltrami-de Sitter black hole with the higher order corrected entropy are also analysed [9]. Here, first and second laws of thermodynamics are established and found that presence of higher order corrections, stem from thermal fluctuations, may remove some instabilities of the black hole. The logarithm-corrected entropy and thermodynamics of a dyonic charged AdS black hole is studied and holographic duality of a van der Waals fluid is established [10]. The effects of first-order correction to the modified Hayward black hole have been studied, where it has been found that corrections reduce the pressure and internal energy of the Hayward black hole [11]. Recently, based on the Jacobson formalism, a method is proposed to test the effects of quantum fluctuations on black holes through the thermal fluctuations on dumb holes [12] We are interested to study the effects of leading-order correction on the stability and thermodynamics of four dimensional charged rotating AdS black hole.

In this paper, we consider the charged rotating black holes as thermal system and try to analyse the effects of thermal fluctuations on the thermodynamics of such black hole. We fist compute the Hawking temperature and leading-order correction to the entropy of the system originated due to the thermal fluctuations which is logarithmic in nature. We see that entropy is an increasing function for large black holes when system is in equilibrium. However, due to thermal fluctuation, the entropy does not exist for smaller black holes. For very large black holes, the thermal fluctuation does not effect significantly. The negative cosmological constant is assumed as the positive thermodynamic pressure. Once the leading-order corrected entropy, the temperature, horizon angular velocity, angular momentum charge and pressure are known, we can easily derive the first-order corrected physical mass of the system. We find that there exists a critical point for physical mass which increases as long as charge of the black hole increases. The mass is a decreasing function before the critical horizon radius and thereafter it is an increasing function. The correction terms with negative correction parameter increases and decreases the values of physical mass before and after the critical horizon radius respectively. Once the expression of corrected physical mass and pressure is known, it is matter of calculation to derive the geometrical volume for a charged rotating AdS black hole. We estimate the correction to internal energy also. We find that internal energy is a decreasing function of horizon radius for smaller black holes. There exists a critical value for internal energy which increases when charge increase of the black hole. The correction term due to thermal fluctuation with negative correction parameter increases and decreases the value of internal energy before and after critical point respectively. We further calculated the corrected value of Helmholtz and Gibbs free energies of the system due to thermal fluctuations. We further study the Van der waals fluid duality to charged rotating black holes and see the typical behavior of the \(P-v\) diagram corresponding to the van der Waals fluid. The stability of such black holes is also checked. We find that the phase transition occurs for such black holes. The specific heat is negative for small black holes which suggests that small black holes are thermodynamically unstable. In fact, the specific heat is always positive for larger black holes which means these black holes are in stable phase. Some stability also occurs for the small black holes due to the correction term with positive correction parameter. However, the correction term with negative correction parameter makes small black holes more unstable.

The paper is organized as follows. In Sect. 2, we first recapitulate the metric and thermodynamical quantities of a charged Kerr-AdS black hole. Then, we study the first-order correction to thermodynamics of such black hole. Further, we analyse the duality between black hole and Van der Waals fluid. We study the stability of such black holes also. Finally, we conclude the results with future directions in Sect. 3.

2 A charged rotating black holes in AdS space

The charged rotating (Kerr) black holes in \(d=4\) AdS space were constructed by Carter [13] and the metric reads,

$$\begin{aligned} ds^2= & {} -\frac{\Delta }{\rho ^2}\left[ dt -\frac{a}{\Sigma }\sin ^2\theta d\phi \right] ^2+\frac{\rho ^2dr^2}{\Delta }\nonumber \\&+\,\frac{\rho ^2d\theta ^2}{\Delta _\theta }+\frac{\Delta _\theta \sin ^2\theta }{\rho ^2}\left[ adt-\frac{r^2+a^2}{\Sigma }d\phi \right] ^2, \end{aligned}$$
(1)

where

$$\begin{aligned} \Delta= & {} (r^2+a^2)\left( 1+\frac{r^2}{l^2}\right) -2mr+q^2,\ \ \ \ \Delta _\theta =1-\frac{a^2}{l^2}\cos ^2\theta ,\nonumber \\ \rho ^2= & {} r^2+a^2\cos ^2\theta ,\ \ \ \ \ \ \Sigma =1-\frac{a^2}{l^2}. \end{aligned}$$
(2)

Here l is the AdS radius and a is the rotation parameter. The associated electromagnetic field is due to the potential one-form \(A_\mu =-\frac{q r}{\rho }\left( dt-\frac{a\sin ^2\theta }{\Sigma }d\phi \right) \), where the parameter q is related to the charge of black hole \(Q=\frac{q}{\Sigma }\). This metric satisfies the vacuum Einstein equations \(R_{\mu \nu }=-3 {g_{\mu \nu }}/{l^2}\). The outer horizon is located at the radius \(r=r_+\) which is determined by the equation

$$\begin{aligned} 2m=\frac{(r_+^2+a^2)(r_+^2+l^2)}{r_+l^2}+\frac{q^2}{r_+}. \end{aligned}$$
(3)

The entropy of the system in thermal equilibrium can be derived in Planck’s unit as

$$\begin{aligned} S_0=\frac{A}{4}=\frac{\pi (r^2_++a^2)}{\Sigma }. \end{aligned}$$
(4)

The Hawking temperature is given by [14]

$$\begin{aligned} T=\frac{\kappa }{2\pi }=\frac{3r^4_++r_+^2l^2+a^2r_+^2-l^2(a^2+q^2)}{4\pi l^2r_+(r_+^2+a^2)}, \end{aligned}$$
(5)

where \(\kappa \) refers to the surface gravity. These black holes have the following roots for the temperature:

$$\begin{aligned} r|_T=\pm \left[ \frac{-a^2-l^2\pm \sqrt{(a^2+l^2)^2 +12l^2(a^2+q^2)}}{6}\right] ^{1/2}. \end{aligned}$$
(6)

It is evident that the values in the square bracket are both positive and negative. So, the existence of a real valued roots for the temperature is limited to the following condition \(-a^2-l^2\pm \sqrt{(a^2+l^2)^2 +12l^2(a^2+q^2)}>0\). Here, we see that for Kerr-AdS black holes two real valued root exist for the temperature.

The other thermodynamic quantities (in Planck units) are given by [14]

$$\begin{aligned} \Omega _H= & {} -\left. \frac{g_{t\phi }}{g_{\phi \phi }}\right| _{r=r_+} =\frac{a(l^2+r_+^2)}{l^2(a^2+r_+^2)},\ \ \ J=\frac{a(r_+^2+a^2)(1+r_+^2l^{-2})+aq^2}{2r_+\Sigma ^2}, \nonumber \\ M_0= & {} \frac{(r_+^2+a^2)(1+r_+^2l^{-2})+q^2}{2r_+\Sigma ^2},\ \ \ \Phi =\frac{qr_+}{r_+^2+a^2}, \end{aligned}$$
(7)

where \(\Omega _H\), J, \(M_0\) and \(\Phi \) denote the horizon angular velocity measured relative to a frame that is non-rotating at infinity, angular momentum, the physical mass (or energy) and the electric potential measured at infinity with respect to the horizon of the black hole, respectively.

2.1 Thermodynamics with first-order correction

In this section, we study the effects of quantum corrections to the thermodynamics of rotating black hole upto first-order. We assume the system of black hole follows the canonical ensemble. In this regard, let us start by defining the density of states with fixed energy as [15, 16]

$$\begin{aligned} \rho =\frac{1}{2\pi i}\int _{c-i\infty }^{c+i\infty }e^{\mathcal{S}(\beta )}d\beta , \end{aligned}$$
(8)

where \(\mathcal{S}(\beta )\) is the exact entropy as a function of temperature \(T=1/\beta \). The above complex integral can be solved by the method of steepest descent around the saddle point \(\beta _0\). Now, by expanding the exact entropy around the saddle point \(\beta =\beta _0\), we have

$$\begin{aligned} \mathcal{S}=S_0+\frac{1}{2}(\beta -\beta _0)^2 S_0''+ \text{(higher } \text{ order } \text{ terms) }, \end{aligned}$$
(9)

where \(S_0=\mathcal{S}(\beta _0)\) refers the zeroth-order entropy and \(S_0'':=\left( \frac{\partial ^2 \mathcal{S}(\beta )}{\partial \beta ^2}\right) _{\beta =\beta _0}\). Inserting this value of \(\mathcal{S}\) given in (9) to (8), and performing integral we get [2]

$$\begin{aligned} \rho =\frac{e^{S_0}}{\sqrt{2\pi S_0''}}. \end{aligned}$$
(10)

This leads to microcanonical entropy

$$\begin{aligned} S=S_0+\alpha \log S_0''+.... . \end{aligned}$$
(11)

where \(\alpha \) is a correction coefficient. By considering most general form of \(\mathcal{S}\), the \(S_0''\) can be determined. Therefore, the generic expression for leading order corrections to Bekenstein-Hawking formula is given by [2]

$$\begin{aligned} S= & {} S_{0} + \alpha \ln (S_{0} T_H^{2}),\nonumber \\= & {} S_{0} + \alpha \ln S_{0}+ 2\alpha \ln T_H. \end{aligned}$$
(12)

The first law of thermodynamics for black holes and Smarr-Gibbs-Duhem relation read,

$$\begin{aligned} dM= & {} TdS+\Omega _H dJ+VdP+\Phi dQ,\nonumber \\ M= & {} 2TS+2\Omega J+ \Phi Q-2PV. \end{aligned}$$
(13)

Here, the negative cosmological constant can be interpreted as the positive thermodynamic pressure

$$\begin{aligned} P=-\frac{\Lambda }{8\pi }=\frac{3}{8\pi l^2}. \end{aligned}$$
(14)

Now, plugging the values of T and \(S_0\) from (5) and (4) respectively to the relation (12), we get the leading-order corrected entropy is given by

$$\begin{aligned} S= & {} \frac{\pi (r^2_++a^2)}{\Sigma }+\alpha \log \frac{\pi (r^2_++a^2)}{\Sigma }\nonumber \\&+ 2 \alpha \log \left[ \frac{3r^4_++r_+^2l^2+a^2r_+^2-l^2(a^2+q^2)}{4\pi l^2r_+(r_+^2+a^2)} \right] . \end{aligned}$$
(15)
Fig. 1
figure 1

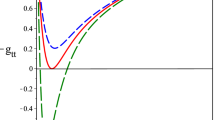
Left: Entropy versus the black hole horizon for \(a=1, q=1\) and \(l=2\). Right: Entropy versus the black hole horizon for \(a=1, q=10\) and \(l=2\). Here, \(\alpha =0\) denoted by blue line, \(\alpha =-\,0.5\) denoted by green line, \(\alpha =0.5\) denoted by red line, and \(\alpha =-\,1.5\) denoted by black line

Full size image

The effects of thermal fluctuation on entropy can be seen in Fig. 1. We see that entropy is an increasing function for large black holes as well as if the system is in equilibrium. Due to thermal fluctuation, the entropy does not exist for smaller black holes. As charge increases the entropy does not occur for even larger black holes. For very large black holes, the thermal fluctuation does not play an important role.

From the first expression of (13), the corrected physical mass for charged rotating black hole is calculated by

$$\begin{aligned} M= & {} \frac{(r_+^2+a^2)(1+r_+^2l^{-2})+q^2}{2r_+\Sigma ^2} +\alpha \frac{6a^4r_++6a^2r_+^3+2a^4r_+-2a^2l^2r_+-l^2q^2r_+}{4\pi l^2a^2(a^2+r_+^2)}\nonumber \\&-\,\alpha \frac{(8a^4+l^2q^2)}{4\pi l^2 a^3}\tan ^{-1}\left[ \frac{r_+}{a}\right] +\alpha \frac{3r^4_++r_+^2l^2+a^2r_+^2-l^2(a^2+q^2)}{2\pi l^2r_+(r_+^2+a^2)}. \end{aligned}$$
(16)
Fig. 2
figure 2

Left: Physical mass versus the black hole horizon for \(a=1, q=1\) and \(l=2\). Right: Physical mass versus the black hole horizon for \(a=1, q=10\) and \(l=2\). Here, \(\alpha =0\) denoted by blue line, \(\alpha =-\,0.5\) denoted by green line, \(\alpha =0.5\) denoted by red line, and \(\alpha =-\,1.5\) denoted by black line

Full size image

We plot Fig. 2 to see the behavior of physical mass with respect to horizon radius. Here, one can see that there exists a critical point for physical mass which increases as long as charge of the black hole increases. The mass is an decreasing function before this critical value of horizon radius and thereafter it is an increasing function. The correction terms with negative correction parameter increases and decreases the values of physical mass before and after the critical horizon radius respectively.

The geometrical volume for charged rotating AdS black hole in \(d=4\) is calculated by

$$\begin{aligned} V= \left( \frac{\partial M_0}{\partial P}\right) _{S_0}=\frac{4}{3} \frac{\pi r_+(r_+^2+a^2)}{\Sigma ^2}. \end{aligned}$$
(17)

Using definition, \(U=M-PV\), the internal energy is calculated by

$$\begin{aligned} U= & {} \frac{(r_+^2+a^2)(1+r_+^2l^{-2})+q^2}{2r_+\Sigma ^2} -\frac{r_+(r^2+a^2)}{2l^2\Sigma ^2}\nonumber \\&+\,\alpha \frac{6a^4r_++6a^2r_+^3+2a^4r_+-2a^2l^2r_+-l^2q^2r_+}{4\pi l^2a^2(a^2+r_+^2)}\nonumber \\&-\,\alpha \frac{(8a^4+l^2q^2)}{4\pi l^2 a^3}\tan ^{-1}\left[ \frac{r_+}{a}\right] +\alpha \frac{3r^4_++r_+^2l^2+a^2r_+^2-l^2(a^2+q^2)}{2\pi l^2r_+(r_+^2+a^2)}.\qquad \end{aligned}$$
(18)
Fig. 3
figure 3

Left: Internal energy versus the black hole horizon for \(a=1, q=1\) and \(l=2\). Right: Internal energy versus the black hole horizon for \(a=1, q=10\) and \(l=2\). Here, \(\alpha =0\) denoted by blue line, \(\alpha =-\,0.5\) denoted by green line, \(\alpha =0.5\) denoted by red line, and \(\alpha =-\,1.5\) denoted by black line

Full size image

We behavior of internal energy with respect to horizon radius can be seen in Fig. 3. We see that internal energy is a decreasing function of horizon radius for smaller black holes. There exists a critical value for internal energy which increases when charge increase of the black hole. The correction term due to thermal fluctuation with negative correction parameter \(\alpha \) increases and decreases the value of internal energy before and after critical point respectively. However, The correction term due to thermal fluctuation with positive correction parameter \(\alpha \) decreases and increases the value of internal energy before and after critical point respectively.

Once the expressions for Hawking temperature, entropy and physical mass are known, it is matter of calculation to evaluate the Helmholtz free energy: \(F=M-TS\). Hence, from (15) and (5), the first-order corrected Helmholtz free energy is calculated by

$$\begin{aligned} F= & {} \frac{1}{4r_+\Sigma ^2}\left( r_+^2 -r_+^4l^{-2}+3a^2 +2a^2r_+^2l^{-2}+3q^2\right. \nonumber \\&\left. +3a^2l^{-4}r_+^4+a^4l^{-4}r_+^2-a^4l^{-2}-a^2q^2l^{-2} \right) \nonumber \\&+\,\alpha \frac{6a^4r_++6a^2r_+^3+2a^4r_+-2a^2l^2r_+-l^2q^2r_+}{4\pi l^2a^2(a^2+r_+^2)}\nonumber \\&-\,\alpha \frac{(8a^4+l^2q^2)}{4\pi l^2 a^3}\tan ^{-1}\left[ \frac{r_+}{a}\right] +\, \alpha \frac{3r^4_++r_+^2l^2+a^2r_+^2-l^2(a^2+q^2)}{2\pi l^2r_+(r_+^2+a^2)}\nonumber \\&-\,\alpha \frac{3r^4_++r_+^2l^2+a^2r_+^2-l^2(a^2+q^2)}{4\pi l^2r_+(r_+^2+a^2)}\log \left[ \frac{\pi (r^2_++a^2)}{\Sigma } \right] \nonumber \\&-\,2\alpha \frac{3r^4_++r_+^2l^2+a^2r_+^2-l^2(a^2+q^2)}{4\pi l^2r_+(r_+^2+a^2)}\log \frac{3r^4_++r_+^2l^2+a^2r_+^2-l^2(a^2+q^2)}{4\pi l^2r_+(r_+^2+a^2)}.\nonumber \\ \end{aligned}$$
(19)

The effects of leading-order correction to Helmholtz free energy can be seen in Fig. 4. It can be seen that the behavior of Helmholtz free energy is decreasing for small black holes and increasing for larger black holes. The value of Helmholtz free energy is always positive. The higher charge increases the value of Helmholtz free energy. Unlike the internal energy, the correction term with negative \(\alpha \) increases the value of Helmholtz free energy always (before and after critical value).

Fig. 4
figure 4

Left: Helmholtz free energy versus the black hole horizon for \(a=1, q=1\) and \(l=2\). Right: Helmholtz free energy versus the black hole horizon for \(a=1, q=10\) and \(l=2\). Here, \(\alpha =0\) denoted by blue line, \(\alpha =-\,0.5\) denoted by green line, \(\alpha =0.5\) denoted by red line, and \(\alpha =-\,1.5\) denoted by black line

Full size image

Since mass of the black hole M is interpreted as the enthalpy, we have the following expression for the Gibbs free energy : \(G=M-TS-\Phi Q\), which can be used to calculate the maximum of reversible work that may be performed by the system of rotating black hole. This is calculated by

$$\begin{aligned} G= & {} \frac{1}{4r_+\Sigma ^2}\left( r_+^2 -r_+^4l^{-2}+3a^2 +2a^2r_+^2l^{-2}+3q^2\right. \nonumber \\&\left. +\,3a^2l^{-4}r_+^4+a^4l^{-4}r_+^2-a^4l^{-2}-a^2q^2l^{-2} \right) \nonumber \\&-\,\frac{q^2r_+}{\Sigma (r_+^2+a^2)} +\alpha \frac{6a^4r_++6a^2r_+^3+2a^4r_+-2a^2l^2r_+-l^2q^2r_+}{4\pi l^2a^2(a^2+r_+^2)}\nonumber \\&-\,\alpha \frac{(8a^4+l^2q^2)}{4\pi l^2 a^3}\tan ^{-1}\left[ \frac{r_+}{a}\right] \nonumber \\&+\, \alpha \frac{3r^4_++r_+^2l^2+a^2r_+^2-l^2(a^2+q^2)}{2\pi l^2r_+(r_+^2+a^2)}\nonumber \\&-\,\alpha \frac{3r^4_++r_+^2l^2+a^2r_+^2-l^2(a^2+q^2)}{4\pi l^2r_+(r_+^2+a^2)}\log \left[ \frac{\pi (r^2_++a^2)}{\Sigma } \right] \nonumber \\&-\,2\alpha \frac{3r^4_++r_+^2l^2+a^2r_+^2-l^2(a^2+q^2)}{4\pi l^2r_+(r_+^2+a^2)}\log \frac{3r^4_++r_+^2l^2+a^2r_+^2-l^2(a^2+q^2)}{4\pi l^2r_+(r_+^2+a^2)}.\nonumber \\ \end{aligned}$$
(20)
Fig. 5
figure 5

Left: Gibbs free energy versus the black hole horizon for \(a=1, q=1\) and \(l=2\). Right: Gibbs free energy versus the black hole horizon for \(a=1, q=10\) and \(l=2\). Here, \(\alpha =0\) denoted by blue line, \(\alpha =-\,0.5\) denoted by green line, \(\alpha =0.5\) denoted by red line, and \(\alpha =-\,1.5\) denoted by black line

Full size image

The graphical analysis of Gibbs free energy for the rotating black hole can be seen in Fig. 5. Here, we observe that correction terms decreases the value of Gibbs free energy for smaller black hole. As long as charge of black hole increases, the correction terms due to thermal fluctuation decrease the Gibbs free energy. For large black hole, the correction terms do not effect the Gibbs free energy much.

2.2 Van der Waals fluid duality

We realize that the rotating black holes behave as Van der Walls fluids. The Van der Walls equation describes the behavior of real fluids and modifies the ideal gas equation of states as

$$\begin{aligned} \left( P+\frac{\mathfrak {a}}{v^2}\right) (v-\mathfrak {b})=T \Rightarrow P=\frac{T}{v-\mathfrak {b}}- \frac{\mathfrak {a}}{v^2}, \end{aligned}$$
(21)

where \(v=V/N\) is the specific volume of the fluid. Here \(N=A/l_P^2\) denotes the number of degrees of freedom associated with the black hole horizon (plank length) \(l_P=\sqrt{G\bar{h}/c^2}\). The constant \(\mathfrak {a} > 0\) is a measure of the interaction between the molecules of a given fluid while the constant \(\mathfrak {b} > 0\) refers to the nonzero size of them. The expression for specific volume [17] is given by

$$\begin{aligned} v= 6\frac{V}{A}=2\frac{r_+}{\Sigma }. \end{aligned}$$
(22)

as in the geometric units (\(G=\hbar =c=k_B=1\)) Planck length is unit. Utilizing the relations (14) and (22), we can plot graph between pressure and specific volume. From the Fig. 6, the typical behavior of the \(P-v\) diagram corresponding to the van der Waals fluid can be seen. The pressure is negative for small black holes with respect to specific volume. To study critical phenomena and van der Waals behavior, we compute the following equation of state:

$$\begin{aligned} P=\frac{3(r_+^2+a^2)T}{2r_+(3r_+^2+a^2)}+\frac{3(a^2+q^2)}{8\pi r_+^2(3r_+^2+a^2)}-\frac{3}{8\pi (3r_+^2+a^2)(r_+^2+a^2)}. \end{aligned}$$
(23)

The critical points can be obtained in this case from conditions \(\left( \frac{\partial P}{\partial r_+}\right) _T=0\) and \(\left( \frac{\partial ^2 P}{\partial r_+^2}\right) _T=0\).

Fig. 6
figure 6

Left: Pressure versus the specific volume for \(a=1\) and \(r_+=1\). Right: Pressure versus the specific volume for \(a=1\) and \(r_+=10\)

Full size image

2.3 Stability

The stability and phase transition of a thermal system can be studied by analyzing the specific heat of the system. The specific heat at constant charge can be calculated from following relation:

$$\begin{aligned} C_Q=T\left( \frac{\partial S}{\partial T}\right) _Q. \end{aligned}$$
(24)

From the above definition, the first-order corrected specific heat for a charge rotating black hole is derived by

$$\begin{aligned} C_Q= & {} \frac{2 \pi r_+^2 \left( a^2+r_+^2\right) \left[ a^2 \left( r_+^2-l^2\right) +l^2 (Q \Sigma +r) (r_+-Q \Sigma )+3 r_+^4\right] }{\Sigma \left[ a^4 \left( l^2+r_+^2\right) +a^2 \left( l^2 \left( Q^2 \Sigma ^2+4 r_+^2\right) +8 r^4\right) -l^2 \left( r_+^4-3 Q^2 r_+^2 \Sigma ^2\right) +3 r_+^6\right] }\nonumber \\&+\,2\alpha \frac{ r_+^2 \left[ a^2 \left( r_+^2-l^2\right) +l^2 (Q \Sigma +r) (r_+-Q \Sigma )+3 r_+^4\right] }{ \left[ a^4 \left( l^2+r_+^2\right) +a^2 \left( l^2 \left( Q^2 \Sigma ^2+4 r_+^2\right) +8 r_+^4\right) -l^2 \left( r_+^4-3 Q^2 r_+^2 \Sigma ^2\right) +3 r_+^6\right] }\nonumber \\&+\,2\alpha . \end{aligned}$$
(25)
Fig. 7
figure 7

Left: Specific heat versus the black hole horizon for \(a=1, q=1\) and \(l=2\). Right: Specific heat versus the black hole horizon for \(a=1, q=10\) and \(l=2\). Here, \(\alpha =0\) denoted by blue line, \(\alpha =-0.5\) denoted by green line, \(\alpha =0.5\) denoted by red line, and \(\alpha =-1.5\) denoted by black line

Full size image

In Fig. 7, we see that the behavior of specific heat of a charged rotating black holes. This diagram suggests that the phase transition occurs for such black hole. The specific heat is negative for small black holes which suggests that small black holes are thermodynamically unstable. On the other hand, the specific heat is always positive for larger black holes which means these black holes are in stable phase. Some stability also occurs for the small black holes due to the correction term with positive correction parameter. However, the correction term with negative \(\alpha \) makes small black holes more unstable.

The divergences occurs at \(l=a\) and

$$\begin{aligned} a^4 \left( l^2+r_+^2\right) +a^2 l^2 \left( Q^2 \Sigma ^2+4 r_+^2\right) +8a^2 r_+^4 -l^2 \left( r_+^4-3 Q^2 r_+^2 \Sigma ^2\right) +3 r_+^6=0.\nonumber \\ \end{aligned}$$
(26)

This can be solved easily and the real solutions are

$$\begin{aligned} r=\pm \left( \frac{\root 3 \of {2}(55 a^4-52 a^2 l^2+ l^4-27 l^2 Q^2 \Sigma ^2)}{9 \root 3 \of {\sqrt{\beta ^2+\gamma }+\beta }} +\frac{l^2-8 a^2}{9}+\frac{\root 3 \of {\sqrt{\beta ^2 +\gamma }+\beta }}{9 \root 3 \of {2}}\right) ^{1/2},\nonumber \\ \end{aligned}$$
(27)

where \(\beta \) and \(\gamma \) are

$$\begin{aligned} \beta= & {} -808 a^6+978 a^4 l^2-156 a^2 l^4+405 a^2 l^2 Q^2 \Sigma ^2+2 l^6-81 l^4 Q^2 \Sigma ^2,\nonumber \\ \gamma= & {} 4 \left( -55 a^4+52 a^2 l^2-l^4+27 l^2 Q^2 \Sigma ^2\right) ^3. \end{aligned}$$
(28)

Here, we assumed that the overall value of expressions inside the bracket in (27) is positive.

3 Concluding remarks

In this paper, we have considered a charged rotating AdS black hole with their thermodynamical quantities when system is in equilibrium and studied the effects of leading-order corrections stemming from thermal fluctuations of charged rotating black holes on equations of states. In particular, we have derived the Hawking temperature and logarithmic correction to the entropy first which leads to correction to other thermodynamical quantities. We found that entropy is an increasing function of horizon radius for large black holes when system is in equilibrium. Due to thermal fluctuation, the entropy does not depend on the horizon radius for smaller black holes. We found that for very large black holes, the thermal fluctuation does not effect significantly. In our analysis, the negative cosmological constant is assumed as the positive thermodynamic pressure. After having expressions of leading-order corrected entropy, the temperature, horizon angular velocity, angular momentum charge and pressure, we have derived the first-order corrected physical mass of the system from the first-law of thermodynamics. We observed that there exists a critical value physical mass which increases as long as charge of the black hole increases. From the plot, one can see that the mass is a decreasing function before the critical point and thereafter it is an increasing function. The correction terms with negative correction parameter increases values of physical mass before the critical point and decreases the physical mass after the critical point. Utilizing the standard relation between physical mass and geometrical volume, we have calculated the geometrical volume of the charged rotating AdS black holes. We have evaluated the leading-order correction to internal energy also. In this regard, we have found that internal energy is a decreasing function of horizon radius for smaller black holes. If fact, there exists a critical value for internal energy as well which increases when charge of the black hole increases. The correction term with negative correction parameter originated from the thermal fluctuation increases the value of internal energy before the critical point and decreases tits value after the critical point. Moreover, we have calculated the corrected value of Helmholtz free energies of the system due to thermal fluctuations. It is observed that the Helmholtz free energy is decreasing function of horizon radius for small black holes and increasing function for larger black holes. The value of Helmholtz free energy is found always positive. The higher value of charge increases the value of Helmholtz free energy. Unlike the internal energy, the correction term with negative \(\alpha \) always increases the value of Helmholtz free energy. We have estimated the correction to Gibbs free energy as well.

We have studied the Van der waals fluid duality to charged rotating black holes and analyzed the typical behavior of the \(P-v\) diagram corresponding to the van der Waals fluid. The stability of such black holes is also checked. We have found that a phase transition occurs for such black holes. For small black holes, the specific heat takes negative values which suggests that small black holes are thermodynamically unstable phase. However, the specific heat is found always positive for larger black holes which means that these black holes are in stable phase. The stability also occurs for the small black holes in case of thermal fluctuations also when correction parameter takes positive values. The correction term with negative correction parameter originated from thermal fluctuations introduces more instabilities to small black holes.