P–v criticality in the extended phase space of a noncommutative geometry inspired Reissner–Nordström black hole in AdS space-time

Abstract

The P–v criticality and phase transition in the extended phase space of a noncommutative geometry inspired Reissner–Nordström (RN) black hole in Anti-de Sitter (AdS) space-time are studied, where the cosmological constant appears as a dynamical pressure and its conjugate quantity is thermodynamic volume of the black hole. It is found that the P–v criticality and the small black hole/large black hole phase transition appear for the noncommutative RN-AdS black hole. Numerical calculations indicate that the noncommutative parameter affects the phase transition as well as the critical temperature, horizon radius, pressure and ratio. The critical ratio is no longer universal, which is different from the result in the van de Waals liquid–gas system. The nature of phase transition at the critical point is also discussed. Especially, for the noncommutative geometry inspired RN-AdS black hole, a new thermodynamic quantity $\varPsi$ conjugate to the noncommutative parameter $\theta$ has to be defined further, which is required for consistency of both the first law of thermodynamics and the corresponding Smarr relation.

1 Introduction

In recent years, noncommutative geometry inspired black holes aroused a lot of interest among researchers because coordinate noncommutativity is supposed to remove the so-called paradox of black hole information loss [1]. Nicolini et al. [2] first found a noncommutative geometry inspired Schwarzschild black hole solution in four dimensions. In their paper, the effect of noncommutativity is incorporated in the mass term of the gravitational source by taking the mass density to be a Gaussian mass distribution instead of the conventional Dirac delta function. Subsequently, the model was extended to include the electric charge [3], rotation [4] and extra-spatial dimensions [5, 6]. From then on, many work on noncommutative geometry inspired black holes were done. Nozari and Mehdipour investigated Parikh-Wilczek tunneling of noncommutative black holes [7,8,9,10]; Giri [11] found out and calculated the asymptotic quasinormal modes of a noncommutative geometry inspired Schwarzschild black hole; the authors of Ref. [12] and the authors of Ref. [13] studied the influence of the noncommutative parameter on the strong field gravitational lensing in the Schwarzschild and RN black hole space-time, respectively; the authors of Refs. [14,15,16,17,18,19] studied black hole thermodynamics in noncommutative spaces (for a comprehensive review of noncommutative geometry inspired black holes, see Ref. [20] and references therein).

On the other hand, in recent years, the idea of including the variation of the cosmological constant $\varLambda$ in the first law of black hole thermodynamics was presented [21,22,23,24,25]. In particular, since the seminal paper of Kubizňák and Mann [26] was published, this idea has attained increasing attention  [27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62]. In the case of an asymptotically AdS black hole in four dimensions, using geometric units $G_{N}=c=\hbar =k=1$, the cosmological constant was treated as a thermodynamic pressure with

$$\begin{aligned} P=-\frac{1}{8\pi }\varLambda =\frac{3}{8\pi }\frac{1}{l^{2}}, \end{aligned}$$

(1)

and and its conjugate quantity as a thermodynamic volume with¹

$$\begin{aligned} V=\left( \frac{\partial M}{\partial P}\right) _{S,Q_{i},J_{k}}. \end{aligned}$$

(2)

Kubizňák and Mann [26] completed the analogy of the RN-AdS black hole with the liquid–gas system. They also calculated the critical exponents and found that the phase transition of the RN-AdS black hole in the extended (including pressure and volume as thermodynamic variables) phase space has the same critical exponents as the van der Waals system. Later their work was generalized to different AdS black hole backgrounds [27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62], and some phenomena were further found, such as reentrant phase transitions [33, 37,38,39, 49, 60], triple points [37, 49] and isolated critical points [49, 51, 60]. For a review, see Ref. [37].

In this paper, we are going to study the P–v criticality and phase transition in the extended phase space of a four dimensional noncommutative geometry inspired RN black hole in AdS space-time. The motivations are as follows: (i) we want to see whether critical phenomena and phase transitions appear or not for the noncommutative geometry inspired RN-AdS black hole. (ii) If P–v criticality and phase transitions appear, is there any effect of the noncommutative parameter on P–v criticality and phase transitions?

The paper is organized as follows: In Sect. 2, we briefly review some basic facts about the noncommutative geometry inspired RN-AdS black hole. In Sect. 3, we will discuss the extended first law of black hole thermodynamics and the corresponding Smarr relation. In Sect. 4, we will analyze P–v criticality in the extended phase space of the noncommutative RN-AdS black hole. In Sect. 5, we will discuss the phase transition at the critical point. Finally, a summary is given in Sect. 6.

2 A brief review of the noncommutative geometry inspired RN-AdS black hole

In the noncommutative geometry inspired RN-AdS black hole model [3, 9], noncommutativity is incorporated by introducing Gaussian smeared density distribution $\rho _{m}$,

$$\begin{aligned} \rho _{m} =\frac{M}{(4\pi \theta )^{\frac{3}{2}}}e^{-\frac{r^{2}}{4\theta }}, \end{aligned}$$

(3)

and Gaussian smeared density distribution $\rho _{c}$,

$$\begin{aligned} \rho _{c} =\frac{Q}{(4\pi \theta )^{\frac{3}{2}}}e^{-\frac{r^{2}}{4\theta }}, \end{aligned}$$

(4)

as the mass density and the charge density of a gravitational source, respectively. Here M and Q are the total mass and the total charge of the source, respectively, and $\theta$ is a positive parameter with dimension of length squared, $\sqrt{\theta }\sim l_{P}$ where $l_{P}=\frac{G_{4}\hbar }{c^{3}}$ is the Plank length.

By solving Einstein equations

$$\begin{aligned} R_{\mu \nu }-\frac{1}{2}Rg_{\mu \nu } = 8\pi T_{\mu \nu }+\frac{1}{l^{2}}g_{\mu \nu }, \end{aligned}$$

(5)

where l is related with the cosmological constant $\varLambda$ by $\varLambda = -\frac{1}{l^{2}}$, one can find that the metric describing the noncommutative geometry inspired RN-AdS black hole is

$$\begin{aligned} ds^{2}=-h_{\theta }(r)dt^{2}+\frac{dr^{2}}{h_{\theta }(r)}+r^{2}d\Omega ^{2}, \end{aligned}$$

(6)

where $h_{\theta }(r)$ is given by

$$\begin{aligned} h_{\theta }(r)=1-\frac{4M}{r\sqrt{\pi }}\gamma \Bigg (\frac{3}{2},\frac{r^{2}}{4\theta }\Bigg )+\frac{Q^{2}}{\pi r^{2}}\Bigg (F_{\theta }(r) +\sqrt{\frac{2}{\theta }} r\gamma \Bigg (\frac{3}{2},\frac{r^{2}}{4\theta }\Bigg )\Bigg ) +\frac{r^{2}}{l^{2}}. \end{aligned}$$

(7)

In the above equation, the lower incomplete Gamma function is defined to be

$$\begin{aligned} \gamma (a,x)=\int _{0}^{x}t^{a-1}e^{-t}dt, \end{aligned}$$

(8)

and $F_{\theta }(r)$ is defined as

$$\begin{aligned} F_{\theta }(r)\equiv \gamma ^{2}\left( \frac{1}{2},\frac{r^{2}}{4\theta }\right) -\frac{r}{\sqrt{2\theta }}\gamma \left( \frac{1}{2},\frac{r^{2}}{2\theta }\right) . \end{aligned}$$

(9)

In the limit of $\frac{r}{\sqrt{\theta }}\rightarrow \infty$, (7) reduces to the form of RN-AdS black hole.

The temperature of the black hole is given by

$$\begin{aligned} T= & {} \frac{1}{4\pi }\frac{\partial h_{\theta }(r)}{\partial r}\Big |_{r=r_{+}}\nonumber \\= & {} \frac{1}{4\pi r_{+}}\left\{ 1+\frac{r^{2}_{+}}{l^{2}}\left( 3-r_{+}\frac{\gamma '\Bigg (\frac{3}{2},\frac{r^{2}_{+}}{4\theta }\Bigg )}{\gamma \Bigg (\frac{3}{2},\frac{r^{2}_{+}}{4\theta }\Bigg )}\right) -r_{+} \frac{\gamma '\Bigg (\frac{3}{2},\frac{r^{2}_{+}}{4\theta }\Bigg )}{\gamma \left( \frac{3}{2},\frac{r^{2}_{+}}{4\theta }\right) }\right. \nonumber \\&-\frac{Q^{2}}{\pi r^{2}_{+}}\left[ \Bigg (F_{\theta }(r_{+})+\sqrt{\frac{2}{\theta }}r_{+} \gamma \Bigg (\frac{3}{2},\frac{r^{2}_{+}}{4\theta }\Bigg )\Bigg )\left( 1+r_{+} \frac{\gamma '\left( \frac{3}{2},\frac{r^{2}_{+}}{4\theta }\right) }{\gamma (\frac{3}{2},\frac{r^{2}_{+}}{4\theta })}\right) \right. \nonumber \\&-2r_{+}\gamma \Bigg (\frac{1}{2},\frac{r^{2}_{+}}{4\theta }\Bigg )\gamma ' \Bigg (\frac{1}{2},\frac{r^{2}_{+}}{4\theta }\Bigg ) +\frac{r^{2}_{+}}{\sqrt{2\theta }}\gamma '\Bigg (\frac{1}{2},\frac{r^{2}_{+}}{2\theta }\Bigg ) +\frac{r_{+}}{\sqrt{2\theta }}\gamma \Bigg (\frac{1}{2},\frac{r^{2}_{+}}{2\theta }\Bigg )\nonumber \\&\left. \left. -\sqrt{\frac{2}{\theta }}r^{2}_{+}\gamma '\Bigg (\frac{3}{2},\frac{r^{2}_{+}}{4\theta }\Bigg ) -\sqrt{\frac{2}{\theta }}r_{+}\gamma \Bigg (\frac{3}{2},\frac{r^{2}_{+}}{4\theta }\Bigg ) \right] \right\} . \end{aligned}$$

(10)

Here $r_{+}$ is the outer horizon radius of the black hole and

$$\begin{aligned} \gamma '\left( \frac{3}{2},\frac{r^{2}_{+}}{4\theta }\right) =\frac{r^{2}_{+}}{4\theta ^{\frac{3}{2}}}e^{-\frac{r^{2}_{+}}{4\theta }},~~~ \gamma '\left( \frac{1}{2},\frac{r^{2}_{+}}{4\theta }\right) =\frac{e^{-\frac{r^{2}_{+}}{4\theta }}}{\sqrt{\theta }},~~~ \gamma '\left( \frac{1}{2},\frac{r^{2}_{+}}{2\theta }\right) =\sqrt{\frac{2}{\theta }} e^{-\frac{r^{2}_{+}}{2\theta }}, \quad \end{aligned}$$

(11)

where the prime denotes the derivative with respect to $r_{+}$.

The mass of the black hole M can be expressed as

$$\begin{aligned} M=\frac{\sqrt{\pi }r_{+}}{4\gamma \Bigg (\frac{3}{2},\frac{r_{+}^{2}}{4\theta }\Bigg )}\Bigg [1+\frac{Q^{2}}{\pi r^{2}_{+}}\Bigg (F_{\theta }(r_{+})+ \sqrt{\frac{2}{\theta }}r_{+} \gamma \Bigg (\frac{3}{2},\frac{r^{2}_{+}}{4\theta }\Bigg )\Bigg ) +\frac{r^{2}_{+}}{l^{2}}\Bigg ]. \end{aligned}$$

(12)

The entropy of the black hole can be obtained as

$$\begin{aligned} S=\frac{A}{4} =\pi r^{2}_{+}, \end{aligned}$$

(13)

where A is the horizon area of the black hole.

3 The extended first law of black hole thermodynamics and the corresponding Smarr relation

In order to analyze whether critical phenomena occur or not in the extended phase space, we identify the pressure with

$$\begin{aligned} P=-\frac{1}{8\pi }\varLambda =\frac{3}{8\pi }\frac{1}{l^{2}}\, \end{aligned}$$

(14)

and consider the mass of the black hole M to be a function of entropy S, pressure P, charge Q and noncommutative parameter $\theta$, $M=M(S,P,Q,\theta )$ (see (12), (13) and (14)). One can check both the extended first law of black hole thermodynamics

$$\begin{aligned} dM=TdS+VdP+\varPhi dQ+\varPsi d\theta \end{aligned}$$

(15)

and the generalized Smarr relation

$$\begin{aligned} M=2TS-2VP+\varPhi Q+2\varPsi \theta \end{aligned}$$

(16)

hold for the noncommutative geometry inspired RN-AdS black hole.² Here,

$$\begin{aligned} V= & {} \Bigg (\frac{\partial M}{\partial P}\Bigg )_{S,Q,\theta }=\frac{2\pi ^{\frac{3}{2}}r^{3}_{+}}{3\gamma (\frac{3}{2},\frac{r_{+}^{2}}{4\theta })}, \end{aligned}$$

(17)

$$\begin{aligned} \varPhi= & {} \Bigg (\frac{\partial M}{\partial Q}\Bigg )_{S,P,\theta } =\frac{Q}{2\sqrt{\pi }r_{+}\gamma \Bigg (\frac{3}{2},\frac{r_{+}^{2}}{4\theta }\Bigg )}\Bigg (F_{\theta }(r_{+})+ \sqrt{\frac{2}{\theta }}r_{+} \gamma \Bigg (\frac{3}{2},\frac{r^{2}_{+}}{4\theta }\Bigg )\Bigg ) \end{aligned}$$

(18)

is the electric potential measured at infinity with respect to the horizon of the black hole, and $\varPsi$ is a quantity we define further conjugate to the noncommutative parameter $\theta$ which is calculated as

$$\begin{aligned} \varPsi= & {} \Bigg (\frac{\partial M}{\partial \theta }\Bigg )_{S,P,Q}\nonumber \\= & {} -\frac{\sqrt{\pi }r_{+}}{4}\Bigg [1+\frac{8\pi r^{2}_{+}P}{3}+\frac{Q^{2}}{\pi r^{2}_{+}}\Bigg (F_{\theta }(r_{+}) +\sqrt{\frac{2}{\theta }}r_{+}\gamma \Bigg (\frac{3}{2},\frac{r^{2}_{+}}{4\theta }\Bigg )\Bigg )\Bigg ] \frac{\dot{\gamma }\Bigg (\frac{3}{2},\frac{r_{+}^{2}}{4\theta }\Bigg )}{\Bigg [\gamma \Bigg (\frac{3}{2},\frac{r_{+}^{2}}{4\theta }\Bigg )\Bigg ]^{2}}\nonumber \\&+\frac{Q^{2}}{4\sqrt{\pi }r_{+}\gamma \Bigg (\frac{3}{2},\frac{r_{+}^{2}}{4\theta }\Bigg )} \Bigg [2\gamma \Bigg (\frac{1}{2},\frac{r_{+}^{2}}{4\theta }\Bigg ) \dot{\gamma }\Bigg (\frac{1}{2},\frac{r_{+}^{2}}{4\theta }\Bigg ) +\frac{r_{+}}{2\sqrt{2}\theta ^{\frac{3}{2}}}\gamma \Bigg (\frac{1}{2}, \frac{r_{+}^{2}}{2\theta }\Bigg )\nonumber \\&-\frac{r_{+}}{\sqrt{2\theta }}\dot{\gamma }\Bigg (\frac{1}{2},\frac{r_{+}^{2}}{2\theta }\Bigg ) -\frac{\sqrt{2}}{2}\frac{r_{+}}{\theta ^{\frac{3}{2}}}\gamma \Bigg (\frac{3}{2},\frac{r^{2}_{+}}{4\theta }\Bigg ) +\sqrt{\frac{2}{\theta }}r_{+}\dot{\gamma }\Bigg (\frac{3}{2},\frac{r^{2}_{+}}{4\theta }\Bigg )\Bigg ] \end{aligned}$$

(19)

where

$$\begin{aligned}&\dot{\gamma }\left( \frac{3}{2},\frac{r^{2}_{+}}{4\theta }\right) =-\frac{r^{3}_{+}}{8\theta ^{\frac{5}{2}}}e^{-\frac{r^{2}_{+}}{4\theta }} =-\frac{r_{+}}{2\theta }\gamma '\left( \frac{3}{2},\frac{r^{2}_{+}}{4\theta }\right) ,\nonumber \\&\dot{\gamma }\left( \frac{1}{2},\frac{r^{2}_{+}}{4\theta }\right) =-\frac{r_{+}}{2\theta ^{\frac{3}{2}}}e^{-\frac{r^{2}_{+}}{4\theta }} =-\frac{r_{+}}{2\theta }\gamma '\left( \frac{1}{2},\frac{r^{2}_{+}}{4\theta }\right) ,\nonumber \\&\dot{\gamma }\left( \frac{1}{2},\frac{r^{2}_{+}}{2\theta }\right) =-\frac{r_{+}}{\sqrt{2}\theta ^{\frac{3}{2}}} e^{-\frac{r^{2}_{+}}{2\theta }} =-\frac{r_{+}}{2\theta }\gamma '\left( \frac{1}{2},\frac{r^{2}_{+}}{2\theta }\right) , \end{aligned}$$

(20)

with the dot denoting the derivative with respect to $\theta$.

We want to stress that even in the case when the cosmological constant $\varLambda$ and the noncommutative parameter $\theta$ are not varied in the first law of black hole thermodynamics, i.e., we have $dM=TdS+\varPhi dQ$, the Smarr relation (16) is valid and the VP and $\varPsi \theta$ terms therein are necessary for it to hold.

4 P–v criticality in the extended phase space of the noncommutative geometry inspired RN-AdS black hole

In this paper, we limit ourselves to the case when the charge Q and the noncommutative parameter $\theta$ are fixed and consider P–v extended phase space, with v being the specific volume of the corresponding fluid (see below).

Substituting (14) into (10), we get the equation of state of the noncommutative geometry inspired RN-AdS black hole

$$\begin{aligned} P= & {} \frac{3\gamma (\frac{3}{2},\frac{r^{2}_{+}}{4\theta })}{3\gamma \Bigg (\frac{3}{2},\frac{r^{2}_{+}}{4\theta }\Bigg ) -\frac{r^{3}_{+}}{4\theta ^{\frac{3}{2}}}e^{-\frac{r^{2}_{+}}{4\theta }}}\Bigg \{\frac{T}{2r_{+}}-\frac{1}{8\pi r^{2}_{+}}+\frac{1}{8\pi r_{+}} \frac{\gamma '\Bigg (\frac{3}{2},\frac{r^{2}_{+}}{4\theta }\Bigg )}{\gamma \Bigg (\frac{3}{2},\frac{r^{2}_{+}}{4\theta }\Bigg )}\nonumber \\&+\frac{Q^{2}}{8\pi ^{2} r^{4}_{+}}\Bigg [\Bigg (F_{\theta }(r_{+})+ \sqrt{\frac{2}{\theta }}r_{+} \gamma \Bigg (\frac{3}{2},\frac{r^{2}_{+}}{4\theta }\Bigg )\Bigg )\Bigg (1+r_{+}\frac{\gamma '\Bigg (\frac{3}{2},\frac{r^{2}_{+}}{4\theta }\Bigg )}{\gamma \Bigg (\frac{3}{2},\frac{r^{2}_{+}}{4\theta }\Bigg )}\Bigg )\nonumber \\&-2r_{+}\gamma \Bigg (\frac{1}{2},\frac{r^{2}_{+}}{4\theta }\Bigg )\gamma '\Bigg (\frac{1}{2},\frac{r^{2}_{+}}{4\theta }\Bigg ) +\frac{r^{2}_{+}}{\sqrt{2\theta }}\gamma '\Bigg (\frac{1}{2},\frac{r^{2}_{+}}{2\theta }\Bigg ) +\frac{r_{+}}{\sqrt{2\theta }}\gamma \Bigg (\frac{1}{2},\frac{r^{2}_{+}}{2\theta }\Bigg )\nonumber \\&-\sqrt{\frac{2}{\theta }}r^{2}_{+}\gamma '\Bigg (\frac{3}{2},\frac{r^{2}_{+}}{4\theta }\Bigg ) -\sqrt{\frac{2}{\theta }}r_{+}\gamma \Bigg (\frac{3}{2},\frac{r^{2}_{+}}{4\theta }\Bigg )\Bigg ]\Bigg \}. \end{aligned}$$

(21)

and the corresponding conjugate quantity, thermodynamic volume (given by (17)), which satisfies the reverse isoperimetric inequality.³

The geometric equation of state (21) can be translated to a physical one

$$\begin{aligned} \mathrm {Press}=\frac{\hbar c}{l^{2}_{P}}P=\frac{\hbar c}{l^{2}_{P}}\frac{T}{2r_{+}}+\cdots =\frac{k\mathrm {Temp}}{2l^{2}_{P}r_{+}}+\cdots \end{aligned}$$

(25)

by using a dimensional analysis and $l_{P}=\frac{G_{4}\hbar }{c^{3}}$ [26]. Here “Press” and “Temp” denote the physical pressure and temperature, respectively.

Comparing (25) with Van der Waals equation

$$\begin{aligned} P=\frac{T}{v-b}-\frac{a}{v^{2}}\approx \frac{T}{v}+\frac{bT}{v^{2}}-\frac{a}{v^{2}}+O(v^{-3}), \end{aligned}$$

(26)

one can find that the specific volume v should be identified with

$$\begin{aligned} v=2r_{+}l^{2}_{P}. \end{aligned}$$

(27)

(27) show that the specific volume v is proportional to the horizon radius $r_{+}$, thus we will just use the horizon radius in the equation of state for the noncommutative geometry inspired RN-AdS black hole hereafter.

We know that the critical point in the P–v diagram is determined from

$$\begin{aligned} \frac{\partial P}{\partial r_{+}}\Big |_{r=r_{+c},T=T_{c}}=0,~~~\frac{\partial ^{2} P}{\partial r_{+}^{2}}\Big |_{r=r_{+c},T=T_{c}}=0 , \end{aligned}$$

(28)

where the subscript “c” denotes the quantity at the critical point. Although we can not, analytically, obtain the critical values of the horizon radius, temperature and pressure, we may investigate them numerically. The numerical results of these critical physical quantities for a fixed noncommutative parameter $\theta$ (using (21) and (28)) are shown in Table 1.

Table 1 Critical physical quantities for some values of the noncommutative parameter $\theta$. We have set $Q=1$

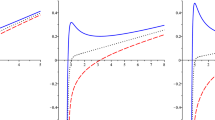
From Table 1, with increase of $\theta$, the critical horizon radius $r_{+c}$ increases, but both of the critical pressure $P_{c}$ and the critical temperature $T_{c}$ decrease. The dependence of the critical horizon radius, pressure and temperature on the noncommutative parameter are correspondingly depicted in Figs. 1, 2 and 3, respectively. In addition, the critical ratio $\frac{P_{c}r_{+c}}{T_{c}}$ is also shown in Table 1, and correspondingly, the dependence of the ratio on the noncommutative parameter is depicted in Fig. 4. This ratio increase with $\theta$, which is different from the result in the van de Waals system, where the universal critical ratio $\frac{P_{c}v_{c}}{T_{c}}=\frac{3}{8}=0.375$ [27].

Fig. 1

Critical horizon radius $r_{+c}$ for $\theta \in [0.1, 10]$. We have set $Q=1$

Fig. 2

Critical pressure $P_{c}$ for $\theta \in [0.1, 10]$. We have set $Q=1$

Fig. 3

Critical temperature $T_{c}$ for $\theta \in [0.1, 10]$. We have set $Q=1$

Fig. 4

Critical ratio $\frac{P_{c}r_{+c}}{T_{c}}$ for $\theta \in [0.1, 10]$. We have set $Q=1$

By the way, we point out, when the value of $\theta$ is very small, the numerical results of the critical specific volume, pressure and temperature are almost identical to those of RN-AdS black hole [26] that is because the noncommutative RN-AdS black hole approaches RN-AdS black hole in this case (see Sect. 2).

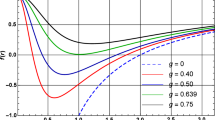
Using (21), we can plot the $P-r_{+}$ diagram for a geometry inspired noncommutative RN-AdS black hole in Fig. 5. Evidently, the $P-r_{+}$ diagram is exactly the same as the P–v diagram of the van der Waals liquid–gas system. Therefore, for $T<T_{c}$, there is a small-large black hole phase transition corresponding to the liquid–gas phase transition of the Van der Waals liquid–gas system, and such phase transition is of first order, while it becomes of second order at $T=T_{c}$ (see Sect. 5) just as in the case of the Van der Waals liquid–gas system.

Fig. 5

$P-r_{+}$ diagram of a noncommutative RN-AdS black hole. The dot-dashed line correspond to the “ideal gas” one-phase behavior for $T>T_{c}$, the critical isotherm $T=T_{c}$ is denoted by dashed line, and the solid line correspond to temperature smaller than the critical temperature. We have taken $\theta =0.1, 0.5, 1.0$ and 5.0 for graphs (a), (b), (c) and (d), respectively, and in addition, we have set $Q=1$ for all graphs

In order to further understand this phase transition, let us analyze the behavior of Gibbs free energy. In the extended phase space, the mass is interpreted as enthalpy rather than as internal energy, thus the Gibbs free energy is given by $G=M-TS$. The behavior of the Gibbs free energy is depicted in Fig. 6.

Fig. 6

Gibbs free energy of a noncommutative Schwarzschild-AdS black hole. The dot-dashed, dashed and solid lines correspond to the cases $\frac{P}{P_{c}}=2$, 1, and 0.2, respectively. I have taken $\theta =0.1, 0.5, 1.0$ and 5.0 for graphs (a), (b), (c) and (d), respectively, and in addition, we have set $Q=1$ for all graphs

From Fig. 6, we see that, for $P<P_{c}$, the Gibbs free energy with respect to temperature demonstrates the characteristic “swallow tail” behavior, therefore, there is a first order small-large black hole phase transition, and at $P=P_{c}$, the “swallow tail” disappears, corresponding to the critical point.

The two-phase coexistence line in the ($P-T$)-plane can be simply obtained by finding a curve in the ($P-T$)-plane for which the Gibbs free energy and temperature coincide for small and large black holes. This is shown in Fig. 7.

Fig. 7

Coexistence line of a noncommutative RN-AdS black hole. The critical point is shown by a small dot at the end of the coexistence line. We have set $Q=1$, and taken $\theta =0.1, 0.5$ and 1.0, respectively

From Fig. 7, one can find that the slope of the coexistence line increases with the increase of $\theta$.

Finally, we briefly mention here, that the critical exponents can been obtained by using a similar analysis done in Ref. [27] and their values coincide with those of the van de waals system.

Fig. 8

Plot of specific heat at constant pressure ($C_{P}$) against horizon radius ($r_{+}$). We have set $Q=1$, and taken $\theta =0.1, 0.5, 1.0$ and 5.0 for (a), (b), (c) and (d), respectively

5 Phase transition at the critical point

The specific heat at constant pressure is defined to be [63]

$$\begin{aligned} C_{P}\equiv C_{P,Q,\theta }=T\left( \frac{\partial S}{\partial T}\right) _{P,Q,\theta }, \end{aligned}$$

(29)

the volume expansion coefficient is defined to be

$$\begin{aligned} \alpha =\frac{1}{V}\left( \frac{\partial V}{\partial T}\right) _{P,Q,\theta } \end{aligned}$$

(30)

and the isothermal compressibility coefficient is defined to be

$$\begin{aligned} \kappa _{T}=-\frac{1}{V}\left( \frac{\partial V}{\partial P}\right) _{T,Q,\theta }. \end{aligned}$$

(31)

The behaviors of $C_{P}$, $\alpha$ and $\kappa _{T}$ are depicted in Figs. 8, 9 and 10, respectively. $C_{P}$, $\alpha$ and $\kappa _{T}$ diverge at the critical point, which allow us to conclude that there is indeed a continuous higher order phase transition at the critical point [63, 64].

Fig. 9

Plot of volume expansion coefficient ($\alpha$) against horizon radius ($r_{+}$). We have set $Q=1$, and taken $\theta =0.1, 0.5, 1.0$ and 5.0 for (a), (b), (c) and (d), respectively

Fig. 10

Plot of isothermal compressibility coefficient ($\kappa _{T}$) against horizon radius ($r_{+}$). We have set $Q=1$, and taken $\theta =0.1, 0.5, 1.0$ and 5.0 for (a), (b), (c) and (d), respectively

Using (29), (30), (31), (13), (17) and (21), one can check the two Ehrenfest’s equations

$$\begin{aligned}&\Bigg (\frac{\partial P}{\partial T}\Bigg )_{V,Q,\theta }=\frac{\alpha ^{(g)}-\alpha ^{(l)}}{\kappa ^{(g)}_{T}-\kappa ^{(l)}_{T}} =\frac{\varDelta \alpha }{\varDelta \kappa _{T}}, \end{aligned}$$

(32)

$$\begin{aligned}&\quad \Bigg (\frac{\partial P}{\partial T}\Bigg )_{S,Q,\theta }=\frac{C^{(g)}_{P}-C^{(l)}_{P}}{TV(\alpha ^{(g)}-\alpha ^{(l)})} =\frac{\varDelta C_{P}}{TV\varDelta \alpha } \end{aligned}$$

(33)

hold at the critical point. Here, the superscripts g and l denote large and small black hole phases, respectively. The validity of the two Ehrenfest’s equations further show that the RN-AdS black hole undergoes a second order phase transition at the critical point [64].

6 Summary

In this paper, we have studied the P–v criticality and phase transition in the extended phase space of a noncommutative geometry inspired RN-AdS black hole in the case when the noncommutative parameter is fixed. It is found that the P–v criticality and the first order small black hole/large black hole phase transition appear for the noncommutative geometry inspired RN-AdS black hole. Numerical calculations indicate that the noncommutative parameter affects the phase transition as well as the critical temperature, horizon radius, pressure and ratio. The critical ratio is not independent of the noncommutative parameter, which is different from the result in the van de Waals system, where the critical ratio is universal. The discussion on the phase transition at the critical point shows that the phase transition at the critical point is of second order.