Black hole evaporation: information loss but no paradox

Abstract

The process of black hole evaporation resulting from the Hawking effect has generated an intense controversy regarding its potential conflict with quantum mechanics’ unitary evolution. A recent set of works by a collaboration involving one of us, have revised the controversy with the aims of, on one hand, clarifying some conceptual issues surrounding it, and, at the same time, arguing that collapse theories have the potential to offer a satisfactory resolution of the so-called paradox. Here we show an explicit calculation supporting this claim using a simplified model of black hole creation and evaporation, known as the CGHS model, together with a dynamical reduction theory, known as CSL, and some speculative, but seemingly natural ideas about the role of quantum gravity in connection with the would-be singularity. This work represents a specific realization of general ideas first discussed in Okon and Sudarsky (Found Phys 44:114–143, 2014) and a complete and detailed analysis of a model first considered in Modak et al. (Phys Rev D 91(12):124009, 2015).

1 Introduction

The surprising discovery of black hole radiation by Hawking [3] in the 1970’s, has had an enormous influence in our ideas concerning the interface of quantum theory and gravitation. For instance, it has changed our perception regarding the laws of black hole thermodynamics, which, before that discovery, could have been regarded as mere analogies to our current view that they represent simply the ordinary thermodynamical laws, as they apply to situations involving black holes (see for instance[69]). This, in turn, has led to the quest to understand, on statistical mechanical terms, and within different proposals for a theory of quantum gravity, the area of the black hole horizon as a measure of the black hole entropy. In fact, the most popular programs in this regard, String Theory and Loop Quantum Gravity, have important success in this front. Furthermore, the fact that as the black hole radiates it must lose mass leads to some tension between the picture that emerges from the gravitational side and the basic tenants of quantum theory. This tension was first pointed out by Hawking [4] and has even been described by many theorists as the “Black Hole Information Paradox” (BHIP). The root of the tension is that, according to the picture that emerges from the gravitational side, it seems that one can start with a pure initial quantum state characterizing the system at some initial stage, which then evolves into something that, at the quantum level, can only be characterized as a highly mixed quantum state, while, the standard quantum mechanical considerations would lead one to expect a fully unitary evolution. There is even some debate as to whether or not this issue should be considered as paradoxical. This question has been discussed in [5] showing that, at the basis of this debate, there are some basic differences of outlook about issues such as the fate of the singularity in the context of a quantum theory that has been extended to cover the gravitational realm (i.e., in what sense will the singularity be resolved by quantum gravity, if at all?), and also, to a certain extent, what should be expected from quantum theory in general (i.e. should it be viewed as describing a “reality out there”, or as just encoding the information we have about a given system?).

One point of view is that the singularity represents an additional boundary of space-time (besides the standard one associated with the asymptotic regions) and thus the discussion about information, or about the nature of the end state, is erroneous if one does not take into account the information codified in such boundary. This point is, of course, completely justified when considering the situation from the purely classical view of space-time. If, however, as it is often expected, quantum gravity resolves the singularity replacing it by a region that can only be described in the appropriate quantum gravity terms, one would be justified in seeking a clarification of the situation without invoking an additional boundary. Moreover, given that such quantum gravity region will leave no trace, as far as asymptotic observers are concerned, in the case of complete evaporation of the black hole, one might want to obtain an effective characterization of the evolution, that corresponds to what is, in principle, accessible to them. For a more extensive discussion of these issues we refer the reader to the work [5].

Leaving aside these issues, a large number of researchers have been searching for a scheme to address the black hole information problem, within the context of various existing proposals for a theory of quantum gravity. This is natural given the fact that, the “paradox” truly emerges only after one assumes that a quantum theory of gravity removes the singularities that appear in association with black holes in General Relativity, and thus, when contemplating any such proposal, the BHIP issue acquires a new urgency. In fact, within the community that follows the most popular approaches to quantum gravity, the subject has recently been the focus of intense attention.

For those researchers arriving at the issue from the String Theory perspective, the importance of the issue is intensified by the AdS/CFT conjecture [6], which indicates that a theory including gravitation on the bulk should be equivalent to a another theory involving no gravitation on the boundary, and, as such, the description of the formation and evaporation of a black hole should be equivalent to the description of a process involving no black holes. Thus, if the evolution is unitary in the no black hole situation, there should be no breakdown of unitarity in the case involving a black hole creation and evaporation. Thus information cannot possibly be lost when a black hole forms and subsequently evaporates via Hawking effect [7].

These arguments have led some physicists to argue that the AdS/CFT duality implies that information must be preserved always. Although there is no clear indication that this duality will hold for asymptotically flat spacetimes, it is conjectured to be valid for situations involving the anti-de Sitter/de Sitter/asymptotically Lifshitz space-times and conformal field theories [6, 8, 9]. Moreover, within that context, there seems to be no clear explanation of how the information is recovered in a black hole evaporation within the space-time description, or where precisely does Hawking’s analysis indicating that the final state is not pure, actually go wrong. These issues are worthwhile revisiting given recent arguments [10] indicating that the three following well known physical principles cannot be satisfied simultaneously in the context of black hole evaporation:

• 1. Hawking radiation is in a pure state, i.e., the evolution of a quantum field state is unitary and there is no loss of information.

• 2. The Effective Field Theory (EFT) approach based on the notion that, although there is a breakdown of physics at some point inside the horizon, EFT should be well defined and a good description of physics outside the horizon.

• 3. The validity of the equivalence principle at the horizon, i.e., the infalling observers feel nothing unusual at the event horizon.

One finds in the literature various approaches to deal with the tension among three principles above. For instance, the proposal in [10] prioritizes (1) and (2) over (3). A consequence of such choice is that the event horizon would be turned into a so called “firewall”, which represents a fundamental inconsistency with basic ideas of general relativity embodied in the equivalence principle which would indicate that, from the local perspective, nothing unusual can be taking place at the event horizon, which after all is only defined globally. The appearance of the firewall would indicate that the event horizon is in a sense the “end point” of the space-time manifold, contrary to the basic views of general relativity, in this regard. Other proposals consider some rather exotic ideas, for example, that the outgoing and infalling particles are connected by a worm-holes, and therefore they are not independent objects [11], the existence of Planck stars [12], and the modeling of the black hole interior with “fuzzballs” [13, 14].

On the Loop Quantum Gravity (LQG) side, it has been argued that the theory seems to be able to resolve the singularities, of both, cosmological (see for instance [15]) and black hole (see for instance [16]) kind. In particular as in that theory there would be no room for divergences of an energy-momentum tensor, there can be no firewalls, and nevertheless, the information would be leaked at late times in the form of unusual quantum correlations.

We must point out, however, that, as the theory of LQG is meant to involve a resolution of the black hole singularity, the corresponding region (i.e. the region which, in the classical characterization, would contain the singularity) would have to be a region with exotic properties, where, in all likelihood, the ordinary space-time notions would cease to be valid. Therefore, it is not completely clear how exactly, the information would traverse across such exotic region: In fact, in the 2 dimensional example based on the CGHS model presented in the work [17], the region corresponding to the “would be singularity” is replaced by a region where the conformal factor (which characterizes the space-time metric which is conformally flat), undergoes fluctuations about zero. That is, we have a region where the metric signature fluctuates¹ and, as far as we know, the evolution of a quantum field through such a region is not well understood (see [18] for a recent work discussing such problems in detail). Another issue that does not seem to be addressed in a satisfactory way in that proposal is related to the problems faced in other attempts to solve the information loss question: if most of the energy of the initial black hole is emitted during the normal Hawking radiation state of the evaporation, then there would be very little energy left to be radiated in the late stages, which are presumably those where QG effects would be relevant. In fact, even if QG resolves the singularity, and information is somehow able to cross to the other side of the quantum gravity region, the amount of information encoded cannot be too large. This is simply due to the limitations associated with the small energy available to populate different highly localized modes of the quantum field. In other words, it seems one would need to face a serious energy deficit if one wants to argue that there are enough modes excited in the radiation which escapes through the singularity, so the complete state of the quantum field in ${\mathscr {I}}^+$ is pure, even though the restriction of the state to the early part of ${\mathscr {I}}^{+}$ is both thermal and contains most of the energy. We believe that these facts cast some doubts on the claims that the information is preserved, and that the final state must be unitarily related to the initial one.

Another important issue that has to be stressed in connection with any such proposal to dealing with the BHIP, is that, among other things, it should account for the fact that a pure state must turn into an ordinary (quantum) thermal state corresponding to a proper mixture (rather then an improper one, see [19] for terminology). Effectively, as the interior region of the black hole disappears when the singularity is removed, the state of the field for asymptotic observers at ${\mathscr {I}}^+$ has to be described by a density matrix representing an ensemble, every element of which, is in a pure state (which one ignores) and not by a density matrix that results from tracing out degrees of freedom of some region of space-time.

In our view, there is little hope that these problems could be completely clarified without first setting them in a proper context. The fact is that there is not even a full consensus about how should we view quantum theory in the absence of the gravitational complications. In fact, the so called “measurement problem” (often characterized as the “reality problem”) in quantum mechanics remains, almost a century after the theory’s formulation, a major obstacle to considering the theory as truly fundamental. We shall see that some related issues appear in unexpected places along our discussion of our proposed resolution of the BHIP.

The search for a satisfactory interpretation of the theory, despite the efforts of many insightful physicists, continues, and all the existing work has not yet yielded a convincing option, at least not one that is universally accepted.

The basic difficulty, as described for instance in [20–26], is the fact that the theory, as presented in textbooks, relies on two different and incompatible evolution processes. As Penrose [25] has characterized them, the theory relies on two different evolution processes: the U (unitary) process, where the state changes smoothly according to Schrödinger’s deterministic differential equation, and the R (reduction) process, in which the state of the system undergoes some instantaneous change or jump, in an un-deterministic fashion. The U process is supposed to control a system’s dynamics all the time that the system is not interfered with, while the R process takes control whenever a measurement is carried out.

The fundamental problem is that no one has been able to characterize, in a general way, when exactly should a physical process be considered as a measurement. This issue has been studied in depth and debated, according to most people, to exhaustion, in the scientific and philosophical literature,² with no universally acceptable resolution (for extensive discussions about dealing with these issues in terms of interpretational proposals, and their related shortcomings see for instance [31–42]). Moreover, the fact that in laboratory situations, one clearly knows when a measurement has been carried out has led some people to claim the debate as irrelevant, and most professional researchers now advice their students not to think about the issue and just calculate. Nonetheless, as characterized by Bell [43, 44], this kind of for all practical purposes (FAPP) approach, is not fully satisfactory at the foundational level, as it involves treating the system differently from the measuring device or the observer, and this division is one for which the theory offers no specific internal rules.

These issues are often dismissed by large segments of the physics community as simple philosophical/interpretational dilemmas with little, if any, relevance for the application of the theory. Needless to say that there are other colleagues who strongly disagree with such characterization, and that, as it is evident, we find ourselves in agreement with this latter group. In fact, it is worthwhile to note a relatively recent work [45], which helps putting the issue in a clear perspective by showing that there is a fundamental incompatibility between the following notions:

• (a) the wave function provides a complete characterization of a system;

• (b) the wave function always evolves according to a deterministic linear dynamical equation;

• (c) measurements always have determinate outcomes.

Thus for instance, hidden variable theories negate (a), objective collapse models negate (b)³, while the many-worlds scenarios negate (c).

The logical self consistency requirement to abandon one of the three desirable items above, clearly illustrates the fact that, when dealing with issues of principle, as we necessarily do when considering questions such as the fate of information, in light of Hawking evaporation of a black holes, we need to consider, with some care, the interpretational aspects of quantum theory.

One approach to deal with this unsatisfactory aspect of standard quantum theory is to consider modifying it by incorporating novel dynamical features that avoid the need to distinguish between the U and the R process (in the sense of having to know when to apply one or the other). That is, the modification incorporates something like “the collapse of the wave function” at the basic dynamical level, and in doing so removes the issue completely. The exploration of these ideas has a long history, with the first suggestions [46] as far back as the mid 60’s. The more recent developments might be traced to the early works of Pearle [47], followed by the first truly viable proposal, the GRW (Ghirardi–Rimini–Weber) theory in [48, 49], which considers individual stochastic collapse events leading to a spontaneous spatial localization of the wave function of multiparticle systems. Further developments led to a continuous version [50] known as CSL (continuous spontaneous localization), and to an improved GRW version [51]. The work along those lines has continued and has led to important insights and even to the development of an experimental program to test these ideas. We suggest the interested reader to consult the relevant and exciting literature.

In this work, we will show, in a simple model, how the incorporation of these modifications of quantum theory, together with a few other more or less natural assumptions, could lead to a resolution to the paradox.

The basic idea, first discussed in [1], is that, as the theories involving dynamical spontaneous reduction of the wave function, do generically prescribe a un-deterministic and non-unitary stochastic evolution, the loss of information occurs, not just in the context of black hole evaporation, but it takes place always. Thus, within this context, the situation involving black holes needs not, in principle, be different from more mundane situations. That is, as the fundamental quantum theory would now involve an actual departure from the simple linear and unitary evolution, the fact that the complete evolution leads us to a loss of information is no longer paradoxical. Information is lost all the time in quantum theory and the unitary evolution is only an approximation.

However, in order to present a convincing argument, we need to do much more than just to point to these simple conceptual changes. Our task is to show how the initially pure state that evolves to form a black hole, will evolve in the remote future into a state that is characterized, to a very good approximation, by the almost thermal state that is inferred from the Hawking type calculations. At the same time, we must ensure that this can be accommodated within the very stringent bounds on departures from ordinary quantum theory that have been obtained when examining the phenomenological manifestations of these theories [52]. In fact, as it was mentioned in [1], and as we will explicitly show here, in order to account for the information loss in black holes, we must introduce a new hypothesis that the rate of such stochastic, dynamical state reduction is enhanced in a region of high spacetime curvature. As the spacetime curvature increases towards the singularity of a black hole, this modified quantum behavior erases almost all the information associated with an otherwise unitary quantum evolution.

We should note that, in the course of this analysis, we would need to deal with at least three additional issues: what does quantum gravity say regarding the black hole singularity and what are the implications of the way in which it presumably resolves the singularity; what is precisely the nature of a mixed state, in general, and of a thermal state in particular? (i.e., does it reflect only our ignorance, or is it essentially attached with ensembles of systems rather than a single one? etc.); and finally, what are the specific attributes required from a theoretical proposal, so that we would consider it to be able to account for the required evolution of the quantum field in the conditions associated with a black hole evaporation?

The article is organized as follows: in Sect. 2 we present a review of the geometry of the CGHS model, and in Sect. 3 we review the standard analysis of QFT and Hawking radiation in this space-time, we also present an analysis of the energy-momentum fluxes across the horizon associated to the quantum field vacuum state, and discuss its renormalizability. Section 4 contains a brief discussion clarifying the nature of the two kinds of mixed/thermal states. In Sect. 5, we review the standard CSL dynamical reduction theory, and in Sect. 6 we present our proposals for adapting CSL to the CGHS scenario, and for what would be the role in the final evolution of a theory of Quantum Gravity. Finally, in Sect. 7, we present the final result of the evolution, and we end with some discussions on Sect. 8. There are four Appendices 1, 2, 3 and 4 at the end of this paper. In “Appendix 1” we discuss the non-Hadamard behavior of certain states, in “Appendix 2” we prove the anticipated behavior of the spacetime foliation, whereas, “Appendix 3” contains some useful expressions, and finally in “Appendix 4” a scheme to incorporate backreaction in presence of the wavefunction collapse is sketched.

Regarding notation, we will use signature $(-+++)$ for the metric, and throughout this paper we set the unit $c=G=\hbar =1$.

2 Brief review of the CGHS model

The Callan–Giddings–Harvey–Strominger (CGHS) model [55] involving black hole formation has very close similarity with the spherical collapse of massless scalar field in four spacetime dimensions.⁴ Furthermore, it provides a consistent theory of a toy version of quantum gravity in two spacetime dimensions coupled to conformal matter. Due to these features, the CGHS model gives a very useful tool for getting insights on the formation and evaporation of four dimensional black holes. In the last twenty years, this model has often been referred toas a “laboratory for testing general ideas on more realistic black holes” (see [56–58] for reviews and the monograph [59]). Particularly, it has been extensively studied to incorporate back reaction effects due to quantum matter fields [60–62], building a toy model for quantum gravity [63, 64], and also shading light on the information loss paradox [17, 62]. We will follow this tradition and use it as a laboratory for testing our ideas about the resolution of the BHIP. The work in this section and the next, is just a review of existing work, and contains nothing original (except, perhaps, for the discussion in Sect. 3.3). Those readers familiar with the model can safely proceed directly to Sect. 5.

The action for the CGHS model [55, 65] is given by

$$\begin{aligned} S=\frac{1}{2\pi }\int d^2x\sqrt{-g}\left[ e^{-2\phi }\left[ R+4(\nabla \phi )^2+4\Lambda ^2\right] -\frac{1}{2}\sum _{i=1}^{N}(\nabla f_{i})^2\right] , \end{aligned}$$

(1)

where $\phi$ is the dilaton field, $\Lambda ^2$ is a cosmological constant, and $f_{i}$ are N matter fields. In this work we will restrict ourselves with only one field f. For the most direct path that leads to a black hole solution one investigates this model in the “conformal gauge”:

$$\begin{aligned} ds^2=-e^{2\rho }dx^{+}dx^{-} \end{aligned}$$

(2)

in null coordinates $x^{+}=x^{0}+x^{1}$, $x^{-}=x^{0}-x^{1}$. In this setting, the field equation for the scalar field f decouples, and the most general solution can be written in the following manner

$$\begin{aligned} f(x^{+},x^{-})=f_{+}(x^{+})+f_{-}(x^{-}). \end{aligned}$$

(3)

This is a characteristic of CGHS model where left and right moving field modes do not interact with each other. Therefore, there is not need to deal with any sort of “back-scattering” effects. For any given functions $f_{+}$ and $f_{-}$, one can then find solutions for $\phi$ and $\rho$ [55]. A particular case is the vacuum solution ($f=0$) [56]

$$\begin{aligned} ds^2= & {} -\frac{dx^{+}dx^{-}}{M/\Lambda -\Lambda ^2 x^{+}x^{-}},\quad (-\infty < x^{+} < \infty ,~-\infty < x^- < \infty ), \end{aligned}$$

(4)

$$\begin{aligned} e^{-2\phi }= & {} \frac{M}{\Lambda }-\Lambda ^2 x^{+}x^{-}, \end{aligned}$$

(5)

which corresponds to a black hole of mass M. This mass is the ADM mass [62]. The case $M=0$ is known as the linear dilaton vacuum solution. One can “glue together” the linear dilaton vacuum and the black hole solutions along the line $x^{+}=x_{0}^{+}$ by considering a pulse of left moving matter with energy momentum tensor

$$\begin{aligned} T_{++}=\frac{1}{2}(\partial _{+}f)^2=\frac{M}{\Lambda x_{0}^{+}}\delta (x^{+}-x_{0}^{+}). \end{aligned}$$

(6)

This gives the solution

$$\begin{aligned} ds^2= & {} -\frac{dx^{+}dx^{-}}{-\Lambda ^2x^{+}x^{-}-(M/\Lambda x_{0}^{+})(x^{+}-x_{0}^{+})\Theta (x^{+}-x_{0}^{+})}, \nonumber \\&(0< x^{+} < \infty ,-\infty < x^- < 0 ), \end{aligned}$$

(7)

$$\begin{aligned} e^{-2\phi }= & {} -\Lambda ^2x^{+}x^{-}-\frac{M}{\Lambda x_{0}^{+}}(x^{+}-x_{0}^{+})\Theta (x^{+}-x_{0}^{+}). \end{aligned}$$

(8)

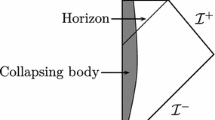
Before (i.e. to the past of) the matter pulse, the space-time metric is just the linear dilaton vacuum solution (regions I and I’ in Fig. 1)

$$\begin{aligned} ds^2=-\frac{dx^{+}dx^{-}}{-\Lambda ^2 x^{+}x^{-}}, \quad (0 < x^{+}< x_{0}^{+},-\infty < x^- < 0 ), \end{aligned}$$

(9)

and after $x_{0}^{+}$ it turns into a black hole solution. For later purposes it is useful to write the metric for the black hole region (regions II and III) as [65]:

$$\begin{aligned} ds^2=-\frac{dx^{+}dx^{-}}{\frac{M}{\Lambda }-\Lambda ^2 x^{+}(x^{-}+\Delta )}, \quad (x_{0}^{+}< x^{+} < \infty ,-\infty < x^- < 0 ), \end{aligned}$$

(10)

where $\Delta =M/\Lambda ^3x_{0}^{+}$. The position of the horizon is given by $x^{-}=-\Delta =-M/\Lambda ^3x_{0}^{+}$. The Ricci curvature scalar has the form

$$\begin{aligned} R = \frac{4 M \Lambda }{M/\Lambda - \Lambda ^2 x^+ (x^- +\Delta )}. \end{aligned}$$

(11)

The position of classical singularity, where R “blows up”, is given by

$$\begin{aligned} M= \Lambda ^3 x^+ (x^- + \Delta ). \end{aligned}$$

(12)

We note that the metric Eq. (10) is asymptotically flat in the black hole region $x^{+}>x_{0}^{+}$. To see this, the first step would be to use null coordinates $\sigma ^{+}$ and $\sigma ^{-}$, where

$$\begin{aligned} e^{\Lambda \sigma ^{+}}=\Lambda x^{+},\quad e^{-\Lambda \sigma ^{-}}=-\Lambda (x^{-}+\Delta ), \end{aligned}$$

(13)

and $-\infty <\sigma ^{\pm }<\infty$. Note that the above relationships between the coordinates $\sigma ^{\pm }$ and $x^{\pm }$ are the Kruskal transformations where the latter represents null Kruskal coordinates. The $\sigma ^{\pm }$ coordinates are only defined outside the event horizon (regions I and II in Fig. 1). In these new coordinates the metric is given by

$$\begin{aligned} ds^2=-\frac{d\sigma ^{+}d\sigma ^{-}}{1+\Delta \Lambda e^{\Lambda \sigma ^{-}}} ; \quad (-\infty < \sigma ^{-} < \infty , -\infty < \sigma ^{+} < \sigma _{0}^{+}), \end{aligned}$$

(14)

if $\sigma ^{+}<\sigma _{0}^{+}$ (region-I in Fig. 1) and

$$\begin{aligned} ds^2=-\frac{d\sigma ^{+}d\sigma ^{-}}{1+(M/\Lambda )e^{\Lambda (\sigma ^{-}-\sigma ^{+)}}} ;\quad (-\infty < \sigma ^{-} < \infty , \sigma ^{+} > \sigma _{0}^{+}), \end{aligned}$$

(15)

if $\sigma ^{+}>\sigma _{0}^{+}$ (Region-II in Fig. 1), where $\Lambda x_{0}^{+}=e^{\Lambda \sigma _{0}^{+}}$. In order to exhibit the asymptotic flatness, we first write the metric in Region-II using coordinates ($t,\sigma$) defined as $\sigma ^{\pm } =t \pm \sigma$ and then it is easy to express the metric in Schwarzschild-like coordinates using the transformation,

$$\begin{aligned} r= \frac{1}{2\Lambda } \ln \left( e^{2\Lambda \sigma } + \frac{M}{\Lambda }\right) . \end{aligned}$$

(16)

The resulting metric in Schwarzschild gauge is,

$$\begin{aligned} ds^2= & {} -\left( 1-\frac{M}{\Lambda }e^{-2\Lambda r}\right) dt^2 + \frac{1}{\left( 1-\frac{M}{\Lambda }e^{-2\Lambda r}\right) } dr^2; \nonumber \\&(-\infty < t < \infty , -\infty < r < \infty ). \end{aligned}$$

(17)

In these coordinates the position of the horizon is given by $r_h= \frac{1}{2\Lambda }\ln (M/\Lambda )$ and singularity is situated at $r= - \infty$. Also at spatial infinity ($r= \infty$) one has the flat metric.

Fig. 1

Penrose diagram for CGHS spacetime created due to matter collapse and evaporated due to Hawking effect

In addition, one can introduce new coordinates $y^{\pm }$ covering the whole manifold (all regions in Fig. 1) in the following way,

$$\begin{aligned} x^{+}=\frac{1}{\Lambda }e^{\Lambda y^{+}},\quad x^{-}=-\Delta e^{-\Lambda y^{-}}. \end{aligned}$$

(18)

These coordinates are particularly helpful to characterize the flat dilaton vacuum region Eq. (9) as there the metric takes the usual Minkwoskian form (regions I and I’ in Fig. 1)

$$\begin{aligned} ds^2=-dy^{+}dy^{-}; ~ \left( -\infty < y^+ < \frac{1}{\Lambda } \ln (\Lambda x_0^+) , -\infty < y^{-} < \infty \right) . \end{aligned}$$

(19)

On the other hand, the black hole regions II and III in Fig. 1 described in terms of $y^\pm$ coordinates [using Eq. (10) and Eq. (18)], takes the form

$$\begin{aligned} ds^2=-\frac{dy^{+}dy^{-}}{e^{\Lambda y^- \left( \frac{M}{\Lambda ^2 \Delta }e^{-\Lambda y^+} + e^{-\Lambda y^-} -1\right) }}; \quad \left( \frac{1}{\Lambda } \ln (\Lambda x_0^+) < y^+ < \infty , -\infty < y^{-} < \infty \right) . \end{aligned}$$

(20)

Although, these coordinates are not truly Schwarzschild-like, they are helpful for various purposes in our study.

Note that unlike the coordinates $\sigma ^{\pm }$ the coordinates $y^{\pm }$ cover the whole space-time. The relation between these two group of coordinates, in the region II of Fig. 1, is the following

$$\begin{aligned} y^+= & {} \sigma ^+ \end{aligned}$$

(21)

$$\begin{aligned} y^-= & {} -\frac{1}{\Lambda }\ln \left( 1+\frac{1}{\Lambda \Delta } e^{-\Lambda \sigma ^-}\right) . \end{aligned}$$

(22)

Note that the event horizon is located at $y^{-}=0$. We shall use these ($y^{\pm }$) coordinates in the construction of the quantum field modes in the CGHS background (particularly in region I, I’ and III in Fig. 1).

3 Quantum fields and energy fluxes in the CGHS model

In this section, we outline the basic framework for studying the quantum real scalar field on the CGHS black hole and calculate the Hawking flux in asymptotic infinity, and the negative flux through the horizon.

3.1 Field quantization and Hawking radiation

The standard framework of Quantum Field Theory (QFT) in curved spacetime is simplified when there are asymptotic regions where one can expand the field in some appropriate canonical basis of mode functions. In this case we will consider ${\mathscr {I}}^{-}_{L}$ and ${\mathscr {I}}^{-}_{R}$ as our asymptotic in region, and the interior of the black hole plus the ${\mathscr {I}}_{R}^+$ region as our asymptotic out region (although in the interior black hole region there is no time-like Killing field, and thus no natural notion of particle and no canonical modes in terms of which to perform the quantization). We are interested in expanding the field f in these two regions of the spacetime. This will allow one to find the energy fluxes in the following subsection.

In the in region the field operator can be expanded as

$$\begin{aligned} \hat{f}(x)=\sum _{\omega }\left( \hat{a}_{\omega }^{R} u_{\omega }^{R} + \hat{a}^{R \dag }_{\omega } u_{\omega }^{R*} + \hat{{a}}^{L}_{\omega } u_{\omega }^{L}+\hat{{a}}^{ L \dag }_{\omega } u_{\omega }^{L*}\right) , \end{aligned}$$

(23)

where, the basis of functions (modes) are as follows:

$$\begin{aligned} u_{\omega }^{R}=\frac{1}{\sqrt{4\pi \omega }}e^{-i\omega y^{-}} \end{aligned}$$

(24)

and

$$\begin{aligned} u_{\omega }^{L}=\frac{1}{\sqrt{4\pi \omega }}e^{-i\omega y^{+}}, \end{aligned}$$

(25)

with $\omega >0$. The superscripts R and L refer to the right and left moving modes. These modes will define an in vacuum right ($\left| 0 \right\rangle ^{in}_{R}$) and in vacuum left ($\left| 0 \right\rangle ^{in}_{L}$) whose tensor product ($\left| 0 \right\rangle ^{in}_{R}\otimes \left| 0 \right\rangle ^{in}_{L}$) will define our in vacuum.

We can also expand the field in the out region in a manner similar to Eq. (23). In this region, the complete set of modes include those that have support on the outside (region II in Fig. 1) and on the inside (region III in Fig. 1) the event horizon. Therefore, the field operator has the following form

$$\begin{aligned} \hat{f}(x)= & {} \sum _{\omega }\left( \hat{b}_{\omega }^{R} v_{\omega }^{R} + \hat{b}^{R \dag }_{\omega } v_{\omega }^{R*} + \hat{{b}}^{L}_{\omega } v_{\omega }^{L}+\hat{{b}}^{ L \dag }_{\omega } v_{\omega }^{L*}\right) \nonumber \\&+ \sum _{\tilde{\omega }}\left( \hat{\tilde{b}}_{\tilde{\omega }}^{R} \tilde{v}_{\tilde{\omega }}^{R} + \hat{\tilde{b}}^{R \dag }_{\tilde{\omega }} \tilde{v}_{\tilde{\omega }}^{R*} + \hat{\tilde{b}}^{L}_{\omega } \tilde{v}_{\tilde{\omega }}^{L}+\hat{\tilde{b}}^{ L \dag }_{\tilde{\omega }} \tilde{v}_{\tilde{\omega }}^{L*}\right) . \end{aligned}$$

(26)

Hereafter, the modes and operators with and without tildes correspond to those associated with the regions inside and outside the horizon, respectively. Note that there is an arbitrariness in the choice of basis inside the horizon, as there is no timelike Killing field, and thus no canonical definition of particles there. However, this arbitrariness is not expected to affect the physical results we will be interested on, as the specific states inside the black hole should not be relevant to any of the quantities of interest, which will be related to things that are, in principle, observable by asymptotic observers.⁵ The convenient basis of modes in the exterior (region-II in Fig. 1) are the following:

$$\begin{aligned} v_{\omega }^{R}=\frac{1}{\sqrt{4\pi \omega }}e^{-i\omega \sigma ^{-}}\Theta (-(x^{-} + \Delta )) \end{aligned}$$

(27)

and

$$\begin{aligned} v_{\omega }^{L}=\frac{1}{\sqrt{4\pi \omega }}e^{-i\omega \sigma ^{+}}\Theta (x^{+} - x_0^{+}). \end{aligned}$$

(28)

Similarly, following [59, 65], one can define a set of black hole interior modes (region III in Fig. 1). For that, we make use of $y^{\pm }$ coordinates which are well defined in region III. The left moving modes (moving from region II to region III) are simply a continuation of each other in the two regions, because they never cross the collapsing matter shell. However, the right moving modes coming from region I’ to region III do cross the matter shell, and therefore will generally lead to non-trivial Bogolubov coefficients. The modes in region I’ are given by Eq. (24), whereas, in region III they can be chosen as [65]:

$$\begin{aligned} {\tilde{v}}_{\omega }^{R} (y^-) \equiv {v}_{\omega }^{R*}(-y^-). \end{aligned}$$

(29)

The above formula, defining the modes in region III, involves using the expression for $\sigma ^- ( y^-)$ (from Eq. (22))and the substitution in the argument $y^-$ by $-y^-$. Usually, the consideration of the operator expansions Eq. (23) and (26), leads to two sets of Bogolubov coefficients for the right moving sector. The first corresponding to the relations between the modes in regions I’ and III, and the second to that between the modes in regions I and region II. One focuses on the transformation from the in to the exterior modes (i.e. regions I and II) because that is what leads to the Hawking flux.

In this way one obtains the Hawking radiation in the asymptotic limit (given by the right moving sector), and the negative flux at the horizon (given by the left moving sector).

In order to provide an appropriate notion of late time particle production (in terms of normalizable modes), it is convenient to replace the above delocalized plane wave type modes Eq. (27) and (28) by a complete orthonormal set of discrete wave packets modes, such as

$$\begin{aligned} v_{jn}^{L/R}=\frac{1}{\sqrt{\epsilon }}\int _{j\epsilon }^{(j+1)\epsilon }d\omega e^{2\pi i\omega n/\epsilon }v_{\omega }^{L/R}, \end{aligned}$$

(30)

where the integers $j\ge 0$ and $-\infty <n<\infty$. These modes correspond to wave packets which are peaked about $\sigma ^{+/-}= 2\pi n/\epsilon$ and which have a width $2\pi /\epsilon$. Taking a small value of epsilon ensures that the modes’ frequency is narrowly centered around $\omega \simeq \omega _{j}=j\epsilon$. This, in turn, gives a clear physical interpretation of the count of a particle detector sensitive only to frequencies within $\epsilon$ of $\omega _{j}$, while switched on for a time interval $2\pi /\epsilon$ at time $2\pi n/\epsilon$. A similar procedure is applied to convert the modes Eq. (24) and (25) into localized modes making up a discrete basis. Writing the modes in discrete basis gives a natural definition of the field operators Eq. (23) and (26) in terms of an orthonormalized set up.

With these basis of modes in the in and out regions defined, we can construct the corresponding Fock space quantization of the field in each region. Using standard procedures [69], one can construct, for example, the Fock space for the right moving sector of the field in the exterior region, ${\mathscr {F}}_{ext}^R$. The Fock spaces for the in and out quantizations are, respectively,

$$\begin{aligned} {\mathscr {F}}_{in}= {\mathscr {F}}_{in}^R \otimes {\mathscr {F}}_{in}^L \end{aligned}$$

(31)

and

$$\begin{aligned} {\mathscr {F}}_{out} = {\mathscr {F}}_{int}^R\otimes {\mathscr {F}}_{int}^L\otimes {\mathscr {F}}_{ext}^R\otimes {\mathscr {F}}_{ext}^L \, . \end{aligned}$$

(32)

Now, consider the distribution of occupation numbers $F=\{\dots , F_{nj}, \dots \}$, $F_{nj}\ge 0$ integer, such that $\sum _{nj} F_{nj}<\infty$ and the normalized state

$$\begin{aligned} \left| F \right\rangle _R^{ext} = C_F \prod _{nj} (\hat{b}_{nj}^\dagger )^{F_{nj}} \left| 0 \right\rangle _R^{ext}, \end{aligned}$$

(33)

where $C_{F}$ is a normalization factor. The set of all possible states of this form, $\{\left| F \right\rangle ^R_{ext}\}$, constitutes a basis of ${\mathscr {F}}_{ext}^R$. Basis for all other Fock spaces can be constructed similarly.

Following [65], one writes the in vacuum state as a superposition of all the particle states of out basis. As we have noted, the non trivial Bogolubov coefficients occur only for the right moving modes and thus, one can expand formally $\left| 0 \right\rangle ^{in}_R$ in the basis of the out (exterior and interior) right moving sector’s Fock space. This is the standard derivation of the Hawking radiation in the CGHS model, which gives [65]⁶:

$$\begin{aligned} \left| 0 \right\rangle ^{in}_R = N \sum _F e^{-\frac{\pi }{\Lambda } E_F} \left| F \right\rangle ^{int}_{R}\otimes \left| F \right\rangle ^{ext}_{R}\,, \end{aligned}$$

(34)

where N is a normalization factor and $E_F \equiv \sum _{nj} \omega _{nj} F_{nj}$ is the energy of state $\left| F \right\rangle ^{ext}_R$ with respect to late-time observers near ${\mathscr {I}}^+_R$ and $\sum _F \equiv \sum _{F_{nj}}\sum _{F_{n'j'}}\dots$ where all the sums run from 0 to $\infty$. Then, the full in vacuum can be expressed as

$$\begin{aligned} \left| 0 \right\rangle ^{in}= & {} \left| 0 \right\rangle ^{in}_{R}\otimes \left| 0 \right\rangle ^{in}_{L} \nonumber \\= & {} N \sum _F e^{-\frac{\pi }{\Lambda } E_F} \left| F \right\rangle ^{int}_{R}\otimes \left| F \right\rangle ^{ext}_{R} \otimes \left| 0 \right\rangle ^{in}_{L} \,. \end{aligned}$$

(35)

In the above expression we have used the fact that the vacuum state for the left movers is unchanged in both quantizations (due to trivial Bogolubov transformations).

With that, we are in a position to move to the remaining part of our work using the above CGHS model as our playground. We start by finding the energy fluxes by calculating the renormalized energy momentum tensor in the in vacuum.

3.2 Energy fluxes

Here we are interested in finding the renormalized energy momentum tensor in the in vacuum. For that we follow the method introduced by Davies, Fulling and Unruh (DFU) [66], and also used by Hiscock [67].⁷

This method uses the property that in two dimensions any spacetime metric can be written in conformally flat coordinates as

$$\begin{aligned} ds^2 = C(u, v) du dv \end{aligned}$$

(36)

where u and v are null coordinates. One can always introduce another set of null coordinates $\overline{u}$ and $\overline{v}$ such that $\overline{u} = \overline{u} (u)$ and $\overline{v} = \overline{v} (v)$. In the DFU method, one defines a vacuum state directly in terms of these $(\overline{u}, \overline{v})$ coordinates. In the in region, this vacuum corresponds to the in vacuum (defined before the gravitational collapse), since in this region the metric is flat, and one has $\overline{u} = u, ~ \overline{v} = v, ~ C(\overline{u},~\overline{v}) =1$. However, in the out (defined long after the gravitational collapse) region this is no longer the vacuum, since $\overline{u}$ and $\overline{v}$ are nontrivial functions of u and v. As a consequence, one finds particle creation and non-zero energy fluxes with respect to the in vacuum. The renormalized energy-momentum tensor in the in vacuum is given by [66]

$$\begin{aligned} \langle 0|^{in} T_{\mu \nu } | 0 \rangle ^{in} = \theta _{\mu \nu } + \frac{R}{48\pi } g_{\mu \nu } \end{aligned}$$

(37)

with

$$\begin{aligned} \theta _{\overline{u}~\overline{u}}= & {} -\frac{1}{12\pi } C^{1/2} \partial _{\overline{u}}^2(C^{-1/2}) \end{aligned}$$

(38)

$$\begin{aligned} \theta _{\overline{v}~\overline{v}}= & {} -\frac{1}{12\pi } C^{1/2} \partial _{\overline{v}}^2(C^{-1/2}) \end{aligned}$$

(39)

$$\begin{aligned} \theta _{\overline{u}~\overline{v}}= & {} \theta _{\overline{v}~\overline{u}} = 0 \end{aligned}$$

(40)

$$\begin{aligned} C= & {} C(\overline{u},\overline{v}). \end{aligned}$$

(41)

Using the above expressions one can obtain the explicit expressions for the renormalized energy-momentum tensor for CGHS model. First for the in linear dilaton vacuum region, we have the metric Eq. (19), (region I and I’ in Fig. 1) and thus one has null coordinates readily available $\overline{u} = y^{-}$ and $\overline{v}=y^{+}$ and $C(y^{-}, y^{+}) =1$. Whereas, for the out region (region II and III in Fig. 1) the metric is given by Eq. (20), and thus the conformal factor is:

$$\begin{aligned} C(y^{-}, y^{+})= -\frac{1}{e^{\Lambda y^- \left( \frac{M}{\Lambda ^2 \Delta }e^{-\Lambda y^+} + e^{-\Lambda y^-} -1\right) }}. \end{aligned}$$

(42)

The resulting components of energy-momentum tensor in $y^{+}, ~ y^{-}$ coordinates are thus,

$$\begin{aligned}&\langle 0|^{in} T_{{y^{+}}y^+} | 0 \rangle ^{in} = -\frac{\Lambda ^2 M e^{\Lambda {y^{-}}} \left( M e^{\Lambda {y^{-}}}+2 \Delta \Lambda ^2 e^{\Lambda {y^{+}}}-2 \Delta \Lambda ^2 e^{\Lambda ({y^{+}}+{y^{-}})}\right) }{48 \pi \left( M e^{\Lambda {y^{-}}}+\Delta \Lambda ^2 e^{\Lambda {y^{+}}}-\Delta \Lambda ^2 e^{\Lambda ({y^{+}}+{y^{-}})}\right) ^2}, \nonumber \\\end{aligned}$$

(43)

$$\begin{aligned}&\langle 0|^{in} T_{y^-y^-} | 0 \rangle ^{in} \nonumber \\&\quad = \frac{\Lambda ^2 e^{\Lambda {y^{-}}} \left( \Delta \Lambda ^2 e^{\Lambda {y^{+}}}-M\right) \left( M e^{\Lambda {y^{-}}}+2 \Delta \Lambda ^2 e^{\Lambda {y^{+}}}-\Delta \Lambda ^2 e^{\Lambda ({y^{+}}+{y^{-}})}\right) }{48 \pi \left( M e^{\Lambda {y^{-}}}+\Delta \Lambda ^2 e^{\Lambda {y^{+}}}-\Delta \Lambda ^2 e^{\Lambda ({y^{+}}+{y^{-}})}\right) ^2}.\nonumber \\ \end{aligned}$$

(44)

Next we write the relevant expression for the energy fluxes in region II of Fig. 1 in terms of the $\sigma ^{+},~\sigma ^{-}$ coordinates. These correspond to $\langle 0|^{in} T_{\sigma ^{\pm } \sigma ^{\pm }} | 0 \rangle ^{in} = (\frac{\partial y^{\pm }}{\partial \sigma ^{\pm }})^2 \langle 0|^{in} T_{{y^{\pm }}y^{\pm }} | 0 \rangle ^{in}$, thus giving,

$$\begin{aligned}&\langle 0|^{in} T_{\sigma ^{-} \sigma ^{-}} | 0 \rangle ^{in} \nonumber \\&\quad = \frac{\Lambda ^2 e^{\Lambda {\sigma ^{-}}} \left( \Delta \Lambda ^2 e^{\Lambda {\sigma ^{+}}}-M\right) \left( M e^{\Lambda {\sigma ^{-}}}+\Delta \Lambda ^2 e^{\Lambda ({\sigma ^{-}}+{\sigma ^{+}})}+2 \Lambda e^{\Lambda {\sigma ^{+}}}\right) }{48 \pi \left( \Delta \Lambda e^{\Lambda {\sigma ^{-}}}+1\right) ^2 \left( M e^{\Lambda {\sigma ^{-}}}+\Lambda e^{\Lambda {\sigma ^{+}}}\right) ^2}, \nonumber \\&\langle 0|^{in} T_{\sigma ^{+} \sigma ^{+}} | 0 \rangle ^{in} = -\frac{M \Lambda ^2 e^{\Lambda \sigma ^{-}} (M e^{\Lambda \sigma ^{-}} + 2\Lambda e^{\Lambda \sigma ^{+}})}{48\pi (M e^{\Lambda \sigma ^{-}} + \Lambda e^{\Lambda \sigma ^{+}})^2}. \end{aligned}$$

(45)

In the asymptotic limit ($\sigma ^{+} \rightarrow \infty$), the flux at ${\mathscr {I}}_R^{+}$ simplifies to

$$\begin{aligned} \langle 0|^{in} T_{\sigma ^{-} \sigma ^{-}}| 0 \rangle ^{in} = \frac{\Lambda ^2}{48\pi } \left( 1-\frac{1}{(1 + \Delta \Lambda e^{\Lambda \sigma ^{-}})^2}\right) , \end{aligned}$$

(46)

corresponding to the results in [55, 56]. In the late time limit (see Fig. 1), this gives the Hawking flux

$$\begin{aligned} \langle 0|^{in} T_{\sigma ^{-} \sigma ^{-}}^{H} | 0 \rangle ^{in} = \frac{\Lambda ^2}{48\pi }. \end{aligned}$$

(47)

On the other hand, near the horizon (in the limit $\sigma ^{-} \rightarrow \infty$), one finds

$$\begin{aligned} \langle 0|^{in}T_{\sigma ^{+} \sigma ^{+}}| 0 \rangle ^{in} = - \frac{\Lambda ^2}{48\pi } \end{aligned}$$

(48)

i.e., an equal amount of negative flux going inside the black hole. As a result of these fluxes the black hole loses energy during its evaporation.

These basic features of the model will be important in our discussion of the end state of the black hole evaporation process.

3.3 Comment on renormalization and Hadamard form

In the standard approach to QFT in flat spacetime, we have an entirely satisfactory prescription of renormalization of the energy-momentum tensor on a suitable class of states in the standard Fock representation. This is given in terms of “normal ordering”, which is well defined due to the fact that there is a unique canonical vacuum state connected to the notions of energy used by all inertial observers. The key problem in extending this idea to curved spacetime is due to the absence of a “preferred” vacuum state. Moreover, even if one chooses such “preferred states”, for example, in the case of stationary spacetimes, there is always “vacuum polarization” that makes $\langle T_{\mu \nu } \rangle \ne 0$. As a result, normal ordering is not a good prescription for renormalization in curved spacetime. Thus, one needs a more general prescription that can be extended to curved spacetime. Fortunately, such an extension exists and it is given by the “Hadamard renormalization”.

The essence of the Hadamard renormalization [68] for the real scalar field $\phi (x)$ is to find out the physically relevant states $\{ |\psi \rangle \}$ in the standard Fock space such that the difference $F(x,x') \equiv \frac{1}{2}(\langle \psi | \phi (x) \phi (x') |\psi \rangle + \langle \psi | \phi (x') \phi (x) |\psi \rangle ) - H (x,x')$ is a smooth function of x and $x'$. Here $H(x,x')$ is the “Hadamard ansatz” for the Green’s function whose precise form, even for the real scalar field, varies depending on the dimensionality. By subtracting this term, one removes the singular behavior in $G^{(1)} (x,x') = \frac{1}{2}(\langle \psi | \phi (x) \phi (x') |\psi \rangle + \langle \psi | \phi (x') \phi (x) |\psi \rangle )$ if and only if $| \psi \rangle$ is a Hadamard state. In other words, if the singular structure of the two point function is purely “Hadamard”, one obtains a well defined renormalized two-point function. Moreover, it eventually gives a physically acceptable renormalized energy-momentum tensor $\langle \psi | T_{\mu \nu } (x) |\psi \rangle$ by: (i) taking appropriate derivatives of $F(x,x')$ with respect to x and $x'$, (ii) taking the coincidence limit $x\rightarrow x'$, and (iii) making this compatible with Wald’s axioms [69] by adding or subtracting local curvature counter-terms.

The reason for using the in vacuum to calculate the fluxes is that this state is known to be a Hadamard state. Thus the DFU approach [66] should be compatible with the Hadamard approach. Thus, one expects that the calculated Hawking fluxes at infinity, and at the horizon would be the correct ones. (On the other hand, as we show in “Appendix 1” by a direct calculation, the generic states in the int, out or $int\otimes out$ bases are non-Hadamard. These states are analogous to the Boulware state, which is known to be divergent at the horizon. This divergence is not of the Hadamard form. This is to say that, although the left hand side of Eq. (35) is Hadamard, the individual terms in the sum on the right hand side are non-Hadamard.

Here, we might become very concerned because, when the state of a quantum field is not of the Hadamard form, one can not define, in a reasonable way, a smooth renormalized energy momentum tensor expectation value for it. Thus, it seems, that allowing such states to appear in the characterization of the evolution of our fields, in the black hole space-time, as we will be doing in the following sections, would be equivalent to allowing the kind of dramatic departures from the smooth physics that have been characterized as “firewalls”, in regions where no drastic departures from semiclassical gravitation should be expected.

In fact, one can find a very similar situation arising in even more mundane situations: consider the Minkowski vacuum as described in terms of the (two wedges) Rindler coordinates. As it is well known, this state, when tracing over, say, the right wedge’s degrees of freedom, corresponds to a thermal state. Let us consider now a detector providing the measurement of the number of particles in a certain mode of the field. The point is that a state with a definite number of particles in the corresponding mode (both in the left and right Rindler wedges) is not a Hadamard state, and thus has an ill defined expectation value for the energy-momentum (precisely at the Rindler horizon), which would have to be considered as a singular state there. Thus, if, as a result of the measurement, the state of the system becomes one such a state, we would have something similar to the emergence of a firewall at the Rindler horizon.⁸ The conclusion we must draw from such analysis is that no detection, that could be modeled in terms of a smooth interaction between a localized detector and the quantum field, could ever provide a precise measurement of the number of Rindler particles in any given mode.

The above discussion illustrates the lesson we should draw regarding the situation involving the quantum field in the case of a black hole subject to the evolution characterized by the modified Schrödinger equation associated with a dynamical collapse theory: If the modification of the evolution equation under consideration, involves only smooth local operators, it would not, in any finite amount of time, result in the collapse of the state of the field into a state with definite number of particles in any of the modes that are associated with unphysical divergences at the horizon. We will have more to say on this issue in the following sections.

4 A word about pure, mixed and thermal states

In quantum mechanics one is often led to consider not just vectors (or more precisely rays) in the Hilbert space, as characterizing the state of a system, but often more general objects known as density matrices are used for that task. The cases where that occurs involve situations where one considers ensembles of identical systems, situations in which one does not know the precise state of the system, or when one considers a subsystem of a larger system.

In the practical usages one very seldom distinguishes among the above situations, a fact that leads to a tendency to simply and generically ignore the differences. However, we believe that when considering issues of principle it is essential to make the appropriate distinctions if one is to avoid generating confusion. One situation where the distinction is very important concerns the analysis of the measurement problem which is often addressed using decoherence arguments.

One simple and very illustrative example is provided by a simple EPR pair of spin 1 / 2 fermions in zero angular momentum state. If we consider the particles moving along the z axis, we can describe the state of the system using the basis of spin states oriented along say the x axis $\lbrace \left| +1/2, x \right\rangle , \left| -1/2, x \right\rangle \rbrace$ for the Hilbert space of each particle. The state of the two particle system is then $\left| \Psi \right\rangle =\frac{1}{\sqrt{2}} (\left| +1/2, x \right\rangle ^{(1)} \otimes \left| -1/2, x \right\rangle ^{(2)} + \left| -1/2, x \right\rangle ^{(1)} \otimes \left| +1/2, x \right\rangle ^{(2)} )$. If we decide to focus on the particle 1, and thus characterize the situation with the reduced density matrix $\rho ^{(1)} \equiv Tr_{2} (\left| \Psi \right\rangle \left\langle \Psi \right| ) = \frac{1}{2} (\left| +1/2, x \right\rangle ^{(1)} \left\langle +1/2, x \right| ^{(1)} + \left| -1/2, x \right\rangle ^{(1)} \left\langle -1/2, x \right| ^{(1)} )$, we might be inclined to consider that the particle 1 is now in a definite state: either $\left| +1/2, x \right\rangle$ or $\left| -1/2, x \right\rangle$, with probabilities 1 / 2 for each alternative. There are at least two things that clearly indicate that such interpretation is not correct. First, the simple fact that had we started describing the system using the basis of spin states oriented along say the y axis $\lbrace \left| +1/2, y \right\rangle , \left| -1/2, y \right\rangle \rbrace$ for the Hilbert space of each particle, we would have ended with the expression $\rho ^{1} \equiv Tr_{2} (\left| \Psi \right\rangle \left\langle \Psi \right| ) = \frac{1}{2} (\left| +1/2, y \right\rangle ^{(1)} \left\langle +1/2, y \right| ^{(1)} + \left| -1/2, y \right\rangle ^{(1)} \left\langle -1/2, y \right| ^{(1)} )$, and according to the above we would be entitled to assert that the particle 1 is in a definite state: either $\left| +1/2, y \right\rangle$ or $\left| -1/2, y \right\rangle$, with probabilities 1 / 2 for each alternative, which is in clear contradiction with the previous conclusion. The second is the existence of the strong non-classical correlations, (which have been experimentally demonstrated by the famous experiments of Aspect et al. [70]) make it clear that, such interpretations are untenable. Thus, we conclude that, the fact that we use the same mathematical objects to describe various physical situations, requires us to be extra careful to avoid the confusion of one such situation with the other, otherwise we could very quickly be driven to erroneous conclusions.

When considering any system one can then wonder if it should be described by a pure or mixed state. When we can identify that the system as part of another larger system, and we know there are correlations between it and other parts, it is clear that it should be described by a mixed density matrix. But, what should be the description if one can not identify the larger system to which our system is a part of? Or if we can point to such a larger system but we also know there are no correlations with the (sub-)system of interests? Should we consider that the appropriate description must be pure, and that, if we consider a density matrix it is only because of our ignorance about that pure state? The problem becomes specially acute when thinking of the universe as a whole, a situation in which, by definition, there can be no larger system. Is the universe necessarily in a pure state? Or can it be in a mixed state which reflects something other than our ignorance about the particular pure state the Universe is?

In order to make progress we will adopt a rather conservative viewpoint and adhere to it consistently throughout the coming discussions. That is, in this work we will take the view that individual isolated systems that are not entangled with others systems are represented by pure states, and can be represented either by the corresponding density matrices that satisfy $\rho ^2 =\rho$, or by the unique ray $\left| \psi \right\rangle$ (the phase is irrelevant) for which one can write $\rho = \left| \psi \right\rangle \left\langle \psi \right|$.

The case where one is concerned with an individual system and one does not know exactly what state the system is in, is in fact a particular situation of the usage of an ensemble. In such situations, as in most usages of probabilistic considerations, the ensemble is employed to represent our lack on knowledge regarding the system’s state. That is the case even if one is dealing, in practice, with a unique specific system. This is just what is done, for instance, in making probabilistic considerations in weather prediction. So regarding issues of principle we have, in fact, to distinguish only between two kinds of situations as far as the characterization of a system via a general density matrix. Thus, mixed states will occur when one considers either:

• (a) An ensemble of (identical) systems each in a pure state. These are the “proper” mixtures.

• (b) The state of a subsystem of a larger system (which is in a pure state), after we “trace over” the rest of the system. These are the “improper” mixtures.

The above characterizations of mixed states as proper or improper follows from the terminology introduced by d’ Espagnat [19]. An ordinary (quantum) thermal state, (such as what occurs in statistical mechanics) represents an ensemble, where the weights are simple functions, characterizable by temperature and chemical potentials (e.g. the ensemble that characterizes a gas at room temperature) and is thus a proper thermal state. An “improper” thermal state is an improper mixed state where the weights happen to be thermal (e.g. the Minkowski vacuum, described in Rindler coordinates, after tracing over the other wedge).

From the above point of view, which seems to be the most demanding in the present context, resolving the BH information paradox would require explaining how a pure state becomes a “proper” thermal state rather than a “improper” one, simply because the region corresponding to black hole interior will disappear.

5 Brief review of the CSL theory

We start our discussion by presenting a particularly simple form of CSL, which describes collapse towards one or another of the eigenstates of an operator $\hat{A}$ with rate $\sim \lambda$. We leave aside, for the moment, the question regarding what dictates the selection of such operator.⁹ Again, the work in this section is just a review of existing work, and contains nothing original. For a very pedagogical and detailed review we suggest turning to [53, 54]. Those readers familiar with the model can safely proceed directly to the next section.

In using the theory, one needs to consider two equations [54]. The first is a stochastically modified version of Schrödinger equation, which in the simple case where we take the hamiltonian $H\equiv 0$ has, as a general solution:

$$\begin{aligned} |\psi , t\rangle = e^{-\frac{1}{4\lambda t} [B(t) - 2\lambda t \hat{A}]^2}|\psi , 0 \rangle \end{aligned}$$

(49)

where B(t) is a stochastic function of time,¹⁰ $\hat{A}$ is a hermitian operator and $\lambda$ is a positive valued parameter. The second is the probability rule for the specific realization of the function B(t). That rule can be presented in terms of the probability that the specific realization at each time t has the value within B(t) to $B(t) + dB(t)$, given by

$$\begin{aligned} P[B(t)] dB(t) = \frac{dB(t)}{\sqrt{2\pi \lambda t}} \langle \psi ,t | \psi , t\rangle , \end{aligned}$$

(50)

with the assumption that the initial state has a unit norm. These two equations define CSL and everything else is derived using these two.

When including a nontrivial Hamiltonian, the state vector dynamics is most easily understood in terms of small individual time “steps”. For that we consider an “infinitesimal” time interval of duration dt, and state the evolution equation (49) during that interval:

$$\begin{aligned} |\psi ,t\rangle = e^{-dt \big [i\hat{H}+\frac{1}{4\lambda }[w(t)-2\lambda \hat{A}]^{2}\big ]}|\psi ,t-dt\rangle , \end{aligned}$$

(51)

where $w(t) = dB(t)/dt$ is a random white noise function. The probability that its value at t lies within the interval $(w(t), w(t) + dw(t))$ is now:

$$\begin{aligned} P(w) dw = \frac{\langle \psi ,t|\psi ,t\rangle }{\langle \psi ,t-dt|\psi ,t-dt\rangle } \frac{dw(t)}{\sqrt{ 2\pi \lambda /dt}} \end{aligned}$$

(52)

Over a finite time interval, say from $t=0$ to t in the step of dt, (51) takes the following form

$$\begin{aligned} |\psi ,t\rangle ={\mathcal {T}}e^{-\int _{0}^{t}dt'\big [i\hat{H}+\frac{1}{4\lambda }[w(t')-2\lambda \hat{A}]^{2}\big ]}|\psi ,0\rangle , \end{aligned}$$

(53)

(where ${\mathcal {T}}$ is the time-ordering operator) and the probability rule again has to be described by a $N\rightarrow \infty$ limiting process involving dividing the interval (0, t) on N steps $(t_0= 0, t_1,\ldots t_N =t)$ with duration $dt_i = t_i-t_{i-1}= dt$. The probability that the function w(t) lies in the tube Dw(t) characterized by the restriction that in the i-th step the white noise function takes a value between $w(t_i)$ and $w(t_i) + dw(t_i)$ is given by:

$$\begin{aligned} P(w) Dw(t) = \langle \psi ,t|\psi ,t\rangle \prod _{i=1}^{N}\frac{dw(t_{i})}{\sqrt{ 2\pi \lambda /dt}}. \end{aligned}$$

(54)

Thus now the probability rule (54) is a joint probability distribution over the entire time interval $t=0$ to t. In deducing (54) from (52), one has to assume that the norm of the initial state vector was unity. For later times the state vector norm evolves dynamically (not equal 1), so Eq. (54) says that the state vectors with largest norm are most probable. Note that the interpretation of the theory does not require the state vector to have norm one as probabilities are now assigned to the realization of the stochastic functions, rather than to the standard quantum mechanical amplitudes. For further discussion see [53, 54].

It is now straightforward to see that the total probability for realization of an arbitrary stochastic function is 1, that is

$$\begin{aligned} \int PDw(t)= & {} \int Dw(t-dt)\int _{-\infty }^{\infty }\frac{dw(t)}{\sqrt{ 2\pi \lambda /dt}}\langle \psi ,t-dt| e^{-dt'\big [-i\hat{H}+\frac{1}{4\lambda }[w(t')-2\lambda \hat{A}]^{2}\big ]} \nonumber \\&\times e^{-\int _{0}^{t}dt'\big [i\hat{H}+\frac{1}{4\lambda }[w(t')-2\lambda \hat{A}]^{2}\big ]}| \psi ,t-dt\rangle \nonumber \\= & {} \int Dw(t-dt)\int _{-\infty }^{\infty }\frac{dw(t)}{\sqrt{ 2\pi \lambda /dt}}\langle \psi ,t-dt| e^{-\frac{1}{2\lambda }[w(t')-2\lambda \hat{A}]^{2}} |\psi ,t-dt\rangle \nonumber \\= & {} \int Dw(t-dt)\langle \psi ,t-dt|\psi ,t-dt\rangle = ... =\langle \psi ,0|\psi ,0\rangle =1. \end{aligned}$$

(55)

As we indicated, the dynamics is designed to drive any initial state towards one of the eigenstates $|a_{n}\rangle$ of $\hat{A}$. We can see this by considering the simplified case where $\hat{H}=0$. As usual, we can write the initial state in terms of those eigenstates as

$$\begin{aligned} |\psi ,0\rangle =\sum _{n=1}^{N}c_{n}|a_{n}\rangle \end{aligned}$$

(56)

and thus, according to Eqs. (49), (50), we find

$$\begin{aligned} |\psi ,t\rangle= & {} \sum _{n=1}^{N}c_{n}|a_{n}\rangle e^{-\frac{1}{4\lambda t}[B(t)-2 \lambda ta_{n}]^{2}}, \end{aligned}$$

(57)

$$\begin{aligned} P[B(t)] dB(t)= & {} \frac{dB(t)}{\sqrt{2\pi \lambda t}} \sum _{n=1}^{N}|c_{n}|^{2}e^{-\frac{1}{2\lambda t}[B(t)-2\lambda t a_{n}]^{2}}, \end{aligned}$$

(58)

According to Eq. (58), the probability is then a sum of gaussians, each drifting by an amount $\sim a_{n}t$, and having a width $\sim \sqrt{\lambda t}$. Therefore, after a while, the result can be described as a sum of essentially separated gaussians. Then, we can identify the various ranges of values of B(t) as corresponding to each one of the possible outcomes. If $-K\sqrt{\lambda t}\le B(t)-2\lambda ta_{n}\le K\sqrt{\lambda t}$, ($K>1$ is some suitably large number), the associated probability integrated over this range of B(t) is essentially $|c_{n}|^{2}$, and the state vector given by Eq. (57) becomes $|\psi ,t\rangle \sim |a_{n}\rangle$.

Note that, when $\hat{H}\ne 0$, the hamiltonian dynamics interferes with the collapse dynamics, and sometimes the full collapse is never achieved, and all that happens is a relative narrowing of the wave function about the eigenstates of $\hat{A}$ leading to a kind of equilibrium stage between the two competing dynamics: the specific CSL dynamics that tends to sharpen the wave function about one of the eigenstates, and the characteristic Schrödinger behavior associated with the spreading of the wave function (such as what occurs with the position). This is mathematically analogous to what one expects when considering in classical physics a cloud of gas subject both to the random fluctuations and the effects of gravity. One part of the dynamics tends to spread the gas cloud and the other tends to contract it. Note however that in the above example the roles of the deterministic and stochastic components of the dynamics, regarding respectively contraction and diffusion (or spatial spreading), are interchanged in comparison with the case of a single free particle and a CSL modified dynamics with a smeared position operator driving the collapse (i.e. playing the role of the operator $\hat{A}$ in Eq. ).

The above, describes in full the evolution of an individual system “prepared” in the initial state: the presence of the stochastic function w(t), however, clearly renders the evolution highly unpredictable, and all one can say is that the system will be driven towards one of the eigenstates of $\hat{A}$. It is often useful to discuss the fate of an ensemble of identically prepared systems. In that case, we consider a collection of systems all prepared in the same initial state and evolve each one of them according to CSL dynamics, which tries to collapse the state vectors towards eigenstates of $\hat{A}$. The result is an ensemble of differently evolved state vectors, each characterized by a different w(t). It is useful to have an expression for the density matrix which describes the ensemble of evolutions. We obtain that simply by considering the density matrix describing the ensemble of vectors evolved using Eq. (53):

$$\begin{aligned} \rho (t)= & {} \int PDw(t)\frac{|\psi ,t\rangle \langle \psi ,t|}{\langle \psi ,t|\psi ,t\rangle }=\int Dw(t)|\psi ,t\rangle \langle \psi ,t|\nonumber \\= & {} \int Dw(t){\mathcal {T}}e^{-\int _{0}^{t}dt'\big [i\hat{H}+\frac{1}{4\lambda }[w(t')-2\lambda \hat{A}]^{2}}\big ]|\psi ,0\rangle \langle \psi ,0|\nonumber \\&\times e^{-\int _{0}^{t}dt'\big [-i\hat{H}+\frac{1}{4\lambda }[w(t')-2\lambda \hat{A}]^{2}\big ]}\nonumber \\= & {} {\mathcal {T}}e^{-\int _{0}^{t}dt'\big [i(\underrightarrow{\hat{H}}-\underleftarrow{\hat{H}}]+\frac{\lambda }{2}[\underrightarrow{\hat{A}}-\underleftarrow{\hat{A}}]^{2}\big ]}\rho (0), \end{aligned}$$

(59)

where the arrows $\rightarrow$, $\leftarrow {}$ under the operator indicate that the operator acts, respectively, on the right or on the left of $\rho (0)$, and the ${\mathcal {T}}$ reverse-time-order operator to the right of $\rho (0)$. It can be shown that the resulting evolution equation for the density matrix is

$$\begin{aligned} \frac{d}{dt}\rho (t)=-i[\hat{H},\rho (t)]-\frac{\lambda }{2}\left[ \hat{A},[\hat{A},\rho (t)]\right] . \end{aligned}$$

(60)

Therefore, the ensemble expectation value of any operator$\overline{\langle \hat{O}\rangle }=\hbox {Tr}\hat{O}\rho (t)$ evolves in time according to

$$\begin{aligned} \frac{d}{dt}\overline{\langle \hat{O}\rangle }=-i\overline{[\hat{O},\hat{H}]}-\frac{\lambda }{2}\overline{\left[ \hat{A},[\hat{A},\hat{O}]\right] }. \end{aligned}$$

(61)

In this case, one can see that the Born rule is recovered in the sense that the portion of the systems that ends up in the eigenstate turns out to be precisely the quantity obtained by projecting the initial state on the corresponding eigenstates (the theory is designed to do this).

Of course, one could now ask: if we still have to determine what is a measurement, and decide, in each situation, what is the relevant operator $\hat{A}$, and determine a phenomenologically suitable value of $\lambda$, what has been gained? The beauty of the proposal is, however, that it intends to use the above mathematical framework in connection with a a general specification of the collapse operator that would cover all situations. The existing proposals, framed in the language of many particle quantum mechanics, the operator is the tensor product of suitable smeared position operators for all the particles. What seems to make this possible is the observation that all measurement situations can be seen as essentially position measurements of a macroscopically large aggregate of particles making, say, a pointer (or in modern devices something like the corresponding position arrangement of a large number of electrically charged particles). The idea is then, that a measurement involves in an essential way the entanglement of the subsystem under observation with the position coordinates of these large number of particles that constitute the pointer and as any of those particles undergoes collapse in their position, the complete system collapses into a state for which the subsystem under observation is in an eigenstate of the measured quantity. This of course can only occur as long as the measurement interaction is strong enough, i.e. it leads to a strong entanglement of the quantity being measured with the fundamental position of the physical system that constitutes the measuring device.

Thus, the CSL proposal involves the selection of a properly smeared position operator for each particle and a universal value of the parameter $\lambda$. In fact, later refinements indicate that the value of $\lambda$ should be universal except for the fact that each type of particle should have its own value which, the detail analysis suggests, should be roughly proportional to the square of the particle’s mass, i.e. $\lambda _i = \lambda _0 (m_i / m_N)^2$ where $\lambda _i$ is the collapse rate for the smeared position of the particles of the ith species, $\lambda _0$ is a universal parameter, $m_i$ is the mass of the ith species of particles and $m_N$ is a fiduciary mass scale usually taken as the nucleon mass (1 GeV).

Of course, this can not be considered yet a satisfactory candidate for a fundamental theory. After all, we know that particles are not the fundamental entities. In fact, Quantum Field Theory teaches us that the fundamental objects are the fields, and that the notion of particle is, in general, ambiguous and tied intrinsically with the particular symmetries of the space-times and the coordinates we use to describe them (see for instance, [68, 69]). Thus, any candidate for a truly fundamental replacement of quantum theory will likely need to be formulated in terms of quantum fields. It is worth mentioning here, anticipating latter discussions, that there do exist some such proposals, involving relativistic versions of dynamical collapse theories.

6 Application of CSL to the CGHS model

In this section, we describe the CSL evolution of states of the real scalar quantum field living on the CGHS black hole. The basic idea is to work in an interaction picture where the free evolution is encoded in the quantum field operators and the CSL effects are treated as an interaction and codified in the evolution of the quantum states.

The results of this section will be used to support our main statement in the next section.

6.1 The foliation of CGHS spacetime

In order to consider the CSL evolution of states of our quantum field on the CGHS background using the interaction picture mentioned above, we have to foliate the space-time, in order to have a well defined evolution operator connecting the states associated with the different specific hypersurfaces. In this subsection, we describe such a foliation.

As described in Sect. 2, the space-time metric in the null Kruskal coordinates ($x^+,~x^{-}$) is given in (Eq. 10). Now we introduce the Kruskal coordinates

$$\begin{aligned} T = \frac{x^+ + x^- + \Delta }{2}, \quad X = \frac{x^+ - x^- - \Delta }{2}. \end{aligned}$$

The metric in the region involving the black hole, both its exterior and interior (regions II and III in Fig. 1 respectively) can be written as

$$\begin{aligned} ds^2=-\frac{dT^2 - dX^2}{\frac{M}{\Lambda }-\Lambda ^2 (T^2-X^2)}, \quad (-\infty \le T \le \infty , -\infty \le X \le \infty ). \end{aligned}$$

(62)

These coordinates can be related with Schwarzschild-like time t and space r coordinates in the following way

$$\begin{aligned}&\tanh (\Lambda t) = \frac{T}{X}, \end{aligned}$$

(63)

$$\begin{aligned}&-\frac{1}{\Lambda ^2} (e^{2\Lambda r} - M/\Lambda ) = T^2 - X^2, \end{aligned}$$

(64)

where the time coordinate t is well defined only in region II similar to the Schwarzschild case. Using Eq. (11) and the coordinate transformations for T and X as defined above, one finds $R= \frac{4M\Lambda }{M/\Lambda -\Lambda ^2(T^2 - X^2) }$. Therefore, the singularity is located at $M/\Lambda = \Lambda ^2(T^2 - X^2)$.

Now, we proceed to define our foliation $\Sigma _\tau$ and related coordinates $(\tau ,\zeta )$ covering the regions II and III. The idea is to define the hypersurface $\Sigma _\tau$ by following in the region III ($e^{2\Lambda r} < M/\Lambda$) a curve with $r=const.$, given by Eq. (64) and in the region II a $t=const.$ line, given by Eq. (63), connecting them via a line $T =const.$.

The prescription is defined once we provide the joining conditions for the above recipe. That will be specified by two functions $T_1(X)$ and $T_2(X)$ determining the points where the matching takes place. The images of $T_1(X)$ and $T_2(X)$ will be located in regions III and II respectively.

More specifically the construction is as follows:

As a first step we choose any value of $\tau$ in the range $(0, \tau _s = \sqrt{M/\Lambda ^3})$. Then we start the $\Sigma _\tau$ following the curve $T^2-X^2 = \tau ^2$ (corresponding to $r = const.$) until the intersection of that curve with the curve $T_1(X)$. From there $\Sigma _\tau$ continues along the line $T= const.$ until the intersection of this line with the curve $T_2(X)$. From there it continues along the line $T/X= const.$ (which corresponds to $t = const.$) all the way to the asymptotic region.

Finally we define $\zeta$ (on the region $X \ge 0$) as the distance of the given space-time point to the T axis (i.e. the line $X=0$) along the hypersurface $\Sigma _\tau$. For the region $X \le 0$ we define $\zeta$ as minus the distance of the given space-time point to the T axis along the hypersurface $\Sigma _\tau$.

In order to complete the specification of the new coordinates and the foliation all that we need are the two curves $T_{1,2}(X)$. They can be chosen to be

$$\begin{aligned} T_1(X) = \left( X^2 + \frac{M}{\Lambda ^3}e^{-2\Lambda /\sqrt{X}}\right) ^{1/2}. \end{aligned}$$

(65)

The other curve that we need can be found by the reflection with respect to the horizon $T=X$, of that given in Eq. (65). This curve is obtained just by interchanging T with X in Eq. (65). That is, $T_2$ is defined via the implicit function theorem, as the solution to the equation:

$$\begin{aligned} X(T) = \left( T^2 + \frac{M}{\Lambda ^3}e^{-2\Lambda /\sqrt{T}}\right) ^{1/2}. \end{aligned}$$

(66)

It is clear from the above recipe that we face smoothness issues at the junction points defining the foliation, and that this is problematic regarding the smoothness of coordinates we have defined. However it seems clear that a simple smoothing procedure should serve to resolve the problem without affecting the essence of the construction (we will not further consider that aspect in the present work).

It is clearly important to ensure that these hypersurfaces do not cross each other. We show this in “Appendix 2”.

Essentially, this construction now divides the spacetime into three regions as shown in Fig. 2. Region-A and C are defined, respectively, at the inside and outside of the event horizon, whereas, Region-B connects them to complete the foliation. Note that due to our choice of intersecting curves Eq. (65) and Eq. (66), Region-B starts from a point and asymptotically it also ends in a point. In Fig. 3 (upper) we plot various space-like hypersurfaces generated by using the above prescription of foliation. As required they “evolve forward in time” (in the sense that $\tau$ is a good time function) and do not cross each other at any stage. An artistic picture of the above scheme in the conformal diagram is also shown in Fig. 3 (lower).

Fig. 2

Division of the CGHS spacetime in Kruskal coordinates due to the foliation. In this plot we have set $M/\Lambda ^3 = 4.42$. For details see the text

Fig. 3

Spacetime foliation of the CGHS spacetime. The upper figure (in Kruskal coordinates) contains mathematical plots of various slices with fixed value $M/\Lambda ^3 = 4.42$. We have chosen $T= 0.1$ (magenta), $T = 0.5$ (blue), $T=1$ (orange), $T = 3$ (green) for connecting $T=const.$ lines. In the lower figure various foliating surfaces are highlighted in the conformal/Penrose diagram of CGHS model. For more details see the text

Now, we give the explicit transformations of coordinates $\tau (T,X), \zeta (T,X)$. For that, let us, for instance, consider the general case of a point in Region-C. All other cases can be easily found using the same recipe. We refer the reader to consult Fig. 4 to get familiar with the scheme as presented below.

Fig. 4

($\tau , \zeta$) parametrization of spacelike hypersurfaces used to foliate the Kruskal diagram of CGHS spacetime. Like before, these mathematical plots have fixed values of $M/\Lambda ^3 = 4.42$. For detailed description see the text

Let’s take a point $T=a,~ X=b$ in Region-C. Given these values we have a unique t from Eq. (63). Now, we follow this line of $t = const.$ until we intersect the curve Eq. (66). This determines a point $T=c,~X=d$. Then we move along $T=const.=c$ until we intersect the curve Eq. (65). This gives a point $T=c,~X=e$. From this point we move along $r=r(c,e)=const.$ given by Eq. (64) until we intersect the axis $X=0$. This gives us a value of $T=f$ and we take this as the value of $\tau =\tau (a,b)$. In this way we assign a unique value of $\tau$ for the entire hypersurface. The other coordinate $\zeta$ is now the distance between $(T=f,X=0)$ and $(T=a, X=b)$ along the hypersurface which determines $\tau$. This distance is given by

$$\begin{aligned} \zeta = \zeta _A + \zeta _B + \zeta _C, \end{aligned}$$

(67)

where

$$\begin{aligned} \zeta _A = \int _{r=const.}ds_{A}= & {} \sqrt{\frac{A}{M/\Lambda - \Lambda ^2 A}}\int _{f-\Delta }^{c-e-\Delta }\frac{dx^{-}}{x^{-}+\Delta }, \end{aligned}$$

(68)

$$\begin{aligned} \zeta _B = \int _{T=const.}ds_{B}= & {} \int _{c-e-\Delta }^{c-d-\Delta } \frac{dx^{-}}{\sqrt{{\frac{M}{\Lambda }} + \Lambda ^2 (x^- +\Delta ) (x^- - 2c)}}, \end{aligned}$$

(69)

$$\begin{aligned} \zeta _C = \int _{t=const.}ds_{C}= & {} \int _{c-d-\Delta }^{a-b-\Delta } \frac{dx^-}{\sqrt{\Lambda ^2 x^- (x^- + \Delta ) + \frac{M(b-a)}{\Lambda (b+a)} }}. \end{aligned}$$

(70)

The explicit values of these integrations are provided in “Appendix 3”. In a similar manner, for other cases when a point belongs to Region-B or Region-A, one should integrate up to $ds_B$ or $ds_C$, compatible with the limits of integrations.

In the $(\tau ,\zeta )$ parametrization the expression of Ricci scalar in Region-A is constant on each $\Sigma _{\tau }$ hypersurface. The explicit expression for R in Region-A follows from Eq. (11) and Eq. (64) and is given by

$$\begin{aligned} R (\tau ) = \frac{4 M \Lambda }{M/\Lambda - \Lambda ^2 \tau ^2}. \end{aligned}$$

(71)

Note that the position of singularity is now given by a finite $\tau _{s} = \frac{M^{1/2}}{\Lambda ^{3/2}}$, and we are interested in using this foliation to evolve various quantum states (using CSL) in the open interval $(0,\tau _s)$.

The foliation can be continued backwards to cover the rest of the space-time before the singularity in an arbitrary way, because its exact form will have very little effect on the final result of the state evolution resulting from the CSL interaction (recall we are using a kind of interaction picture and treating the CSL specific modifications of the dynamics as an ineteraction) simply because in our proposal the CSL parameter will only become large in the regions of large curvature which are precisely those covered by the specific foliation presented above. This assumption will be central to the picture whereby, information loss in black hole evaporation is controlled by the same process that, according to collapse theories, controls everyday situations, and helps resolve the measurement problem.

6.2 Specification of collapse operators in modified CSL

The CSL theory can be generalized so as to drive/collapse an initial state into a joint eigenstate of a set of mutually commuting operators $\lbrace A^\alpha \ \rbrace$. This requires the introduction of a white noise function $w^\alpha$ for each one of the $A^\alpha$’s. In this case, the equation corresponding to Eq. (59) takes the form:

$$\begin{aligned} \rho (t) = {\mathcal {T}}e^{-\int _{0}^{t}dt'\big [i[\underrightarrow{\hat{H}}-\underleftarrow{\hat{H}}]+\frac{\lambda }{2}\sum _\alpha [\underrightarrow{\hat{A}}^\alpha -\underleftarrow{\hat{A}}^\alpha ]^{2}\big ]}\rho (0). \end{aligned}$$

(72)

We call $\{A^\alpha \}$ the set of collapse operators. In order to adapt CSL evolution to the CGHS scenario, a situation that involves both quantum fields and gravitation, and as anticipated in the previous subsection, we will consider that the rate of collapse is enhanced by the curvature of the space-time, so that, as the evolution approaches the singularity (in a finite time) the rate of collapse will diverge. This will ensure that a complete collapse of the state of the field to one of the eigenstates of the chosen operators occurs in a finite time. Far from the singularity the rate of collapse will be much smaller, and thus the effects of CSL evolution will be negligible.

Also, for this matter, collapse operators have to be smooth and locally constructed from the quantum fields. From these considerations, we choose the collapse operators as the operators that count the number of right-moving particles inside the black hole in a definite state, as described by observers in late times (that is, for observers that describe the Hawking radiation¹¹). Recall that the right moving modes of the field inside the black hole are given by Eq. (29), and the left moving remain the same as in Eq. (28). The Fock space of states of the quantum field in the interior black hole region, ${\mathscr {F}}^{int}_R\otimes {\mathscr {F}}^{int}_L$ has as a basis the set $\{\left| F \right\rangle ^{int}_R\otimes \left| G \right\rangle ^{int}_L\}$.

The action of the right-moving particles number operator¹² $(N^{int}_{R})_{nj} = \hat{\tilde{b}}^{R\,\dagger }_{nj} \hat{\tilde{b}}^{R}_{nj}$ acting on ${\mathscr {F}}^{int}_R$ is the following:

$$\begin{aligned} (N^{int}_R )_{nj} \left| F \right\rangle ^{int}_R= F_{nj} \left| F \right\rangle ^{int}_R. \end{aligned}$$

(74)

The set of collapse operators we are proposing for the modification of CSL is $\{\tilde{N}_{nj}\}$, where

$$\begin{aligned} \tilde{N}_{nj} \equiv (N^{int}_R)_{nj} \otimes \mathbb {I}^{int}_L\otimes \mathbb {I}^{ext}_R\otimes \mathbb {I}^{ext}_L \end{aligned}$$

(75)

where $\mathbb {I}^{int}_L$, $\mathbb {I}^{ext}_R$, and $\mathbb {I}^{ext}_L$ are the identity operators in the corresponding Fock spaces. Any state in the basis of ${\mathscr {F}}^{out}$ [see Eq. (32)] is now an eigenstate of the collapse operators $\tilde{N}_{nj}$:

$$\begin{aligned} \tilde{N}_{nj} \left| F \right\rangle ^{int}_R \otimes \left| G \right\rangle ^{int}_L \otimes \left| H \right\rangle ^{ext}_R \otimes \left| I \right\rangle ^{ext}_L=F_{nj} \left| F \right\rangle ^{int}_R \otimes \left| G \right\rangle ^{int}_L \otimes \left| H \right\rangle ^{ext}_R \otimes \left| I \right\rangle ^{ext}_L. \end{aligned}$$

(76)

As we already noted, the states characterized by a definite number of particles in the individual modes we are working with, are not of the Hadamard form and they correspond to a singular behavior of the energy-momentum tensor expectation value, precisely along the black hole horizon. However, we must note that the standard CSL evolution controlled by a fixed value of $\lambda$ is meant to be a smooth one and, in fact, it only drives the state to one of the eigenstates of the collapse operator in the limit $t \rightarrow \infty$.

In our case, as we already anticipated, we will choose a variable but smooth $\lambda$ which, however, will be bounded except as one approaches the singularity where, one expects, quantum gravity effects to become dominant, and where the space-time picture will likely break down. Moreover, in our case we will chose the CSL evolution that is driven by collapse operators that are smooth and locally constructed from the quantum fields, the initial state of the field [as defined in past null infinity as in Eq. (78)] is a regular (Hadamard) state with a smooth expectation value for the energy-momentum tensor, and thus the state resulting from the evolution at any hypersurface of our foliation lying before the singularity, will also be a regular (Hadamard) state with a smooth expectation for the energy momentum tensor. Again this is just as it occurs in the case of the state resulting from the Minkowski vacuum of a quantum field interacting with a physical detector which is characterized by a smooth operator and thus, as we discussed, can not measure the precise number of Rindler particles in a particular mode in a finite amount of time.

6.3 The curvature dependent coupling $\lambda$ in modified CSL

As we have said, in the toy model of CSL we are proposing the rate of collapse is enhanced by the curvature of the spacetime. This mechanism is introduced in terms of the rate of collapse $\lambda$, which will be dependent, in this case, on the Ricci scalar:

$$\begin{aligned} \lambda (R) = \lambda _0 \left[ 1+\left( \frac{R}{\mu }\right) ^\gamma \right] , \end{aligned}$$

(77)

where R is the Ricci scalar of the CGHS space-time and $\mu$ and $\gamma \ge 1$ are constants.

This is a key hypothesis made in the paper, which states that there is some connection between the physics that underlies the dynamical collapse of quantum states with gravity. The argument is that assuming the rate of collapse intensifies in a region of high curvature, information might be completely destroyed due to the stochastic nature of this process. Of course, this hypothesis cannot be confirmed or ruled out as of now. In order to do that, one would need to perform experiments or analyze observations of a quantum process in presence of ultra-strong gravity.¹³

Note that the hypersurfaces given by the foliation in Sect. 6.1 have constant R inside the black hole (in almost all the part of $\Sigma _\tau$ that lies inside). Then, from Eq. (71) we have that for the region of interest, the rate of collapse depends on the time parameter defined by the foliation, $\lambda =\lambda (\tau )$. Standard CSL is defined for a constant value of $\lambda$, however, the generalization to time-dependent $\lambda$ is simply done by making the substitution $\lambda \rightarrow \lambda (\tau )$.

This choice for the curvature dependence of the CSL parameter is meant to ensure that the initial state would be driven to an eigenstate of the collapse operators in a finite amount of time $\tau$ so that, if we were to continue the evolution up to the singularity (we will not contemplate that simply because, as we indicated, it is within this region where we expect quantum gravity effects to dominate and the space time picture to break down, invalidating most of our considerations), the state of the field would be one with definite number of particles in each mode. The point, however, is that such (singular) state would only be approached as one approaches the singularity, and the state of the field, in the region before the singularity where semiclassical considerations are expected to hold, will be a state with a smooth expectation value for the energy-momentum tensor.

At this point, we must comment on the importance of the dimensionality of the model under consideration in selecting the curvature dependent coupling of the parameter $\lambda$. Clearly, for a more realistic, four dimensional models, this choice has to be done in a way that it does not lead to big deviations in the evolution of the early Universe. Otherwise such changes would have to be carefully investigated. In making our proposal we take Penrose’s Weyl curvature hypothesis [71] as a guiding principle. As already mentioned in the earlier work [1], in a four dimensional model, $\lambda$ can be naturally taken to be a function of Weyl scalar $W_{abcd}W^{abcd}$ and, as the early Universe is thought to have a comparatively small value of such quantity, the deviations from the standard quantum mechanical consideration can be expected to be insignificant. However, for the two dimensional case at hand, Ricci scalar can be chosen to be the only one algebraically independent component of the Riemann-tensor, and thus we take $\lambda$ to depend on R as defined in (77).

6.4 Initial state and modified CSL evolution

As we have mentioned in Sect. 2, a left-moving pulse of matter produces the CGHS black hole. Then, the initial state of the quantum field, defined in ${\mathscr {I}}^-$, that will evolve in this space-time is

$$\begin{aligned} \left| \Psi _{i} \right\rangle= & {} \left| 0 \right\rangle ^{in}_R\otimes \left| Pulse \right\rangle _L\nonumber \\= & {} N \sum _F e^{-\frac{\pi }{\Lambda } E_F} \left| F \right\rangle ^{int}_{R}\otimes \left| F \right\rangle ^{ext}_{R} \otimes \left| Pulse \right\rangle _L, \end{aligned}$$

(78)

where we have used Eq. (35). The state $\left| Pulse \right\rangle _L$ can be considered as a very localized left-moving wave packet. Because of the dependence of the CSL parameter $\lambda$ on the curvature we can assume that the state $\left| \Psi _i \right\rangle$ will remain mostly unchanged as it evolves outside the horizon since $\lambda$ would be very small (recall we are working in the interaction picture) until it reaches some hypersurface $\Sigma _{\tau _0}$ described by the foliation given in Sect. 6.1. In this section we derive the final density matrix for the modified CSL evolution of the initial state $\left| \Psi _{i} \right\rangle$, Eq. (78), from the initial hypersurface $\Sigma _{\tau _0}$ to a final hypersurface $\Sigma _{\tau }$.

The final state of this evolution will depend on the particular set of stochastic functions $w^\alpha$ that occurred during the evolution. In order to take into account our ignorance on this particular realization of the $w^\alpha$, we will describe the evolution by considering an appropriate ensemble. So let us consider an ensemble of systems identically prepared in the same initial state $\left| \Psi _{i} \right\rangle$.¹⁴ This ensemble is described by the pure density matrix $\rho (\tau _0) = \left| \Psi _i \right\rangle \left\langle \Psi _i \right|$. Note that even though we are talking about an ensemble, the density matrix is pure because all systems are in the exact same state. The evolution of this density matrix can be done simply using CSL.

Then, for the free field evolution, Eq. (72) reads:

$$\begin{aligned} \rho (\tau ) = {\mathcal {T}}e^{-\int _{\tau _0}^{\tau }d\tau '\frac{\lambda (\tau ')}{2}\sum _{nj} [\underrightarrow{\tilde{N}}_{nj}-\underleftarrow{\tilde{N}}_{nj}]^{2}}\rho (\tau _0). \end{aligned}$$

(79)

Note that $\rho (\tau _0) = \left| \Psi _i \right\rangle \left\langle \Psi _i \right|$ can be expressed as:

$$\begin{aligned} \rho (\tau _0) = \left| 0 \right\rangle ^{in}_R\left\langle 0 \right| ^{in}_R \otimes \left| Pulse \right\rangle _L \left\langle Pulse \right| _L = \rho _R (\tau _0) \otimes \left| Pulse \right\rangle _L \left\langle Pulse \right| _L . \end{aligned}$$

(80)

The evolution operator in Eq. (79) acts only on $\rho _R (\tau _0)$. The right-moving initial density matrix, $\rho _R (\tau _0)$ takes the following form when expressed in terms of the out quantization:

$$\begin{aligned} \rho _R (\tau _0) = N^2 \sum _{F,G} e^{-\frac{\pi }{\Lambda } (E_F +E_G )} \left| F \right\rangle ^{int}_R\otimes \left| F \right\rangle ^{ext}_R \left\langle G \right| ^{int}_R \otimes \left\langle G \right| ^{ext}_R . \end{aligned}$$

(81)

On the other hand, we have

$$\begin{aligned}&\sum _{nj} [\underrightarrow{\tilde{N}}_{nj} - \underleftarrow{\tilde{N}}_{nj}]^2 \left| F \right\rangle ^{int}_R\otimes \left| F \right\rangle ^{ext}_R \left\langle G \right| ^{int}_R \otimes \left\langle G \right| ^{ext}_R \nonumber \\&\qquad = \sum _{nj} (F_{nj}-G_{nj})^2 \left| F \right\rangle ^{int}_R\otimes \left| F \right\rangle ^{ext}_R \left\langle G \right| ^{int}_R \otimes \left\langle G \right| ^{ext}_R . \end{aligned}$$

(82)

The calculation is facilitated by the fact that the $\tilde{N}_{nj}$ and their eigenvalues do not depend on $\tau$. Thus, for any $\tau$, we have:

$$\begin{aligned} \rho _R (\tau )= & {} N^2 \sum _{F,G} e^{-\frac{\pi }{\Lambda } (E_F +E_G )} e^{- \sum _{nj} (F_{nj}-G_{nj})^2\int _{\tau _0}^{\tau }d\tau '\frac{\lambda (\tau ')}{2}} \left| F \right\rangle ^{int}_R\otimes \left| F \right\rangle ^{ext}_R \nonumber \\&\times \left\langle G \right| ^{int}_R \otimes \left\langle G \right| ^{ext}_R. \end{aligned}$$

(83)

In general, this density matrix does not represent a thermal state. Nevertheless, as $\tau$ approaches the singularity, say at $\tau =\tau _s$, the integral¹⁵

$$\begin{aligned} \int _{\tau _0}^{\tau }d\tau '\lambda (\tau ') = \lambda _0 \left( \frac{4 \sqrt{M\Lambda } \tanh ^{-1}\left( \frac{\Lambda ^{3/2}}{\sqrt{M}}\tau \right) }{\mu }+\tau \right) _{\tau _{0}}^{\tau _s = \frac{\sqrt{M}}{{\Lambda ^{3/2}}}}, \end{aligned}$$

(84)

diverges simply because of the way $\lambda (\tau )$ increases with curvature. Therefore, as $\tau \rightarrow \tau _s$ the non diagonal elements of $\rho (\tau )$ vanish and we have in this limit:

$$\begin{aligned} \lim _{\tau \rightarrow \tau _s} \rho _R (\tau ) = N^2 \sum _{F} e^{-\frac{2\pi }{\mu } E_F} \left| F \right\rangle ^{int}_R\otimes \left| F \right\rangle ^{ext}_R \left\langle F \right| ^{int}_R \otimes \left\langle F \right| ^{ext}_R. \end{aligned}$$

(85)

Thus, when $\tau \rightarrow \tau _s$, the complete density matrix that represents the evolution of state Eq. (78) is given by

$$\begin{aligned} \lim _{\tau \rightarrow \tau _s} \rho (\tau ) = N^2 \sum _{F} e^{-\frac{2\pi }{\mu } E_F} \left| F \right\rangle ^{int}_R\otimes \left| F \right\rangle ^{ext}_R \left\langle F \right| ^{int}_R \otimes \left\langle F \right| ^{ext}_R \otimes \left| Pulse \right\rangle _L\left\langle Pulse \right| _L. \end{aligned}$$

(86)

Note that $E_F$ represents the energy of state $\left| F \right\rangle ^{ext}_R$ as measured by late time observers. The operator given by Eq. (86) represents the ensemble when the evolution has almost reached the singularity (at the hypersurface $\Sigma _{\tau \rightarrow \tau _s}$). However, we want to describe the evolution beyond the singularity for which we have to consider the effects of a plausible quantum theory of gravity. We elaborate on this matter in the next subsection.

6.5 A task for quantum gravity

The fact that CSL evolves states towards one of the eigenstates of the collapse operators ensures that as the result of our evolution, the state at hypersurfaces $\tau$ constant but very close to the singularity would be of the form

$$\begin{aligned} \left| \Psi _{\tau \rightarrow \tau _s} \right\rangle = \left| F \right\rangle ^{ext}_R \otimes \left| F \right\rangle ^{int}_R\otimes \left| Pulse \right\rangle _{L} \end{aligned}$$

(87)

for some particular number of particles distribution F. Note that in the expression above there is no summation implied over the F. The state is a pure one, with a definite occupation number in each of the field’s modes.

Next, we consider the role that is reserved for a quantum theory of gravity: We will assume that a reasonable theory of QG will resolve the singularity and lead, on the other side, to a reasonable space-time. Moreover, we will assume that such a theory will not lead to large violations of the basic space-time conservation laws.

On the basis of these assumptions, we consider the situation on the hypersurface that lies “just before the singularity” (we could define such hypersurface more precisely by requiring that the curvature reaches a particular value close to that where quantum gravity effects should become important, say, half the Planck scale). There, from the “energetic point of view”, we would have the following:

• (i) The positive energy flux associated with the incoming left moving pulse that formed the BH.

• (ii) The negative flux associated with the remaining left moving modes in a vacuum state (from Region-II to Region-III in Fig. 1) which is known to correspond essentially to the negative of the total Hawking radiation flux (see Sect. 3.2).

• (iii) The flux associated with the right moving modes which crossed the collapsing matter and which went directly into the singularity (from Region-I’ to Region-III in Fig. 1).

The only part missing in the above energy budget is that corresponding to the Hawking radiation flux. If, as we have assumed, energy is to be essentially conserved by QG, it seems that the only possibility for the state in the post singularity region is one corresponding to a very small value of the energy. It is possible that such state of negligible energy would be associated with a small amount of remnant radiation, or perhaps some kind of stable Planck mass remnant.Those possibilities would represent a situation where some of the initial information survives the whole process. For simplicity, we will ignore that alternative, and replace it by the simplest thing: a zero energy momentum state corresponding to a region of space-time that would necessarily be trivial. We denote it by $\left| 0^{post-singularity} \right\rangle$.

Therefore, we can complete the description of the evolution of the initial situation, by assuming that the effects of QG can be represented by: (a) the cure of the singularity and (b) the transformation of the state just before to that one just after the would be singularity (or more precisely, the quantum gravity region) represented as s follows;

$$\begin{aligned} \left| \Psi _{\tau \rightarrow \tau _s} \right\rangle= & {} \left| F \right\rangle _R^{ext} \otimes \left| F \right\rangle _R^{int}\otimes \left| Pulse \right\rangle _{L}\nonumber \\\longmapsto & {} \left| F \right\rangle _R^{ext} \otimes \vert 0^{post-singularity}\rangle . \end{aligned}$$

(88)

The above result is a bit unsettling because we end up with a pure quantum state, but we do not know which one. That selection, according to CSL, is determined by the particular realization of the collection of random functions $w^\alpha$ that appear in the evolution equation for the state. That is, it depends on precisely the stochastic aspects of the CSL evolution of the quantum state.

One might be concerned about the naturalness of the choice for the collapse operators used to drive the CSL modifications. It might be argued that it does not seem to be a very natural one as the notion of particle number in the interior region is completely ad hoc because there is not even a time-like Killing field. One can argue that the choice is made because of the correlations that occur in the in-vacuum, between those states and the states with well defined energy in the asymptotic region, which are states with a definite number of particles in the outside region. We will not attempt to further justify such choice here, and will only note the relative robustness of the analysis that is expected to emerge from the fact that the density matrix characterizing a subsystem of a system in a pure state (resulting from tracing the rest of the system’s degrees of freedom) is independent of the choice of basis. In fact, as we will see in the next section, the final result we obtain characterizes the end point of the black hole evaporation, in terms of a density matrix. We will mention some subtleties in this regard after that discussion.

7 The final result

Now we are ready to proceed to the effective description of the end state taking into account the effects of a quantum theory of gravity. In Sect. 6.4 we have already described the evolution up to a hypersurface “just before the singularity”. The ensemble at this hypersurface ( $\Sigma _{\tau _s- \epsilon }$) is described by the density operator

$$\begin{aligned} \lim _{\tau \rightarrow \tau _s} \rho (\tau ) = N^2 \sum _{F} e^{-\frac{2\pi }{\mu } E_F} \left| F \right\rangle ^{int}_R\otimes \left| F \right\rangle ^{ext}_R \left\langle F \right| ^{int}_R \otimes \left\langle F \right| ^{ext}_R \otimes \left| Pulse \right\rangle _L\left\langle Pulse \right| _L. \end{aligned}$$

(89)

If we now take into account what we have assumed about QG, we end up with a density matrix characterizing the ensemble after the region that would have corresponded to the singularity, (i.e for instance on the hypersurface appearing in Fig. 5 with no name), which is given by

$$\begin{aligned} \rho _{final}= & {} N^2 \sum _{F} e^{-\frac{2\pi }{\Lambda } E_F} \left| F \right\rangle ^{ext}_R \otimes \left| 0^{post-sing} \right\rangle \left\langle F \right| ^{ext}_R \otimes \left\langle 0^{post-sing} \right| \nonumber \\= & {} \left| 0^{post-sing} \right\rangle \left\langle 0^{post-sing} \right| \otimes \rho ^{ext}_{thermal}. \end{aligned}$$

(90)

That is, we started with an initial pure state (characterizing the ensemble of identical systems in the same state) of the quantum field corresponding to an initially collapsing pulse, which we can imagine as being given together with the initial space-time data on past null infinity, and we ended up with a situation where the ensemble is characterized by a proper mixture with thermal characteristics on the early part of future null infinity and followed by an empty region. That is precisely what was needed in order to reconcile the Hawking evaporation of a black hole with Quantum Theory. Of course in this case, the result arises from the modified quantum evolution provided by CSL.

Fig. 5

Plausible spacetime structure including the post-singularity region. For details see the text

Here, we see that the questions concerning the choice for the collapse operators used to drive the CSL modifications, which are connected to the details of the collapse taking place in the inside region should have essentially no effects on the overall result simply because, as a result of the quantum gravity resolution of the singularity, and the considerations regarding overall energy conservation, the details of the state characterizing the field just before the region requiring an essential quantum gravity description (i.e., the “would be singularity”) are simply erased. That is, as argued above, the crossing of the “would be singularity” should lead to:

$$\begin{aligned} \left| F \right\rangle ^{ext}_R \otimes {\left| Pulse \right\rangle }_{L} \longmapsto \left| 0^{post-singularity} \right\rangle . \end{aligned}$$

(91)

In fact, if we concern ourselves with the quantities that are conceivable measurable by observers in the outside, the issue of exactly what operators drove the collapse in region III, would be analogous to Bob’s question regarding the orientation of the spin that was measured by Alice on an EPR situation.¹⁶ That is, the answer can not be determined by any measurement conceivably made by Bob without input of regarding what Alice does.

8 Discussions

We have presented a proposal to address the issue known as the “Black Hole Information Paradox”. The picture that emerges is represented in Fig. 5, which is essentially the same as the one presented in [17]; however, in our proposal the answer to the question about the fate of information is completely opposite to that advocated in that work. According to the picture we have presented here, the state of the quantum field (corresponding to the ensemble of identically prepared systems) on a very early hypersurface, such as $\Sigma _0$ (in Fig. 5), is pure, and then evolves according to CSL resulting at late hypersurfaces (which are still to the past of the singularity), such as $\Sigma _{\tau _s -\epsilon }$, in a mixed state (representing, as discussed in Sect. 4, an ensemble of systems) that is in fact thermal, according to the set of asymptotic observers of the ensemble of evaporating black holes. That state corresponds to a situation where essentially all the initial energy (corresponding to the matter pulse in $\Sigma _0$) appears as radiation crossing the $\Sigma _{\tau _s -\epsilon }$ hypersurface towards the asymptotic region. Thus, when considering the state on $\Sigma _{\tau _s -\epsilon }$, the information has already been lost, and the state is non unitarily related to that in $\Sigma _0$. A theory of quantum gravity must then be evoked as resolving the singularity, and leading to a state of the matter fields containing essentially no energy. That is, the state of the fields in the region just after the singularity must be a sort of local vacuum corresponding to a flat region of space-time (i.e., the effects of quantum gravity must be represented by Eq. (91)). Then, on ${\mathscr {I}}^{+}_{R}$, we will have a situation corresponding to a thermal state in the early times, a small pulse containing very little energy and associated with the start of the shadow of the would be singularity (i.e, the boundary of the causal future of the region containing the singularity), a point where there could be some influence of a complex back reaction, and perhaps also some traces of influences of quantum gravity, and to the future of that point, the state is just the vacuum. To make the point more forcefully, Fig. 5 also depicts a hypersurface (with no particular name) that encodes everything that is left after the singularity disappears. The hypersurface has no points to the past of the quantum gravity region that replaces the singularity. On such hypersurface the state of the field represents the Hawking radiation and nothing else. According to this picture, during the black hole evaporation information is lost, however, that is just the result of the modified evolution described by a dynamical reduction theory such as CSL (which is meant to be the correct theory that replaces ordinary quantum mechanics). In other words, information is lost, in this case, just as it is lost in all physical process, with the only difference being the effective rate for this loss which, in the case of the black hole, is enhanced by our hypothesis regarding the dependence of $\lambda$ on curvature.

There are, of course, many issues that are not completely satisfactory in the specific account given throughout this work and shortly we shall elaborate on them. However, we feel that the essential picture would remain valid in more realistic treatments. To start with, the example which we worked is two dimensional while our space-time has 4 dimensions. We do not think that this poses a serious problem. Among others, one issue that concerns people regarding the notion of information loss, are the arguments that any such process must be accompanied by the unacceptable breakdown of either, causality, or energy-momentum conservation [79]. Such arguments have been confronted in [80], by providing examples of evolution laws capable of leading from pure states to mixed states under conditions involving Planck scale physics, while locality and causality are preserved, and where the deviations from ordinary dynamics are exceedingly small, and thus empirically acceptable for laboratory situations.

As we explained, the BHIP appears if one assumes that quantum gravity resolves the BH singularity, and, therefore, removes the need to incorporate an additional space-time boundary. One might argue that, even if quantum gravity resolves the singularity, one should still keep an additional boundary where information is registered. One might, for instance, take the view that quantum gravity itself leads to the loss of information and that an extra boundary has to be added in any description of a classical space-time, if it is known that there is a non-classical region, that can only be characterized in terms of a quantum gravity language. The boundary could then be thought as the receptacle for the apparently lost information, and the inclusion and characterization of the quantum state there, as restoring a fully unitary evolution. One fact that suggests that it is worthwhile looking for a different solution from the one considered above, is that the hypersurface where the lost information is supposed to be encoded (i.e., that representing the new boundary of space-time), would have to be contained in a region where, as a result to the negative Hawking flux, there should be very little or no energy remaining at all. Thus, if we were to adopt such a view, we would be considering the near singularity region, and whatever replaces the singularity in a theory of quantum gravity, as the region that contains the missing information, despite the fact that such region must be deemed to contain essentially no energy. That is, even before considering the singularity, we can think that there is a problem similar to that in the standard BHIP, simply because an enormous amount of information must be contained in a region having essentially no energy. The scheme we have been considering in this manuscript clearly eliminates also that aspect of the problem.

Furthermore, in taking a view like the last one considered above, one ends up acknowledging that the quantum gravity effects that resolve the singularity are, at the same time, responsible for the information loss. The idea would be then, that such information loss occurs only in connection with regions that would correspond to classical singularities, and which we normally associate with very special conditions such as those connected with black holes. However, at the fundamental level, one would have to say that a theory of quantum gravity, which is in principle able to lead to information loss, also underlies our notions of space-time in general. Thus, one might wonder, why would such quantum gravity effects not make an appearance in ordinary situations, perhaps only as highly suppressed effects, associated with radiative corrections involving things like virtual black holes?

At this point, it seems natural to offer the following speculative idea (first described in [1]): If we accept that the Hawking evaporation of large black holes leads to a loss of information and to the associated deviation from quantum mechanical unitary evolution, one might wonder about the effects of virtual black holes that can be expected to contribute, just as any other quantum process to the sum over histories associated with a quantum theory that includes the space-time degrees of freedom. One might at first argue that such objects might have to correspond to something like the Planck scale mass, and that their corresponding Compton wavelength would be too large for the formation of a black hole, however after a second look, it seems unclear why should larger virtual black holes be excluded from contribution, even if only with an exceedingly small amplitude, and furthermore, why such classical considerations, regarding for instance the ratio of mass to size for the formation of a black hole, should apply to virtual objects which can, in principle, be “off-shell”.¹⁷ Needless is to say that we can not expect clear cut answers to the above questions in the absence of a fully satisfactory and workable theory of quantum gravity. However, if we accept that something that might be characterized, loosely speaking, as virtual black holes, should contribute, given the quantum nature of gravity, to all physical process, we would be led to expect, that some amount of information loss, and of departure of unitarity evolution should be an intrinsic part of the effective description of quantum evolution in general. This, in turn, seems to bring us to expect a departure from Schrödinger evolution, not unlike the one consider in the modified theories involving spontaneous collapse such as GRW and CSL. The global picture that emerges requires adopting a view about our theories of nature that allows for a kind of self referral, which reminds us of the boot-strap ideas in the physics of strongly interacting particles, and that is discussed in more detail in [1]. We should note that, in a sense, this views do not seem to be very distant, at least in spirit, to those in work [80], although there, the connection with the measurement problem seems not to have been made.

We should note here the early arguments [81] made by Penrose in connection of the possibility of thermal equilibrium and ergodic behavior in situations involving matter in quasi-flat space-time and fully formed black holes. Those arguments strongly indicated the need to incorporate something like the stochastic reduction of the quantum state of matter fields in ordinary conditions, in order to have a self consistent picture of such equilibrium situations.

One aspect of the present proposal that we find particularly appealing is the fact that, in contrast with most other attempts to offer a resolution of the BHIP, and which are designed specifically to address just that specific problem, the dynamical collapse theories were designed to address a very different difficulty in our current theoretical description of nature: the measurement problem in quantum mechanics. We find it truly remarkable that such proposals seem to be able (when appropriately refined and modified) to deal also with the BHIP. Furthermore, as was already pointed out in [1], the scheme we have presented has the appealing feature of connecting the plausible resolution of other problems afflicting our understanding of the workings of nature in a single unified picture: the measurement problem, the emergence of the primordial inhomogeneities during inflation [82–85], and the problem of time in canonical quantum theories of gravitation.

It should also be pointed out, that part of the emphasis in looking for a resolution of the black hole evaporation problem, in a way that ensures the unitary connection between initial and final states, comes from the AdS/ CFT conjecture. However, if the quantum mechanical evolution on the two sides of the duality, is controlled by a modified evolution law, involving non-unitarity and stochasticity, such as GRW or CSL, the duality might still be possible even if the end result of the evolution of a black hole that forms out of a pure state is a thermal state.

It is clear that in the course of the present analysis we have assumed that a theory of quantum gravity would “resolve” the singularity, and that it leads to no gross violations of conservation laws (which would otherwise have potentially observable implications) in the regions where something close to a classical space-time description is expected to be a very good approximation

We acknowledge that we made several simplifying assumptions and that we have ignored certain delicate and difficult issues. However we can expect the general picture we obtained to be rather robust. We next deal briefly with the most important of these approximations and issues:

• 1. Choice of collapse operators The question of what are the operators $A_{\alpha }$ which control the CSL dynamics as a unified and universal rule is an open issue. It is clear a complete theory should specify what determines such operators, for all possible circumstances, and in a manner that depends only on the dynamics of the system in question. The early studies in the context on the non-relativistic many particle quantum theory indicate that they must correspond to a kind of smeared position operators. In Sect. 6.2 we took these to be the particle number operator for each of our partially localized modes in the interior of black hole region. That choice was done for calculational convenience. On the other hand it is clear that within the context of a fully covariant theory these fundamental operators should to be locally constructed from the quantum fields, and the number operators we have used are clearly non-local. This might seem like a serious concern. However, it turns out that in these theories, one can rewrite the same CSL evolution in terms of various different choices of operators. In fact, in the work [87], a CSL evolution that was in principle controlled by operators associated with modes of definite wavenumber $\vec {k}$, was shown to be easily expressed in terms of a CSL evolution controlled by operators associated with local field operators, directly connected with the quantum field and its momentum conjugate. Moreover, as it is well known from considerations of EPR situations, the collapse of the state into eigenvalues of an operator associated with a certain space-time region, has no influence whatsoever in the effective description in terms of density matrix for the state restricted to space-time regions that are causally disconnected (that is the reason one can not use an EPR pair to send information in a causal way). To see the point more clearly lets focus on the case of an EPR pair with correlated spin 1/2 particles, and use the standard Alice and Bob description. We know that what exactly is the operator measured by Bob has no influence in the density matrix that describes the particle still in the hands of Alice, but which she has yet to subject to a measurement (that is the reason such non-locallity can not be used to send signals faster than light). The situation with the CSL collapse is just like that (as it involves a kind of non-locality that can not be used to send a causal signals¹⁸). That is, the exact nature of the quantity controlling the CSL collapse that occurs in the inside region (that with high curvature) will have no effect in the density matrix that describes the situation outside the black hole. On the other hand while in the case of a standard type of EPR setting, we might analyze the correlations between the outcomes of Alice versus Bob measurements which will depend on the quantities measured by each one (i.e. for instance of the various components of the spin), it is clear that things change dramatically in our setting, because the state of the subsystem corresponding to Bob (i.e. the matter field in the inside BH Region) will simply disappear. In other words, the state of the quantum field in the region just after the would be singularity or Quantum Gravity region, should correspond to something like a vacuum state with negligible amounts of energy and of information, an thus there would be essentially no nontrivial correlations to look for. Thus, we can expect such robustness (i.e., independence of the precise choice of collapse operators in the region III) will apply to the density matrix that describes of the quantum field state on ${\mathscr {I}}^{+}_{R}$.

• 2. Choice of foliation We have performed the present study using a particular foliation, which is adapted to the fact that, in our proposal, the CSL parameter $\lambda$ depends on the scalar curvature R. However, if the fundamental collapse theory is fully covariant as should be expected from a realistic collapse theory, the evolution of the state in the interaction picture approach we have been using, should be describable in terms of a Tomonaga–Schwinger equation¹⁹ where, instead of the interaction hamiltonian, we would have the corresponding collapse theory density operator. In such setting, any specific physical prediction would be foliation independent. Furthermore, when considering a foliation of a region of space-time lying away far from the singularity, the changes in the state around any point, associated with the CSL type evolution should be describable in terms of regular local operators. In that case these changes in the state will be very small, as the CSL-like parameter $\lambda$ will remain small in regions where the curvature is small, and, in particular, these changes should not lead to anything like “firewalls” on the part of the horizon²⁰ which is far from the singularity. See the related comments at the end of Sect. 3.3.

• 3. Relativistic Covariance The issue above clearly illustrates not only the conceptual importance, but the great relevance for the problem at hand, of the question of general covariance of the full scheme. We have based our treatment on a non-relativistic model of spontaneous collapse theory, while a truly satisfactory proposal to deal with the issue should be based on a fully covariant theory. Fortunately, the early studies [72, 73], and the recent specific proposals for special relativistic versions of these type of theories [74–78] indicate that we should be able to address this shortcoming in near future. We just note again that in those theories the interaction picture evolution should be describable in terms of a Tomonaga–Schwinger equation where the interaction hamiltonian is replaced by the corresponding collapse theory density operator. In that case we should be able to carry the study, within those theories, of the present proposal, although it is clear that the task would be far from trivial.

• 4. Energy conservation When considering an individual situation, rather than an ensemble, the energy of the initial pulse of matter will, in general, not be exactly equal to that corresponding to the state with definite number of particles $\left| F \right\rangle ^{ext}_R$ that characterizes the modified matter content in the asymptotic region, once the black hole has evaporated completely.²¹ In this regard we note that CSL, in general, leads to small violations of energy conservation, a fact that has led to establish the most stringent bounds on the parameter $\lambda$ (although modified covariant theories might evade this problems altogether. See for instance discussions in [76, 77, 80]). Moreover, we note that if there is a small amount of energy remaining inside the black hole region, and very close to the singularity, simply because the positive and negative energy fluxes do not precisely cancel each other, there would be no problem, at least in principle, if such energy were to be radiated after the singularity. In such case, the resulting picture would be one in which most of the initial energy making the in-falling pulse of matter would have been radiated in standard Hawking radiation, and a small amount of energy would remain to be radiated towards infinity from the “quantum gravity region”.

• 5. Possibility of radiation after the singularity If, as described above, there is some energy left to be emitted from the quantum gravity region, the corresponding radiation might, in principle, contain a small amount of the initial information, and its state could even be correlated with the radiation emitted in the earlier stages. However, as such energy will be minuscule compared with the initial energy that led to the formation of the black hole, following standard arguments, we do not expect the amount of information that the corresponding field can encode, to be significant, thus even when contemplating this possibility, the essence of the picture we have presented here, would remain unchanged.

• 6. Backreaction In the discussion so far, we have omitted the very important issue of back reaction. The changes in the space-time metric as a response to those in the state of the matter fields, are crucial in accounting for the decrease of the mass of the black hole that must accompany the Hawking radiation. This is essential for the arguments involving overall energy conservation which, in turn, underlay all arguments concerning the nature of the space-time that emerges on the other side of the quantum gravity region which replaces the classical singularity. In a more realistic model, and as a result of the the backreaction, the space-time metric, and the black hole’s mass would change, and so would its “instantaneous Hawking temperature”. Then the “late time” radiation would be, in a sense, emitted at a higher temperature than the “early times” one, leading to the runaway effects that are associated with the expected explosive disappearance of the black hole itself. All such effects are extremely important to obtain a realistic picture of the entire history of formation and complete evaporation of a black hole, but none of that seems to require an essential modification of the proposal we have put forward in this work.

  In fact, the back reaction is responsible for the decrease of the Bondi mass to a very small value, as one considers the very late parts of ${\mathscr {I}}^{+}_{R}$ (in Fig. 3), and that is what allows us to consider, matching our space-time, at least in the the asymptotic region, with the one essentially empty, and flat one expected to emerge on the other side of the quantum gravity region.

• 7. Reliance on semi-classical gravity The issue discussed above led to us to reconsider the basic viability of semi-classical gravity, the framework in which all the present approach is based. Before engaging in this discussion we should note that the alternative to semi-classical treatment of gravity, would entail the use of some quantum theory of gravitation. The issue is, however, not only that do we lack, at this point, any such theory that is sufficiently developed to offer us in general a satisfactory characterization of quantum space-time, but that, as indicated in the introduction, these theories (at least the ones based on a canonical approach) suffer from the so called “ problem of time” as exemplified by the Wheeler de Witt, and the Loop Quantum Gravity proposals, a fact that impedes the presentation of a truly space-time description of any situation. In fact, the recovery of such a space-time picture, in general, is an open problem, and the only situations in which that seems to be possible require some sort of approximated treatment, that involves selecting some physical observable to play the role of a clock, and then resorting to some king of relative wave-function characterization of the remaining variables. It is not clear at all how exactly the questions of unitarity and information should be addressed in that context.

  In the semi-classical gravity scheme one treats the space-time metric at the classical level, but uses as a source in Einstein’s equation the quantum expectation value of the energy momentum tensor, and clearly, this is by no means free of problems. The issue was considered in [94], a manuscript that is often referred to, as showing that semi-classical gravity is at odds with experimental results. However, it is not often emphasized that such conclusion is only valid in those contexts where quantum mechanical evolution does not include any sort of measurement-related or spontaneous collapse of the quantum state. Therefore, it is clear that such conclusion would not be relevant for our present proposal. On the other hand, it is clear that if one wants to incorporate the instantaneous (or even the continuous) reduction or collapse of the quantum state of matter fields, Einstein’s semi-classical equation can not be taken as fundamental and 100% accurate. That would be simply inconsistent: The fact is that in general $\nabla ^a \langle T_{ab} \rangle \not = 0$ as the collapse of the quantum state takes place, and therefore $\langle T_{ab} \rangle$ can not be equated with $G_{ab}$, which satisfies $\nabla ^a G_{ab}=0$ identically. The point however, is that when viewing the metric description of space-time as just an effective and approximate characterization of the fundamental entity, in analogy, say, with the way the Navier -Stokes (NS) equation can be used in hydrodynamics, that basic problem might be bypassed. That is, in the same way that one would not expect the NS equation to hold exactly, or to be valid universally, one would not take the semiclassical Einstein’s equation as a fundamental description. In other words, just as one could easily envision situations where the NS would not be an appropriate characterization of the fluid, such as when an ocean wave breaks, or when the fluid is undergoing a phase transition, situations in which one can expect important local departures from the equation, one can expect something similar to happen with the semi-classical Einstein equation. However, we must emphasize that this would not negate the validity of the equation, at least as a good approximation, for describing a large class of regimes in terms of macroscopic and approximate characterizations. It is clear that more precise characterizations, both in the treatment of fluids and of gravitation, would involve higher order and more complicated terms. In fact, eventually, as the phenomena in question become associated with a scale that is closer to the natural scale of the more fundamental underlying theory, one would expect the complete breakdown of such effective description. The initial steps in the exploration of the formal adaptation of this approach to the use of semi-classical gravity in a context involving spontaneous collapse has been developed [86]. There the issue has been explored in detail in the cosmological setting as part of the attempts to understand the breakdown of the symmetries of the quantum vacuum during inflation, and the generation via quantum fluctuations of the primordial inhomogeneities and an-isotropies, an issue that has been the focus of various previous studies [82]. A brief review of that formalism is presented in “Appendix 4”. One should note in this regard, the work [95] which considers in some detail the general arguments against semi-classical gravity, and which indicates that they are not as conclusive as they are sometimes presented.

One more thing that is worth discussing at this stage, is the contrast in the overall picture that emerges in the present approach with that which would result from schemes in which information is preserved due to some exotic quantum gravity features.

To clarify this it is convenient to recall one of the early arguments against the information preserving proposal that would rely on things like Planck mass remnants from the black hole evaporation. In those proposals one would need the complete quantum state describing the Hawking thermal radiation and the degrees of freedom of the remnant to be pure. We have of course no proof that this is impossible, however the resulting picture seems rather unnatural simply because the internal degrees of freedom of the remnant, whose mass would be of the order of $10^{-5}$ gr. would have to be essentially equal to the number of degrees of freedom associated with the radiation, which in this case would have the same total energy as the corresponding collapsing star (or gas cloud) that led to the formation of the black hole in the first place. Thus, the essential argument against these kind of proposals is that it requires us to accept the existence of objects with an incredible disparity between their energy content and their number of available degrees of freedom.²² It is worth noting therefore that if, as suggested in some proposals, information is fully preserved, via the escape of quantum correlations through the quantum gravity region which resolved the singularity, we would have a very similar situation. Namely, in those schemes, the picture would be that long after the black hole had evaporated completely, the quantum state describing the complete set of degrees of freedom would be 100 % pure, and yet its energy will be essentially associated with the quasi-thermal subset (taking into account the increase of Hawking temperature as the black hole mass decreases), characterizing the radiation at infinity, while the post quantum gravity region would have very small energy content, and yet it will have an exceedingly large number of degrees of freedom available.²³ Furthermore, even if we wanted to consider a scheme whereby information is lost, but only in association with the quantum gravity region, we might face a similar naturalness problem. That is, when considering an hypersurface that passes in the black hole interior just to the past of the singularity (or more precisely, the quantum gravity region) the same issues would arise. In other words, the state of the quantum field associated with such hypersurface would be pure, and yet its energy content would be divided into the overwhelmingly large component being carried away towards infinity by the Hawking radiation and the tiny amount remaining in the very low mass black hole that would be there at the very late times. The point again would be that these two components would have to have essentially the same number of available degrees of freedom despite being so energetically dissimilar. In contrast, in the proposal we have considered here the information is erased as the mass of the black hole decreases leading to a more natural type of situation where the available degrees of freedom in a system is bound by some monotonic function of its total energy.

The discussion above indicates that the picture we have discussed in this work should be rather robust, however we reiterate that, at this point, what we have presented must be regarded as a toy model. A truly satisfactory and realistic version of these ideas should be based on a generalized theory, adapted generically to quantum field theory on curved spacetimes, which should be fully covariant and in a 4 dimensional setting. However we believe that reasonable models with the basic features we have discussed here do offer one of the best hopes for resolving, the long standing question known as the “Black Hole Information Loss Paradox”.

Appendices

Appendix 1: Non-Hadamard behavior in the $\varvec{out}$ region

In this section we shall follow the standard Hadamard prescription to prove the non-Hadamard behavior of an arbitrary particle state (including the zero particle state, i.e, vacuum) in the out quantization defined in the case of evaporating black hole.

1.1 The two-point function

We use the discrete basis by working with wave packets. In this basis the modes are orthonormalized unlike the continuous counterpart. The field operator has the following form

$$\begin{aligned} \hat{f}^{L/R}(x)= & {} \displaystyle \sum _{n,j}\frac{1}{\epsilon ^{1/2}}\int _{j\epsilon }^{(j+1)\epsilon } d\omega \left( e^{2\pi i \omega n/ \epsilon }~\hat{b}_{\omega }^{L/R} v_{\omega }^{L/R}+ e^{-2\pi i \omega n/ \epsilon }~ \hat{b}^{L\dag /R\dag }_{\omega }v_{\omega }^{L*/R*} \right. \nonumber \\&+ \left. e^{2\pi i \omega n/ \epsilon }~ \hat{\tilde{b}}^{L/R}_{\omega }\tilde{v}_{\omega }^{L/R}+ e^{-2\pi i \omega n/ \epsilon }~\hat{\tilde{b}}^{L\dag /R\dag }_{\omega }\tilde{v}_{\omega }^{L*/R*}\right) \end{aligned}$$

(92)

$$\begin{aligned}= & {} \hat{f}_{1}^{L/R} (x) + \hat{\tilde{f}}_{2}^{L/R} (\tilde{x}). \end{aligned}$$

(93)

In the above expression we again used tilde to denote that these modes are defined interior to the black hole.²⁴ The wave packets defined exterior to black hole, similar to Eq. (30), are given by

$$\begin{aligned} v_{jn}^{L/R}=\epsilon ^{-1/2}\int _{j\epsilon }^{(j+1)\epsilon }d\omega e^{2\pi i\omega n/\epsilon }v_{\omega }^{L/R}, \end{aligned}$$

(94)

where the modes $v_{\omega }^{L/R}$ are given in Eq. (109) and Eq. (111). Below we provide an explicit calculation only for the right-moving modes since the other left-moving sector is fully analogous.

We calculate the two-point function in an arbitrary state, say, $\left| \psi \right\rangle =\left| F \right\rangle ^{int}\otimes \left| F \right\rangle ^{ext}$ of the joint basis. The two-point function takes the following form

$$\begin{aligned} \left\langle \psi \right| \hat{f}^R(x) \hat{f}^R(x') \left| \psi \right\rangle = \left\langle F \right| ^{ext} \hat{f}_{1}^R(x) \hat{f}_{1}^R (x') \left| F \right\rangle ^{ext} + \left\langle F \right| ^{int} \hat{\tilde{f}}_{2}^R (\tilde{x}) \hat{\tilde{f}}_{2}^R (\tilde{x}') \left| F \right\rangle ^{int}\nonumber \\ \end{aligned}$$

(95)

Note that the contributions from the exterior (region II, Fig. 1) and interior (region III, Fig. 1) of the black hole decouples from one another. Let us first focus on the first term defined exterior. Calculations involving the other term defined in the interior to the black hole is exactly similar. Writing this term explicitly yields

$$\begin{aligned}&\left\langle F \right| ^{ext} \hat{f}_{1}^R(x) \hat{f}_{1}^R (x') \left| F \right\rangle ^{ext} = \left\langle F \right| ^{ext} \displaystyle \sum _{n,j} \displaystyle \sum _{n',j'} \frac{1}{\epsilon } \int _{j\epsilon }^{(j+1)\epsilon }d\omega \int _{j'\epsilon }^{(j'+1)\epsilon }d\omega ' \nonumber \\&\quad \times \left( e^{2\pi i (n \omega - n' \omega ')/ \epsilon }~v_{\omega } v_{\omega '}^{*} \hat{b}_{nj}{{\hat{b}}^{\dagger }}_{n'j'} + e^{-2\pi i (n \omega - n' \omega ')/ \epsilon }~v_{\omega '} v_{\omega }^{*} \hat{b}^{\dagger }_{nj}\hat{b}_{n'j'}\right) \left| F \right\rangle ^{ext} \end{aligned}$$

(96)

while the other terms do not contribute. The next step would be to use the commutator relation between the creation and annihilation operators and orthonormality condition $\left\langle F_{nj} \right| {F_{n'j'}}\rangle ^{ext} = \delta _{nn'}\delta _{jj'}$. This simplifies Eq. (96) to the following form

$$\begin{aligned} \left\langle F \right| ^{ext} \hat{f}_{1}^R (x) \hat{f}_{1}^R (x') \left| F \right\rangle ^{ext} = \displaystyle \sum _{n,j} \frac{(2F_{nj} + 1)}{\epsilon }~I_{1}(\omega ) I_{1}^{*}(\omega ') \end{aligned}$$

(97)

where,

$$\begin{aligned} I_{1} (\omega )= & {} \int _{j\epsilon }^{(j+1)\epsilon }\frac{d\omega }{\sqrt{4\pi \omega }} e^{\frac{i\omega }{\Lambda }\log (-\Lambda x)+ 2\pi i n \omega /\epsilon } \end{aligned}$$

(98)

$$\begin{aligned} I_{1}^{*} (\omega ')= & {} \int _{j\epsilon }^{(j+1)\epsilon }\frac{d\omega '}{\sqrt{4\pi \omega '}} e^{\frac{-i\omega '}{\Lambda }\log (-\Lambda x)- 2\pi i n \omega '/\epsilon }. \end{aligned}$$

(99)

In the expression Eq. (97), the integration over the term that includes $F_{nj}$ gives

$$\begin{aligned}&\displaystyle \sum _{n,j} \frac{F_{nj}}{\epsilon \left( \frac{1}{\Lambda }\log (-\Lambda x)+ \frac{2\pi n}{\epsilon }\right) ^{1/2}\left( \frac{1}{\Lambda }\log (-\Lambda x')+ \frac{2\pi n}{\epsilon }\right) ^{1/2}}\nonumber \\&\qquad \times \left( \gamma \left[ \frac{1}{2},(j+1)\epsilon \right] - \gamma \left[ \frac{1}{2},j\epsilon \right] \right) ^2 \end{aligned}$$

(100)

Note that since $\left| F \right\rangle ^{ext}$ is a well defined state in the out Fock space it may have arbitrary number of particles but in no case it can be infinity. Therefore not all $F_{nj}$-s are nonzero when n and j are changing their values. On the other hand the term without $F_{nj}$ in Eq. (97) can be simplified in the following manner. We first use the identity

$$\begin{aligned} \displaystyle \sum _{n} e^{2\pi i n (\omega -\omega ')/ \epsilon } = \epsilon \delta (\omega - \omega '). \end{aligned}$$

(101)

As a result the integrations of the two integrals over $\omega$ and $\omega '$ transforms into a single integral, and then, by appropriately using the definition of the function $\gamma$ to turn the the sum over j into an integral, we obtain the final expression for the two-point function

$$\begin{aligned}&\left\langle F \right| ^{ext} \hat{f}_{1}^R (x) \hat{f}_{1}^R (x') \left| F \right\rangle ^{ext} \nonumber \\&\quad = - \frac{1}{4\pi } \log |\log (x/x')| + \displaystyle \sum _{n,j} \frac{F_{nj}}{2\pi \epsilon h(x) h(x')} \left( \gamma \left[ \frac{1}{2},(j+1)\epsilon \right] -\gamma \left[ \frac{1}{2},j\epsilon \right] \right) ^2,\nonumber \\&\quad h(x) = \left( \frac{1}{\Lambda }\log (-\Lambda x)+ \frac{2\pi n}{\epsilon }\right) ^{1/2}. \end{aligned}$$

(102)

In order to check the Hadamard behavior, as explained in Sect. 3.3, we need to construct the symmetrized two-point function

$$\begin{aligned} G^{(1)} (x, x') = \frac{1}{2}(\left\langle F \right| ^{ext} \hat{f}_{1}(x) \hat{f}_{1} (x') \left| F \right\rangle ^{ext} + \left\langle F \right| ^{ext} \hat{f}_{1}(x') \hat{f}_{1} (x) \left| F \right\rangle ^{ext}) \end{aligned}$$

(103)

and subtract the “Hadamard ansatz”. If the quantum state is Hadamard then we expect no singular behavior after the above said subtraction.

1.2 The Hadamard Ansatz

In two dimensions it seems to be a non-agreement about precise form of the “Hadamard ansatz” [88] and [89]. Usually the differences in opinion comes through the finite terms that are present in the Hadamard ansatz. Nevertheless, for our purpose we are interested to extract the singular behavior due to coincidence limit. We restrict to the following singular behavior of the Hadamard ansatz

$$\begin{aligned} H (x, x') = -\frac{1}{4\pi } \log \sigma , \end{aligned}$$

(104)

where $\sigma$ is half of the geodesic distance square between two close points x and $x'$ in the normal neighborhood.

Now let us proceed to calculate the geodesic distance between x and $x'$. We will do it in null coordinates. The calculations of this section are based on section 2 of chapter II of [90]. The geodesic distance is given by

$$\begin{aligned} \sigma =\frac{1}{2}u_{1}^{2}g_{\mu '\nu '}U^{\mu '}U^{\nu '}, \end{aligned}$$

(105)

where $u_{1}$ is the affine parameter of the geodesic at $x'$, $U^{\mu '}=\frac{dx}{du}$ is the tangent vector to the geodesic and $g_{\mu '\nu '}$ is the metric of space-time. Now we use that

$$\begin{aligned} u_{1}U^{\mu '}=\xi ^{\mu }+\frac{1}{2}\Gamma ^{\mu '}_{\alpha '\beta '}\xi ^{\alpha }\xi ^{\beta }, \end{aligned}$$

(106)

where $\xi ^{\mu }=x^{\mu }-x^{\mu '}$ and $\Gamma ^{\mu '}_{\alpha '\beta '}$ are the usual Christoffel symbols. By using Eq. (106) in Eq. (105) we obtain

$$\begin{aligned} \sigma =\frac{1}{2}g_{\mu '\nu '}\left( \xi ^{\mu }+\frac{1}{2} \Gamma ^{\mu '}_{\alpha '\beta '}\xi ^{\alpha }\xi ^{\beta }\right) \left( \xi ^{\nu }+\frac{1}{2}\Gamma ^{\nu '}_{\gamma '\eta '}\xi ^{\gamma }\xi ^{\eta }\right) . \end{aligned}$$

(107)

Up to cubic order in $\xi ^{\mu }$ we obtain

$$\begin{aligned} \sigma =\frac{1}{2}\left( g_{\mu '\nu '}\xi ^{\mu }\xi ^{\nu }+\frac{1}{2}g_{\mu '\nu '}\Gamma ^{\mu '}_{\alpha '\beta '}\xi ^{\alpha }\xi ^{\beta }\xi ^{\nu }+\frac{1}{2}g_{\mu '\nu '}\Gamma ^{\nu '}_{\gamma '\eta '}\xi ^{\mu }\xi ^{\gamma }\xi ^{\eta }+ ...\right) . \end{aligned}$$

(108)

Now we find that the only Christoffel symbols different from zero are²⁵

$$\begin{aligned} \Gamma ^{x}_{xx}=x^{+}\Omega \Lambda ^{2},\quad \Gamma ^{x^{+}}_{x^{+}x^{+}}=x\Omega \Lambda ^{2}, \end{aligned}$$

(109)

where $\Omega =\frac{1}{\frac{M}{\Lambda }-xx^{+}\Lambda ^{2}}$ and $g_{xx^{+}}=g_{x^{+}x}=-\frac{1}{2}\Omega$. Then the geodesic distance is given by

$$\begin{aligned} \sigma= & {} \frac{1}{2}\left( 2g_{x'x'^{+}}\xi ^{x}\xi ^{x^{+}}+\frac{1}{2}g_{x'x'^{+}}\Gamma ^{x}_{xx}\xi ^{x}\xi ^{x}\xi ^{x^{+}}+\frac{1}{2}g_{x'x'^{+}}\Gamma ^{x'^{+}}_{x'^{+}x'^{+}}\xi ^{x^{+}}\xi ^{x^{+}}\xi ^{x}\right. \nonumber \\&+ \left. \frac{1}{2}g_{x'x'^{+}}\Gamma ^{x'^{+}}_{x'^{+}x'^{+}}\xi ^{x}\xi ^{x^{+}}\xi ^{x^{+}}+\frac{1}{2}g_{x'^{+}x'}\Gamma ^{x'}_{x'x'}\xi ^{x^{+}}\xi ^{x}\xi ^{x}\right) . \end{aligned}$$

(110)

This simplifies to

$$\begin{aligned} \sigma =g_{x'x'^{+}}\xi ^{x}\xi ^{x^{+}}\left( 1+\frac{1}{2}\Gamma ^{x'}_{x'x'} \xi ^{x}+\frac{1}{2}\Gamma ^{x'^{+}}_{x'^{+}x'^{+}}\xi ^{x^{+}}\right) . \end{aligned}$$

(111)

Using Eq. (109) and the expression for the metric in Eq. (111) we finally obtain

$$\begin{aligned} \sigma =-\frac{1}{2}\Omega \Delta x\Delta x^{+}\left( 1-\frac{\Omega \Lambda ^{2}}{2}(x^{+}\Delta x+x\Delta x^{+})\right) , \end{aligned}$$

(112)

where $\Delta x=x'-x$ and $\Delta x^{+}=x'^{+}-x^{+}$. This geodesic distance is clearly an approximation, but for our purposes is seems to be enough.

1.3 The non-Hadamard behavior

In order to check the Hadamard property we substitute Eq. (112) in Eq. (104) and subtract the result from Eq. (102). We obtain the following expression

$$\begin{aligned} F(x, x')= & {} - \frac{1}{8\pi } \log (xx') - \log \left[ -\frac{1}{2}\Omega \Delta x^{+}\left( 1-\frac{\Omega \Lambda ^{2}}{2}(x^{+}\Delta x+x\Delta x^{+})\right) \right] \nonumber \\&+ \displaystyle \sum _{n,j} \frac{F_{nj}}{2\pi \epsilon h(x) h(x')} \left( \gamma \left[ \frac{1}{2},(j+1)\epsilon \right] - \gamma \left[ \frac{1}{2},j\epsilon \right] \right) ^2. \end{aligned}$$

(113)

Note that with the above expression for the renormalized two-point function we have a well defined coincidence limit with x and $x'$. However while approaching the horizon $x= x^- + \Delta =0$, there appears another divergence of the form $\log x$ which is not of the Hadamard form. Therefore clearly the state $|F\rangle ^{ext}$ is not Hadamard. Similarly one can prove that the particle state $|F\rangle ^{int}$ is also non-Hadamard. This obviously implies that the states $|F\rangle ^{int}\otimes |F\rangle ^{ext}$ of the joint Hilbert space is non-Hadamard.

Appendix 2: Proof of well defined foliation

The intersecting curves Eq. (65) and Eq. (66) are very important since they determine the foliation of the space-time. One might be concerned with the possibility that the foliating surfaces may cross each other at some region of the space-time. If this happens then one fails to associate a well defined evolution of the quantum states. Here we give a proof that such crossings among foliating surfaces does not take place.

The most general situation where this crossing can happen is shown on the left in Fig. 6. From the figure we can see that such crossings can take place both in regions II and III. Let us first consider the situation in region III. A zoomed version highlighting this aspect is shown on the right of Fig. 6. In the figure $T_{r_1} (r_1, X)$ and $T_{r_2}(r_2, X)$ are two $r=const.$ curves and the points A and B are on curves $T_{r_1}$ and $T_{r_2}$ respectively. The slope of the line joining A and B is given by

$$\begin{aligned} m_{BA} = \frac{T_{A} - T_{C}}{X_C - X _B}. \end{aligned}$$

(114)

This can be easily expressed in terms of the slopes of the line joining the points E with A and E with C such that

$$\begin{aligned} m_{BA} = m_{EA} - m_{EC}. \end{aligned}$$

(115)

Now making use of the mean-value theorem and $\Delta X = X_C - X _B \rightarrow 0$ we can associate the slope $m_{BA}$ with the slope of the guiding curve (generated by all intersecting points) and $m_{EA}$ with the curve $T_{r_1}$. Then Eq. (115) clearly tells us that the slope of the guiding curve should be less than the slope of $r=const.$ curve. But this is clearly in contradiction with our choice Eq. (65). Actually, it is trivial to verify that the slope of Eq. (65) is always greater than the slope of Eq. (64) provided $r<r_h$. With this we rule out the crossing behavior showing in Fig. 6. Similarly, for region-II, in order to have a crossing it is necessary that the slope of the guiding curve is less that the $t= const.$ curve. However, by comparing the slopes of Eq. (66) and Eq. (63) one can conclude that this situation does not appear given the condition $X>T$ in region II.

Fig. 6

Possible crossing between hyper-surfaces due to a bad choice of foliation. We show this situation does not take place in our construction. For details see the text

Appendix 3: Useful integrals to define $\zeta$

Here we provide the explicit results of various integrals defined in Sect. 6. These integrals measure the distance of a point in a particular foliating hypersurface. This distance is the parameter $\zeta$ Eq. (67) used together with $\tau$ for locating a point in CGHS space-time.

$$\begin{aligned} \zeta _{A}= & {} \left( \frac{A}{M/\Lambda - \Lambda ^2 A}\right) ^{1/2} \ln \left| \frac{c-e}{f}\right| \\ A= & {} \frac{e^{2\Lambda r (c,e)}}{\Lambda ^2},\\ \zeta _{B}= & {} \frac{1}{\Lambda } \log \left( -2 c \Lambda \right. \\&+\left. 2 \sqrt{\frac{-2 c \Delta \Lambda ^3-2 c \Lambda ^3 x+M+\Lambda ^3 x^2+\Delta \Lambda ^3 x}{\Lambda }}+\Delta \Lambda +2 \Lambda x\right) _{c-e-\Delta }^{c-d-\Delta } \\ \zeta _{C}= & {} \frac{1}{\Lambda }\log \left( \Delta \Lambda +2 \Lambda x \right. \\&+ \left. 2 \sqrt{\frac{-a M+a \Lambda ^3 x^2+a \Delta \Lambda ^3 x+b M+b \Lambda ^3 x^2+b \Delta \Lambda ^3 x}{\Lambda (a+b)}}\right) _{c-d-\Delta }^{a-b}. \end{aligned}$$

Appendix 4: The SSC formalism and the sudden collapse of the quantum state

When one considers a description of a situation requiring a quantum treatment of matter fields and at the same time requires a classical picture of space-time, allowing the consideration of questions such as those that usually as arise in the context of the BHIP; one is in the realm of semi-classical gravity. As discussed in this can not considered as a truly fundamental characterization of the physical situation, but only as an effective description. Nevertheless it is convenient among other reasons for the sake of conceptual clarity to have a well defined framework, where various issues can be studied in a self consistent manner. This can be thought as analogous to, say, the Navier Stokes equation in hydrodynamics, which even though can not be considered as a fundamental description of a fluid, and which is known not to be valid under various kind of circumstances, leads to an internally self consistent description, that can be the subject of rigorous mathematical analysis. A scheme which is hoped to offer a similar characterization has been developed for semi-classical gravity, and it is defied as follows.

Definition

The set $\left\{ g_{\mu \nu }(x),\hat{\varphi }(x),\hat{\pi }(x),{\mathscr {H}},\vert \xi \rangle \ in {\mathscr {H}}\right\}$ represents a Semiclassical Self-Consistent Configuration SSC if and only if $\hat{\varphi }(x)$, $\hat{\pi }(x)$ and ${\mathscr {H}}$ correspond to a quantum field theory constructed over a space-time with metric $g_{\mu \nu }(x)$ (as described in, say [69]), and the state $\vert \xi \rangle$ in ${\mathscr {H}}$ is such that

$$\begin{aligned} G_{\mu \nu }[g(x)]=8\pi G\langle \xi \vert \hat{T}_{\mu \nu }[g(x),\hat{\varphi }(x),\hat{\pi }(x)]\vert \xi \rangle \end{aligned}$$

(116)

for all the points x in the space-time manifold.

The point however is that such rigid definition does not allow for the incorporation of something like a collapse of the quantum state of the matter fields. However we can extend the scheme by incorporating a transition from one SSC to a another associated to a sudden change in the state of the system, as an analog of the matching used in the treatment of thin shells in general relativity developed in [93]. That is, just as in the later case, one matches two space-times across a time-like boundary representing the thin matter shell, in the situation at hand, one matches two space-times across a space-like hypesurface taken to represent the excitation of the fundamental underlying DOF of quantum gravity that must occur in association with what we call the collapse of the quantum state of the matter fields.

The basic idea is then that a collapse is associated not just with the sudden transition from one state $\vert \xi _1\rangle$ in ${\mathscr {H}}$ to another $\vert \xi _2\rangle$ in ${\mathscr {H}}$ but with a the transition of a complete SSC to another $SSC_1 \rightarrow SSC_2$, which not only involves a jump in the state but also the jump in the space-time metric and even in the Hilbert space. The analysis performed in [86] indicates that the matching of space-times might be done while requiring continuity of the induced metric across the collapse hypersurfae, but allowing for a discountinuity of the extrinsic curvature.

The above scheme is clearly designed to deal with a single spontaneous collapse of the quantum state, but it seems in principle extendable to deal with proposals involving continuous reduction processes such as those considered in CSL.

It is clear however that further research on the details of these formalism as applied to theories like CSL is required.