1 Introduction

The possibility of a nonsingular early de Sitter phase driven by a decaying vacuum was phenomenologically proposed to solve several problems of the Big-Bang cosmology [34, 35]. It traces back to some early attempts to solve (or at least to alleviate) several cosmological puzzles, in particular the “graceful exit” problem plaguing most variants of inflation (for recent reviews [26, 36]). Difficult and arduous as all these theoretical conundrums are, the most serious one is the cosmological constant problem [13, 41, 43, 45, 58], which remains as the main challenge also for inflationary theories of the cosmic evolution.

Later on, new developments have appeared which could mitigate some of these problems. For instance, by combining the phenomenological approach with the renormalization group (RG) theoretical techniques of quantum field theory (QFT) in curved spacetimes, a large class of dynamical \(\Lambda \)(H)-models described by an even power series of the Hubble rate was proposed [47–49].

More recently, we have proposed a large class of nonsingular cosmologies providing a complete cosmological history evolving between two extreme (early and late-time) de Sitter phases supported by a dynamical decaying vacuum energy density [3, 33, 44, 54]. Unlike many inflationary variants which are usually endowed with a preadiabatic phase, this nonsingular decaying vacuum is responsible by an increasing entropy evolution since the start of the primeval de Sitter phase.

The consistency and constraints imposed by the generalized second law (GSL) on this class of nonsingular cosmologies, including the matter-energy content and the horizon entropy of both de Sitter phases, were investigated [38]. The model approaches thermodynamic equilibrium in the last de Sitter era in the sense that the entropy of the apparent horizon plus that of matter and radiation inside it increases and is concave. It was also found that the consistency with the GSL is maintained even when quantum corrections to the Bekenstein–Hawking entropy are considered.

Here, instead to analyze the general thermodynamic conditions that must be obeyed in principle by such spacetimes, we focus our attention on the CMB entropic content generated by this kind of \(\Lambda (H)\) nonsingular cosmology. We know that the amount of radiation entropy contained within our horizon, \(S_{r0} \sim 10^{88}\) (in natural units), is lesser than the current estimates of supermassive black holes, \(S_{BH} \sim 10^{103}\), and much lower than the holographic bound, \(S_{H} \sim 10^{123}\) [17, 18]. However, it is still enormous and well quantified, and this fact creates severe theoretical problems since we cannot trace back the origin of that entropy within the conventional description of the cosmic evolution. Perhaps more interesting, in our model the very early and late time Universe have the same nonsingular de Sitter structure which seems to be in agreement both with the old suggestion of an early de Sitter phase supported by quantum corrections for the general relativity [55, 57], as well as with the present observed ‘quasi’ de Sitter Universe.

In the picture explored here the universe starts from an unstable vacuum de Sitter phase with no matter or radiation. The decay of this primeval vacuum state generates all the energy (and entropy) of the matter-energy content. At the end of the process, an extremely small remnant of vacuum energy survives. As we shall see, the continuous generation of entropy is very large and its final value coincides with the present radiation entropy existing within the Hubble radius. The early decaying vacuum process is not plagued with the inflationary “exit problem” and generates the correct number, \(S_0 \simeq 10^{88}\) [27]. In addition, the ratio between the primeval and the present day vacuum energy densities is \(\rho _{vI}/\rho _{v0} \simeq 10^{123}\).

The paper is organized as follows. In Sect. 2 we provide a brief discussion of the dynamical \(\Lambda (H)\) model and in Sect. 3 we set up the basic equations driving its complete evolution. In Sect. 4, we discuss the transition from an early Sitter to the radiation phase. How inflation ends “gracefully” and some estimates of the corresponding reheating temperature are presented in Sect. 5, while the entropy production generated by the vacuum decaying component is addressed in Sect. 6. Finally, in the last section the main conclusions are delivered.

2 Minimal model for a complete cosmic history

The simplest \(\Lambda (H)\)-scenario accounting for the general chronology of the universe from inflation until our days is based on the following expression for the vacuum energy density ([33], from now on LSB paper):

$$\begin{aligned} \Lambda (H)= c_0+3\nu H^2 +3\alpha \frac{H^4}{H_I^2}, \end{aligned}$$
(2.1)

where \(H\) is the Hubble rate and by definition \(\rho _{\Lambda }(H)=\Lambda (H)/8\pi \,G\) is the corresponding vacuum energy density (\(G\) being Newton’s constant). The even powers of \(H\) were selected due the general covariance of the effective action as required by the QFT treatment in curved spacetime [47–49, 51].

The constant \(c_0\) in the above expression yields the dominant term at low energies, when \(H\) approaches the measured value \(H_0\) (from now on the index “0” denotes the present day values). The dimensionless parameter \(\nu \) can be determined from observations [5, 6, 14, 15, 25]Footnote 1 from a joint likelihood analysis involving SNe Ia, Baryonic Acoustic Oscillations (BAO) and Cosmic Background Radiation (CMB) data, with the result \(|\nu | \equiv \mathcal{O}(10^{-3})\). It is of course small, since a dynamical model of the vacuum energy cannot depart too much from the phenomenologically successful \(\Lambda \)CDM. It is also encouraging that within a generic grand unified theory (GUT) one can estimate its value theoretically in the range \(|\nu | \sim 10^{-6}-10^{-3}\) [49]. Finally, the dimensionless \(\alpha \)-parameter can be fixed to unity since it can be absorbed by the undetermined scale \(H_I\).

As it appears, such dynamical vacuum model is able to link the fast dynamics of the primordial vacuum state with the much more relaxed evolution of the presently observed Universe. At early times, the primeval de Sitter phase (supported by a huge pure vacuum energy density \(\rho _{I} = 3H_I^{2}/8\pi G\)) is unstable and drives the model continuously to a late time de Sitter state characterized by the remnant vacuum energy density today.

3 \(\Lambda (H\)) model: basic equations

It is widely known that the bare cosmological constant appearing on the geometric side of the Einstein field equations (EFE) can be absorbed on the the matter-energy side in order to describe the effective vacuum contribution with energy density \(\rho _{\Lambda }=\Lambda /(8\pi G)\) and pressure \(p_{\Lambda }=-\rho _{\Lambda }\). Hence, by assuming a spatially flat FLRW (Friedmann–Lemaître–Robertson–Walker) metric, the EFE can be written as

$$\begin{aligned} 8\pi G \rho _m+\Lambda (H)= & {} 3H^2, \end{aligned}$$
(3.1)
$$\begin{aligned} 8\pi G p_m-\Lambda (H)= & {} - 2{\dot{H}} - 3H^2, \end{aligned}$$
(3.2)

where an overdot means cosmic time differentiation and the index \(m\) refers to the dominant fluid component (nonrelativistic matter or radiation). The above expressions are valid irrespective of the constant or variable nature of \(\Lambda \), provided it only evolves with the cosmic time, but not with space (as this would violate the cosmological principle). Thus, in our case, the only difference with respect to the more conventional field equations is the fact that \(\Lambda =\Lambda (H)\). In this framework, the local energy-conservation law [\(u_{\mu } (T_{m}^{\mu \nu } + T_{\Lambda }^{\mu \nu })_{;\nu } =0\)] reads:

$$\begin{aligned} \dot{\rho }_{m}+3(1+\omega )H\rho _{m}=-\dot{\rho _{\Lambda }}, \end{aligned}$$
(3.3)

where the equation of state (EoS), \(p_m = \omega \rho _m\), has been adopted for the fluid component. We recall that the above result can also be derived directly from the EFE, as the expression (3.3) is actually a first integral of the original equations.

Finally, by combining the matter EoS with (3.1), (3.2) and inserting (2.1) into the result one finds:

$$\begin{aligned} \dot{H}+\frac{3}{2}(1+\omega )H^2\left[ 1-\nu -\frac{c_0}{3H^2} -\alpha \frac{H^2}{H_I^2}\right] =0. \end{aligned}$$
(3.4)

The most interesting aspect of such cosmology is that it encompasses in a single unified approach both the inflationary and the current dark energy phases. Concerning the latter, let us emphasize that since \(|\nu |\ll 1\) at low redshifts the model becomes almost indistinguishable from the cosmic concordance model. The influence of the \(\nu \)-parameter in the current Universe is qualitatively new: it endows the vacuum energy of a mild dynamical evolution (which could be observed nowadays and appear as dynamical dark energy). The low-energy behavior is thus very close to the concordance model, but it is by no means identical. It could actually lead to distinctive new features in different domains such as the possible variation of the fundamental constants [19–21, 52, 53].

Most conspicuously, at high energies the model (2.1) leads to inflation. The reason is because Eq. (3.4) has the particular solution \(H_p=\sqrt{\frac{1-\nu }{\alpha }} H_I\), which is only valid in the high energy scope where the term \(c_0/H^2\ll 1\) of (3.4) can be neglected. That solution obviously corresponds to an inflationary (de Sitter) phase marking a (nonsingular) starting point of the cosmic evolution (see LSB for more details).

4 Deflation from the primeval de Sitter stage

In this and the following sections, without loss of generality, we fix \(\nu =0\) (which is not essential for the study of the early universe) and \(\alpha = 1\) (since we can rescale the value of \(H_I\)). In this case, it is easy to check that the solution of (3.4) at early times (i.e. when \(c_0\) can be neglected), can be written as

$$\begin{aligned} H(a)=\frac{H_{I}}{\sqrt{D\,a^{3(1+\omega )}+1}}. \end{aligned}$$
(4.1)

Upon integration we find the time evolution:

$$\begin{aligned} H_It=\int _{a_i}^a\frac{d\tilde{a}}{\tilde{a}}\left[ 1+D\,\tilde{a}^{3 (1+\omega )}\right] ^{1/2}. \end{aligned}$$
(4.2)

Here \(t\) is the time elapsed since the scale factor increased from some arbitrary initial point \(a_i\) up to the final one \(a(t)\). The constant \(D>0\) will be specified in the next section.

Using Eq. (4.1) and integrating the EFE (3.1)–(3.2) we obtain the corresponding energy densities:

$$\begin{aligned} \rho _{\Lambda }(a)= & {} \frac{\Lambda (a)}{8\pi G}= \frac{\rho _I}{\left[ Da^{3(1+\omega )}+1\right] ^2},\end{aligned}$$
(4.3)
$$\begin{aligned} \rho _m(a)= & {} \rho _I\, \frac{Da^{3(1+\omega )}}{\left[ Da^{3(1+\omega )}+1\right] ^2}, \end{aligned}$$
(4.4)

where \(\rho _{I}\) is the energy density associated to the primeval de Sitter stage:

$$\begin{aligned} \rho _{I}=\frac{3H_{I}^{2}}{8\pi G}. \end{aligned}$$
(4.5)

From Eq. (4.1) we find that \(H \sim H_I\) while the condition \(Da^{3(1+\omega )}\ll 1\) is fulfilled, and from (4.2) we learn that the evolution of the scale factor during this initial period is exponential: \(a(t)\sim a_i e^{\,H_I\,t}\). It means that the Universe is initially driven by a pure de Sitter vacuum state, and therefore is inflating.

The above mentioned de Sitter inflationary phase, however, is only ephemeral. For as soon as the condition \(Da^{3(1+\omega )} \ll 1\) is relaxed, Eq. (4.3) implies that the vacuum energy density \(\rho _{\Lambda }(a)\) decays. Not only so, it decays quite fast because \(\rho _{\Lambda }\sim a^{-6(1+\omega )}\) while \(\rho _m\sim a^{-3(1+\omega )}\). By assuming that the vacuum decays mainly into relativistic particles (\(\omega = 1/3\)) one finds that \(\rho _{\Lambda }\sim a^{-8}\) and \(\rho _{r} \sim a^{-4}\).

In effect, it is easy to check from Eq. (4.2) that in the post-inflationary regime, i.e. for \(a\gg a_i\) (with \(Da_i^{3(1+\omega )}\gg 1\)), we are led to \(a\sim t^{1/2}\) for \(\omega = 1/3\). This confirms that the Universe evolves continuously from inflation towards the standard (FLRW) radiation dominated stage.

The upshot is that the Universe becomes rapidly dominated by radiation and free from the vacuum energy. The cosmic expansion tends automatically to approach the conventional FLRW regime. This means that the primordial Big Bang Nucleosynthesis (BBN) epoch can proceed fully standard, with no interference at all from an unduly large amount of vacuum energy, thereby preserving all the virtues of the conventional BBN picture.

In Fig. 1, we display the early period of the nonsingular model described above, putting emphasis on the transition from the the inflationary epoch to the standard FLRW radiation regime. More details on this transition (in particular, the so-called “graceful exit”, as well as the temperature evolution) will be discussed in the next section.

Fig. 1
figure 1

Evolution of the energy densities as a function of the scale factor during the primeval vacuum epoch (inflationary period) and their transition into the FLRW radiation era. The densities are normalized with respect to the primeval vacuum energy density \(\rho _I\), and the scale factor with respect to \(a_{eq}\), the value for which \(\rho _{\Lambda } = \rho _r\) (see the text). The curves shown are: ultrarelativistic particles (black dashed line) and vacuum (red solid line). See also LSB for more details

Full size image

5 The “graceful exit”

Let us now demonstrate that in the present nonsingular framework the inflationary phase (\({\ddot{a} > 0}\)) finishes naturally when the radiation dominated era starts. From Eqs. (4.3) and (4.4) the exact ratio of the radiation energy density (\(\omega =1/3\)) to the vacuum energy density is given by:

$$\begin{aligned} \frac{\rho _{r}(a)}{\rho _{\Lambda }(a)} = D a^{4}. \end{aligned}$$
(5.1)

We denote by \(a_{eq}\) the scale factor at the point of vacuum-radiation “equality”, i.e. the precise value marking the beginning of the radiation phase at the end of the vacuum-dominated period.Footnote 2 It is obtained from the condition \(\rho _{r}(a_{eq}) =\rho _{\Lambda }(a_{eq})\), which renders \(D\,a_{eq}^4 = 1\). The last relation enables us to rewrite the expression (4.1) for the Hubble parameter in the following way:

$$\begin{aligned} H = \frac{{H}_I}{\sqrt{1 + (\frac{a}{a_{eq}})^{4}}}. \end{aligned}$$
(5.2)

It follows that the value of the Hubble function at the vacuum-radiation equality is simply related to the corresponding value at the beginning of the de Sitter phase:

$$\begin{aligned} H_{eq} \equiv H(a_{eq})= \frac{{H}_I}{\sqrt{2}}. \end{aligned}$$
(5.3)

It is also useful to understand dynamically the physical meaning of the pair (\(a_{eq}, H_{eq}\)). In principle, we expect that the outset of the radiation-dominated era should be defined from the condition that the Universe performs the transition from acceleration into deceleration, or more precisely when the deceleration parameter moves from \(q=-1\) to \(q=1\). From the equation of motion (3.4) one may check that the decelerating parameter, \(q=-{\ddot{a}}/aH^{2}=-1-\dot{H}/H^2\), reads:

$$\begin{aligned} q(H) = 2 \left[ 1 - \left( \frac{H}{{H}_I}\right) ^2 \right] - 1, \end{aligned}$$
(5.4)

so that the condition \(H=H_{eq}\) implies that \(q=0\)—see Eq. (5.3). However, the start of the radiation phase in this model is not characterized by the canonical radiation value \(q=1\), as one might have naively expected.

In point of fact, there is some delay in acquiring this value, that is, there is an interpolation period during which \(q\) moves continuously from \(q = 0\) to the standard result \(q = 1\). This happens because at the equality scale factor the vacuum is still powerful and continues draining photons in an appreciable rate to the radiation component (see Fig. 1). However, we can estimate when the standard radiation phase (\(q=1\), \(H=H_{rad}\), \(a = a_{rad}\)) begins in our model. The decelerating parameter once the adiabatic radiation regime applies reads:

$$\begin{aligned} q(H_{rad}) = 2 \left[ 1 - \left( \frac{H_{rad}}{{H}_I}\right) ^2 \right] - 1. \end{aligned}$$
(5.5)

For all practical purposes, we may assume that the radiation phase has been attained when, say, \(q(H_{rad}) \cong 0.999\). As one may check from (5.5), this happens for \(H_{rad}=H_I/(2\times 10^{3})^{1/2}\). On inserting this value into Eq. (5.2) we obtain the ratio \(a_{rad}/a_{eq} \simeq (2\times 10^{3})^{1/4}\). In general, by assuming that \(q \simeq 1-10^{-x}\) one may show that \(a_{rad}/a_{eq} \simeq (2\times 10^{x})^{1/4}\gg 1\) for \(x\gg 1\). Thus, the scale factor value at the time when the Universe enters in full the radiation epoch can be one order of magnitude, or more, larger than the corresponding value at the vacuum-radiation equality.Footnote 3 Subsequently, the Universe enters the cold dark matter [Einstein-de Sitter, \(a(t)\propto t^{2/3}\)] dominated phase; and, finally, makes its way to the present vacuum-dust epoch, in which \(\Lambda \simeq \Lambda _{0}=const.\) This will play a role in the subsequent considerations.

6 Radiation temperature law

As shown long ago, when the vacuum decays “adiabatically”, that is, in such a way that the specific entropy of the massless particles remains constant (despite the total entropy may be increasing), some equilibrium relations are preserved [29, 30]. In particular, this happens with the energy density versus temperature relation (\(\rho _r \propto T_r^{4}\)) and particle number (\(n_r \propto T^{3}\)). However, the temperature does not satisfy the standard scaling law, \(Ta =\) constant. In the present scenario, the evolution law for \(T\) can be determined as follows.

In terms of the scale factor at equality (\(a_{eq}\)) and using (4.4), the radiation density can be rewritten as:

$$\begin{aligned} \rho _{r} ={\rho }_I \frac{\left( a/a_{eq}\right) ^4}{\left[ 1 + (a/a_{eq})^{4}\right] ^{2}}. \end{aligned}$$
(6.1)

Now, under such “adiabatic” condition the above expression can be identified with the formula relating \(\rho _r\) with the radiation temperature \(T_r\) (see also [32]). By adding all the degrees of freedom (d.o.f.) of the created massless modes through the \(g_{*}\)-factor, we may write [27]:

$$\begin{aligned} \rho _{r} =\frac{\pi ^2}{30} g_{*} T_{r}^{4}, \end{aligned}$$
(6.2)

and combining with (6.1) we obtain for the radiation temperature law:

$$\begin{aligned} T_r = \sqrt{2}T_{rm}\frac{(a/a_{eq})}{\left[ 1 + (a/a_{eq})^{4}\right] ^{1/2}}, \end{aligned}$$
(6.3)

where \(T_{rm}=T_r (a_{eq})\). The maximum value of the radiation temperature is given by:

$$\begin{aligned} T_{rm} = \left( \frac{15\,\rho _I}{2\pi ^{2}g_*}\right) ^{1/4} = \left( \frac{45\,H_I^{2}}{16\pi ^{3}Gg_*}\right) ^{1/4}, \end{aligned}$$
(6.4)

which depends solely on the arbitrary initial scale of the primeval de Sitter phase (\(\rho _I\), or equivalently \(H_I\)).

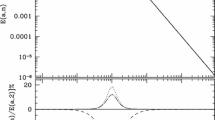
The evolution of the temperature of the universe in our model is shown in Fig. 2 (top plot). For small values of the scale factor (\(a \ll a_{eq}\)), the radiation temperature (6.3) raises linearly with the scale factor, \(T_r\propto a\), attaining its maximum value at the vacuum-radiation equality (\(a=a_{eq}\)). Therefore, instead of having a highly non-adiabatic “reheating” event, as typically occurring in the inflaton-like formulations—see the conventional picture in e.g. [27] and reference therein—in our case we have a relatively long non-equilibrium heating period in which the vacuum instability drives progressively the model to the radiation phase. During this period there is a continuous increase of the temperature and the entropy (see the next section). As mentioned, the temperature reaches a maximum given by (6.4), and for \(a>a_{rad}\) it decreases in the standard way according to the adiabatic scaling regime, \(T_r \sim a^{-1}\) (cf. Fig. 2, top). The linear raising of the temperature and its subsequent evolution until attaining the perfect fluid adiabatic phase is, in our context, directly responsible for the large radiation entropy observed in the present Universe.

The following question is in order: Can we calculate the characteristic quantities ( \(\rho _I, H_I\) ) from first principles or by some reasonable physical condition? This is indeed a relevant question because an affirmative answer opens the possibility to predict the present day values (\(\rho _{r0}\), \(T_{r0}\)) and, naturally, also the value of the radiation entropy, \(S_{r0}\), associated to the CMB thermal bath.

Fig. 2
figure 2

Top the evolution of the radiation temperature (normalized with respect to its maximum value) during the inflationary period and its transition into the FLRW radiation era. The horizontal axis is as in the previous figure; bottom the corresponding evolution of the normalized comoving entropy from the inflationary period (where it increases) until reaching the saturation plateau for \(a/a_{rad} \ge 1\). The asymptotic value corresponds the total entropy at present

Full size image

In principle, the primeval parameters (\(\rho _I, H_I\)) can be defined by different approaches. For instance, we may associate directly the initial de Sitter energy density \(\rho _I\) with the Planck (\(M_{P}^{4})\) or GUT (\(M_X^{4}\)) scales. Another possibility which will be adopted here is to consider the event horizon (EH) of a pure de Sitter space-time. As discussed long ago by Gibbons and Hawking [22], the temperature of the de Sitter EH is \(T_\mathrm{GH}=(\hbar /k_B)(H/2\pi )\), where \(k_B\) is Boltzmann’s constant and \(H\) is the (constant) Hubble rate of such initial epoch. In natural units, we have \({T}_{GH}={{H}_I}/{2\pi }\). Following this prescription, and relating \(\rho _I\) and \(T_{GH}\) according to Eq. (6.2), and with the help of (4.5), we find:

$$\begin{aligned} {H}_I=\left( \frac{180\pi }{g_*}\right) ^{1/2}\,M_{P}, \quad \rho _I = \frac{135}{2g*}M_{P}^{4}, \end{aligned}$$
(6.5)

and from Eq. (6.4) the characteristic radiation temperature reads:

$$\begin{aligned} {T}_{rm}=\left( \frac{45}{2\pi \,g_*}\right) ^{1/2}M_{P}. \end{aligned}$$
(6.6)

Therefore, since \(g_{*}=\mathcal{O}(100)\) it follows that all primeval characteristic scales in the above equations are slightly below the corresponding Planck scales, and in this sense still within the classical regime. For example, for \(g_{*}=106.75\) we have \({T}_{rm}\simeq 0.26\, M_P\). If we would take into account the number of light d.o.f in a GUT we would find it even lower, typically the temperature would be around 10 % of the Planck scale. This means it is still safe to consider a semi-classical QFT treatment in curved spacetime.

7 Generation of the radiation entropy

In natural units, the radiation entropy contained in the present horizon distance (\(d_H\sim H_0^{-1}\)) is given by:

$$\begin{aligned} S_{0}\simeq \frac{2\pi ^2}{45}\,g_{s,0}\,T_{r0}^3\,H_0^{-3}\simeq 2.3 h^{-3} 10^{87}\sim 10^{88}. \end{aligned}$$
(7.1)

Here \(T_{r0}\simeq 2.725\,^{\circ }\)K \(\simeq 2.35\times 10^{-13}\) GeV is the current CMB temperature, \(H_0=2.133\,h\times 10^{-42}\) GeV (with \(h\simeq 0.67\)) is the current Hubble function, and the coefficient \(g_{s,0}=2+6\times (7/8)\left( T_{\nu ,0}/T_{r0}\right) ^3\simeq 3.91\) is the entropy factor for the light d.o.f. today, which involves the well-known ratio \(T_{\nu ,0}/T_{r0}=\left( 4/11\right) ^{1/3}\) of the current neutrino and photon temperatures [27].

Naturally, if our model is to be a realistic description of the cosmic history, the total entropy measured today should be computable from the primeval entropy generated by the decaying vacuum. Let us now check this feature.

Under “adiabatic” conditions (see Sect. 6), the entropy equilibrium formula also remains valid because only the temperature law is modified [29, 30]. Therefore, the radiation entropy per comoving volume reads:

$$\begin{aligned} S_{r} \equiv \left( \frac{\rho _{r} + p_{r}}{T_{r}} \right) a^3 = \frac{4}{3} \frac{\rho _{r}}{T_r} a^3= \frac{2\pi ^2}{45} g_{s} T_{r}^{3} a^3, \end{aligned}$$
(7.2)

where in the last step we have inserted the expression for the radiation density, Eq. (6.2). In the above equation, \(g_s\) is the entropy factor at temperature \(T_r\).Footnote 4

With the help of Eqs. (7.2) and (6.3) the comoving entropy can be expressed as a function of the scale factor:

$$\begin{aligned} S_{r} = \frac{2^{5/2}\pi ^2g_{s}}{45}\,T_{rm}^{3}a_{eq}^{3} f(r), \end{aligned}$$
(7.3)

where we have defined the following function of the ratio \(r\equiv a/a_{eq}\):

$$\begin{aligned} f(r)=\frac{r^6}{\left( 1+r^4\right) ^{3/2}}. \end{aligned}$$
(7.4)

Notice that \(\lim _{a \rightarrow 0} S_{r} = 0\), as should be expected since the initial de Sitter state is supported by a pure vacuum (no radiation fluid). However, during the early stages of the evolution, deep in the inflationary phase (\(a\ll a_{eq}\)), the total comoving entropy of the Universe increases very fast; in fact, proportional to \(\sim \) \(a^{6}\). Note also that for \(a=a_{eq}\), \(f(r)=1/\sqrt{8}\) and the associated value \(S(a_{eq})\) is still not the total comoving entropy that the decaying vacuum is able to generate [see discussion below Eq. (5.4)]. This occurs only when \(a=a_{rad}\) so that \(r^{4}=(a_{rad}/a_{eq})^{4} \gg 1\) and \(f(r) \simeq 1\) for all practical purposes. At this point the comoving entropy \(S_r\) saturates to its final value, \(S^{f}_{rad}=S_r(a_{rad})\), thereby marking the very beginning of the standard radiation phase. The evolution of the radiation entropy normalized to that value is shown in Fig. 2 (bottom plot), where the rapid raising of the entropy during inflation and the final saturation plateau are clearly seen.

It thus follows that the asymptotic adiabatic behavior of (7.3), defined by \(f(r) \simeq 1\) for \(r\gg 1\), is given by:

$$\begin{aligned} S_{r}\rightarrow S_{rad}^f= \left( \frac{2^{5/2}\pi ^2g_{s}}{45}\right) T_{rm}^{3}a_{eq}^{3}, \end{aligned}$$
(7.5)

and, as remarked before, such a quantity is the total comoving entropy predicted by our model. Naturally, its value must be compared with the present day entropy.

In Fig. 2 we display the evolution of the entropy as a function of the ratio \(r=a/a_{eq}\), normalized to its value at the vacuum-radiation equality. Notice that \(S_r(a)/S_r(a_{eq})\rightarrow \sqrt{8}\) for \(a\gg a_{eq}\). The plateau characterizes the standard adiabatic phase, which is sustained until the present days because the bulk of the vacuum energy already decayed. There is, however, a remnant vacuum energy parametrized by \(c_0\) and \(\sim \) \(\nu \,H^2\) in Eq. (2.1), which is small (recall that \(c_0\sim \rho _{\Lambda }^0\lll \rho _I\) and \(|\nu |\lesssim 10^{-3}\)). This residual vacuum energy should describe the current dark energy (DE) epoch (see LSB for details).

Let us finally check the prediction of the total entropy within the current horizon volume \(\sim \) \(H_0^{-3}\). From the temperature evolution law [see Eq. (6.3)] one may check that the product \(T_{rm}^{3}a_{eq}^{3}\) appearing in the final entropy as given by (7.5) is equal to \(2^{-3/2}T_{rad}^{3}a_{rad}^{3}\), where \(T_{rad}=T_r(a_{rad})\) and \(a_{rad}\) was defined in Sect. 5. The result does not depend on the \(x\)-parameter provided \(x\gg 1\), which holds indeed deep in the radiation epoch. We find

$$\begin{aligned} S_{rad}= \left( \frac{2\pi ^2g_{s}}{45}\right) {T_{rad}^{3}\,a_{rad}^{3}}=S_0, \end{aligned}$$
(7.6)

where \(S_0\) is given by (7.1). In the last step we used the entropy conservation law of the standard adiabatic radiation phase, which implies that \(g_s\,T_{rad}^{3}\,a_{rad}^{3}= g_{s,0}\,T_{r0}^3\,a_0^{3}\).

In the beginning of the evolution (de Sitter phase), the radiation entropy is zero. It increases steadily during inflation but it asymptotes deep in the radiation epoch. However, as indicated, the asymptotic value does not depend on the x-parameter used to measure the degree of approximation to the subsequent phase fully dominated by ultra relativistic particles i.e. when \(q=1\) [see discussion below (5.5) and the associated footnote]. Later on, the entropy content evolved to a plateau and remained constant till the observed present day value (see Fig. 2). The model provides a comprehensible past evolution to the present \(\Lambda \)CDM cosmology by evolving smoothly between two extreme phases driven by the vacuum medium [see Eq. (3.4)]. In particular, the ratio between the associated vacuum energy densities can be computed using the Gibbons–Hawking ansatz which led to Eq.  (6.5). The final result is:

$$\begin{aligned} \frac{\rho _{vI}}{\rho _{v0}}= \frac{H_I^{2}}{H_0^{2}\Omega _{\Lambda _0}}= \frac{180\pi }{g_*}\,\frac{M_{P}^{2}}{H_0^{2}\Omega _{\Lambda _0}} \simeq 10^{123}, \end{aligned}$$
(7.7)

in accordance with usual estimates based on QFT [41, 58]. The model is thus able to explain the radiation entropy content and also to reconcile the observations with the so-called cosmological constant problem. Remarkably, the obtained description of the cosmic history is based on a unified dynamical \(\Lambda (H)\)-term accounting for both the vacuum energy of the early and of the current universe.

8 Conclusions

In this work we have discussed some thermodynamical aspects of a non-singular decaying vacuum model [3, 33] describing the entire cosmological history of the Universe (namely from inflation to the current dark energy epoch). The model belongs to a large class of dynamical vacuum models based on a truncated series of even powers of the Hubble rate. Such series is theoretically well motivated within the so-called renormalization group approach to cosmology [47–49, 51], and hence carries essential ingredients for a fundamental description of inflation. Here we have focused on the minimal implementation in which the highest power triggering inflation is \(H^4\). The \(H^{2}\) term, which is also present, is neglected for the description of the early universe, but it can play an important role for the late time evolution.

The main conclusions of our analysis read as follows:

  1. (i)

    The decaying vacuum cosmological models based on the “running” (renormalization group evolution) of the fundamental gravitational parameters provide a new, qualitatively different, approach to the description of primordial inflation which is different from the traditional, inflaton based, mechanisms. The general form of the decaying vacuum energy density is represented by an even power series of the Hubble rate that is consistent with the general covariance of the effective action of quantum field theory in curved spacetime.

  2. (ii)

    The decaying of the primeval vacuum energy into radiation can provide a successful account of the “graceful exit” from the de Sitter phase into the standard FLRW radiation epoch, from which the expansion of the Universe can then follow the concordance \(\Lambda \)CDM scenario.

  3. (iii)

    At the same time we find that the massive decay of the vacuum energy in this context can explain the large amount of entropy that we observe in the present Universe. The entropy production can be explained from a continuous “heating up” (rather than the usual “reheating” caused by inflaton decay), in which the radiation temperature rises initially (i.e. during the vacuum phase) linearly with the scale factor \(a\), reaches a maximum at the vacuum-radiation equality and then decreases inversely proportional to \(a\) (as in the standard adiabatic regime). During the heating up of the Universe the comoving entropy rockets as the sixth power of \(a\) until it reaches a saturation plateau in the radiation-dominated phase, and thereafter follows the standard adiabatic regime as well.

  4. (iv)

    Lastly, the decaying vacuum energy is already largely subdominant during the radiation phase, and therefore the primordial BBN processes can occur normally. Similarly, the vacuum stays subdominant during the entire CDM-dominated epoch and the late time evolution of the Universe can be very close to the \(\Lambda \)CDM model, except for a mild dynamical evolution of the form \(\rho _{\Lambda }(H)\simeq c_0+c_2 H^2\), which asymptotes to a constant value (\(\rho _{\Lambda }\rightarrow c_0\)) as we measure at present.

Let us finally note that, shortly after this work was issued, an alternative decaying vacuum framework was proposed by [12] in which the vacuum energy density \(\rho _{\Lambda }\) is also described in terms of a truncated series of the Hubble rate. It involves, as in our case, the powers \(H^2\) and \(H^4\). However, in their proposal the initial tiny quantum fluctuations are treated as a manifestation of the thermal nature of quantum fields in a curved background. Therefore the Universe starts in their case from a state of radiation with black-body spectrum (\(\rho _r\propto T^4\)) at a very high temperature proportional to the Hubble rate (specifically it is given by the Gibbons–Hawking temperature, \(T_\mathrm{GH}=H/2\pi \)), and as a result \(\rho _r\propto H^4\). In our setup we make also use of the Gibbons–Hawking temperature as a reasonable ansatz, but we assign this temperature to the initial vacuum state rather than to a primordial radiation heat bath. For this reason the behavior of the two inflationary pictures is rather different. In particular, in contrast to our model, the alternative framework develops a curvature singularity at early times where both the vacuum energy and the radiation densities become infinite and with opposite signs (\(\rho _r\rightarrow +\infty \) and \(\rho _{\Lambda }\rightarrow -\infty \) for \(t\rightarrow 0\)). The Clifton & Barrow scenario is nevertheless interesting, as it illustrates with a concrete example that inflation through vacuum decay is possible even when the energy density of the vacuum is large and negative. In the particular implementation that they consider, they find that the very late stage of the universe becomes dominated by radiation. This is in contradistinction to the situation with our vacuum decay model, where the asymptotic behavior leads to a cosmological constant just as in the concordance \(\Lambda \)CDM model. It is remarkable that different inflationary mechanisms based on vacuum decay dynamics can provide alternative descriptions of inflation which differ substantially from the usual reheating process in conventional inflationary theories.

In summary, we think it is advisable to keep in mind the mechanisms of inflation based on vacuum decay. They do not rely directly on the traditional inflaton fields, but can provide new useful insights on the inflationary universe that might eventually help to resolve, or at least highly alleviate, some of the most fundamental cosmological problems.