1 Introduction

After the 1980s, surface wave techniques became popular in many disciplines, such as seismology, geophysics, material science, and engineering. The application of these methods in geotechnical engineering was initiated by the introduction of the spectral analysis of surface waves (SASW) method in 1994 (Stokoe et al. 1994), but its widespread use began after the development of array-based methods such as the multichannel analysis of surface waves (MASW) in 1999 (Park et al. 1999; Xia et al. 1999). MASW utilizes the dispersive nature of Rayleigh- or Love-type surface waves propagating through geomaterials to estimate the variation of shear wave velocity (Vs) with depth. MASW has several advantages over the traditional two-sensor SASW. For MASW, data processing and data interpretation become faster, less subjective, and require less operator knowledge (Foti et al. 2014).

Currently, MASW is widely used in geotechnical engineering for various applications, including but not limited to near-surface site characterization (Rix et al. 2002; Socco and Strobbia 2004; Hebeler and Rix 2006; Lai et al. 2002; Wood et al. 2017), liquefaction assessment (Wood et al. 2017; Rahimi et al. 2020a), infrastructure evaluation (Cardarelli et al. 2014; Rahimi et al. 2019, 2021a), and VS30 estimation (Comina et al. 2010; Martínez-Pagán et al. 2012; Rahimi et al. 2020b). The standard procedure for MASW involves three steps: field measurements, data processing, and inversion. A key part of MASW data processing that controls the final results is developing the experimental dispersion curve (i.e., phase velocity versus frequency plot). This is a critical step in the MASW method because the higher the resolution of the experimental dispersion curve, the higher the reliability of the inverted Vs profile. Therefore, the resolution of the experimental dispersion image is of primary importance in the MASW method. An experimental dispersion image is defined as high resolution if the spectrum peaks are narrow, and one can easily identify a consistent, clear, and meaningful trend for different modes of propagation. Generally, the fundamental mode is the main mode of interest for the inversion process.

To develop the experimental dispersion curve, wavefield transformation techniques are commonly used to transfer the original time–space (t − x) domain data into another domain, such as the frequency-wavenumber (f − k), the frequency-slowness (f − p), or the frequency-velocity (f − v) domains. The advantages of transforming the data into another domain are that in the transformed domain, the propagation properties of surface waves can be easily identified as spectral maxima, and different modes of propagation can often be detected and separated even when they are not clearly visible in the original time–space domain (Foti et al. 2014). Resolving different modes of propagation is important because the inversion analysis's accuracy can be enhanced by including multiple modes in the inversion process (Xia et al. 2003).

Four transformation techniques are commonly used in the MASW method for developing the experimental dispersion curve. These include slant stack or frequency-slowness (τp) (McMechan and Yedlin 1981), frequency-wavenumber (FK) (Nolet and Panza 1976; Yilmaz 1987; Foti et al. 2000), frequency domain beamformer (FDBF) (Hebeler and Rix 2007; Zywicki 1999), and phase shift (PS) (Park et al. 1998). Additionally, varying approaches within the FDBF method can model a planar or cylindrical wavefield (Zywicki and Rix 2005). These methods are explained in detail in the next section. While differences may appear in the experimental dispersion curves developed using each transformation technique, to date, no study has exclusively compared the limitations and advantages of each transformation technique considering different subsurface layering and wavefield conditions. In this regard, the limited previous studies (Dal Moro et al. 2003; Tran and Hiltunen 2008) only compared the performance of transformation techniques for a specific subsurface layering, meaning that their results are site-specific and cannot be applied to other site conditions. For instance, Dal Moro et al. (2003) mentioned that the PS method provides the highest resolution dispersion curve compared to the FK and τp methods for sites with unconsolidated sediments. Tran and Hiltunen (2008) compared the four transformation techniques for a particular site. They claimed that the results from all the transformation techniques are in good agreement, but the FDBF cylindrical leads to a slightly higher resolution dispersion curve. While these previous studies provide relevant insight, they did not provide all critical characteristics of their study area (e.g., sharp impedance contrast depth, wavefield noise conditions). These characteristics are important to truly understand the differences observed in the experimental dispersion curves from different transformation techniques. Despite the lack of investigation in this regard, it is important to understand each transformation technique's limitations and advantages. This is particularly important for identifying multiple modes of propagation and the low-frequency portion of the dispersion curve, where near-field effects or low signal-to-noise ratios typically corrupt the experimental data.

This study evaluates the performance of four common MASW wavefield transformation techniques when used to develop experimental Rayleigh and Love wave dispersion curves. Toward this end, more than 500 MASW tests were conducted at sites with different subsurface layering, wavefield, and noise conditions to understand potential differences between the transformation techniques. The paper begins by reviewing the four common transformation methods, and the issues most often encountered in the MASW technique. Information regarding the field measurements, subsurface layering, and wavefield conditions of each study site is then provided. Finally, the resolution of the Rayleigh and Love experimental dispersion curves generated using the four transformation methods is compared for sites with deep and shallow sharp impedance contrast (i.e., bedrock), sites with a velocity reversal layer, sites in noisy and quiet environments, sites with apparent near-field effects, and sites with clear higher modes. The conditions where each transformation technique performs well and poorly are highlighted and discussed with conclusions on the most appropriate method based on the available data.

2 Common Transformation Techniques used for MASW Data Processing

Four wavefield transformation techniques are commonly used in MASW data processing for developing the experimental dispersion curve. Researchers and consultants have extensively used these transformation techniques from different institutions and in various software packages, as summarized in Table 1. Due to the lack of investigations regarding the advantages and limitations of each transformation technique, users generally ignore potential differences and assume similar performance from these four transformation techniques.

Table 1 Summary of different transformation methods used by researchers and consultants from different institutions and software packages
Full size table

All transformation methods used in MASW are aimed at converting the raw time–space domain data into another domain where the propagation properties of the surface waves (i.e., frequency, wavenumber, and phase velocity) can be identified as a spectral peak (maximum energy). Once the data are converted into such a domain, the experimental dispersion curve is generated by identifying the wavenumber and the phase velocity associated with the maximum energy at each frequency. The procedure used by each method to transform the data is discussed below.

2.1 Slant Stack (τp)

The τp method also called the slant stack or frequency-slowness was first introduced by McMechan and Yedlin (1981). This method utilizes two linear transformations that allow the decomposition of the shot-gather into its plane-wave linear components. The two linear transformations include a slant stack and a one-dimensional Fourier transform. Using the slant stack transformation, the original time (t)-space (x) domain data are converted into the time intercept (τ)-slowness (p) domain. A one-dimensional (1D) Fourier transform is then applied to the τp domain data to transform the data into the frequency (f)-slowness (p) domain (McMechan and Yedlin 1981; Foti et al. 2014). The linear relationship that relates the four variables t, x, τ, and p is given by:

$${\text{t}} = {\text{t}} + {\text{px}}$$
(1)

The slant slack transform is expressed as follows:

$${\text{f}}\left( {\tau ,{\text{p}}} \right) = \mathop \int \limits_{ - \infty }^{ + \infty } {\text{U}}\left( {x,t} \right)\;{\text{d}}x = \mathop \int \limits_{ - \infty }^{ + \infty } {\text{U}}\left( {x,\tau + px} \right)\;{\text{d}}x$$
(2)

where \({\text{U}}\left( {x,t} \right)\) is the signal recorded at distance x from the source. For each value of τ in the slant stack transformation, the data in the time–space domain are stacked along a straight line with a slope of p. Therefore, each straight line in the time–space domain is associated with a constant data pair of τ-p in the τp domain. Finally, by applying a one-dimensional Fourier transform over the time intercept variable, the data are transformed into the frequency-slowness domain:

$${\text{F}}\left( {{\text{f}},{\text{p}}} \right) = \mathop \int \limits_{ - \infty }^{ + \infty } {\text{f}}\left( {\tau ,{\text{p}}} \right)e^{ - i2\pi f\tau } \;{\text{d}}\tau$$
(3)

2.2 Frequency-Wavenumber (FK)

The frequency-wavenumber transformation method was first proposed by Nolet and Panza (1976) and then used by other researchers for surface wave data processing (Yilmaz 1987; Gabriels et al. 1987; Foti et al. 2000). FK is the simplest and fastest method for MASW data processing. In the FK method, the time–space domain data are decomposed into its components at different frequencies and wavenumbers. In this regard, the data in the time–space domain are transformed into the frequency-wavenumber domain using a two-dimensional (2D) Fourier transform:

$${\text{F}}\left( {f,k} \right) = \mathop {\iint }\limits_{ - \infty }^{ + \infty } {\text{U}}\left( {x,t} \right)e^{{ - 2\pi i\left( {ft + kx} \right)}} \;dx\;dt$$
(4)

2.3 Frequency Domain Beamformer (FDBF)

Frequency domain beamformer (FDBF) was first introduced by Gabriels et al. (1987) and then modified and popularized by Zywicki (1999) for surface wave data processing. The basic concept of this method is very similar to τp. The term beamformer refers to the ability of an array or signal processing method to focus on a particular direction and the mainlobe of an array smoothing function (ASF), which is called a beam (Gabriels et al. 1987). The FDBF method utilizes a steering vector, which is an exponential phase shift vector, to calculate the power associated with each particular frequency-wavenumber data pair (Zywicki 1999; Hebeler and Rix 2006):

$${\text{e}}\left( {\text{k}} \right) = \left[ {e^{{ - ik.x_{1} }} , e^{{ - ik.x_{2} }} , \ldots ,e^{{ - ik \cdot x_{m} }} } \right]^{T}$$
(5)

where \({\text{e}}\left( {\text{k}} \right)\) is the phase shift vector, k is the vector wavenumber, xm denotes the sensor m position in the array, T denotes the transpose of the vector, and i is the imaginary number. For a particular f − k data pair, the power is calculated by multiplying the spatiospectral correlation matrix (R) by the steering vector and then summing the total power over all receivers. The steered power spectrum is given by:

$${\text{P}}_{{{\text{BF}}}} \left( {{\text{k}},\omega } \right) = {\text{e}}^{{\text{H}}} {\mathbf{WRW}}^{{\text{H}}} {\text{e}}$$
(6)

where H denotes the Hermitian transpose of the vector, and W is a diagonal matrix, containing the shading weights of each receiver:

$${\mathbf{W}} = \left[ {\begin{array}{*{20}c} {{\text{w}}_{1} } & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & {{\text{w}}_{{\text{m}}} } \\ \end{array} } \right]$$
(7)

The spatiospectral correlation matrix (R) is expressed by:

$${\mathbf{R}} (\omega ) = \left[ {\begin{array}{*{20}c} {{\text{R}}_{1,1} (\omega )} & \cdots & {{\text{R}}_{{1,{\text{m}}}} (\omega )} \\ \vdots & \ddots & \vdots \\ {{\text{R}}_{{{\text{m}},1}} (\omega )} & \cdots & {{\text{R}}_{{{\text{m}},{\text{m}}}} (\omega )} \\ \end{array} } \right]$$
(8)

where Rm,n is the cross-power spectrum between receivers m and n:

$${\text{R}}_{{{\mathbf{m,n}}}} \left( {\varvec{\omega}} \right) = {\text{S}}_{{\text{m}}} \left( \omega \right){\text{S}}_{{\text{n}}}^{*} \left( \omega \right)$$
(9)

where Sm and Sn are the Fourier spectra of the mth and nth receivers, respectively, and * denotes the complex conjugate. The first version of the FDBF transformation method was proposed assuming a plane wavefield. This assumption is also made in all other transformation methods (τp, FK, and PS). This assumption is reasonable for passive surface wave methods, as ambient vibrations are typically generated by sources located at far distances. However, for active surface wave methods (e.g., MASW), it is not always valid to assume a pure plane wavefield because active surface waves are generated at relatively close source offsets (i.e., distance between the first receiver in the array and the shot location). This means that the active waves can propagate cylindrically in the near-field zone. The near-field effect of modeling a cylindrical wavefield with a plane wavefield is called the model incompatibility effect. The FDBF transformation was modified in 2005 to account for the model incompatibility effect (Zywicki and Rix 2005). In the updated version of the FDBF, a new steering vector was defined to account for the cylindrical wavefield:

$${\text{h}}\left( {\text{k}} \right) = [{\text{e}} ^{{ - {\text{i}}\phi ({\text{H}}_{0} \left( {{\text{k}} \cdot {\text{x}}_{1} } \right)}} ,{\text{e}} ^{{ - {\text{i}}\phi ({\text{H}}_{0} \left( {{\text{k}} \cdot {\text{x}}_{2} } \right)}} , \ldots , {\text{e}} ^{{ - {\text{i}}\phi ({\text{H}}_{0} \left( {{\text{k}} \cdot {\text{x}}_{{\text{m}}} } \right)}} ]^{{\text{T}}}$$
(10)

where \(\phi\) is the phase angle of each argument in parentheses, \({\text{h}}\left( {\text{k}} \right)\) is the Hankel steering vector, and Hankel function H0 is given by:

$${\text{H}}_{0} \left( {{\text{k}} \cdot {\text{x}}} \right) = {\text{J}}_{0} \left( {{\text{k}} \cdot {\text{x}}} \right) + {\text{iY}}_{0} \left( {{\text{k}} \cdot {\text{x}}} \right)$$
(11)

where J0 is Bessel function of the first kind of order zero, and Y0 is Bessel function of the second kind of order zero. Then, the steered power spectrum for the cylindrical wavefield is given by:

$${\text{P}}_{{{\text{CBF}}}} \left( {{\text{k}},\omega } \right) = {\text{h}}^{{\text{H}}} {\mathbf{WRW}}^{{\text{H}}} {\text{h}}$$
(12)

Zywicki and Rix (2005) claimed that the updated version of the FDBF overcomes the limitations of the plane wavefield assumption by accounting for the cylindrical wavefield in the near-field zone.

2.4 Phase Shift (PS)

The phase shift method for surface wave data processing was proposed by Park et al. (1998). In this method, the time–space domain data are first converted into the circular frequency (\(\omega\))-space (x) domain using a one-dimensional Fourier transform:

$${\text{U}}\left( {\omega ,{\text{x}}} \right) = \mathop \int \limits_{ - \infty }^{ + \infty } {\text{f}}\left( {{\text{t}},{\text{x}}} \right)e^{{{\text{i}}\omega {\text{t}}}} \;{\text{d}}t$$
(13)

The transformed function is then defined as the multiplication of two separate terms, the phase [\({\text{P}}\left( {\omega ,{\text{x}}} \right)\)] and amplitude spectrum [\({\text{A}}\left( {\omega ,{\text{x}}} \right)\)]:

$$U\left( {\omega ,x} \right) = P\left( {\omega ,x} \right)A\left( {\omega ,x} \right)$$
(14)

The amplitude parameter preserves the information about the signal attenuation and geometrical spreading, whereas the phase velocity parameter preserves all the information regarding the dispersion properties. Therefore, \({\text{U}}\left( {\omega ,{\text{x}}} \right)\) function can also be given by:

$${\text{U}}\left( {{\upomega },{\text{x}}} \right) = e^{ - i\emptyset x} {\text{A}}\left( {\omega ,{\text{x}}} \right) = e^{{ - i\frac{w}{{V_{R} }}x}} {\text{A}}\left( {\omega ,{\text{x}}} \right)$$
(15)

The final equation is obtained by applying an integral transformation to \({\text{U}}\left( {\omega ,{\text{x}}} \right)\) function:

$${\text{V}}\left( {\omega ,\emptyset } \right) = \mathop \int \limits_{ - \infty }^{ + \infty } e^{i\emptyset x} \frac{{{\text{U}}\left( {\omega ,{\text{x}}} \right)}}{{\left| {{\text{U}}\left( {\omega ,{\text{x}}} \right)} \right|}}\;{\text{d}}x$$
(16)

3 Common Issues in Active Surface Wave Methods

3.1 Near-Field Effects

Near-field effects are the most commonly encountered issue in MASW data processing, significantly reducing the maximum resolvable depth, resolution, and reliability of the derived dispersion data. Near-field effects are mainly caused due to two assumptions: (1) plane wavefield surface waves and (2) pure surface waves in the wavefield with no interference from body waves. The regions where these assumptions are invalid are called the near-field. The near-field effect of modeling a cylindrical wavefield with a plane wavefield is called the model incompatibility effect. The model incompatibility effect can lead to a clear roll-off (Fig. 1a) in the phase velocity at low frequencies, whereas the interference of the body waves can generate some oscillations in the phase velocity at low frequencies (Fig. 1b). It should be mentioned that Park and Carnevale (2010) claimed that the clear roll-off in the phase velocity at low frequencies is caused by the Gibb’s phenomenon. However, all other previous studies referred to such behavior as near-field effects (e.g., Zywicki 1999; Yoon and Rix 2009; Tremblay and Karray 2019; Roy and Jakka 2017; Bodet et al. 2009). Therefore, in this study, this behavior is also referred to as near-field effects. These near-field effects are corrupting the low-frequency portion of the dispersion data so that they cannot be reliably used for the inversion process.

Fig. 1
figure 1

Example of near-field effects: a clear roll-off in phase velocity in the low-frequencies portion of the dispersion curve due to model incompatibility, b apparent oscillations in phase velocity in the low-frequencies portion of the dispersion curve due to body waves interference

Full size image

A limited number of studies have investigated near-field effects and suggested some methods to mitigate such effects. These methods include modifying the transformation technique to account for the cylindrical wavefield (Zywicki and Rix 2005), increasing the distance between the source and receivers (Xu et al. 2006; Yoon and Rix 2009; Tremblay and Karray 2019), using multiple source offsets (Wood and Cox 2012), and increasing the number of receivers (Yoon and Rix 2009). One of the primary investigations regarding near-field effects was conducted by Yoon and Rix (2009), in which they defined two normalized parameters, including a normalized phase velocity defined as the ratio of the experimental phase velocity to the true phase velocity and a normalized array center distance given by:

$$\frac{{{\overline{\text{x}}}}}{\lambda } = \frac{{(1/{\text{M}})\mathop \sum \nolimits_{{{\text{m}} = 1}}^{{\text{M}}} {\text{x}}_{{\text{m}}} }}{\lambda }$$
(17)

where \({\overline{\text{x}}}\) is the mean distance of all receivers relative to the source, \(\lambda\) is the wavelength, and M is the number of receivers. To date, the majority of the previous investigations have focused on the geometry of the MASW test to investigate the near-field effects, and no attempt has been made to assess the influence of different transformation methods on near-field effects. Therefore, this topic is investigated in this study by comparing the performance of different transformation techniques for sites with apparent near-field effects.

3.2 Mode Misidentification or Mode-Kissing

In the MASW method, it is possible to observe multiple modes of propagation at a single temporal frequency for sites with a heterogeneous soil profile. In other words, different phase velocities can be associated with a given frequency for sites where multiple modes of propagation exist. Different modes are often observed at sites with a velocity reversal (Teague et al. 2018). Additionally, the existence of a strong velocity contrast (i.e., very shallow bedrock) within the penetration depth of the surface waves increases the possibility of higher modes generation (Stokoe et al. 1994; Gao et al. 2016). Identifying different modes of propagation is important in the MASW method because it can prevent mode misidentification, and it can enhance the accuracy of the inversion results by including multiple modes in the inversion process. However, the presence of different modes of propagation in the experimental dispersion data makes the mode identification complex, and sometimes it can lead to mode misidentification (Foti et al. 2014; Gao et al. 2014, 2016; Zhang and Chan 2003). This means that the dispersion data points related to the effective or higher modes may be mistaken as the fundamental mode for sites with a poor-resolution dispersion image. Therefore, for sites where different modes of propagation are expected, the experimental dispersion curve's resolution is critical to avoid mode misidentification. One of the parameters that may affect the resolution of the experimental dispersion curve is the transformation method used for data processing. This topic has not received adequate attention in the literature. Therefore, one of the present study goals is to examine the capability of different transformation methods for multi-mode detection.

4 Field Measurements and Study Areas

To investigate the performance of the four transformation methods for developing the experimental dispersion curve, more than 500 MASW tests were collected at eight different sites located in the USA. The sites were carefully selected in such a way to cover a wide range of subsurface layering, wavefield, and noise conditions. Summarized in Table 2 are the key characteristics of each site, including site location, sharp impedance contrast or bedrock depth (shallow or deep), whether or not a velocity reversal is present, noise conditions (ranked high to low), geophone coupling (spike or landstreamer), surface wave type (Rayleigh or Love), number of geophones, geophone spacing, and number of setups. It should be mentioned that for all sites in the present study, the sharpest impedance contrast in the subsurface, which significantly alters the shape of the experimental dispersion curve if it’s within the resolvable depth of the MASW measurements, is located at the soil/bedrock interface. Therefore, depth to the sharpest impedance contrast is called hereafter bedrock depth. The bedrock layer located within the top 15 m is classified as very shallow, bedrock depth ranging between 15 and 35 m is classified as shallow, and the bedrock layer located at depths greater than 100 m is classified as deep.

Table 2 Key characteristics of the study areas and field measurements
Full size table

For each site, both Rayleigh- and Love-type surface waves were first used for several array setups to determine the wave type that resulted in a higher resolution experimental dispersion curve. Therefore, the results presented in this study include both Rayleigh- and Love-type surface waves. Testing was performed using 24 vertical or horizontal geophones spaced 1 or 2 m apart. For sites where a significant number of MASW tests were performed, a landstreamer system was used to increase the rate of field measurements. However, spikes generally result in better coupling to the ground surface. Surface waves were generated at different source offsets to improve the reliability of the experimental data and to estimate the uncertainty associated with them. For sites with a very shallow to shallow bedrock layer, various source offsets ranging between 1 and 20 m were included. For sites with a very deep bedrock layer, source offsets of 2, 5, 10, 20, 30, and 40 m were included.

Based on a review of the geology at each site and the shape of the experimental dispersion curves, the majority of the sites in this study are normally dispersive, meaning that Vs increases with depth. However, irregular dispersion curves were observed at some locations along the Melvin-Price site, indicating the presence of a velocity reversal layer (i.e., a low-velocity layer underneath a stiffer layer) in the near-surface. More information regarding the site locations, subsurface layering, and field measurements of each site are provided in Rahimi et al. (2018), Wood and Himel (2019), and Rahimi et al. (2020c).

Sites with high noise levels were located near busy highways or in highly urbanized environments, sites with medium noise levels were located near roads with medium traffic volume, and sites with low noise levels were located far away from highways and urbanized areas. In this regard, representative signal-to-noise ratio (SNR) curves in decibels (dB) for sites with high (Ozark), medium (Melvin-Price), and low noise (Hardy) levels is shown in Fig. 2. From this figure, the SNRs are considerably different for all ranges of frequencies (1–100 Hz). However, this becomes more important for the low-frequency range, where the SNR is typically low and can corrupt the experimental dispersion data points. For this study, a value of 10 dB (as recommended by Wood and Cox 2012) is considered as the threshold SNR, below which the experimental dispersion data points become unreliable due to the substantial contribution of the background noise. Accordingly, the frequency associated with the threshold SNR is considered as the threshold frequency. As observed in Fig. 2, while the threshold frequency is very low (~ 1 Hz) for sites with a low noise level, this value abruptly increases for sites with a high noise level (~ 16 Hz). It should be noted that this threshold does not necessarily mean reliable data will be retrieved to those frequencies, just that the SNR is high at those frequencies. The SNR can be improved by stacking several shots at a source offset; however, the signal stacking method can only improve the SNR to a certain level. In this study, a minimum of three shots was stacked at each source offset to improve the SNR of the experimental data.

Fig. 2
figure 2

Representative signal-to-noise ratio (SNR) for sites with low, medium, and high noise levels

Full size image

5 Results and Discussion

All MASW data collected from different sites were used to develop the experimental dispersion curves using the four transformation methods. The data were processed using in-house MATLAB codes developed by the authors to generate the experimental dispersion curves using the four transformation methods. The accuracy of the in-house MATLAB codes was evaluated by comparing the results with other available software packages such as the MASWaves software package developed by Olafsdottir et al. (2018). Due to the large number of the experimental dispersion curves processed for this study, only a few examples of each type of behavior are presented here to highlight the influence of the transformation method on the derived dispersion data. Furthermore, for each of the topics discussed in detail in this section, an additional experimental result is provided in the supplementary materials to support the discussions. Moreover, for each topic, an example experimental dispersion results from Rayleigh- and Love-type waves (either in the paper or electronic supplement) is provided to investigate whether the same performance is observed for each transformation method for both Rayleigh and Love surface waves. However, for some sites (e.g., Melvin-Price), only Rayleigh- or Love-type surface waves were used. Therefore, only one type of surface wave is included in the discussions for these sites (see Table 2).

For the FDBF transformation, the experimental dispersion curve can be developed assuming either a plane or cylindrical wavefield (see Sect. 2.3). In this study, only the cylindrical FDBF (FDBF-cylindrical) is used for the comparisons since the experimental dispersion curve generated using the FDBF-plane was found to be nearly identical to the FK for the sites considered in this study. To better illustrate this point, example experimental dispersion curves generated using the FDBF-cylindrical and FDBF-plane, and FK methods are provided in Fig. 3 for an MASW setup at the Hardy site. In Fig. 3a, while the dispersion curves of the FDBF-plane and FK methods are nearly identical (see Fig. 3a), differences are observed in the dispersion curves generated using the FDBF-cylindrical and FDBF-plane (see Fig. 3b). As shown in Fig. 3b, the phase velocity estimated using the FDBF-cylindrical is slightly higher (< 8%) than the FDBF-plane at high frequencies, as shown in the zoomed-in view. Moreover, the differences between the two methods are significant at low frequencies (< 20 Hz), where near-field effects are noticeable. More discussions in this regard are provided later in the paper. Therefore, given these differences, the FDBF-cylindrical is utilized to compare the performance of the four transformation methods for developing the experimental dispersion curve.

Fig. 3
figure 3

Comparison between the cylindrical and plane FDBF and FK methods. λp is the maximum wavelength resolved using FDBF-plane and is λc the maximum wavelength resolved using FDBF-cylindrical

Full size image

5.1 Sites with Different Subsurface Conditions

This section compares the four transformation methods for varying site conditions, including (1) sites with deep bedrock, uniform soil, and low noise conditions, (2) sites with very shallow and highly variable bedrock depth and high and low noise levels (using traditional spikes and a landstreamer), and (3) sites with a velocity reversal layer.

5.1.1 Sites with Deep Bedrock, Uniform Soil Conditions, and Low Noise Levels

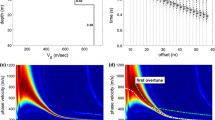
Provided in Fig. 4 are the experimental Rayleigh wave dispersion curves generated using the four transformation methods for the PVMO site, which has a deep bedrock depth (~ 591 m) and low noise levels. The same input parameters (e.g., frequency interval) were used to generate each transformation method's dispersion image. Additionally, to avoid spatial aliasing, the data related to wavelengths less than the minimum resolvable wavelength are removed from the dispersion images. In Fig. 4, the dispersion curve can be divided into two main portions, a flat portion for frequencies ranging between 50 and 9 Hz, and a curved portion with a nearly continuous increase in phase velocity for frequencies lower than 9 Hz. The frequency at the start of the curved portion, which separates these two portions (9 Hz for this example), is termed the point of curvature herein and is important for assessing the performance of the transformations.

Fig. 4
figure 4

Rayleigh wave dispersion curves generated using the four transformation methods for the PVMO site with a deep bedrock layer, a low-frequency point of curvature, and low noise levels: a FDBF-cylindrical, b FK, c PS, and d τp

Full size image

As shown in Fig. 4, the four transformation methods have produced almost identical dispersion curves for the frequency range of interest (5–50 Hz). This is clearer in Fig. 5, where the spectral peak dispersion curves from the four transformation methods are plotted in one figure using different markers. The dashed lines in this figure illustrate the minimum (4 m) and maximum (75 m) resolved wavelengths. These values are important since the characterization depth of the surface waves is a function of the resolved wavelengths. As a rule of thumb, the characterization depth of surface waves is approximately equal to half of the maximum resolved wavelength (37.5 m for this setup). Therefore, the maximum resolved wavelength is critical as it defines the maximum depth sampled by the surface waves. In Fig. 5, it is apparent that the results from the four dispersion curves are identical for the wavelengths ranging between 4 and 75 m. Similar behavior was observed in terms of the dispersion curve resolution for the other MASW tests at this site and the other sites with low noise levels and, more importantly, with a similarly deep bedrock layer and a low-frequency point of curvature (< 10 Hz) (CUSSO and PEBM sites in Table 1). In this regard, another example dispersion image from the PEBM site is provided in Supplement A. To investigate this topic for both Rayleigh and Love waves, the example provided in Supplement A is for Love waves, whereas the one in the paper is for Rayleigh waves. These indicate that for sites with a deep bedrock layer with a low-frequency point of curvature, relatively uniform soil conditions, and low noise levels, the performance of the four transformation methods is almost identical for both Rayleigh and Love waves. This is likely because for such site conditions: The contribution of the surface waves is significant compared to the background noise in the recorded signal, and the dispersion data are mainly dominated by the fundamental mode with no complication from effective or higher modes.

Fig. 5
figure 5

Comparison of the four transformation methods for Rayleigh waves for the PVMO site

Full size image

5.1.2 Sites with a Very Shallow and Highly Variable Bedrock Depth

To evaluate the performance of each transformation method for sites with a very shallow and highly variable bedrock depth for both Rayleigh and Love waves, examples from both Rayleigh (Ozark site) and Love (Hot Springs site) waves are provided in this section.

5.1.2.1 Site with High Noise Levels using Spikes

Presented in Fig. 6 are the experimental Rayleigh wave dispersion curves generated using the four transformation methods for the Ozark site with a very shallow and highly variable bedrock topography and high noise levels. For this site, geophones were coupled to the ground via spikes. From this figure, a high-frequency point of curvature (~ 40 Hz) is observed for this site.

Fig. 6
figure 6

Rayleigh wave dispersion curves generated using the four transformation methods for the Ozark site with a very shallow and highly variable bedrock topography, a high-frequency point of curvature, and high noise levels: a FDBF-cylindrical, b FK, c PS, and d τp

Full size image

As shown in Fig. 6, the FDBF-cylindrical, FK, and τp methods generated a high resolution and almost identical dispersion image (Fig. 6a, b, d). However, the PS method generated a very poor-resolution dispersion image (see Fig. 6c) with no clear trend for the fundamental mode of propagation. A better illustration of the PS resolution issue is provided in Fig. 7, in which the spectral peak dispersion data points from the FDBF-cylindrical, FK, and τp methods are shown in Fig. 7a, and the spectral peak dispersion data points of the PS method are shown in Fig. 7b. As observed in Fig. 7a, the dispersion data points of the FDBF-cylindrical, FK, and τp methods are clear and relatively consistent for wavelengths ranging between 2.1–29.7 m. However, the PS method results in very poor-resolution dispersion data (see Fig. 7b) in such a way that only a small portion of the dispersion curve (wavelengths ranging between 8.9 and 16.7 m) is clear. This type of behavior is observed for most of the dispersion curves generated using the PS method for sites with very shallow and highly variable bedrock depth (e.g., Ozark, Hot Springs, and Hardy) and a high-frequency point of curvature (> 20 Hz). To provide further evidence in this regard, another example of MASW results from the Ozark site with the same issue for the PS method is provided in Supplement B. The example in Supplement B is from a different MASW setup and location at the Ozark site. It should be noted that the poor performance of the PS method was verified by processing the same MASW setups with PS issues using the MASWaves software package (Olafsdottir et al. 2018).

Fig. 7
figure 7

Comparison of the four transformation methods for Rayleigh wave for the Ozark site: a FDBF-cylindrical, FK, and τp, b PS

Full size image

To better understand the poor performance of the PS method, the normalized spectrum for frequencies of 46 and 47 Hz is shown in Fig. 8 for each transformation method. As observed in Fig. 8a, b, and d, the normalized spectrum plots of the FDBF-cylindrical, FK, and τp methods have a clear and dominant peak, indicating most of the energy concentrates at this peak. However, the normalized spectrum plot for the PS method (see Fig. 8c) has several ripples, causing a significant difference in the phase velocities associated with the peak frequencies (i.e., 723 m/s at the frequency of 46 Hz and 342 m/s at the frequency of 47 Hz) due to the spread between the various ripples.

Fig. 8
figure 8

Comparison of the normalized spectrum plots for the four transformation methods at 46 and 47 Hz frequencies for the Ozark site: a FDBF-cylindrical, b FK, c PS, and d τp

Full size image

Another important point regarding the differences between various transformation methods is that the phase velocity estimated using the FDBF-cylindrical is slightly higher than the other methods for all ranges of frequencies, as shown in the zoomed view dispersion curve in Fig. 7a (also see Fig. 3b). This behavior is observed in all the dispersion images of the current study. These differences are caused due to the model incompatibility effects in the FK, PS, and τp methods, in which the cylindrical spreading wavefield is modeled using a plane wavefield. This results in biased phase velocity estimates for the surface waves using these three transformation methods. The higher phase velocity estimates in the FDBF-cylindrical is also confirmed by Zywicki and Rix (2005). This indicates that the FDBF-cylindrical may provide more correct estimates of the phase velocity of surface waves compared to the other transformation methods by using a cylindrical model.

5.1.2.2 Site with low noise levels using a landstreamer

Shown in Fig. 9 are Love wave dispersion curves generated using the four transformation methods for the Hot Springs site with very shallow and highly variable bedrock topography and low noise levels. To increase the rate of field measurements for this site, MASW testing was conducted using a landstreamer system, which typically reduces the dispersion data quality because of poorer geophone coupling to the ground surface compared to traditional spikes. Like the Ozark site, a high-frequency point of curvature (~ 45 Hz) is observed for this site, as shown in Fig. 9. Additionally, in Fig. 9, it is clear that the FDBF-cylindrical, FK, and τp methods yield an identical dispersion image dominated by the fundamental mode of propagation. However, the PS method leads to a poor-resolution dispersion image dominated by higher modes, as observed in Fig. 9c. The resolution issue with the PS method is more apparent in Fig. 10, which represents the dispersion data points measured at three different source offsets of 5, 10, and 15 m. For the FDBF-cylindrical, FK, and τp methods in Fig. 10, the dispersion data points from source offsets at 5 and 10 m are dominated by the fundamental mode of propagation, and only the data points from the 15-m source offset are dominated by higher modes at frequencies greater than 50 Hz. Additionally, these methods result in a similar dispersion curve for wavelengths ranging between 2 and 24.6 m with some variations at the low-frequency portion of the dispersion curve due to near-field effects.

Fig. 9
figure 9

Love wave dispersion curves generated using the four transformation methods for the Hot Springs site with a very shallow and highly variable bedrock topography, high-frequency point of curvature, and low noise levels: a FDBF-cylindrical, b FK, c PS, and d τp

Full size image
Fig. 10
figure 10

Love wave dispersion data points generated from different source offsets using the four transformation methods for the Hot Springs site: a FDBF-cylindrical, b FK, c PS, and d τp

Full size image

On the other hand, for the PS method in Fig. 10c, the dispersion data points from all three source offsets are dominated by higher modes for a wide range of frequencies (from 41 to 95 Hz), and the fundamental mode dominates only a small portion of the dispersion curve. This leads to a very low-resolution experimental dispersion curve from the PS method. While only two example experimental dispersion images are provided here (see Figs. 6, 9), the resolution issue of the PS method is also observed for most of the sites with a very shallow and highly variable bedrock depth and a high-frequency point of curvature (> 20 Hz). From 670 MASW setups processed at four different sites with a very shallow and highly variable bedrock depth and at different source offsets, approximately 360 of them had the PS resolution issue compared to the other transformation techniques. Another example experimental dispersion curve showing the PS issue is provided in Supplement C. The example in Supplement C is from a different MASW setup and location at the Hot Springs site.

Overall, the PS method is one of the most popular transformation methods for MASW data processing and is the method initially used for MASW data processing. However, in this study, it has been shown that the PS method has resolution issues for some datasets for both Rayleigh (Fig. 6 and Supplement B) and Love (Fig. 9 and Supplement C) surface waves for sites with very shallow and highly variable bedrock depth and a high-frequency point of curvature (> 20 Hz), regardless of the geophone coupling conditions (good coupling using spikes or poor coupling using landstreamer) and site noise levels. This contrasts with previous studies that have claimed that the PS method provides the best resolution experimental dispersion curve (Dal Moro et al. 2003) compared to the FK and τp methods. It is worth mentioning that the primary difference between this study and previous studies (Dal Moro et al. 2003; Tran and Hiltunen 2008) is that the previous studies did not include various subsurface layering, wavefield, and noise conditions. Therefore, their results are site-specific and cannot be applied by other researchers for sites with different conditions. While not enough information is available to determine the exact cause for the PS issues, one of the differences between the PS method and other transformation methods is that while both amplitude and phase terms are included in the PS calculations, other transformation techniques only consider the phase term in their calculations. This may contribute to the observed behavior at these complex sites.

5.1.3 Site with Velocity Reversal

Presented in Fig. 11 are the Rayleigh wave dispersion curves generated using the four transformation methods for one of the MASW setups at the Melvin-Price site that includes a velocity reversal layer (i.e., reversal in velocity at depth or irregular dispersion curve) and medium noise levels. The velocity reversal presence is evident from the dispersion images (e.g., Figure 11a) since the phase velocity decreases with frequency at frequencies ranging between 7 and 30 Hz. Additionally, the existence of the velocity reversal is also confirmed by geologic information available for the site (Rahimi et al. 2018). In Fig. 11, the dispersion data associated with the fundamental mode of propagation are clear for the FDBF-cylindrical, FK, and PS methods over a broad range of frequencies (3–90 Hz). However, the τp method (see Fig. 11d) fails to provide any clear dispersion data at frequencies less than 17 Hz, which is related to the layers below the velocity reversal. This portion of the dispersion curve is important since it has information regarding the deeper layers, including the inverse layer, stiff soils, and bedrock layers. This issue is further highlighted in Fig. 12, in which the dispersion curves are presented on a semi-log scale. In Fig. 12a, it is apparent that similar dispersion curves are generated using the FDBF-cylindrical, FK, and PS methods for wavelengths ranging between 2 and 72 m. However, for the τp method in Fig. 12b, the low-frequency portion of the dispersion image is missing, and so the maximum resolvable wavelength is ~ 14 m, which is significantly lower than the other transformation methods (72 m). This issue with the τp method is observed for all the MASW setups that include a velocity reversal in this study. In this regard, another example of this issue with the τp method is provided in Supplement D from a different MASW setup and location at the Melvin-Price site. It is also worth mentioning that the resolution of the PS method is lower than the FDBF-cylindrical and FK methods.

Fig. 11
figure 11

Rayleigh wave dispersion curves generated using the four transformation methods for the Melvin-Price site with a velocity reversal layer and moderate noise levels: a FDBF-cylindrical, b FK, c PS, and d τp

Full size image
Fig. 12
figure 12

Comparison of the four transformation methods for Rayleigh wave for the Melvin-Price site for a location with a velocity reversal layer (irregular dispersive dispersion curve): a FDBF-cylindrical, FK, and PS, b τp

Full size image

To ensure this is not a common issue for all dispersion curves when using the τp method at the Melvin-Price site, dispersion curves are generated using the four transformation method for another location at the Melvin-Price site where no velocity reversal layer is present, but similar subsurface layering exists otherwise. These results are shown in Fig. 13. As observed in the figure, the dispersion curve from the τp method (Fig. 13b) is similar to those of the FDBF-cylindrical, FK, and PS methods (Fig. 13a) in terms of the shape and the minimum (2 m) and maximum (24 m) resolvable wavelengths for a normally dispersive subsurface layering. This confirms that the issue with the τp method in Figs. 11 and 12 is likely related to the presence of a velocity reversal in the near-surface, and it is not related to the other factors such as wavefield and noise conditions. However, it should be mentioned that all the results presented in this section, regarding the issue with τp method for sites with a velocity reversal layer, are only based on the experimental data from one site at multiple locations; therefore, there is a need for more investigations to confirm this issue with the τp method.

Fig. 13
figure 13

Comparison of the four transformation methods for Rayleigh wave for the Melvin-Price site at a location without a velocity reversal layer (normally dispersive dispersion curve): a FDBF-cylindrical, FK, and PS, b τp

Full size image

5.2 Near-Field Effects

Shown in Fig. 14 are Love wave dispersion curves generated using the four transformation methods for the Hot Springs site with clear near-field effects. As shown in this figure, the near-field effects are caused by model incompatibility because of the clear roll-off in the phase velocity without any oscillations in the low-frequency portion of the dispersion curve. For the FK and τp methods in Fig. 14b, d, respectively, it is apparent that the near-field effect corrupts a large portion of the low frequency (< 23 Hz) dispersion data. However, for the FDBF-cylindrical and PS methods in Fig. 14a, c, respectively, a smaller portion of the dispersion curve is corrupted by the near-field effect. The FDBF-cylindrical provided the highest resolution (i.e., longest resolvable wavelength) experimental dispersion curve.

Fig. 14
figure 14

Love wave dispersion curves generated using the four transformation methods for the Hot Springs site with clear near-field effects and low noise levels: a FDBF-cylindrical, b FK, c PS, and d τp

Full size image

To better compare the performance of the four transformation methods in the presence of clear near-field effects, the experimental dispersion data points of the four transformation methods are plotted together in Fig. 15. As shown in this figure, the majority of the dispersion data points are related to the fundamental mode of propagation except for frequencies ranging between 47 and 67 Hz, which are dominated by a higher mode. The capability of each transformation method to mitigate the near-field effect is visible in this figure. The differences between the four methods regarding the near-field effect are highlighted in the zoomed view in Fig. 15. From this figure, the maximum resolved wavelength using the FK, and the τp methods is 19 m, whereas this value is 37 m for the PS method and 51 m for the FDBF-cylindrical method, illustrating significant differences between the transformation methods. This indicates that in the presence of model incompatibility effects, the performance of the FDBF-cylindrical is considerably better than the other transformation techniques because it mitigates the near-field effect by using a cylindrical wavefield model. Similar behavior is observed for all the MASW dispersion data with clear near-field effects. To provide more evidence in this regard, another example of an experimental Rayleigh wave dispersion image with clear near-field effects is provided in Supplement E. It should be noted that the example in Supplement E is for Rayleigh waves, whereas the example in the paper in Fig. 14 is for Love waves. While Rayleigh and Love waves are very different in terms of wave characteristics, wave propagation, and near-field effects, both examples illustrate the superior performance of the FDBF-cylindrical over the other methods when considering near-field effects (Rahimi et al. 2021b).

Fig. 15
figure 15

Comparison of the four transformation methods for Love wave for the Hot Springs site with clear near-field effects using Love-type surface waves

Full size image

5.3 Multiple Mode Detection

Shown in Fig. 16 are the Rayleigh dispersion curves generated using the four transformation methods for the Ozark site. From this figure, it is apparent that the four transformation methods have different sensitivities to higher modes. While most of the dispersion data points from the FDBF-cylindrical are related to a higher mode (see Fig. 16a), the other transformation methods contain more evidence of the fundamental mode. The differences between the FDBF-cylindrical and the other transformation methods are clearer in Fig. 17, in which the dispersion data points of the FDBF-cylindrical and the other methods (FK, PS, and τp) are shown in Fig. 17a, b, respectively. As observed in Fig. 17a, for the FDBF-cylindrical, all the dispersion data points with a frequency greater than 35 Hz are related to the first higher mode. However, for the FK, PS, and τp, only the dispersion data points for frequencies ranging between 40 and 66 Hz and 90 and 100 Hz are associated with the first higher mode. This behavior is observed for several other dispersion images with apparent higher modes. Another example in this regard from a different MASW setup and location at the Ozark site is provided in Supplement F. It should be mentioned that while for the example presented here, the FDBF-cylindrical contained more data from the higher modes compared to the other methods, this was not the case for all sites as other transformation techniques were dominated by higher modes for other datasets. This indicates that the four transformation techniques have different sensitivities to higher modes.

Fig. 16
figure 16

Rayleigh wave dispersion curves generated using the four transformation methods for the Ozark site with the FDBF-cylindrical method dominated with a higher mode: a FDBF-cylindrical, b FK, c PS, and d τp

Full size image
Fig. 17
figure 17

Rayleigh wave dispersion curves for the Ozark site: a FDBF-cylindrical with clear first higher mode (R1) domination, b FK, PS, and τp methods dominated with the fundamental mode (R0)

Full size image

Therefore, given that the four transformation techniques were observed to have different sensitivities to higher modes, the composite dispersion curve approach is recommended to be used as the best practice for sites with a complex mode assignment where multiple modes are present. To demonstrate the advantages of the composite dispersion curve approach, the dispersion data of a single transformation technique (FK) and the dispersion data of the composite dispersion curve approach (using the four different transformation techniques) from another MASW setup are shown in Fig. 18a, b, respectively. From Fig. 18a, one can only identify the fundamental mode and a small portion of the higher mode. On the other hands, using the composite dispersion method (see Fig. 18b), one can easily identify the trend of the fundamental and the higher mode with much more detail. Therefore, the composite dispersion approach can be used as a way to (1) avoid mode misidentification, (2) define multiple modes of propagation, (3) increase the reliability of the experimental dispersion data, (4) estimate the uncertainty associated with the experimental dispersion data, and (5) enhance the accuracy of the retrieve Vs profile from the inversion process through multimodal inversion.

Fig. 18
figure 18

Combination of all transformation methods with clear fundamental and first higher Rayleigh mode dispersion curves

Full size image

6 Conclusions

This study examines the performance of the four transformation methods (FDBF-cylindrical, FK, PS, and τp), which are commonly used for MASW data processing to develop the experimental dispersion curve. In this regard, extensive MASW measurements were conducted at sites with different subsurface layering and noise conditions, including sites with deep and shallow bedrock, sites with a velocity reversal, sites in a noisy and quiet environment, sites with apparent near-field effects, and sites with clear higher modes. Based on the comparison of the performance of the four transformation methods for developing the experimental dispersion curves, the following conclusions are derived.

  1. 1.

    The performance of the four transformation methods is judged to be identical for both Rayleigh and Love waves for sites with a deep bedrock layer, a low-frequency point of curvature (< 10 Hz), relatively uniform soil conditions, and a low noise level (see Fig. 4). Therefore, any of the four transformation methods can be used for these sites.

  1. 2.

    It is observed that for sites with a very shallow and highly variable bedrock depth and a high-frequency point of curvature (> 20 Hz), regardless of the site noise level and geophone coupling conditions, the PS method resulted in a very poor-resolution dispersion image for approximately half our datasets for both Rayleigh and Love waves in such a way that no clear dispersion curve could be extracted from the experimental results (see Figs. 6, 9, Supplement B, and Supplement C). However, the other transformation methods (FDBF-cylindrical, FK, and τp) generated a clear, high-resolution dispersion image for both Rayleigh and Love waves for the same sites. Therefore, it is recommended that if the PS method is used for sites with very shallow and highly variable bedrock topography with a high-frequency point of curvature (> 20 Hz), the experimental dispersion curve of the PS method should be compared to one of the other transformation methods to ensure the accuracy of the derived dispersion data.

  2. 3.

    According to the results of this study, for sites with a velocity reversal (i.e., stiff over soft soil layer), the τp method fails to generate Rayleigh dispersion data points for the layers located below the velocity reversal layer. However, the other transformation methods developed an experimental Rayleigh dispersion curve that contains information from the velocity reversal layer and the layers below it (see Fig. 11 and Supplement D). Therefore, if the τp method is used for sites with a velocity reversal layer located within the MASW target depth, it is recommended to verify the accuracy of the τp dispersion image by comparing the results with other transformation techniques. Additionally, since this conclusion is made based on limited experimental data, more investigations are needed to confirm the performance of τp method for sites with a velocity reversal layer.

  3. 4.

    For sites with clear near-field effects, the FDBF-cylindrical method provided a significantly higher resolution dispersion image than the other transformation methods (FK, PS, and τp), which were corrupted by near-field effects at low frequencies (see Fig. 15 and Supplement E). It is observed that the FDBF-cylindrical method mitigates the near-field effects compared to the other transformation methods for both Rayleigh and Love waves, particularly the effects of model incompatibility by using a cylindrical wavefield model rather than a plane wavefield model.

  4. 5.

    It was determined that the four transformation techniques have different sensitivity to higher modes. Therefore, for complex sites where multiple modes are present, the best practice is to use the composite dispersion approach (using the four transformation techniques) to avoid mode misidentification. This method can be employed as a means to (1) prevent mode misidentification, (2) detect multiple modes of propagation, (3) improve the reliability of the experimental dispersion image, (4) estimate the uncertainty associated with the experimental dispersion data, and (5) improve the accuracy of the final Vs profile by multimodal inversion.

  5. 6.

    By comparing the performance of the four common transformation methods for both Rayleigh and Love waves for sites with different subsurface layering, wavefield, and noise conditions, it was observed that the FDBF-cylindrical generally outperforms the other (FK, PS, and τp) transformation methods. The FDBF-cylindrical provides a stable, high-resolution dispersion image for various subsurface layering and noise conditions, mitigates the near-field effects by modeling a cylindrical wavefield, and provides a high-resolution dispersion image over a broad range of frequencies, including the low-frequency portion of the dispersion curve. The FDBF-cylindrical is, therefore, recommended to be used as the primary method if users are willing to only use one transformation technique for MASW data processing.

  6. 7.

    Since there are some conditions that could not be tested in the current study, it is recommended that if one of the transformation techniques leads to a poor-resolution dispersion image for a particular site condition, the same site should be processed using the other transformation techniques to ensure that the selected transformation technique is not causing the poor quality dispersion image.

  7. 8.

    Overall, the best practice is to use the composite dispersion approach by combining all the transformation methods or at least use two different transformation methods (FDBF-cylindrical and one of the other transformation techniques) for MASW data processing, particularly for complex stratigraphy environments (e.g., sites where higher modes are present). The composite dispersion approach can be used as a means to enhance the quality and reliability of the experimental dispersion curve, reduce the uncertainty regarding the experimental dispersion curves and the final inverted Vs profile, accurately determine different modes of propagation, and define and remove data corrupted by near-field effects if any are present.