1 Introduction

One of the useful and effective techniques in tunnel designing is the Convergence Confinement Method (CCM). It is a simplified approach used to analyze the interaction between the ground and support. The CCM consists of three basic components in the form of graphs: the ground reaction curve (GRC), the longitudinal deformation profile (LDP), the support characteristic curve (SCC), (Fig. 1). The GRC can be defined as a curve that describes the reduction in inner pressure and the increase in radial displacement of the tunnel wall. The relationship between the tunnel deformations with the distance from the tunnel face is called LDP. Correlation of the stress–strain in the support system is identified as the SCC (Carranza-Torres and Fairhurst 2000; Guan et al. 2007). The most important applications of the CCM method in tunneling are as follows:

  • Round length (maximum unsupported excavation length)

  • Stress relaxation factor (for 2D numerical design)

  • Timing of support installation

  • Rock load determination

  • Support and pre-support measures

Fig. 1
figure 1

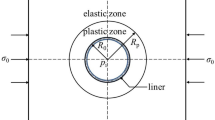
Main components of the CCM method (Bour and Goshtasbi 2019)

Full size image

The GRC is generally evaluated by closed form solutions and based on plane strain assumption. These solutions are applied to a circular tunnel section, hydrostatic in-situ stresses and elastic perfectly plastic (EPP) constitutive model (Brown et al. 1983; Ogawa and Lo 1987; Duncan-Fama, 1993; Panet 1995; Wang 1996; Carranza-Torres and Fairhurst 2000). However, a number of solutions have been presented for strain softening (SS) (Alonso et al. 2003; Guan et al. 2007; Park and Kim 2008; Lee and Pietruszczak 2008; Fahimifar et al. 2015) and elastic-brittle-plastic (EBP) behavior of the rock mass (Carranza-Torres and Fairhurst 2004; Sharan 2003, 2005; Park and Kim 2006; Wang and Yin 2011). These methods are based on plasticity theory and application of elastic or plastic strain parameter to introduce the post-failure behavior of the rock mass.

The LDP was initially calculated by elastic behavior of the rock mass (Panet 1993, 1995; Unlu and Gercek 2003). Then, further analytical equations are developed to obtain this curve, assuming EPP behavior and circular cross section (Panet and Guenot 1982; Chern et al. 1998; Carranza-Torres and Fairhurst 1999; Rooh et al. 2018). Distance from the tunnel face and tunnel radius are the only input parameters to these equations. Vlachopoulos and Diederichs (2009) proposed a new formulation for the LDP calculation that considers the maximum plastic radius. The method for obtaining the SCC curve was initially proposed for different types of supports by Brown and Hoek (1980) and then further discussed by other researchers (Peila and Oreste 1995; Hoek 1999; Carranza-Torres and Fairhurst 2000; Oreste 2003a, b; Oreste 2008). Carranza-Torres (2004); Panet et al. (2001).

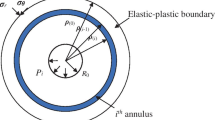
After tunnel excavation in strain softening materials, according to different inner pressures applied by the tunnel face and the support, three regions around the tunnel are created: residual, softening and elastic regions. The plastic zone refers to the residual and softening regions which creates a load on the structure. As the excavation continues and the internal pressure in tunnels falls below a critical support pressure (\({p}_{i}^{*}\)), a plastic zone develops around the tunnel. There are few equations to assess the plastic radii and especially how to expand it. For this reason, it is necessary in the design phase to consider the size, shape and development of the plastic zone ahead and behind of the tunnel face.

As mentioned above, CCM curves are often evaluated by EPP or EBP analyses for all kinds of rock masses. However, for rocks with average quality (25 < GSI < 75) which shows SS behavior, if failure occurs, none of these simple behavior models adequately show the post-failure behavior of the rock mass (Hoek and Brown 1997; Kaiser et al. 2000; Cai et al. 2004). Therefore, description and quantification of an appropriate constitutive model is still the main problem in application of the CCM method.

In this paper, post-failure behavior of the rock mass with average quality is formulated and incorporated in the constitutive model by the finite difference method (FDM). In order to verify the numerical approach, the results are compared with experimental results. In addition to apply the numerical method in the CCM tool, plastic zone extension and critical support pressure are investigated.

2 Problem Description

2.1 Convergence Confinement Method (CCM)

Tunnel excavation causes a disturbance of the initial state of stress in the ground and creates a three dimensional stress regime. The CCM method is a convenient tool to solve three-dimensional problems of rock-support interaction and estimate the applied load on the support. A plot of internal support pressure (\({p}_{i}\)) versus tunnel wall deformation (\({u}_{r}\)) is known as the GRC curve (Fig. 2a). The critical support pressure (\({p}_{i}^{*}\)) represents the boundary between the elastic and plastic response of the rock mass in the GRC curve. In rock masses with strain softening behaviour, there is another critical support pressure (\({p}_{i}^{**}\)) indicates the boundary between the softening and residual regions. Since the rock mass still has strength and can undergo the applied loads, the plastic failure of the rock mass does not necessarily mean the collapse of the tunnel. When the internal support pressure (\({p}_{i}\)) is less than (\({p}_{i}^{**}\)), tunnel starts to collapse and the radius of the plastic zone begins to increase. Therefore, the best time to install the support system or determine the round length is within these two critical support pressures.

Fig. 2
figure 2

Schematic representation of the CCM curves in SS rock mass behavior (a) GRC (b) LDP

Full size image

If a measuring point ahead of the advancing tunnel is considered, the displacement of this point is increased as the tunnel face approaches. The displacement is gradually increased as the face advances, and when the face exceeds the measuring point and is far enough away, the maximum displacement occurs. The relation between the displacement of the tunnel wall and the position of the tunnel face is defined as the longitudinal displacement profile (LDP) (Fig. 2b). In order to determine the appropriate timing for support installation and round length, a three-dimensional analysis should be carried out to establish this profile. Also, this curve is used to obtain the stress relaxation factor corresponding to the round length to be utilized in two-dimensional analysis. As mentioned, and shown in Fig. 2b, the three elastic, softening and residual regions are also in the LDP curve.

For unsupported tunnels with 2D analysis, the excavation process and plastic zone formation are simulated by gradually reduction in internal pressure from in situ stress value to null (Fig. 3a). When the internal support pressure (\({p}_{i}\)) is less than (\({p}_{i}^{*}\)), the rock mass is transmitted from elastic region to the softening region and the plastic zone develops around the tunnel. The plastic radii are also increased as the decreasing trend in the internal pressure applied to the tunnel wall continues. The transition from the softening to the residual region takes place for a value of the internal pressure less than (\({p}_{i}^{**}\)). As shown in Fig. 3b, the formation and evolution of the plastic zone begins from ahead of the tunnel face and continues to the behind of it. Therefore, 3D analysis should be carried out to estimate the accurate plastic radii and apply to the rock load determination.

Fig. 3
figure 3

Schematic representation of the CCM curves in SS rock mass behavior (a) GRC, (b) LDP

Full size image

2.2 Rock Mass Constitutive Model

It is important to have a comprehensive knowledge of the rock mass constitutive model and the parameters to obtain CCM curves for a tunnel. The three behavioural models for rock mass are: elastic perfectly plastic (EPP), elastic brittle plastic (EBP) and strain softening (SS). Most of the available equations to calculate the GRC and LDP curves include the EPP and EBP constitutive models. Based on a wide experience and study, rock masses with poor quality (GSI < 25), show the EPP behaviour. For rock masses with high quality (GSI > 75), the EBP model could be suitable and the SS constitutive model is more effective in terms of rock masses with average quality (25 < GSI < 75) (Fig. 4) (Hoek and Brown 1997; Kaiser et al. 2000; Cai et al. 2004).

Fig. 4
figure 4

Different post-failure modes in different GSI quantities (Hoek and Brown 1997)

Full size image

2.2.1 Strain Softening Behavior

Strain softening behavior of the rock mass can be studied and characterized by means of a failure criterion \(f\) and a plastic potential \(g\) which depend on the plastic softening parameter or plastic shear strain (\(\eta\)). As can be seen in Fig. 5, the softening state and the residual state take place in \(0 < \eta < \eta^{*}\) and \( \eta^{*} < \eta\), respectively. The critical value which establishes the change between the softening and residual states is defined as \(\eta^{*}\). The EBP behavior occurs when the slope of the softening state which is defined as drop modulus (M), has tendency to infinity. If M has a tendency to zero, the EPP behavior happens.

Fig. 5
figure 5

Three different states of a confined compressive test in a sample with SS behavior (Alejano et al. 2009)

Full size image

2.2.2 Failure Criterion and the Flow Rule

In order to study the strain softening behaviour in this research, it is assumed that the yielding of the rock mass is governed by Mohr–Coulomb yielding criterion (\(f\)) and plastic potential function (\(g\)). The yield criterion and plastic potential function are provided as follows:

$$ f\left( {\sigma_{r} ,\sigma_{\theta } ,\eta } \right) = \sigma_{\theta } - k_{\varphi } \left( \eta \right)\sigma_{r} - 2C\left( \eta \right)\sqrt {k_{\varphi } \left( \eta \right)} $$
(1)
$$ \sigma_{r} = \sigma_{3} \quad \sigma_{\theta } = \sigma_{1} $$
$$ {\text{g}}\left( {\sigma_{r} ,\sigma_{\theta } ,\eta } \right) = \sigma_{\theta } - k_{\psi } \left( \eta \right)\sigma_{r} $$
(2)

where, \({\sigma }_{\theta }\) and \({\sigma }_{r}\) denote the tangential and radial stresses, respectively. The parameters of cohesion (C), friction angle (\(\varphi \)), and dilation angle (\(\psi \)) are used to obtain dilation and friction coefficients are as follows:

$$ k_{\psi } \left( \eta \right) = \frac{1 + \sin \psi \left( \eta \right)}{{1 - \sin \psi \left( \eta \right)}} $$
(3)
$$ k_{\varphi } \left( \eta \right) = \frac{1 + \sin \varphi \left( \eta \right)}{{1 - \sin \varphi \left( \eta \right)}} $$
(4)

2.2.3 Evolution of Strength Parameters

When the rock mass failure occurs, it doesn’t have its original strength and the reduction in the strength parameters can be observed. This reduction depends on the confinement stress (\({\sigma }_{3}\)) and the softening parameter (\(\eta\)) (Arzúa and Alejano 2013). In our approach, it is assumed that strength parameters (\(c\),\(\varphi \),\(\psi \)) have a decreasing linear relationship with the softening parameter (\(\eta\)) (Fig. 6).

Fig. 6
figure 6

Variation of strength parameters with the softening parameter

Full size image

In plastic regime, the strength parameters can be expressed as follows:

$$ c\left( \eta \right) = \left\{ \begin{gathered} c^{peak} - \frac{{c^{peak} - {\text{c}}^{res} }}{\eta }\eta ,\quad 0 < \eta < \eta^{*} \hfill \\ c^{res} ,\quad \quad \quad \quad \quad \quad \quad \quad \;\eta^{*} < \eta \hfill \\ \end{gathered} \right. $$
(5)
$$ \varphi \left( \eta \right) = \left\{ \begin{gathered} \varphi^{peak} - \frac{{\varphi^{peak} - \varphi^{res} }}{{\eta^{*} }}\eta ,\quad 0 < \eta < \eta^{*} \hfill \\ \varphi^{res} ,\quad \quad \quad \quad \quad \quad \quad \quad \quad \eta^{*} < \eta \hfill \\ \end{gathered} \right. $$
(6)
$$ \psi \left( \eta \right) = \left\{ \begin{gathered} \psi^{peak} - \frac{{\psi^{peak} - \psi^{res} }}{{\eta^{*} }}\eta ,\quad 0 < \eta < \eta^{*} \hfill \\ \psi^{res} ,\quad \quad \quad \quad \quad \quad \quad \quad \quad \eta^{*} < \eta \hfill \\ \end{gathered} \right. $$
(7)

2.2.4 Post-failure Behaviour

To describe and obtain a complete stress–strain behaviour of the rock mass, drop modulus (M) and critical softening parameters (\(\eta^{*}\)) are needed. According to Fig. 7, the major principal stress for a value of \({\sigma }_{3}\) and peak and residual states, can be defined as follows:

$$ \sigma_{1}^{peak} \left( {\sigma_{3} } \right) = \frac{{2c^{peak} \cos \varphi^{peak} }}{{1 - \sin \varphi^{peak} }} + \frac{{1 + \sin \varphi^{peak} }}{{1 - \sin \varphi^{peak} }}{ }\sigma_{3} $$
(8)
$$ \sigma_{1}^{res} \left( {\sigma_{3} } \right) = \frac{{2c^{res} \cos \varphi^{res} }}{{1 - \sin \varphi^{res} }} + \frac{{1 + \sin \varphi^{res} }}{{1 - \sin \varphi^{res} }}{ }\sigma_{3} $$
(9)
Fig. 7
figure 7

Calculation of the critical softening parameter based on the stress–strain curve of the rock (Alejano et al. 2010)

Full size image

The values of the major and minor principal strains can be obtained by means of the following equations (Alejano et al. 2010):

$$ \varepsilon_{1}^{peak,elas} = { }\frac{{\sigma_{1}^{peak} \left( {\sigma_{3} } \right)}}{E} $$
(10)
$$ \varepsilon_{1}^{\eta ,drop} = \frac{{\left[ {\sigma_{1}^{peak} \left( {\sigma_{3} } \right) - [\sigma_{1}^{res} \left( {\sigma_{3} } \right)} \right]}}{ - M} $$
(11)
$$ \varepsilon_{1}^{elas} = \frac{{\sigma_{1}^{res} \left( {\sigma_{3} } \right)}}{E} $$
(12)
$$ \varepsilon_{1}^{plas} = \varepsilon_{1}^{peak,elas} + \varepsilon_{1}^{\eta ,drop} - \varepsilon_{1}^{elas} $$
(13)
$$ \varepsilon_{1}^{plas} = \left[ {\sigma_{1}^{peak} \left( {\sigma_{3} } \right)} \right] - \left[ {\sigma_{1}^{res} \left( {\sigma_{3} } \right)} \right]\left[ {\frac{1}{E} - \frac{1}{M}} \right] $$
(14)
$$ \varepsilon_{3}^{plas} = - \frac{1}{2}\frac{1 + \sin \psi \left( \eta \right)}{{1 - \sin \psi \left( \eta \right)}}\varepsilon_{1}^{plas} = \frac{{ - k_{\psi } }}{2}\varepsilon_{1}^{plas} $$
(15)

As can be seen in Fig. 7, it is assumed that the relationship between the plastic strains is linear.

Now, the critical softening parameter (\(\eta^{*}\)) for the assumed amount of (\(\sigma_{3}\)) can be obtained as below:

$$ \eta^{*} \left( {\sigma_{3} } \right) = \varepsilon_{1}^{plas} - \varepsilon_{3}^{plas} = \left( {1 - \frac{E}{M}} \right) \left( {\frac{{\sigma_{1}^{peak} \left( {\sigma_{3} } \right) - \sigma_{1}^{res} \left( {\sigma_{3} } \right)}}{E}} \right)\left( {1 + \frac{{k_{\psi } }}{2}} \right) $$
(16)

Since the drop modulus (M) depends on the geological strength index (GSI) of the rock mass and confinement stress (\({\sigma }_{3}\)), the critical softening parameter can be calculated as follows (Alejano et al. 2009):

$$ \eta^{*} = \varepsilon_{1}^{plas} - \varepsilon_{3}^{plas} = \left( {1 - \frac{E}{M}} \right)\left( {\frac{{\sigma_{1}^{peak} \left( {\sigma_{3} } \right) - \sigma_{1}^{res} \left( {\sigma_{3} } \right)}}{E}} \right)\left( {1 + \frac{{k_{\psi } }}{2}} \right) = f_{\eta } \left( {\sigma_{3} ,GSI} \right)\left( {\frac{{\sigma_{1}^{peak} \left( {\sigma_{3} } \right) - \sigma_{1}^{res} \left( {\sigma_{3} } \right)}}{E}} \right)\left( {1 + \frac{{k_{\psi } }}{2}} \right) $$
(17)

Based on the findings of the laboratory tests, Alejano et al. (2009) suggested the following equation to estimate the confinement stress dependent critical softening parameter:

$$ f_{\eta } \left( {\sigma_{3} ,GSI} \right) = \left[ {\left( {\frac{225 - GSI}{{1000}}} \right).\sigma_{3} + \left( {\frac{55 - 0.6GSI}{8}} \right)} \right]for{ }25 < GSI < 75 $$
(18)

3 Verification of the Strain Softening Constitutive Model

The results of the laboratory tests (triaxial test, uniaxial compressive test, density test, etc.) that performed on the granite specimens by Arzúa and Alejano (2013), are used to verify the proposed equations for the SS constitutive model. Based on the equations as mentioned above, a calculation algorithm has been presented to simulate the rock behaviour (Fig. 8). This algorithm, along with the modified SS behaviour model has been implemented into the numerical codes \({FLAC}^{2D \& 3D}\) by using the embedded FISH program language.

Fig. 8
figure 8

Numerical simulation procedure for the SS constitutive model

Full size image

In order to show the applicability of the proposed procedure, several tests of triaxial compression test are simulated (\({\sigma }_{3}\)=2, 6, 10 MPa). The parameters used in numerical simulation are presented in Table 1. The model has a height of 108 mm and a diameter of 54 mm (Fig. 9).

Table 1 Mechanical parameters used in numerical simulation of triaxial test
Full size table
Fig. 9
figure 9

Boundary conditions of the cylindrical sample for numerical simulation

Full size image

Figure 10 shows the comparison between the results of the triaxial test modelling with the EPP constitutive model and the experimental results. As can be seen, in elastic state the simulated stress–strain curves are in good accordance with the experimental results. When the failure occurs, these curves continue linearly and are constant in the plastic state. However, in reality, the strength parameters soften after the onset of plastic yield, and this matter affects the stress–strain curve. This indicates the inefficiency of the EPP constitutive model for the rock masses with average quality.

Fig. 10
figure 10

Comparison of stress- strain curves of numerical approach (EPP model) and experimental result

Full size image

The results of numerical and experimental tests for the modified SS model are given in Fig. 11. It can be seen that in softening and residual states, there is a good consistency between numerical and experimental approaches. Both peak and residual strength increase with increasing the confining pressure (\({\sigma }_{3}\)), however, according to Fig. 11, the rate of growth for peak strength is more than for residual ones.

Fig. 11
figure 11

Comparison of stress- strain curves of numerical approach (SS model) and experimental result

Full size image

The effect of increasing the confining pressure on the ductility of the samples is well illustrated in Fig. 11. The values of drop modulus (M) in softening region decreases with increasing confining pressure and the behaviour of the sample is transitioning from brittle to ductile type (M = -18, -17, -16 GPa). In addition, the value of the critical softening parameter (\(\eta^{*}\)) in each element is not constant in the plastic state and varies according to the corresponding confining pressure.

4 Application of the CCM Method

4.1 Numerical Approaches

In the present study, a circular tunnel of 7 m diameter and 450 m deep has been chosen for the CCM application. Two constitutive models of the EPP and the proposed SS through the M-C failure criterion have been used to show the behaviour of the surrounding rock mass. The rock mass has been assumed to be homogeneous and isotropic and the parameters are shown in Table 2.

Table 2 Rock mass geological parameters (Alejano et al. 2009)
Full size table

The finite difference numerical program \({FLAC}^{2D \& 3D}\) is used to simulate the tunnel excavation process (Itasca Inc. 2013, 2016). The analysis has been carried out for three cases of in-situ stress ratios (K) of 0.5, 1.0 and 1.5. As shown in Fig. 12, the dimensions of the model are designed to minimize the boundary effects. The lateral and bottom surfaces of the model are fixed horizontally and vertically, respectively. A fine grid is employed at the vicinity of the tunnel boundary in order to increase the accuracy of the results.

Fig. 12
figure 12

Dimensions and Finite difference mesh used for numerical modeling in both 2D and 3D approaches

Full size image

4.2 The CCM Curves

Figure 13 shows the CCM curves for the K = 0.5 associated with EPP and SS constitutive models. It can be seen that the maximum displacement in EPP model altered by 65 mm to 330 mm in SS model. The displacement in the tunnel face for EPP and SS model are 27 mm and 147 mm, respectively. In addition, from 30 to 40% of stress relaxation, GRCs are in good accordance. In other words, the elastic response of the ground to the tunnel is similar for both constitutive models. The critical support pressure (\({p}_{i}^{*}\)) between the elastic and plastic states will be 60–70% of the in-situ stress. The distinct differences between GRCs can be observed about the 70% of stress relaxation and is increased with increasing stress relaxation.

Fig. 13
figure 13

CCMs for K = 0.5

Full size image

GRCs for K = 1 and with these two constitutive models are shown in Fig. 14. As can be seen, the deformation in SS model is greater than in EPP model. The maximum displacement for the EPP model is increased from about 100 mm to 530 mm in the SS model. The displacement in the tunnel face in EPP and SS model are 32 mm and 176 mm, respectively. According to Fig. 14, up to 70% of stress relaxation, GRCs are in good accordance and therefore the critical support pressure (\({p}_{i}^{*}\)) is 30% of the in-situ stress.

Fig. 14
figure 14

CCMs for K = 1.0

Full size image

GRCs for K = 1.5 are shown in Fig. 15. As can be seen in this figure, the maximum displacement in EPP model is altered by 240 mm to 940 mm in SS model. The displacement in the tunnel face in EPP and SS model is 35 mm 138 mm, respectively. Since GRCs are similar up to 60% of stress relaxation, it can be concluded that the critical support pressure (\({p}_{i}^{*}\)) is 50% of the in-situ stress.

Fig. 15
figure 15

CCMs for K = 1.5

Full size image

5 Plastic Zone

The shape and size of the plastic zone are accounted as the key factors to design the tunnel support and the results of the CCM method. In addition, the rock load can be estimated by the plastic radii. As mentioned above, the maximum extension of the plastic zone occurs when the internal pressure (\({p}_{i}^{*}\)) is equal to zero. Figure 16 shows the results of two-dimensional analysis for the plastic zone around the circular and for both mentioned constitutive models. As can be seen, the maximum plastic radii in the case of the SS model and for all different values of K, is greater than the EPP model. According to Fig. 16, it can be said that the maximum plastic radii for the SS model is almost twice the EPP model.

Fig. 16
figure 16

Plastic zone thickness around the tunnel (2D analysis)

Full size image

Instability of the face and unsupported span are common problems in low and average quality of the rock masses. At this situation, pre-support measures or change in excavation method are used to ensure the stability (Klotoé and Bourgeois 2019; Zhang et al. 2020). The main challenge to design the pre-support measures and particularly their lengths is the accurate estimation of the plastic zone extension in front of the face. Figure 17 shows the results of three-dimensional analysis for the plastic zone ahead of the tunnel face. As can be seen, the plastic zone extension in front of the face for the case of SS model is greater than EPP model. The important point in this figure for K = 0.5 is that the extension of the plastic zone in front of the face is greater comparing to the walls. While for other two values of in-situ stress ratios, plastic zone extension in front of the face and the walls are the same.

Fig. 17
figure 17

Longitudinal section of the plastic zone extension ahead of the tunnel (3D analysis)

Full size image

As mentioned, three elastic, softening and residual regions are formed in front of the tunnel face and walls due to the tunnel excavation. The extension of each of these regions depends on the factors such as the in-situ and induced stress values, geomechanical parameters, tunnel geometry and tunnel excavation method. Therefore, a comparison has been made between these regions for the SS model and different values of in-situ stress ratios (Fig. 18). It can be seen that the thickness of softening and residual regions for K = 1.5 is higher than other values and is constant around the tunnel. While, for K = 0.5 the thickness of residual region in front of tunnel face is higher than tunnel walls.

Fig. 18
figure 18

States of zones around the tunnel

Full size image

6 Critical Support Pressure

Failure of the rock mass surrounding the tunnel occurs when the internal pressure provided by the tunnel lining is less than the critical support pressure (\({p}_{i}^{*}\)). Closed form solutions are available to determine this pressure for hydrostatic stress field and two constitutive models (EPP and EBP). While for critical support pressure (\({p}_{i}^{**}\)) that rock mass changes from softening to residual region, there is no analytical solutions but it can be obtained by numerical simulation. For this purpose, the values of the cohesion parameter for a point on the tunnel crown are monitored during the gradual reduction in internal pressure (\({p}_{i}\)). The values of this parameter versus normalized pressure on the tunnel wall (\({p}_{i}/{p}_{0}\)) are shown in Fig. 19. It can be seen that the value of this pressure (\({p}_{i}^{**}\)) for K = 1.5, is 30% of the in situ stress, and for K = 0.5, 1.0, it is 20% of in situ stress. Furthermore, the amount of critical support pressure (\({p}_{i}^{*}\)) that defines the boundary between the elastic and plastic regions, can be also determined by this diagram.

Fig. 19
figure 19

Determination of (\({p}_{i}^{**}\)) based on the distribution of cohesion value

Full size image

7 Conclusions

In order to take into account, the effect of constitutive models on CCM method, the rock masses with average quality (30 < GSI < 75) that show strain softening behavior, is used in this research. An important factor to define the CCM curves is the behavioral model selection and particularly post-failure behavior of the rock. For this purpose, the complete stress − strain curve for strain softening materials is quantified. It includes evolutional behavior of the strength parameters based on confining pressure (\({\sigma }_{3}\)) and GSI. Then a simple procedure is implemented into the numerical codes \({FLAC}^{2D \& 3D}\) by using the embedded FISH program language. In order to validate the equations, the simulated results based on the proposed procedure are in good accordance with the laboratory results.

To investigate the application of the proposed procedure in CCM method, a series of 2D and 3D analysis with SS and EPP behavior are carried out for circular tunnel and in-situ stress ratios of K = 0.5, 1.0 and 1.5. The following conclusions are drawn from the analysis:

  • According to results, there are considerable differences between the constitutive models of LDPs and GRCs in plastic region. When the rock mass failure occurs, this difference begins and increases with the face advance.

  • The maximum deformation for SS model is more than three times of EPP model. This is due to low confining pressure (\({\sigma }_{3}\)) adjacent to the tunnel boundary and the consequent decrease in the strength parameters of the rock mass. While this issue is not considered in the EPP constitutive model.

  • The plastic radii for SS model are about two times of EPP model in both two-dimensional and three-dimensional sections. As mentioned above, this is due to evolutional behavior of the strength parameters in the SS model.

  • The procedure used in this paper, can determine the critical pressure (\({p}_{i}^{*}\)) between the residual and softening regions. This issue in CCM design can be helpful to determine the safe round length and stress relaxation coefficient.