Conceptual p–y Curve Framework for a Single Pile in Cohesionless Soils with Variable Degrees of Saturation

Abstract

P–y curves are commonly used in geotechnical engineering practice to predict the lateral resistance of soils and corresponding lateral displacements when piles are subjected to lateral forces and moments. The original formulation for p–y curves in cohesionless soils was developed in 1974 based on the behavior of a pile in a fully saturated soil layer. This paper focuses on modifying the p–y curve formulation to incorporate unsaturated soil mechanics in cohesionless soils. Key variables that are impacted by the soils’ degree of water saturation are adjusted and new mathematical models are presented. Then, these new models are assessed using numerical solutions. The new approach is validated against the original version in fully saturated soils. To capture the significance of the degree of saturation in the p–y curve formulation, a set of sensitivity analyses is performed. Specifically, the effects of water table level, soil water retention characteristics, and flow discharge rate on ultimate lateral resistance, horizontal subgrade reaction, and fully constructed p–y curves were investigated. Overall, the results emphasize the importance of the water level fluctuation and climatic conditions on the lateral pile response, while ignoring such conditions may lead to inaccurate performance assessment of deep foundation systems.

1 Introduction

The introduction of p–y curves for lateral resistance of soils began in the 1950s for analysis and installation of offshore rigs in the oil industry (Terzaghi 1955; McClelland and Focht 1958). Since then, the approach has been further developed and extended to consider various soils and loading conditions (Matlock 1970; Reese et al. 1974; Reese and Welch 1975; Mokwa et al. 2000). The method is also widely used by practicing geotechnical engineers worldwide and programmed in different computer software (Reese and Wang 2006; Isenhower et al. 2019a). A review of current literature on lateral soil-pile interaction show different analytical, numerical, field, and experimental use of p–y curves in geotechnical applications. For example, Rathod et al. (2020) discussed the relevant approaches for the analysis of laterally loaded piles under static and cyclic loading conditions. They reviewed the common theoretical and analytical design methodologies such as the beam on wrinkler elastic foundation (Hetényi 1946), the ultimate load method (Broms 1964a, b), the p–y curve approach, and elastic continuum numerical techniques (Poulos and Davis 1980). However, the discussion from this review study showed that the p–y curve approach is usually regarded as one of the best methods to reflect the non-linearity of lateral soil-pile response.

The formulation of the p–y curve in cohesionless soils was initially developed by Reese et al. (1974), and later, there were modifications to the original approach by the American Petroleum Institute (2010). In the original formulation, the soil was idealized by a set of finite, elastic Wrinkler springs. Two expressions were derived for the ultimate lateral resistance of the soil; one for the near soil surface condition and one at a depth far from the soil surface. The formulations were then validated using the field lateral load test results in Mustang Island, and it was recommended that caution be taken when applying them on other sites (Isenhower et al. 2019b). Some recent studies have also proposed modified p–y curves for different applications (Choo and Kim 2016; Suryasentana and Lehane 2016; Komolafe and Aubeny 2020). For example, Rathod et al. (2018, 2019) developed p–y curves showing the effect of sloping ground on single piles in soft clay. They conducted a number of 1 g tests on an instrumented aluminum pile embedded atop the sloping ground at various angles and pile depth embedments. Results from their analysis showed that steeper soil slopes reduced the soil reactions and increased the pile lateral displacement due to the reduced mass of soil in front of the pile. Additionally, the effect of the sloping ground on the p–y curves below the depth of fixity along the pile was not significant.

In recent years, unsaturated soil mechanics has evolved by extending the Terzaghi (1943) soil mechanics and introducing variables such as matric suction, degree of saturation, suction stress, and soil–water retention (van Genuchten 1980; Lu and Likos 2004, 2006; Fredlund et al. 2012). More specifically, Bishop (1959) effective stress formulation for unsaturated soils has shown promising results when consistently used across the degrees of saturation in different deep foundation-related applications such as estimating lateral earth pressure coefficients, Poisson’s ratio, and seismic behavior of piles, to mention a few (Vahedifard et al. 2015; Ghadirianniari et al. 2017; Ghayoomi et al. 2018; Thota et al. 2021). For example, Cheng and Vanapalli (2021) studied the nonlinear behavior of laterally loaded rigid piles using the mechanics of unsaturated soils. Also, Lalicata et al. (2019, 2020) investigated the response of laterally loaded piles in unsaturated soils through centrifuge and finite element modeling (FEM).

The original p–y curve approach by Reese et al. (1974) for lateral soil resistance is founded on cohesionless soils in the fully saturated state and does not consider the mechanics of unsaturated soils. Based on the review of current literature, little has been done to extend the p–y curve approach to unsaturated cohesionless soils and understand how climatic conditions affect the lateral resistance of the soil, especially during extreme events. Additionally, examining the saturation state of soils can enhance foundation performance and lead to a potentially cost-effective design, thereby improving the state of practice (Komolafe and Ghayoomi 2021). The strength and stiffness of unsaturated soils differ from those of saturated and dry soils due to inter-particle suction and three-phase material response (Lu et al. 2010). Hence, the theoretical ultimate lateral resistance and the p–y curves in unsaturated soils would vary from fully saturated soils. Therefore, the inclusion of the effects of the degree of water saturation in soil layers into the p–y curve formulations would benefit the performance assessment of deep foundations. This becomes critical when dealing with fluctuating groundwater levels within different vadose zone thicknesses. This paper presents the derivation and modifications of the p–y curve formulation and ultimate lateral strength constitutive models of cohesionless soil by incorporating unsaturated soil mechanics in soil layers with variable groundwater levels. The updated formulations were numerically programmed to develop p–y curves demonstrating the influence of soil degree of saturation. Finally, the extent of this influence was investigated by a set of local sensitivity analyses.

2 Theoretical Ultimate Lateral Resistance for Unsaturated Cohesionless Soils

The effective stress in unsaturated soils can be expressed using suction stress characteristic curve (SSCC) formulation (Lu and Likos 2006; Lu et al. 2010), as shown below

$$\sigma_{v}^{^{\prime}} = \sigma_{v} - u_{a} - \sigma_{s}$$

(1)

where ${\sigma }_{v}$ is the total vertical stress, ${u}_{a}$ is the pore air pressure, ${\sigma }_{s}$ is the suction stress. Suction stress is an essential state of stress in unsaturated soils and can be defined as (Lu and Likos 2004; Lu et al. 2010),

$$\sigma_{s} = - (u_{a} - u_{w} )\left[ {1 + \left[ {\alpha_{VG} \left( {u_{a} - u_{w} } \right)} \right]^{{n_{VG} }} } \right]^{{\frac{{1 - n_{VG} }}{{n_{VG} }}}}$$

(2)

where $u_{w}$ is the pore water pressure. $u_{a} - u_{w}$, the difference between pore air and pore water pressure constitutes matric suction. $\alpha_{VG}$ and $n_{VG}$ are the van Genuchten (1980) fitting parameters for the soil–water retention curve (SWRC) representing the parameter related to the inverse of the air-entry value and the pore size distribution, respectively.

The degree of saturation profile in the depth of a soil layer depends on the depth of the water table and climatic impacts, including precipitation and evaporation. In the absence of any water influx or outflux, suction will take a hydrostatic form above the groundwater level (i.e., negative pore water pressure), while beneath the water level, the pore water pressure is considered positive. However, the matric suction profile would vary when evaporation and precipitation occur. For example, Fredlund and Rahardjo (1993) emphasized that matric suction in the field can decrease or increase based on variations in precipitation and evaporation due to climatic conditions. Liu et al. (2014) investigated how seepage influences consolidation in unsaturated soils and discussed that infiltration due to rainfall and evaporation rate have a considerable effect on suction development and pore water pressure, respectively, in unsaturated soils. Mirshekari et al. (2018) also evaluated the effects of water flux on unsaturated sand using centrifuge tests, and they inferred that there was a substantial effect of hysteresis due to wetting and drying on the soil water retention curve under steady-state infiltration. Hence, the evaluation of water flux would play a key role in understanding the influence of climatic conditions on the lateral resistance of unsaturated cohesionless soils, which is an objective of this study. Positive values of vertical discharge $(+q)$ signify evaporation, and negative values of vertical discharge $(-q)$ signify infiltration. However, in fully saturated conditions, $q=0$. Consequently, matric suction profile in depth can be written based on Lu and Likos (2004) as

$${u}_{a}-{u}_{w}=-{{\alpha }_{VG}}^{-1}\mathrm{ln}\left[\left(\frac{{k}_{s}+q}{{k}_{s}}\right){e}^{-{\alpha }_{VG}{\gamma }_{w}\left({H}_{w}-z\right)}-\frac{q}{{k}_{s}}\right]$$

(3)

where ${H}_{w}$ is the depth of the groundwater level and ${k}_{s}$ is the saturated hydraulic conductivity.

The estimation of the ultimate lateral resistance near the soil surface takes a similar approach to the one proposed by Reese et al. (1974), except with a modification of the state of water saturation. One important note is that the soil unit weight changes due to the variation of the volumetric water content in the soil layer. Using van Genuchten’s SWRC model, the soil water content can be estimated as a function of suction

$$\theta ={\theta }_{r}+\left({\theta }_{s}-{\theta }_{r}\right){S}_{e}={\theta }_{r}+\left({\theta }_{s}-{\theta }_{r}\right){\left[1+{\left[{\alpha }_{VG}\left({u}_{a}-{u}_{w}\right)\right]}^{{n}_{VG}}\right]}^{\frac{1-{n}_{VG}}{{n}_{VG}}}$$

(4)

where ${\theta }_{r}$ and ${\theta }_{s}$ are residual and saturated volumetric water content, respectively, and ${S}_{e}$ is the effective degree of saturation. From this, the soil unit weight can be calculated as

$$\gamma =\left[\frac{{G}_{s}\left(1+w\right)}{1+e}\right]{\gamma }_{w}=\frac{{G}_{s}{\gamma }_{w}}{1+e}+{\gamma }_{w}\theta$$

(5)

where ${G}_{s}$ is the specific gravity, $e$ is the void ratio, and ${\gamma }_{w}$ is the unit weight of water.

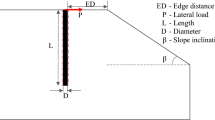
The mathematical formulation of the ultimate lateral resistance in cohesionless soils for the near soil surface and far from soil surface conditions based on the Reese et al. (1974) method is unraveled and discussed in Appendix 1. Rankine (1857) earth pressure theory was considered for evaluating the failure wedge for the unsaturated cohesionless soil. The assumption of Reese et al.’s wedge for lateral resistance analysis of unsaturated soil layers involves a challenge where both suction and water content change in depth. Depending on where the water table is located, the wedge may be fully saturated, unsaturated, or a mix of both conditions. Thus, this spatial variability should be considered either through discretized finite layers or numerical solution. Also, to be inclusive, it was assumed that the depth of the water table ${H}_{w}$ is somewhere within the wedge, as shown in Fig. 1. In this figure, $H$ is the wedge depth, $b$ is the diameter of the pile, ${\phi }^{^{\prime}}$ is the effective friction angle, $\alpha$ is the angle of the wedge fan with respect to the horizontal direction taken as$\frac{{\phi }^{^{\prime}}}{2}$, $\beta$ is taken as$45+\frac{{\phi }^{^{\prime}}}{2}$, $x$ is the length of the wedge fan, and ${\text{a}}$ is the length of the fan hypotenuse.

Fig. 1

Representation of the unsaturated–saturated cohesionless soil wedge modified from Reese et al. (1974)

The total vertical stress of the soil, ${\sigma }_{v}$, at the depth of the wedge, a critical component in the ultimate lateral resistance formulation, can be numerically integrated as

$$\sigma_{v} = \mathop \smallint \limits_{0}^{z} \gamma dz$$

(6)

where $z$ is any depth within the wedge, and $dz$ is the thickness of the finite soil strip layer at each interval. Putting the total stress from Eq. (6) and suction stress from Eq. (2) for different depths into Eq. (1) and assuming zero pore air pressure in the field would lead to the effective stress profile in depth.

Determining the lateral earth pressures acting on the unsaturated, cohesionless soil wedge requires estimating lateral earth pressure coefficients for unsaturated soils. Lu and Likos (2004) proposed the following expressions for active and passive coefficients in cohesionless soil; ${K}_{pu}$ and ${K}_{au}$ are the passive and active lateral earth pressure coefficient for the cohesionless unsaturated soils, respectively.

$${K}_{pu}={K}_{p}+\frac{{\sigma }_{s}\left(1-{K}_{p}\right)}{\sigma -{u}_{a}}$$

(7)

$${K}_{au}={K}_{a}+\frac{{\sigma }_{s}\left(1-{K}_{a}\right)}{\sigma -{u}_{a}}$$

(8)

where ${K}_{p}$ and ${K}_{a}$ are Rankine’s passive and active earth pressure coefficients, respectively.

The coefficient of at-rest lateral pressure for unsaturated soil can be expressed in terms of soil’s Poisson’s ratio based on elastic theory (Cornforth 1964; Federico and Elia 2009; Fredlund et al. 2012; Komolafe and Ghayoomi 2021; Turner et al. 2022), as presented below,

$${K}_{ou}=\frac{\mu }{1-\mu }$$

(9)

The expression in Eq. (9) is stable and does not yield negative values when the water table is close to the soil surface within small wedge depths. Further, Poisson’s ratio (shown as $\mu$ in this paper) also varies with the degree of saturation. Inspired by SSCC, Thota et al. (2021) proposed a Poisson’s ratio characteristic curve (PRCC) formulation for unsaturated soil as

$$\mu = \mu_{d} + \left( {\mu_{s} - \mu_{d} } \right)\left[ {1 - \left\{ {1 + \left( {\frac{S}{{1.04S_{r} }}} \right)^{{0.19n_{VG} + 2.71}} } \right\}^{{\frac{1}{{\left( {0.19n_{VG} + 2.71} \right)}} - 1}} } \right]$$

(10)

where ${\mu }_{d}$ is the dry state Poisson’s ratio, ${\mu }_{s}$ is the fully saturated state Poisson’s ratio of the soil, $S$ is the degree of saturation, and ${S}_{r}$ is the residual degree of saturation.

After determining the key input parameters within Reese et al.’s failure wedge (schematically shown in Fig. 1), the ultimate lateral resistance in unsaturated cohesionless soils near the soil surface condition can be numerically derived. Although some integral expressions may not result in an exact solution, they were numerically integrated through discretization.

The components of the resultant passive force, ${F}_{p}$, are based on the wedge geometry. Considering the unsaturated soil condition above the water table, which depends on the depth of the water table, slight modifications were made to $x$ and ${\text{a}}$, which are the length of the wedge fan and the length of the fan hypotenuse, respectively. Although still yielding the same results when used for the fully saturated wedge, they are now expressed as:

$$x=\left(H-z\right)\mathrm{tan}\beta \mathrm{tan}\alpha$$

(11)

$${\text{a}}=\frac{\left(H-z\right)\mathrm{tan}\beta }{\mathrm{cos}\alpha }$$

(12)

The cross-sectional area across the soil wedge is thus expressed as:

$$A=\left(H-z\right)b\mathrm{tan}\beta +{\left(H-z\right)}^{2}{\mathrm{tan}}^{2}\beta \mathrm{tan}\alpha$$

(13)

Hence the effective weight of the cohesionless soil wedge, if unsaturated, is expressed as:

$$W^{\prime } = \int\limits_{0}^{H} {\gamma Adz} = \int\limits_{0}^{H} {\gamma \left[ {\left( {H - z} \right)b\tan \beta + \left( {H - z} \right)^{2} \tan^{2} \beta \tan \alpha } \right] dz}$$

(14)

Equation (14) can also be written in its full form by substituting with the expression for $\gamma$ in Eq. (5) to give:

$$\begin{aligned} W^{\prime } = & \int\limits_{0}^{H} {\left[ {\frac{{G_{s} \gamma_{w} }}{1 + e} + \gamma_{w} \left( {\theta_{r} + \left( {\theta_{s} - \theta_{r} } \right)\left[ {1 + \left[ {\alpha_{VG} \left( {u_{a} - u_{w} } \right)} \right]^{{n_{VG} }} } \right]^{{\frac{{1 - n_{VG} }}{{n_{VG} }}}} } \right)} \right]} \\ & \left[ {\left( {H - z} \right)b\tan \beta + \left( {H - z} \right)^{2} \tan^{2} \beta \tan \alpha } \right] dz \\ \end{aligned}$$

(15)

It is necessary to note that when $z\ge {H}_{w}$ and the soil becomes fully saturated, ${\gamma }^{^{\prime}}=\gamma -{\gamma }_{w}$ should be used for calculating the effective weight. Thus, Eq. (15) should be modified to capture a general solution form with the water table somewhere within the wedge; as presented below

$$\begin{aligned} W^{\prime } = & \int\limits_{0}^{{H_{w} }} {\left[ {\frac{{G_{s} \gamma_{w} }}{1 + e} + \gamma_{w} \left( {\theta_{r} + \left( {\theta_{s} - \theta_{r} } \right)\left[ {1 + \left[ {\alpha_{VG} \left( {u_{a} - u_{w} } \right)} \right]^{{n_{VG} }} } \right]^{{\frac{{1 - n_{VG} }}{{n_{VG} }}}} } \right)} \right]\left[ {\left( {H - z} \right)b\tan \beta + \left( {H - z} \right)^{2} \tan^{2} \beta \tan \alpha } \right]dz} \\ & \quad + \int\limits_{{H_{w} }}^{H} {\gamma^{\prime } \left[ {\left( {H - z} \right)b\tan \beta + \left( {H - z} \right)^{2} \tan^{2} \beta \tan \alpha } \right] dz} \\ \end{aligned}$$

(16)

Also, there is a need to consider the active and at-rest coefficients of lateral earth pressure for the unsaturated–saturated cohesionless soil wedge, which are defined as:

$$K_{au}^{^{\prime}} = \left\{ {\begin{array}{*{20}l} {K_{au} z < H_{w} } \hfill \\ {K_{a} z \ge H_{w} } \hfill \\ \end{array} } \right.$$

(17)

$$K_{ou}^{^{\prime}} = \left\{ {\begin{array}{*{20}l} {K_{ou} z < H_{w} } \hfill \\ {\left( {1 - \sin \phi^{\prime } } \right)OCR^{{\sin \phi^{\prime}}} z \ge H_{w} } \hfill \\ \end{array} } \right.$$

(18)

In Eq. (18), when the depth of consideration is equal to or below the water table $(z\ge {H}_{w})$, the expression to determine ${{K}_{ou}}^{^{\prime}}$ was based on Mayne and Kulhawy (1982). Additionally, in purely cohesionless soils, $OCR$ (over consolidation ratio) can be approximately taken equal to 1.

The side area of the wedge can be expressed as

$$A_{s} = \int\limits_{0}^{H} {\left( {H - z} \right)\frac{\tan \beta }{{\cos \alpha }}dz}$$

(19)

Hence, the force normal to each side of the cohesionless soil wedge $F_{n}$ using the estimated $A_{s}$ can be calculated as

$$F_{n} = \int\limits_{0}^{H} {K_{ou}^{^{\prime}} \sigma_{v}^{^{\prime}} \left( {H - z} \right)\frac{\tan \beta }{{\cos \alpha }}dz}$$

(20)

The effect of friction on the sliding cohesionless soil wedge $F_{s}$ is estimated using

$$F_{s} = \int\limits_{0}^{H} {K_{ou}^{^{\prime}} \sigma_{v}^{^{\prime}} \left( {H - z} \right)\frac{{\tan \beta \tan \phi^{\prime}}}{\cos \alpha }dz}$$

(21)

The force at the underside of the cohesionless soil wedge acting at an angle ${\phi }^{^{\prime}}$, then, can be calculated as

$$F_{\phi } = \frac{{W^{\prime } + 2F_{s} \cos \beta }}{{\sin \left( {\beta - \phi^{\prime } } \right)}}$$

(22)

The passive force acting on the cohesionless soil wedge is expressed as

$$F_{p} = \frac{{W^{\prime } + 2F_{s} \cos \beta \cos \left( {\beta - \phi^{\prime } } \right)}}{{\sin \left( {\beta - \phi^{\prime } } \right)}} + 2F_{s} \sin \beta \cos \alpha - 2F_{n} \sin \alpha$$

(23)

Also, the active force based on Rankine’s theory is calculated as

$$F_{a} = \int\limits_{0}^{H} {K_{au}^{^{\prime}} \sigma_{v}^{^{\prime}} b dz}$$

(24)

Using the integral expressions above, for the near soil surface condition, the total ultimate lateral force of the cohesionless soil wedge is expressed as:

$${F}_{u}={F}_{p}-{F}_{a}$$

(25)

Similar to the fully saturated case, differentiating ${F}_{u}$ with respect to $H$ (the wedge depth) results in the theoretical ultimate lateral resistance of the cohesionless soil near the soil surface, while the wedge constitutes a mix of unsaturated and saturated soils. Therefore, the ultimate lateral resistance of the cohesionless soil near the soil surface can be evaluated using numerical differentiation.

$${p}_{ua}=\frac{d{F}_{u}}{dH}$$

(26)

The failure mode for the case of soils far from the surface is shown in the Appendix in Fig. 17, and the mathematical derivation for the ultimate lateral resistance expression of fully saturated soils is described in Eqs. (52)–(58). It should be noted that often the soil far from the surface is fully saturated. However, for alternating saturated–unsaturated conditions, the theoretical ultimate lateral resistance at a depth far from the soil surface can be estimated as

$$p_{ub} = \left( {\sigma_{VI}^{\prime } - \sigma_{V}^{\prime } } \right)b = \sigma_{v}^{^{\prime}} b\left[ {K_{au}^{\prime } \left\{ {\tan^{8} \beta - 1} \right\} + K_{ou}^{\prime } \tan^{4} \beta \tan \phi^{\prime } } \right]$$

(27)

Hence, the theoretical ultimate lateral resistance for the unsaturated–saturated cohesionless soil can be considered as

$${p}_{ut}=\mathrm{min}p\left({p}_{ua}, {p}_{ub}\right)$$

(28)

where $\mathrm{min}p$ signifies minimum positive values only.

The theoretical ultimate lateral resistance obtained for the near soil surface and far from soil surface scenarios need to be adjusted to field values for static and cyclic loading, and the necessary modification plots based on Reese et al. (1974) are shown in Appendix 2. A set of approximate empirical relationships were derived for this adjustment for static loading conditions, and they are also presented in Appendix 2.

3 Coefficient of Subgrade Reaction

The coefficient of horizontal subgrade reaction, ${k}^{^{\prime}}$, has been a widely investigated parameter over the years (Terzaghi 1955; Vesic 1961; Habibagahi and Langer 1984; Bowles 1996; Isenhower et al. 2019b). ${k}^{^{\prime}}$ is a reflection of the soil modulus variation with depth. Vesic (1961) proposed a popular representation of ${k}^{^{\prime}}$ that takes into consideration a reflection of the soil-pile stiffness. This equation also incorporates the soil Poisson’s ratio, and it can be used to obtain the initial value of ${k}^{^{\prime}}$ to get the initial straight-line portion of the p–y curve. Therefore, the initial value of ${k}^{^{\prime}}$ shown as ${k}_{i}$ can be determined as

$${k}_{i}=\frac{0.65}{b}\left[\frac{{E}_{s}}{1-{\mu }^{2}}\right]\sqrt[12]{\frac{{E}_{s}{b}^{4}}{{E}_{p}{I}_{p}}}$$

(29)

where ${E}_{s}$ is the Young’s modulus of the soil at very small strains, ${E}_{p}$ is the elastic modulus of the pile, and ${I}_{p}$ is the second moment of area for the pile section. It is also important to note that the ${k}^{^{\prime}}$ value for the unsaturated–saturated soil wedge used in this study was determined based on an average in depth,

$$k^{\prime } = \frac{{\mathop \smallint \nolimits_{0}^{H} k_{i} Adz}}{{\mathop \smallint \nolimits_{0}^{H} Adz}}$$

(30)

${E}_{s}$ can be evaluated based on elastic theory in relation to the small strain shear modulus of the soil ${G}_{max}$ and the Poisson’s ratio. ${G}_{max}$ can be obtained for cohesionless soils using the Hardin and Drnevich (1972) relationship form, which various researchers have used and modified for different soil types (Kramer 1996; Khosravi et al. 2009; Ghayoomi and McCartney 2011). A popular expression generally applicable to various types of cohesionless soils is based on Kramer (1996) and Hardin (1978) equations; hence, ${E}_{s}$ and ${G}_{max}$ can be expressed as:

$${E}_{s}=2{G}_{max}\left(1+\mu \right)$$

(31)

$$G_{\max } = 625\left[ {\frac{1}{{0.3 + 0.7e^{2} }}} \right]OCR^{k} P_{a}^{{1 - n^{\prime}}} \left[ {\frac{{\sigma_{v}^{^{\prime}} + 2K_{ou}^{^{\prime}} \sigma_{v}^{^{\prime}} }}{3}} \right]^{{n^{\prime}}}$$

(32)

where ${P}_{a}$ is the atmospheric pressure (in the same units as ${{\sigma }_{v}}^{^{\prime}}$ and ${G}_{max}$) which can be taken as 101.3 kPa, $OCR$ can be assumed to be 1 for purely cohesionless soils, $k$ is the overconsolidation ratio exponent, which can be taken as 0 when the plasticity index is 0, and ${n}^{^{\prime}}$ is the stress exponent, which can be taken as 0.5.

Equations (31) and (32) are approximately applicable to saturated and unsaturated soils if suction-dependent effective stress formulation is used (Ghayoomi and McCartney 2011). However, some researchers encouraged the additional direct inclusion of suction effects in the shear modulus formulation (Dong et al. 2016; Le and Ghayoomi 2016; Ghayoomi et al. 2017).

4 Construction of the p–y Curve

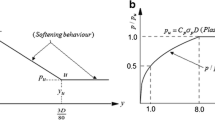
The Reese et al. (1974) p–y curve is constructed through several key points. The typical p–y curve forms are shown in Fig. 2. These include: the point $u$ where a lateral displacement ${y}_{u}$ corresponds to ultimate lateral resistance, ${p}_{u}$; the point $m$ with ${y}_{m}$ and ${p}_{m}$ coordinates, and the point $k$ at the end of the initial straight-line portion of the curve starting from the origin. There is a parabola that defines the p–y curve between the points $k$ and $m$. The rest of the p–y curve from point $m$ to point $u$ is an intermediate straight-line. From the point $u$ and beyond, the horizontal straight-line signifies that the soil has reached the ultimate lateral resistance or displacement.

Fig. 2

Different forms of a typical p–y curve in cohesionless soil

$${p}_{k}={k}^{^{\prime}}H{y}_{k}$$

(33)

The parabolic p–y function between the points $k$ and $m$ warrants

$${p}_{pb}=\overline{c}{y }^\frac{1}{n}$$

(34)

$$n=\frac{{p}_{m}}{s . {y}_{m}}$$

(35)

$$\overline{c }=\frac{{p}_{m}}{{{y}_{m}}^\frac{1}{n}}$$

(36)

where $s$ is the slope of the line between points m and u.

$${y}_{k}={\left[\frac{\overline{c}}{{k }^{^{\prime}}H}\right]}^{\frac{n}{n-1}}$$

(37)

For an aesthetic look of the p–y curve, the horizontal straight-line beyond point $u$ can be extended beyond ${y}_{u}$ (or ${y}_{k}$, when ${y}_{k}>{y}_{u}$). Additionally, the maximum value of the p–y curve modulus ${E}_{p-y (max)}$, being a function of the relative density and unit weight of sand as suggested by Terzaghi (1955), can be estimated as:

$${E}_{p-y \left(\mathrm{max}\right)}={k}^{^{\prime}}H$$

(38)

5 Validation of the Proposed p–y Curve Model With Reese et al. (1974)

Comparing the original p–y curve formulation in sand and the method proposed in this study is an essential first step to confirm the consistency of the approach. To this end, a case example was defined, and the associated p–y curves were compared. In order to ensure that the conditions governing the determination of the ultimate lateral resistance were satisfied, the ultimate lateral resistance was analyzed at two sample depths, one near the soil surface and far from the soil surface. For the near soil surface condition, a shallow depth was required to obtain the minimum ${p}_{ua}$ based on Eq. (28). Hence, a depth of 1.5 m was selected and found to satisfy this criterion. On the other hand, ${p}_{ub}$ had to be minimum for the case far from soil surface. Results from Reese et al. (1974) showed that ${p}_{ub}$ reflected the theoretical ultimate lateral resistance at a depth of about 12 m. Therefore, for this study, a depth of 12 m was selected as a point far from the soil surface that satisfies the criteria in Eq. (28). Fine sand similar to the properties of Ottawa Sand was assumed for the validation of the p–y curves. The soil is classified as SP based on the USCS classification. Table 1 shows details of the geotechnical and soil–water retention curve (SWRC) parameters of this soil using van Genuchten model, while Fig. 3 shows the SWRC both for the drying and wetting paths.

Table 1 Case example numerical modeling parameters

Fig. 3

SWRC hysteresis paths for the cohesionless soil

Similar to the pile and test setup by Cox et al. (1974), which is a companion paper to Reese et al. (1974), the pile evaluated for the first stage of the validation of the proposed p–y curve model was assumed to be a free-head steel pile with the pile bending stiffness of 8.697 × 10⁴ kN.m². Based on the classification of the relative soil-pile stiffness ${K}_{R}$ proposed by Poulos and Hull (1989), the pile has a ${K}_{R}$ of 2 × 10^–5 and thus can be classified as a flexible pile (Hong et al. 2017; Yang et al. 2019). Furthermore, the lateral loads on the pile were evaluated at 0.305 m above the soil surface. Supplementary details on the magnitude of the lateral loads applied on the pile, and load test results can be found in the Cox et al. (1974) paper. Additional information about the pile is also shown in Table 1, and the p–y curve results from the analysis are shown in Figs. 4 and 5.

Fig. 4

p–y curve at a depth of 1.5 m. a for the fully saturated condition; b for ${H}_{w}/H = 3$

Fig. 5

p–y curve at a depth of 12 m for the fully saturated condition

The Isenhower et al. (2019b) design approach recommended in the LPile 2019 software was used to obtain p–y curves based on the Reese et al. (1974) formulation. The numerical integration approach proposed in this paper was programmed in MATLAB. The comparison of p–y curves obtained from the two approaches for a near soil surface consideration are shown in Figs. 4a and b for hydrostatic fully saturated and dry soil layers, respectively. The dry case in the proposed method was simulated by a deep water table (i.e., ${H}_{w}/H=3$). Similarly, the comparison of p–y curves far from soil surface based on the two approaches is shown in Fig. 5 for the hydrostatic fully saturated condition.

The results in Fig. 4a and b show that the modified saturated–unsaturated p–y curve formulation presented in this study was consistent with the one proposed by Reese et al. (1974) with slight variations in the initial straight-line portion of the p–y curve due to differences in the method of obtaining the ${k}^{^{\prime}}$ values. The dry model (unsaturated with deep water table for the case of the proposed method), presented in Fig. 4b, resulted in relatively larger values of lateral soil resistance than the fully saturated conditions in Fig. 4a throughout the measured displacement along the p–y curve. As expected, this is due to the impact of effective stress on ${k}^{^{\prime}}$ and the ultimate lateral resistance. Similar trends to Fig. 4a were also observed in Fig. 5 for the p–y curves far from the soil surface. The lateral soil resistance values obtained for the soil far from the surface were usually higher than those of the near soil surface due to the influence of higher effective vertical stress at greater depths.

6 Validation of the Proposed p–y Curve Model with Centrifuge Data

The proposed method was also compared with experimental data using soil and pile properties based on the centrifuge modeling of pile lateral loading. The experimental data were published by Georgiadis et al. (1992) and Zhu et al. (2016) for dry and fully saturated conditions, respectively. Simulating pile lateral loading in a dry soil condition using the centrifuge tests results from Georgiadis et al. (1992), a soil with unit weight of 16.3 kN/m³ with friction angle of 36° and a pile with diameter of 1.092 m and $E_{p} I_{p} = 3878.5 {\text{MN}}/{\text{m}}^{2}$ were used. The void ratio was taken as 0.595, and the water table was assumed to be far below the depth of consideration. The results of their analysis with the proposed method are shown in Fig. 6a and b at $H=$ 1, 2, 3, and 4 m. For the fully saturated condition, displacement-controlled pile lateral loading results from the centrifuge tests of Zhu et al. (2016) were simulated using the proposed approach as shown in Fig. 7a and b. Specifically, a soil with saturated unit weight of 18.99 kN/m³, void ratio of 0.745, and friction angle of 35°, a pile diameter of 0.75 m, and $E_{p} I_{p} = 466 {\text{MN}}/{\text{m}}^{2}$ were considered. The p–y curves were evaluated at $H=$ 0.375, 0.75, 1.5, 2.25, and 3 m, as shown in Fig. 7a and b.

Fig. 6

Comparison of p–y curves for the dry cohesionless soil based on the proposed method and experimental data. a when using the Reese et al. (1974) constants; b when using fitted parameters

Fig. 7

Comparison of p–y curves for the fully saturated cohesionless soil based on the proposed method and experimental data. a when using the Reese et al. (1974) constants; b when using fitted parameters

A sample comparison of the maximum lateral resistances from the p–y curves in Fig. 6a is presented in Table 2. Results from the proposed method showed reasonable agreement with experimental data, and the maximum observed deviation was 33% at the 1 m depth due to lower values of lateral resistance. Moreover, as the maximum lateral resistance increased with depth, there was a reduction in the percentage difference between the results from the experiment and the proposed method. However, the results from Figs. 6a and 7a reveal that the p–y curves obtained using the key constants provided by Reese et al. (1974) do not closely align with the experimental data. In general, the proposed Reese et al. (1974) constants are not applicable for all laterally loaded piles in different cohesionless soils due to their empirical nature, as they were developed based on limited field cases. Therefore, a set of fitted parameters were used to match the experimental data.

Table 2 Sample comparison of maximum observed lateral resistance based on the Reese et al. (1974) constants for the dry soil

The fitting parameters were based on the constants $k^{\prime }$, $y_{u}^{\prime }$, $y_{m}^{\prime }$, $A_{s}^{\prime }$, and $B_{s}^{\prime }$, necessary for constructing the p–y curves similar to the Reese et al. (1974) approach. To obtain these parameters, first, the initial slope of the p–y curves was obtained using Eq. (33) and macthing $k^{\prime }$ values with the experimental data. Thereafter, it was observed that the lateral displacements $y_{u}^{\prime }$ and $y_{m}^{\prime }$ (proposed in the original p–y curve approach) matched the experimental data at 0.3 $b$ and 0.2 $b,$ respectively. Next, $A_{s}^{\prime }$ and $B_{s}^{\prime }$ values that were used for field adjustment of the theoretical lateral resistance were estimated using best-fit polynomial functions (similar to Eqs. 65 and 66 in the Appendix) to the experimental data presented by Georgiadis et al. (1992) and Zhu et al. (2016).

Details of the fitted parameters used for constructing the p–y curves from the centrifuge experimental data are presented in Table 3, and the fitted p–y curves are shown in Figs. 6b and 7b. The curves are in reasonable agreement with the experimental data for the dry and fully saturated soils. Nevertheless, since this study aims to understand how the unsaturated soil parameters affect the p–y curve, the Reese et al. (1974) constants are used for generating the p–y curves for the rest of the paper.

Table 3 Parameters fitting p–y curves to the evaluated experimental data

7 Impact of Water Table Depth on the Coefficient Subgrade Reaction

The values of ${k}^{^{\prime}}$ based on the proposed method founded on the Vesic (1961) recommendation are shown for a near soil surface ($H=1.5 m$) and a far from the soil surface ($H=12 m$) condition under different groundwater depths with hydrostatic water distribution in Fig. 8. The plots are based on the drying SWRC soil parameters in Table 1. The values of ${k}^{^{\prime}}$ near the soil surface were lower than the ones far from the soil surface for all water tables, as expected, due to the pronounced influence of the effective vertical stress on the soil elastic modulus at very small strains. For the near soil surface point ($H = 1.5 m$), the ${k}^{^{\prime}}$ values increased steadily when the water table was lowered from the soil surface up to about ${H}_{w}/H=0.25$. In this case, both total stress and pore water pressure reduced simultaneously, but the reduction in pore water pressure outweighed the total stress reduction. As the water table continued to increase, the ${k}^{^{\prime}}$ values slightly increased but then started to decrease and plateau after about ${H}_{w}/H=1.5$. This highlights the impact of suction stress for soils slightly above the water table. However, for soils well above the water table, the reduction in total stress dominated the overall response until the soil reached a residual water content where no significant changes in either water content and total stress is expected. For points far below the soil surface ($H=12 m$) similar increasing trend in ${k}^{^{\prime}}$ was observed to ${H}_{w}/H=0.25$; but then, there was a sharp drop to a constant ${k}^{^{\prime}}$. This is due to negligible impact of suction stress in comparison with very high values of total stress in deep soil. These results highlighted the role of the depth of water table or the state of saturation on the soils’ elastic modulus that forms the initial slope of p–y curves, especially in shallow depths.

Fig. 8

The variation of the coefficient of horizontal subgrade reaction with water table depth. a for the depth of 1.5 m; b for the depth of 12 m

8 Impact of Water Table Depth on the Ultimate Lateral Resistance

The effect of varying water table depth under hydrostatic conditions on the ultimate lateral resistance is depicted in Fig. 9. This is shown for both drying and wetting paths of Soil–Water Retention Curve (SWRC), using the van Genuchten (1980) parameters, ${\alpha }_{VG}$ and ${n}_{VG}$, listed in Table 1, and also for both near the soil surface and far from the soil surface conditions (i.e., Fig. 9a and b, respectively). In both cases, the ultimate lateral resistance increased by lowering the water table level due to an increase in the effective stress and then started to decrease until it reached a constant value. These trends highlight the role of water table location on the ultimate lateral resistance of soils.

Fig. 9

Effect of water table variation on the ultimate lateral resistance for the drying and wetting paths. a for the depth of 1.5 m; b for the depth of 12 m; c for the depth of 1.5 m when $0.5\le {H}_{w}/H\le 1.5$; d for the depth of 12 m when $0.5\le {H}_{w}/H\le 1.5$

For the near surface soil ($H=1.5 m$), the drying SWRC path yielded larger values of ultimate lateral resistance, mainly between ${H}_{w}/H=0.5$ and ${H}_{w}/H=1.5$, when compared with the ones obtained from the wetting SWRC path, shown in Fig. 9a. This difference is minimal for the cases far from the soil surface due to the small impact of SWRC wetting and drying parameters on effective stress in deeper ground, as shown in Fig. 9b. To better illustrate the peak ultimate lateral resistance point for the near and far from the soil surface conditions, closer views of the variations around the peaks are shown in Fig. 9c and d, for $0.5\le {H}_{w}/H\le 1.5$. The results indicate that maximum values of the ultimate lateral resistance occurred at about ${H}_{w}/H=0.8$ for both drying and wetting SWRC paths in the near soil surface, while the peak was at about ${H}_{w}/H=1$ in the case of deeper soil. Peak values of lateral resistance, observed when the water table was close to the wedge depth for the near soil surface condition, could be attributed to the suction stress (Komolafe and Ghayoomi 2021). The influence of suction stress was more noticeable as the water table was lowered within the wedge, thereby increasing the soil stiffness, which led to higher lateral resistance. However, the effect of suction stress on the results began to diminish as the water table was further lowered from the soil surface and beyond the depth of the wedge.

9 p–y Curves Under Fluctuating Water Table Levels

The estimated p–y curves under different groundwater levels with hydrostatic water distribution for near surface ($H=1.5 m$) and far from the surface ($H=12 m$) are shown in Fig. 10a and b, respectively. These plots are based on the drying SWRC parameters in Table 1. In both figures, the fully saturated condition (${H}_{w}/H=0$) resulted in the least values of lateral soil resistance for all the lateral displacements considered. As the water table depth increased, the degree of saturation within the depth of considered wedge reduced, changing the effective stresses and earth pressure values. The reduction in the degree of saturation increased the value of lateral soil resistance and ultimately changed the p–y curves. This increase continued to a peak value at ${H}_{w}/H=1$ before it started to reduce and finally reached a constant curve. Similar curves for ${H}_{w}/H=1.5$, ${H}_{w}/H=2$, and ${H}_{w}/H=3$ indicate that the soil within the wedge was at a state close to its residual degree of saturation, and the response became insensitive to the location of the water table. Also, by comparing Fig. 11a and b, it is evident that lowering the water table level from the surface would have more immediate impact on near soil surface p–y curves than the ones far from the surface. Both figures, however, emphasize the importance of water level fluctuation on p–y curves. Ignoring the effect of this fluctuation, depending on the depth of water level, could result in either a conservative or unconservative performance assessment. Further, Fig. 11 shows the impact of the use of wetting or drying SWRC parameters on p–y curves. It can be seen that the water hysteresis impact is relatively small for near-soil surface soils while negligible for soils far from the surface.

Fig. 10

p–y curves based on water table variation. a for the depth of 1.5 m; b for the depth of 12 m

Fig. 11

p–y curves for the drying and wetting paths at $H_{w} /H = 1$. a for the depth of 1.5 m; b for the depth of 12 m

10 Effect of Discharge Rate on the p–y Curve

The consideration of climatic impacts on the ultimate lateral resistance and the p–y curve is essential in foundation response assessment and design. Thus, the influence of discharge rates, i.e., infiltration and evaporation rates, on pile lateral response should be evaluated. In this study, a normalized flow rate, which is defined as the ratio of the flow rate to the soil’s saturated hydraulic conductivity ($q/{k}_{s}$), was considered. This was in conjunction with the corresponding drying and wetting SWRC parameters in Table 1. In addition, a steady-state condition was assumed, and Eq. (3) was used to estimate the suction profile in depth. Negative flow rates indicate infiltration, while positive flow rates mark evaporation. The extreme infiltration and evaporation conditions are marked as $q/{k}_{s}=- 1$ and $q/{k}_{s}=1$, respectively. The results were evaluated for soils at both near surface and far from the surface conditions, but plots are presented for near surface condition only. Similar trends were observed in both cases, although as expected, often the impact of discharge rate on deeper soil response became minimal.

The variation of the near surface ultimate lateral resistance ($H=1.5 m$) with absolute values of normalized flow rates (both under infiltration and evaporation) for ${H}_{w}/H=0$, ${H}_{w}/H=0.5$, ${H}_{w}/H=1$, and ${H}_{w}/H=3$, are shown in Fig. 12a–d, respectively. Since flow through the fully saturated soil layer does not impact the state of saturation, the ultimate lateral resistance remained constant for all flow rates, as in Fig. 12a. Figure 12b and c show that when the water table was lowered from the surface, it led to a gradual drop by a small amount in the ultimate lateral resistance during the evaporation regime and by increasing the evaporation rate due to small changes in unit weight. However, during an infiltration event, when the water level was below the soil surface, the ultimate lateral resistance increased with increasing flow rates. This is due to the increase in the effective stress of the unsaturated soil due to high infiltration. When the water table is far below the point of interest (i.e., ${H}_{w}/H=3$ in Fig. 12d), the ultimate resistance became insensitive to drying because the soil was already at the residual degree of saturation, while increasing infiltration after at a certain rate would become pronounced and increase the lateral resistance mainly due to an increase in the soil density and consequently the effective stress.

Fig. 12

Effect of discharge on the ultimate lateral resistance for the depth of 1.5 m. a $H_{w} /H = 0$; b $H_{w} /H = 0.5$; c $H_{w} /H = 1$; d $H_{w} /H = 3$

Lu and Griffiths (2004) noted that suction stress could decrease and tend toward zero after exceeding its maximum value during evaporation conditions. Their results further showed that suction stress increased to an asymptotic value under large steady infiltration as the water table was further lowered in the soil. This explains why there was a reduction of lateral resistance in the unsaturated cohesionless soil during intense evaporation and there were greater values of ultimate lateral resistance as the flow rate increased at values closer to the saturated hydraulic conductivity of the soil.

Figure 13 shows the developed p–y curves under different steady-state flow conditions for the near soil surface. Consistently with the ultimate resistance, the p–y curves in the fully saturated soil layer (Fig. 13a) were not affected by the flow. Figure 13b and c also reflect the trends observed in Fig. 12b and c with varying discharge rate from $q/{k}_{s}=- 1$ to $q/{k}_{s}=0$, and then to $q/{k}_{s}=1$. The soil’s lateral resistance will follow a complex trend. Starting from an extreme infiltration and lowering the flow rate to hydrostatic conditions, the lateral resistance decreased. Then, the resistance continued to decrease by further increasing the evaporation rate. Finally, Fig. 13d, for a water table at a considerable depth from the wedge depth and the soil surface, indicates that, under this condition, the effect of evaporation on the lateral resistance was insignificant, while the effect of infiltration could become noticeable at high infiltration rates. Overall, the data from Figs. 12 and 13 clearly highlight the impact of water flow on the soil’s lateral resistance, which can become critical on seasonal pile response or under changing climate.

Fig. 13

Effect of discharge on the p–y curves for the depth of 1.5 m. a $H_{w} /H = 0$; b $H_{w} /H = 0.5$; c $H_{w} /H = 1$; d $H_{w} /H = 3$

11 Effect of the Soil–Water Retention Parameters on the Ultimate Lateral Resistance

The van Genuchten (1980) SWRC parameters, ${\alpha }_{VG}$ and ${n}_{VG}$, are the ones that were used for modeling the effect of soil water retention in this study. Since different cohesionless soils with various amount fines content may result in different water retention, it is important to investigate the effects of these parameters on soil lateral response. Figure 14 reveals how the SWRC parameters affected the ultimate lateral resistance of the soil based on water table variations. ${\alpha }_{VG}$ was varied between 0.1 and 0.7 kPa⁻¹ at intervals of 0.1 kPa⁻¹ while ${n}_{VG}$ was between 3 and 9 at intervals of 1, representing the typical ranges for many cohesionless soil types (Lu and Likos 2004; Mirshekari and Ghayoomi 2017; Komolafe and Ghayoomi 2021). Figure 14 only shows the near soil surface condition ($H=1.5 m$) because previous figures indicated a minimal impact of soil water retention on lateral soil response in deeper ground. Water table levels at ${H}_{w}/H=0$, ${H}_{w}/H=0.5$, ${H}_{w}/H=1$, and ${H}_{w}/H=3$ were considered. Regardless of the retention parameter, i.e., ${\alpha }_{VG}$ or ${n}_{VG}$ in Fig. 14a and b, respectively, a maximum value of ultimate lateral resistance was observed at ${H}_{w}/H=1$. Comparing the trends in Fig. 14a and b, it is evident that the near surface ultimate lateral resistance was more sensitive to ${\alpha }_{VG}$ than ${n}_{VG}$, which indicates the influence of air entry value as the soil transitions from saturated or unsaturated condition. Nevertheless, in both figures, increasing ${\alpha }_{VG}$, which means lower air entry value due to less fines content, and increasing ${n}_{VG}$, which means more uniformly distributed pore space, would lead to a reduction in ultimate lateral resistance. However, these effects are negligible for the fully saturated soil layer or when the water table is at a meaningful distance below the point of interest, the former being due to irrelevance of water retention in saturated soil and the latter being due to soil reaching the state of residual degree of saturation.

Fig. 14

Variation of the ultimate lateral resistance based on the van Genuchten SWRC parameters for the depth of 1.5 m. a $\alpha_{VG}$; b $n_{VG}$

12 Effect of the Soil–Water Retention Parameters on the p–y Curve

Evaluating the effects of soil–water retention characteristics based on the van Genutchen SWRC parameters is beneficial to understanding the effect of water table variation on the p–y curve for different soil types. Four additional cohesionless soil types with similar geotechnical properties to those in Table 1 while only differing in their ${\alpha }_{VG}$ values which indicate the amount of fines content in the soil and the ${n}_{VG}$ values that reflect the soil gradation were considered. The p–y curves based on the analysis of the near soil surface condition were compared in Fig. 15. Specifically, two additional ${\alpha }_{VG}$ values of 0.1 and 0.7 and two additional ${n}_{VG}$ values of 3 and 9 were evaluated covering different soil fines contents and particle gradations.

Fig. 15

Effect of SWRC of various soil types on the p–y curve

Results from Fig. 15 show that the SWRC parameters considerably affect the soil lateral response, assessed by comparing the near surface p–y curves when the water table is at wedge depth (i.e., $Hw/H=1$) and when it is at wedge mid-depth (i.e., $Hw/H=0.5$). This impact is more pronounced when a larger portion of the wedge is unsaturated (i.e., $Hw/H=0.5$). Overall, the results indicate that higher fines content (lower ${\alpha }_{VG}$) would increase the effect of suction stress resulting in higher lateral resistance. In addition, better-graded soil particle distribution (lower ${n}_{VG}$) also has a meaningful impact on lateral soil resistance. Therefore, water table fluctuation in soils with higher water retention will have a more significant impact on the ultimate lateral resistance and the p–y curve, and ignoring this effect will induce greater uncertainty in the soil lateral response assessment.

13 Conclusions

A modified p–y curve approach was proposed to assess lateral response in unsaturated cohesionless soils. The proposed model was developed based on the effective stress approach using the concept of a unified failure envelope for the unsaturated cohesionless soil. Different key parameters were adjusted to reflect the unsaturated soil condition, such as the unit weight of the soil, the effective vertical stress, Poisson’s ratio, coefficients of lateral earth pressures, and the coefficient of horizontal subgrade reaction. The proposed method was validated using the original p–y formulations by Reese et al. (1974) for fully saturated soil conditions and published centrifuge experimental results for the dry and fully saturated cases. Although the ultimate lateral resistance values between the proposed method and experiments are within a reasonable range, the lateral displacements required to mobilize the ultimate lateral resistance based on the experimental data considered herein were greater than those predicted theoretically. Reese et al. (1974) acknowledged this difference and considered their method relatively conservative.

Ultimate lateral resistances and subgrade reactions in the near soil surface and far from the soil surface in unsaturated soils were generally greater than the fully saturated soil conditions due to the presence of suction stresses. However, based on the case example evaluated, the competing effects of lower density and higher suction in unsaturated soils led to a reversal in this trend from the peak value of ultimate lateral resistance when the depth of the water table increased to about 0.9 times the wedge depth for the near surface soil and about 1.1 times the wedge depth for the soil far from the surface. The lateral resistance and subgrade reaction both remained unchanged after the water level was lowered deep enough due to minimal changes in soil moisture at the residual degree of saturation. Additionally, the lateral resistance was higher for far from the surface in comparison with near the surface; but less sensitive to water fluctuation and flow and soil water retention characteristics. Further, the higher soil water retention (higher fines content) resulted in higher lateral resistance and had a greater influence on p–y curve values near the soil surface.

Sensitivity analysis of the effect of discharge rate during a steady-state flow on the p–y curves revealed that the ultimate lateral resistance and p–y curves could vary significantly depending on the water table level and the extent of infiltration or evaporation. Soil lateral resistance can increase or decrease depending on whether the soil is experiencing infiltration or evaporation and also the location of the initial water table. However, this sensitivity was more evident in near soil surface as the effective stress in depth was more influenced by the changes in water content. Evaluating the influence of discharge rate for the near surface soil further reveals that when the water table is far from the soil surface, the infiltration condition can considerably increase the lateral resistance of the soil provided the discharge rate is very close to or is equal to the saturated hydraulic conductivity of the soil. This situation was evident when ${H}_{w}/H = 3$ where the lateral resistance increased from about 199 kN/m² at $\left|q/{k}_{s}\right|=0.01$ to 267 kN/m² at $\left|q/{k}_{s}\right|=1$, which reflects a 34% lateral resistance increase.

The p–y formulation and approach proposed in this paper would help to improve the performance assessment of laterally loaded pile foundations in unsaturated cohesionless soils. Especially amid changing climate and more frequent water level fluctuation and extreme climatic conditions, incorporating the effects of degree of saturation both hydrostatically and under moisture flow on pile lateral response would lead to safer and more sustainable foundation systems.

Appendices

Appendix 1: Unraveling the Theoretical Ultimate Lateral Resistance Formulation in Cohesionless Soils

In this section, the detailed components of the original p–y curve formulation by Reese et al. (1974) are presented and discussed. It will form a foundation for the modified version that includes the effects of the degree of water saturation. It should be noted that the presented complete derivations are not available in the original Reese et al. (1974) paper.

The theoretical ultimate lateral resistance was derived by considering the soil-failure mechanism within a wedge-shaped failure zone, shown in Fig. 

Fig. 16

The failure wedge concept of the ultimate lateral resistance near the soil surface in cohesionless soils by (Adapted from Reese et al. (1974)). a The soil wedge; b The forces on the soil wedge; c The resultant forces acting on the pile

16, for the near soil surface condition. Rankine (1857) earth pressure theory was considered for evaluating the failure wedge. In this figure, $H$ is the wedge depth, $b$ is the diameter of the pile, ${\gamma }^{^{\prime}}$ is the effective soil unit weight, which equals the submerged unit weight if the wedge is under the water level, ${\phi }^{^{\prime}}$ is the angle of internal friction, $\alpha$ is the angle of the wedge fan with respect to the horizontal direction taken as $\frac{{\phi }^{^{\prime}}}{2}$, $\beta$ is taken as $45+\frac{{\phi }^{^{\prime}}}{2}$, $x$ is the length of the wedge fan and equals $H\mathrm{tan}\beta \mathrm{tan}\alpha$, and ${\text{a}}$ is the length of the fan hypotenuse and equals $\frac{H\mathrm{tan}\beta }{\mathrm{cos}\alpha }$.

${W}^{^{\prime}}$, the effective (submerged) weight of the cohesionless soil wedge was estimated using the following equation,

$$W^{\prime } = \gamma^{\prime } \times b \times \frac{1}{2} \times H \times H\tan \beta + \int\limits_{0}^{H} {2 \times \frac{1}{2} \times \gamma^{\prime } \times H\tan \beta \times H\tan \beta \tan \alpha dH}$$

(39)

While integrating the formulations for homogenous dry or saturated soils, Eq. (39) will turn into Eq. (40).

$$W^{\prime } = \frac{{\gamma^{\prime } bH^{2} \tan \beta }}{2} + \frac{{\gamma^{\prime } H^{3} \tan^{2} \beta \tan \alpha }}{2}$$

(40)

As proposed by Reese et al. (1974), $K_{o}$, which is the coefficient of lateral earth pressure at rest condition, was recommended to set to a constant value of 0.4. Also, $K_{a}$, the coefficient of active lateral earth pressure, and $K_{p}$, the coefficient of passive lateral earth pressure, were estimated using Rankine’s theory as shown in Eqs. (41) and (42), respectively.

$$K_{a} = \tan^{2} \left[ {45 - \frac{{\phi^{\prime } }}{2}} \right]$$

(41)

$$K_{p} = \tan^{2} \left[ {45 + \frac{{\phi^{\prime } }}{2}} \right] = \tan^{2} \beta$$

(42)

$F_{n}$ is the normal force on the sides of the wedge and can be calculated as:

$$F_{n} = K_{o} \gamma^{\prime } H \times \int\limits_{0}^{H} {\frac{1}{2} \times \frac{H\tan \beta }{{\cos \alpha }} dH} = \int\limits_{0}^{H} {\frac{{K_{o} \gamma^{\prime } H^{2} \tan \beta }}{2\cos \alpha } dH} = \frac{{K_{o} \gamma^{\prime } H^{3} \tan \beta }}{6\cos \alpha }$$

(43)

$F_{s}$ is the frictional force on the sides of the wedge and can be expressed as:

$$F_{s} = F_{n} \tan \phi^{\prime } = \frac{{K_{o} \gamma^{\prime } H^{3} \sin \beta \tan \phi^{\prime } }}{6\cos \beta \cos \alpha }$$

(44)

${F}_{\phi }$ is the force at the underside of the cohesionless soil wedge at an angle ${\phi }^{^{\prime}}$, which can be determined by considering a vertical force equilibrium; therefore:

$$F_{\phi } \sin \left( {\beta - \phi^{\prime } } \right) = W^{\prime } + 2F_{s} \cos \beta$$

(45)

Rearranging and expanding Eq. (45), $F_{\phi }$ can be written as:

$$F_{\phi } = \gamma^{\prime } \left[ {\frac{{bH^{2} \tan \beta }}{{2\sin \left( {\beta - \phi^{\prime } } \right)}} + \frac{{H^{3} \tan^{2} \beta \tan \alpha }}{{3\sin \left( {\beta - \phi^{\prime } } \right)}}} \right] + \frac{{K_{o} \gamma^{\prime } H^{3} \tan \phi^{\prime } \sin \beta }}{{3\sin \left( {\beta - \phi^{\prime } } \right)\cos \alpha }}$$

(46)

$F_{a}$ and $F_{p}$ are the active and passive forces on the pile that can be estimated using Eqs. (47) and (48), respectively.

$$F_{a} = \frac{{K_{a} \gamma^{\prime } H^{2} b}}{2}$$

(47)

$$\begin{aligned} F_{p} = & \;\frac{{\gamma^{\prime } bH^{2} \tan \beta }}{{2\tan \left( {\beta - \phi^{\prime } } \right)}} + \frac{{\gamma^{\prime } H^{3} \tan^{2} \beta \tan \alpha }}{{3\tan \left( {\beta - \phi^{\prime } } \right)}} + \frac{{K_{o} \gamma^{\prime } H^{3} \tan \phi^{\prime } \sin \beta }}{{3\tan \left( {\beta - \phi^{\prime } } \right)\cos \alpha }} \\ & \quad + \frac{{K_{o} \gamma^{\prime } H^{3} \tan \beta \tan \phi^{\prime } \sin \beta }}{3} - \frac{{K_{o} \gamma^{\prime } H^{3} \tan \beta \tan \alpha }}{3} \\ \end{aligned}$$

(48)

The total ultimate lateral resistance force for the near soil surface condition, $F_{u}$, can then be calculated as:

$$\begin{aligned} F_{u} = & \;\frac{{\gamma^{\prime } bH^{2} \tan \beta }}{{2\tan \left( {\beta - \phi^{\prime } } \right)}} + \frac{{\gamma^{\prime } H^{3} \tan^{2} \beta \tan \alpha }}{{3\tan \left( {\beta - \phi^{\prime } } \right)}} + \frac{{K_{o} \gamma^{\prime } H^{3} \tan \phi^{\prime } \sin \beta }}{{3\tan \left( {\beta - \phi^{\prime } } \right)\cos \alpha }} \\ & \quad + \frac{{K_{o} \gamma^{\prime } H^{3} \tan \beta \tan \phi^{\prime } \sin \beta }}{3} - \frac{{K_{o} \gamma^{\prime } H^{3} \tan \beta \tan \alpha }}{3} - \frac{{K_{a} \gamma^{\prime } H^{2} b}}{2} \\ \end{aligned}$$

(49)

Differentiating the total ultimate lateral resistance with respect to $H$ will result in the theoretical ultimate lateral resistance for the near soil surface condition and can be expressed as:

$$\begin{aligned} p_{ua} = & \;\frac{{\gamma^{\prime } bH\tan \beta }}{{\tan \left( {\beta - \phi^{\prime } } \right)}} + \frac{{\gamma^{\prime } H^{2} \tan^{2} \beta \tan \alpha }}{{\tan \left( {\beta - \phi^{\prime } } \right)}} + \frac{{K_{o} \gamma^{\prime } H^{2} \tan \phi^{\prime } \sin \beta }}{{\tan \left( {\beta - \phi^{\prime } } \right)\cos \alpha }} \\ & \quad + K_{o} \gamma^{\prime } H^{2} \tan \beta \tan \phi^{\prime } \sin \beta - K_{o} \gamma^{\prime } H^{2} \tan \beta \tan \alpha - K_{a} \gamma vH^{2} b \\ \end{aligned}$$

(50)

Simplifying Eq. (50), the theoretical ultimate lateral resistance for the near soil surface condition can be rewritten as:

$$p_{ua} = \gamma^{^{\prime}} H\left[ {\frac{{K_{o} H\sin \beta \tan \phi^{\prime } }}{{\cos \alpha \tan \left( {\beta - \phi^{\prime } } \right)}} + \frac{\tan \beta }{{\tan \left( {\beta - \phi^{\prime } } \right)}}\left( {H\tan \alpha \tan \beta + b} \right) + K_{o} H\tan \beta \left( {\sin \beta \tan \phi^{\prime } - \tan \alpha } \right) - K_{a} b} \right]$$

(51)

Reese et al. (1974) proposed that the failure mode at a depth far from the soil surface is different from the near soil surface condition. Such a failure mechanism was conceptualized using failure blocks instead of a wedge. Fig. 

Fig. 17

Failure mode indicating lateral movement around the pile at a depth far from the soil surface based on Reese et al. (1974)

17 shows the failure mode, indicated by horizontal movement around the pile, used to obtain the ultimate lateral resistance at a depth far from the soil surface. The stress behind the pile must be higher than or equal to the minimum active lateral pressure to prevent the collapse of the soil. According to Reese et al. (1974), failure would occur through the following process: (1) Block I would fail along the diagonal lines by shearing and follow the pile movement; (2) Block II would fail along the diagonal line; (3) Block III would slide laterally; (4) Block IV would fail in a similar pattern as Block II due to the sliding effect of Block II, and (5) Block V would be in the condition necessary for failure as the pile also pushes against it. Accordingly, the following steps should be taken to determine the ultimate lateral resistance at a depth far from the soil surface:

At Block I:

$$\sigma_{I}^{\prime } = K_{a} \gamma^{\prime } H$$

(52)

In this block, $\sigma_{I}^{\prime }$ is at active condition, which is the minimum lateral earth pressure; thus, $\sigma_{II}^{\prime }$ would entail a higher value. Therefore, $\sigma_{II}^{\prime }$ and $\sigma_{I}^{\prime }$ are the major and minor principal stresses, respectively; i.e. $\sigma_{1}^{\prime } = \sigma_{II}^{\prime }$ and $\sigma_{3}^{\prime } = \sigma_{I}^{\prime }$. When the block is at failure condition, and for a Mohr circle tangent to the Mohr–Coulomb failure envelope, $\sigma_{1}^{\prime } = \sigma_{3}^{\prime } \tan^{2} \left[ {45 + \frac{{\phi^{\prime } }}{2}} \right] = \sigma_{3}^{\prime } \tan^{2} \beta$.

Therefore,

$$\sigma_{II}^{\prime } = \sigma_{I}^{\prime } \tan^{2} \beta = K_{a} \gamma^{\prime } H\tan^{2} \beta$$

(53)

Using the same process in Block II, one can obtain:

$$\sigma_{III}^{\prime } = \sigma_{II}^{\prime } \tan^{2} \beta = \sigma_{I}^{\prime } \tan^{4} \beta = K_{a} \gamma^{\prime } H\tan^{4} \beta$$

(54)

$\tau$ is the shear stress that is introduced during pile sliding against Block III and equals $\sigma_{o}^{\prime } \tan \phi^{\prime }$ where $\sigma_{o}^{\prime } = K_{o} \gamma^{\prime } H$ is the at-rest lateral earth pressure. Using horizontal equilibrium,

$$\sigma_{IV}^{\prime } = \sigma_{III}^{\prime } + \tau = K_{a} \gamma^{\prime } H\tan^{4} \beta + K_{o} \gamma^{\prime } H \tan \phi^{\prime }$$

(55)

At Block IV and V, the same process as in Block I and II can be followed, which results in,

$$\sigma_{VI}^{\prime } = \sigma_{V}^{\prime } \tan^{2} \beta = \sigma_{IV}^{\prime } \tan^{4} \beta = K_{a} \gamma^{\prime } H\tan^{8} \beta + K_{o} \gamma^{\prime } H \tan \phi^{\prime } \tan^{4} \beta$$

(56)

Subtracting the active force on the right side of the pile from the passive force from the left side of the pile will result in the theoretical ultimate lateral resistance at a depth far from the soil surface, given as:

$$p_{ub} = \left( {\sigma_{VI}^{\prime } - \sigma_{I}^{\prime } } \right)b = K_{a} b\gamma^{\prime } H\tan^{8} \beta + K_{o} b\gamma^{\prime } H\tan \phi^{\prime } \tan^{4} \beta - K_{a} b\gamma^{\prime } H$$

(57)

Simplifying Eq. (57), the expression can be rewritten as:

$$p_{ub} = K_{a} b\gamma^{\prime } H\left( {\tan^{8} \beta - 1} \right) + K_{o} b\gamma^{\prime } H\tan \phi^{\prime } \tan^{4} \beta$$

(58)

Appendix 2: Adjustments to the Theoretical Ultimate Lateral Resistance

Reese et al. (1974) discovered that the ultimate lateral resistance values measured at the Mustang Island site did not correspond accurately with the computed theoretical values. Therefore, coefficients $A$ and $B$ were used to adjust the theoretical values based on the ratio of the observed field values to the theoretical values. The coefficient $A$ (${A}_{s}$ for static and ${A}_{c}$ for cyclic) that was used to obtain the ultimate lateral resistance of cohesionless soil, ${p}_{u}$; is shown in Fig. 18a. Also, the coefficient $B$ (${B}_{s}$ for static and ${B}_{c}$ for cyclic) that was used to obtain the lateral resistance of the cohesionless soil at the point where the lateral displacement of the pile is 1/60 of the pile diameter (or width), ${p}_{m}$; is shown in Fig. 

Fig. 18

a Coefficient $A$ for obtaining the ultimate lateral resistance of cohesionless soil based on Reese et al. (1974); b Coefficient $B$ for obtaining the lateral resistance of cohesionless soil when the lateral displacement is 1/60 of the pile diameter (or width) based on Reese et al. (1974)

18b.

Therefore, ${p}_{u}$ and ${p}_{m}$ are defined as

$${p}_{u}={p}_{ut}{A}_{s} (\mathrm{for\,static\,loading})$$

(59)

$${p}_{u}={p}_{ut}{A}_{c} (\mathrm{for\,cyclic\,loading})$$

(60)

$${p}_{m}={p}_{ut}{B}_{s} (\mathrm{for\,static\,loading})$$

(61)

$${p}_{m}={p}_{ut}{B}_{c} (\mathrm{for\,cyclic\,loading})$$

(62)

Additionally, the lateral displacements ${y}_{u}$ and ${y}_{m}$ corresponding to ${p}_{u}$ and ${p}_{m}$, respectively, are determined as

$${y}_{u}=\frac{3b}{80}$$

(63)

$${y}_{m}=\frac{b}{60}$$

(64)

Further research and field testing are necessary to validate that the empirical adjustment coefficients $A$ and $B$ are suitable for use in unsaturated cohesionless soils using field or laboratory studies.

The coefficients $A$ and $B$ can be approximately obtained from Fig. 18 for the static loading condition as

$$A_{s} = \left\{ {\begin{array}{*{20}l} {0.1\left( \frac{H}{b} \right)^{2} - 0.9\left( \frac{H}{b} \right) + 2.9 0 \le \frac{H}{b} \le 4.2 } \hfill \\ {0.88 \frac{H}{b} > 4.2} \hfill \\ \end{array} } \right.$$

(65)

$$B_{s} = \left\{ {\begin{array}{*{20}l} {0.07\left( \frac{H}{b} \right)^{2} - 0.69\left( \frac{H}{b} \right) + 2.15 0 \le \frac{H}{b} \le 4.1 } \hfill \\ {0.50 \frac{H}{b} > 4.1} \hfill \\ \end{array} } \right.$$

(66)