1 Introduction

The methods used to evaluate the bearing capacity of shallow foundations have been progressively developed since the twentieth century. The bearing capacity of strip footings under vertical loading has been investigated using different methods such as the limit equilibrium method (e.g. Terzaghi 1943; Meyerhof 1963; Vesic 1973), the upper bound method (e.g. Michałowski 1997; Soubra 1999; Hjiaj et al. 2004), the slip-line method (e.g. Hansen 1970; Bolton and Lau 1993; Martin 2005) and the elasto-plastic analysis based on the finite-element and the finite-difference methods (Griffiths 1982; Frydman and Burd 1997; Loukidis and Salgado 2009; Mabrouki et al. 2010). The exact bearing-capacity factor for cohesionless soils was first found by Prandtl (1920). Most of the results obtained by mentioned theories are validated using experimental data. Many researchers studied the bearing capacity of footings by taking into account various parameters that affect the limit load, such as load inclination, load eccentricity, shape of footing, embedment and inclination of the base.

The effect of load inclination has been included in design by introducing a correction coefficient, known as the inclination factor. In this approach, the inclination factors for the bearing capacity of strip footings were derived from a combination of experimental data and theoretical analysis. This traditional approach was initially suggested by Meyerhof (1953). Then, several other expressions for this factor were obtained by many investigators (e.g. Hansen 1970; Vesic 1975; Saran et al. 1971; Michalowski and You 1998; Ouahab et al. 2017).

The approach used to determine the inclination factors has recently been replaced by the failure envelope approach (Butterfield and Ticof 1979; Butterfield and Gottardi 1994). This approach consists in determining the loading components (V-H) which cause the footing failure. This approach has also been adopted, using finite element method in order to take into account the effect of inclined loading, footings geometries and soil conditions (e.g. Martin and Houlsby 2001; Gourvenec and Randolph 2003; Hjiaj et al. 2004; Randolph et al. 2004; Loukidis et al. 2008; Gourvenec and Barnett 2011; Lee et al. 2015; Yahia-Cherif et al. 2017).

In practice, the soils are not homogeneous and the footings are generally located on layered soils, especially in offshore regions. Many theories have been developed in order to investigate the vertical bearing capacity of a two layered soil by using various techniques, such as the limit equilibrium method, the semi-empirical method and numerical analyses, such as the finite element method (FEM) and finite difference method (FDM). Button (1953) presented a solution for strip footings on a two-layer soil using the limit equilibrium method. Terzaghi and Peck (1948), Meyerhof and Hanna (1978) and Houlsby et al. (1989) proposed a semi-empirical technique, based on small scale tests, to address this problem. Huang and Qin (2009) adopted the upper-bound limit analysis for multi-rigid-block with a modified failure mechanism, to calculate the bearing capacity of rigid strip footings on two layered soils. Also, numerical models for footings on two layered soils were developed by Burd and Frydman (1997), Merifield et al. (1999), Shiau et al (2003) and more recently, by Ismail Ibrahim (2014). These models are all based on the use of finite element analysis.

Most of the previous studies on the ultimate bearing capacity concentrated on the cases of surface strip footings subjected to inclined loading on homogeneous soils. The problem of a footing subjected to inclined loadings on layered soils is very rarely treated in the literature. Meyerhof (1974) studied the bearing capacity of shallow strip and circular footings on sand layer of finite thickness over clay. Also, Meyerhof and Hanna (1978) investigated the ultimate bearing capacity of footings resting on a strong layer overlaying a weak deposit, and then on a weak layer overlaying a strong deposit. The results of the analyses of different soil failure modes were then compared with those of model tests for circular and strip footings on layered sand and clay soils. Michalowski and Shi (1995) used the kinematic approach of limit analysis to evaluate the vertical ultimate bearing capacity of strip footings on granular soils overlies cohesive soils. These authors developed an approximate theory of the bearing capacity of layered soils under vertical loading and inclined loading conditions.

Georgiadis and Michalopoulos (1985) developed a numerical method of slip surfaces in layered soils with both eccentric and inclined loads. Furthermore, Youssef-Abdel Massih et al. (2005) investigated the bearing capacity of a strip footing resting on a two-layered foundation soil (sand and clay) in the case of inclined and/or eccentric loads, using the kinematic approach of limit analysis. Moreover, Zhan (2011) used the finite element method to examine the bearing capacity of strip footings resting on the surface of an undrained two-layer clay soil, under inclined and eccentric loadings. More recently, Rao et al. (2015) used the lower bound limit analysis in conjunction with finite elements and second-order cone programming to determine the bearing capacity of a rigid strip footing placed on two-layered clay subjected to inclined or eccentric loading. The numerical results are presented in the form of failure envelopes in the loading plane.

The exact solution for the bearing capacity of strip footings on two-layered soils subjected to inclined loading has not yet been demonstrated and, in the absence of a rigorous analytical solution, the numerical methods may give valuable information about the problem. The main objective of this research is to carry out numerical computations, using the finite difference code, Fast Lagrangian Analysis of Continua FLAC (2005), to evaluate the bearing capacity of a rigid strip footings placed on uniform sand layer overlying clay under inclined loads.

2 Problem Definition

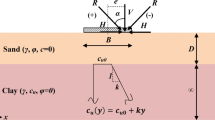
The bearing capacity problem considered in this paper is illustrated in Fig. 1. This paper is concerned with the study of the bearing capacity of a rigid strip footing of width B, located on the surface of a sand layer underlain by a clay layer. The footing is subjected to centered inclined load R characterized by the load inclination α. This loading can also be represented by two statically equivalent forces V (V = Rcosα) and H (H = Rsinα), as shown in Fig. 1.

Fig. 1
figure 1

Problem geometry and boundary conditions

Full size image

The boundary conditions are presented in Fig. 1, The vertical sides of the model were constrained in the horizontal direction only. The bottom side was constrained in all directions. The boundaries were sufficiently distant from the footing to ensure that the mesh contained the entire plastic zone. In all cases, the analyses were based on meshes with a depth of 20B and extend 40B as shown in Fig. 2.

Fig. 2
figure 2

Finite-difference mesh

Full size image

3 Numerical Modeling Procedure

The parametric study was carried out using the finite difference code FLAC (2005). The entire soil domain was considered because of the asymmetrical loading. The domain was subdivided into a mesh composed of quadrilateral elements. Larger concentration of elements is needed where large stress gradients are expected i.e., neighborhood of strip footings. Frydman and Burd (1997) studied the effect of vertical velocity and mesh refinement on the bearing capacity factor. They found that refinement of mesh with a small velocity led to better results.

In this study, the soils are modeled as a linear elastic-perfectly plastic material obeying Mohr–Coulomb criterion and the normality rule is adopted. The layer of sand is characterized by the shear modulus Gs, bulk modulus Ks, unit weights γ, internal friction φ = 30° and 35°, and thickness D. In each case, five values of ratio D/B were investigated (D/B = 0.25, 0.5, 1, 2 and 3). The parameters needed for the lower layer of clay are: shear modulus Gc, bulk modulus Kc, undrained shear strength su, internal friction φ = 0, and the unit weights of the clay γc. It is important to mention that the undrained bearing capacity of a footing is not sensitive to the soil unit weight (Shiau et al. 2011).

The values of shear strength ratio su/γB adopted in present study have the following values: 0.25, 0.5, 1, 2, 3 and 4. It should be noted that the values of shear modulus and the bulk modulus (equivalent to a Young’s modulus E and a Poisson’s ratio υ) affect the footing settlement but have an insignificant effect on the bearing capacity (Mabrouki et al. 2010).

The concrete footing was assumed linear elastic material with Young’s modulus of E = 30 GPa and Poisson’s ratio υ = 0.2. In all cases, for a more realistic modeling of footing behavior, the soil-footing interface is assumed to be perfectly rough (Loukidis et al. 2008). The code FLAC (2005) provides interface models that are characterized by Coulomb sliding and/or tensile separation. The interface elements placed between the soil and the footing are defined by its normal stiffness Kn = 2 × 109 Pa/m and shear stiffness Ks = 2 × 109 Pa/m, these parameters do not have a major influence on the failure load. To simulate a rough footing, the same friction angle of the upper layer was assigned to the interface elements.

In order to estimate the bearing capacity under inclined loads, the probe loading method was used. In this technique, a vertical stress (smaller than the ultimate vertical bearing capacity) is applied until equilibrium; then, horizontal velocity is applied at the footing nodes. The progressive displacement of the footing is accompanied by an increase of the shear stress along the soil-footing interface until collapse. The magnitude of chosen horizontal velocity is 2 × 10–7 m/step. In the probe analysis, the value of α at collapse is not known a priori; it represents an output variable. Full details of the numerical procedures of probe analysis can be found in Loukidis et al. (2008).

4 Model Validation

In this section, the bearing capacity is studied by several examples, in order to validate the proposed procedure with previous investigations. Three cases are considered: (1) strip footings on homogeneous sand under inclined load, (2) strip footings on sand layer overlying clay under vertical loading and, (3) strip footings on two-layered clays subjected to inclined loads.

4.1 Bearing Capacity of a Sand Soil Under Inclined Load

The numerical modeling procedure was first used to evaluate the bearing capacity of a rough strip footing resting on cohesionless soil under the action of an inclined loading. The analyses were performed for an angle of internal friction φ = 35° with an associated flow rule. The effect of inclined load is estimated by inclination factor iγ, defined as the ratio of the bearing capacity for a strip footing under inclined load to that of the footing under vertical load (iγ = V/Vult).

The values of the inclination factor iγ derived from the FLAC computation are presented in Fig. 3 for different load inclination α (tanα = H/Vult). The computed values of iγ are compared with those obtained by the semi-empirical formulas of Meyerhof (1963), Hansen (1970), also the results of kinematic approach of Michalowski and You (1998), and with the numerical results of Loukidis et al (2008). Figure 3 clearly shows that iγ decrease with an increase in the load inclination α. It can also be noted that the present study are in excellent agreement with the solutions obtained by Hansen (1970). Meyerhof’s method (1963) gives smaller results; however, Loukidis et al (2008) found greater results than those obtained with the other methods.

Fig. 3
figure 3

Comparison of obtained iγ with other results for φ = 35°

Full size image

4.2 Bearing Capacity of Strip Footings on a Sand Layer Overlying Clay Under Vertical Loading

The numerical analyses were performed using FLAC in order to evaluate the bearing capacity of a strip footing resting on a sand layer over clay soil. The problem addressed in this section is the same as the one illustrated in Fig. 1, except that the footing is subjected to a vertical loading (α = 0). Figure 4 displays the dimensionless bearing capacity (qu/γB) as a function of the dimensionless parameter (su/γB) of the clay layer, for the case of D/B = 1 and φ = 40°.

Fig. 4
figure 4

Comparison of the dimensionless bearing capacity (qu/γB) for different dimensionless parameter su/γB with other results, in the case φ = 40° and D/B = 1

Full size image

Where: qu = the bearing capacity of footing.

The results obtained from the present study were compared with those previously reported by other authors. It was noted that the dimensionless bearing capacity qu/γB increases with increasing su/γB. Figure 4 shows that the bearing capacity values obtained by the present study are slightly higher than those found by Burd and Frydman (1997) using the displacement finite element method. In addition, the two solutions are located inside the interval defined by the upper and lower bounds presented by Shiau et al. (2003), using the finite-element limit analysis. However, the analytical kinematic approach of limit analysis of Michalowski and Shi (1995) overestimate the bearing capacity.

4.3 Bearing Capacity of Strip Footings on Two-layered Clays Under Inclined Load

A series of numerical computations have been carried out to investigate the bearing capacity of a strip footing on two-layered clay soils subjected to inclined loading. Figure 5 displays the failure envelopes, in term of the dimensionless limit loads V/Bsu1 and H/Bsu1, obtained for D/B = 1 and su1/su2 = 3. The comparison was made with the results of the numerical limit analysis previously obtained by Rao et al. (2015) and Zhan (2011). As seen from Fig. 5, the bearing capacity under pure horizontal load is Hu = 0.996Bsu1, this value is found to be in good agreement with the exact value for a homogenous soil (Hu = Bsu1), because in the case of pure horizontal load, the failure occurs in the upper layer. In addition, it is clearly noted that the current bearing capacity agree well with the results of Rao et al. (2015) using the lower bound analysis.

Fig. 5
figure 5

Failure envelope for two-layered clay in term of V/Bsu1 and H/Bsu1, for D/B = 1 and su1/su2 = 3

Full size image

5 Results and Discussions

5.1 Failure Envelopes

Failure envelopes with vertical and horizontal loads are shown in Figs. 6 and 7 in terms of their normalized values V/Vult and H/Vult, where Vult is the ultimate vertical load (α = 0). The failure envelopes were expressed as functions of the dimensionless shear strength of clay layer (su/γB = 0.25, 0.5,1, 2, 3 and 4). The curves are presented for different values of relative thickness of sand layer (D/B = 0.25, 0.5, 1, 2 and 3) and two values of the friction angle of sand layer (φ = 30° and 35°).

Fig. 6
figure 6figure 6

Normalized failure envelopes of vertical and horizontal normalized bearing capacity V/Vult and H/Vult, for φ = 30°

Full size image
Fig. 7
figure 7figure 7

Normalized failure envelopes of vertical and horizontal normalized bearing capacity V/Vult and H/Vult, for φ = 35

Full size image

These plots clearly show that both the relative size and the shape of the failure envelopes are affected by the friction angle of the soil φ, the ratio D/B and the dimensionless shear strength su/γB.

It is noted that the size of relative failure envelopes decreases significantly with increasing su/γB, for φ = 30° and 35°. The decrease of the size of failure envelopes means that the bearing capacity increases by increasing the lower layer strength.

For given depth of the clay layer, there is a value of its strength (su/γB)crit such that it will force the mechanism to be confined to the upper layer. Further increase in the clay strength will not change the bearing capacity. As shown in Fig. 6c and d, for φ = 30° the value of (su/γB)crit is equal 2 and 0.5, respectively, when D/B = 1 and 2. Moreover, for φ = 35° the value of (su/γB)crit is equal 2 and 1, respectively, when D/B = 2 and 3 (Fig. 7d and e). This fact means that the value of the critical shear strength depends on the depth and the friction angle of the upper layer. As seen from Fig. 6e, there is no effect of the shear strength of clay on the failure envelopes, when D/B is approximately equal to 3, which indicates that the failure mechanism is entirely contained within the upper soil layer. The same observation was made by Shiau et al. (2003) and Burd and Frydman (1997) in the case of strip footings on sand layer overlaying clay under vertical loading.

Figures 6e and 7f compare the failure envelopes obtained from our computations in the case of D/B = 3, for φ = 30° and 35°, respectively, with the results of the earlier theoretical and numerical solutions of Hansen (1970), Vesic (1975) and Loukidis et al. (2008). It can be observed that for φ = 30°, the present results are in good agreement with the semi-empirical data given by Vesic (1975), and slightly lower than those found by Loukidis (2008). However, φ = 35° the present solution is close to the results obtained by Hansen (1970).

5.2 Failure Mechanism

Figures 8 and 9 show the contours of maximum shear strain for different load inclinations with various values of φ, D/B and su/γB. It is worth noting that the analyses with a displacement control do not maintain a constant load inclination, which can be obtained from the output (tanα = H/Vult). Figures 8a and 9a are obtained for su/γB = 0.25, it is observed that shear zone decreases when the load inclination increases. Moreover, there is an expansion of the failure mechanism in both layers, especially for small values of load inclination (V/Vult = 0.8). It is also seen that the failure mechanism is asymmetrical and becomes largely one-sided for higher values of α. By contrast, in the case of sand overlying a strong layer of clay (Fig. 9b), the mechanism is almost symmetrical and concentrated in the upper layer even if this top layer is thin.

Fig. 8
figure 8

Contours of maximum shear strain for different load inclinations, for φ = 30° and D/B = 1

Full size image
Fig. 9
figure 9

Contours of maximum shear strain for different load inclinations, for φ = 35° and D/B = 0.25

Full size image

It can be seen from Fig. 8b, for all load inclination and φ = 30°, D/B = 1, su/γB = 3, the failure mechanism is fully contained within the upper layer, which explains the convergence between the failure envelopes obtained in this case with those of homogenous sand (Fig. 6c). It is also noted that, for pure vertically loaded footing (α = 0), there is a triangular wedge immediately underneath the footing and the shear zone is in close agreement with the failure mechanism found by Terzaghi (1943) in the analysis of a strip footing on homogeneous soil.

The failure mechanism under vertical loading for φ = 30°, D/B = 1 and su/γB = 0.25 is shown Fig. 8a, it is seen that when the strong sand layer on top of a soft layer of clay, the top layer acts as a rigid column of soil that punches through into the bottom layer. Also, one can observe a prismatic elastic wedge forms immediately underneath the footing. In this case, the failure mechanism is deeper and extends to the underlying softer layer, even when the top layer has a large thickness. The form of the mechanism is similar to the punching shear failure obtained by Meyerhof (1974); this finding has also been reported by Shiau et al. (2003).

6 Conclusion

The finite difference code FLAC was employed to evaluate the bearing capacity of rough strip footings on sand underlying clay subjected to inclined loadings. The numerical procedure was validated through a comparison with the solutions available in the literature. It was found that the results obtained in this study and those reported in the literature are in good agreement, therefore the proposed approach can be used to study the problems related to layered soils. In all analyses the probe analysis technique was used and the results obtained were then presented in the form of failure envelopes.

The shape and the size of failure envelopes depend significantly on the values of the friction angle φ, ratio D/B and the shear strength of the lower layer su/γB. For all friction angles φ and ratio D/B, considered in this study, the size of the failure envelopes increases as the relative strength of the lower-layer rises. The relative failure envelopes and the failure mechanisms are similar to those found in the case of homogenous sand soils, when su/γB ≥ (su/γB)crit. In this case, a good agreement was observed between the present results and those of Vesic (1975) and Hansen (1970) for φ = 30° and 35° respectively. However, for su/γB ≤ (su/γB)crit, the failure mechanism reaches the lower layer especially for low values of α and su/γB. Otherwise the mechanism is entirely confined within the upper layer.