Numerical Investigation of the Bearing Capacity of Strip and Rectangular Shallow Footings on Cohesive Frictional Soils Under Eccentric Loads

Abstract

Safe performance of structures founded on shallow footings necessitates that: (a) the ground settlements are kept within acceptable threshold limits; and (b) the bearing capacity is always higher than the imposed stress, by thus giving an acceptable factor of safety. Regardless of minor alterations on the original bearing capacity expression by (Terzaghi K (1943) Theoretical Soil Mechanics. Wiley), most terms are used routinely in engineering practice to date. This paper revisits the bearing capacity of strip and rectangular footings on cohesive frictional soils under eccentric loads, by means of two- and three-dimensional numerical analyses in the finite element code Simulia Abaqus. The geomaterial is described by means of the Mohr–Coulomb failure criterion and works at a null dilation angle, while the footing remains undeformed regardless of the ground stiffness. The ground-footing interface allows for separation and slippage to account for cases where the ground detaches or slips beneath and around the footing. The paper studies the effect of: (a) elastic Young’s Modulus; (b) width; (c) cohesion; (d) surcharge; (e) dilation; (f) strain-softening; and (g) interface roughness on the bearing capacity. The paper shows that the Eurocode 7 underestimates the bearing capacity by up to 60% compared to the numerical solution. Revised bearing capacity and shape factors are developed to enhance the accuracy of the bearing capacity equation.

1 Introduction

Structures founded on soft soils can suffer significant settlements, even under low stresses. At high shear stress levels however, even hard soils can exhibit inelastic behavior which can lead to failure. Safe performance of shallow footings necessitates that the following two conditions are always justified: (a) the ground settlements are kept within acceptable threshold limits; and (b) the unit bearing capacity is always higher than the imposed stress, by thus securing an acceptable safety factor. The bearing capacity of shallow foundations is typically calculated based on Terzaghi’s (1943) original formula:

$$q_{u} = c \cdot N_{c} + q \cdot N_{q} + \frac{1}{2} \cdot \gamma \cdot B \cdot N_{\gamma }$$

(1)

where "q_u" is the unit bearing capacity, "c" is the ground cohesion, "q" is the surcharge at the foundation level, "γ" is the ground unit weight, "B" is the foundation width and "N_c", "N_q" and "N_γ" are the bearing capacity factors, which depend on the internal friction angle "φ". This expression computes the bearing capacity for centrally vertical loaded strip footings embedded at depth D (giving a surcharge q = γ·D); the ground response is described by a perfectly plastic Mohr–Coulomb material. Bearing capacity expressions used widely in engineering practice to date work and further extend Terzaghi’s original formulation by superimposing three components: (a) the cohesion term; (b) the overburden or surcharge term; and (c) the term of foundation width related to the length of shear stress area. Each of the aforementioned terms is usually determined separately by eliminating the remaining components. Thus, (a) the cohesion term is calculated for a weightless (γ = 0) and frictionless ground mass (φ = 0); (b) the component of width works at null cohesion (c = 0) and zero surcharge (q = 0), and the surcharge term computes for a weightless (γ = 0) ground mass with null cohesion (c = 0). The ground and the footing remain undeformed until the full formation of the failure surface, at which point the ground fails as it cannot withstand any further stress increase. Most bearing capacity formulations (e.g., Terzaghi, 1943; Meyerhof, 1951, 1963; Brinch Hansen, 1970; Vesic, 1973) work on rough ground-footing interfaces.

The bearing capacity factors "N_c", "N_q" and "N_γ" depend solely on the internal friction angle "φ", with:

• "N_q" traditionally given by $N_{q} = \tan^{2} \left( {45^{^\circ } + {\varphi \mathord{\left/ {\vphantom {\varphi 2}} \right. \kern-\nulldelimiterspace} 2}} \right) \cdot e^{\pi \cdot \tan \varphi }$ (Reissner, 1924);

• "N_c" traditionally given by $N_{c} = \left( {N_{q} - 1} \right) \cdot \cot \varphi$ (Prandtl, 1920); and

• "N_γ" typically given by $N_{\gamma } = \left( {N_{q} - 1} \right) \cdot \tan \left( {1.4 \cdot \varphi } \right)$ (Meyerhof, 1963) or $N_{\gamma } = 2 \cdot \left( {N_{q} - 1} \right) \cdot \tan \varphi$ (Caquot and Kerisel, 1953; Chen, 1975). Both DIN4017 and the Eurocode 7 methodology use the latter expression to describe the width term in the bearing capacity expression.

Meyerhof (1953) included the inclination of loading in Equation (1) and further extended the bearing capacity formula (in 1963), through the load inclination ("i_c", "i_q", "i_γ") and shape factors ("s_c", "s_q", "s_γ"):

$$q_{u} = i_{c} \cdot s_{c} \cdot c \cdot N_{c} + i_{q} \cdot s_{q} \cdot q \cdot N_{q} + i_{\gamma } \cdot s_{\gamma } \cdot \frac{1}{2} \cdot \gamma \cdot B \cdot N_{\gamma }$$

(2)

Brinch Hansen (1970) later proposed slightly different expressions for the inclination and shape factors. The base inclination factors ("b_c", "b_q", "b_γ") were included in Equation (2) by Brinch Hansen (1970) and Vesic (1973), by thus modifying the bearing capacity formula in its most common form:

$$q_{u} = i_{c} \cdot s_{c} \cdot b_{c} \cdot c \cdot N_{c} + i_{q} \cdot s_{q} \cdot b_{q} \cdot q \cdot N_{q} + i_{\gamma } \cdot s_{\gamma } \cdot b_{\gamma } \cdot \frac{1}{2} \cdot \gamma \cdot B \cdot N_{\gamma }$$

(3)

Without excluding experimentally based formulations of the bearing capacity equation and relevant factors (e.g., Prakash and Saran, 1971; Purkayastha and Char, 1977; Zadroga, 1994; Georgiadis and Butterfield, 1988; Gottardi and Butterfield, 1993), most bearing capacity methodologies build on the following theories:

• Limit equilibrium analyses (e.g., Terzaghi, 1943; Meyerhof, 1951) working on predetermined failure surfaces.

• Method of characteristics (e.g., Prandtl 1920; Reissner, 1924; Sokolovskii, 1965; Brinch Hansen, 1961; Bolton and Lau, 1993) which gives accurate limit loads for parabolic failure surfaces, in cases where the calculation of the bearing capacity formula is consistent with a single collapse mechanism and the soil further works on a dilation angle equal to the internal friction angle ψ = φ (Martin, 2005; Smith, 2005). However, it is highly unlikely that the collapse mechanism remains intact for different overburden heights, friction angles and cohesion values, the accuracy of this method is not consistent.

• Upper-bound plastic limit theorem (e.g., Shield, 1954a,b; Chen, 1975; de Borst and Vermeer, 1984; Sarma and Iossifelis, 1990; Drescher and Detournay, 1993; Michalowski, 1997; Soubra, 1999) which gives upper-bound solutions of the bearing capacity loads based on the limit analysis theory. The upper-bound theorem assumes a perfectly plastic soil model working on an associated flow rule. The upper-bound plastic limit analysis needs to be used in tandem with the lower bound theorem, to bracket the solution within a relatively accurate confidence interval for design purposes. Upper-bound plastic limit loads need to be handled with caution, especially when the lower-bound solution differs significantly from it.

• Numerical analyses integrated in Finite Element and Finite Difference codes (e.g., Zienkiewicz et al., 1975; Griffiths, 1982; Mizuno and Chen, 1983; Frydman and Burd, 1997; Yin et al., 2001; Ericson and Drescher, 2002; Loukidis and Salgado, 2009; Benmebarek et al., 2012; Remadna et al. 2017). These methods can accurately compute the unit bearing capacity of shallow footings, depending on the selected ground model parameters and ground-footing interface parameters.

This paper studies bearing capacity of strip and rectangular shallow footings on cohesive frictional soils under eccentric loads, by means of two- and three-dimensional numerical analyses in the finite element code Simulia Abaqus. The study investigates the effect of: (a) the Young’s Modulus; (b) the foundation width; (c) the cohesion; (d) the surcharge; (e) dilation; (f) strain-softening; and (g) the interface roughness on the bearing capacity. The numerical model is firstly verified against Prandtl’s (1920) analytical solution; interface parameters and the dilation angle are then calibrated to match the bearing capacity values computed by means of the Meyerhof and Eurocode 7 methodologies. This process ensures that the bearing capacity founds safely on well-known and extensively used (in engineering practice) bearing capacity formulations, by further enhancing their accuracy. The effect of each of the aforementioned parameters is examined separately scoping to deconvolve its importance on bearing capacity. Revised bearing capacity and shape factors are developed to most accurately compute the ultimate bearing load, based on the numerical observations.

2 Numerical Investigation of the Bearing Capacity of Shallow Footings

2.1 Geometry and Model Parameters

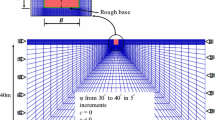
The numerical investigation studies the bearing capacity of both strip and rectangular shallow footings, by means of two-dimensional and three-dimensional numerical analyses in the commercial Finite Element Code Simulia Abaqus. Figure 1 shows the finite element mesh in two and three dimensions. The lateral and bottom boundaries extend more than 7B to each side to ensure that all boundary effects are minimal. The plane-strain analyses for the strip footing work on 8-node biquadratic elements (CPE8), while the three-dimensional finite element mesh works on 20-node quadratic brick (C3D20) elements.

Fig. 1

Mesh configurations for a a strip (left figure) and b a square footing (right figure). The figures also show the lateral roller supports and the pinned supports at the bottom nodes

The numerical study investigates the effect of the internal friction angles, ranging from φ = 20° to φ = 40° (φ = 20°, 25°, 30°, 35°, 40°), on the bearing capacity. The bearing capacity study of rectangular shallow footings works on commonly used L/B ≤ 4 ratios in engineering practice (L/B = 1, 2, 4 and L/B →  + ∞). The following embedment ratios D/B = 0, 0.5 and 1 are considered to study the effect of the surcharge on the bearing capacity; the soil unit weight is kept constant to γ = 20kN/m³. The maximum simulated foundation embedment is D/B = 1, which is typical for shallow footings. The numerical investigation studies the effect of cohesion, ranging from c = 0 to c = 200 kPa, on the bearing capacity. The examined dilation angles range from ψ = 0 to ψ = φ, for an associated flow rule. The effect of the ground Young’s modulus, ranging from E = 3 MPa to E = 200 MPa for the soil materials under examination based on Bowles (1996), on the bearing capacity is also examined in a separate section.

The footing behaves elastically at an infinite stiffness, as the footing remains undeformed regardless of the ground stiffness. Both strip and rectangular shallow footings were modeled using 8-node biquadratic (CPE8) and 20-node quadratic brick (C3D20) continuum elements. The surface interaction between the footing and the underlying soil is described by the Coulomb friction law, allowing for slippage of the footing in cases where the interface shear strength is exceeded. The interface in the normal direction can account for possible uplift of the footing, in cases where the eccentricity of the load causes the footing to detach from the ground surface as the footing tilts; the numerical investigation studies the effect of the eccentricity, ranging from e/B = 0 to e/B = 0.315, on the bearing capacity. The contact pressure interface follows the exponential law shown in Fig. 2.

Fig. 2

Contact pressure–overclosure exponential law describing the mechanical behavior of the soil-footing interface

2.2 Model Verification

This study verifies the numerical model against Prandtl’s (1920) analytical solution. Prandtl’s solution addresses the bearing capacity of a strip load applied on the ground surface. The geomaterial works on a null internal friction angle (φ) and a cohesion (c) equal to the undrained shear strength (C_u). The analytical solution gives a unit bearing capacity equal to q_u = (π + 2)·C_u.

Figure 3 compares the numerical solution based on the 2D analyses in Simulia Abaqus against Prandtl’s analytical formula for three values of the undrained shear strength C_u = 20, 50 and 100 kPa. Prandtl’s solution is indicative of a fully flexible strip footing resting on the ground surface. The numerical solution (shown in the black solid line – indicated C_u) compares well to Prandtl’s analytical solution (shown in the black dashed line – indicated as "Prandtl—EC7") for all the examined C_u values. The methods differ by less than 3%, with the discrepancy attributed to approximations during the numerical integration of the governing equations.

Fig. 3

Comparative plots of the numerical solution (in the black solid line) against Prandtl’s analytical solution (in the dashed line), for three values of the undrained shear strength Cu = 20, 50 and 100 kPa (from top to bottom). The diagrams plot the settlement (in m) as a function of the imposed Load (in kN/m)

Eurocode 7 adopts Prandtl’s analytical formula to describe the bearing capacity of strip shallow footings on null internal friction angles. This contradicts the Eurocode 7 bearing capacity working hypothesis building on perfectly stiff shallow foundations, as Prandtl’s solution gives the bearing capacity of a strip load applied on the ground surface (rather than imposed displacement applied through the loading of an unbending footing).

2.3 Ground–Footing Interface Calibration

The roughness of the footing is long known to control the bearing capacity mainly through the bearing capacity factor N_γ (e.g., Meyerhof, 1951 & 1955; Griffiths, 1982; Bolton and Lau, 1993; Michalowski, 1997; Kumar and Kouzer, 2007; Kumar, 2009). This is attributed to the inclusion or not of the nonplastic wedge below the footing base in the case of rough (e.g., Terzaghi, 1943; Meyerhof, 1957 & 1963; Chen, 1975; Bolton and Lau, 1993; Michalowski, 1997, Soubra, 1999; Kumar, 2003; Chen and Xiao, 2020) or smooth shallow (e.g., Hill, 1950; Meyerhof 1951; Sokolovski, 1960; Bolton and Lau, 1993; Michalowski, 1997) footings. As the aforementioned methods do not explicitly control the roughness of the soil – footing surface interaction in the shear direction (described by the Mohr–Coulomb failure criterion on a null surface cohesion) there is some ambiguity involved stemming from the mobilization of the exact failure mechanism.

This section calibrates the interface friction angle "δ", for the numerical solution to match the bearing capacity values computed by means of the Meyerhof (1963) and and the Caquot and Kerisel (1953) (used in the EC7) methodologies. The calibration focuses on the proper determination of the interface friction angle as the remaining model parameters (c, φ) are well defined, for the numerical finite element solution to match the ultimate loads computed by means of the aforementioned methodologies, regardless of their limit state origin. The calibration process works on strip foundations resting on the ground surface at null cohesion under central vertical loading.

Figure 4 compares the numerical solutions from the two-dimensional numerical analyses in Abaqus against the bearing capacity loads of Meyerhof and EC-7 for three soil internal friction values φ = 25°, 30° and 35°. The numerical solution working on a soil–footing interface friction angle equal to δ = ${\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$·φ (shown in the black solid line) gives about the same (± 5% ÷ 6%) ultimate loads as the EC-7 method (shown in the black dashed line), while the numerical solution working on a soil–footing interface friction angle equal to δ = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$·φ (shown in the grey solid line) approximates well (± 5%) the ultimate loads of the Meyerhof method (shown in the grey dashed line). While the calibration process scopes primarily for the numerical solution to match the aforementioned methodologies of EC-7 and Meyerhof through the proper determination of the interaction friction angle (δ), it can act as a guideline for the footing interface smoothness, with rough footings working typically on δ = ${\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$·φ and smooth footings working on δ = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$ φ. The numerical analyses work on a non-associated flow rule at a null dilation angle ψ ≈ 0. Use of a finite dilation angle (0 ≤ ψ ≤ φ) gives higher bearing capacity loads, as will be shown in a following section.

Fig. 4

Calibration of the ground-footing interface friction angle (δ), shown in the solid lines, for the numerical solution to match the ultimate load computed by means of the Meyerhof and the EC-7 methodology, for strip footings (with width B = 2 m) resting on the ground surface with internal friction angles φ = 25°, 30°, 35° (from top to bottom). The EC-7 ultimate load (shown in the black dashed line) is shown to match the numerical solution for δ = ${\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$·φ (shown in the black solid line), while the numerical solution working on δ = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$·φ (shown in the grey solid line) gives approximately the same ultimate load as Meyerhof (shown in the grey dashed line)

Henceforth, all numerical analyses will be working on a soil–footing surface friction angle equal to δ = ${\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$·φ, matching the EC-7 solution. This assumption founds safely on the well-known and extensively used (in engineering practice) EC-7 bearing capacity methodology, by further enhancing its accuracy and applicability.

2.4 Necessity of the Work–Comparison with Late Novel Studies

This section scopes to highlight the necessity of the work by comparing the numerical method, working on the aforementioned calibration procedure of the surface interaction friction law for strip footings resting on the ground surface with zero dilation angle, with the late novel studies by Lyamin et al. (2007) and Salgado (2008). The works by Lyamin et al. (2007) and Salgado (2008) focus on the determination of the bearing capacity of shallow footings by means of two- and three-dimensional numerical analyses. The lower bound calculation satisfies solely the stress equilibrium, while calculation of the upper bound gives the velocity distribution which satisfies the compatibility, the (associated) flow rule, the velocity boundary conditions and further minimizes the internal power dissipation less the rate of work due to external tractions and body forces.

Figure 5 compares the numerical results based on the ensuing calibration process (in the dark grey solid line) against the F.E. solution, lying between the upper- and lower-bound solutions, based on the works of Lyamin et al. (2007) and Salgado (2008), shown in the light grey line. The figure also includes the Eurocode 7 ultimate load in the black solid line. The difference between the dark and light grey lines may exceeds 50% and increases with increasing "φ". It is attributed to the working hypotheses of the works of Lyamin et al. (2007) and Salgado (2008) working on: (a) an associated flow rule (ψ = φ) and (b) complete roughness of the strip footing (δ = φ).

Fig. 5

Comparative plots of a the load-settlement curve of shallow footings (with width B = 2 m) resting on the ground surface (shown in the dark grey solid line), calibrated to match b the EC-7 ultimate loads (shown in the black solid lines), against c the finite element numerical solution working on the model parameters (ψ = φ, δ/φ = 1, where ψ is the ground dilation angle), reported by Lyamin et al. (2007) and Salgado (2008)

It is shown that strip footings with a perfectly rough base founded on the surface of a soil with a dilation angle (ψ = φ) give considerably higher ultimate loads compared to the Eurocode methodology. As the EC-7 method was shown to work on a null dilation angle and a ground-footing surface friction angle δ =  2/3·φ, it is important to investigate whether theses working hypotheses apply in the actual bearing capacity problem. Soils at failure work on zero dilation, by thus justifying the use of a non-associated flow rule. In addition, rough ground-concrete footing base interfaces can work on friction angles (δ) ranging from ${\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$·φ to φ, which places the calibrated value of δ = ${\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$·φ at the lower bound. Hence, the calibrated interface and model parameters are relevant to engineering practice and ground response. This means that the bearing capacity computed by means of the methodologies by Lyamin et al. (2007) and Salgado (2008) may work on the unsafe side, by thus justifying the necessity to revisit the bearing capacity theory and revise the bearing capacity and shape factors to enhance the accuracy and applicability of the method.

3 Numerical Results

This section studies the effect of: (a) the Young’s Modulus; (b) the internal friction angle; (c) the ground cohesion; (d) surcharge; (e) dilation; and (f) strain-softening on the bearing capacity of strip and rectangular shallow footings by means of two- and three-dimensional numerical analyses in the Finite Element Code Simulia Abaqus.

3.1 Effect of Young’s Modulus

Figure 6 studies the effect of the Young’s modulus on the bearing capacity of strip footings founded on the ground surface for three internal friction values φ = 25°, 30° and 35° (from top to bottom). The EC-7 ultimate load is shown in the black solid line and is matched by the main load – settlement curve (depicted in the dark grey line) working on a Young’s modulus E (E = 13 MPa for φ = 25°, E = 52 MPa for φ = 30°, E = 91 MPa for φ = 35°) showing failure at approximately 10 cm of settlement. The figures also include three curves for fractions of the aforementioned Young’s modulus E: (a) ¾·E in the dark grey dashed line; (b) ½·E in the light grey solid line; and (c) ¼·E in the light grey dashed line.

Fig. 6

Comparative plots of the load-settlement curves of strip shallow footings (with width B = 2 m) resting on the ground surface for three internal friction angles φ = 25°, 30° and 35° (from top to bottom), studying the effect of Young’s modulus. The analyses show that the ultimate load is independent of the Young’s modulus

The figure shows that the bearing capacity is independent of the Young’s modulus of the soil, as all the curves give the same ultimate load at different settlements. Soils on low elastic moduli reach the ultimate load at higher settlement values, as the load – settlement curve bends smoothly towards its final resting bearing capacity load. On the other hand, soils on high elastic moduli necessitate considerably smaller deformations to reach the ultimate load, as the load – settlement curve bends sharply downwards reaching a plateau at lower settlement values.

3.2 Effect of Width

This section studies the effect of the term of width "Β" on the bearing capacity, by eliminating the surcharge (q = 0) and the cohesion (c = 0) terms. Cohesionless soils are not irrelevant as sands, gravels and even NC (Normally Consolidated) Clays work on null cohesion.

Figure 4 compares the numerical solution in the black solid line against the ultimate loads computed by means of the EC-7 methodology for strip footings with width equal to B = 2 m. The numerical solution was shown to perform well against the EC-7 ultimate loads for all the internal friction values (φ = 25°, 30° and 35°), by thus proving the appropriateness of the calibration procedure. As however, this does not ensure that the calibration process performs well for other footing widths, Fig. 7 compares the numerical solution (in the black solid line) against the ultimate loads computed by means of the EC-7 methodology (in the black dashed line) for strip footings with width equal to B = 4 m. The calibrated numerical solution shown in the grey dashed line matches systematically the EC-7 ultimate loads for a wide range of internal friction values "φ".

Fig. 7

Comparative plots of the load-settlement curves of strip shallow footings with width B = 4 m resting on the ground surface for two internal friction angles φ = 25° and 35° (from top to bottom). The figure shows that the calibrated numerical solution performs well for a wide range of internal friction values, as the numerical solution in the black dashed line matches the EC-7 ultimate load in the black solid line. The figure also shows the numerical solution for c = 10 kPa in the grey dashed line giving systematically higher ultimate loads compared to the EC-7 methodology depicted in the grey solid line

Hence, the bearing capacity factor "N_γ" can be expressed accurately through the following formula:

$$N_{\gamma } = 2 \cdot \left[ {\tan^{2} \left( {45^{^\circ } + {\varphi \mathord{\left/ {\vphantom {\varphi 2}} \right. \kern-\nulldelimiterspace} 2}} \right) \cdot e^{\pi \cdot \tan \varphi } - 1} \right] \cdot \tan \varphi$$

(4)

based on the formulations by Caquot and Kerisel (1953) and Chen (1975). Eurocode 7 uses this expression to compute the bearing capacity factor of width. This expression will be used henceforth to give the bearing capacity width factor. The following section investigates the effect of surcharge and cohesion on the bearing capacity of strip foundations by studying the standalone effect of each term.

3.3 Effect of Cohesion

While the numerical solution converges to the EC-7 ultimate load for strip footings on the ground surface at null cohesion, Fig. 7 shows that the numerical solution for c = 10 kPa depicted in the grey solid line diverges from the EC-7 ultimate load (in the grey dashed line) for strip footings with width equal to B = 4 m. The numerical solution working on c > 0 gives systematically higher ultimate loads compared to the EC-7 methodology.

Figure 8 compares the numerical solution of the bearing capacity problem of strip footings with zero surcharge for different values of the soil cohesion c = 5, 10 and 15 kPa against the EC-7 ultimate loads. The cohesion values are relevant for soils with internal friction angles of φ = 25°, 30° and 35°. The figure shows that as the cohesion increases the numerical solution gives systematically higher ultimate loads compared those computed by means of the EC-7 methodology. This effect is more pronounced at low internal friction values, with the numerical solution giving ultimate loads up to 35% higher compared to the EC-7 counterpart loads.

Fig. 8

Comparative plots of the load-settlement curves of strip shallow footings (with width B = 2 m) resting on the ground surface for two internal friction angles φ = 25°, 30° and 35° (from top to bottom). The figure shows that as the cohesion increases the numerical solutions shown in the dashed curves lay systematically significantly higher than the EC-7 ultimate loads shown in the solid lines of the same color

By accounting for the soil cohesion (and further assuming a fixed Young’s modulus), the footing tends to fail not only at higher ultimate loads, which is to be expected as the soil strength increases, but also at higher settlements. This is due to the fact that the elastic regime is bigger (compared to the cohesionless counterpart), by thus necessitating additional deformation to reach failure which in turn manifests in greater settlement values to reach the ultimate load.

As the numerical solution for cohesive soils gives systematically higher ultimate loads for strip shallow foundations compared to the counterpart loads computed by means of the EC-7 formula, it is necessary to revise the bearing capacity cohesion factor in order to account for this excess load. A following section introduces a revised formula giving the bearing capacity factor "N_c" as a function of the internal friction angle.

3.4 Effect of Surcharge

This section studies the effect of surcharge on the bearing capacity of strip shallow footings. The surcharge can be applied either directly as a uniform pressure on the ground surface or through the overburden depth in cases where the footing is embedded at depth "D". As simulation of surcharge by means of constant uniform load cannot account for the excess resistance of the overlying soil on the bearing capacity load, this section studies this effect through the simulation of the embedment. The surrounding vertical footing-ground interfaces work on a fraction of the ground internal friction angle with δ = arctan(5%·tanφ), while the base footing-ground interface works on a δ = ${\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$·φ based on the previous calibration of Sect. 2.3. While perfect smoothness of the vertical footing-ground interface is not relevant for typical shallow footings, the numerical solution scopes to produce conservative ultimate loads. Use of typical vertical footing-ground interface friction angles in the range of δ = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$·φ ÷ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}$·φ or even equal to that of the base soil–footing interface δ = ${\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$·φ, which is relevant for cast-in-place concrete–rough–footings, gives significantly higher ultimate loads.

Scoping to investigate the standalone effect of the surcharge on the ultimate load, Fig. 9 compares the numerical solution against the ultimate loads computed by means of the EC-7 methodology for strip shallow footings embedded at depth "D" on cohesionless soils. The overburden depths range from D = 0, for surface-based strip footings, to D = B which is typical for shallow footings. The figure shows that as the embedment increases the numerical solution gives ever-higher ultimate loads compared to the counterpart loads computed by means of the EC-7 methodology. This effect is more pronounced at low internal friction values, with the numerical solution giving ultimate loads up to 55% higher compared to the Eurocode.

Fig. 9

Comparative plots of the load-settlement curves of strip shallow footings (with width B = 2 m) for three internal friction angles φ = 25° and 35° (from top to bottom) and null cohesion. The figure shows that as the depth increases the numerical solutions shown in the dashed curves lay systematically significantly higher than the EC-7 ultimate loads shown in the solid lines of the same color

By accounting for the embedment on a fixed Young’s modulus, the footing tends to fail not only at higher ultimate loads, which is to be expected as the soil strength increases, but also at higher settlements. The ultimate load increases as the failure surface needs to propagate through the overlying soil to emerge to the surface. For the formation of the final failure surface, the full shear strength of the soil needs to be mobilized along the shear band. Hence, as the slip surface is longer the ultimate load of the embedded strip footing is higher.

Figure 10 compares the numerical solution against the ultimate loads computed by means of the EC-7 methodology for strip shallow footings embedded on depth "D" on soils with cohesion c = 10 kPa. The figure shows that as the embedment increases the numerical solution gives ever-higher ultimate loads compared to the ultimate loads computed by means of the EC-7 methodology. The combined effect of surcharge and cohesion becomes more pronounced at low internal friction values, with the numerical solution giving ultimate loads up to 60% higher than the Eurocode. This agrees with the observations of Meyerhof (1963), Brinch Hansen (1970), Vesic (1973) and Lyamin et al. (2007), where the bearing capacity increase is included in the depth factors.

Fig. 10

Comparative plots of the load-settlement curves of strip shallow footings (with width B = 2 m) for three internal friction angles φ = 25° and 35° (from top to bottom) and cohesion c = 10 kPa. The figure shows that as the depth increases the numerical solutions shown in the dashed curves lay systematically (significantly) higher than the EC-7 ultimate loads shown in the solid lines of the same color

As the numerical solution for embedded strip footings gives systematically higher ultimate loads compared to the EC-7 methodology, it is necessary to revise the bearing capacity surcharge factor in order to account for this excess load. A following section introduces a revised formula giving the bearing capacity factor "N_q" as a function of the internal friction angle.

3.5 Dilation Effect

This section studies the dilation effect on the bearing capacity of strip footings on the ground surface. The bearing capacity terms for the surcharge and the cohesion are eliminated, as the investigation focuses on the mechanical response of strip foundations resting on the surface of a cohesionless geomaterial, by thus giving the standalone dilation effect. As the geomaterial response is described by the Mohr–Coulomb failure criterion, the dilation works through the dilation angle "ψ".

Figure 11 studies the dilation effect on the ultimate load of a strip footing resting on the ground surface with an internal friction angle φ = 35° and cohesion c = 0. The figure shows the numerical solutions for: (a) the associated flow rule (ψ/φ = 1) in the light-grey dashed line; and non-associated flow rules with (b) ψ/φ = ${\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$ in the mid-grey dashed line; (c) ψ/φ = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$ in the dark-grey dashed line; and (d) ψ/φ = 0 in the black dashed line from left to right respectively. The figure includes the EC-7 ultimate load in the black solid line acting as a baseline for comparison.

Fig. 11

Effect of dilation on the ultimate load of a strip footing (with width B = 2 m) resting on the surface of a cohesionless soil (c = 0) with φ = 35°. The figure shows the numerical solutions for: (a) the associated flow rule (ψ/φ = 1) in the light-grey dashed line; and non-associated flow rules with (b) ψ/φ = ${\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$ in the mid-grey dashed line; (c) ψ/φ = ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$ in the dark-grey dashed line; and (d) ψ/φ = 0 in the black dashed line from left to right respectively. The figure also includes the EC-7 ultimate load in the black solid line acting as a baseline for comparison

The figure shows that as the dilation angle (ψ) increases the numerical solution gives ever-higher ultimate loads compared to the loads computed by means of the EC-7 methodology. It is noted that most limit state approaches, including the EC-7 methodology, use an associated flow rule to describe the evolution of the plastic straining after yielding. The increase in the ultimate load exceeds 23% for the associated flow rule working on ψ = φ which agrees with observations by Frydman and Burd (1997), Yin et al. (2001) and Loukidis and Salgado (2009). As however, use of a null dilation angle is relevant for soils at failure, the bearing capacity formula needs not to account for the dilation effect as typical dilation angles for soils ψ = 0 ÷ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$·φ gives slightly higher ultimate loads (by up to 7%) compared to the calibrated numerical solution against the EC-7 methodology.

3.6 Strain-Softening Effect

This section studies the standalone effect of the soil strain-softening on the bearing capacity of strip footings on the ground surface. Scoping to isolate the effect of strain-softening, the investigation focuses on cohesionless soils. The strain-softening mechanism works by reducing the internal friction angle from its initial value φ_in to its residual value φ_res, by means of an exponentially decaying formula which works on the accumulated shear plastic strain ε_q^p (= ∑dε_q^p).

Figure 12 studies the effect of strain-softening on the ultimate load of strip footings on the ground surface. The figure includes the numerical solutions for fixed internal friction angles: (a) φ = 25° in the light-grey solid line; (b) φ = 30° in the dark-grey solid line; and (c) φ = 35° in the black solid line. The effect of strain-softening is highlighted through: (a) the reduction from φ_in = 35° to φ_res = 30° in the dark-grey dashed line; and (b) the reduction from φ_in = 30° to φ_res = 25° in the light-grey dashed line. In both cases, the footing founded on a soil undergoing strain-softening tends to fail at loads slightly higher (by up to 7.5%) than the ones computed numerically for the (fixed) residual value φ_res. The "plateau" in the load-settlement curve signifies failure of the strip footing on a friction angle slightly higher from its residual value φ_res. Note that as the settlement increases any further the shear plastic strain measure ε_q^p continues to accumulate, by thus decreasing the internal friction angle to the residual. The damage rate, however, is smaller as the degradation mechanism decelerates when approaching the residual value due to the nature of the exponentially decaying formula. Hence, the dashed lines will reduce to their residual solid counterpart lines (of the same color) with settlement.

Fig. 12

Effect of strain-softening on the ultimate load of a strip footing (with width B = 2 m) resting on the ground surface of a cohesionless soil. The figure includes the numerical solutions of the bearing capacity problem for: a φ = 25° in the light-grey solid line; b φ = 30° in the dark-grey solid line; and c φ = 35° in the black solid line. The effect of strain-softening is portrayed through the degradation of φ (with accumulated plastic shear strains): a from φ = 35° to φ = 30° in the dark-grey dashed line; and b from φ = 30° to φ = 25° in the light-grey dashed line

As the ultimate load of strip footings on the ground surface, of soils undergoing strain-softening, depends on the residual internal friction angle rather than its initial value, the ultimate load needs to work on this.

3.7 Other Bearing Capacity Factors (Shape and Eccentricity)

Additional factors affecting the response of shallow footings involve the shape of the foundations and the eccentricity of the imposed loading. While these parameters are of no less importance from the above, they apply only in specific cases of footing shapes and types of loading. In this regard, they differ from the bearing capacity factors "N_c", "N_q" and "N_γ" and the dilation and strain-softening effects, which depend on the soil internal parameters, as the shape and eccentricity characterize the footing itself and the type of loading.

As the shape factors account primarily for the B/L ratios it is important to study their performance against the numerical solutions via 3D numerical analyses in cases of null eccentricity. Figure 13 compares the numerical solutions, via the three-dimensional (3D) numerical analyses, for the following different L/B ratios: (a) L/B →  + ∞ (characteristic of a strip footing) in the black solid line; (b) L/B = 4 in the black dashed line; (c) L/B = 2 in the grey dashed line; and (d) L/B = 1 (characteristic of a square footing) in the grey solid line. The figure shows that as the L/B ratio increases the bearing capacity load decreases towards a limiting threshold, computed for the case of a strip footing. While this observation agrees with Lyamin et al. (2007), it works opposite to the Eurocode giving lower ultimate loads for decreasing L/B ratios. Figure 14 shows indicative results of the bearing capacity problem in both 2D and 3D conditions for nil cohesion (c = 0), nil embedment (D = 0) and internal friction angle φ = 35°, under central vertical loading. The figures highlight the observed failure mechanism and the proper placement of the boundary conditions.

Fig. 13

Comparative diagram of the numerical bearing capacity solution of shallow footings (with width B = 2 m) for different L/B ratios on an internal friction angles φ = 35° and null cohesion. The figure shows the numerical solutions for: a a strip fooring with L/Β →  + ∞ in the black solid line; b a rectangular footing with L/Β = 4 in the black dashed line; c a rectangular footing with L/Β = 2 in the grey dashed line; and d a square footing with L/Β = 1 in the grey solid line. The bearing capacity decreases with L/Β increasing

Fig. 14

Indicative numerical results of the bearing capacity problem in both 2D and 3D conditions for nil cohesion (c = 0), nil embedment (D = 0) and internal friction angle φ = 35°, under central vertical loading. The analyses of the 2D analysis of the strip foundation is shown in the top left figure, while the remaining figures highlight the failure mechanism of a BxL rectangular footing in 3D conditions. The boundary effect is minimal, as the failure mechanism does not extend close to the lateral and bottom boundaries

Figure 15 compares the numerical solutions via the 2D finite element analyses of the bearing capacity problem of strip footings (with width B = 2 m) resting on the ground surface, in terms of load versus settlement. The comparative diagrams work on the following mechanical soil properties: (a) internal friction angles φ = 25° and φ = 35°; and (b) cohesion c = 0 and c = 10 kPa. The numerical solutions investigate eccentricity ratios: (a) e/B = 0, shown in the black dashed line, (b) e/B = 0.125, shown in the dark-grey dashed line; and (c) e/B = 0.25, shown in the light-grey dashed line. The respective Eurocode ultimate loads working on the aforementioned eccentricity ratios are depicted in solid lines of the same color. For an eccentricity ratio equal to e/B = 0.125 < ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 6}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$6$}}$ the full width of the footing sustains the reaction of the underlying ground, while for an eccentricity ratio equal to e/B = 0.25 < ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$ only part of the footing width sustains the ground reactions to the imposed loading as there is an uplift of the soil shown in Fig. 16. For null cohesion, the strip footings subjected to eccentric vertical loading tend to fail at higher ultimate loads compared to the Eurocode. As the effect of eccentricity in the bearing capacity equation is typically accounted through the substitution of the total width "Β" by the working width Β′ = B−2·e, it is necessary to either introduce a new factor multiplying the working length (Β′), to account for the excess load, or revise the shape factors accordingly. Scoping to enhance the accuracy of the bearing capacity expression (3) without jeopardizing its wide-spread validity and use of the formula, the eccentricity effect will be accounted for in the revised definition of the shape factors. The combined effect of cohesion and eccentricity, is shown to give ever higher bearing capacity loads compared to the Eurocode.

Fig. 15

Comparative diagrams of the load-settlement curves of strip shallow footings (with width B = 2 m) for different normalized eccentricities e/B (0; 0.125; 0.25), on two internal friction angles φ = 25° and 35° (from top to bottom) and two cohesion values c = 0 and c = 10 kPa. The figure compares: a the numerical solution for e/Β = 0 in the black dashed line to the Eurocode ultimate load in the black solid line; b the numerical solution for e/Β = 0.125 in the dark-grey dashed line to the Eurocode ultimate load in the dark-grey solid line; and c the numerical solution for e/Β = 0.125 in the light-grey dashed line to the Eurocode ultimate load in the light-grey solid line

Fig. 16

Contour plot of the total displacement magnitude U (in m) showing the uplift at the left of the strip footing under eccentric vertical loading with e/B = 0.25

The bearing capacity for strip shallow foundations reduces to equation (1) for: (a) vertical loads deviating from the footing axis (i_c = i_q = i_γ = 1); (b) horizontal footing base (b_c = b_q = b_γ = 1); and (c) B′/L = (B − 2·e)/L = 0 (s_c = s_q = s_γ = 1), with the sole difference that the bearing capacity width term works on the active working width B′ = (B − 2·e) rather than the total "B". Hence, the aforementioned revision of the shape factors needs to account for the eccentricity effect by giving values greater than unity for strip footings with B′/L = 0. The overburden shape factors also depend on the eccentricity e/B and L/B ratios, as eccentricity ratios e/B = 0.25 can reduce the bearing capacity by half, while square footings (L/B = 1) fail at loads considerably higher (by more than 100%) compared to those of strip footings (L/B →  + ∞), for D/B = 1 and typical internal friction values φ = 25° ÷ 35°.

Hence, the shape factors need to be revised to account for the excess load stemming from: (a) the eccentricity of the loading; and (b) the L/B ratios. A following section introduces the revised formulae giving the shape factors as a function of the internal friction angle and the L/B ratio.

4 Proposed Formulae

This section develops revised formulations, based on the aforementioned observations of Sect. 3, for: (a) the bearing capacity cohesion factor "N_c"; (b) the bearing capacity surcharge factor "N_q"; (c) the shape factors ("s_c", "s_q", "s_γ") accounting for the combined effect of cohesion and eccentricity. It is noted that the eccentricity effect is included in the ensuing formulations on the basis of 2D numerical finite element results, later extrapolated for the rectangular footings.

4.1 Revised Bearing Capacity Cohesion Factor "N _c"

The bearing capacity cohesion factor "N_c", traditionally given by $N_{c} = \left( {N_{q} - 1} \right) \cdot \cot \varphi$ (Prandtl, 1920), where $N_{q} = \tan^{2} \left( {45^{^\circ } + {\varphi \mathord{\left/ {\vphantom {\varphi 2}} \right. \kern-\nulldelimiterspace} 2}} \right) \cdot e^{\pi \cdot \tan \varphi }$ (Reissner, 1924), was shown to systematically underestimate the bearing capacity based on the observations of paragraph §3.3, for cohesion values c > 0. This effect was more pronounced at low internal friction values where the importance of the cohesion bearing capacity term becomes important (e.g., Fang, 2013), with the numerical solution giving ultimate loads up to 35% higher compared to the EC-7 methodology.

The bearing capacity cohesion factor "N_c" can be computed for strip footings on the ground surface via numerical analyses, by first eliminating the term of width. Subtracting the bearing capacities for c > 0 and c = 0 gives the effect of cohesion. The regression analysis associates the numerically computed bearing capacity factor "N_c" to the internal friction angle "φ", by means of the following formula:

$$N_{c} = \left[ {e^{1.287 \cdot \pi } \cdot \tan^{2} \left( {45^{^\circ } + {\varphi \mathord{\left/ {\vphantom {\varphi 2}} \right. \kern-\nulldelimiterspace} 2}} \right) \cdot \tan \varphi } \right]^{0.828}$$

(5)

Figure 17 compares the proposed formula shown in the black solid line against the Eurocode bearing capacity factor "N_c", based on the solution of Prandtl (1920), in the grey solid line. The proposed formula is shown to systematically produce higher bearing capacity cohesion factors "N_c" compared to the Eurocode methodology. The numerically computed bearing capacity factors "N_c", shown in the black solid circles laying systematically higher from the Eurocode "N_c" values, align perfectly (R² = 0.99) with the graphical representation of equation (5). For a null internal friction angle, the cohesion bearing capacity factor "N_c" is equal to $N_{c} = 1.1 \cdot \left( {\pi + 2} \right)$. This "N_c" value is 10% higher compared to Prandtl’s solution, as the numerical analyses work on an unbending footing (of infinite stiffness and strength) rather than on a fully flexible footing of null stiffness.

Fig. 17

Comparative diagram of the bearing capacity cohesion factor "N_c" for strip footings on the ground surface (D = 0) over a wide range of friction angles. The figure shows: a the computed "N_c" via numerical analyses in Simulia Abaqus in the black solid circles; b the proposed formula for "N_c", working on eq. (5), in the black solid line; and c the Eurocode "N_c" values, based on the solution of Prandtl (1920), in the grey solid line

4.2 Revised Bearing Capacity Surcharge Factor "N _q"

The bearing capacity surcharge factor "N_q", traditionally given by $N_{q} = \tan^{2} \left( {45^{^\circ } + {\varphi \mathord{\left/ {\vphantom {\varphi 2}} \right. \kern-\nulldelimiterspace} 2}} \right) \cdot e^{\pi \cdot \tan \varphi }$ (Reissner, 1924), was shown to systematically underestimate the bearing capacity based on the observations of paragraph §3.4 for embedment D > 0. Based on Fig. 9, as the embedment increases the numerical solution gives ever-higher ultimate loads compared to the counterpart loads computed by means of the EC-7 methodology. This effect was more pronounced at low internal friction values, with the numerical solution giving ultimate loads up to 55% higher than the Eurocode.

The bearing capacity surcharge factor "N_q" can be computed for strip footings embedded on cohesionless geomaterials via numerical analyses, by first eliminating the term of width. Subtracting the bearing capacities for D > 0 and D = 0 gives the effect of surcharge. The regression analysis associates the numerically computed bearing capacity surcharge factor "N_q" to the internal friction angle "φ":

$$N_{q} = 2.447 \cdot e^{4.368 \cdot \tan \varphi }$$

(6)

Figure 18 compares the proposed formula of eq. (6) depicted in the black solid line against the Eurocode bearing capacity surcharge factor "N_q", based on the solution of Reissner (1924), in the grey solid line. The proposed formula is shown to systematically produce higher "N_q" values compared to the Eurocode methodology. The numerically computed bearing capacity factors "N_q", shown in the black solid circles laying systematically higher from the Eurocode "N_q" values, align perfectly (R² = 1) with the graphical representation of equation (6).

Fig. 18

Comparative diagram of the bearing capacity surcharge factor "N_q" for strip footings embedded on a cohesionless geomaterial (c = 0), over a wide range of friction angles. The figure shows: a the computed "N_q" via numerical analyses in Simulia Abaqus in the black solid circles; b the proposed formula for "N_q", working on eq. (6), in the black solid line; and c the Eurocode "N_q" values, based on the Reissner’s solution (1924), in the grey solid line

4.3 Revised Shape Factors

The shape factors describe the dependence of the bearing capacity on the eccentricity ratio e/B and the shape of the footing described by means of the B/L ratio. The shape factor "s_γ", associated with the width term, can be computed straight forward from the computed bearing capacities of shallow footings resting on the surface (D/B = 0) of a cohesionless soil. The solution is shown to depend on the active working width B′ = (B − 2·e):

$$s_{\gamma } = \frac{{\left( {1 - 2.335 \cdot \frac{e}{B}} \right)}}{{\left( {1 - 2 \cdot \frac{e}{B}} \right)}} \cdot \left\{ {1 + \frac{B}{L} \cdot \left[ { - 0.137 + 1.325 \cdot \left( {\tan \varphi } \right)^{3.146} } \right]} \right\}$$

(7)

The term (1–2.335·e/B)/ (1–2·e/B) gives the dependence of the safety factor "s_γ" on the load eccentricity for e/B ≤ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$ ratios, while the remaining term 1 + B/L·[− 0.137 + 1.325·(tanφ)^3.146] gives the dependence on the shape of the footing described by means of the B/L ratio and the internal friction angle (φ). Expression (7) shows a minimal effect of the eccentricity on the shape factor "s_γ" for e/B ≤ ${\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 6}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$6$}}$ ratios, while this effect tends to become important as the e/B ratio increases.

Figure 19 compares the proposed formula of eq. (7) against the numerical results of the shape factor "s_γ". The Eurocode formula working on s_γ = 1 − 0.3·Β′/L′ acts as baseline for comparison. The comparative diagrams of the shape factor "s_γ" study the effect of: (a) L/B for rectangular footings on the surface of a cohesionless geomaterial (c = 0), under central loading (left diagram); and (b) e/B for strip footings on the surface of a cohesionless geomaterial (c = 0), under eccentric vertical loading (right diagram), over a wide range of friction angles. The numerical results depicted in symbols (circles, squares, rhombi, triangles, crosses and X-marks) are shown to compare well to the proposed formula (7).

Fig. 19

Comparative diagrams of the shape factor "s_γ": a for rectangular footings on the surface of a cohesionless geomaterial (c = 0) under central loading, over a wide range of friction angles (left figure); and b for strip footings on the surface of a cohesionless geomaterial (c = 0) under eccentric vertical loading, over a wide range of friction angles (right figure). The numerical results depicted in symbols (circles, squares, rhombi, triangles, crosses and X-marks) compare well to the proposed formula (7). The figures also include the Eurocode shape factors acting as baseline for comparison

The shape factor "s_c" describes the dependence of the bearing capacity cohesion term from the eccentricity (e/B) and the footing shape (B/L). This parameter describes the standalone effect of the eccentricity and shape on the term of the cohesion, by first eliminating the effect of the width term; this is performed by normalizing: (a) the decrease in the bearing capacity due to a non-null eccentricity; and/or (b) the increase in the bearing capacity due to a non-null B/L ratio, with the difference between the bearing capacities of two shallow footings (with zero eccentricity) with one resting on the surface of cohesionless soil (c = 0) and the other resting on the surface of cohesive soil with c > 0. The shape factor "s_c" works by means of the following formula:

$$s_{c} = \left( {1 + \lambda_{1} \cdot \frac{e}{B}} \right) \cdot \left( {1 + \lambda_{2} \cdot \frac{B}{L}} \right)$$

(8.a)

$$\lambda_{1} = - 2.028 - 0.396 \cdot \ln K_{p} + 1.188 \cdot \left( {\ln K_{p} } \right)^{2} - 0.566 \cdot \left( {\ln K_{p} } \right)^{3}$$

(8.b)

$$\lambda_{2} = 1 + \left( {0.216 \cdot e^{3.185 \cdot \tan \varphi } } \right) \cdot \left[ {1 - 0.393^{{\left( \frac{B}{L} \right)}} } \right]$$

(8.c)

where K_p denotes the passive lateral earth pressure coefficient given by K_p = tan²(45° + φ/2). The term (1-λ₁·e/B) gives the dependence of the safety factor "s_c" on the load eccentricity, while the remaining term 1 + λ₂·B/L gives the dependence on the shape of the footing. Note that the multiplying factors λ₁ and λ₂ are functions of the internal friction angle and the B/L ratio. Expression (8) gives positive shape factors "s_c" for the parameters range (φ = 20° ÷ 40°, B/L = 0 ÷ 1) examined in this study.

Figure 20 compares the proposed formula of eq. (8) against the numerical results of the shape factor "s_γ". The Eurocode formula working on s_c = [(1 + Β′/L′·sinφ)·K_p·exp(π·tanφ) − 1]/[K_p·exp(π·tanφ) − 1] acts as baseline for comparison. The comparative diagrams of the shape factor "s_c" study the effect of: (a) L/B for rectangular footings on the ground surface, under central loading (left diagram); and (b) e/B for strip footings on the ground surface, under eccentric vertical loading (right diagram), over a wide range of friction angles. The numerical results depicted in symbols (circles, squares, rhombi, triangles, crosses and X-marks) are shown to compare well to the proposed formula (8).

Fig. 20

Comparative diagrams of the shape factor "s_c": a for rectangular footings on the ground surface under central loading, over a wide range of friction angles (left figure); and b for strip footings on the ground surface under eccentric vertical loading, over a wide range of friction angles (right figure). The numerical results depicted in symbols (circles, squares, rhombi, triangles, crosses and X-marks) compare well to the proposed formula (8). The figures also include the Eurocode shape factors acting as a baseline for comparison

Finally, the shape factor "s_q" describes the standalone effect of the eccentricity and shape on the term of the surcharge, by first eliminating the effect of the term; this is performed by normalizing: (a) the decrease in the bearing capacity due to a non-null eccentricity; and/or (b) the increase in the bearing capacity due to a non-null B/L ratio, with the difference between the bearing capacities of two shallow footings (with zero eccentricity) with one resting on the ground surface and the other resting on depth D > 0 of a cohesionless geomaterial. The shape factor "s_q" works by means of the following formula:

$$s_{q} = \left[ {1 - 0.516 \cdot \tan^{2} \left( {45^{ \circ } + \frac{\varphi }{2}} \right) \cdot \frac{e}{B}} \right] \cdot \left[ {1 + 0.497 \cdot \tan^{2} \left( {45^{ \circ } + \frac{\varphi }{2}} \right) \cdot \frac{B}{L}} \right]$$

(9)

The term [1 − 0.516· tan²(45° + φ/2)·e/B] gives the dependence of the safety factor "s_q" on the load eccentricity, while the remaining term [1 + 0.497· tan²(45° + φ/2)·B/L] gives the dependence on the shape of the footing.

Figure 21 compares the proposed formula of eq. (9) against the numerical results of the shape factor "s_q". The Eurocode formula working on s_q = (1 + Β′/L′·sinφ) acts as baseline for comparison. The comparative diagrams of the shape factor "s_q" study the effect of: (a) L/B for rectangular footings embedded at depth D, under central loading (left diagram); and (b) e/B for strip footings embedded at depth D, under eccentric vertical loading (right diagram), over a wide range of friction angles. The numerical results depicted in symbols (circles, squares, rhombi, triangles, crosses and X-marks) are shown to compare well to the proposed formula.

Fig. 21

Comparative diagrams of the shape factor "s_q": a for rectangular footings embedded at depth D of a cohesionless geomaterial (c = 0) under central loading, over a wide range of friction angles (left figure); and b for strip footings embedded at depth D of a cohesionless geomaterial (c = 0) under eccentric vertical loading, over a wide range of friction angles (right figure). The numerical results depicted in symbols (circles, squares, rhombi, triangles, crosses and X-marks) compare well to the proposed formula (9). The figures also include the Eurocode shape factors acting as a baseline for comparison

5 Summary and Conclusions

This paper studied the bearing capacity of shallow strip and rectangular footings on cohesive soils under eccentric loads, by means of two- and three-dimensional numerical analyses in Simulia Abaqus. It built on the traditional bearing capacity equation by further developing revised expressions of the bearing capacity and shape factors. The soil was described by means of the Mohr–Coulomb failure criterion, while the footing remained always elastic and undeformed. The soil Young’s modulus is inconsequential, based on its negligible effect on the bearing capacity.

The model was initially verified against Prandtl’s analytical solution for fully flexible strip footings resting on the ground surface. The flow rule and interface friction angle "δ" were calibrated in order for the numerically computed bearing capacity to match the capacity computed by means of the Eurocode methodology. The numerical bearing capacities were shown to match the EC-7 counterpart capacities for a typical ground-footing friction angle δ = ${\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$·φ and a null dilation angle ψ ≈ 0 for the soil. Use of a finite dilation angle (0 ≤ ψ ≤ φ) gives ever-higher bearing capacity values. Soils at failure work on zero dilation, by thus justifying the use of a non-associated flow rule. Rough soil-concrete footing base interfaces also worked on friction angles (δ) ranging from ${\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$·φ to φ, by thus placing the calibrated value of δ = ${\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$·φ at the lower bound. Hence, the approximations of the numerical solution calibrated to match the EC-7 methodology were found to be relevant to engineering practice and ground response. Use of an associated flow rule, working on ψ = φ, and the complete roughness of the strip footing (δ = φ) gives considerably higher bearing capacity values as compared to the previous calibration and thus may work on the unsafe side.

Based on the results of the numerical investigation presented in this paper, the following conclusions can be drawn:

• (1) As the soil cohesion increases, the numerical solution diverges from the EC-7 methodology; this effect becomes more pronounced at low internal friction values, where the numerical solution gives ultimate loads up to 35% higher compared to the EC-7 counterpart loads.

• (2) As the embedment increases, the numerical solution diverges from the EC-7 methodology; this effect is more pronounced at low internal friction values, with the numerical solution giving ultimate loads up to 55% higher compared to the Eurocode.

• (3) As the dilation angle (ψ) of the soil increases, the numerical solution gives ever-higher ultimate loads compared to the counterpart loads computed by means of the EC-7 methodology. The increase in the ultimate load exceeds 23% for the associated flow rule working on ψ = φ.

• (4) The ultimate load of shallow footings, resting on soils experiencing strain-softening, depends on the residual internal friction angle rather than on the initial value. The friction angle damage decelerates, as the friction angle continues to degrade towards its residual value, until it reduces fully on it with increasing settlement.

• (5) As the eccentricity (e/B) increases, the bearing capacity decreases. The numerical solution gives ultimate loads up to 60% higher as compared to the counterpart loads computed by means of the EC-7 methodology. This observation is in line with the works of Michalowski and You (1998) and Pham et al. (2019).

• (6) As the shape ratio (L/B) of the footing transitions from unity to infinity, the bearing capacity decreases towards its limiting value for the case of strip footings. The numerical solution gives bearing capacity values up to 40% higher as compared to the bearing capacities computed by means of the EC-7 methodology.

The paper proposes revised formulas for the bearing capacity cohesion factor "N_c", bearing capacity surcharge factor "N_q" and the shape factors ("s_c", "s_q", "s_γ"), by thus enhancing the accuracy of the bearing capacity equation.