1 Introduction

Stability analysis of tunnel is one of the most crucial requirements for the successful completion of tunnelling projects. The key geological factors that directly influence the stability of tunnels are mechanical properties of the rock mass, in situ stress environment and groundwater influx through the discontinuities (Panthi 2012; Bahaaddini et al. 2016; Sazid and Ahmed 2019). The discontinuities (joints) are the most common type of geological structure found in rockmass and it affects the mechanical behavior of the rock mass (Jia and Tang 2008). Most rock masses are discontinuous over a wide range of scales (from cm to m) and there are two major sources of discontinuities exist in case sedimentary rocks, i.e. the bedding planes and joints, the intersection of which forms the ‘‘blocky’’ rock mass. These discontinuities are fractured surfaces along or across which there has been little or no displacement and many catastrophes during or after tunnel construction are closely related to joints (Das et al. 2017a; Yang et al. 2019). The mechanical behavior of jointed blocks with non-persistent joints is more complicated than having persistent joints. The mechanical behavior of the jointed rockmass is governed by the number of joint sets, joint orientation, infilling materials, joint roughness joint spacing, and whether the joints are open or closed, etc. (Fan et al. 2015).

Generally, several joint sets occur together in rockmass and for this reason, the rock mass is broken up into a blocky structure. Normally, the joint strength is much less than the intact rock strength, hence their (joints) contribution during a failure of the rockmass is very high. The two most important effects of joints are: (a) their presence itself decreases the overall rockmass strength and (b) initiation of new discontinuities via linkage of other cracks which further decreases the rockmass strength. Also, the joints allow the rock blocks to slide along the joint surface. For these reasons, jointed rockmass displays complex mechanical behavior like anisotropy, irreversible strain, and strongly path-dependent stress–strain relationships (Madkour 2012). Hence, determining the effects of joints on the mechanical behavior of a rock mass is an important factor for the safe design of underground structures (Jaeger et al. 2007; Wang et al. 2011; Singh et al. 2013, 2016; Bahaaddini et al. 2016; Li et al. 2016; Panthee et al. 2018a, b).

There are four basic methods to study the deformation and examine the stability of underground tunnels i.e. analytical method, empirical method, Physical method, and numerical methods. All four methods have their inherent advantages and disadvantages. The analytical methods consist of equations that are used to determine the stress and deformation around circular openings but they can not provide satisfactory solutions for complex geometries (Kirsch 1898; Brady 1977). On the other hand, the empirical methods are based on past experiences, reported case studies, and rock mass classification systems. These methods do not comprise all the factors influencing the stability of the underground opening. They only use a few geomechanical properties of the rock mass to deliver an estimated solution for the rock support system design (Abdellah et al. 2018). Also, physical methods are very laborious and time-consuming method. They also have many other limitations, like the proper selection of structural models, the nonlinearity of rocks, scale effect, high experimental setup cost, etc. (Yang et al. 2010; Das et al. 2017b). That is why these methods are widely replaced by numerical methods. The numerical methods are a powerful, reliable, and robust technique that can also handle very complex geometries. They can also be adopted before actual excavation, to select the optimum design sequence (Lee and Pietruszczak 2008; Bobet et al. 2009; Bahaaddini et al. 2016; Sazid 2017).

Shen and Barton (1997) present the failure zone around the tunnel in jointed rockmass with the help of a distinct element code. They studied three different types of zones created around the tunnel i.e. failure zone, open zone, and shear zone with different joint spacing and orientation. Jia and Tang (2008) numerically investigated the influence of layered joints dip angle and the lateral pressure coefficient on the stability of tunnel in a jointed rock mass and concluded with the changes in the failure modes of the tunnel. Fuenkajorn and Phueakphum (2010) performed extremely simplified conditions of joints and stress states in numerical simulation tests to assess the effects of tunnel depth, joint spacing/orientation on the maximum unsupported span of a shallow tunnel under static and cyclic loading condition. Nikadat et al. (2016) performed numerical tests to observe the effects of joint spacing/dips on the stress distribution around rock tunnels and concluded that the tensile and compressive tangential stresses at the tunnel boundary are inversely proportional to the joint spacing. Panthee et al. (2016) numerically studied the deformation of tunnel (Kulekhani III hydroelectric project in Lesser Himalaya, Nepal) due to structurally controlled joints (mainly joint persistence and spacing). Their results showed that the slate and garnetiferous schist with high persistence and low joint spacing develop huge plastic zone around the tunnel. Whereas marble and quartzite with low persistency and low joint spacing create roof failure condition. Yang et al. (2019) carried out a tunnel physical model experiment to investigate the effect of non-persistent joints on a rock mass, with seven joint inclinations tested under uniaxial compression. Although researchers have studied the influences of rock joints on the stability of underground structures, either numerically or experimentally, the failure mechanism of jointed rockmass in underground excavations is still far from being satisfactory. Hence, a sound understanding of this subject is highly required for appropriate support system design and safe excavation.

This paper discusses the effect of closely spaced non-persistent joints on rockmass deformation during the construction of a tunnel in weak jointed rockmass. To present the author's views, a similar situation has been selected in the Himachal Himalayan region, India. The study comprises the extensive field study, laboratory testing of mechanical properties of the intact rock samples, numerical modelling, and comparison of data from the existing tunnel with other similar project sites reported by researchers.

1.1 A general overview of the study area

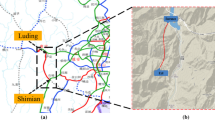
The project, “Kainchi-mod neirchowck tunnel” is located in Kiratpur-Neirchowck national highway in the south of the Sutlej River, Bilaspur district of Himachal Pradesh, India (lesser Himalayan rock formation). The twin tunnels, trending N40°E were constructed across the gray sandstone (GS) and maroon sandstone (MS) of Lower Dharamshala formation of Sirmur Group (Eocene-Miocene age). The rocks in the study area have suffered extreme deformation and are heavily influenced by jointing. The two asymmetric horseshoe-shaped parallel tunnels are 1.8 km in length and they are referred to as the main tunnel (MT) and escape tunnel (ET) with diameters (B) of 12 m and 8.5 m, respectively (Fig. 1). The grain size of these sandstones varies from fine to very fine. The heading and benching excavation technique is adopted in the MT and the full-face excavation method is adopted for ET. Both tunnels are excavated by the drilling and blasting methods. The SW portal of both the tunnels is kept at an elevation of 719.84 m while the northeastern portal is at 680.42 m above sea level.

Fig. 1
figure 1

Location of the study area, a South-west (SW) portal of the twin tunnel, b Tunnel face at 12 + 803 m chainage from the SW portal (modified after Das et al. 2017a, b)

Full size image
Fig. 2
figure 2

Stress–strain curve of gray and maroon sandstone

Full size image

2 Methodology

2.1 Intact Rock Properties

Intact rock samples were collected from the study area and tested in the laboratory to determine its mechanical properties. Tests like the Uniaxial Compressive Strength (UCS) (σci) (Fig. 2), Brazilian tensile strength (σt), Elastic modulus (Eci), P-wave velocity (VP), Poisson's ratio (υ), Density (ρ), and Point load index (PLI), were conducted based on methods prescribed by the ASTM/ISRM standards and the results are tabulated below (Brown 1981a; ASTM 1985; ASTM:E132-04(10) 2011; ASTM:D7012-14 2014).

2.2 Rock Mass Characteristics

The Bieniawski, (1989)’s rock mass rating (RMR) at chainage 12 + 803 m from the SW portal is determined. The UCS of the intact rock ranging between 50 and 70 MPa (rating 7), rock quality designation (RQD) is varied between 70 and 85 (rating 17), joint spacing is varied between 0.08 m and 0.5 m (rating 8), condition of discontinuity (persistency rating 2, aperture rating 1, joint roughness rating 3, infilling rating 4, weathering of discontinuity surface rating 5), and dry water condition (rating 15). The rocks contain three dominant joint sets. The attitudes of the joints J1, J2, and J3 are S42°E/62°, N40°W/20°, and S83°E/78°, respectively. The J3 joints were very few in numbers. Considering the ratings for orientation of discontinuities the RMR varies between 40 and 60, i.e. “class III rock” or “Fair quality rockmass” (Fig. 3). The Hoek and Brown, (1997)’s geological strength index (GSI) is based on visual inspection of geological conditions for both hard and weak rock masses. A peak GSI value of 55 (fair quality rockmass) is directly calculated from the field observations.

Fig. 3
figure 3

a Bedding plane with joint orientations, b joint density (spacing, persistency), c RQD measurements d joint aperture with the infilling study

Full size image

2.3 Numerical Analysis

The numerical method is a powerful technique to replace the problem with an approximate problem which is easier to be solved, with the solution as close as possible to the original solution (Nikadat et al. 2016). There are several numerical methods available to examine the stability of a tunnel, among which the finite element method (FEM) is the most effective and popular choice in dealing with anisotropic and nonlinear problems (Sellers and Klerck 2000; Yang et al. 2010, 2015; Zhang et al. 2017; Das and Singh 2020). The FEM is used for solving science and engineering problems that are described by partial differential equations (PDE) or can be formulated as functional minimization. Almost any physical problem can be expressed by its governing equation and boundary conditions in some PDE’s. But these PDE’s are difficult to solve. The FEM can converts the PDE’s into algebraic equations by taking approximations which are easy to solve.

The FEM involves four fundamental steps; domain discretization, local approximation, global matrix assembly, and solution (Nikadat et al. 2016). The FEM converts the whole problem domain into a number of “finite elements” with a regular shape and fixed number of nodes, that converts PDE into algebraic equations and give results, taking into consideration of all the algebraic equations from all finite elements. One of the major advantages of using FEM is that the FEM can handle anisotropic as well as non-homogeneous material with complex geometries and complex boundary conditions.

2.3.1 Model Description

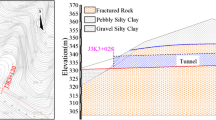
This study concentrates on the effect of joint density in tunnel boundary deformation and for this purpose, a 2D finite element (FE) software “Phase2 v.8.0” is used (Rocscience Inc. 2016). To model the rockmass, three-node triangular elements (or plane elements) were used to mesh the problem domain. The triangular-shaped elements are easy to develop and they can accommodate irregular boundaries. Almost any plane structural shape can be discretized with triangular finite elements, though individual triangular finite elements may be different in size (Carroll 1998). The graded mesh type is used with a gradation factor of 0.1. In Fig. 4, the model geometry is shown, i.e. the dimensions of tunnel, topographic undulation, and lithology variation, etc. Two sets of ubiquitous joints were explicitly modeled as a Joint boundary, i.e. J1 and J2, and they were assigned strength and stiffness properties.

Fig. 4
figure 4

Tunnel cross-section at chainage 12 + 803 m from the SW portal. (yellow: J1 Joint set, dark green: J2 joint set)

Full size image

The numerical model represents a plane strain analysis which assumes that the excavations are of infinite length in the out-of-plane direction, and therefore the strain in the out-of-plane direction is zero. To solves the matrix representing the system of equations defined by our model, the “Gaussian Elimination Method (GEM)” is used. This method is also known as the “Row Reduction Method (RRM)”, which is an algorithm in linear algebra for solving a system of linear equations. It is usually understood as a sequence of operations performed on the corresponding matrix of coefficients.

2.3.2 Boundary Condition

It is well known to all that the tunnels are often located in an essentially infinite or semi-infinite rock mass. The "boundaries" of numerical models are often just some artificial cutting planes which separate our region of interest from the rest of the rock mass (Shen and Barton 1997). It is clear from the previous literature that the most affected area around an excavation in terms of stress redistribution and resulting strain is approximately two to three times the diameter of the opening (Brown 1981b; Hoek et al. 2008; Yang et al. 2017). Keeping this in consideration, the outer boundary was constructed three times the diameter of the opening. Fixed restraints were applied to the bottom and sidewalls of the model (i.e. no movement in X and Y directions), while the top ground surface is left free. As reported by Zhang (2013), complex topographic conditions such as hills or valleys, the rock mass is assumed to be under gravitational load. Hence, the model used in this study are assumed to be under gravity field stress and the actual ground surface is selected. The field stress ratio “k” is assumed to be 1.

2.3.3 Material Model

The generalized Hoek and Brown failure criterion (Hoek et al. 2002) for rock mass is used, which is expressed as

$${{\sigma }^{{\prime}}}_{1}={{\sigma }^{{\prime}}}_{3}+{{\sigma }^{{\prime}}}_{\text{ci}}{\left({m}_{b}\frac{{{\sigma }^{{\prime}}}_{3}}{{{\sigma }^{{\prime}}}_{\text{ci}}}+s\right)}^{a}$$
(1)

where \({\sigma }_{1}^{{\prime}}\) and \({\sigma }_{3}^{{\prime}}\) are the major and minor effective principal stress respectively, \({\sigma }_{\mathrm{ci}}^{^{\prime}}\) is the UCS of intact rock, and \({m}_{\mathrm{b}}\) is the reduced value of material constant mi. Here, \({m}_{\mathrm{b}}\) can be calculated according to the following equation:

$${m}_{\mathrm{b}}={m}_{\mathrm{i}}\mathrm{exp}\frac{GSI-100}{28-14D}$$
(2)

where mi is the Hoek–Brown rock material constant, which is obtained from triaxial tests on rock cores, and GSI is the geological strength index.

In Eqs. (3) and (4), s and a are constants for the rock mass and are obtained by the following equations:

$$s=\mathrm{exp}\frac{GSI-100}{9-3D}$$
(3)
$$a=\frac{1}{2}+\frac{1}{6}\left({\mathrm{e}}^{-GSI/15}-{\mathrm{e}}^{-20/3}\right)$$
(4)

where D is the disturbance factor that depends on whether the rock mass has been subjected to blast damage and stress relaxation, and it varies from 0 to 1. The geomechanical properties of rock used in the numerical simulation are described in Table 1. The properties of loose unconsolidated overburden material were not determined in the laboratory, hence their values were taken from Ameri et al. (2009).

Table 1 Physico-mechanical properties of the intact rock samples
Full size table

For static FE analysis, the equilibrium equation in the following matrix form

$$K\Delta U = P - F$$
(5)

where P is the vector of applied loads, K is the non-linear stiffness of the spring element, ΔU is the vector of current nodal displacements, and F the vector of internal forces. FE analysis involves solving the equation above for ΔU. For the n-th load step, the equation is often solved through iterations of the form:

$$K\Delta U_{{\left( {i + 1} \right)}} = P_{\left( n \right)} - F_{\left( i \right)} \,\,\,\,\,\,\,\,for\,\,iterations\,\,\,i = 0,1,2,3.......$$
(6)

2.3.4 The FE Convergence Criteria

The non-linear response of a spring to applied load is depicted in Fig. 5. Here, the displacement Un and Un+1 are assumed at load Pn and Pn+1, respectively. Before applying the new load step, the resisting (internal) force F(0) in the spring due to its current deformed state is in equilibrium with the applied (external) load F(n).

Fig. 5
figure 5

Typical non-linear response of a spring element to applied loads

Full size image

The tangent stiffness, K(0) at the origin of the displacement-load curve is the initial stiffness, which will be used throughout all iterations for the new load step. Accordingly, the current displacement increment and updated solution can be expressed as

$$\left\{ \begin{array}{l} K_{\left( 0 \right)} \Delta U_{\left( 1 \right)} = P_{{\left( {n + 1} \right)}} - F_{\left( 0 \right)} \hfill \\ \Delta U_{\left( 1 \right)} = K_{\left( 0 \right)}^{ - 1} (P_{{\left( {n + 1} \right)}} - F_{\left( 0 \right)} ) \hfill \\ U_{{\left( {n + 1} \right)}} = U_{\left( n \right)} + \Delta U_{\left( 1 \right)} \hfill \\ \end{array} \right\}$$
(7)

From the current displacement state, the internal force, F(1), in the spring can be calculated. At this stage, the current load imbalance is quite large. From the figure above it is evident that a key aim of the iterations is to reduce the load imbalance to zero, or at least a very small number. Similarly, with continued iterations, not only does the load imbalance P(n+1) − F(1), grow smaller and smaller, the displacement increments ΔU(i) also approach zero, and updates of U(n+1) approach the true solution. In order not to iterate unnecessarily long, we can decide to terminate calculations when the results are “sufficiently close” according to some stopping criteria. In the FE analysis, we used the Absolute Energy Criterion which is satisfied when

$$\left. {\left| {\frac{{\Delta U_{\left( i \right)}^{T} (P_{\left( n \right)} - F_{\left( i \right)} )}}{{\Delta U_{\left( 0 \right)}^{T} (P_{\left( n \right)} - F_{\left( 0 \right)} )}}} \right.} \right|\,\,< \,\,(specified\,\,\,energy\,\,\,tolerance)$$
(8)

For the present study, we have taken the maximum number of iteration as 500 with a tolerance of 0.001.

2.3.5 Joint Slip Criterion

The Barton-Bandis joint slip criterion is used in this study to model the joints (Barton 1973, 1976; Barton and Choubey 1977). The parameters used are the joint wall compressive strength (JCS), joint wall roughness coefficient (JRC), and residual friction angle (ϕr), which can be expressed by the following equation:

$$\tau = \sigma_{n} \tan \left[ {\phi_{r} + JRC\log_{10} \left( {\frac{JCS}{{\sigma_{n} }}} \right)} \right]$$
(9)

where τ is the shear strength of joint, σn is the normal stress. In this study, the joints are modeled assuming a linear elastic behavior. So, the influence parameters on the joint behavior (closed joints) are joint's normal stiffness (Kn) and shear stiffness (Ks) which is based on the following constitutive law:

$$\sigma_{n} = K_{n} v_{j}$$
(10)
$$\tau = K_{s} d_{h}$$
(11)

where Vj is the normal displacements, and dh is the shear displacement. The joint geometrical and mechanical properties are tabulated in Table 2. The joint's normal stiffness (Kn) and shear stiffness (Ks) values were taken from the literature with a similar jointed rockmass model (Shen and Barton 1997).

Table 2 Geometrical and mechanical properties of the joint set J1 and J2
Full size table

For unweathered joints, the JCS may be equal to the UCS of rock material (Singh and Goel 2011). Hence the JCS value 60 MPa is assigned for this study. The joint persistency is a measure of joint continuity along a given plane, which defines the ratio of joint length to total length along any joint plane. For the Parallel deterministic joint model, the persistence is a constant value and defines a uniform length of intact material between each joint segment. The joint persistency or continuity factor (k) can be calculated as follows:

$$k = \frac{{L_{j} }}{{L_{j} + L_{r} }}$$
(12)

where Lj is the lengths of the joint and Lr is the rock bridge. Both the joints have a persistence value of 20% or 0.20 (Field condition).

3 Results and Discussion

It is well known that the underground excavation in a jointed rock mass disturbs the initial equilibrium, and the rock mass stresses attempts to readjust itself until a new equilibrium is attained. During this stress readjustment process, some level of rock blocks displacement takes place. These displacements and block rotations are only possible across these discontinuities because they are sources of weakness in the rockmass (Tsesarsky and Hatzor 2006). In some cases, the stresses can not readjust themselves to form a stable, load resisting structure, and the rockmass around the tunnel fails. Mostly, this type of situation arises due to two major reasons i.e. when the induced stresses exceeded material strength at some locations, or when movements of rock blocks prevent the development of a stable geometric configuration. However, the second reason is more common in the case of shallow tunnel excavation. The formation of rock blocks of different shapes and sizes is primarily dependent on joint spacing and joint persistency.

3.1 Influence of the Joint Spacing

Joint spacing is one of the most important geological factors influencing rockmass deformation surrounding an excavation. Extensive field investigation shows that the deformational behavior of jointed rock mass around the tunnel opening is highly affected by the mechanical properties of intact rock and geometrical characteristics of joints, such as joint spacing, density, orientations, and predominant shear loading directions. FEM is employed, to study the influence of the closely spaced non-persistent joint network in a tunnel located in Himachal Himalaya (Kainchi-mod neirchowck highway tunnel). In numerical modeling, the geometrical properties of the J2 joint set were kept constant, while the J1 joint spacing was varied to observe the deformational characteristics. In the field, the average J1 joint spacing was recorded is 0.2 m. In this research, a parametric study is conducted to see the effect of J1 joint spacing (changed from js = 0.1 m to js = 0.7 m) on tunnel boundary deformation (Fig. 6). The results of the numerical simulations were validated with a simpler closed-form solution for an ideal situation, such as total vertical stress at a particular depth from the surface. The author also validated the model with Das et al., (2017a, b).

Fig. 6
figure 6

Main tunnel boundary deformation for varied J1 joint spacing, a 0.1 m, b 0.2 m, c 0.3 m, d 0.4 m, e 0.5 m, f 0.6 m

Full size image

The values of the failure zone volume increase significantly with the decrease in discontinuity spacing. The test results showed that the decrease in the joint spacing significantly increases the total displacement at the tunnel boundary and the maximum displacement is observed at the crown (Fig. 7). Similar observations were also reported by Yeung and Leong, (1997). This is because of the formation of small-sized blocks is observed due to closely spaced J1 joints. Zhang et al., (2020) reported that the discontinuities spacing controls the block sizes of the surrounding rock masses. Also, both the joint, J1 and J2 are placed in such a way that they can initiate kinematic sliding along those joint surfaces. For the rockmass with largly spaced joints, the stability is mostly governed by the key blocks. Their shapes permit free kinematic movement through either by key block sliding or falling into the opening (Boon et al. 2014). The sliding rock blocks smoothen the joint plane and the JRC is reduced. The reduced JRC value reduces the shear strength of the individual joint (see Eq. 9) and resulted in the overall strength reduction of the rockmass. It is also important to mention that the same joint spacing may also result in different block sizes and shapes w.r.t. different joint persistency values, leading to different degrees of tunnel stability.

Fig. 7
figure 7

Total displacement along tunnel boundary (data acquisition from the tunnel bottom left corner in an anticlockwise direction), for varied J1 joint spacing (i.r. 0.1 m, 0.2 m, 0.3 m, 0.4 m, 0.5 m,0.6 and 0.7 m)

Full size image

Based on the results, it can be concluded that there is an inverse relationship between tunnel boundary displacement and joint spacing and a correlation equation has been proposed between these parameters (see Fig. 8). As the joint spacing increases from 0.2 m to 0.6 m, accordingly, the total boundary displacement reduces. A further increase in the joint spacing above 0.6 m does not affect the change in total boundary deformation. This suggests that the influence of the joint spacing on tunnel deformation is negligible if the discontinuity spacing is more than or equal to 0.05 times the span of the tunnel (js/B ≥ 0.6/12). Based on the observation the following equation has been proposed:

$$\delta = 0.00162j_{s}^{ - 0.50}$$
(13)

where js is the joint spacing and δ is the maximum displacement.

Fig. 8
figure 8

Maximum displacement (m) versus joint spacing (m) for given set of parameters

Full size image

In jointed rockmass, the maximum deformation (δ) is dependent on the sliding of keyblocks formed due to the intersection of two joint sets. The keyblocks are expected to move into the tunnel, without support installation. According to the block theory, the size and shape of possible key blocks adjacent to the excavation can be predicted by the orientation of discontinuity, along with the geometry and alignment of the proposed tunnel. Depending upon joint characteristics and the in situ stress condition, the keyblock may be initially stable but could become unstable due to dynamic loading or the reduction of joint strength and slide into the tunnel (Fig. 9). There may be a few possible scenarios where potential keyblocks, can develop. The potential keyblocks are in a position to slide into the excavation, but will not because the available joint friction or joint shear strength on the faces in contact is sufficient for maintaining the equilibrium. The author is aware of the fact that many times the circumstances are unavoidable. Hence, the design engineers must ensure that the tunnel in jointed rockmass encounters in such a way that the blocks are in the shape of a “normal keystone”. This is because normal keystone are unlikely to fall into the tunnel. Whereas an “inverted keystone” may possess difficulty during tunnel construction. Kuszmaul, (1999) reported that the probability of failure (Pf) increases with the decrease in keyblock sizes (Fig. 10).

Fig. 9
figure 9

Formation of keyblock in jointed rockmass due to excavation

Full size image
Fig. 10
figure 10

Probability of failure as a function of the keyblock size fraction (modified after Kuszmaul, 1999)

Full size image

In Fig. 10, the parameter x represents keyblock size fraction, that varies between 0 and 1 or it can be expressed as,

$$x = \frac{minimum \, keyblock \, size \, of \, interest}{{maximum \, possible \, keyblock \, size \, \left( {i.e. \, B} \right)}}$$
(14)

where x minimum keyblock size of interest/maximum possible keyblock size (i.e. B).

3.2 Plastic Zone Distributions around the Tunnel

The Fig. 11 shows the plastic zone distributions and yielding elements around the tunnel (js = 0.2 m) after the excavation. The results confirm that the number of joints has a huge influence on the plastic zone distributions in a jointed rock mass. Also, the shape as well as the extent of the plastic zone is strongly controlled by the joint spacing. The yielding around tunnels occurs when the tangential stresses overcome to rocks strength. This is why the yielded elements have an important role in the analysis of the stability of underground excavation. If the rockmass surrounding the tunnel is devoid of joints then the plastic zone distribution around the tunnel is symmetric (Zhang et al. 2020). But in the case of the blocky rock mass, the plastic zone distribution becomes asymmetric (Fig. 11). The plastic zone areas in the discontinuity positions are large, which can be observed from the figure below. The more complex the joint structures in jointed rock masses are, the more unstable rock masses are formed. The radius of the plastic zone developed around the tunnel excavation is inversely proportional to the joint spacing (see Fig. 12). There are wedge-shaped rock blocks (potential keyblocks) formed at the tunnel crown, which are displaced under the force of gravity. In this situation, there is a chance of the creation of an overbreak zone in the roof.

Fig. 11
figure 11

Plastic zone distribution and yielded element contours around the main tunnel (js = 0.2 m)

Full size image
Fig. 12
figure 12

Joint spacing versus plastic zone radius (measured from the tunnel center) developed around the tunnel boundary

Full size image

4 Conclusion

This study intends to demonstrate the effect of closely spaced, non-persistent ubiquitous joint on tunnel stability considering a Himalayan tunnel as a case study. A parametric study is conducted to see the effect of J1 joint spacing (changed from js = 0.1 m to js = 0.7 m) on tunnel boundary deformation. And for that a 2D finite element method is employed to observe the effects. The salient findings of the analysis are drawn as follows:

  • Increasing the joint spacing from js/B = 0.1/12 to js/B = 0.6/12 significantly reduces the total displacement at the crown.

  • It is concluded that the displacements are dying out with a further increment of joint spacing js/B ≥ 0.6/12 and stable arching begins at the crown.

  • A correlation equation between joint spacing vs total displacement around tunnel periphery has been proposed based on the observed results.

  • For safe construction of a tunnel, the orientation of the tunnel should be selected in such a way that it produces the smallest maximum keyblock size in a given rock mass. Because, the probability of failure (Pf) increases with the decrease in keyblock sizes or increase in joint spacing (js).

  • The plastic zone distribution becomes more and more asymmetric with decreasing discontinuity spacing i.e. the height of loose zone above the excavation is controlled by the ratio between joint spacing and excavation span (js/B). Also, the radius of the plastic zone developed around the tunnel excavation is inversely proportional to the joint spacing.