Longitudinal Deformation Profiles for Sequentially Supported Deep Tunnels in Strain-Softening Hoek–Brown Rock Mass

Abstract

Numerical methods are commonly applied in tunneling design practice for the prediction of rock mass behavior during tunnel construction and for primary support dimensioning. Although the sequential excavation and primary support installation in phases is a complex three-dimensional problem, in practice it is usually approximated with plane strain simulations. For their correct application, the knowledge of the confinement level prior to the installation of the support is necessary and requires the construction of an accurate longitudinal deformation profile. This study presents a practical methodology for the estimation of the confinement level at the support installation position based on the execution and interpretation of a large number of plane strain, axisymmetric and 3D numerical simulations. All simulations incorporate sequential excavation and support cycles in confinement depended strain-softening Hoek–Brown rock mass. The results indicate the importance of the post-peak rock mass behavior and the influence of the installed support to the confinement level for both top-head and bench excavation and support stages.

1 Introduction

Numerical methods are commonly applied in tunneling design practice for the prediction of rock mass behavior during tunnel construction and for the dimensioning of the primary support. Although the sequential excavation and primary support installation in phases is a complex three-dimensional problem, in practice it is usually approximated with plane strain simulations, normal to the tunnel axis, where the effect of the rotation of the principal stresses axes near the tunnel face are accounted for by considering a fictitious internal pressure acting on the tunnel boundary. For their correct application, the knowledge of the confinement level prior to the installation of the support is necessary. The confinement level apart from the rock mass characteristics and in situ stress conditions is also correlated to the vicinity of the tunnel face, the geometry of the excavated section and the primary support scheme itself. The ground reaction curve (GRC) and the longitudinal deformation profile (LDP) is essential for the estimation of the confinement level.

The GRC can be estimated with various methods according to the numerical code used or the solution scheme. In the numerical approach, a gradual relaxation of the core of the un-supported section can be applied in plane strain models. The minor principal stress and the deformation at the crown of the excavation define the GRC. All modern two-dimensional numerical codes provide also the ability to establish axisymmetric models. With axisymmetric simulations the longitudinal deformation profile of an equivalent circular tunnel can be evaluated. Such models provide all the necessary information for the estimation of the confinement level prior to the installation of the support. Additionally, the sequential excavation and support of the tunnel can be incorporated in axisymmetric models. With that procedure, the significant influence of the supported section of the tunnel to the deformation at the vicinity of the tunnel face can be introduced to the LDP. The influence of the support to the LDP is generally ignored in the current design practice, with relevant impact to the support pressure estimation. This simplification is usually overcome with conservative support selection, often without adequate justification.

1.1 Background

The convergence-confinement method and particularly the construction of the ground reaction curve (GRC) have been discussed by numerus pioneer researchers. Benchmark solution methods described by Duncan Fama (1993), with small strain theory for Mohr–Coulomb medium with dilation, and Carranza-Torres (2004), with small strain theory for Generalized Hoek–Brown medium with dilation and brittle post peak residual strength, guided the research on this field. More resent works such as Vrakas and Anagnostou (2014), with large strain theory for Mohr–Coulomb strength envelope with dilation, and Lee and Pietruszczak (2008), for Mohr–Coulomb or Hoek–Brown strain softening medium with dilation, are notable. Alejano et al. (2009, 2010) examined numerically the influence of the strain softening behavior on the GRC with practical and detailed proposals regarding the estimation of the critical plastic strain for various rock masses.

The longitudinal deformation profile (LDP) was initially described for an elastic rock mass by Panet (1995). Measurements of deformations along the tunnel axis with respect the distance of the tunnel face were presented by Chern et al. (1998). An empirical best fit of a radial deformation—face vicinity equation was proposed by E. Hoek and presented by Carranza-Torres and Fairhurst (2000). Based on axisymmetric numerical simulations, Bernaud and Rousset (1996) introduced an implicit method that incorporates the stiffness of the lining on the determination of the LDP. The influence of the support on the stress relief factors was numerically investigated by Graziani et al. (2005) and the results were compared with monitoring data. The expected discontinuity of the longitudinal deformation profile at the tunnel face was firstly introduced by Vlachopoulos and Diederichs (2009) with a large number of numerical simulations on unsupported tunnels. With numerical modeling, Alejano et al. (2012) extended the Vlachopoulos and Diederichs (2009) approach to strain softening behavior and rock masses with a geological strength index 30 < GSI < 75. For supported tunnels, Vlachopoulos and Diederichs (2014) developed a sigmoid LDP function that includes face distance and support installation position. The aforementioned function requires the unknown maximum supported deformation that is related to the support installation position and the stiffness of the support. Finally, Oke et al. (2018) included a method to take into account the support installation proximity and stiffness on the Vlachopoulos and Diederichs (2009) LDP.

1.2 Motivation

Although the construction of LDP has been the subject of previous research by many authors offering rigorous, simplified and approximate solutions, numerical data and in situ measurements, a practical approach for a reliable and fast estimation of the relaxation of a supported tunnel in a strain softening rock mass is not well established.

This study presents a practical methodology for the estimation of the relaxation of supported tunnels in strain-softening rock mass, both for top-head and bench excavation and support stages. The suggested procedures result in the evaluation of the radial displacement and pressure at the support installation position, which are necessary components to be known for tunnel support dimensioning. The proposed methodology is based on the execution and interpretation of a large number of plane strain, axisymmetric and 3D numerical simulations with the three dimensional finite differences code FLAC 3D (Itasca Consulting Group Inc., 2017). The Hoek–Brown failure criterion is employed for both peak and residual rock mass strength. The transition from peak to residual strength follows a strain softening rule with confinement depended critical plastic strain. The post peak behavior of the rock mass is assumed to be brittle or abrupt strain softening for unconfined conditions with a gradual progression to ductile—perfectly plastic for a confining stress of the order of rock mass uniaxial compressive strength ($\sigma_{c}$), defined according to Hoek – Brown failure criterion (Hoek et al. 2002).

2 Tunnels, Rock Masses and Support

2.1 Tunnel Geometry and Support Selection Criteria

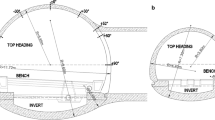
The geometry of the tunnel excavation is derived from the geometry of the final lining with provision of an additional free space for the installation of the primary support and the waterproofing, construction tolerances, expected convergence of the surrounding rock mass and possible acceptable over-excavations. The cross sections of the examined tunnels are presented in Fig. 1 and represent the geometry of typical two-lane single branch tunnels and vehicle escape tunnels, respectively. The excavation geometry derived from these typical cross sections, with 6.0 and 4.0 m external crown radius respectively, was introduced for the three-dimensional and plane strain models, while for the axisymmetric models an equivalent cylindrical excavation with 6.0 and 4.0 m radius was assumed. Although the actual excavation geometry varies for different primary support categories the impact on the numerical results is insignificant compared to the required effort to construct different 3D meshes for each support category. The thickness of the final lining is beyond the scope of the current research.

Fig. 1

Typical cross sections of the examined tunnels: a main tunnel, b vehicle escape tunnel

A crude support selection criterion was established in order to assign an appropriate primary support for each examined case based on the in-situ stresses and the rock mass strength and deformability. The criterion was based on the tunnel strain approach, presented by Hoek and Marinos (2000), which was adjusted for the current study according to the range of the strain levels estimated from a series of numerical simulations. For every combination of tunnel geometry, in situ stress and rock mass properties, a set of plane strain and axisymmetric simulations were carried out in order to determine the maximum strain of the unsupported tunnel and to confirm that the calculated deformations of the two approaches match. With the results of the aforementioned simulations, primary support categories A, B, C and D were assigned to the two-lane tunnel for percent strain $\varepsilon$ = 0–0.1%, 0.1–0.2%, 0.2–0.3% and > 0.3% respectively. The primary support used for the vehicle escape tunnel was based on the results of the two-lane tunnel. In cases were support classes A or B were selected for the two-lane tunnel, support class AB was applied at the vehicle escape tunnel, while for support type C and D for the two-lane tunnel, support class CD was introduced for the vehicle tunnel. Since the contribution of the steel sets – lattice girders and of rock bolts on the stiffness of the support scheme is minor compared to its total stiffness, only shotcrete was considered in the numerical simulations, with a Young’s modulus of 15 GPa and a Poisson’s ratio of 0.25. The aforementioned support classes are summarized in Table 1.

Table 1 Support classes used in numerical simulations

2.2 Rock Mass Quality and in situ Stress Assumptions

The strength of the intact rock is a nonlinear function of its confinement. The Hoek–Brown failure criterion incorporates such behavior with plenty of experience gained from practical applications. In conjunction with the characterization of the rock mass with the geological strength index-GSI (Marinos et al. 2007), the generalized Hoek–Brown criterion (Hoek and Brown 2019) creates a practical and powerful tool for the description of the rock mass strength in engineering practice. In order to cover a wide range of rock masses, a range between 10 and 100 MPa was selected for the uniaxial compressive strength σ_ci of the intact rock. Each case of intact rock strength was paired with a typical intact rock Young’s modulus $E_{i}$, $m_{i}$ value and dilation angle $\psi_{i}$ expressed as a function of the instantaneous equivalent friction angle $\phi_{i}$ of the Mohr–Coulomb strength criterion evaluated during the numerical solution. It is noted here that the true nature of each rock is much more complex than simply combining strength and deformability indices. It is believed however that the selected $\sigma_{ci}$ and $E_{i}$ values cover common combinations that can be found in a wide variety of rocks (e.g. Deere and Miller 1966). The selected values of $\sigma_{ci}$, $E_{i}$, $m_{i}$ and $\psi_{i}$ are summarized in Table 2. No disturbance factor was introduced, reflecting the modern excavation and blasting techniques employed to minimize rock mass damage.

Table 2 Selected values of $\sigma_{ci}$, $E_{i}$, $m_{i}$ and $\psi_{i}$

The fracturing of the rock mass was introduced with three $GSI$ values, i.e. $GSI$ = 30, 50 and 70, for each intact rock category. These values represent a disturbed, a very blocky and a blocky rock mass, respectively, commonly encountered in tunnels. Extremely high $GSI$ values were not examined since the structure of such rock masses requires numerical techniques that explicitly simulate joints. Conversely, extremely low $GSI$ values may lead to severe squeezing problems or are unlikely to be found in intact rocks with high strength.

For the three-dimensional models, tunnel depths of 100 m, 300 m and 600 m were considered while for the axisymmetric models tunnel depths varied from 50 to 600 m with 50 m intervals.

In all numerical simulations a rock mass unit weight of 25 kN/m³ was considered and a hydrostatic natural stress field.

3 Numerical Models

3.1 Simulation Approach

All the numerical simulations were carried out using FLAC 3D finite differences code. The external dimensions of the three-dimensional models were 90 m along the tunnel axis. In order to minimize the influence of the lateral model boundaries a minimum distance of five tunnel diameters on each side of the tunnel was selected vertically and horizontally. The actual geometry of the tunnels was used to create the 3D mesh. All the lateral external boundaries were fixed in the normal direction (zero velocities perpendicular to the external boundary faces) while a normal stress was applied at the top of the model in order to initialize the primary stress field of each case. For the three depths considered and the combinations of rock masses used, only the models with values of $\sigma_{c} /P_{o}$ between 0.2 and 1.3 were examined. Values below 0.2 were rejected in order to avoid squeezing problems and values above 1.3 due to practically elastic behavior of the rock mass. With the aforementioned limitations and assumptions, a total of 22 three dimensional models were examined. Nine models were with support class A, 6 models with support class B, 2 models with support class C and 5 models with support class D. The number of top heading excavation and support stages varied from 30 to 90 depending on the support class. The number of bench—invert excavation and support stages were the half of those of the top heading stages and varied between 15 and 45. In total approximately 1800 excavation and support stages were solved. An indicative view of the 3D model is presented in Fig. 2b.

Fig. 2

View and dimensions of the models: a axisymmetric, b three dimensional

The axisymmetric models consisted of a slice of a cylinder (cylindrical sector) with 80 m radius and 4° internal angle. The length of the model was 150 m and the face of the final excavation stage was set at a tunnel advance of 110 m. All the lateral external boundaries of the model were fixed normal to their plane, in order to achieve axisymmetric boundary conditions while in the outer boundary a normal stress equal to the stress of the primary stress field was applied. A total of 115 models were solved with the range of $\sigma_{c} /P_{o}$ being between 0.2 and 2.0. 49 models were with support class A, 30 models with support class B, 14 models with support class C and 22 models with support class D. The total excavation and support steps where of the order of 7500. A view of the axisymmetric models is depicted in Fig. 2a. Both the 3D and the axisymmetric models were also solved for unsupported tunnel in a single step each. Additionally, plane strain models with the actual tunnel geometry were used for the selection of the support and the investigation of the relaxation of the top heading and the bench – invert. A fully structured hexahedral mesh was generated for both three dimensional and plane strain models.

In order to investigate the influence of the support stiffness and support installation position, 242 additional axisymmetric numerical models were solved assuming 12 combinations consisting of excavation round lengths from 1 to 3 m and support thickness from 0.1 to 0.4 m. The tunnel depths and the rock mass strength examined are those used in the 22 three dimensional models. The total excavation and support steps were of the order of 15000. It should be noted that, since support classes similar to A to D presented in Table 1 are commonly used in tunneling, the application of significantly different excavation rounds and support thickness might result in stability problems and/or in increased construction cost.

For the evaluation and interpretation of the results, the deformation profiles along the tunnel axis were exported both for the axisymmetric and the three-dimensional models respectively. The deformations at critical positions along the profile were extracted and individually evaluated. Those were the radial deformation at the tunnel face ($u^{face}$), at the middle of each support cycle ($u^{support}$) and the maximum deformation away from the tunnel face ($u^{total}$). The same applied for both the supported (indicated by the subscript “s”, $u_{s}$) and the unsupported (indicated by the subscript “u − s”, $u_{u - s}$) models, where for the unsupported tunnel models $u_{u - s}^{support}$ was measured at the same position as for the supported tunnel models. The aforementioned deformations and their measurement positions are presented in Fig. 3. Since the deformations along a support cycle vary with respect to the vicinity to the tunnel face, the value at the middle of each support cycle is used for further interpretation. The distance from the tunnel face to the middle point of each support cycle is half the excavation round length and equal to 0.5 m, 1 m and 1.5 m for support classes D or C, B and A respectively.

Fig. 3

Positions of critical deformations along a longitudinal deformation profile with excavation round length S = 2 m

3.2 Constitutive Model

All the numerical simulations were carried out using the Hoek–Brown Failure criterion (Hoek and Brown, 2019). The peak strength envelope was estimated with the parameters presented in Table 2 for $GSI$ = 30, 50 and 70. For the residual strength parameters, a reduction of the $GSI$ value was introduced, as suggested by Cai et al. (2007), in order to represent the increased fracturing of the rock mass, where the strength of the intact rock is assumed to remain constant after the peak strength. Equation (1) proposed by Alejano et al. (2012) was used in this study for the estimation of the residual $GSI_{r}$.

$$GSI_{r} = 17.25e^{0.0107 \cdot GSI}$$

(1)

The rock mass deformation modulus was estimated with the parameters of Table 1 and the equation proposed by Hoek and Diederichs (2006). A confinement stress depended critical plastic shear strain was used in all the numerical models. The critical plastic shear strain is the strain level after which the material retains only its residual strength. The ratio of the drop modulus was estimated by using the methodology of Alejano et al. (2010) for unconfined conditions and by considering a softening branch of $2G\eta$ as per Cundall et al. (2003). The $\eta$ values for each peak $GSI$ value are shown in Table 3.

Table 3 Softening branch $\eta$ values for each peak $GSI$ value

The expression proposed by Cundall et al. (2003) was used for the estimation of critical plastic shear strain (Eq. 2), by using the peak values of Hoek–Brown strength parameters $m_{b}$, $s$ and $a$, and considering unconfined conditions ($\sigma_{3}$ = 0):

$$\gamma_{p}^{cr} \left( {\sigma_{3} = 0} \right) = \frac{\beta }{2G}\left( {\frac{\eta + 1}{\eta }} \right)\sigma_{ci} s^{\alpha }$$

(2)

The parameter $\beta$, defined by Eq. (3), relates the peak and residual $GSI$ values. Note that Cundall et al. (2003) proposed the parameter $\beta$ to calculate a multiplier by $\left( {1 - \beta } \right)$ for $m_{b}$ and $\sigma_{ci}$ so that the residual parameters are achieved. However, in this study, it is assumed that the residual parameters depend only on the additional fracturing introduced in the residual state.

$$\beta = 1 - \frac{{GSI_{r} }}{GSI}$$

(3)

The confinement stress dependency of the critical plastic shear strain was based on a multiplier ($\mu$) of the latter according to Cundall et al. (2003) methodology, as presented with Eqs. (4) and (5). The multiplier was estimated in order to achieve the ductile behavior at the confinement level $\sigma_{3}^{dc} = \sigma_{c}$, where $\sigma_{c}$ is the uniaxial compressive strength of the rock mass, defined according to the Hoek–Brown strength criterion (Hoek et al. 2002) as $\sigma_{c} = \sigma_{ci} s^{a}$.

$$\mu = \frac{{\gamma_{p}^{cr} \left( {\sigma_{3} } \right)}}{{\gamma_{p}^{cr} \left( {\sigma_{3} = 0} \right)}} = \frac{{\sigma_{3}^{dc} }}{{\sigma_{3}^{dc} - \sigma_{3} }} = \frac{{\sigma_{c} }}{{\sigma_{c} - \sigma_{3} }}, \quad \text{for} \, \sigma_{3} < \sigma_{c}$$

(4)

$$\mu \to \infty , \quad \text{for}\, \sigma_{3} \ge \sigma_{c}$$

(5)

To summarize the constitutive low used in the numerical models, the material initially behaves linearly in the elastic region according to the rock mass Young’s modulus. After achieving its peak strength, as specified by the nonlinear generalized Hoek–Brown failure criterion with the peak $GSI$ value, a softening branch is used for any further deformations. For very low confining levels the material behaves in a brittle manner. As the confinement increases, the critical plastic shear strain of the softening branch increases gradually according to the multiplier $\mu$. For elevated values of the confining stress, equal or greater than the uniaxial compressive strength of the rock mass, the slope of the softening branch is mild enough that approximates ductile behavior. At the critical plastic shear strain of each confining stress level the material constantly retains its residual strength for any further deformations, as specified by the nonlinear generalized Hoek – Brown failure criterion with the residual $GSI_{r}$ values. A linear transition of the Hoek–Brown parameters at peak strength to the residual parameters at the critical plastic shear strain was assumed.

To validate the behavior of the model, triaxial tests were numerically performed at three confinement levels in a rock mass with σ_ci = 50 MPa, GSI = 50, GSI_r = 29, m_i = 15, ψ_i = φ_i/8, η = 0.33 and β = 0.41. The tests were simulated at a single hexahedral element and loading was introduced by applying a constant normal velocity of 10^–9 m/s at the top of the specimen.

The results of a set of triaxial tests for a single rock mass are presented in Fig. 4b along with the peak and residual strength envelope at Fig. 4a. The model behaves exactly as expected and specified by the constitutive low. Under unconfined conditions, a small strain-softening branch is observed according to the initially estimated critical plastic shear strain. For increased confinement, a gradual strength loss, up to the residual strength, with a wider softening branch is obtained. At confinement levels equal to the unconfined compressive strength of the rock mass, the critical plastic shear strain is magnified up to a point where a ductile behavior is approximated for strain levels that concern underground excavations. The equivalent post peak cohesion and friction parameters of the Mohr–Coulomb criterion versus the plastic shear strain are presented in Fig. 4c and d respectively. A post peak cohesion degradation is observed for low confinement of the rock mass during triaxial loading. The cohesion degradation gradually dissipates as confinement increases and tends to a constant cohesion value as σ₃ approaches σ_c. Post peak friction is further mobilized for small confinement levels, degradates for medium confinement and practically remains constant for confinement level of the order of rock mass uniaxial compressive strength (σ_c).

Fig. 4

Triaxial tests in a rock mass with σ_c≈3 MPa and softening parameter $\beta$ = 0.41: a peak and residual strength envelope, b principal stress difference versus axial strain for three confinement levels, c post peak instantaneous cohesion (c_i) normalized with peak cohesion (c_o) versus plastic shear strain, d) post peak instantaneous friction (φ_i) normalized with peak friction (φ_o) versus plastic shear strain

4 Results and Discussion

4.1 Percent Strain

A first indication of the difficulties associated with tunneling is the percent tunnel “strain” $\varepsilon$, defined as the ratio of the radial deformation to the tunnel radius multiplied by 100, $\varepsilon = 100 \times u/R$. This approach was firstly introduced by Sakurai (1983) and was the bases of extended further research. Hoek (1999) noted the significant importance of the rock mass strength to the in-situ stress for the prediction of the potential tunnel squeezing. Further, Hoek and Marinos (2000) proposed a practical support selection criterion, based on the percent strain of the tunnel, that remains a baseline in tunnel design.

The results for the percent tunnel strain versus $\sigma_{c} /P_{o}$ ratio of the axisymmetric and three-dimensional numerical simulations of this study are presented in Fig. 5a, both for the supported and the unsupported tunnel models. The percent strain of the supported tunnels is significantly lower, as expected, due to the beneficial reaction of the support. Further, in Fig. 5b the best fit curve of the percent strain for the unsupported tunnels of the current study are compared to the results obtained by using the analytical solution of Carranza-Torres (2004) for Hoek–Brown rock mass. As expected, the percent strains of the unsupported tunnels, obtained from the numerical models for strain softening rock mass, are within the range of values calculated by the analytic solution for the brittle and perfectly plastic rock mass. In all cases the rock mass deformation modulus was calculated with the Hoek and Diederichs (2006) method.

Fig. 5

Percent strain for different rock masses: a results of supported and unsupported tunnel models, b comparison of the unsupported tunnel best fit curve of the numerical results to the results of the Carranza-Torres (2004) analytical solution

4.2 The Effect of Strain Softening in Supported Tunnels

In the diagrams of Fig. 6 the deformations of the supported axisymmetric tunnels at the tunnel face ($u_{s}^{face}$), at the support installation position ($u_{s}^{support}$) and at a long distance from the tunnel face ($u_{s}^{total}$) are normalized with the deformation of the unsupported tunnels at the same positions. Further, the deformation of the supported tunnels at the support installation position ($u_{s}^{support}$) are normalized with the final deformation of the unsupported tunnels ($u_{u - s}^{total}$). The normalized deformations values are indicated with symbols F_A, S_A, T_A and D_A respectively, with subscript “A” denoting the axisymmetric conditions. These ratios are plotted with respect to the normalized rock mass strength $\sigma_{c} /P_{o}$ and allow for the assessment of the influence of the support.

Fig. 6

Variation of the normalized deformations of the supported tunnel, to the deformations of the unsupported tunnel, with respect to the normalized rock mass strength: a total—away from tunnel face (T_A), b at the support installation position (S_A), c at the tunnel face (F_A), d at the support installation position normalized to the total deformation of the unsupported tunnel (D_A)

For all diagrams, a smooth variation of the normalized deformations with respect to the $\sigma_{c} /P_{o}$ is observed, indicating that the $\sigma_{c} /P_{o}$ factor is a reliable and practical way to present and interpret the results for the combinations of rock masses and support classes examined in this study.

In all cases, the influence of the softening parameter $\beta$ was found to be critical. For increasing the parameter $\beta$ (i.e. more abrupt decrease of the post-peak rock mass strength to the residual strength) the restrain of the rock mass deformations due to the presence of the support increases, which is more pronounced for low $\sigma_{c} /P_{o}$ values. Further, the effect of the support is more considerable as the tunnel face moves away from each supported section.

For a range of the strain softening parameter $\beta$ between 0.2 and 0.5 and for values of $\sigma_{c} /P_{o}$ larger than 0.2, the results depicted in Fig. 6 can be expressed with Eqs. (6), (7) and (8). In all cases the ratios evaluated from these expressions cannot exceed a value of 1.0. Indicatively, the results of the Eqs. (7) and (8) are presented in Fig. 7a and b respectively, for four characteristic values of the strain softening parameter $\beta$ and for $\sigma_{c} /P_{o} \ge 0.2$. Note that due to the limited distance of the support installation middle point and the tunnel face position, the results of Fig. 7a and b are similar.

$$T_{A} = \frac{{u_{s}^{total} }}{{u_{u - s}^{total} }} = \left[ {\left( {0.20\beta + 0.30} \right)\ln \frac{{\sigma_{c} }}{{P_{o} }}} \right] - 0.73\beta + 1.12 \le 1.0$$

(6)

$$S_{A} = \frac{{u_{s}^{support} }}{{u_{u - s}^{support} }} = \left[ {\left( {0.56\beta + 0.03} \right)\ln \frac{{\sigma_{c} }}{{P_{o} }}} \right] - 0.25\beta + 1.09 \le 1.0$$

(7)

$$F_{A} = \frac{{u_{s}^{face} }}{{u_{u - s}^{face} }} = \left[ {\left( {0.41\beta + 0.04} \right)\ln \frac{{\sigma_{c} }}{{P_{o} }}} \right] - 0.33\beta + 1.09 \le 1.0$$

(8)

Fig. 7

Visualization of proposed equations: a at support installation position (S_A), b at the tunnel face (F_A)

4.3 Influence of the True Three-Dimensional Conditions

The same evaluation scheme presented in Sect. 4.2 for the axisymmetric models was also applied for the three-dimensional models. The calculated normalized deformations T_3D, S_3D, F_3D, D_3D were compared to the relevant results of the axisymmetric models T_A, S_A, F_A, D_A and they are presented in Fig. 8. The subscript “3D” indicates the normalized deformations that correspond to the results of the three-dimensional models. Figure 8 practically compares the performance of an axisymmetric and a true three-dimensional support. It is observed that for low $\sigma_{c} /P_{o}$ values, the three-dimensional models generally yield higher normalized deformations than the axisymmetric ones. This may be attributed to the actual geometry and stress redistribution at the vicinity of the tunnel face, and the actual three-dimensional function of the support. The bending of the three-dimensional support in both hoop and longitudinal direction results in a lower stiffness in comparison with the generally stiff circular support of the axisymmetric models. Regarding the strain softening parameter $\beta$, since both three dimensional and axisymmetric models incorporate the same constitutive law, the results are independent from this parameter.

Fig. 8

Variation of the normalized deformations of axisymmetric and three dimensional models with respect to the normalized rock mass strength: a total—away from tunnel face (T_3D/T_A), b at the support installation position (S_3D/S_A), c at the tunnel face (F_3D/F_A), d at the support installation position normalized to the total deformation of the unsupported tunnel (D_3D/D_A)

4.4 Effect of the Support Stiffness and Excavation Round Length

Support systems such as those presented in Table 1 are commonly used in tunneling practice and may be considered as a baseline for common tunneling conditions. The percent strain according to axisymmetric models of tunnels supported with those support systems with respect to the normalized rock mass uniaxial compressive strength are presented in Fig. 9a. Figure 9b presents the percent strain of the relevant unsupported tunnels based on plane strain models. Those two figures along with Table 1 summarize the support systems used, the support selection criterion established, and the results of the numerical simulations with those commonly used support systems. In some cases, the evaluation of various alternative support systems might be required or examined. This exercise must be done with extreme caution since significant variations from commonly applied support systems might lead to unstable conditions and/or expensive construction. Hence, engineering judgment is required and the deviations of an examined support system and round length from the commonly applied is proposed to be limited.

Fig. 9

Percent strain for different rock masses and primary support used in numerical simulations: a supported axisymmetric models, b unsupported plane strain models

To this respect, the effect of the support stiffness and of the excavation round length was parametrically investigated with axisymmetric numerical simulations. The tunnel depths and the rock mass strength examined are those used in the three-dimensional models presented in §4.3. For each 3D model, 11 additional axisymmetric models with round length (S’) within a range of 1.0 to 3.0 m and shotcrete shell thickness (t’) from 10 to 40 cm were solved. The additionally calculated normalized deformations T_S, S_S, F_S and D_S, with subscript “S” denoting the support stiffness parametric investigation, along with the initial values T_A, S_A, F_A and D_A make a total of 12 models for each of the 22 combinations of tunnel depths and the rock mass parameters examined.

Figure 10 presents the results for a tunnel with σ_c/P_o = 0.40 and strain softening parameter β = 0.41. The proposed support system for the tunnel according to Table 1 is PS-B with round length S = 2.0 m and shell thickness t = 20 cm. The area of the left-top to bottom-right diagonal represents commonly used support systems according to Table 1 and engineering practice. From Fig. 10a, the T_S value for round length S′ = 1.0 m and shell thickness t′ = 10 cm is 0.62 and practically identical with the T_A value of the proposed support (S = 2.0 m, t = 20 cm). In that case the capacity of the support might be lower than the demand leading to unstable conditions. On the contrary, T_S is approximately the same (0.62) for round length S′≈2.3 m and shell thickness t′ = 40 cm. The increased thickness of the support affects the construction cost and leads to a possible excess of the required safety factors. For all the examined combinations, T_S varies between a range from 0.53 to 0.72. According to Fig. 10b, S_S depends more to the excavation round length due to the proximity to the tunnel face and less to the support stiffness due to the limited contribution of the support reaction at the specific location. Finally, F_S and D_S values depicted in Fig. 10c and d respectively are practically independent form the support stiffness in comparison with the excavation round length.

Fig. 10

Contour plot with the effect of the shell thickness and excavation round length to the normalized deformations for a tunnel with σ_c/P_o = 0.40, β = 0.41: a total—away from tunnel face (T_S), b at the support installation position (S_S), c at the tunnel face (F_S), d at the support installation position normalized to the total deformation of the unsupported tunnel (D_S)

In the contour plots of Fig. 11, the T_S, S_S, F_S and D_S values are normalized to the respective values of the initially proposed support system T_A, S_A, F_A and D_A. The normalized values are plotted with respect to the excavation round length (S′) normalized to the round length of the suggested supported system (S) and to the shell thickness (t′) normalized to the shell thickness of the suggested support system (t). The suggested support systems are presented in Table 1 and the corresponding T_A, S_A, F_A and D_A vales were discussed in detail in §4.2. For normalized round length and shell thickness equal to 1, S′ = S, t′ = t, T_S = T_A, S_S = S_A, F_S = F_A and D_S is equal to D_A. Note that S′ must be within a range of 1.0 to 3.0 m and t’ within 10 cm to 40 cm.

Fig. 11

Contour plot with the variation of the normalized T_S, S_S, F_S and D_S values to the respective T_A, S_A, F_A and D_A values. The values are plotted with respect the round length (S’) normalized to the relevant length of the proposed support (S) and the shell thickness (t’) normalized to the thickness of the proposed support (t): a total—away from tunnel face (T_S/T_A), b at the support installation position (S_S/S_A), c at the tunnel face (F_S/F_A), d at the support installation position normalized to the total deformation of the unsupported tunnel (D_S/D_A). Note that S, S’ must be within a range of 1.0 to 3.0 m and t, t’ within 10 cm to 40 cm

The normalized total displacements T_S/T_A presented in Fig. 11a are correlated to both round length and shell thickness. T_S is equal to T_A for t’ = 0.5t with S’ = 0.5S and for t′ = 2t with S′ = 1.3S. In the first case, unstable tunnel conditions are expected, while in the latter case the construction cost will be affected. The normalized face displacement S_S/S_A is minorly affected due to the normalization process since both numerator and denominator are related to support installation position. Finally, F_S/F_A and D_S/D_A values depicted in Fig. 11c and d respectively, are more sensitive to the excavation round length than the support stiffness.

4.5 Excavation Sequence

In tunnel design, it is common practice to use the same stress relaxation factor in order to simulate the 3D advance for all the excavation stages (e.g. Vlachopoulos and Diederichs 2014). This is a rough approximation, since the excavation round length of the top-head is generally shorter than the excavation round length of the bench. Additionally, the excavation of the top head has already introduced a relaxation to the area of the bench.

In order to estimate the pressure that should be applied at the tunnel boundary to account for the 3D tunnel advance in 2D plane strain numerical simulations, a series of plane strain models was solved for various relaxation levels. The simulation of the top heading excavation and support is performed in two stages for each gradually reduced internal pressure. At the 1^st stage of every relaxation round, the core of the tunnel top heading was removed and an internal pressure was applied normal to the boundary of the excavation. At the 2nd stage, the internal pressure was removed and the relevant support was installed. The internal pressure where the deformations at the crown of the tunnel are approximately equal to those calculated from the three-dimensional models, at the same position and excavation stage, approximates the relaxation pressure of the top heading ($P_{i}^{top}$).

The same sequence was applied for the bench of the tunnel. In that case, the initial stage of the plane strain models was the stage of the supported top-head with crown deformation equal to the relevant three-dimensional model. The deformations were compared at two control points. The first control point was at the crown of the tunnel and the second at the middle of the bench wall of the excavation. The internal pressure of this excavation stage ($P_{i}^{bench}$) was estimated by comparing the deformations at the two control points of every relaxation stage with the deformations obtained from the three-dimensional models at the same position and excavation stage.

The ratio of the internal support pressure at the bench and at the top heading simulation that matched the 3D numerical deformation is shown in Fig. 12 with respect to the $\sigma_{c} /P_{o}$ ratio. The results indicate that the assumption of the same pressure reduction for the two excavation stages may be justified only for low $\sigma_{c} /P_{o}$ values. For higher $\sigma_{c} /P_{o}$ values a higher bench relaxation is observed which results in lower loading levels of the bench wall support. However, it is noted that in reality other factors, such as the load transfer from the top heading support to the bench, may increase the loading of the support there. Hence, it is proposed that the same support scheme for the top heading and the bench is used.

Fig. 12

Variation of the normalized confinement pressure at bench with respect to the normalized rock mass strength

5 Proposed Design Methodology

The sequential tunnel excavation and support is a three-dimensional problem and only three-dimensional simulations integrate the actual stress and deformations redistribution along the tunnel. However, such analysis is time consuming and is usually avoided in design practice. An accurate alternative is the combination of a plane strain model and of an axisymmetric one with sequential excavation and support installation incorporated at the latter. In that case, the same constitutive law should be used in both models. This study presents a design methodology that takes into account the effect of the support to the longitudinal deformation profiles.

5.1 Ground Reaction Curve

The estimation of the confinement pressure prior to the support installation requires the estimation of the ground reaction curve (GRC) of the tunnel and of the deformations at the support installation position of the supported tunnel. The GRC can be constructed with plane strain models and simulation of the gradual relaxation of the top head core area of the tunnel. All modern geotechnical numerical programs incorporate various methods that can accomplish this procedure. Additionally, many analytic solution schemes exist that can approximate the GRC of an equivalent circular tunnel. For a given GRC, the only required component for the estimation of the confinement pressure prior to the support installation is the deformation at the support installation position. The results of this paper provide a practical way to calculate the required deformation at the support installation position.

5.2 Example Application

The GRC of a tunnel with radius $R$ = 6 m excavated in a rock mass with $\sigma_{c} /P_{o}$ = 0.62 and softening parameter $\beta$ = 0.48 is presented in Fig. 13a. The LDP along the unsupported tunnel is presented in Fig. 13b. Τhe deformations of the unsupported tunnel at the three examined critical points presented in Fig. 3 are $u_{u - s}^{total}$ = 1.0 cm, $u_{u - s}^{support}$ = 0.51 cm and $u_{u - s}^{face}$ = 0.28 cm. Considering that the tunnel is supported with support class PS-B with round length S = 2 m, $u_{u - s}^{support}$ and $u_{s}^{support}$ are located at a distance of S/2 = 1 m (half excavation round length) from the tunnel face. The values T_A = 0.6, S_A = 0.8, F_A = 0.8 and D_A = 0.4 can be found from Fig. 6 and the relevant values of a supported axisymmetric tunnel can be approximated as $u_{s}^{total} = T_{A} u_{u - s}^{total}$, $u_{s}^{support} = S_{A} u_{u - s}^{support}$ or $u_{s}^{support} = D_{A} u_{u - s}^{total}$ and $u_{s}^{face} = F_{A} u_{u - s}^{face}$. The calculated values presented in Fig. 13b with red circles are $u_{s}^{total} = 0.61\;{\text{cm}}$, $u_{s}^{support} = 0.41\;{\text{cm}}$ and $u_{s}^{face} = 0.22\;{\text{cm}}$_. Those values are within the range of the numerical results for the supported axisymmetric tunnel presented in Fig. 13b.

Fig. 13

Results of a tunnel constructed within a rock mass with $\sigma_{c} /P_{o}$ = 0.62 and softening parameter β = 0.48, a GRC, b LDP

From Fig. 13a, a confining pressure for the top head $P_{i}^{top}$ = 500 kPa can be estimated from the GRC and for $u_{s}^{support}$ = 0.41 cm calculated with the proposed method. From the supported tunnel numerical simulation the deformation at the support installation position was $u_{s}^{support}$ = 0.44 cm and the equivalent confining pressure for the top head is $P_{i}^{top}$ = 450 kPa. The numerically calculated value is in a good correlation with the value estimated with the proposed method. According to Fig. 12 the confining pressure for the bench is of the order of $P_{i}^{bench}$ = 50 kPa.

With both methods the confining pressure is significantly higher than the value $P_{i}^{top}$ = 200 kPa estimated from the LDP of the unsupported tunnel. Note that those are confining pressures and not the final pressure that will act to the support. The support system will react to that pressure (according to the so-called support reaction curve) and will deform with the rock mass until the final equilibrium of the system to a reduced pressure. The higher confining pressure indicates that the resulted loading on the support at the final equilibrium of the model will be underestimated if the used LDP does not incorporate the effect of the support.

6 Conclusion

Based on the results of this paper, the following conclusions are summarized:

• (a) It is generally proposed to use three dimensional simulations with sequentially excavated and supported tunnels, since tunneling is a three-dimensional problem.

• (b) The influence of strain softening constitutive models is significant in terms of deformations along the tunnel.

• (c) It is essential to incorporate the effect of the support to estimate the confinement level prior to the support installation.

• (d) The results of this paper provide a practical and easy way to take into account the effect of the support to the longitudinal deformation profile

• (e) The equations proposed should be used with caution and taking into account the limitations of the current study and also the variation of the numerical results as presented in the relevant diagrams.

• (f) The confinement of the bench was found to be lower or equal to the confinement of the top head. Since in reality other factors, such as the load transfer from the top heading support to the bench, may increase the loading of the support there, it is proposed that the same support scheme for the top heading and the bench is used.