1 Introduction

The direct discharge of wastewater is one of the major factors of marine environment degradation because this water is collected and discharged directly into the sea with high concentrations of pollutants. However, if the discharge area is not controlled properly, the effluent can return along the coast without being sufficiently diluted and may then contaminate fishing grounds, areas for farming, collecting shells and or crustaceans, as well as beaches. Incidentally, all parts of the Moroccan coast, including the Bay of Tangier, are lined with popular tourist beaches and fishing areas. This bay faces a real critical problem of coastal pollution, a problem the complexity of which involves many factors. The coastal pollution does not affect only the marine environment but also the soil, especially the unsaturated soils. Indeed, the polluted water discharged through rivers, wadis and marine disposals contaminates the soil structure by means of its porosity. This contamination has major consequences on human health, growth of plants and soil yield. Hence, the description of the flow in the unsaturated zone is very important for predictions of the movement of pollutants into ground water aquifers.

The unsaturated soils play an important hydrologic role that influences water quality and quantity. Indeed, the water movements in these soils are essential for assessing the water demand of the vegetation and the ground water storage. This mechanism is governed by the infiltration process that indicates the soil ability to allow water movement into and through the soil. The infiltration depends on soil texture (percentage of sand, silt, and clay) and its mineralogy.

For experimental and analytical studies about soil moisture regime, many factors must be taken into account. For example, evaporation, evapotranspiration and humidity are classified as climatic factors. However, the soil factors include, for example, hydraulic conductivity and water content relationship of the soil, saturated/unsaturated hydraulic conductivity and effective porosity.

Unsaturated hydraulic conductivity is one of the main properties considered to govern a flow. Knowledge of the highly nonlinear relationship between unsaturated hydraulic conductivity (K) and volumetric water content (θ) is required for models of water flow and solute transport processes in the unsaturated zone. Measurement of unsaturated hydraulic conductivity is experimentally expensive and sometimes impossible. Therefore, the use of models that estimate this relationship is required. Indeed, the most experimental methods used to measure directly the unsaturated hydraulic conductivity are limited to climatic soil conditions and very slow where they require sometimes months for single K measurement (Conca and Wright 1998; Nimmo and Perkins 2002).

Various models have been developed, for example, HYDRUS (Kool and Van Genuchten 1991). However, most of these models are one-dimensional and limited to the unsaturated zones. HYDRUS-2D has been developed by Simunek et al. (1996). It simulates two-dimensional water flow and solute transport in saturated and unsaturated porous soils. Later, a HYDRUS 2D/3D is distributed by Simunek et al. (2012a, b) for simulating the two- and three-dimensional movement of water, heat, and multiple solutes in variably saturated media. To our knowledge, a study using HYDRUS 2D/3D for simulating transport process either in unsaturated or saturated zones of Tangier’s bay region has not been reported in the literature.

In the present study, numerical simulations using the model HYDRUS 2D/3D have been carried out to analyze the hydrologic behavior of Tangier’s bay region near the Meghogha wadi. The aim was to simulate the infiltration of polluted water from saturated zones of the Meghogha wadi and the Tangier’s bay into the unsaturated environment soil for different ranges of water content. Numerical results represented by water retention and unsaturated hydraulic conductivity curves near the saturation are obtained to discuss the studied infiltration process.

2 Experimental Site

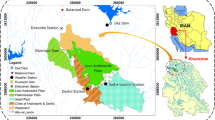
The Bay of Tangier is located in the north-western extremity of Morocco, on the southern border of the strait of the Gibraltar, between parallel of 35°46′ and 35°48′ North and meridians of 5°45′ and 5°49′ West. It has a dense river network in the form of low wadis flowing through the city from south to north (Fig. 1) (El Hatimi et al. 2002). The intensity of their flow is especially remarkable in their upstream course, while downstream they are almost perennial because of drainage of wastewater from the city. Moreover, these wadis can make a significant contribution in water during rainy seasons, causing severe flooding, and often flooding the neighborhoods in low areas (valleys) of the city because of the impermeability of the soil and the steep slopes of surrounding hills. These wadis by order of hydrological and hydraulic importance are: Meghogha, Souani, Lihoud. Meghogha wadi flow represents 70% of the total flow rate discharged into the bay. It runs through urban and industrialized areas of the city of Tangier and leads to the strait of Gibraltar. The Meghogha wadi discharge and its dispersion into the bay (Belcaid et al. 2012) is one of the major factors of marine environment degradation. It has been demonstrated (Achab et al. 2007) that highest concentrations of heavy metals (Pb, Cu, Ni, Cr) are located in the western sector of the bay, in particular between the port and the mouth of Meghogha wadi. The well drained Meghogha wadi soil consists of a fine clay, while the excessively drained bay Tangier’s bay soil consists of a fine sandy–clay (Eddine and Abdellaoui 2007). These two soil types are widespread in the Tangier’s bay area and are representative of different vulnerabilities to groundwater contamination. Soil horizons are listed in Table 1.

Fig. 1
figure 1

Geographical position and drainage network of the bay of Tangier (El Hatimi et al. 2002)

Full size image
Table 1 Hydraulic parameters optimized from water retention data
Full size table

3 Model Description

Water movement was simulated using the HYDRUS 2D/3D model developed by Simunek et al. (2012a, b). The HYDRUS 3D numerical model is based on the modeling environment for analysis of water flow and solute transport in incompressible and variably saturated porous soils and groundwater. The program numerically solves the Richards’ equation for saturated–unsaturated water flow and the Fickian-based advection–dispersion equation for solute transport. Applications involve a steady/unsteady water flow, solute transport, and/or heat transfer problems (Simunek et al. 2012a, b). The transport equation includes provisions for linear equilibrium adsorption, zero-order production, and first-order degradation. The governing flow and transport equations are solved using a Galerkin type linear finite element scheme.

In porous soils, the water occurs below the surface at depths, where all the pore spaces are completely filled with water (Groundwater). Firstly, this water passes through the vadose zone (the unsaturated zone) where the soil pores are primarily filled with air. Then, the infiltration process continues until the water reaches the aquifer (the saturated zone) (Fig. 2). Hence, infiltrated water flows through the connected pore spaces to the various zones, and therefore a contamination can be transported by advection.

Fig. 2
figure 2

Divisions of subsurface water (Meinzer 1923)

Full size image

3.1 Governing Equation: Richard’s Equation

Water movement in unsaturated soil was simulated by the model of Simunek et al. (2012a, b). This model uses a modified form of the Richards’ equation as follow:

$$\frac{\partial \theta }{\partial t} - \frac{\partial }{{\partial x_{i} }}\left[ {K\left( {K_{ij}^{A} \frac{\partial h}{{\partial x_{j} }} + K_{iz}^{A} } \right)} \right] + S = 0$$
(1)

where θ is the volumetric water content [−], h is the soil water pressure head [L], t is time [T], the subscripts i, j and z in the equation are the space direction indices depending on the origin of the surface flux, and S is the sink term for root water uptake rate [T−1]. \(K_{ij}^{A}\) and \(K_{iz}^{A}\) are components of a dimensionless anisotropy tensor KA. K is the unsaturated hydraulic conductivity [LT−1].

The volumetric water content θ and unsaturated hydraulic conductivity K, as functions of h, are given in the Van Genuchten Equation (Van Genuchten 1980) as follows:

$$\theta \left( h \right) = \left\{ {\begin{array}{*{20}l} {\theta_{r} + \frac{{\left( {\theta_{s} - \theta_{r} } \right).}}{{\left( {1 + \left| {\alpha h} \right|^{n} } \right)^{m} }}} \hfill & {h < 0} \hfill \\ {\theta_{s} } \hfill & {h \ge 0} \hfill \\ \end{array} } \right.$$
(2)
$$K\left( h \right) = \left\{ {\begin{array}{*{20}l} {K_{s} S_{e}^{l} \left[ {1 - (1 - S_{e}^{1/m} )^{m} } \right]^{2} } \hfill & {h < 0} \hfill \\ {K_{s} } \hfill & { h \ge 0} \hfill \\ \end{array} } \right.$$
(3)
$$m = 1 - 1/n \quad (n > 1)$$

where θr and θS are the residual and saturated volumetric water contents, respectively. n is an empirical parameter related to the pore-size distribution. α is an empirical parameter, often assumed to be related to the inverse of the air-entry section (L−1).

Ks is the saturated hydraulic conductivity [LT−1]. Se is the effective saturation; l is the pore connectivity parameter and is about 0.5 for many soils (Mualem 1976).

In the numerical simulations, two basic soil textures were used: sandy–clay, and clay (Eddine and Abdellaoui 2007). Thus, the initial inputs of θr and θS, α, n, l and Ks are estimated from measured water retention data using the Rosetta package (Schaap and Leij 2000) which is embedded in HYDRUS 2D/3D.

3.2 Boundary and Initial Conditions

Boundary and initial conditions of the model described above are:

$$H = h_{i} \left( z \right)\quad {\text{at}}\quad - L \le z \le 0, \quad {\text{when}}\,t = 0$$
(4)
$$- K\left( {\frac{\partial h}{\partial z} + 1} \right) = E\left( t \right)\quad {\text{at}}\quad z = 0,\quad {\text{when}}\,t > 0$$
(5)
$$\frac{\partial h}{\partial z} = 0\quad {\text{at}}\quad z = - L, \quad {\text{when}}\,t > 0$$
(6)

E(t) is the rate of infiltration or evapotranspiration (cm day−1) at different times, hi is the initial soil water pressure head (cm). L is the maximum soil depth.

Therefore, Eq. (6) has considered that dh/dz = 0. In Eq. (6), z = − L was considered due to the maximum soil depth and root depth.

According to geochemical analysis (Achab et al. 2007), the results show that the discharge of Meghogha wadi contains high contents of heavy metals coming from domestic and industrial liquid and solid discharges. Statistical data shows that the dominant association is represented by Pb > Cu > Ni > Cr. Therfore, for our simulations, the water flow has been tracked by the transport of the dominant solute: Pb. The value of the taken Pb concentration was about 500,000 mmol/m3.

The measured daily potential infiltration for the whole simulation period (10 days) was used as a time-variable boundary for the soil surface of the application area (Meghogha wadi). The soil surface outside the application area, vertical boundaries within the unsaturated zone, and the lower boundary fixed at 12 m below water table were assumed to be no-flow boundaries. The vertical boundaries within the saturated zone were assumed to have constant pressure heads calculated from the hydraulic gradient of the groundwater. In this study, simulation would focus on horizontal movement of water in the unsaturated zone and horizontal movement and transport within the groundwater.

Solute was introduced to the model domain through the amount and concentration water on the application day. Initial concentration of the solute was set to zero in the whole unsaturated domain as initial condition indicated no pollution present.

Simulations were carried out for 4 cases of various values of initial soil water pressure head hi in both saturated and unsaturated soils (Table 2).

Table 2 Initial values of water pressure head taken into account for the simulations
Full size table

The size of computational domain (Fig. 3) is 350 m in length, 156 m in width and 12 m in depth. This domain is divided in two connected sub-domains; (1) a parallelepiped of 156 m in length, 150 m in width and 12 m in depth. The surface wadi is placed in the middle of this sub-domain and it is of 150 m in length and 36 m in width. (2) the second sub-domain presents a slop of an angle about 87° to the vertical (the depth) and extends to the rest of the global domain. This later sub-domain represents the bay soil. The wadi and the bay soils are considered as saturated zones and the rest of the domain as unsaturated zone.

Fig. 3
figure 3

Scheme and dimensions of computational domain

Full size image

The mesh as shown in Fig. 4 has been generated by 7044 nodes and 12,320 non-structured triangular prisms (3D) elements. Twelve layers were distinguished for the domain depth. Each layer was assumed to have uniform physical and chemical properties. The mesh density near the Meghogha wadi mouth is refined in order to have more precision in the numerical results. Time discretizations were as follows: initial time step Δt = 0.01 day, minimum time step Δt = 0.001 day and maximum time step Δt = 2 days. The whole simulation period is of 10 days.

Fig. 4
figure 4

Mesh details of computational domain

Full size image

4 Numerical Modeling

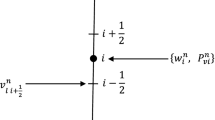
The resolution of Richard’s equation is done by the Galerkin finite element method with linear basis functions. The first step is to divide the flow region into a number of triangular (2D) or tetrahedral (3D) elements. The corners of these elements are taken to be the nodal points. The dependent variable, the pressure head function h(x, y, z, t), is approximated by a function h’(x, y, z, t) as follows:

$$h^{{\prime }} \left( {x,y,z,t} \right) = \mathop \sum \limits_{n = 1}^{N} \emptyset_{n} \left( {x,y,z,} \right)h_{n} \left( t \right)$$
(7)

where \(\emptyset_{n}\) are piecewise linear basis functions satisfying the condition \(\emptyset_{n}\) (xm, zm) = δnm (where is the Kronecker delta [−], xm maximum rooting length in the x-direction and zm maximum rooting length in the x-direction). hn are unknown coefficients representing the solution of (Richard’s equation) at the nodal points, and N is the total number of nodal points.

The Galerkin method postulates that the differential operator associated with the Richards’ equation is orthogonal to each of the N basis functions:

$$\int\limits_{\Omega } {\left\{ {\frac{\partial \theta }{\partial t} - \frac{\partial }{{\partial x_{i} }}\left[ {K\left( {K_{ij}^{A} \frac{\partial h}{{\partial x_{j} }} + K_{iz}^{A} } \right)} \right] + S} \right\}} \, \phi_{n} d\Omega = 0$$
(8)

Applying Green’s first identity to Eq. (8) and replacing h by hn, leads to:

$$\sum\limits_{e} {\int\limits_{{\Omega e}} {\left( {\frac{\partial \theta }{\partial t} \, \phi_{n} + KK_{ij}^{A} \frac{{\partial h^{\prime } }}{{\partial x_{j} }}\frac{{\partial \phi_{n} }}{{\partial x_{i} }}} \right)} \, d\Omega } = \sum\limits_{e} {\int\limits_{{\Gamma e}} {K\left( {K_{ij}^{A} \frac{{\partial h^{\prime } }}{{\partial x_{j} }} + K_{iz}^{A} } \right)} \, n_{i} \phi_{n} d\Gamma + } \sum\limits_{e} {\int\limits_{{\Omega e}} {\left( { - KK_{iz}^{A} \frac{{\partial \phi_{n} }}{{\partial x_{i} }} - S\phi_{n} } \right)} \, d\Omega }$$
(9)

where Ωe represents the domain occupied by element e, and Гe is a boundary segment of element e. Natural flux-type (Neumann) and gradient type boundary conditions can be immediately incorporated into the numerical scheme by specifying the line integral in Eq. (9). Hence, this later can be written in matrix form as:

$$\left[ F \right]\frac{\partial \theta }{\partial t} + \left[ A \right]\left\{ h \right\} = \left\{ Q \right\} - \left\{ B \right\} - \left\{ D \right\}$$
(10)

where

$$\begin{aligned} A_{nm} & = \sum\limits_{e} {K_{l} K_{ij}^{A} \int\limits_{{\Omega e}} {\phi_{l} \frac{{\partial \phi_{n} }}{{\partial x_{i} }}\frac{{\partial \phi_{m} }}{{\partial x_{j} }}} \, d\Omega } \\ B_{n} & = \sum\limits_{e} {K_{l} K_{iz}^{A} \int\limits_{{\Omega e}} {\phi_{l} \frac{{\partial \phi_{n} }}{{\partial x_{i} }}} \, d\Omega } \\ F_{nm} & = \delta_{nm} \sum\limits_{e} {\int\limits_{{\Omega e}} {\phi_{n} } \, d\Omega = } \delta_{nm} \sum\limits_{e} { \, \frac{{V_{\text{e}} }}{ 4}\quad {\text{for}}\, 3 {\text{D }}} \\ Q_{n} & = - \sum\limits_{e} {\sigma_{1l} \int\limits_{{\Gamma e}} {\phi_{l} \phi_{n} } \, d\Gamma = } - \sum\limits_{e} {\sigma_{1n} L_{n} } \\ D_{n} & = - \sum\limits_{e} {S_{l} \int\limits_{{\Omega e}} {\phi_{l} \phi_{n} } \, d\Omega = } \sum\limits_{e} {\frac{{V_{\text{e}} }}{20}} (4\overline{S} + S_{n} )\quad {\text{for}}\, 3 {\text{D}} \\ \end{aligned}$$

The subscripts i, j and z in equations are the space direction indices. Ve is the volume of a three-dimensional element e, \(\overline{S}\) is the average root water extraction values over element e, Ln is the length of the boundary segment connected to node n. The symbol σn represents the flux [LT−1] across the boundary in the vicinity of boundary node n. The boundary flux is assumed to be uniform over each boundary segment. The entries of the vector Qn are zero at all internal nodes, which do not act as sources or sinks for water.

In time, the integration of Eq. (10) is based on the discretizing of the time domain into a sequence of finite intervals and replacing the time derivatives by finite differences. An implicit (backward) finite difference scheme is used for both saturated and unsaturated conditions:

$$\left[ F \right]\frac{{\left\{ \theta \right\}_{j + 1} - \left\{ \theta \right\}_{j} }}{{\Delta t_{j} }} + \left[ A \right]_{{_{j + 1} }} \left\{ h \right\}_{{_{j + 1} }} = \left\{ Q \right\}_{j} - \left\{ B \right\}_{j + 1} - \left\{ D \right\}_{j}$$
(11)

where j + 1 presents the current time level at which the solution is being considered, j refers to the previous time level, and Δtj = tj+1 −tj. Equation (last) represents the final set of algebraic equations to be solved.

The Eq. (11) is nonlinear. Hence, to obtain solutions at each new time step, an iterative process must be used. For each iteration a system of linearized algebraic equations is first derived from (last equation), which, after incorporation of the boundary conditions, is solved using either Gaussian elimination (Joseph 2011). After inversion, the coefficients in (Eq. 11) are re-evaluated using the first solution, and the new equations are again solved. The iterative process continues until a satisfactory degree of convergence is obtained. According to Simunek and Van Genuchten (1994), the convergence is verified when at all nodes, the absolute change in pressure head (or water content) between two successive iterations becomes less than some small value determined by the imposed absolute pressure head (or water content) tolerance.

5 Results and Discussion

As explained above, simulations of three-dimensional modeling were made for a period of 10 days. As the infiltration is an indicator of the soil’s ability to allow water movement into and through the soil profile, results simulations are based on water infiltration evolution during the transport process (Figs. 5, 6, 7, 8).

Fig. 5
figure 5

Evolution of water infiltration from saturated zones to unsaturated zones during 10 day of the transport process for a pressure head of hi = (25; − 25): a after 1 day, b after 3 days, c after 5 days and d after 10 days

Full size image
Fig. 6
figure 6

Evolution of water infiltration from saturated zones to unsaturated zones during 10 days of the transport process for a pressure head of hi = (50; − 50): a after 1 day, b after 3 days, c after 5 days and d after 10 days

Full size image
Fig. 7
figure 7

Evolution of water infiltration from saturated zones to unsaturated zones during 10 day of the transport process for a pressure head of hi = (100; − 100): a after 1 day, b after 3 days, c after 5 days, and d after 10 days

Full size image
Fig. 8
figure 8

Evolution of water infiltration from saturated zones to unsaturated zones during 10 day of the transport process for a pressure head of hi = (175; − 175): a after 1 day, b after 3 days, c after 5 days and d after 10 days

Full size image

5.1 Infiltration Water Process

During the first day, water begins to infiltrate from the saturated zones (Meghogha wadi and Tangiers’ bay) into the adjacent unsaturated zones through the limits (Figs. 5a, 6a, 7a, 8a). The water infiltration is manifested horizontally in the direction of descending potentials. The infiltration process continues and the water expands to the unsaturated zones and becomes more important towards the 10 days where it reaches the steady rate (Figs. 5d, 6d, 7d, 8d). Indeed, water infiltrates rapidly in dry soils. The maximum infiltration rate prevailing at the beginning of the process is called initial infiltration rate. The air in the pores is replaced by the water as this later continues to infiltrate. Gradually, the infiltration process slows down and a steady rate is reached (the basic infiltration rate).

The infiltration rate depends on soil texture (percentage of sand, silt, and clay) and the arrangement of soil particles. Because of the large porosity of sandy soils, water moves more rapidly than through the small pores of clay soils (Table 3). Hence, in our simulations where the unsaturated soil is a clay one, it was noted that the infiltration process was relatively slow.

Table 3 Steady infiltration rates for general soil texture groups (Diamond and Shanley 1998)
Full size table

Clay soil of our site (Tangier’s bay region) has the specified characteristic that as it dries, it develops shrinkage cracks (El Ouahabi et al. 2014). These later promote and accelerate the infiltration process. However, when cracks are not present, the infiltration process is slow.

As the pressure head was an essential parameter of infiltration process simulations, it was noted that the higher initial pressure head is, the higher water infiltration rate is (it appears when we compare for example Figs. 5d, 6d, 7d, 8d). This observation was translated into the curve of water content variation in function of pressure head (Fig. 9). In the same figure, numerical results are compared with the general curve of Musy and Soutter (1991).

Fig. 9
figure 9

Evolution of pollutant concentration infiltration from the free surface into a depth of 1 m of the soil: a after 1 day, b after 2 days and c after 3 days

Full size image

To have an idea about the infiltration process of the Pb concentration in the different levels of the soil depth (Fig. 3), Fig. 9 shows that the solute transport is done progressively between the different layers of the soil. It takes about 2 days to cover a depth of 1 m.

Over time, and due to the soil porosity, the infiltration process continues. Hence, the concentration of pollutant becomes more important in the lower layers and spreads laterally into the soil neighboring the wadi and its mouth.

5.2 Water Retention Curve

Figure 9 suggests that simulations in water content agreed well with the general trend obtained by Musy and Soutter (1991). The predicted θ(h) values matched reasonably well with analytical values for the clay soils. This curve represents the intensity variation of the capillarity forces and the adsorption in function of water content, and it is called water retention curve. This later is the main base of the unsaturated porous soils characterization.

The volumetric water content of the clay soil starts to decrease while the material remains saturated. Indeed, since water is expelled from the pores because of suction, the volumetric water content in compressible materials starts to decrease while the degree of saturation remains constant.

The water retention curve depends essentially on the soil pore size and the compressibility of the material. Hence, It is affected directly by the initial water content (Simms and Yanful 2002; Smith and Mullins 2000). Indeed, all volumetric changes (induced during the shrinkage) can affect the calculated volumetric water content, and hence the shape of water retention curve.

As water is infiltrating, soil remains at saturation. At this later, soil porosity corresponds to the volumetric water content θ. Soil with the greatest pore space would be a well aggregated clay. According to simulations (Figs. 5, 6, 7, 8), after about 3 days of infiltration process, the amount of water, that is held in soil after it has been fully wetted and all gravitational water has been drained away, becomes remarkable. Hence, field capacity is reached. This later depends on the size and the type of soil particles (soil texture) where it is reached more rapidly in a coarser textured soil (high proportion of sand) than in a fine textured soil (high proportion of clay). At field capacity, the soil holds the maximum amount of water that can be stored and can be used by plants. For practical purposes, clay soil holds much more water than, for example, sandy–clay soil.

5.3 Unsaturated Hydraulic Conductivity Curve

One of the main properties considered to govern flow is the unsaturated hydraulic conductivity. Knowledge of the highly nonlinear relationship between unsaturated hydraulic conductivity K and volumetric water content θ is required for widely-used models of water flow and solute transport process in the unsaturated zone. Hence, Fig. 10 represents the curve of the variation of unsaturated hydraulic conductivity in function of volumetric water content.

Fig. 10
figure 10

Water retention curve of unsaturated zone of our study

Full size image

Figure 10 shows that the numerical results of our simulations agreed well with the general trend (Musy and Soutter 1991). However, a small deviation is observed and it is essentially due to the relative difference between the composition (percentage of each component) of our clay soil and that of the clay studied by Musy and Soutter (1991). We note here, that the trend obtained by these later represents the general variation of hydraulic conductivity for all clay soil types independently of the details of their components (Fig. 11).

Fig. 11
figure 11

Variation of unsaturated hydraulic conductivity K in function of volumetric water content θ

Full size image

In unsaturated soils, hydraulic conductivity is highly affected by the volumetric water content of soil. According to Fig. 9, the water content θ decreases with the increase of the pressure head h. Hence, this decrease induces, according to Fig. 10, a brief decrease of the unsaturated hydraulic conductivity K. This later decreases as the vadose zone dries out and it induces the increase of the resistance of unsaturated system to releasing the surplus water. In other words, K remains very low (with values less than 0.003 m/day) until 80% from the saturation (where water content values are about 0.35 m3/m3) and it increases rapidly near the saturation (for θ ~ 0.42 m3/m3).

The properties of soil matrix affect strongly the hydraulic conductivity. For example, for the clay soils, the fine texture (especially its small pores size) affects directly the water immigration and decreases the hydraulic conductivities. The hydraulic conductivity of these materials is generally smaller than 10−4 ms−1 (Schuhmann et al. 2011).

6 Conclusion

Our numerical results have shown that the polluted water issue from Meghogha wadi discharged into the Tangier’s bay does not spread just into the bay under a hydrodynamic process (Belcaid et al. 2012), but it also infiltrates into the environment soil by means of its porosity. Indeed, our study discusses the ability of the soil of Tangier’s bay region to receive the water drained at once by the Meghogha wadi and the bay.

Our simulations show that the water infiltration process from the saturated zones (Meghogha wadi and the bay) to the unsaturated zone (environment soil of the wadi) is relatively slow. However, this process accelerates as the pressure head h increases. Indeed, the water infiltrates to unsaturated zone until this later reaches the saturation. Consequently, the maximum water content θmax is reached. Soils remain at saturation so long as water is infiltrating. As the pressure head increases, the water is expelled from the pores because of suction. So that, the volumetric water content starts to decrease while the degree of saturation remains constant.

Unsaturated hydraulic conductivity K is affected by the volumetric water content θ. Indeed, when this later decreases, the vadose zone dries out. As a consequence, the resistance of unsaturated system increases releasing surplus water. Hence, the K decreases.