1 Introduction

Underground roadway and railway tunnels, tunnels for utility lines and water pipelines are indivisible parts of the civil infrastructure. In the recent decades, explosion incidents caused by terrorist activities inside underground infrastructure have proved to be a growing threat to the human civilization. Internal explosion in a tunnel is often more hazardous than an explosion above ground due to multiple reflections of the blast-induced shock wave on the tunnel wall causing channeling of the shock wave. Hence, in order to safeguard the tunnels from explosion incidents, it is necessary designing the tunnel adequately to sustain the blast loading and for this, it is necessary to understand the response of the tunnel subjected to blast loading, experimentally and numerically. The present work focuses on the advanced numerical analysis of tunnels subjected to blast loading.

Numerical analysis of tunnels subjected to blast loading has been reported in the literature by several researchers. Chille et al. (1998) investigated dynamic response of an underground electric power plant subjected to internal explosive loading using three-dimensional (3-D) numerical analysis procedures. Coupled fluid–solid interaction was considered in their study, however, the nonlinearity and failure behavior of rock and concrete, as well as the interaction between different solid media, were not simulated. Choi et al. (2006) used 3-D finite element (FE) method and coupled fluid–solid interaction to study the blast pressure and resulting deformation in concrete lining for traffic tunnels in rock. They reported that the blast pressure on tunnel lining was not the same as the reflected pressure obtained using conventional weapons (CONWEP; Department of the Army, the Navy, and the Air Force 1990). Lu (2005), Gui and Chien (2006), Liu (2009) used FE procedure to perform blast analysis of tunnel in soil subjected to external blast loading and reported stresses and deformations in the tunnel. However, they did not consider high strain rate behavior of soil. Also, blast load was simulated using CONWEP. Feldgun et al. (2008a, b) and Karinski et al. (2008) used the variational difference method to analyze tunnels and cavities subjected to blast loads. Yang et al. (2010) studied the response of metro tunnels subjected to above ground explosion through finite element analysis procedure and von-Mises material model for soil. Liu (2011, 2012) performed finite element analysis of tunnel with cast-iron lining subjected to blast loading simulated using CONWEP. Nateghi (2012) evaluated blast-induced ground vibration for minimizing negative effects on surrounding structures. Higgins et al. (2012) carried out plain strain analysis of tunnels in sand subjected to internal blast loading considering high strain rate stress–strain response of soil simulated using a bounding surface plasticity constitutive model. However, their study assumed elastic stress–strain response for concrete lining in the tunnel. Qiu et al. (2011) used the CEL tool available in Abaqus for simulation of large deformation problem of geomechanics. Chakraborty et al. (2013) compared the performance of steel and concrete conventional tunnel linings with sandwich panel linings made up of shock absorbing foam material as the core of the sandwich panels in tunnel subjected to blast loading. The blast load was calculated through a coupled fluid dynamics simulation and applied as a pressure pulse on the tunnel lining. Sainoki and Mitri (2014) studied rock mass vibration subjected to blast loading. However, advanced 3-D nonlinear dynamic analyses of tunnel in soil with reinforced concrete (RC) tunnel lining, rigorous modeling of the reinforcement cage inside the lining, properly simulated explosive load using the Jones-Wilkins-Lee (JWL) equation of state (EOS), interaction between explosive cloud and the surrounding lining and soil are rather unavailable in the literature, perhaps due to the extremely challenging nature of the problem. The present investigations are addressing these issues by conducting rigorous and detailed FE analysis of tunnels in soil subjected to internal blast loading.

The specific objectives of the present study are to perform 3-D nonlinear dynamic FE analysis of tunnel subjected to internal blast loading and to understand the response of tunnel lining and surrounding soil when subjected to blast loading. The FE analyses are performed herein using the commercially available FE software Abaqus version 6.11 (Abaqus manual version 6.11). The soil and RC lining of the tunnel are modeled using Lagrangian elements. The trinitrotoluene (TNT) explosive and the surrounding air have been modeled using the Eulerian elements. Blast loading may generate up to 104/s strain rate in any material (Ngo et al. 2007; Dusenberry 2010). Hence, strain rate dependent material properties have been used for all materials used herein. Soil stress–strain response is simulated using the Drucker–Prager constitutive model (Lee and Salgado 1999; Liu 2009). The stress–strain response of concrete lining is simulated using the concrete damaged plasticity model (Chakraborty et al. 2013). The stress–strain behavior of steel reinforcement is simulated using the Johnson–Cook (J–C) plasticity model (Johnson and Cook 1983). The pressure–volume relationship of the explosive is simulated using the JWL EOS. Parametric sensitivity studies have been performed by varying (1) concrete lining thickness (t w), (2) weight (W) of TNT explosive used and (3) angle of internal friction of soil (ϕ). The analysis results have been studied for stress and deformation of RC lining, lining reinforcement and soil, pressure on the lining, damage and plastic strain in lining and attenuation of shock wave velocity in soil with distance from the source of the blast.

2 Three-Dimensional Finite Element Modeling

2.1 Lagrangian Finite Element Modeling of Soil and RC Lining

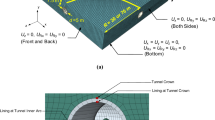
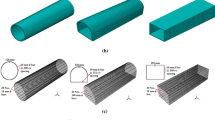
The 3-D FE model of the tunnel in soil is developed using Abaqus version 6.11 software using the Lagrangian analysis option. The FE mesh of the soil, tunnel lining and reinforcement inside the lining are shown in Fig. 1a–c. A 20 m long tunnel geometry has been considered in soil with the central axis of the tunnel assumed at a depth of 7.5 m from the ground surface as shown in Fig. 1a. Figure 1b presents an enlarged mesh and various points in the mesh where the results have been studied. It may be noted that in the present study, the stress and displacement results are studied at tunnel crown, tunnel side wall, lining at tunnel crown and lining at tunnel side wall. Here, tunnel crown and tunnel side wall represent the locations in the soil at the lining-soil interface whereas lining at tunnel crown and lining at tunnel side wall represent the locations on the inner surface of the lining as shown in Fig. 1b. The concept of the segmental lining has been ignored herein in order to simplify the modelling. The steel reinforcement has been modeled with 10 and 12 mm diameter bars with yield strength of 300 MPa in longitudinal and hoop reinforcement directions, respectively. The hoop reinforcement rings are placed at 250 mm centre-to-centre spacing. The longitudinal reinforcement bars are placed at a distance of 850 mm centre-to-centre. Two layers of hoop reinforcement have been placed with 120 mm distance between the inner and the outer hoop reinforcement rings. Reinforcement specifications are obtained from a metro rail corporation in India and simplified for the purpose of simulation. The 20 m long and 5 m diameter tunnel is placed in a soil domain of 20 m long and 15 m × 15 m cross-section. The dimensions of the soil domain are considered larger than the size of the tunnel in the present study so as to minimize the reflection of the shock wave from the soil boundaries. The FE models of the soil and concrete lining are developed in Abaqus/CAE using the 3-D part option. The eight-node brick element (C3D8R) with reduced integration, hourglass control, and finite membrane strains are used in the FE mesh which are available in Abaqus/Explicit. The C3D8R elements are capable of simulating the blast response of the structure. Mesh convergence and boundary convergence studies have been performed and higher mesh density with a minimum element size of 10 mm has been used in tunnel lining and soil close to the lining to achieve higher accuracy. The steel reinforcement has been modeled using the two node beam elements (B31; Tan 2010, Mosallam et al. 2015). Proper bonding between concrete and reinforcement bars is assured by embedding the reinforcement bars in the RC lining. The contact between tunnel lining and soil has been modeled with the general contact option in Abaqus with hard contact in the normal direction and frictionless contact in the tangential direction. The effect of excavation and construction stages are not considered in the present study. Among the boundary conditions, the bottom plane of the soil domain has been fixed in all Cartesian directions, e.g. x, y and z. The vertical side planes and the front and back side planes of the soil domain and the lining have been constrained as detailed in Fig. 1a, by constraining the normal displacements perpendicular to the plane (U x, U y and U z). Figure 1d shows the location of explosive inside the tunnel modeled using the Eulerian elements.

Fig. 1
figure 1

Tunnel geometry and reinforcement details. a Typical geometry, mesh and boundary conditions for tunnel in soil. b Enlarged mesh for tunnel with tunnel lining. c Tunnel lining and reinforcement details. d Explosive inside tunnel

Full size image

2.2 Eulerian Finite Element Modeling of Explosive

The explosive material has been modeled using the Eulerian modeling technique in Abaqus. Figure 1d shows the location of TNT explosive inside the tunnel. In Abaqus coupled Eulerian–Lagrangian (CEL) modeling option, the Eulerian material flows through the finite element mesh. Thus, the simulation that generates a large amount of deformation and stress in the elements and thus, results in an error or inaccuracy in the Lagrangian analysis may be successfully carried out using the CEL tool. Herein, Eulerian continuum 3-D eight node reduced integration elements (EC3D8R) are used (Abaqus/Explicit user manual 2011) to model the explosive material and the surrounding air domain inside the tunnel. These Eulerian elements are completely or partially filled with explosive material, while the rest of the Eulerian grid is void. In the Eulerian analysis, the material is tracked by means of Eulerian volume fractions (EVF) when it flows through the mesh. The EVF represents the ratio by which each Eulerian element is filled with material; i.e. EVF = 1 representing element completely filled with material and EVF = 0 representing completely void elements. The boundary of Eulerian material may not match the element geometry during the analysis and has to be recomputed at each time instance when the material flows through the mesh. Dimensions of the grid containing Eulerian elements are taken sufficiently large to prevent the loss of air from the Eulerian grid after the blast as this would have lead to artificial loss of kinetic energy and consequently reduce the accuracy of the obtained results. The Eulerian and Lagrangian elements can interact with each other through the general contact defined between explosive, air and tunnel lining surface. Free outflow boundary conditions are defined by the boundaries of the air domain, thus, blast pressure when reaches the boundaries of air domain, it propagates freely out of the air domain without any reflection. A fine mesh of Eulerian elements is necessary to efficiently capture the propagation of the blast wave through the air, surrounding concrete lining and soil. The mesh convergence study has been performed in the present study to decide the smallest element size in the Eulerian domain.

The pressure (p) for the TNT explosive can be calculated using Jones-Wilkins-Lee (JWL) equation of state (EOS; Larcher and Casadei 2010) given by

$$ p = A\,\left( {1 - \frac{\omega }{{R_{1} \bar{\rho }}}} \right)e^{{ - {\text{R}}_{1} \bar{\rho }}} + B\,\left( {1 - \frac{\omega }{{R_{2} \bar{\rho }}}} \right)e^{{ - {\text{R}}_{2} \bar{\rho }}} + \omega \rho {\kern 1pt} e_{\text{int}} $$
(1)

where A, B, R 1, R 2 and ω are material constants for TNT explosive. Parameters A and B represent the magnitudes of pressure, \( \bar{\rho } \) is the ratio of the density of the explosive in the solid state (\( \rho_{\text{sol}} \)) to the current density (ρ) and e int is the specific internal energy at atmospheric pressure. In the JWL equation of state, the first two exponential terms on the right-hand side represent high pressure generated during the explosion and the last term on the right-hand side is a low-pressure term which deals with high volume due to the explosion. Table 1 shows the material properties used herein for the JWL EOS, as suggested by Larcher and Casadei (2010).

Table 1 JWL material properties for TNT explosive.
Full size table

2.3 Constitutive Models of Materials

2.3.1 Constitutive Model of Concrete

Concrete in RC lining has been modeled as M30 grade (maximum compressive strength 30 MPa) using the concrete damaged plasticity model in Abaqus. The stress–strain relation of concrete damaged plasticity model is given by

$$ \upsigma_{\text{t}} = \left( { 1- d_{\text{t}} } \right)D_{ 0}^{\text{el}} :\left( {\upvarepsilon -\upvarepsilon_{\text{t}}^{\text{pl}} } \right) $$
(2)
$$ \sigma_{\text{c}} = \left( { 1- d_{\text{c}} } \right)D_{ 0}^{\text{el}} :\left( {\upvarepsilon -\upvarepsilon_{\text{c}}^{\text{pl}} } \right) $$
(3)

where t and c represent tension and compression behavior, respectively. Here, \( \sigma_{\text{t}} \) and \( \sigma_{\text{c}} \) are tensile and compressive stress vectors, respectively; \( \varepsilon_{\text{t}}^{\text{pl}} \) and \( \varepsilon_{\text{c}}^{\text{pl}} \) are plastic strains; \( d_{\text{t}} \) and \( d_{\text{c}} \) are the damage variables which are considered functions of plastic strain; \( D_{ 0}^{\text{el}} \) is the undamaged initial elastic modulus. The yield function in the considered damaged plasticity model is given by Lubliner et al. (1989) and later modified by Lee and Fenves (1998), given by

$$ F = \left( {\sqrt {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}} \sqrt {\bar{s}:\bar{s}} } \right) - 3\upalpha\bar{p} +\upbeta\left\langle {{\hat{\bar{\sigma }}}_{\hbox{max} } } \right\rangle - \gamma \left\langle { - {\hat{\bar{\sigma }}}_{\hbox{max} } } \right\rangle - \left( {1 -\upalpha} \right){\bar{\sigma }}_{c} = 0 $$
(4)

where

$$ \upalpha = \frac{{\left( {{{\upsigma_{{{\text{b}}0}} } \mathord{\left/ {\vphantom {{\upsigma_{{{\text{b}}0}} } {\upsigma_{{{\text{c}}0}} }}} \right. \kern-0pt} {\upsigma_{{{\text{c}}0}} }}} \right) - 1}}{{2\left( {{{\upsigma_{{{\text{b}}0}} } \mathord{\left/ {\vphantom {{\upsigma_{{{\text{b}}0}} } {\upsigma_{{{\text{c}}0}} }}} \right. \kern-0pt} {\upsigma_{{{\text{c}}0}} }}} \right) - 1}} $$
(5)
$$ \upbeta = \frac{{\bar{\sigma }_{c} }}{{\bar{\sigma }_{t} }}\left( {1 - \alpha } \right) - \left( {1 + \alpha } \right) $$
(6)
$$ \gamma = \frac{{3\left( {1 - K_{\text{c}} } \right)}}{{2K_{\text{c}} - 1}} $$
(7)
$$ {\bar{\sigma }}_{\text{c}} = \frac{{\upsigma_{\text{c}} }}{{\left( {1 - d_{t} } \right)}} $$
(8)
$$ {\bar{\sigma }}_{\text{t}} = \frac{{\upsigma_{\text{t}} }}{{\left( {1 - d_{\text{t}} } \right)}} $$
(9)

where \( {\hat{\bar{\sigma }}}_{\hbox{max} } \) is the maximum principal effective stress; \( \bar{s} \) is the deviatoric stress tensor; \( {{\sigma_{\text{b0}} } \mathord{\left/ {\vphantom {{\sigma_{\text{b0}} } {\sigma_{\text{c0}} }}} \right. \kern-0pt} {\sigma_{\text{c0}} }} \) is the ratio of initial equibiaxial compressive yield stress to initial uniaxial compressive yield stress; d t is the damage variable and \( K_{\text{c}} \) is the ratio of the second deviatoric stress invariant on the tensile meridian to that on the compressive meridian at initial crushing for any given value of effective mean stress, \( \bar{p} = \, \left( {\bar{\sigma }_{ 1} + \bar{\sigma }_{ 2} + \bar{\sigma }_{ 3} } \right) / 3 \).

The concrete damaged plasticity model assumes a non-associated plastic flow. The plastic potential function G p used for this model is given by

$$ G_{\text{p}} = \sqrt {\left( {\varepsilon \sigma_{\text{t0}} \tan \psi } \right)^{2} + \left( {\frac{3}{2}s:s} \right)} - \bar{p}\tan \psi $$
(10)

where ψ is the dilation angle at mean stress-deviatoric stress plane; \( \sigma_{\text{t0}} \) is the uniaxial tensile stress at failure, value of which is set by the user and ɛ is the eccentricity parameter. If the eccentricity is zero, the plastic potential function becomes a straight line. In the present study, the modulus of elasticity of concrete E c = 27.4 GPa, compressive strength of concrete f ck = 30 MPa, mass density ρc = 2400 kg/m3 and Poisson’s ratio νc = 0.2 have been considered. The material properties used herein for the concrete are listed in Table 2. Figure 2a, b show the stress–strain curves for M30 concrete in compression and tension, respectively (Carreira and Chu 1985, 1986). Figure 2c, d show the damage density-strain curves for M30 concrete in compression and tension, respectively (Al-Rub and Kim 2010). Damage density is defined as the ratio of the total damaged area to the whole cross sectional area; damage density value is varied from 0 to 1—density = 0 means the material is undamaged and density = 1 means the material is completely damaged. The strain rate dependent strength properties of concrete and the dynamic increment factor (DIF) under compressive and tensile loading are obtained from Bischoff and Perry (1991). Herein, DIF values of 2.1 and 6 at 100/s strain rate have been used on the static compressive and tensile strength values of concrete, respectively.

Table 2 Material properties for concrete
Full size table
Fig. 2
figure 2

(Carreira and Chu 1985, 1986; Al-Rub and Kim 2010)

Static stress–strain and damage-strain curves for M30 grade of concrete under compression and tension at 100/s strain rate.

Full size image

2.3.2 Constitutive Model of Steel

The stress–strain behavior of steel reinforcement has been modeled using Johnson–Cook (J–C) model (Johnson and Cook 1983). The dynamic yield stress (σ)–strain (ε) relationship of the J–C model is given by

$$ \upsigma = \left( {A + B\upvarepsilon^{\text{n}} } \right){\kern 1pt} \left( {1 + C\log_{\text{e}}\upvarepsilon^{*} } \right)\left( {1 - T^{{*{\text{m}}}} } \right) $$
(11)

where \( \varepsilon^{ *} \) is a dimensionless plastic strain; \( \upvarepsilon^{*} = {{{\dot{\varepsilon }}} \mathord{\left/ {\vphantom {{{\dot{\varepsilon }}} {{\dot{\varepsilon }}_{0} }}} \right. \kern-0pt} {{\dot{\varepsilon }}_{0} }} \) in which \( \dot{\varepsilon } \) is the equivalent plastic strain rate and \( {\dot{\varepsilon }}_{0} \) = 1/s is the reference strain rate. Here, A, B, C, m and n are the model parameters; T *is the homologous temperature. In the present study, the temperature dependence of material stress–strain response has not been considered. For steel, modulus of elasticity E s = 210 GPa, tensile yield strength f s = 300 MPa, density ρs = 7800 kg/m3 and Poisson’s ratio ν = 0.3 have been considered. For strain rate dependent modeling using the J–C model, the material constants are obtained from mechanical testing and adopted herein as A = 360 MPa, B = 635 MPa, C = 0.075, n = 0.114 for strain rate of 100/s. The material properties used herein for steel are listed in Table 3. These values are computed based on tensile test data of the material as per the J–C model by neglecting the temperature effects (Goel et al. 2012).

Table 3 Material properties for steel
Full size table

2.3.3 Constitutive Model of Soil

The stress–strain response of soil has been simulated using the Drucker–Prager plasticity model. The yield criterion of the Drucker–Prager model is given by

$$ F = \frac{q}{2}\left[ {1 + \frac{1}{K} - \left( {1 - \frac{1}{K}} \right)\left( {\frac{r}{q}} \right)^{3} } \right] - p'\tan \beta - d = 0 $$
(12)

where q is the deviatoric stress \( \left[ { = \sqrt {{ 3\mathord{\left/ {\vphantom { 3{ 2 { }}}} \right. \kern-0pt} { 2 { }}}} \sqrt {s_{\text{ij}} :s_{\text{ij}} } } \right] \), \( s_{\text{ij}} \) is the deviatoric stress tensor, p′ is the mean stress = (σ′1 + σ′2 + σ′3)/3, K is a scalar parameter that determines the shape of the yield surface and maintains the convexity of the yield surface in the deviatoric (π) plane, r is the third invariant of the deviatoric stress tensor. The parameter β is related to the angle of internal friction \( \upphi \) at the stage of no dilatancy, i.e. the critical state of sand using a correlation given by

$$ \tan\upbeta = \frac{\sqrt 3 \sin \upphi }{{\sqrt {1 + \left( {{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}} \right)\sin^{2} \upphi } }} $$
(13)

and d is the hardening parameter related to cohesion, c through a correlation given by

$$ \frac{d}{c} = \frac{\sqrt 3 \cos \upphi }{{\sqrt {1 + \left( {{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}} \right)\sin^{2} \upphi } }} . $$
(14)

For sands, the cohesion (c) is considered to be zero. The plastic potential surface, G P of the model is given by

$$ G_{\text{P}} = \frac{q}{2}\left[ {1 + \frac{1}{K} - \left( {1 - \frac{1}{K}} \right)\left( {\frac{r}{q}} \right)^{3} } \right] - p^{\prime}\tan \psi_{\text{tp}} $$
(15)

where \( \psi_{\text{tp}} \) is related to the dilatancy angle, ψ through a correlation given by

$$ \tan \psi_{\text{tp}} = \frac{\sqrt 3\sin \psi }{{\sqrt { 1 { + (1/3)}\sin^{2} \psi } }} . $$
(16)

A non-associated flow rule is considered in the present analysis by considering the dilatancy angle of sand to be different from the angle of internal friction. For sand, modulus of elasticity E sand = 28 MPa, mass density ρsand = 1560 kg/m3 and Poisson’s ratio νsand = 0.2, angle of internal friction ϕ = 30° and dilation angle ψ = 5° have been considered. The material properties used herein for the Ottawa sand are listed in Table 4. The strain rate dependent stress–strain response of sand has been obtained from Veyera and Ross (1995). Figure 3 shows the stress–strain relationship of Ottawa sand at 1000/s strain rate as obtained from Veyera and Ross (1995).

Table 4 Material properties for sand
Full size table
Fig. 3
figure 3

(Veyera and Ross 1995)

Stress–strain curve for Ottawa sand at 1000/s strain rate

Full size image

2.4 Solution Scheme

The dynamic explicit analyses using the CEL approach have been performed using central difference integration scheme in a single step. This scheme uses a time increment (Δt) that is smaller than the Courant time limit, Δt ≤ l/c, where l is the smallest element dimension and c is the speed of the sound wave in the medium in which it travels. For studying the response of the complete 20 m tunnel section, the duration of analysis is maintained at 16 ms (msec) such that the shock wave can travel through the complete length of the tunnel. In order to properly represent the propagation of the blast-induced compressive stress wave, the artificial bulk viscosity is activated by employing quadratic and linear functions of volumetric strain rates with default values of 1.2 and 0.06, respectively (Abaqus/Explicit user manual 2011).

3 Validation Studies for Fe Model and CEL Procedure

To ensure the validity of the present numerical simulations the results of CEL analyses of blast loading on a concrete slab have been compared with (1) the analysis results when blast loading is simulated using a pressure pulse calculated using UFC 3-340-02 manual and the modified Friedlander’s equation, (2) numerical simulation results collected from Du and Li (2009) and (3) results of experimental investigation carried out by Zhao and Chen (2013).

3.1 Validation for Capability of JWL EOS in Blast Simulation

The capability of JWL EOS in simulating blast load has been checked by comparing numerical simulation results for blast-induced displacement of a concrete slab for blast pressures simulated using JWL and that calculated using UFC 03-340-02. Herein, a 1.2 m × 1.2 m × 90 mm concrete slab subjected to a blast load caused by 1.69 kg TNT charge weight (W) at three different scaled distances of 0.5, 1 and 2 m/kg1/3 have been analyzed numerically using the CEL method. In the CEL method, the TNT explosive has been simulated using the JWL EOS. The M25 concrete has been modeled with a compressive strength of 25 MPa, mass density of 2500 kg/m3, Young’s modulus of 25 GPa and Poisson’s ratio of 0.2. The boundaries of the concrete slab are restrained in all three Cartesian directions, e.g. x, y and z. In another set of analysis, the blast load is calculated using the UFC 3-340-02 (2008) manual and the modified Friedlander’s equation for the same scaled distances mentioned above and the same charge weight of 1.69 kg. Figure 4a, c show the comparison of central node displacement of the concrete slab calculated from the analysis results using the JWL model and its comparison with the results obtained from the simulation using UFC 03-340-02. From Fig. 4 it is observed that the results obtained from both the analyses compare with reasonable accuracy. Figure 5a–c show the pressure time histories calculated using JWL EOS. The peak pressure values are compared with the pressure magnitudes obtained from UFC 3-340-02 manual. The blast pressure generated using JWL EOS is observed to be slightly higher as compared to that calculated using UFC 3-340-02 which is conservative.

Fig. 4
figure 4

Comparison of central node displacement time histories for simulations using JWL EOS and pressure time history calculated from UFC 3-340-02 and modified Friedlander’s equation

Full size image
Fig. 5
figure 5

Pressure time histories obtained from CEL simulations using JWL EOS and comparison of peak pressure obtained from UFC 3-340-02

Full size image

3.2 Validation for Blast Analysis Using JWL with the Numerical Analysis Results

The validity of the current modeling approach using the CEL method and JWL EOS for explosive is also ensured by comparing the current analysis results with the numerical simulation results collected from Du and Li (2009). Du and Li analyzed the dynamic behavior of RC slabs under blast loading. A RC slab of size 2 m × 1 m × 100 mm is used in these analyses. The slab has been reinforced with 10 and 12 mm diameter bars at 100 mm centre-to-centre spacing, in both the directions placed at the mid-depth of the slab. A charge weight of 1000 kg TNT is placed at a stand-off distance of 10 m from the centre of the slab. The boundaries of the concrete slab are restrained in three Cartesian directions, e.g. x, y and z. The FE software LS-Dyna was used for the analysis performed by Du and Li (2009). The Johnson–Holmquist material model was used to simulate concrete stress–strain response whereas the Cowper and Symond’s model was used for steel. In the present study, the RC slab model with the same explosive charge weight and scaled distances as considered by Du and Li (2009) is prepared using the CEL procedure. The JWL EOS has been used to model the explosive material. The material properties of steel and concrete have been considered to be the same as that assumed by Du and Li (2009). The concrete damaged plasticity model has been used to simulate the stress–strain response of concrete whereas von-Mises model has been used for steel. The concrete in RC slab has been modeled with a compressive strength of 23.7 MPa, mass density of 2400 kg/m3, the shear modulus of 12.7 GPa and Poisson’s ratio of 0.2 as mentioned in Du and Li (2009). Steel in RC slab has been modeled with yield strength of 335 MPa, mass density of 7800 kg/m3, Young’s modulus of 207 GPa and Poisson’s ratio of 0.3. Figure 6 shows the maximum displacement of the concrete slab when subjected to blast load for 80, 90, 100, 110 and 120 mm slab thicknesses. It is observed that the current simulation results compare with that from the literature with reasonable accuracy, thus duly validating the CEL method based simulation approach adopted herein.

Fig. 6
figure 6

Variation of maximum displacement for different concrete slab thicknesses obtained from CEL simulations using JWL EOS with the results reported by Du and Li (2009)

Full size image

3.3 Validation for Blast Analysis Using JWL with the Experimental Data

The CEL simulation results have also been compared with experimental data for different charge weights, e.g. 0.2, 0.31 and 0.46 kg placed at a stand-off distance of 400 mm from the centre of the slab as reported by Zhao and Chen (2013). A RC slab of size 1 m × 1 m × 40 mm has been used for the analyses. The RC slab has been reinforced with 6 mm diameter bars, spaced at 75 mm centre-to-centre in both the directions. The boundaries of the RC slab are restrained in three Cartesian directions, e.g. x, y and z along two sides. In the present study, a similar model has been prepared using the CEL procedure and the charge weights as considered by Zhao and Chen (2013) are taken. The material properties of steel and concrete have been considered to be the same as assumed by Zhao and Chen (2013). Concrete in RC slab has been modeled with a compressive strength of 39.5 MPa and Young’s modulus of 28.3 GPa. Steel in RC slab has been modeled with yield strength of 600 MPa and Young’s modulus of 200 GPa. The concrete damaged plasticity model has been used for concrete whereas the von-Mises model has been used for steel. Table 5 shows the central node displacement of the concrete slab under blast load for different slab thicknesses. Reasonable agreement of the current simulation results with that from experimental and numerical investigations reported by Zhao and Chen (2013) is observed in Table 5.

Table 5 Comparison of numerical simulation results with experimental data.
Full size table

4 Results and Discussion on Parametric Studies

Parametric sensitivity studies are carried out for two RC lining thicknesses (t w) = 350 and 550 mm, three different angles of internal friction of soil (ϕ) = 25°, 30°, 35° and three different charge weights of explosive (W) = 25, 50 and 100 kg. Table 6 presents the different analysis cases considered herein to study the response of tunnel subjected to blast loading. Figure 7 shows the expansion of explosive gas cloud inside the tunnel at 0, 0.4 and 1.2 ms for 100 kg explosive charge. Figure 8a–d show a typical deformed cross-section of soil around the tunnel at different time instances from the time of detonation, e.g. 0, 5, 10 and 15 ms for 100 kg charge weight. Soil deformation increases with increase in time. Figure 8e shows the deformed soil and lining mesh at the end of the analysis. Substantial deformation is observed in both the lining and the surrounding soil. Figure 9 shows the paths along which the results are extracted and presented herein. It may be noted that for minimizing the boundary effect, only central 10 m path length has been considered for extracting the results. Herein, tensile stresses are considered positive and displacement values in the direction of the positive x, y and z-axes are considered positive.

Table 6 Cases considered for numerical simulations of tunnel
Full size table
Fig. 7
figure 7

Propagation of explosion cloud for 100 kg charge weight

Full size image
Fig. 8
figure 8

Deformation of soil surrounding the tunnel at different time instances subjected to 100 kg charge weight

Full size image
Fig. 9
figure 9

Paths defined for visualization

Full size image

4.1 Variation of RC Lining Thickness

Figure 10a, b show the displacement of RC lining along two paths—one along tunnel crown and the other along tunnel side wall, for 350 and 550 mm RC lining thicknesses at 4 ms for 50 kg TNT charge weight. The 350 mm RC lining thickness show maximum displacement at its crown just above the explosive. It is observed that just after the explosion, explosive cloud propagates towards the tunnel boundaries and hits the RC lining. Irregular peak displacement in the soil is observed in Fig. 10c, d due to the damage of RC lining at few places and lesser modulus of soil as compared to the RC lining. Figure 11a, b show the displacement of reinforced concrete lining along two paths—one along tunnel crown and the other along tunnel side wall, for 350 and 550 mm RC lining thicknesses at 16 ms for 50 kg TNT charge weight. Higher damage and displacement are observed in the 350 mm thick tunnel lining as compared to the 550 mm thick tunnel lining when subjected to blast loading. The magnitudes of deformation in the lining at tunnel crown and tunnel left side wall for 550 mm thick tunnel lining are almost 90.7 and 66.7% lesser than that of 350 mm thick tunnel lining, respectively. The tunnel crown moves downward, i.e. in the negative y-direction and the left side wall moves inward, i.e. in positive x direction when subjected to blast. Hence, displacement of the crown is negative and that of the left side wall is positive. The deformed shape of the tunnel cross-section can be seen in the inset of Fig. 11c. Figure 11c shows the displacement time history at tunnel crown in the lining immediately above the explosive. For both the lining thicknesses, displacement at the tunnel crown increases with time. Figure 11d, e show the displacement of soil along the tunnel crown and the left side wall surrounding the RC lining. Irregular displacement pattern is observed in the soil for 350 mm thick tunnel lining due to complete damage of the lining. The 550 mm thick lining exhibits comparatively lesser damage. Thus, soil displacement remains uniform along the path. The magnitudes of soil deformation at tunnel crown and left side wall for 550 mm thick tunnel lining are almost 39.4 and 92.2% lesser than that of 350 mm thick tunnel lining, respectively. Figure 11f shows the displacement time history of soil at the tunnel crown. For 350 mm thick tunnel lining, shock wave propagates through the soil and pushes the soil in the upward direction. However, for 550 mm thick lining, soil moves in the downward direction along with the tunnel lining. It is observed that the upward soil displacement for 350 mm thick lining is much higher in magnitude than the downward displacement of soil for 550 mm thick lining.

Fig. 10
figure 10

Displacement of RC lining and soil for different lining thicknesses subjected to 50 kg charge weight at 4 ms

Full size image
Fig. 11
figure 11

Displacement of RC lining and soil for different lining thicknesses subjected to 50 kg charge weight

Full size image

Figure 12a, b show the hoop stress time histories in tunnel lining for two different lining thicknesses at the crown and at left side wall respectively, when subjected to 50 kg charge weight. The hoop stress increases with increasing time. In the tunnel lining, 75 MPa stress is induced which is higher than the maximum dynamic tensile strength of concrete, i.e. 11 MPa. The stresses developed at the soil-lining interface are presented in Fig. 12c, d, respectively. High value of stress is generated in soil. However, soil is weak in tension and cannot sustain tensile stress. Hence, failure of soil at the interface happens under blast loading.

Fig. 12
figure 12

Hoop stress in different RC lining thickness subjected to 50 kg charge weight

Full size image

Figure 13a, b show the y-directional displacement of soil at tunnel crown and x directional displacement of soil at the left side wall along a path at 250 mm inside the soil from the lining. It is observed that displacement in the soil surrounding the 350 mm thick RC lining is more as compared to that for 550 mm thick RC lining. Up to 400 mm displacement is observed in the soil due to blast. The magnitudes of soil deformation along tunnel crown and left side wall for 550 mm thick tunnel lining are almost 28.6 and 9.2% lesser than that of 350 mm thick tunnel lining, respectively. Figure 13c shows the y-directional displacement of soil mass from tunnel crown to the ground level. It may be observed that under the effect of the shock wave, RC lining, and soil, both are showing higher deformation up to 250 mm height from the tunnel crown. However, above 250 mm, the deformation of soil decreased due to the attenuation of the shock wave. Hence, for the safe design of tunnel, 250 mm soil domain above the lining should be reinforced to prevent soil damage in this region.

Fig. 13
figure 13

Displacement of soil 250 mm inside the lining crown and left side wall for different lining thicknesses at 16 ms subjected to 50 kg charge weight

Full size image

Figure 14a, c show the pressure generated in the RC lining at three different time instances—2, 5, and 10 ms. Maximum blast pressure generates at 2 ms, i.e. 3.76 MPa and gradually decreases with time. At 10 ms, a maximum of 0.28 MPa pressure remains on the tunnel lining. In the soil, however, the pressure increases with increasing time due to increasing damage of concrete and propagation of shock wave. At 2 ms, maximum 13.32 MPa pressure is exhibited close to the middle of the path whereas at 5 and 10 ms, 31.32 and 46.03 MPa pressures generate towards the side of the path. Figure 15a–c show the displacement contours surrounding the tunnel at 5, 10, and 15 ms time instances. As time progresses, the influence zone affected by the internal blast also increases.

Fig. 14
figure 14

Pressure in RC lining and soil for different lining thicknesses subjected to 50 kg charge weight

Full size image
Fig. 15
figure 15

Deformation contours in soil at different time instances subjected 50 kg charge weight and 350 mm lining thickness (deformation in m)

Full size image

4.2 Variation of Charge Weights

For understanding the response of tunnel under different charge weights, three different charge weights of 25, 50, and 100 kg have been considered in the current investigations. Lining thickness has been maintained 350 mm in all cases. Stiffness degradation of concrete is defined using concrete tension damage (DAMAGET) parameter, available in concrete damaged plasticity model. Damage value equal to 0 means material is undamaged and damage value equal to 1 means material is completely damaged. Figure 16a–c show the tensile damage contours in the concrete lining (DAMAGET) for 25, 50, and 100 kg charge weights at 10 ms time. It may be clearly seen from the plots that as the charge weight increases, the damage contours extend along the length of the tunnel. It is observed that the propagation of damage is not uniform with respect to charge weight. For 50 kg charge weight, more damage was observed in tunnel roof close to support whereas for 100 kg charge weight, more damage was observed in the side wall and tunnel roof immediately above explosive. Effect of blast loading was also observed in the steel reinforcement inside the RC lining. Figure 16d–f show the deformation contours in reinforcement for three different charge weights at 15 ms. Displacement in the reinforcement increases with increase in the charge weight.

Fig. 16
figure 16

Tensile damage and reinforcement deformation contours for 350 mm thickness RC lining at 15 ms for different charge weights (deformation in m)

Full size image

Figure 17a, b show the displacement response of RC lining for the paths along the tunnel crown and the left side wall. Higher displacement is observed in lining for 100 kg charge weight as compared to 25 kg charge weight which is reasonable. At tunnel crown, 50 kg explosive produces a higher displacement in the lining, however, at tunnel side wall, 100 kg explosive produces the maximum displacement in the lining. The magnitudes of deformation in lining at tunnel crown for 25 kg charge weight are almost 74.9% lesser than that of 50 kg charge weight. Figure 17c shows displacement time history plot of lining at tunnel crown. The displacement of lining at the crown increases with increasing time for all charge weights. Figure 17d, e show the displacement response in soil, both at the tunnel crown and at the side wall. In both the cases, higher displacement is observed for 100 kg charge weight as compared to that for 25 kg charge weight. The magnitudes of soil deformation at tunnel crown for 25 and 50 kg charge weights are almost 58.4 and 3.3% lesser than that of 100 kg charge weight, respectively. Figure 17f presents the displacement in soil at the tunnel crown. It is observed that the displacement of soil is not consistent with increasing charge weight. Downward soil displacement is observed for 25 and 100 kg explosives whereas upward soil displacement is observed for 50 kg explosive due to irregular damage pattern under 50 kg charge explosion.

Fig. 17
figure 17

Displacement of RC lining and soil mass for different charge weights with 350 mm RC lining thickness and 30° angle of internal friction

Full size image

4.3 Variation of Angles of Internal Friction of Soil

Herein, three different angles of internal friction of soil, e.g. 25°, 30° and 35° have been considered for the analyses. The analyses have been performed using 50 kg TNT explosive and 350 mm tunnel lining thickness. Figure 18a, b show the deformation of the RC lining for the paths along the tunnel crown and the left side wall. The results show clearly that the deformation of the lining decreases with increasing angle of internal friction of the surrounding soil. The magnitudes of deformation in lining at tunnel crown for 35° angle of internal friction of soil is almost 56.8 and 43.7% lesser than that of 25° and 30° angle of internal friction of soil, respectively. Figure 18c shows the time history of deformation at the tunnel crown. Deformation of tunnel lining decreases with increasing angle of internal friction of the surrounding soil. Thus, sands with a higher angle of internal friction may be used in blast resistant design of tunnels. Figure 18d, e show the deformation in soil. Soil deformation decreases significantly for 30° and 35° angles of internal friction as compared to that for 25° angle of internal friction. The magnitudes of soil deformation at tunnel crown for 35° angle of internal friction of soil is almost 70.2 and 60.3% lesser than that of 25° and 30° angle of internal friction of soil, respectively. Figure 19a–c show the deformation contours surrounding the tunnel for three different angles of internal friction values. As the angle of internal friction increases, the deformation of tunnel decreases which is reasonable. The hoop stress generated in tunnel lining has been presented in Fig. 20a, b for tunnel crown and left side wall, respectively for three different angles of internal friction values. The stress generated at the soil-lining interface has been presented in Fig. 20c, d for tunnel crown and left side wall, respectively for three different angles of internal friction values. Higher stress is observed for 25° angle of internal friction as compared to that for 35° angle of internal friction in both soil and tunnel lining.

Fig. 18
figure 18

Displacement of RC lining and soil mass for different angles of internal friction subjected to 50 kg charge weight and 350 mm RC lining thickness

Full size image
Fig. 19
figure 19

Deformation of soil mass for different angles of internal friction at 15 ms, subjected to 50 kg charge weight, 350 mm lining thickness (deformation in m)

Full size image
Fig. 20
figure 20

Hoop stress for different angles of internal friction with 350 mm RC lining thickness subjected to 50 kg charge weight

Full size image

4.4 Comparison of Displacement, Plastic Strain, and Spatial Velocity

Figure 21a–c show the generation of plastic strain in the tunnel lining for all the different cases considered in this study. The maximum plastic strain is observed in tunnel lining for 25° angle of internal friction of soil. Also, the higher plastic strain is exhibited in the lining in 350 mm thick RC lining as compared to that in 550 mm thick tunnel lining. Figure 22a–c show the particle velocity in soil at the soil-lining interface, 1 m from tunnel crown and at the ground surface. Particle velocity decreases from the interface to the ground surface. Faster decrease in particle velocity is observed for the higher value of the angle of internal friction.

Fig. 21
figure 21

Plastic strains at lining reinforcement

Full size image
Fig. 22
figure 22

Spatial velocities from tunnel crown (soil level) to ground subjected to 50 kg charge weight

Full size image

5 Conclusions

Three-dimensional nonlinear finite element analyses of the tunnel in soil subjected to internal blast loading are carried out using the coupled Eulerian–Lagrangian analysis tool in finite element software Abaqus/Explicit. The soil and reinforced concrete lining have been modeled using the Lagrangian elements. The explosive TNT has been modeled using the Eulerian elements. Parametric sensitivity studies have been performed for different (1) tunnel lining thicknesses, (2) explosive charge weights and (3) angles of internal friction of soil. The following conclusions are drawn:

  1. 1.

    The blast induced pressure on the tunnel lining increases with the increase in charge weight. Both the lining and the surrounding soil undergo significant deformation which also increases with increasing charge weight.The magnitudes of soil deformation at tunnel crown for 25 and 50 kg charge weights are almost 58.4 and 3.3% lesser than that of 100 kg charge weight, respectively.

  2. 2.

    Deformation of tunnel lining decreases with increasing lining thickness and increasing friction angle of soil. The 550 mm thickness RC lining shows 90% lesser deformation than the 350 mm thickness RC lining. The soil with 35° angle of internal friction shows 70% lesser deformation than 25° angle of internal friction of soil.

  3. 3.

    Blast-induced velocity in soil attenuates with increasing distance from the source of the blast. Faster reduction in soil particle velocity is observed for the higher value of friction angle.

  4. 4.

    Plastic strain in tunnel lining increases with increasing charge weight, decreasing friction angle and decreasing lining thickness.