1 Introduction

The fracture toughness of a tough material can be related to crack tip constraint at the crack tip. Classically, the characterization of crack tip stress–strain fields was founded on two-dimensional asymptotic plane strain \(HRR\) fields (Hutchinson 1968; Rice and Rosengren 1968) which established the concept of single parameter elastic–plastic fracture mechanics, \(J\). The limitation of the single parameter elastic–plastic fracture mechanics has been demonstrated by (McMeeking and Parks 1979) and a similar conclusion was also derived from (Shih and German 1981) in which the loss of \(J\)-dominance was scaled through a non-dimensional classification parameter, \(\mu\), which gave a scale of 25 and 200 for bending and tension respectively.

Using Williams asymptotic polynomial expansion (Williams 1957), the loss of \(J\)-dominance was correlated by a second term of the asymptotic expansion known as the \(T\)-stress (Rice 1974). Subsequent finite-element results of (Betegon and Hancock 1991) proposed a two-parameter approach (\(K\)–\(T\)) while (O'Dowd and Shih 1991, 1992) proposed a two-parameter \(J\)–\(Q^{2D}\) approach to characterize the plane strain crack tip fields. To extend the two-parameter approach to characterize deformation fields away from the tip, a higher order crack tip deformation was proposed through the \(J\)–\(A_{2}\) approach (Yang et al. 1993).

Based on the two-parameter \(J\)–\(Q^{2D}\) approach (O'Dowd and Shih 1991), the parameter \(Q^{2D}\) is an amplitude factor and a second order non-singular term of the \(HRR\) field. Following the \(Q^{2D}\) stress description of constraint loss, a positive \(Q^{2D}\) was related to a fully constrained field while a negative \(Q^{2D}\) meant that the crack tip stress field, has lost constraint in accord with the drop from the fully constrained field usually taken to refer to a plane strain \(HRR\) or a small-scale yielding reference field:

$$ \sigma_{ij}^{2D} = \left( {\sigma_{ij} } \right)^{HRR} + Q^{2D} \sigma_{o} \delta_{ij} $$
(1)

where \(\sigma_{ij}\) are the Cartesian components of the stress tensor and \(\sigma_{o}\) is the initial yield stress based on a von Mises plastic yielding solution in uniaxial tension. The difference between the cracked geometry and the reference stress field was found to be relatively constant at both angular and radial positions in the forward sector of a crack tip \(\left( { - \pi /4 < \theta < \pi /4} \right)\). Therefore \(Q^{2D}\) can be inferred from the constant stress difference field through the uniform hydrostatic stress field ahead of the crack tip. Taking the hoop stress, \(\sigma_{\theta \theta }\), \(Q^{2D}\) is generally defined as:

$$ Q^{2D} = \frac{{\sigma_{\theta \theta }^{2D} - \sigma_{\theta \theta }^{HRR} }}{{\sigma_{o} }}\; at\; \theta = 0^\circ \;and\; r = \frac{2J}{{\sigma_{o} }} $$
(2)

The \(J\)–\(Q^{2D}\) provided a systematic approach to the determination of the stresses at the crack tip and allowed the prediction of the toughness of materials in problems related to elastic–plastic fracture. This approach has been suited to failure assessment diagrams and implemented in codes (R6 2001; BS7910 2005) to estimate the integrity of structures containing defects.

Classically, the assessment of a three-dimensional elastic–plastic crack tip field was usually based on a condition that a three-dimensional elastic–plastic crack tip field was bounded by the extremes of a plane strain field at the mid-plane of a crack front and a plane stress field at the crack front enjoining a free surface. Notable publications based on finite-element analysis of three-dimensional elastic–plastic crack tip analysis before the establishment of the in-plane constraint effects can be seen in (Wellman et al. 1985; Brocks and Olschewski 1986; Sorem et al. 1989). As the second terms \(T\), \(Q^{2D}\) and \(A_{2}\) were identified, attempts were made to use these parameters to quantify three-dimensional elastic–plastic crack tip stress fields. However, it seemed that the \(T\), \(Q^{2D}\) and \(A_{2}\) approaches were unable to uniquely quantify the out-of-plane constraint loss because the way the stresses develop in three-dimensional elastic–plastic field was different from the two-dimensional plane strain elastic–plastic crack tip field. Significantly, three-dimensional elastic–plastic crack tip stress fields were not distanced independent ahead of the crack as compared to the two-dimensional plane strain fields. Moreover, the asymptotic fields near the free surface do not conform to a plane stress field as expected at the crack tip (\(x_{3}\)/\(B\) = 0.5, \(r\) = 0). (Newman et al. 1993; O'Dowd 1995; Nevalainen and Dodds 1995; Yuan and Brocks 1998; Kim et al. 2001, 2003) concluded that the \(Q^{2D}\) and the \(A_{2}\) terms were able to characterize three-dimensional fields that approach a plane strain field, but some aspects of three-dimensional elastic–plastic crack tip fields were not fully characterized through the \(Q^{2D}\) and the \(A_{2}\) terms. Due to the findings of the \(Q^{2D}\) and \(A_{2}\) dominance to characterize three-dimensional elastic–plastic crack tip fields, other directly derived techniques also faced a similar limitation such as the \(h\) term (Henry and Luxmoore 1997) to characterize three-dimensional elastic–plastic crack tip fields.

A three-dimensional elastic–plastic crack tip stress field characterization was presented following the concept based on the HRR fields as the \(J\)–\(Tz\) approach, to describe out-of-plane crack tip stress fields (Guo 1993a, b, 1995). Using the \(J\)–\(Tz\) approach, (Graba 2017) proposed that a three-dimensional elastic–plastic crack tip constraint can be quantified through:

$$ Q^{*} = \frac{{\sigma_{22}^{{3D\left( {FE} \right)}} - \sigma_{22}^{{\left( {J - Tz} \right)}} }}{{\sigma_{o} }} ;\;r = \frac{2J}{{\sigma_{o} }}\; at\; \theta = 0^\circ $$
(3)

where the \(Q^{*}\) is the stress difference of the opening stress (\(\sigma_{22}\)) from a cracked three-dimensional elastic–plastic finite-element results to a \(J\)–\(Tz\) deduced opening stress. The inherent limitation of the \(HRR\) fields to characterize the in-plane constraint effect was apparent in the \(J\)–\(Tz\) approach and was remedied through a \(J\)–\(Tz\)–\(Q^{2D}\) solution (Zhao et al. 2008). However, (Hebel et al. 2007; Shlyannikov et al. 2014; Yusof and Leong 2019) demonstrated insensitivity of the \(J\)–\(Tz\)–\(Q^{2D}\) approach in characterizing highly compressive \(T\) or \(Q^{2D}\) geometries.

Detailed finite-element formulations of (Nakamura and Parks 1990; Hom and McMeeking 1990) demonstrated that straight-through cracks in a fully constrained field (\(T\)/\(Q\) = 0) was found to be bounded by a plane strain field at the mid-plane (\(x_{3}\)/\(B\) = 0) of the model and at the free surface (\(x_{3}\)/\(B\) = 0.5, \(r_{p}\)/\(B\) > 1.5) a plane stress field. In a different development, (Yusof and Hancock 2005) demonstrated that at the free surface, an elastic–plastic corner field was shown to develop with a uniaxial tension field ahead of the crack. Using non-hardening thin plate and full-field fully constrained and unconstrained deep cracks, (Yusof 2019) demonstrated that three-dimensional constraint fields differ hydrostatically but are similar in respect of the maximum stress deviator independent of distance, \(r\), and position along the crack front, \(z\), while the normal stresses of a three-dimensional elastic–plastic crack tip field can be described through:

$$ \frac{{\sigma_{ij} }}{{\sigma_{o} }}^{op} = \left[ {\left( {\frac{{\sigma_{ij} }}{{\sigma_{o} }}} \right)_{T,Q}^{pl.\varepsilon } - \left( {\frac{{\sigma_{ij} }}{{\sigma_{o} }}} \right)^{pl.\sigma } } \right]\exp \left( {\frac{{\gamma_{{\left( {r,n} \right)}} J_{loc} }}{{z\sigma_{o} }}} \right) + \left( {\frac{{\sigma_{ij} }}{{\sigma_{o} }}} \right)^{pl.\sigma } for \left( {\theta = 0^\circ and\,i = j} \right) $$
(4)

while the constraint sensitivity parameter \(\gamma_{{\left( {r,n} \right)}}\) was given as:

$$ \gamma_{{\left( {r,n} \right)}} = \left[ {2.3\left( {\frac{{r\sigma_{o} }}{{J_{loc} }}} \right) + 4.3} \right]\exp \left( { - 0.4n} \right) + \left[ {1.7\left( {\frac{{r\sigma_{o} }}{{J_{loc} }}} \right) + 3.7} \right] $$
(5)

within a micro-separation distance of \(2J_{loc} /\sigma_{o} \le r \le 5J_{loc} /\sigma_{o}\) and strain hardening range of \(\left( {1 < n \le \infty } \right)\).

From the \(J\)–\(T\) and the \(J\)–\(Q^{2D}\) approaches, it was shown that highly constrained crack tip fields such as a deep crack in bend bar lose in-plane constraint in shallow cracks because the plastic zone spread to the cracked face and demonstrated loss of crack tip constraint (Al-Ani and Hancock 1991; O'Dowd and Shih 1991). Analyses of three-dimensional effects on shallow cracks discussed by (Nevalainen and Dodds 1995; Kim et al. 2001, 2003) demonstrated that crack tip constraint behaved as expected in that it was highly constrained at the mid-plane (\(x_{3}\)/\(B\) = 0) and constraint was lost along the crack front to the free surface (\(x_{3}\)/\(B\) = 0.5). However, the stress fields from the shallow cracked bend models were not unique and depended on geometry, crack length, loading level, and hardening response when characterized by the second parameter \(A_{2}\). Based on these reviews, it can be deduced that the characterization of three-dimensional elastic–plastic crack tip stress–strain fields of shallow cracks in fully constrained and unconstrained flow fields problems is still unsatisfactory in some respects.

Although the two-dimensional two-parameter approaches provided a conservative estimate of crack tip constraint loss through a plane strain approximation field, toughness of real cracks is affected by the three-dimensional state of crack tip constraint. Further discussions on the characterization of the three-dimensional elastic–plastic crack tip problem within a contained yielding limit can be found from the scaling approach \(\sigma_{1}\)/\(\sigma_{y}\) (Dodds et al. 1991) and the \(T_{33}\) approach (Meshii and Tanaka 2010). The scaling approach became the basis of the \(J\)–\(\sqrt \phi\) approach, (Mostafavi et al. 2010) and \(J\)–\(\sqrt {A_{p} }\) approach, (Yang et al. 2013). It was apparent that these approaches have been used to explain the combined effects of the in-plane and the out-of-plane constraint, but some questions are still open in regard to non-cleavage type fracture ensued by large scale crack tip yielding due to the understanding that these approaches were based on cleavage fracture with weakly compressive \(T\)/\(Q^{2D}\) cracked configurations.

In this paper, a further investigation on the application of (Yusof 2019) approach to characterize three-dimensional elastic–plastic crack tip fields of shallow crack affected by thickness was carried out. Systematic analyses of three-dimensional elastic–plastic crack tip fields were undertaken to understand the effect of crack lengths, geometries, thickness, full strain hardening range, and loading modes through models of fully constrained single-edge notch bend and unconstrained center crack panels in tension.

2 Numerical methods and material responses

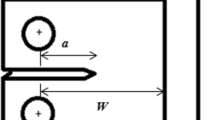
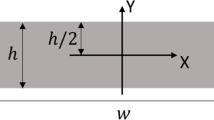
The crack tip plasticity of deep to shallow crack problems in full-field single edge notch bend (henceforth SENB) and center crack panel in tension (henceforth CCP) solutions have been studied by modeling a range of thicknesses and lengths of cracked models. Figure 1 shows the height and width of the SENB geometries were in accordance with the size requirement given in ASTM-E1820 (ASTM-E1820-11 2011), by maintaining a consistent size ratio of \(H/W\) = 2. A total of four crack length sizes considered for the finite-element models were (\(a/W\) = 0.1, 0.2, 0.3 and 0.5). The crack lengths were chosen based on the definition of deep and shallow cracks demonstrated by (Al-Ani and Hancock 1991). The SENB geometries with a crack to ligament length ratio, \(a/W\) < 0.3 and the CCP model with \(a/W\) < 0.5 were categorized as shallow cracked models. The models were also defined with two normalized thicknesses, \(B\)/\(\left( {W - a} \right)\) = 1 and 0.05. The model with \(B\)/\(\left( {W - a} \right)\) = 1 represented a thick cracked model while \(B\)/\(\left( {W - a} \right)\) = 0.05 was at a one-twentieth thickness of the thick model represented a thin cracked model. The crack tip constraint fields from deep to shallow cracks in different model thicknesses and the cracked models required 16 full-fields SENB and CCP cracked finite-element models. The form factors considered for the SENB and CCP geometries in this paper are summarized in Table 1.

Fig. 1
figure 1

Schematics of the SENB and the CCP models implemented in the finite-element analysis

Full size image
Table 1 The form factors of the SENB and the CCP models
Full size table

To facilitate the creation of the finite-element models, a meshing algorithm was developed as discussed in (Leong et al. 2021). Input files generated by the algorithm were transferred and processed with the finite-element code ABAQUS (ABAQUS 2012). The models were meshed with twenty-noded brick elements as typified by the crack tip meshes depicted in Fig. 2a and b. Along the model thickness direction, the thickness of each element layer decreases gradually from the mid-plane (\(x_{3} /B\) = 0) to the free surface (\(x_{3} /B\) = 0.5) as illustrated in Fig. 3. It is also helpful to measure the distance along the crack front from the free surface to the mid-plane using the notation \(z\) = (\(B/2\))-\(x_{3}\) where \(B\) is the thickness of the model, which in such instance would be \(z/B\) = 0 at the free surface and \(z/B \)  = 0.5 at the mid-plane.

Fig. 2
figure 2

a A focused mesh at a sharp crack tip. b The full field mesh of SENB and CCP models for each (\(a\)/\(W\)) configuration

Full size image
Fig. 3
figure 3

The thickness mesh configuration for \(B\)/(\(W\)–\(a\)) = 1 (thick) and 0.05 (thin)

Full size image

The meshing pattern adopted for the semi-annular region was highly focused at the crack tip and was similar for all the crack geometries as depicted in Fig. 2. The nodes at the crack tip along the \(X_{1}\) and \(X_{2}\) coordinates at the crack tip, (0,0), were collapsed to become coincident but independent which cause the crack tip to demonstrate a 1/\(r\) singularity in the strains on all radial fans of the mesh. Within region A, twenty-four concentric rings of elements in the semi-annular region, with each one consisting of 24 elements spaced equally at an angle interval of 7.5°. The size of the elements was increased gradually with a bias ratio of 5 from the crack tip to the outermost boundary of region B. The ratio of the smallest element, \(r_{e}\), to the radius of the semi-annular region, rsa was given as re/rsa = 0.02. The models were loaded on the remote boundary by either a pure couple or by uniform displacement as shown in Fig. 1.

In the present paper, the plastic stress–strain response was represented by a Ramberg–Osgood power law of the form:

$$ \frac{\varepsilon }{{\varepsilon_{o} }} = \frac{\sigma }{{\sigma_{o} }} + \alpha \left( {\frac{\sigma }{{\sigma_{o} }}} \right)^{n}, \quad \sigma \ge \sigma_{o} $$
(6)

The material constants \(\alpha\) and \(n\) were set at 3/7 and 3, 6, 13 and \(\infty\) respectively, although most results were shown for \(n\) = 13. The exponent \(n\) = \(\infty \) is to model non-hardening plasticity. Equation (6) was generalized into \(J_{2}\) flow theory to give an incremental relation, which for the Ramberg–Osgood relation takes the form:

$$ d\varepsilon_{ij} = \frac{1}{E}\left[ {\left( {1 + \nu } \right)d\sigma_{ij} - \nu \delta_{ij} d\sigma_{kk} } \right] + \frac{3}{2} \alpha n\left( {\frac{{\sigma_{e} }}{{\sigma_{o} }}} \right)^{n - 2} \frac{{S_{ij} }}{E} \frac{{d\sigma_{e} }}{{\sigma_{o} }} $$
(7)

The material model employed in this paper was based on an incremental isotropic elastic–plastic model as described in ABAQUS, (ABAQUS 2012). The problem presented in this paper is similar to the case of monotonously increasing loading for a stationary crack in which the domain integral method (Shih et al. 1986; Moran and Shih 1987) was used to infer a path-independent \(J\) as discussed in (Kuna 2013) and implemented in ABAQUS, (ABAQUS 2012). With a sufficiently refined finite element mesh as described in (Leong et al. 2021), a prevalent \(HRR\) field was ensured, thereby allowing \(J\) as a characteristic parameter that defined the elastic–plastic three-dimensional crack tip fields. The technique to extract \(J\) adopted in this paper has been demonstrated in (Nakamura and Parks 1990; Betegon and Hancock 1991; Al-Ani and Hancock 1991), and more recently in (Yusof 2019).

Although, the use of strain hardening plasticity is an appropriate description to engineering materials, however, the analysis of crack tip fields through non-hardening plasticity provides insight into the stresses around the crack tip through slip-line fields proposed by (Prandtl 1920) and applied in small-scale yielding crack tip fields analysis by (Rice 1968; Du and Hancock 1991). To achieve non-hardening crack tip deformation plastic flow, the Poisson’s ratio was set to \(v = 0.49\) to prevent element locking while the Poisson’s ratio \(v = 0.3\) was adopted for the strain hardening materials.

The deformation level for the SENB and CCP models was measured by the non-dimensional classification parameter, \(\mu\), given as:

$$ \mu = \frac{{c\sigma_{o} }}{{J_{loc} }} $$
(8)

where \(c\) = (\(W\)–\(a\)) is the uncracked ligament. The local \(J\), \(J_{loc}\), is the \(J\) values extracted along the crack front tip, \(x_{3}\)/\(B\) = 0 (known as the mid-plane) to \(x_{3}\)/\(B\) = 0.5 (known as the free surface) and vary weakly as the free surface was approached. The parameter \(\mu\) is related to the \(J\)-dominance criterion for plane strain fields discussed by (McMeeking and Parks 1979) and (Shih and German 1981) in which a limit of plane strain \(J\)-dominance for SENB and CCP at \(\mu\) > 25 and 200 was proposed respectively. The restriction of plane strain \(J\)-dominance has been applied in related analysis at \(\mu\) = 50 and 200 for the SENB and CCP models respectively to ensure numerical stability of finite-element solutions.

3 Results and discussions

3.1 \(Q^{3D}\) fields along the crack front

In a through cracked three-dimensional geometries, crack tip constraint can be assessed through proximity to a plane strain field at the mid-plane and to a plane stress field at the free surface. Assessment of three-dimensional crack tip constraint can be quantified through a difference of the constant stress sector to a reference \(HRR\) field, \(Q^{3D}\):

$$ Q^{3D} = \frac{{\sigma_{\theta \theta }^{{3D\left( {FE} \right)}} - \sigma_{\theta \theta }^{HRR} }}{{\sigma_{o} }};\;r = \frac{{2J_{loc} }}{{\sigma_{o} }}\; at\; \theta = 0^\circ $$
(9)

Table 2 shows that at the maximum applied load, plasticity has spread to an equivalent of the thickness of the plate in the thick SENB and CCP geometries and was greater than six times in the thin SENB models of the smallest crack length. In the thin CCP, the plastic zone, \(r_{p}\), extended to twenty times the thickness, \(B\), of the model.

Table 2 The size of the plastic zone as a function of load, \(\mu\)
Full size table

Figure 4 shows the deep to shallow cracks of the SENB and the CCP models plotted along the crack front at \(r\) = 2 \(J_{loc}\)/\(\sigma_{o}\) for hardening case \(n\) = 13 at the limit of \(J\)-Dominance defined in Table 2. For the thick SENB in Figs. 4a, the \(Q^{3D}\) fields start slightly below the \(Q^{3D}\) = 0 as expected from a thick and deep crack similar to results presented in (O'Dowd and Shih 1991). As the crack lengths are reduced, the \(Q^{3D}\) field drops in accord to the reduction of crack length within \(x_{3}\)/\(B\) < 0.4 but near the free surface, the \(Q^{3D}\) fields are reversed to become less negative in the shallow cracks compared to the deep cracks. Figure 4b shows the \(Q^{3D}\) fields for the thin SENB whereby at the limit of \(J\)-Dominance, the deep crack has a highly negative \(Q^{3D}\) compared to other examined crack lengths. It is shown that the shallowest crack (\(a\)/\(W\) = 0.1) developed the least negative \(Q^{3D}\) field. Unlike the thick SENB which shows a \(Q^{3D}\) field rank change close to the free surface, the thin SENB \(Q^{3D}\) field drops continuously from the mid-plane to converge to a similar \(Q^{3D}\) field level of other crack lengths at the free surface.

Fig. 4
figure 4

\(Q^{3D}\) fields for thick and thin SENB and CCP with different crack lengths along the crack front at r = 2 \(J_{loc}\)/\(\sigma_{o}\) for strain hardening models, \(n\) = 13 at load, \( \mu\) = 50 (SENB) and 200 (CCP)

Full size image

The \(Q^{3D}\) fields for the thick CCP models are shown in Fig. 4c in which at the limit of \(J\)-Dominance, the deep crack develops the highest negative \(Q^{3D}\) field while the intermediate crack lengths of \(a\)/\(W\) = 0.2 and 0.3 show a reduced negative \(Q^{3D}\) field. The shallowest crack demonstrated a \(Q^{3D}\) field slightly above the deep crack but lower than the intermediate crack lengths. Figure 4d shows the \(Q^{3D}\) fields for the thin CCP, here the \(Q^{3D}\) field pattern is similar to the thin SENB but at a different amplitude.

Analyses of the three-dimensional elastic–plastic crack tip constraint based on a \(Q^{3D}\) parameter demonstrated that out-of-plane constraint drops from a level of constraint initially affected by the associated in-plane effect (at the mid-plane to a low constraint at the free surface) for various SENB and CCP geometries regardless of the crack length and thickness combinations. However, the combinations of crack length and thickness caused the rank of the out-of-plane constraint loss to decrease from the shallow crack to deep crack for the thin SENB and CCP geometries and the thick CCP geometries. In contrast, the thick SENB geometries showed an out-of-plane constraint decrease from the deep crack to shallow crack in a similar trend shown in two-dimensional plane strain problems of (Al-Ani and Hancock 1991; O'Dowd and Shih 1991).

3.2 Hoop stress ahead of the crack front

The state of the three-dimensional elastic–plastic crack tip hoop stress (\(\sigma_{\theta \theta }\)/\(\sigma_{o}\)) in all crack lengths examined are compared to the \(HRR\) plane strain and \(HRR\) plane stress fields data given in (Shih 1983) are shown in Fig. 5. Even at the highest plastic loading level, a fully constrained plane strain field is maintained at the crack tip of the deep cracked thick SENB geometry as illustrated in Fig. 5a in which the hoop stress in the deep thick SENB approaches the \(HRR\) plane strain field \(Q^{2D}\) = 0 fields. At different crack lengths, the hoop stresses ahead of the crack are dependent on the distance at the mid-plane. For the same load, the reduction of the crack length caused the hoop stress to drop in accord with the reduction of \(Q^{3D}\) field from slightly negative in the thick deep SENB to highly negative in the thick shallow SENB models as indicated in Fig. 4a.

Fig. 5
figure 5

The hoop stress for the thick and thin SENB and CCP models at the mid-plane for various crack lengths at load, \( \mu\) = 50 and 200 respectively

Full size image

Figure 5b shows the thin SENB models hoop stress and for all the crack length considered, approach the \(HRR\) plane strain field at distances of \(r\) very close to the crack tip but the stress field drop rapidly ahead of the crack tip with the thin deep SENB model demonstrating the largest hoop stress loss. The hoop stress fields for different crack lengths ahead of the crack has been ranked according to the \(Q^{3D}\) drop because from Fig. 4b, the \(Q^{3D}\) field for deep thin SENB is highly negative and develop hoop stress lower than the shallow thin SENB (\(a\)/\(W\) = 0.1) which shows a less negative \(Q^{3D}\). Eventually, the hoop stress for all crack lengths approaches the \(HRR\) plane stress field at distances away from the crack tip.

Figure 5c depicts the effect of the crack lengths on the thick CCP models. Here, the crack tip constraint loss first arises from in-plane effects and is followed by out-of-plane effects. The thick CCP models exhibit highly negative \(Q^{3D}\) field (Fig. 4c) and demonstrate a large drop of crack tip constraint from the \(HRR\) plane strain field even in deep cracks (\(a\)/\(W\) = 0.5). A similar trend of crack tip constraint loss is seen in shallower crack lengths and constraint loss is also distance-dependent from the crack tip similar to the hoop stress state ahead of the crack in the SENB geometries.

The thin CCP models hoop stress fields can be evaluated from Fig. 5d. The loss of crack tip constraint in the thin CCP due to the out-of-plane effect has a similar trend to the thin SENB. Ahead of the crack, the hoop stress drops rapidly in the thin deep crack CCP than the shallow cracked thin CCP. The shallow cracked thin CCP has a lower negative \(Q^{3D}\) than the deep cracked thin CCP in Fig. 4d, which in turn shows higher hoop stress in the shallow cracked thin CCP than the thin cracked deep CCP model.

3.3 Effect of crack length on the Hoop stress

To examine the effect of constraint in different crack lengths along the crack front, the hoop stress along the crack front from the mid-plane (\(x_{3}\)/\(B\) = 0) to the free surface (\(x_{3}\)/\(B\) = 0.5) for deep to shallow cracks of the SENB and CCP models at loads near \(J\)-dominance (\(\mu\) = 50 and 200 for SENB and CCP respectively) at a distance \(r\) = 2 \(J_{loc}\)/\(\sigma_{o}\) are shown in Fig. 6. The thick SENB model is shown in Fig. 6(a) and for the deepest crack (\(a\)/\(W\) = 0.5), the crack tip constraint approaches the \(HRR\) plane strain field at the mid-plane but as the crack length at the mid-plane is reduced, the hoop stress for shallower crack length is lost. Along the crack front, away from the mid-plane, the hoop stress decays as the crack lengths become shorter but the hoop stress is slightly elevated as the free surface is approached for crack lengths \(a\)/\(W\) < 0.3.

Fig. 6
figure 6

The hoop stress in SENB and CCP thick and thin models along the crack front from the mid-plane to the free surface at \(r\) = 2 \(J_{loc}\)/\(\sigma_{o}\) at load \(\mu\) = 50 and 200 respectively

Full size image

The thin SENB hoop stress along the crack front is shown in Fig. 6b. At the mid-plane, the deep thin SENB lose constraint and approached the \(HRR\) plane stress field but as the crack length is reduced, the hoop stress increases slightly but within a range considered to have experienced constraint loss as it is more than ten percent drop from the \(HRR\) plane strain field following the (Shih and German 1981) criterion for \(HRR\) dominance. Along the crack front, the hoop stresses for \(a\)/\(W\) > 0.3 approach the \( HRR\) plane stress but as the crack lengths become shallower \(a\)/\(W\) < 0.3, the hoop stress demonstrates a slight increase.

The hoop stress for the thick CCP geometries is shown in Fig. 6c. Thick CCP geometries for all crack lengths demonstrate a highly negative \(Q^{3D}\) field as shown in Fig. 4c and exhibit loss of crack tip constraint due to the in-plane effect. At the mid-plane, initially, the hoop stress is lost due to the in-plane effect for the deep thick CCP geometries, and the level of hoop stress is maintained for deep shallow cracks as well. Along the crack front from the mid-plane, the hoop stress drops and approach the \(HRR\) plane stress field near the free surface (\(x_{3}\)/\(B\) = 0.5) from the deep crack to the shallow crack.

The thin CCP hoop stress is shown in Fig. 6d. For the thin deep CCP at the mid-plane at \(r\) = 2 \(J_{loc} /\sigma_{o}\) the hoop stress demonstrates a large departure from the \(HRR\) plane strain field but as the crack lengths become shallower, the hoop stress increases to a level equivalent to the thin SENB and is retained at that level for the shallow crack. At other crack front distances, the hoop stress constraint demonstrates a similar pattern of reduction from the mid-plane curve to the free surface.

For both the thick and thin SENB and CCP models, at all crack lengths, the free surface field does not conform to the \(HRR\) plane stress field at the measured distance of \(r\) = 2 \(J_{loc}\)/\(\sigma_{o}\). This is consistent with the three-dimensional elastic perfectly-plastic fields described in (Yusof and Hancock 2005) and (Yusof 2019) in which the stress field at the vertex of the intersection of the free surface and the crack front develops into a corner field and diminishes when the plane stress field dominates ahead of the free surface crack as discussed by (Nakamura and Parks 1990; Hom and McMeeking 1990).

3.4 Three-dimensional crack tip constraint characterized by \(J\)–\(\Delta \sigma\)

Three-dimensional assessments of crack tip constraint by (Yusof 2019) indicated that the out-of-plane effect at \(r\) = 2 \(J_{loc}\)/\(\sigma_{o}\) was the change of the strain state from a near plane strain conditions at the mid-plane to a plane stress field at the free surface. It was found that the three-dimensional elastic–plastic crack tip stress field can be described by \(J_{loc}\)/\(z\sigma_{o}\) from which three-dimensional elastic–plastic crack tip fields were expected to develop near plane strain fields remote from a free surface, (\(z\) → ∞), and at small deformation levels, (\(J_{loc}\) → 0). While crack tip stress field was expected to be lost near a free surface, and at large deformation levels (\(z\) → 0, \(J_{loc}\) → \(\infty\)). In a three-dimensional elastic–plastic crack tip field, the in-plane constrained effect (\(Q^{2D}\) < 0) caused the crack tip stress fields to lose constraint as crack tip plasticity increased, and then the out-of-plane constraint caused the loss of constraint across the thickness.

Conventionally, the hoop stress and the mean stress were used in the description of the stress state at the crack tip because both were identified as the main drivers for cleavage and ductile mechanisms of crack extension. In cleavage, failure was associated by low energy separation of atomic planes which occurs when the crack opening stress attains a critical value, \(\sigma_{\theta \theta }\) = \(\sigma_{critical}\) and usually at two-grain diameters ahead of the crack at \(\theta\) = 0 \(^\circ\) as discussed by (Ritchie et al. 1973). (Rice and Tracey 1969) showed that ductile failure occurs by nucleation, growth, and coalescence of micro-voids which forms at inclusion and second phase particles by interface decohesion or particle cracking. The voids grow by plastic strain and mean stress \(\left( {\sigma_{m} = \sigma_{kk} /3} \right)\) and finally coalesce with the blunting crack tip. The crack opening stress \(\left( {\sigma_{\theta \theta } } \right)\) and the mean stress \(\left( {\sigma_{m} } \right)\) are thus important drivers for the two mechanisms of crack extension.

The hoop stress (Fig. 7) and the mean stress (Fig. 8) for different hardening rates (\(n\) = 3, 6, 13, \(\infty\)) for the SENB and CCP geometries for different crack lengths at \(r\) = 2 \(J_{loc}\)/\(\sigma_{o}\) are shown to compare the state of the stresses in cracked geometries at different crack lengths. Firstly, the SENB geometries are associated with a fully constrained flow field which shows that the highly constrained flow fields that approach the equivalent strain hardening \(HRR\) fields are found near the mid-plane or when the load is below the small-scale yielding load. With increasing load and as the hoop stress and the mean stress are examined along the crack front, the stresses drop according to Eq. (4) and approach the \(HRR\) plane stress field. The CCP geometries initially demonstrate in-plane constraint loss as plasticity starts to develop at the crack tip as the highest stresses attained at the mid-plane are below the \(HRR\) fields and then the out-of-plane constraint develops similar to the decay seen in the SENB geometries.

Fig. 7
figure 7

The hoop stress, \(\sigma_{\theta \theta }\), ahead of the crack at \(r\sigma_{0} /J_{loc} = 2\) for the thick and thin SENB and CCP models at crack lengths 0.1 \(\le\) \(a\)/\(W\) \(\le\) 0.5 for strain hardening index (\(n\) = 3, 6, 13, \(\infty\)) at increasing load levels for SENB and CCP geometries respectively

Full size image
Fig. 8
figure 8

The mean stress, \(\sigma_{m}\), ahead of the crack at \(r\sigma_{0} /J_{loc} = 2\) for the thick and thin SENB and CCP models at crack lengths 0.1 \(\le\) \(a\)/\(W\) \(\le\) 0.5 for strain hardening index (\(n\) = 3, 6, 13, \(\infty\)) at increasing load levels for SENB and CCP geometries respectively

Full size image

Figures 7 and 8 demonstrate that both Eqs. (4) and (5) can represent three-dimensional elastic–plastic stress fields of different crack lengths, strain hardening responses, thickness, and crack configurations. To connect the out-of-plane constraint loss to the in-plane constraint loss scheme (\(J\)–\(Q^{2D}\)) widely used for a conservative estimate of fracture, a scheme for three-dimensional elastic–plastic crack tip constraint is proposed as follows:

$$ \frac{{{\Delta }\sigma }}{{\sigma_{o} }}^{3D} = \frac{{{\Delta }\sigma }}{{\sigma_{o} }}^{ip} + \frac{{{\Delta }\sigma }}{{\sigma_{o} }}^{op} $$
(10)

where \({\Delta }\sigma^{ip}\)/\(\sigma_{o}\) is the in-plane constraint loss and \({\Delta }\sigma^{ip}\)/\(\sigma_{o}\) = \(Q^{2D}\) = 0 in cases of the fully constrained plane strain flow field. For fully constrained three-dimensional elastic–plastic flow fields, \({\Delta }\sigma^{ip}\)/\(\sigma_{o}\) = 0 and \({\Delta }\sigma^{3D}\)/\(\sigma_{o}\) = \({\Delta }\sigma^{op}\)/\(\sigma_{o}\). However for unconstrained flow fields, \({\Delta }\sigma^{ip}\)/\(\sigma_{o}\) is the stress difference of the geometries due to the in-plane effect.

The change of the out-of-plane constraint loss is the change of normal stress at a fixed distance ahead of the crack. In this respect, the change of the maximum stresses, \(\sigma_{\theta \theta }\) and \(\sigma_{m}\) as indicated in (Yusof 2019) is:

$$ \frac{{{\Delta }\sigma }}{{\sigma_{o} }}^{op} = \frac{{\left( {\sigma_{\theta \theta }^{op} - \sigma_{\theta \theta }^{ref} } \right)}}{{\sigma_{o} }} = \frac{{\left( {\sigma_{m}^{op} - \sigma_{m}^{ref} } \right)}}{{\sigma_{o} }} $$
(11)

Using the out-of-plane constraint loss Eqs. (4) in (11) and taking the hoop stress \(\left( {\sigma_{\theta \theta } } \right)\) as an example:

$$ \frac{{{\Delta }\sigma }}{{\sigma_{o} }}^{op} = \left( {\frac{{\sigma_{\theta \theta }^{op} }}{{\sigma_{o} }}} \right) - \left( {\frac{{\sigma_{\theta \theta } }}{{\sigma_{o} }}} \right)^{ref} $$
(12)

where

$$ \left( {\frac{{\sigma_{\theta \theta } }}{{\sigma_{o} }}} \right)^{ref} = \left( {\frac{{\sigma_{\theta \theta } }}{{\sigma_{o} }}} \right)_{{Q^{2D} }}^{HRR/SSY pl.\varepsilon } $$
(13)

Assuming the reference stress, \(\sigma_{\theta \theta }^{ref} /\sigma_{o}\) is the small-scale yielding (SSY) plane strain field,

$$ \frac{{{\Delta }\sigma }}{{\sigma_{o} }}^{op} = \left( {\frac{{\sigma_{\theta \theta } }}{{\sigma_{o} }}^{op} } \right) - \left( {\frac{{\sigma_{\theta \theta } }}{{\sigma_{o} }}} \right)_{{Q^{2D} }}^{pl.\varepsilon } $$
(14)

substituting Eqs. (4) into (14):

$$ \frac{{{\Delta }\sigma }}{{\sigma_{o} }}^{op} = \left\{ {\left[ {\left( {\frac{{\sigma_{\theta \theta } }}{{\sigma_{o} }}} \right)_{{Q^{2D} }}^{pl.\varepsilon } - \left( {\frac{{\sigma_{\theta \theta } }}{{\sigma_{o} }}} \right)^{pl.\sigma } } \right]\exp \left( {\frac{{\gamma_{{\left( {r,n} \right)}} J_{loc} }}{{z\sigma_{o} }}} \right) + \left( {\frac{{\sigma_{\theta \theta } }}{{\sigma_{o} }}} \right)^{pl.\sigma } } \right\} - \left( {\frac{{\sigma_{\theta \theta } }}{{\sigma_{o} }}} \right)_{{Q^{2D} }}^{pl.\varepsilon } $$
(15)

rearranging

$$ \frac{\Delta \sigma }{{\sigma_{o} }}^{op} = \left( {\exp \left( {\frac{{\gamma_{{\left( {r,n} \right)}} J_{loc} }}{{z\sigma_{o} }}} \right) - 1} \right)\left( {\frac{{\sigma_{\theta \theta } }}{{\sigma_{o} }}} \right)_{{Q^{2D} }}^{pl.\varepsilon } - \left( {\exp \left( {\frac{{\gamma_{{\left( {r,n} \right)}} J_{loc} }}{{z\sigma_{o} }}} \right) - 1} \right)\left( {\frac{{\sigma_{\theta \theta } }}{{\sigma_{o} }}} \right)^{pl.\sigma } $$
(16)

resulting

$$ \frac{{{\Delta }\sigma }}{{\sigma_{o} }}^{op} = \left[ {\left( {\frac{{\sigma_{\theta \theta } }}{{\sigma_{o} }}} \right)_{{Q^{2D} }}^{pl.\varepsilon } - \left( {\frac{{\sigma_{\theta \theta } }}{{\sigma_{o} }}} \right)^{pl.\sigma } } \right]\left[ {\left( {\exp \left( { - \frac{{\gamma_{{\left( {r,n} \right)}} J_{loc} }}{{z\sigma_{o} }}} \right) - 1} \right)} \right] $$
(17)

Using Eq. (17) and taking the non-hardening material response (\(n\) = \(\infty\)), the change of the out-of-plane constraint loss parameter \({\Delta }\sigma^{op}\)/\(\sigma_{o}\) for the hoop stress (\(\sigma_{\theta \theta }\)/\(\sigma_{o}\)) at the mid-plane for different crack lengths and thicknesses are shown in Fig. 9. For non-hardening perfectly-plastic crack tip fields, the stresses around the crack tip can be determined following the method described by (Rice 1982). Figure 9 illustrates that the thick and deeply cracked SENB out-of-plane constraint \({\Delta }\sigma^{op}\)/\(\sigma_{o}\) approaches zero towards the plane strain fully constrained hoop stress. Thin SENB with different crack lengths show a large constraint drop and develop a distinctive constraint loss curve (as shown by the continuous blue line) that starts from the fully constrained level near the plane strain field for the non-hardening crack tip field which corresponds to \(\sigma_{\theta \theta }\) = 2.96 \(\sigma_{o}\) and decays to a negative \({\Delta }\sigma^{op}\)/\(\sigma_{o}\) that approach a non-hardening plane stress field \(\sigma_{\theta \theta }\)/\(\sigma_{o}\) = 1.15 \(\sigma_{o}\). However, the thick and thin shallow cracked SENB geometries demonstrate in-plane constraint loss with the hoop stress level below the perfectly-plastic plane strain hoop stress and thus develop an independent out-of-plane constraint loss curve (as indicated by the dashed blue line). With increasing load, the constraint loss curve (dashed blue line curve) merges with the continuous blue line curve. CCP geometries that lose in-plane constraint develop a hoop stress level lower than the thick and thin SENB geometries and are shown by the red-dashed-dot line curve. With increasing load, the CCP out-of-plane stress difference drops and merges with the main out-of-plane constraint loss curve. Although Fig. 9 shows the change of the out-of-plane stress for the non-hardening material response, it is expected that a similar constraint loss decay trend will also develop for strain hardening responses as the out-of-plane constraint loss trend is similar to non-hardening responses as depicted in Figs. 7 and 8.

Fig. 9
figure 9

The hoop stress ahead of the crack at the mid-plane \(x_{3}\)/\(B\) = 0 at distance \(r\) = 2 \(J_{loc}\)/\(\sigma_{o}\) as a function of \({\Delta }\sigma^{3D} /\sigma_{o}\) for non-hardening (\(n = \infty\)) SENB and CCP geometries at all applied loads, \(\mu\)

Full size image

3.5 Crack tip plastic zones

The shape of the plastic zone at the crack tip has traditionally been used to relate to the state of the stresses at the crack tip, (Larsson and Carlsson 1973; Rice 1974; Bilby et al. 1986) and was key to understanding the effect of in-plane constraint (Du and Hancock 1991; Al-Ani and Hancock 1991; O'Dowd and Shih 1991). Therefore, the shapes of the plastic zones of the cracked SENB and CCP geometries are examined to relate to the three-dimensional elastic–plastic crack tip stresses as shown in Fig. 10.

Fig. 10
figure 10

Plastic zone for non-hardening thick and thin geometries for various crack lengths at the mid-plane at \(\mu\) = 50 and 200 for SENB and CCP respectively

Full size image

Detailed investigation of Fig. 10a in which the thick SENB with the different crack length for crack length \(a\)/\(W\) ≥ 0.3 shows the plastic zones envelop the crack tip and the change of the out-of-plane constraint \(\Delta \sigma^{3D}\)/\(\sigma_{o}\) approaches zero and the hoop stress is near the fully constrained level \(\sigma_{\theta \theta }\)/\(\sigma_{o}\) = 2.96 as demonstrated in Fig. 9. For the shallow cracked thick SENB, \(a\)/\(W\) ≤ 0.3, the plastic zones envelop the crack tip and spread to the crack face because the crack face for crack length \(a\)/\(W\) = 0.2 and 0.1 are given by the \(X\)-axis = − 200 and − 100 respectively. The spread of plastic zone to the crack face for \(a\)/\(W\) = 0.2 and 0.1 are consistent with the result shown by (Al-Ani and Hancock 1991) from two-dimensional plane strain shallow crack geometries. The thick cracked shallow SENB geometries showed that the effect of thickness is to reduce the toughness attained because increasing the thickness in the thick shallow cracked geometries caused the plastic zone lobe to swing backward relative to the thick deeply cracked SENB geometry.

Figure 10b shows the thin cracked SENB with different crack lengths developed plastic zones that do not fully envelop the crack tip. The thin cracked SENB with deep cracks \(a\)/\(W\) ≥ 0.3 shows the plastic zones swing forward and from Fig. 9 the change of the out-of-plane constraint \(\Delta \sigma^{3D}\)/\(\sigma_{o}\) is highly negative and the hoop stress drops away from the fully constrained level as the load is increased for the thin deep cracks. For the thin SENB with shallow crack length \(a\)/\(W\) < 0.3, the plastic zones lobes swing backward and the change of the three-dimensional crack tip constraint, \(\Delta \sigma^{3D}\)/\(\sigma_{o}\), loses negativity (as shown in Fig. 9). The increase of thickness in the thin shallow cracks at low load initially cause a reduction of the out-of-plane constraint loss but with increase load, the out-of-plane constraint increase as shown in Fig. 9. Unlike the thick shallow SENB, the thin shallow SENB plastic zones do not spread to the crack faces.

Figure 10c and d show that the plastic zones do not fully envelop the crack tip for the thick and thin CCP models. This is in agreement with the non-hardening asymptotic crack tip fields of CCP geometries shown in (Yusof 2019) in which an elastic wedge appears near the crack flanks and the angle of the wedge is dependent on the state of in-plane constraint and out-of-plane constraint along the crack front. In geometries that develop a combined \({\Delta }\sigma^{ip}\)/\(\sigma_{o}\) field and \(\Delta \sigma^{op}\)/\(\sigma_{o}\) that are less than zero, plasticity does not surround the crack tip. For the thick CCP models, the plastic zones swing backward with a reduction in crack length, which agree with the change of the three-dimensional crack tip constraint, \(\Delta \sigma^{3D}\)/\(\sigma_{o}\) that approach zero (shown in Fig. 9) but the hoop stress drops due to in-plane constraint loss. Thin CCP models with deep and shallow cracks developed similar plastic zones sizes that swing forward indicating a negative out-of-plane constraint.

In general, the reduction of the crack length in the SENB and the CCP models demonstrated that the plastic zones show a tendency to lean backward for the thick SENB and CCP geometries (Fig. 10a and c). For the thin SENB and CCP geometries, the plastic zone leans forward with the deep thin geometries showing the steepest forward lean as shown in Fig. 10b and d. The tendency of the plastic zones to lean backward and forward is analogous to the two distinct features highlighted by (Du and Hancock 1991) for plane strain crack tip fields in which the tensile or positive \(T\)-stress geometries cause the plastic zone to rotate backwards and associated by crack tip constraint approaching the \(HRR\) field while compressive or negative \(T\)-stress cause the plastic zone to swing forward and associated with loss of constraint. From the SENB and CCP geometries dealt in this paper, it can be deduced that when the change of the out-of-plane constraint \(\Delta \sigma^{3D}\)/\(\sigma_{o}\) \(\to\) 0 the plastic zone of in such geometries to lean backward and when \(\Delta \sigma^{3D}\)/\(\sigma_{o}\) becomes negative, the plastic zone tends to lean forward.

4 Conclusions

The effects of crack length and thickness of three-dimensional elastic–plastic crack tip fields can be summarized as listed below:

  1. 1.

    Deep and shallow cracks of three-dimensional elastic–plastic crack tip fields demonstrate a transition from a plane strain to a plane stress field and the transition of the field at the onset of the out-of-plane effect can be determined through a non-dimensional parameter \(J_{loc}\)/\(z\sigma_{o}\) and the sensitivity of the change is demonstrated through a constraint sensitivity parameter \(\gamma\).

  2. 2.

    The change of the out-of-plane constraint parameter, \(\Delta \sigma^{op}\)/\(\sigma_{o}\) = 0 and a maximum hoop or mean stress designate a plane strain field at the fully constrained limit.

  3. 3.

    Increased thickness in shallow cracked geometries can reduce enhanced toughness but can be ranked within the change of maximum stress \(\Delta \sigma^{3D}\)/\(\sigma_{o}\) parameter.

  4. 4.

    The effect of the thickness on thick and thin, deep and shallow cracks can be seen in the way the shape of the plastic zone developed and changed at the crack tip. For fully constrained geometries, three-dimensional plastic zone shapes that swing forward are associated with the loss of the out-of-plane constraint, and in contrast, plastic zone shape that swings backward demonstrated out-of-plane constraint that approaches a fully constrained \(HRR\) field.

  5. 5.

    A measure of the three-dimensional elastic–plastic constant stress sector difference fields, \(\Delta \sigma^{3D}\)/\(\sigma_{o}\) established a way to link in-plane and out-of-plane crack tip constraint loss in three-dimensional geometries. Therefore, an elastic–plastic stress distribution within a three-dimensional annulus can be identified through a stress difference field \(\Delta \sigma^{3D}\)/\(\sigma_{o}\) when the crack tip deformation size scale is set by \(J\) hence this approach extended a two-parameter fracture mechanics \(J\)-\(\Delta \sigma\) approach in three-dimensional elastic–plastic cracks.