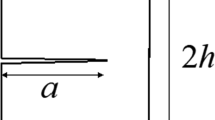1 Introduction

In a classical formulation of plasticity or visco-plasticity, no lengthscale-effects are included. However, a range of micro-scale experiments have shown distinct size effects associated with plasticity (Fleck et al. 1994; Ma and Clarke 1995; Stölken and Evans 1998; Shrotriya et al. 2003) even at high-temperatures (Gan and Tomar 2010). Strain-gradient plasticity theories have been developed to introduce an intrinsic material length parameter (Fleck and Hutchinson 1993; Gao et al. 1999; Huang et al. 2000, 2004) in order to account for the observed size effects. The intrinsic lengthscale then relates to the scale of deformation at which effects due to plastic strain gradients becomes significant (Wei and Hutchinson 1997). The response of a mechanical model accounting for plastic strain gradients in the formulation of the constitutive model converges to that obtained with a conventional plasticity model if the characteristic length of the plastic deformation process is considerably larger than the intrinsic material length l (Huang et al. 2004).

In elasto-plastic solids, the local flow stress and strain hardening conditions determine the crack tip fields, and thus also the crack growth resistance through the energy dissipation associated with plastic deformation. The small size of the plastic zone at the crack tip and the large plastic strain gradients can promote a strong size effect associated with cracks (Sevillano 2001; Qu et al. 2004). In (Chen et al. 1999; Huang et al. 1999; Qu et al. 2004; Martínez-Pañeda and Betegón 2015; Martínez-Pañeda and Niordson 2016) it was shown that plastic strain gradient effects increase the stresses at the crack tip significantly. The radius of the influence zone of the strain gradients at the crack tip is on the order of \(10\, \upmu \hbox {m}\) which is on the same order of magnitude as intrinsic lengthscales in strain gradient plasticity models. Thus, local mechanisms associated with plastic strain gradients can play an important role on fracture processes.

The seminal work of (Tvergaard and Hutchinson 1996)—employing a boundary layer model in combination with cohesive zone elements—established important knowledge on to the processes of mode I crack growth in an elasto-plastic solid. The ratio of cohesive strength to yield strength, and the strain hardening exponent N were found to be key parameters determining fracture toughness and crack growth resistance. Using a similar model, Wei et al. (2004) demonstrated that once plastic strain gradients are accounted for in the constitutive model, a reduced steady state toughness emerges. In (Wei and Hutchinson 1997) a comparable model was used to study steady-state crack growth, again including plastic strain gradients. These authors found that larger values of the intrinsic length would lead to increased stresses near the crack tip but at the same time results in lower stresses away from the crack tip, all compared to a response based on strain-only plasticity. In additional, accounting for plastic strain gradients lead to an increase of the predicted plastic zone size while at the same time resulting in a decreased crack opening displacement and steady state toughness.

Visco-plastic strain gradient theories have been considered by several authors. In  (Gurtin 2002, 2003) single-crystal and higher order small deform visco-plastic strain gradient plasticity theories, respectively, were defined. A small deformation visco-plastic strain gradient theory was proposed in (Gudmundson 2004), and applied in (Fredriksson and Gudmundson 2005) to the analysis of thin films but rate-effects were not considered explicitly for the analysis of this boundary value problem. In (Borg et al. 2006) a visco-plastic strain gradient formulation based on (Fleck and Hutchinson 2001) and (Niordson and Redanz 2004) was introduced and applied to inclusion and void growth problems. The results demonstrate an increased rate sensitivity when strain gradient effects are accounted for in the visco-plastic formulation. A small- and large-deformation visco-plastic strain gradient theory was introduced by Lele and Anand (2008, (2009). Both theories are higher order gradient models accounting for microscopic boundary conditions. The model was applied to several boundary value problems but rate effects were not explored. Recently, in (Nielsen and Niordson 2014) a rate-dependent implementation of the corresponding rate-independent models of (Fleck and Willis 2009) was presented. Loading rate conditions considered in that study were such that stress relaxation was dominant. Visco-plastic effects were found to be more pronounced for larger (dissipative) lengthscale parameters.

In the context of fracture problems few prior investigations exist that have investigated the effects of visco-plasticity combined with strain gradients effects. In Nielsen et al. (2012) and Nielsen and Niordson (2012) steady state crack growth in mode I and mixed mode, respectively, was analyzed by combining a steady-state crack growth model with a strain gradient visco-plastic constitutive model. These authors applied a model for cleavage cracking proposed by Suo et al. (1993). It was found that hardening due to plastic strain gradients decreases the macroscopic toughness independent of the crack tip velocities. Strain gradients also alter the stress triaxiality, and visco-plastic effects appear to stabilize this effect. A characteristic velocity delineating domains of increased and decreased toughness with the degree of visco-plasticity was found to exist not only for the case of a lengthscale independent constitutive formulation but persisted in the case of a gradient theory as well. What has not been documented so far in the literature are details of crack tip field and transient crack growth response characteristics in problems considering viscoplasticity and strain gradients.

The present study considers a visco-plastic strain gradient model for the analysis of transients as these arise in stresses and strains associated with a crack tip. The study considers a finite element representation of a modified boundary layer model. Two scenarios are investigated: (1) a model with a stationary crack (Sect. 3.1) and (2) a model with crack growth under monotonic loading (Sect. 3.2). The cohesive zone model approach is employed for crack growth studies. This approach has been successful for such studies in a range of material systems, amongst many studies see (Roychowdhury et al. 2002; Park and Paulino 2011; Turon et al. 2007; McGarry et al. 2014). The parameters of the visco-plastic strain gradient model are motivated by the high temperature properties of Nickel based superalloys and varied parametrically covering small and large visco-plastic power exponent, as well as a range of relevant intrinsic material length values. The cohesive zone response is considered as rate independent, similar to (Bouvard et al. 2009). Thereby, the assumption is that the rate processes of material deformation are much faster than those of material separation.

The main research questions addressed in this paper are:

  1. 1.

    Accounting for plastic strain gradients, how do stresses and strains at a crack tip evolve over time while holding at constant load?

  2. 2.

    How do the plastic strain gradients, visco-plastic rate-dependency, and strain hardening interact to influencing crack growth under monotonic loading and varying loading rates?

The implications of the results on the fracture process are discussed.

2 Methodology

This study employs a boundary layer model and considers mode I loading. The solid is described by a visco-plasticity constitutive model that includes length-scale effects via the conventional theory of mechanism-based strain-gradient approach. Crack growth is accounted for through the use of the cohesive zone model approach. Material parameters are motivated by high temperature properties of Nickel-based superalloys.

2.1 Modified boundary layer model

A modified boundary layer (MBL) model is applied  (Tvergaard and Hutchinson 1996; Wang and Siegmund 2005; Ren et al. 2011; Nielsen et al. 2012; Nielsen and Niordson 2012; Martínez-Pañeda and Betegón 2015; Martínez-Pañeda and Niordson 2016). Plane strain conditions are assumed. The MBL model contains the crack tip inside a circular zone, with the crack tip near domain meshed by a regular quadrilateral mesh. Considering isotropic, linear elasticity, the asymptotic crack tip solution is applied at the outer circular boundary by an imposed time-dependent displacement u(t) in x- and y-directions. Under these conditions, an elastic zone at the boundary constrains the small creep zone at the crack tip, Riedel and Rice (1980). A solution for the displacements can be obtained by the Williams-expansion under mode I (Williams 1957; Xiao and Karihaloo 2002). The first order terms of the displacements \(u_x\) and \(u_y\) as a function of the radial and angular coordinates r and \(\theta \) are

$$\begin{aligned} u_x(t)= & {} K_{\mathrm {I}}(t)\sqrt{\frac{r}{2\pi }}\frac{1}{2\mu }\cos \left( {\frac{\theta }{2}}\right) (3-4\nu -\cos \theta ) \nonumber \\ \end{aligned}$$
(1)
$$\begin{aligned} u_y(t)= & {} K_{\mathrm {I}}(t)\sqrt{\frac{r}{2\pi }}\frac{1}{2\mu }\sin \left( {\frac{\theta }{2}}\right) (3-4\nu -\cos \theta )\nonumber \\ \end{aligned}$$
(2)

where \(K_I(t)\) is the prescribed time dependent stress intensity factor. The prescribed displacements due to a given remote \(K_I\) are applied as boundary conditions to every node on the outer boundary of the MBL model. The boundary conditions are implemented by applying the Disp user subroutine in Abaqus Standard.

Figure 1 shows the global FE mesh and the mesh refinement near the crack tip. Only a half-model is considered due to symmetry under mode I loading. The model consists of 3892 plane strain elements and 123 cohesive zone elements, both being linear elements. The cohesive elements are defined along the symmetry line starting at the crack tip in the direction of x in Fig. 1. The nodes of the cohesive elements coincidental with the symmetry line of the model are restricted to move only in x-direction. Symmetry conditions also dictate that the the \(u_x\) displacement of the nodes of the cohesive elements are pairwise tied to each other. The maximum crack advance is much smaller than \(R_\mathrm {MBL}\).

Fig. 1
figure 1

Global (a) and refined finite element mesh (b) near the crack tip of the modified boundary layer model. The applied displacement u(t) calculated by Eqs. (1) and (2) at the circular outer boundary is illustrated by arrows

Full size image

The initial crack was modeled with a sharp crack tip. This mesh geometry is justified by the results of Martínez-Pañeda and Niordson (2016) which shows comparable response of a plastic strain gradient formulation including an initially blunted crack. A mesh geometry including a sharp crack tip is ideal for crack propagation problems as is considered here in the monotonic loading case.

The MBL model is an approximation of the conditions near the crack tip. For example, if the geometry of a compact tension (CT) specimen is analyzed, higher-order terms have an influence on the stress field near the crack tip which have to be considered. T-stresses can change the shape of the visco-plastic zone (Ren et al. 2011) which influences the fracture toughness (Tvergaard and Hutchinson 1994). In addition, the time-dependent deformation of the circular boundary during loading (predominantly for a prolonged hold time) has not been taken into account in the model. This is seen as a secondary effect and could be accounted for by adjusting the load adaptively during the hold time.

2.2 Visco-plastic strain gradient formulation

A constitutive model of conventional theory of mechanism-based strain-gradient visco-plasticity (CMSG-vp) is considered in order to model the time and lengthscale dependent constitutive response. The model is based on the formulation of (Huang et al. 2004). An intrinsic material length parameter l which is defined for a face-centered cubic (FCC) crystal as

$$\begin{aligned} l=18\alpha ^2\left( \frac{\mu }{\sigma _Y} \right) ^2b \end{aligned}$$
(3)

where b is the magnitude of the Burgers vector, \(\mu \) is the shear modulus, \(\sigma _Y\) is the yield strength, and \(\alpha \) is an empirical prefactor (\(0.2<\alpha <0.5\)) (Gao et al. 1999). Employing summation notation of continuum mechanics, the increment of the effective visco-plastic strain gradient \(\dot{\eta }^{vp}\) is calculated as Gao et al. (1999)

$$\begin{aligned} \dot{\eta }^{vp}=\sqrt{\frac{1}{4}\dot{\eta }^{vp}_{ijk}\dot{\eta }^{vp}_{ijk}} \end{aligned}$$
(4)

where

$$\begin{aligned} \dot{\eta }^{vp}_{ijk}=\dot{\varepsilon }^{vp}_{ik,j} + \dot{\varepsilon }^{vp}_{kk,i} - \dot{\varepsilon }^{vp}_{ij,k} \end{aligned}$$
(5)

and

$$\begin{aligned} \eta ^{vp}= \int {\dot{\eta }^{vp} \mathrm {d}t} \end{aligned}$$
(6)

with the visco-plastic strain rates \(\dot{\varepsilon }^{vp}_{ij}\). A visco-plastic constitutive model is used leading to the visco-plastic strain rate \(\dot{\varepsilon }^{vp}\) via a Norton visco-plastic model:

$$\begin{aligned} \dot{\varepsilon }^{vp}=A\sigma ^m =\frac{\dot{\varepsilon _0}}{\sigma _Y^m}\left[ \frac{\sigma _e}{\sqrt{f^2(\varepsilon ^{vp})+l\eta ^{vp}}} \right] ^m, \end{aligned}$$
(7)

where A is the visco-plastic prefactor, m is the visco-plastic exponent, and \(\dot{\varepsilon }_0\) is the reference strain rate. Also, a flow stress is defined as \(\sigma _\mathrm{flow}=\sigma _Y \sqrt{f^2(\varepsilon ^{vp})+l\eta ^{vp}}\). The non-dimensional function \(f(\varepsilon ^{vp})\) in Eq. (7) is defined for a power-law hardening solid

$$\begin{aligned} f(\varepsilon ^{vp})=\left( 1+\frac{E\varepsilon ^{vp}}{\sigma _{Y}}\right) ^N \end{aligned}$$
(8)

with the plastic strain hardening exponent N, the Young’s modulus \(E=2\mu (1+\nu )\), and the Poisson’s ratio \(\nu \). A basic Norton model can be obtained with \(N=0\) and \(l=0\) and describes a steady-state secondary creep regime. Additional strain hardening \(N>0\) for \(l=0\) corresponds to the conventional primary creep regime (Reed 2006; Rösler et al. 2007) for short loading times which passes into a steady-state regime in the long term. Strain gradients affect the hardening response of the model if gradients are sufficiently large. All calculations are isothermal and the intrinsic material length is considered as constant during one simulation. The constitutive model was implemented as a Umat subroutine for the implicit commercial finite element solver Abaqus Standard. The model is based on the rate-independent Umat created by Huang et al. (2004).

2.3 Cohesive zone model

Cohesive-zone (CZ) elements with a traction-separation relationship as motivated by (Needleman 1990, 1992) are applied on the plane ahead of the crack tip. The relationship between the cohesive traction in the normal direction T and the associated material separation \(\delta \) is defined as

$$\begin{aligned} T(\delta ) = \sigma _{\mathrm {max}}e\exp \left( -\frac{\delta }{\delta _0}\right) \left( \frac{\delta }{\delta _0} \right) \end{aligned}$$
(9)

with the cohesive strength \(\sigma _{\mathrm {max}}\), the cohesive length \(\delta _0\), and \(e=\exp (1)\), Fig. 2. Only the normal traction has to be considered due to symmetric conditions. The parameter \(\delta _0\) equals the material separation under normal loading necessary to reach cohesive strength. The CZ elements are considered as failed if the critical normal separation \(\delta = 5\delta _0\) is reached. At this magnitude of material separation the value of cohesive tractions has declined substantially from the peak value and crack faces are nearly traction free. This condition defines the location of crack tip. Crack advance \(\varDelta a\) is related to the undeformed mesh.

Fig. 2
figure 2

Traction–separation relationship and definition of the normal crack opening displacement \(\delta \)

Full size image

The cohesive energy \(\varGamma _0\) is calculated as the integral over the traction–separation response from \(\delta =0\) to \(\delta = 5\delta _0\) as \(\varGamma _0=\zeta \mathrm{e} \sigma _\mathrm{max} \delta _0\) and \(\zeta =0.98\) for the selected crack tip definition \(\delta = 5\delta _0\). Following arguments on the relationship between stress intensity factor and energy release rate under plane strain conditions a reference stress intensity factor \(K_0\) is introduced as (Tvergaard and Hutchinson 1994)

$$\begin{aligned} K_0=\left( \frac{E\varGamma _0}{1-\nu ^2} \right) ^{1/2}. \end{aligned}$$
(10)

Then, following from \(K_0\) a respective reference plastic zone size \(R_{p,0}\) is given employing (Rice 1967)

$$\begin{aligned} R_{p,0}=\frac{1}{3\pi }\frac{K_0^2}{\sigma _Y^2}. \end{aligned}$$
(11)

2.4 Model parameters

The constitutive parameters of the visco-plastic strain gradient formulation are \(\mu \), \(\sigma _Y\), \(\nu \), N, A, m, and l. The model parameter values employed in this study are related to the high temperature properties of Ni-based superalloys. Following (Benz et al. 2014) the present study considers \(\mu /\sigma _Y=214\). Motivated by the creep data in (Benz et al. 2014) \(m=5.6\) as well as \(m=5.0\) and 6.0 are employed. The creep prefactor is \(A=5 \times 10^{-18}\) MPa\(^m\) s\(^{-1}\), Consequently each m-case possesses a different reference strain rate (\(m=5.0\) \(\dot{\epsilon }_0=2.2 \times 10^{-6}\) s\(^{-1}\); \(m=5.6\) \(\dot{\epsilon }_0=5.6 \times 10^{-5}\) s\(^{-1}\); \(m=6.0\) \(\dot{\epsilon }_0=4.8 \times 10^{-4}\) s\(^{-1}\)). In a parametric sense, the strain hardening parameters N is varied from \(N=0\) (Norton model response) to \(N=0.15\). Several levels of strain gradient hardening are considered and compared to results with a conventional visco-plastic constitutive theory (\(l=0\)). Values of l are in the range of typical values for this parameter in CMSG theory based studies.

It is well understood that the value of cohesive strength strongly affects the amount of plastic dissipation during crack growth (Tvergaard and Hutchinson 1996; Wei and Hutchinson 1997; Landis et al. 2000). For values of \(\sigma _\mathrm {max}/\sigma _Y < 2\) little or no dissipation occurs while for \(\sigma _\mathrm {max}/\sigma _Y > 4\) crack growth is generally absent. Consequently, for the present study the cohesive strength was selected as \(\sigma _{\mathrm {max}}=3.5\sigma _Y\).

Considering the model with the cohesive zone, the two fundamental model length quantities are l and \(\delta _0\). The values of the ratio of the intrinsic lengthscale to the cohesive length are in the range \(l/\delta _0\)=0 to 1000. The cohesive length also sets a size of the reference plastic zone, here \(R_{p,0}/\delta _0=581\). Consequently, the values of the ratios of intrinsic lengthscale l to reference plastic zone size \(l/R_{p,0}\) are between 0.0 and 1.7. This order of values for \(l/R_{p,0}\) was also considered in (Wei and Hutchinson 1997). Considering the model with a stationary crack, the intrinsic lengthscale l is normalized with the size of the plastic zone at the maximum value of the applied stress intensity factor, here \(K_{I,\mathrm {max}}=2.5K_0\). Consequently, the values of the ratio of intrinsic lengthscale to the corresponding plastic zone size \((l/R_P)\) are in the range from 0.0 to 0.28, again of the order of values in (Wei and Hutchinson 1997).

The radius of the MBL model is selected such that the visco-plastic zone at the crack tip remains well contained in the model domain. This is ensured by considering that the radius of the outer perimeter of the MBL model is large relative to the reference plastic zone size, here \(R_{\mathrm {MBL}}/R_{p,0}=42\). Also, maximum value considered for the applied stress intensity factor, \(K_{I,\mathrm {max}}=2.5K_0\), the size of the the plastic zone remains contained in the MBL model, \(R_{\mathrm {MBL}}/R_{p}=6\). Furthermore, the maximum amount of crack advance \(\varDelta a_\mathrm {max}\) is limited to the structured mesh region at the center of the MBL (\(\varDelta a_\mathrm {max}=288\delta _0\)). Finally, the smallest element length near the crack tip is \(2.5\delta _0\).

3 Results and discussion

Results of simulations are presented first for the case of a stationary crack tip, and the evolution of crack tip fields over time are documented. Then, crack growth resistance curves and their characterizing parameters (initiation toughness and tearing modulus) are discussed and loading rate effects are considered. Crack tip fields for growing cracks are analyzed. For all cases, specific attention is paid to the effect of the length scale in the visco-plastic strain gradient model in its influence on computed quantities.

3.1 Stationary cracks

Considering the stationary crack model, the load is ramped for \(5\, \mathrm{s}\) until \(K_{I,\mathrm {max}}=2.5K_0\) is reached, followed by a hold step of \(t_\mathrm {hold}={100}\hbox {s}\). In order to gain insight into the interaction of visco-plastic deformation and plastic strain gradient hardening, identical load and hold times were considered for all computations. The hoop stress values \(\sigma _{\theta \theta }\) are evaluated ahead of the crack tip for \(\theta ={0}^{\circ }\). Two cases are examined: (1) a conventional Norton model (\(l=0\), \(N=0\)) and (2) the strain gradient constitutive model with \(l/R_p\), m, and N varied.

Figure 3 depicts the hoop-stress values \(\sigma _{\theta \theta }\) normalized by \(\sigma _Y\) ahead of the crack tip over the distance r in front of the crack tip for computations considering a range of \(l/R_p\) and m values with \(N=0\) in all cases. Solid lines correspond to the stresses after ramp loading is complete and dashed lines correspond to stresses after the subsequent hold step. Overall, the highest values of \(\sigma _{\theta \theta }\) were found for \(m=5.0\) caused by the limited visco-plastic deformation in the case of low visco-plastic powers. For the Norton model (\(l=0\), \(N=0\)) the highest \(\sigma _{\theta \theta }\) stresses are reached slightly ahead of the crack tip. This breakdown of the singularity type solution of the stress field around the crack tip is due to crack blunting (McMeeking and Parks 1979; Bassani and Hawk 1990; Anderson 2005). The distance between the location of the maximum stress and the crack tip equals approximately two times the crack tip opening displacement (Anderson 2005). For \(l/R_p>{0}\), the presence of hardening due to the plastic strain gradients alters the crack tip fields. Now, the location of the maximum stress is shifted towards the crack tip. This change in crack tip fields occurs already for small values of \(l/R_p\).

Fig. 3
figure 3

Normalized hoop-stresses \(\sigma _{\theta \theta }/\sigma _Y\) versus the normalized distance \(r/\delta _0\) for stationary cracks ahead of the crack tip after loading (\(t_\mathrm {hold}={0}\,\hbox {s}\), solid lines) and after (\(t_\mathrm {hold}={100}\, \hbox {s}\), dashed lines), several values of the ratio of intrinsic material length to plastic zone size \(l/R_p\), and visco-plastic exponents: a \(m=5.0\), b \(m=5.6\), and c \(m=6.0\). For all cases \(N=0.0\)

Full size image

Near the crack tip (e. g. for \(r/\delta _0 <10\) in Fig. 3a) the level of the hoop stresses predicted by use of a strain gradient formulation is 2–3.5 times higher compared to the conventional Norton model case (\(l=0, N=0\)), and that ratio increase increases with \(l/R_p\). The present results indicate an increase in the crack tip near stress levels as l is increased from zero, and that relative sensitivity increase with m. The maximum stress level on the order of \(10\sigma _Y\). This finding extends the results by Martínez-Pañeda and Betegón (2015) on crack tip stresses in models with a rate-independent formulation of strain gradient plasticity. Stress levels are similar to what was found in (Wei and Hutchinson 1997; Qu et al. 2004). During the hold time, stresses decrease due to stress relaxation. Stress relaxation is caused by constraining the visco-plastic deformation by the surrounding elastic domain  (Riedel and Rice 1980; Bassani and Hawk 1990). The amount of stress relaxation was found to most pronounced for \(l=0\) and low values of m. As m is increased the predicted stress relaxation declines for cases with \(l=0\) but increases for non-zero l values. It is found that the influence zone of the plastic strain gradients grows over time. This change in the stress fields can be explained by higher visco-plastic strain rates caused by the initial higher crack tip stresses in cases with \(l>0\) which then cause more pronounced relaxation processes, similar to what was found even for \(l=0\) in (Bassani and Hawk 1990). Further away from the crack tip (e. g. for \(r/\delta _0>10\) in Fig. 3a) hoop stresses for cases \(l/R_p>0\) are slightly below the hoop stresses of the Norton model case. This is due to the necessary force equilibrium which has to be maintained also in the case of higher hoop stresses at the crack tip for \(l/R_p>0\). This was also found in rate-independent solids by Wei and Hutchinson (1997). During hold, stress levels decay as well in this region. As expected, far away from the crack tip for \(r/\delta _0\gg 0\) the stresses of the strain gradient model equals the stresses of the Norton model case. In this domain the influence of the plastic strain gradients is negligible and the response of the strain gradient formulation passes into a conventionally Norton model.

To quantify the area influenced by strain gradients, Martínez-Pañeda and Niordson (2016) suggested to calculate a distance \(r_{\mathrm {SGVP}}\) from the crack tip where the computed hoop-stresses from plastic strain gradient formulation are significantly higher than the stresses predicted in a strain-only plasticity model. This strategy is adapted here as well and used to compare the results obtained with the conventional visco-plastic model to those obtained with the strain gradient visco-plasticity. The distance \(r_\mathrm {SGVP}\) (normalized by \(\delta _0\)) defines the size of the domain in which the hoop-stresses \(\sigma _{\theta \theta }\) following for the visco-plastic strain gradient model are significantly higher than the stresses predicted by use of the conventional Norton model, (\(\sigma _\mathrm {SGVP} = 1.5\sigma _\mathrm {Norton}\), Fig. 4).

Fig. 4
figure 4

Definition of \(r_\mathrm {SGVP}/\delta _0\) to quantify the area affected by the visco-plastic strain gradient plasticity in comparison to the Norton visco-plastic model

Full size image

Figure 5 depicts \(r_\mathrm {SGVP}/\delta _0\) over hold time \(t_\mathrm {hold}\) for computations considering three visco-plastic exponents and \(N=0\). A steady-state (Bassani and Hawk 1990) was not fully reached over the hold time considered here. For all cases considered \(1/\dot{\epsilon }_0 > t_\mathrm {hold}={100}\,\hbox {s}\). As expected, for all cases \(r_\mathrm {SGVP}/\delta _0\) increases with hold time. In François et al. (2012) the growth of the visco-plastic zone near the crack tip with time was demonstrated. Here, not only does the visco-plastic zone grow during hold, but the domain of influence of the plastic strain gradient expands as well.

Fig. 5
figure 5

Distance effected by plastic strain gradients \(r_\mathrm {SGVP}/\delta _0\) for stationary cracks versus hold time \(t_\mathrm {hold}\) for \(N=0.0\), several values of ratio of intrinsic material length to plastic zone size \(l/R_p\), and visco-plastic exponents: a \(m=5.0\), b \(m=5.6\), c \(m=6.0\)

Full size image

By comparing parameter sets with different visco-plastic exponents m it can be seen that \(r_\mathrm {SGVP}/\delta _0\) is larger for cases with large visco-plastic power (Fig. 5c) compared to cases with small visco-plastic power (Fig. 5b). Plastic strain gradients also affect the magnitude of \(r_\mathrm {SGVP}/\delta _0\), and it is found that the influence size of the gradients increases with increasing values of l. The change in \(r_\mathrm {SGVP}/\delta _0\) over time is strongest for small values of m, and in that case the temporal and relative change in \(r_\mathrm {SGVP}/\delta _0\) decreases with l. On the other hand, for large values of m an overall reduced rate of change in \(r_\mathrm {SGVP}/\delta _0\) is present, but now the change the temporal and relative change in \(r_\mathrm {SGVP}/\delta _0\) increases with l.

The rate \(\dot{r}_\mathrm {SGVP}/\delta _0\) was found to increase with increasing \(l/R_p\). The relaxation of the crack tip stresses leads to a decreasing \(\dot{r}_\mathrm {SGVP}/\delta _0\) with hold time until a near steady-state stress distribution is reached at long hold times. The rate \(\dot{r}_\mathrm {SGVP}/\delta _0\) also increases with increasing m for large \(l/R_p\) (the increase of \(r_\mathrm {SGVP}/\delta _0\) with hold time at \(m=6.0\) is about twice as large as at \(m=5.0\)) but can be considered as constant for \(l/R_p=0.03\).

Next, computations with \(N=0\) and \(N>0\) are considered. Figure 6 shows \(r_\mathrm {SGVP}\) at the end of the hold time in dependence of the hardening exponent N varied in the region \(0\le N \le 0.15\) for \(m = 5.0,5.6,6.0\) and four values of \(l/R_p\). The higher the strain hardening degree the lower the influence of the size effect in a visco-plastic strain gradient formulation for all \(l/R_p\). An increasing N results in an increase of the non-dimensional function \(f(\varepsilon ^{vp})\) in Eq. (8) and therefore in an increase of the flow stress \(\sigma _\mathrm {flow}\) in Eq. (7). A higher flow stress implies smaller values of visco-plastic strains, and thus a smaller influence of plastic strain gradients. This behavior was also found by Martínez-Pañeda and Betegón (2015) in a rate-independent strain gradient model.

Fig. 6
figure 6

Distance effected by plastic strain gradients \(r_\mathrm {SGVP}\) for stationary cracks versus hardening exponent N at \(t_\mathrm {hold}={100}\,\hbox {s}\) for several values of visco-plastic exponents m and ratio of intrinsic material length to plastic zone size: a \(l/R_p=0.03\), b \(l/R_p=0.06\), c \(l/R_p=0.11\), and d \(l/R_p=0.16\)

Full size image

In summary, considering the results obtained for the stationary crack case, the following key discussion points emerge. Results on computations employing conventional Norton model agree well with the results obtained using a visco-plastic strain gradient formulation far away from crack tip. In this area, no influence of local hardening effects due to strain gradient plasticity can be found. When approaching the crack tip, significant difference are predicted in the stresses between the computation with the conventional Norton model and the strain-gradient visco-plastic model. The results in the model with the stationary crack show that size of the zone influence by visco-plastic strain gradients, \(r_\mathrm {SGVP}\), expands with time. The computations predict that the interaction of m and l in their influence on crack tip fields and the time related changes in these fields is non-trivial, and that the effects of these two parameters interact strongly.

3.2 Crack growth under monotonic loading

Simulations of crack growth under monotonic loading consider the cohesive zone model to capture crack advance. Two set of computations are conducted: (1) with a fixed \(\dot{K}_I=2.5 \times 10^{-3} K_0/{s}\) increase load until \(K_{I,\mathrm {max}}=2.5K_0\), thereby vary the parameter values of \(l/R_{p,0}\), m, and N to establish their influence on crack growth, and (2) for a subset of m and \(l/R_{p,0}\) values, all with \(N=0\) consider various load rates \(\dot{K}_I\) to establish the rate sensitivity of crack growth. For all cases, the initiation toughness and the tearing modulus are evaluated. Details of the crack tip fields are evaluated.

3.2.1 Crack initiation and crack growth

Figure 7 shows the computed (normalized) crack growth resistance curves, \(K_I/K_0\) vs. \(\varDelta a/\delta _0\), for various combinations of \(l/R_{p,0}\), N, and m, all for \(\dot{K}_I=2.5 \times 10^{-3} K_0/{s}\). For the limiting elastic case, the crack initiates at \(K_0\) and propagates unstable instantly. If visco-plasticity is considered, crack growth initiation occurs at \(K_I/K_0 >1\) and that increase over the elastic case increases depends on the magnitude of the parameters m, N, and \(l/R_{p,0}\). Similarly, the subsequent crack growth resistance increases with increasing \(\varDelta a\) and that increase over the initiation toughness depends again on the magnitude of m, N, and \(l/R_{p,0}\).

Fig. 7
figure 7

Normalized crack advance \(\varDelta a/\delta _0\) versus the loading \(K_I/K_0\) under monotonic loading for several visco-plastic exponents: a \(m=5.0\), b \(m=5.6\), and c \(m=6.0\)

Full size image

The overall resistance to crack growth was found to increase with the magnitude of the visco-plastic power. At low value of m it is found that \(l/R_{p,0}\) has little effect on toughness and crack growth resistance and only N influences crack growth. For larger values of m both \(l/R_{p,0}\) and N are relevant.

Figure  8a summarizes the predicted initiation toughness values and the normalized tearing moduli as a function of the intrinsic lengthscale ratio \(l/R_{p,0}\), for three values of the visco-plastic power m and two values of N.

Fig. 8
figure 8

a Normalized initiation toughness \(K_{I,\mathrm {init}}/K_{0}\) (arrows indicating data point representing the smallest \(l/R_{p,0}\) value for crack initiation) and b normalized tearing modulus \((K_I/\varDelta a)/(K_0/\delta _0)\) (arrows indicating data point represents the smallest \(l/R_{p,0}\) value for crack growth past crack initiation) as a function of the intrinsic material length to reference plastic zone size \(l/R_{p,0}\) for constant loading rate

Full size image

It is found that initiation toughness values \(K_{I,\mathrm {init}}/K_0\) predicted by computations accounting for plastic strain gradients and \(l >0\) are in all considered cases smaller than those predicted by the corresponding model with \(l=0\), Fig. 8a. A similar influence of the effects of plastic strain gradients on crack growth was described in  Nielsen et al. (2012). For crack initiation, this effect is particularly pronounced for the case with \(m=6.0\) where for \(l=0\) no crack initiation takes place, but crack growth initiates for \(l>0\). The dependence of the initiation toughness on \(l/R_{p,0}\) is strongest at small values of \(l/R_{p,0}\) and saturates for large \(l/R_{p,0}\). The dependence of \(K_{I,\mathrm {init}}\) on \(l/R_{p,0}\) is more pronounced for cases with large value of m and low N. The decrease of \(K_{I,\mathrm {init}}\) with increasing \(l/R_{p,0}\) is due to higher stresses near the crack tip as a result of strain gradient hardening, see also Fig. 3. This allows to overcome the cohesive strength of the first CZ element more readily. The highest levels of stress near the crack tip are expected for cases with a small visco-plastic power (here \(m=5.0\)), and indeed the lowest values of \(K_{I,\mathrm {init}}\) can be found there. Since, failure of the cohesive elements is faster than the possible evolution of visco-plastic strain, the magnitude of plastic strain is small and only a minor influence of \(l/R_{p,0}\) on the initiation toughness can be found. On the other hand, in case of a large visco-plastic powers (here \(m=\)5.6 and 6.0) a distinct influence of \(l/R_{p,0}\) on initiation toughness is present. For small values of \(l/R_{p,0}\), additional strain hardening (\(N>0\)) further reduces the initiation toughness. However, for large \(l/R_{p,0}\) the initiation toughness is not effected by N, or even slightly higher for \(N>1\) compared to \(N=0.0\).

Figure 8b shows the computed normalized tearing modulus \((K_I/\varDelta a)/(K_0/\delta _0)\). The tearing modulus represents the slope of the curves presented in Fig. 7 at crack initiation. For a small visco-plastic power (\(m=5.0\)) the tearing modulus is small, independent of all other parameters. For larger visco-plastic powers (\(m=5.6\) and 6.0) higher tearing moduli are observed for the dependence of \((K_I/\varDelta a)/(K_0/\delta _0)\) on \(l/R_{p,0}\) is most pronounced at small values of \(l/R_{p,0}\) and saturates as \(l/R_{p,0}\) increases. In particular, for small \(l/R_{p,0}\) and high values of m, computations predict crack initiation but no subsequent crack growth. For large values of \(l/R_{p,0}\) the dependence of \((K_I/\varDelta a)/(K_0/\delta _0)\) on \(l/R_{p,0}\) saturates. In all cases, additional strain hardening (\(N=0.1\)) further lowers the tearing modulus, similar to results in Tvergaard and Hutchinson (1996). This effect is more prominent for low \(l/R_{p,0}\). The reduced influence of N with an increase in \(l/R_{p,0}\) can be explained by the growing influence of the plastic strain gradients acting in front of the current crack tip: higher stresses in this area make it easier to overcome the traction of the CZ elements.

Figure 9 shows the predicted initiation toughness and tearing modulus values in dependence of the loading rate \(\dot{K}_I/K_0\). The dependence of both initiation toughness and tearing modulus on loading rate is stronger for small values of \(l/R_{p,0}\) than for larger values of \(l/R_{p,0}\). At low loading rates a distinct influence of \(l/R_{p,0}\) on initiation toughness and tearing modulus is present, but as the loading rate is increased the amount of visco-plastic deformation is reduced and the dependence on \(l/R_{p,0}\) subsides at high loading rates.

Fig. 9
figure 9

Normalized initiation toughness \(K_{I,\mathrm {init}}/K_{0}\) (a) and tearing modulus \(K_I/\varDelta a\) (b) (arrows indicating data point represents the smallest \(\dot{K}_I/K_0\) value for crack growth past crack initiation) as a function of the loading rate \(\dot{K}_I/K_0\) for \(N=0.0\)

Full size image

3.2.2 Strains and strain gradients at the growth crack tip

To further understand the influence of intrinsic lengthscales on crack growth, visco-plastic strain \(\varepsilon ^{vp}\) and plastic strain gradients \(\eta ^{vp}\) are analyzed. The values of \(\dot{\varepsilon }^{vp}\) and \(\dot{\eta }^{vp}\) were evaluated along the row of elements right above the crack path. Figure 10 shows the position of the maximum values of \(\dot{\varepsilon }^{vp}\), \(\dot{\eta }^{vp}\), respectively, together with the crack tip position in dependence of the applied load for \(m=5.6\) and 6.0, both for \(N=0\) and 0.1. For cases in which there is substantive crack extension, e.g. Fig. 10b, the position of the maximum in \(\dot{\eta }^{vp}\) is in front of the current crack tip, and the position of \(\dot{\varepsilon }^{vp}\) is behind the current crack tip. However, if the magnitude of crack extension is small and crack tip blunting is substantial, e.g. Fig. 10d, then the location of maximum of \(\dot{\varepsilon }^{vp}\) and \(\dot{\varepsilon }^{vp}\) move closer together, and both are positioned ahead of the current crack tip. This shift occurs gradually, depending on the relative influence of the material parameters considered, Fig. 10a.

Fig. 10
figure 10

Position of the maxima of \(\dot{\varepsilon }^{vp}\) and \(\dot{\eta }^{vp}\) together with the position of the crack tip versus \(K_I/K_0\) for several visco-plastic exponents m and strain hardening exponents N: a \(m=5.6\), \(N=0.0\); b \(m=5.6\), \(N=0.1\); c \(m=6.0\), \(N=0.0\); d \(m=6.0\), \(N=0.1\)

Full size image

In Fig. 8 it was shown that initiation toughness and tearing modulus depend little on N for large values of \(l/R_{p,0}\). In such instances the crack growth resistance is overall low and a substantive amount of crack growth occurs. In such cases, the maximum plastic strain rate occurs behind the current crack tip. Consequently, a change in the crack tip fields due to a change in N has only a minor influence on the deformation processes associated with overcoming the cohesive strength. If, on the other hand \(l/R_{p,0}\) is small, and the location of the maximum of the plastic strain rate moves closer to that of the maximum of the plastic strain gradient rate, both the intrinsic lengthscale and strain hardening affect the crack growth resistance.

4 Conclusion

A visco-plasticity strain gradient formulation was applied in a modified boundary layer (MBL) model. The MBL model was loaded using a mode I asymptotic crack tip solution, in which the stress intensity factor \(K_I\), relative to the reference stress intensity factor \(K_0\) set by the cohesive zone properties was used to calculate the boundary displacement. Two loading scenarios were considered: (1) a stationary crack with no crack advance and a hold time and (2) a crack advance using a cohesive zone formulation under monotonic loading and no hold time. The parameters of the constitutive visco-plastic model and the intrinsic material length were varied. The primary findings of this study are:

  • Plastic strain gradient hardening and rate effects are found to interact strongly in their influence on crack tip fields;

  • The influence of plastic strain gradient hardening increases with hold time;

  • Under monotonic loading, plastic strain gradients reduce crack initiation toughness and crack growth resistance and that effect is more pronounced for large visco-plastic powers;

  • The dependence of initiation toughness and tearing modulus on the ratio between intrinsic lengthscale and plastic zone size is most pronounced at small value of this ratio but saturates as the ratio increases.

  • The influence of the intrinsic lengthscale on initial toughness and tearing modulus is found to decreases with an increase in loading rate, and this rate dependence is more pronounced for smaller values of the intrinsic lengthscale.

  • In reference to the crack growth direction, the spatial location of the maximum in the rate of the plastic strain gradient is always ahead of the location of the maximum plastic strain, but the position relative to the crack tip is found to depend on the magnitude of blunting accompanying the crack advance.

The strong dependence of initiation toughness and tearing modulus on the ratio between intrinsic lengthscale and plastic zone size is one key finding of this study. It demonstrates, that the influence of the intrinsic material length at the crack tip should be considered even for small measured values of the intrinsic lengthscale. Further studies with an expansion to a rate-dependent cohesive zone model will shed light on the competing material separation and rate processes as influenced by plasticity related length scales.