1 Introduction

One of the hallmarks of dynamic fracture processes is the apparent rise in the stress intensity factor at initiation with loading rates. Smith (1975) first examined the dependence of the critical stress intensity factor on the rate of applied loading. This work was extended by Ravi-Chandar and Knauss (1984) who showed that at higher loading rates, the stress intensity factor (SIF) at initiation increases significantly. However, the effect of the rate of loading on the initiation SIF is negligible when the time to fracture is within a characteristic time scale. This result was further verified by the experiments of Liu et al. (1998). This characteristic time scale is a material-dependent property and depends on the intrinsic rate of microscopic nucleation and growth processes. At low loading rates, rate-independent results are obtained. When the loading rate is larger, the microscopic processes are incompletely developed and hence higher loads are sustained. Ravi Chandar and Knauss postulate that the fracture properties of materials such as the initiation SIF depend on the strain rate at the fracture-tip as well as the external load.

A substantial theoretical and experimental effort has been made toward developing initiation and propagation theory using SIF’s for a variety of geometries and loading conditions (Anderson 2005). This theory is routinely used to describe fracture propagation criteria in numerical tools that are used to model fracture. These criteria, which are empirical relations between the fracture geometry and the SIF’s, are usually used to decide if a fracture propagates, and if so, determine the direction of fracture propagation. These criteria include stress based criterion (Dumstroff and Meschke 2007), energy based criterion (Shen and Stephansson 2007) and fracture toughness based criterion (Duarte et al. 2001). While they all give reasonable predictions for the direction of fracture propagation they seldom give accurate predictions for the rate of fracture extension. Furthermore, these criteria are limited to quasi-static propagation and are generally lacking for more complex fracture phenomenon like dynamic fracture propagation and branching. This is because there is no unified theory that describes the micromechanical modeling of dynamic fracture propagation. This limits the applicability of conventional numerical tools to advance understanding of dynamic fracture processes.

It is the goal of this study to develop techniques to estimate dynamic stress intensity factors for a variety of loading conditions using a novel numerical technique called peridynamics (Silling 2000). This is intended to promote understanding of fracture initiation and propagation and formulate failure theories in a standard manner for the purposes of comparison to analogous results from linear elastic fracture mechanics (LEFM). Peridynamics is a non-local formulation of the classical continuum mechanics wherein the conservation of momentum equation is reformulated so as to replace the traditional spatial derivatives with suitable integral counterparts. Non-locality in peridynamics allows for evolution of discontinuities such as fractures spontaneously, which is a distinct advantage over continuum based finite element models (Belytschko et al. 2003).

Peridynamics, originally designed  for modeling  dynamic fracture, was first introduced by Silling (2000). Since its inception, several researchers have published results pertaining to its verification (Silling and Lehoucq 2008; Ha and Bobaru 2011). However, these results have largely consisted of qualitative comparisons. Quantitative comparisons to experimental results have been limited to the general profile of the fracture propagation speed (Ha and Bobaru 2010). Direct comparisons to LEFM via stress intensity factor analysis, which is the foundation of traditional fracture mechanics, has received little attention. Recently Hu et al. (2012) derived the peridynamic formulation of the J-integral which is used to uniquely derive the SIF’s. In their analysis, they used peridynamics to estimate the J-integral for single edge notch and double edge notch configurations. They showed that in both cases the peridynamic results for the J-integral approached the numerical solutions obtained using finite element methods. However, their analysis was limited to quasi-static fractures.

Computing dynamic stress intensity factors from peridynamic data for comparison with LEFM serves two purposes. First, it provides a direct means of validation of the numerical method, as most experimental and numerical results in the literature are expressed in terms of SIFs. These include dynamic SIFs at initiation and of propagating fractures. Second, as previously noted, most conventional numerical techniques use a stress intensity factor based fracture criterion to propagate fractures. While analytical and empirical relations exist for cases of fracture propagation in 2D, criteria for more complex fracture phenomena, such as fracture branching and coalescence, and 3D fracture propagation are scarce. The ability to calculate SIF’s provides a path for peridynamics to be used in conventional numerical methods as a means to calculate fracture criteria on the fly. Furthermore, peridynamic analysis of SIF’s can be extended to study more complex fracture physics, such as, initiation, branching, arrest and interaction of stress waves with propagating fractures, that are difficult using conventional numerical methods. While SIF’s are not strictly needed in peridynamics to propagate a fracture, they provide a useful way to analyze dynamic fracture behavior.

In this paper we present a new technique to compute peridynamic stress intensity factors for quasi-static as well as dynamic fracture initiation and propagation. The new method is computationally inexpensive and straightforward to implement while giving accurate predictions. We then apply this technique to a variety of relevant fracture problems with different geometry and loading conditions. Although the examples shown in this study focus on initiation and propagation of a single fracture, the technique can be easily extensible for more complicated fracture problems such as fracture branching. We begin this paper with a brief overview of the peridynamic theory and methodology employed to model dynamic fracture followed by a brief discussion of stress intensity factors. Next, we introduce several examples and present peridynamic results used for verification of the numerical method. Finally, for a particular geometry of an internally loaded fracture, we investigate a wide range of loading conditions, looking at the influence of loading rate on dynamic fracture. Predictions for the SIF at initiation and propagation as well as the fracture velocity are compared with known theoretical and experimental solutions found in the literature.

2 Modeling

Peridynamic theory can be derived from the classical momentum equation for solid mechanics given by

$$\begin{aligned} \rho _0(\mathbf {x}) \ddot{\mathbf {u}}(\mathbf {x},t) = \nabla \cdot \varvec{\sigma } + \mathbf {b}(\mathbf {x},t), \end{aligned}$$
(1)

where \(\mathbf {x}\) is a point in the body, \(\mathbf {u}(\mathbf {x},t)\) is the displacement of point \(\mathbf {x}\) at time t, \(\rho _0\) is the mass density in the undeformed body, and \(\mathbf {b}\) is an external body force density. Here, \(\nabla \) is the material derivative and \(\varvec{\sigma }\) is the Cauchy stress. As spatial derivatives do not exist on fracture surfaces and at other singularities, Eq. (1) cannot be applied at these points. In peridynamics, Eq. (1) is reformulated so as to replace the traditional spatial derivatives with suitable integral counterparts, as the integral equations of the peridynamic theory can be applied to fracture solutions without any mathematical difficulty. For a full introduction to the peridynamic theory, see (Silling 2000; Silling et al. 2007). Briefly, the peridynamic equation of motion is

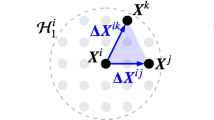
$$\begin{aligned} \rho _0(\mathbf {x}) \ddot{\mathbf {u}}(\mathbf {x},t) = \int _{\mathscr {H}_\mathbf {x}} \mathbf {f}( \mathbf {x}^\prime ,\mathbf {x},t) dV_{\mathbf {x}^\prime } + \mathbf {b}(\mathbf {x},t) \end{aligned}$$
(2)

where the vector valued function \(\mathbf {f}\) is the force density per volume squared that \(\mathbf {x'}\) exerts on \(\mathbf {x}\). Here, \(\mathscr {H}_\mathbf {x}\) is a spherical region of radius \(\delta \) centered at \(\mathbf {x}\) and is the family of \(\mathbf {x}\). In the literature \(\delta \) is often referred to as the peridynamic horizon.

The notion of damage at a point is incorporated in the force function by allowing bonds to break when their elongation  exceeds some prescribed value \(s_0\) referred to as the critical stretch. After a  bond breaks, the material points are effectively disconnected from each other and the load the bond was carrying is redistributed to other bonds that have not yet broken. This increased load makes it more likely that these other bonds will break, leading to progressive failure. Fractures propagate in the peridynamic model through this process of bond breakage and load redistribution, leading to further breakage. Damage at any point is represented as the ratio of number of broken bonds in the current configuration to the undeformed configuration.

In this study we use a linear peridynamic solid material model (LPS). The elastic properties of the LPS model are determined by the bulk modulus k, the shear modulus \(\mu \) and the horizon \(\delta \). The critical stretch is related to the critical energy release rate \(G_c\) as

$$\begin{aligned} s_0 = \sqrt{\frac{5 G_c}{9 k \delta }}, \end{aligned}$$
(3)

where \(G_c\) is related to the fracture toughness \(K_f\) as \( G_c = K_f^2 * (1 - \nu ^2) / E\). Here, E is the Young’s modulus and \(\nu \) is the Poisson’s ratio. A consequence of the LPS model is that the fracture toughness is independent of fracture velocity. This results in the measured dynamic stress intensity factor of a running crack to be very weakly influenced by its velocity. This presents no particular issues for the purposes of this study, but it is worth noting that more complex material models can be developed to investigate the effects of dynamic loading on the initiation and propagation characteristics of a fracture. Additional details on the LPS model can be found in Silling et al. (2007).

2.1 Path independent integrals

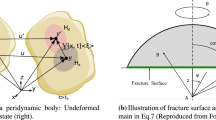
In linear elastic fracture mechanics, stress intensity factors (K) are used to describe the concentration of stress close to the fracture tip. They are evaluated using path-independent energy integrals, and are primarily used to describe fracture/failure criterion used in most numerical techniques. For the case of a running fracture, as shown in Fig. 1a, the stress field in the vicinity of the fracture tip is given by the theory of elastodynamics as (Freund 1990)

$$\begin{aligned} {\varvec{\sigma }}_{ij}(r,\theta ) = \frac{K(t,v_c)}{\sqrt{2\pi r}}{\varvec{\varTheta }}_{ij}(\theta ,r), \end{aligned}$$
(4)

where \({\varvec{\varTheta }}_{ij}\) is a function of the radial distance from the fracture tip r and the direction \(\theta \). The stress intensity factor may depend on geometry of the fracture, the material properties of the body, and loading. It is usually expressed as a function of fracture length a, fracture speed \(v_c\) and loading \(p_f\). The fracture is assumed to propagate if \(K \ge K_{cr}\). Here, \(K_{cr}\) represents the dynamic fracture toughness, which is a material property.

Fig. 1
figure 1

a Schematic of a internally pressurized dynamic fracture propagation. The 1 and 2 axes are global x and y axes. The 1\(^\prime \) and 2\(^\prime \) axes are aligned with the current fracture direction. b Schematic of the contour path used to calculate path independent J integral

Full size image

Path-independent integrals are used in physics to calculate the intensity of a singularity of a field quantity without knowing the exact shape of the field in the vicinity of the singularity. They are derived from conservation laws. For two dimensional problems Nishioka and Atluri (1983) derived the path-independent integral used to estimate stress intensity factors as:

$$\begin{aligned} J_{k = 1,2} \equiv \lim _{\varepsilon \rightarrow 0} \int _{\varGamma _{\varepsilon }} [(w + \kappa )\mathbf{n}_k - {\varvec{\sigma }}_{ij}{} \mathbf{n}_j\mathbf{u}_{i,k}]~d\varGamma \end{aligned}$$
(5)

where \(\varepsilon \) is the radius of a small spherical volume (\(\varOmega _{\varepsilon }\)) close to the fracture tip and \(\varGamma _{\varepsilon }\) is the surface of that volume. Here, \(dw = {\varvec{\sigma }}_{ij}d{\varvec{e}}_{ij}\) and \(\kappa = (1/2)\rho \dot{\mathbf{u}}\dot{\mathbf{u}}\) are the strain and kinetic energy density, respectively. \({\varvec{e}}\) is the strain tensor and \(\mathbf{u}_{i,k}\) is the displacement gradient field. \(\mathbf{n}\) denotes the outward unit normal to the contour path. The above expression is also referred to in the literature as the dynamic J integral. A peridynamic J-integral was established in Silling and Lehoucq (2010) where it was shown that it is consistent with the classical J-integral in the limit as the peridynamic horizon approaches zero.

Equation (5) can be further expanded using the divergence theorem as

$$\begin{aligned} J_{k = 1,2}\equiv & {} \lim _{\varepsilon \rightarrow 0} \int _{\varGamma _{-\varepsilon }} [(w + \kappa )\mathbf{n}_k - {\varvec{\sigma }}_{ij}{} \mathbf{n}_j\mathbf{u}_{i,k}]~d\varGamma \nonumber \\&+ \int _{\varOmega _{-\varepsilon }} [\rho \ddot{\mathbf{u}}{} \mathbf{u}_{,k} + \rho \dot{\mathbf{u}}\dot{\mathbf{u}}_{,k}]~d\varOmega \end{aligned}$$
(6)

where \(\varGamma _{-\varepsilon } = \varGamma + \varGamma _c^+ + \varGamma _c^{-} - \varGamma _{\varepsilon }\) and \(\varOmega _{-\varepsilon } = \varOmega - \varOmega _{\varepsilon }\). Here, \(\varOmega \) is the volume enclosed by the contour \(\varGamma + \varGamma _c^+ + \varGamma _c^{-}\) as shown in the figure. \(\dot{\mathbf{u}}\), \(\ddot{\mathbf{u}}\) are the velocity and acceleration fields, respectively. \(\dot{\mathbf{u}}_{,k}\) is the velocity gradient. The first and second term in the above expression correspond to the surface and volume integral. Once the components of the J-integral are calculated the energy release rate for fracture growth is given by

$$\begin{aligned} G_0 = J_1cos(\theta ) + J_2sin(\theta ) \end{aligned}$$
(7)

In their work, Nishioka and Atluri (1983), extensively show the derivation of the relationship between the mixed-mode stress intensity  factors and the  energy release rate. For brevity, these results are not rederived in this paper but only the final result is summarized. Nishioka and Atluri give the formula for calculating the mode I, II, III dynamic stress intensity factors (\( K_{I}\), \( K_{II}\), \( K_{III}\), respectively) from the J integrals as

$$\begin{aligned} J_1^{'} = \frac{1}{2\mu }\left[ K_{I}^2 A_I(v_c) + K_{II}^2 A_{II}(v_c) + K_{III}^2 A_{III}(v_c)\right] \end{aligned}$$
(8)

and

$$\begin{aligned} J_2^{'} = -\frac{A_{IV}(v_c)}{\mu }[ K_{I}* K_{II}] \end{aligned}$$
(9)

where \(J_1^{'}\) and \(J_2^{'}\) are the components of the J integral rotated into the coordinate axes parallel and perpendicular to the fracture. Here, \(A_{I}\), \(A_{II}\), \(A_{III}\) and \(A_{IV}\) are functions of the fracture speed \(v_c\) given in (Nishioka and Atluri 1983).

2.2 Discretization of J-integral

To numerically estimate the energy release rate from peridynamic data, the expression for the J-integral shown in Eq. (6) is discretized. To this end, the fracture tip is identified as the peridynamic particle with damage greater than 0.35 that is furthest from the loading region. The value of 0.35 is chosen because it represents the value of damage of any peridynamic particle that is on the surface of a fracture (Ha and Bobaru 2010). Second, a closed path is chosen to encompass the fracture tip as shown in Fig. 2. In this study the contour integral size is fixed (2r \(= 5\delta \)), unless otherwise mentioned. It is important to note that in cases where the fracture propagates, the dynamic stress intensity factor of the propagating fracture is computed by drawing the contour path around the current location of the fracture tip. As shown in Fig. 2, the contour includes a portion of the crack surface. The “skin effect” of the peridynamic particles close to the crack surface, as described by Hu et al. (2012), is compensated for by scaling the elastic properties of these particles by the ratio of the number of bonds of the particles on the boundary to the number of bonds of particles in the bulk. No modifications are made to the critical stretch.

Fig. 2
figure 2

Schematic of the discretized J-integral contour path used to estimate stress intensity factors

Full size image

In this study, as the domain is discretized using a regular lattice on a Cartesian co-ordinate system, the natural choice of the contour path is a square of side length 2r. To calculate the stress intensity factor, Eq. (6) is decomposed into a contour integral component and an area integral component as

$$\begin{aligned} J_k = J_{k,C} + J_{k,A}, \end{aligned}$$
(10)

where \(J_{k,C}\) is the contour integral component given by

$$\begin{aligned} J_{k,C} = \sum _{p = 1}^{n}\left( F_k^{p}\right) ~\varGamma _d. \end{aligned}$$
(11)

Here, the contour around the fracture is discretized using n nodes into segments \(\varGamma _d\) as shown in Fig. 2, and the integrand at each node, \(F_k^{p}\), is

$$\begin{aligned} F_k^{p} = [(w + \kappa )\mathbf{n}_k - ({\varvec{\sigma }}_{ij}{} \mathbf{n}_j\cdot \mathbf{u}_{i,k})]^{p}. \end{aligned}$$
(12)

\(J_{k,A}\) is the area integral component given by

$$\begin{aligned} J_{k,A} = \sum _{q = 1}^{m} \left( H_k^{q}\right) ~{\varOmega _d}. \end{aligned}$$
(13)

Here, the area inside the contour is discretized into m discrete regions \(\varOmega _d\) as shown in Fig. 2, and the integrand in each discrete region, \(H_k^{q}\), is

$$\begin{aligned} H_k^{q} = [\rho \ddot{\mathbf{u}}{} \mathbf{u}_{,k} + \rho \dot{\mathbf{u}}\dot{\mathbf{u}}_{,k}]^{q}. \end{aligned}$$
(14)

In their study, Hu et al. (2012) presented a rigorous derivation of the non-local J-integral for bond based peridynamics from first principles. In contrast to our approach they estimate the strain energy term (\(w \mathbf{n}_k\)) by summing over all particles on the contour path, while the traction term (\({\varvec{\sigma }}_{ij}{} \mathbf{n}_j\cdot \mathbf{u}_{i,k}\)) is estimated by replacing the stress tensor with the peridynamic bond force and summing over the bonds of all particles, on either side of the contour, that are within a horizon from the contour. In our analysis, we estimate an approximate non-local peridynamic stress tensor from peridynamic bond forces and use it directly in Eq. (6). This method is easier to implement and computationally less expensive that the technique described by Hu et al. (2012).

3 Verification

The following examples intend to demonstrate the applicability of peridynamics to predict key quasi-static and dynamic fracture initiation  and propagation processes. The predictions for the quasi-static and dynamic stress intensity factors, fracture path and fracture speed are expected to qualitatively and quantitatively match other analytical, experimental and numerical results found in the literature. For the purposes of this study two model problems were considered:

  1. 1.

    Quasi-static tensile loading of a notched body

  2. 2.

    Dynamic impact loading of a double-edge notched body

The initial system setup for the problems is shown in Figs. 3 and 4.

Fig. 3
figure 3

Pre-notched body subject to quasi-static tensile loading

Full size image
Fig. 4
figure 4

Double notched body subject to impact loading imposed using velocity boundary condition

Full size image

The schematic of the quasi-static test case shows a pre-notched body subjected to tensile loading. The width and height of the body are 200 mm. It has a notch 40 mm in length. The tensile stress is denoted by \(\sigma \). The stress is linearly increased in increments of \(\Delta \sigma = .05~\hbox {MPa}\). At each loading step, the incremental stress is applied on the boundaries and the net potential energy of the system is minimized using the FIRE algorithm (Bitzek et al. 2006). This process is repeated until fracture initiation.

The second test case is a  double edge notched body dynamically loaded in impact compression between the two notches. The problem setup mimics the well known Kalthoff–Winkler experiment (Kalthoff and Winkler 1987). The width and height of the body are 100 mm and 200 mm respectively. The parallel notches are 50 mm long and are separated by 50 mm. A velocity boundary condition of 16.5 m/s is applied instantaneously on a portion of the boundary of the body at time \(t = 0\) and is sustained for the remainder of the simulation. Due to the symmetric nature of the problem, analysis for this case is shown only for the top half of the body. For both cases, the body is assumed to be isotropic, elastic, and homogeneous. Also, for both cases periodic boundary conditions are imposed in the out-of-plane direction to mimic plane strain conditions. The relevant material parameters used for the two cases are given in Table 1.

Table 1 Elastic and fracture properties of the materials used in this study
Full size table

Calculations were performed using the Peridynamic extensions (Parks et al. 2008) implemented in LAMMPS (Plimpton 1995), and modifications therein. The domain was discretized on a simple cubic lattice The horizon is set to three times the lattice spacing such that each particle in the bulk has 122 bonds. The discretized equations of motion are integrated using a velocity Verlet algorithm. In this work the pre-notch in the peridynamic material was created by identifying and deleting the set of peridynamic particles that lie on the plane of the notch. The stiffness, critical stretch and horizon of all bonds passing through the plane of the notch were initialized to zero. Due to the nature of the discretization, the tip of the notch is not sharp but is represented by three peridynamic particles. Corners are introduced on either side of the central peridynamic particle. These corners also provide a seeding mechanism for fracture initiation. Depending on the loading conditions and in the absence of any special treatment fractures will initiate and propagate from the notch tip as well as the corners. In cases where noted, care was taken to ensure that fractures initiate and propagate in the expected direction.

3.1 Quasi-static fracture propagation due to tensile loading of a notched plate

Predictions for the variation of the mode I quasi-static stress intensity factor (\(K_{Iq}\)) with respect to the tensile load stress are presented in Fig. 5. To verify the path independence of the J-integral estimation, profiles of \(K_{Iq}\) versus load are calculated for several closed contours around the fracture tip. Predictions are shown in Fig. 5a for contour widths of 2r = 20, 40 and 60 mm. Load is plotted on the horizontal axis and the stress intensity factor is plotted on the vertical axis. The predictions indicate that the stress intensity factor increases linearly with loading up to a maximum value of \(1.2892~\hbox {MPa}\sqrt{\hbox {m}}\). This compares very well with the input fracture toughness value of \(1.26~\hbox {MPa}\sqrt{\hbox {m}}\). Also, for different contour paths, the profiles of \(K_{Iq}\) remain nearly unchanged.

Fig. 5
figure 5

a Sensitivity of quasi-static stress intensity factor to contour path. b Comparison of the numerically obtained quasi-static stress intensity factor to analytical solutions Eqs. 15 and 16

Full size image

Shown in Fig. 5b is the comparison between the numerically obtained solution for the stress intensity factor and analytical solutions obtained from the literature (Anderson 2005). For an edge fracture in an infinite plate the analytical solution is given as

$$\begin{aligned} K_{Iq} = 1.12 \sigma _0 \sqrt{\pi a}, \end{aligned}$$
(15)

where, \(\sigma _0\) is the tensile load on the boundary. For a finite plate more accurate solutions are given by

$$\begin{aligned} K_{Iq} = \sigma _0 \sqrt{\pi a} \left[ \frac{2W}{\pi a}tan\left( \frac{\pi a}{2W}\right) \right] , \end{aligned}$$
(16)

where, W is the width of the body. The numerical results compare very well to the analytical solutions.

3.2 Dynamic fracture propagation due to impact loading of a notched plate

Predictions pertaining to the peridynamic modeling of the Kalthoff–Winkler experiment Kalthoff and Winkler (1987) are presented next. The numerical predictions for the fracture propagation, fracture speed, and the transient stress intensity factor are compared to numerical predictions obtained using other numerical methods found in the literature. Specifically, predictions for the fracture geometry are compared with the results of Belytschko et al. (2003), Huespe et al. (2006) and Kosteski et al. (2012). Predictions for the mode I and II SIF’s are compared with the results of Batra and Ching (2002), Guo and Nairn (2004) and Kosteski et al. (2012). The studies use very different numerical techniques to solve the problem. Belytschko et al. (2003) use the finite element method (FEM) whereas Batra and Ching (2002), Guo and Nairn (2004) and Kosteski et al. (2012) use meshless discrete element methods (DEM). It is important to note that there are several similarities as well as differences in the solution procedure of the aforementioned studies. The material properties used to model the material behavior is consistent for all the studies. However, they use different criteria to propagate fractures. For example, Belytschko et al. (2003) use the cohesive zone model with the tensile stress criterion to propagate fractures. Kosteski et al. (2012) use a bi-linear constitutive law to model material behavior between DEM particles. The load carrying capacity within each element is characterized by the critical strain, where damage first occurs, and limit strain that determines material failure. Both these parameters are determined from the elastic properties and fracture toughness. The studies also impose different boundary conditions to simulate the impact loading. While Belytschko et al. (2003) and Kosteski et al. (2012) use velocity boundary conditions to simulate impact (16.5 m/s), Batra and Ching (2002) and Guo and Nairn (2004) use traction boundary conditions (200 MPa). In spite of all the differences our predictions compare very well with all their results. Other notable numerical studies of the Kalthoff–Winkler experiment include those of Amani et al. (2016) using a non-ordinary state-based strain-hardening peridynamics model, Braun and Fernandez-Saez (2014) using discrete element model, Raymond et al. (2014) using smooth particle hydrodynamics and Song et al. (2008) using finite element method.

The loading applied in this setup is primarily mode II. Upon application of the velocity boundary condition a compressive wave is generated which propagates parallel to the notches. The pressure wave reaches the notch tip at approximately 7.5 \(\upmu \)s. Soon after the arrival of the wave, the stresses at the notch tip increase with the stress component parallel to the notch being significantly larger than the perpendicular component. The stress concentration then intensifies with maximum principal tensile stress oriented at \(\theta = 68^{\circ }\). Peridynamic bonds break when the strain exceeds the critical stretch \(s_0\). As bonds break their stress is redistributed to their neighbors which results in further bond breaking. This cascading effect finally results in fracture initiation at 23 \(\upmu \)s. After initiation, the fracture propagates at a constant speed of \(1725~\hbox {m/s}\) which is approximately 60 % of the Rayleigh wave speed (2800 m/s). The fracture speed is computed by post-processing peridynamic data. To this end, first we plot the fracture tip displacement versus time. The fracture speed is then given by the slope of that profile. For the same problem Belytschko et al. (2003) and Kosteski et al. (2012) predict that the average fracture speed is 1800 m/s and 1600 m/s respectively. Our result for the fracture speed agrees very well with both results.

Fig. 6
figure 6

Time evolution of fracture process and circumferential stress in the body. Circumferential stress is calculated in the coordinate system with the fracture tip as the origin. Due to symmetry only the upper half (100 mm by 100 mm) of the body is shown in the figures. The color bar is in MPa

Full size image

Figure 6 shows the contours of circumferential stress at different snapshots in time. The circumferential stress is calculated using a moving Cartesian coordinate system with the fracture tip as the origin. Also plotted in black is the time evolution of the fracture path. The figures show that the interaction of the mode II loading produces a region of tension and compression on either side of the fracture tip. As loading continues the maximum circumferential stress increases up to the fracture toughness of the material, at which point fracture initiates. As the fracture propagates the fracture tip is easily identified by the concentration in the hoop stress. The pressure wave generated due to the loading reaches the opposite boundary at approximately 20 \(\upmu \)s. The reflection from the boundary induces tensile stress in the direction perpendicular to the original notch due to Poisson effect. As shown in the figures this tensile stress region is originally separated from the stress concentration close to the propagating fracture tip. These regions interact between 30 \(\upmu \)s and 60 \(\upmu \)s. However, this induces only a marginal change in the direction of fracture propagation.

Fig. 7
figure 7

Results from (I) DEM (Kosteski et al. 2012) (II) XFEM (Belytschko et al. 2003) (III) FEM (Huespe et al. 2006) (IV) Peridynamics for the final configuration of the fracture. The authors would like to acknowledge Springer Publishing Company for allowing us to reprint the figure from the paper Kosteski et al. (2012)

Full size image

The position of the fracture at the end of the simulation is shown in Fig. 7 along with comparable predictions from three other numerical techniques used to solve the same problem. The solutions shown are adapted from the works of (I) Kosteski et al. (2012) using DEM (II) Belytschko et al. (2003) using XFEM and (III) Huespe et al. (2006) using FEM with embedded discontinuities. The final result (IV) is obtained using peridynamics. In their studies Kosteski, Belytschko and Huespe also assumed plane strain boundary conditions. Also, Kosteski applied the impact loading using a Heaviside function from \(t = 0\), whereas, Belytschko and Huespe imposed a prescribed velocity on the boundary. Predictions show that the orientation and position of the main fracture are comparable for all the numerical techniques. The fracture propagates and an angle of \(68^{\circ }\)–\(70^{\circ }\) to the original notch and reaches close to the boundary at end time. However, there are also differences between the four predictions. First, predictions for the fracture path from Kosteski et al. (2012) and Huespe et al. (2006) indicate bending of the main fracture as it reaches the boundary which is absent in the peridynamics result. Second, unlike the peridynamics result, the other three numerical techniques predict the presence of an additional fracture that initiates from the boundary and propagates inwards. The experimental evidence presented by Kalthoff and Winkler does not indicate the presence of the secondary fracture. They note that in all their experiments complete failure of the specimen was observed, i.e. damage spreads across the entire specimen dividing it into two. By contrast, the studies of Braun et. al. Braun and Fernandez-Saez (2014) predict the occurrence of a single progressing fracture, and Kosteski et al. (2012) note in their work that the second fracture is replaced by a diffuse damage zone upon mesh refinement.

To investigate the influence of mesh resolution and non-locality on our fracture predictions, we follow the approach of Hu et al. (2012) and examine so-called \(\delta \)-convergence and m-convergence properties of the simulations. For \(\delta \)-convergence, the peridynamic lattice spacing \(\Delta x\) is lowered while keeping the ratio of the horizon to the lattice spacing fixed, with the expectation that the influence of nonlocality diminishes and converges to the local solution as \(\delta \rightarrow 0\). Simulations were performed on systems with \(\Delta x = \) 0.25, 0.5, 1.0, and 2.0 mm with a horizon of \(\delta = 3{\Delta x}\), and the final fracture configurations are depicted in Fig. 8. These results clearly show that the secondary fracture attenuates and finally disappears completely as the horizon is reduced.

Fig. 8
figure 8

\(\delta \)-Convergence results for the final configuration of the fracture. In all the cases shown the horizon \(\delta \) was set to three times the lattice spacing \(\Delta x\)

Full size image

For m-convergence properties, the size of the horizon is kept fixed while the mesh spacing is lowered, such that \(m = \frac{\delta }{\Delta x}\) increases. As m becomes large, any spatial integration errors associated with discretizing the system with a lattice should become negligible, and the solution should converge for the specified non-local approximation associated with the finite horizon. Simulations were performed on multiple grids with \(\Delta x =\) 1.0, 0.75, and 0.5 mm and horizon size fixed to 3 mm. As depicted in Fig. 9, the results of these simulations show the consistent appearance of the secondary fracture for all cases we considered. This tentatively suggests that, for the given level of non-locality in the model, mesh discretization does not have an influence on the resulting fracture patterns. It would be desirable to conduct similar m-convergence tests for the system that exhibits the appearance of a single fracture (\(\Delta x = \) 0.25 mm), but we found the simulations to be computationally intractable given the number of particles and memory requirements required to resolve the system.

Nonetheless, these observations suggest that the appearance of the secondary fracture must result from the complex interaction of the reflected stress waves associated with the initial loading of the sample and the waves associated with the propagating primary fracture. Figure  8 suggests that the dispersive character of the waves, which increases with non-locality, plays a strong role in this interaction, and as the horizon is reduced, the results from peridynamics become consistent with the experimental observations.

Fig. 9
figure 9

m-Convergence results for the final configuration of the fracture. In all the cases shown the horizon \(\delta \) was set to 3 mm

Full size image
Fig. 10
figure 10

Time evolution of the mode I and II SIF’s obtained using peridynamics. Also plotted are comparable data from Kosteski et al. (2012), Guo and Nairn (2004) and Batra and Ching (2002)

Full size image

Finally, Fig. 10 depicts the time evolution of the dynamic stress intensity factor up to fracture initiation. Also shown in the figure are comparable predictions for the same example by Kosteski et al. (2012), Batra and Ching (2002) and Guo and Nairn (2004). In all the cases shown in the figures, including peridynamics, a prescribed stress excitation of 200 MPa was applied as a Heaviside function at time \(t = 0\). Both the mode I and mode II stress intensity factors, \(K_{I}\) and \( K_{II}\) respectively, are unchanged until approximately \(7.5~\upmu \)s when the pressure wave first interacts with the fracture tip. The interaction of the stress wave with the tip results in negative values of \(K_{I}\) which indicates that the fracture is closed. The sign of \(K_{II}\) is arbitrary. As shown in the figure the predictions for \(K_{I}\) and \( K_{II}\) from peridynamics generally agree with the other numerical predictions. Plotted in Fig. 11 are the predictions for the mode II SIF from peridynamics for several closed contours around the fracture tip. Predictions are shown for contour widths of \(2\hbox {r} = 3.75, 7.5\;\hbox {and}\;15\) mm. The predictions demonstrate that for different contour paths, the profiles of \(K_{II}\) remain nearly unchanged.

Results from the \(\delta \) and m convergence studies for the time evolution of the mode II SIF obtained using peridynamics are shown in Figs. 12 and  13 respectively. The \(\delta \)-convergence results shows that the mode II SIF converges as the mesh and the peridynamic horizon is refined. The results of the m-convergence shows that the profiles for the mode II SIF remain unchanged as the size of the horizon is held constant (\(\delta = 3~\hbox {mm}\)) and the mesh is refined. It is important to note that the in all the cases shown the size of the contour integral depends only on the size of the horizon (2r \(= 5\delta \)). Therefore for a fixed horizon all the SIF’s profiles in the m-convergence studies collapse to solution to the non-local problem for a given horizon.

Fig. 11
figure 11

Sensitivity of mode II dynamic SIF to contour path

Full size image
Fig. 12
figure 12

\(\delta \)-Convergence results for the time evolution of the mode II SIF. In all the cases shown the horizon \(\delta \) was set to three times the lattice spacing \(\Delta x\)

Full size image
Fig. 13
figure 13

m-Convergence results for the time evolution of the mode II SIF. In all the cases shown the horizon \(\delta \) was set to 3 mm

Full size image

4 Application

4.1 Investigation of fracture initiation and propagation using peridynamic stress intensity factors

In the previous section, predictions of dynamic and quasi-static stress intensity factors were presented to compare and verify peridynamic results against other numerical techniques for known test cases found in the literature. In the current section we use stress intensity factors to investigate the sensitivity of loading rate on fracture initiation and propagation criteria. These include the critical stress intensity at initiation, dynamic SIF of a running fracture and the correlation of fracture velocity to dynamic SIF. To this end a test case as shown in Fig. 14a is chosen. The test specimen has a width and height of 30 m. It has a pre-fracture that is 3 m long. A large domain size was chosen to allow the fracture to propagate in a interior stress field unpolluted by reflections from the boundaries. Load is applied on a portion of the interior surfaces of the fracture leaving the near-tip fracture faces of length 0.75 m traction free. The load on the fracture surfaces increases linearly from zero at \(t = 0\) to a maximum load denoted by \(P_0\) over a rise time denoted by \(t_0\) as shown in Fig. 14b. To resist fracture initiation from the corners of the discretized notch tip the critical stretch of the central peridynamic particle immediately ahead of the tip was reduced to half that of the bulk material. In this way we overcome discretization errors and ensure that fracture initiation occurs at the notch tip rather than the corners.

Fig. 14
figure 14

a Pre-notched body subject to dynamic loading on internal fracture surfaces. b Loading conditions for the dynamic test case

Full size image

A similar geometry was employed by Kim (1985) to study experimentally the transient variation of stress intensity factor of a running fracture resulting from impact loading on the fracture faces. Unlike this study, in his experiments, Kim used a smaller specimen size and a step loading function to load the fracture faces. To study the influence of loading rate on fracture initiation and propagation simulations were performed using different loading rates. The peak pressure was held fixed at 10 MPa and the rise time was modified from 100 ms to 1 ms. The relevant elastic material properties for all the cases presented in this section are shown for Case1 in Table 1. Predictions for the case with a peak pressure of 10 MPa and rise time of 10 ms are discussed first. These predictions highlight characteristics of initiation and propagation of dynamic fractures as described by stress intensity factors. Note that for all the cases the pressure pulse was applied on only a portion of the initial fracture surface. Any newly created fracture surfaces are assumed to be traction free for the computation of the stress intensity factors. Periodic boundary conditions are imposed in the out-of-plane direction to mimic plane strain conditions.

Fig. 15
figure 15

Contour plots of pressure at \(t = 2, 4, 8\) ms for case \(P_0 = 10\) MPa and \(t_0 = 10\) ms. Color bar is in MPa

Full size image

Figure 15 shows contours of the pressure for the test case at time \(\hbox {t} = 2, 4\) and 8 ms. The color bars are given in MPa. The stress contours display a region of compression near the pre-fracture resulting from pressure pulse and a localized region in tension near the fracture tip. As load on the pre-fracture increases linearly, at 2.3 ms the tensile stress at the tip of the pre-fracture exceeds the fracture toughness of the material. As a result, a fracture initiates and propagates perpendicular to the applied load. As the loading increases, the fracture grows, while the stress state near the fracture tip remains nearly unchanged.

Shown in Fig. 16 is the variation of the mode I dynamic stress intensity factor (\(K_{Id}\)) with time. Also shown is the fracture tip position. The quasi-static critical stress intensity factor is plotted using the dashed line for reference. Upon application of the load the dynamic stress intensity first decreases and then increases sharply but smoothly to a value close to the input fracture toughness. At time t \(= 2.0\) ms, the first peridynamic bond breaks. Subsequent bond breakage finally results in fracture initiation at t \(= 2.3\) ms. Shown in the figure is the displacement of the fracture tip with time. The slope of this line is the fracture velocity given by \(v_c =\) 880 m/s.

Fig. 16
figure 16

Time evolution of dynamic stress intensity factor for case \(P_0 = 10\) MPa and \(t_0 = 10\) ms. Also plotted is the fracture tip position versus time

Full size image

In Fig. 16, the dynamic critical stress intensity factor at initiation is estimated as \(K_{Icr} = 1.53~\hbox {MPa}\sqrt{\hbox {m}}\), which is higher than the quasi-static stress intensity factor. Immediately after initiation, the inertia effect of a running fracture and the effect of fracture extending away from the loading edge results in a drop in the stress intensity factor. Similar effects were observed by Kim (1985) in his experimental studies of transient variation of stress intensity factor of a running fracture resulting from impact loading on the fracture faces. After the initial drop, the profile for \(K_{Id}\) stabilizes at \(1.35~\hbox {MPa}\sqrt{\hbox {m}}\) and remains nearly constant thereafter. This is referred to as the dynamic stress intensity factor of a running fracture. As the fracture propagates, bonds break and high frequency stress waves are generated from these individual events. These waves propagate through the material resulting in oscillatory compression and expansion of neighboring bonds. The effect of these oscillations results is captured by the profile of the stress intensity factor as shown in the figure.

Fig. 17
figure 17

Initial time response of dynamic stress intensity factor for case \(P_0 = 10\) MPa and \(t_0 = 10\) ms

Full size image

Figure 17 magnifies the early time response of the stress intensity factor. As shown in the figure, the initial stress intensity factor of the pressure loading decreases from the time the pressure wave generated at the loading edge arrives at the fracture tip until the Rayleigh wave arrives. After the Rayleigh wave arrives, the stress intensity factor increases monotonically until fracture initiation. This was also observed by Kim (1985) in his studies. Kim explains that the initial negative stress-intensity factor is due to the surface displacement on the traction-free surface bulges out due to the uniform pressure loading. The propagating bulge tends to close the fracture when it arrives at the fracture tip.

In what follows we highlight the influence of loading rate on key fracture initiation and propagation properties such as time to initiation (\(t_i\)), critical stress intensity (\(K_{Icr}\)), dynamic stress intensity of a running fracture (\(K_{Id}\)), and fracture speed (\(v_c\)). Shown in Fig. 18 are the peridynamic predictions for the variation of the stress intensity factor required for initiation with the time to fracture. The predictions show that the critical stress intensity is insensitive to loading rate when the fracture initiation time is on the order of 1 ms. This corresponds to a loading rate of 5 MPa/ms. With higher loading rates the critical stress intensity factor increases markedly. This effect has also been demonstrated by the experiments of Ravi-Chandar and Knauss (1984).

Fig. 18
figure 18

Variation of the stress intensity factor required for initiation with time to fracture

Full size image

In a heterogeneous material it is energetically favorable for the weakest bonds to break first. A certain number of bonds need to break before a fracture is assumed to initiate. The process of bond breakage and stress redistribution is therefore not instantaneous. There is a finite duration of time from the point the first bond breaks to fracture initiation which we denote as \(\Delta t_f\). As loading rate increases energy is supplied at a faster rate to the fracture tip. Stress increases rapidly near the fracture tip and damage occurs earlier at higher loading rates. The time to initiation \(t_i\) is a sum of the time taken for energy to be supplied to the crack tip \(t_0\) which depends on the wave speed and \(\Delta t_f\). In this case \(t_0\) is approximately constant at 0.7 ms. However, \(\Delta t_f\) decreases rapidly with increasing loading rate. The peridynamic results show that \(\Delta t_f = 8, 0.6\) and 0.2 ms for loading rates of \(\dot{L} = 0.1, 1\) and 10 MPa/ms respectively.

Fracture initiation is determined by the combination of the rate of energy supply and the intrinsic rate of stress equilibriation near the tip. In the material energy is transmitted via stress waves and is dissipated by breaking bonds. When bonds break due to the applied loading the stress carried by those bonds is redistributed to neighboring particles at a fixed rate determined by the wave speed of the material. As loading rate increases and \(\Delta t_f\) decreases more energy is supplied to the particles near the fracture tip than that can be transmitted to neighboring particles or dissipated. This promotes stress localization at the tip resulting in higher critical stress intensity factors.

Table 2 Loading rate of the pressure loading on the internal surfaces of the fracture
Full size table

A few other observations are shown in Table 2. Here \(\overline{K}_{Id}\) is the averaged dynamic SIF of a propagating fracture estimated by averaging the data for \(K_{Id}\) over the propagation time. As loading rate increases the fracture propagates faster. The fracture speed increases from 360 m/s for a loading rate of \(\dot{L} = 0.1\) AMPa/ms to approximately 55 % of the Rayleigh wave speed for \(\dot{L} = 2.5\) MPa/ms, at which point branching occurs. In our simulations fracture branching was obtained for all loading rates above 2.5 MPa/ms. Predictions for \(\overline{K}_{Id}\) showed that it is not sensitive to loading rate although the fracture speed was sensitive to loading rate. This indicates that \(\overline{K}_{Id}\) is independent of fracture speed which is in contrast to the well known hypothesis that \(K_{Id}\) is an increasing function of the instantaneous fracture tip speed (Freund 1990). This is a consequence of using a constant fracture toughness and a rate-independent material model in peridynamics. Additional work on peridynamic material model development is ongoing to reproduce the velocity dependence of \(K_{Id}\) observed in experiments.

In the current example the critical stretch of all bonds connected to the peridynamic particle at the center of the tip of the fracture was modified. The ratio of the critical stretch of this particle to the bulk material is \(S_0^*/S_0\) = 0.5. This is done to ensure initiation occurs at a predetermined location ahead of the fracture tip. Modifying the critical stretch at the crack tip introduces an additional material heterogeneity that can have a significant influence on the strength of the stress singularity. Although the ratio \(S_0^*/S_0\) is unknown for a particular fracture, its effect on the fracture propagation can be studied using numerical simulations. To investigate the influence of the heterogeneity on fracture initiation simulations were performed by varying the ratio of the critical stretch. Predictions for the variation in critical SIF with time to fracture for these cases are shown in Fig. 19a.

Fig. 19
figure 19

a Variation of the stress intensity factor required for initiation with time to fracture for varying ratios of critical stretch at the fracture tip to the bulk material. b Variation of the stress intensity factor required for initiation with time to fracture for varying Young’s modulus

Full size image

As shown in the figure, the predictions are qualitatively similar for all cases of the critical stretch ratio. As expected, as the ratio of the critical stretch at the tip to the bulk material is decreased, both \(K_{Icr}\) and \(t_i\) decrease. In all cases, the critical SIF is insensitive to loading rate when the fracture initiation time larger than the characteristic time to fracture of \(\approx \)1 ms. With higher loading rates the critical stress intensity factor increases markedly. This indicates that the characteristic time to fracture is independent of the strength of the singularity at the fracture tip. Rather, it depends on the bulk elastic properties of the material. To further investigate this simulations were performed on a stiffer material with a higher Young’s modulus of \(30.2\times 10^{10}\). Predictions for the variation in the critical SIF with time to fracture for both the Young’s modulus are shown in Fig. 19b. From the figure, two observations are evident. First, the characteristic time to fracture decreases as the material stiffness increases. As the Young’s modulus increases the wave speed increases and the critical stretch \(s_0\) decreases (Eq. (3)). At high loading rates, energy is supplied faster to the crack tip for the stiffer material thereby reducing \(t_0\). Lower \(s_0\) results in speeding up the process of bond breaking resulting in a smaller \(\Delta t_f\). Both these factors contribute to lower the characteristic time. Second, at low loading rates where the time to initiation is greater than the characteristic time, the critical SIF is higher for the softer material. At low loading rates, the combination of faster stress redistribution due to higher wave speed and lower load carrying capacity of the peridynamic bonds due to the lower critical stretch of the stiffer material results in lower stress concentration at the crack tip.

5 Conclusions

A novel non-local numerical technique called peridynamics was used to study the influence of loading conditions on fracture initiation and propagation resulting from the dynamic loading of the surfaces of a pre-notch. A new post-processing technique for estimating stress intensity factors from peridynamic data was introduced. Peridynamic stress intensity factors were estimated for two test cases: (1) quasi-static tensile loading of a material with a pre-notch and (2) the Kalthoff–Winkler experiment Kalthoff and Winkler (1987). Predictions for the fracture evolution and stress intensity factors were verified against known analytical and numerical solutions in the literature.

Peridynamic stress intensity factors were used to study fracture initiation and propagation resulting from dynamic loading of the interior surfaces of a pre-notch. The predictions showed that upon application of load, the dynamic stress intensity first decreases due to interaction of the pressure and shear wave and then increases sharply due to interaction with the Rayleigh wave. The stress intensity factor increases smoothly to a value above to the input fracture toughness at which point initiation occurs. After initiation, the stress intensity factor remained nearly constant in time. Predictions showed that the critical stress intensity is insensitive to loading rate when the fracture initiation time is on the order of 1 ms. As loading rate increased the time to fracture decreased and the critical stress intensity increased markedly.

Our predictions show that path-independent J-integrals can be accurately estimated by post-processing peridynamic data. These predictions can be used to understand key aspects of fracture initiation, propagation and branching, that results from the interplay of loading rate, and wave interaction with propagating fractures. This opens doors for incorporating peridynamic stress intensity factors into conventional numerical techniques that model fracture. These techniques generally employ ad-hoc fracture criteria to motivate fracture initiation and direction of fracture propagation. Our work provides an effective way of replacing these criteria with peridynamic stress intensity factors. This allows for peridynamics to be used in conventional numerical methods in a convenient and robust manner. Furthermore, peridynamic SIF’s can be used to study complex fracture physics, such as, branching and interaction of stress waves with propagating fractures that would otherwise be difficult to do using conventional numerical methods.